Experimentally guided modelling of dendritic excitability in rat neocortical pyramidal neurones

Abstract

Constructing physiologically relevant compartmental models of neurones is critical for understanding neuronal activity and function. We recently suggested that measurements from multiple locations along the soma, dendrites and axon are necessary as a data set when using a genetic optimization algorithm to constrain the parameters of a compartmental model of an entire neurone. However, recordings from L5 pyramidal neurones can routinely be performed simultaneously from only two locations. Now we show that a data set recorded from the soma and apical dendrite combined with a parameter peeling procedure is sufficient to constrain a compartmental model for the apical dendrite of L5 pyramidal neurones. The peeling procedure was tested on several compartmental models showing that it avoids local minima in parameter space. Based on the requirements of this analysis procedure, we designed and performed simultaneous whole-cell recordings from the soma and apical dendrite of rat L5 pyramidal neurones. The data set obtained from these recordings allowed constraining a simplified compartmental model for the apical dendrite of L5 pyramidal neurones containing four voltage-gated conductances. In agreement with experimental findings, the optimized model predicts that the conductance density gradients of voltage-gated K⁺ conductances taper rapidly proximal to the soma, while the density gradient of the voltage-gated Na⁺ conductance tapers slowly along the apical dendrite. The model reproduced the back-propagation of the action potential and the modulation of the resting membrane potential along the apical dendrite. Furthermore, the optimized model provided a mechanistic explanation for the back-propagation of the action potential into the apical dendrite and the generation of dendritic Na⁺ spikes.

Over 50 years ago Hodgkin and Huxley transformed neurophysiology with their mechanistic explanation of the action potential (AP) in the squid giant axon (Hodgkin & Huxley, 1952). Since then, many investigations of cellular excitability have attempted to provide a mechanistic description of neuronal excitability. In recent decades the pace of research in neuroscience has increased dramatically, with mechanistically oriented research on neuronal excitability making great strides. This considerable acceleration is partly due to the rapid increase in computer power and to the availability of advanced numerical simulation packages such as NEURON (Hines & Carnevale, 1997, Hines & Carnevale,2000) and GENESIS (Bower & Beeman, 1994). Modelling of many cellular processes contributing to neuronal excitability can now be performed relatively easily on an ordinary desktop computer.

One field enjoying vigorous activity is research on dendritic synaptic integration (for reviews see Stuart et al. 1999; Migliore & Shepherd, 2002; Johnston et al. 2003; London & Häusser, 2005; Magee & Johnston, 2005; Sjöström et al. 2008; Spruston, 2008). APs initiated at or near the soma actively back-propagate into the dendritic tree (Stuart & Sakmann, 1994; Häusser et al. 1995; Spruston et al. 1995; Bischofberger & Jonas, 1997; Chen et al. 1997,Chen et al. 2002). In addition, dendrites generate complex regenerative Ca²⁺ and Na⁺ spikes (Amitai et al. 1993; Schiller et al. 1997; Magee et al. 1998; Martina et al. 2000; Zhu, 2000; Migliore & Shepherd, 2002; Antic, 2003; Ariav et al. 2003; Johnston et al. 2003). They modulate synaptic potentials (Magee & Johnston, 1995; Magee, 1999), contain electrically and chemically defined compartments (Hoffman et al. 1997; Schiller et al. 1997; Larkum et al. 1999b; Magee, 1999; Bekkers, 2000; Korngreen & Sakmann, 2000; Schiller et al. 2000; Larkum et al. 2001; Gasparini & Magee, 2006; Losonczy & Magee, 2006), and influence the induction and expression of synaptic plasticity (Magee & Johnston, 1997; Markram et al. 1997; Golding et al. 2002). The exciting finding of regenerative Ca²⁺ spikes in the apical dendrite of neocortical L5 pyramidal neurones (Amitai et al. 1993; Schiller et al. 1997; Larkum et al. 1999a,Larkum et al. 1999b,; Zhu, 2000; Larkum et al. 2001) revived the discussion on the computational properties of single neurones (Koch, 1999; Poirazi et al. 2003; Polsky et al. 2004; London & Häusser, 2005).

In several types of neurones the density of voltage-gated ion channels varies as a function of the distance of the dendritic section from the soma (Migliore & Shepherd, 2002), contrary to the Hodgkin–Huxley model with its homogeneous conductance densities. The varying densities add considerable complexity to modelling dendritic physiology and make hand-tuning of compartmental models a daunting task. Thus, the goal of describing neuronal excitability from the bottom up by measuring ion channel properties followed by modelling appeared to be much harder to achieve than previously expected. However, given sufficient recordings of the membrane potential from the soma, dendrites and axon, it may be possible to automatically constrain a compartmental model of the neurone, even if it contains dendritic gradients of ion channels (Keren et al. 2005; Huys et al. 2006). Using numerical simulations with genetic search algorithms, we predicted that recording from the soma, axon and three locations along the apical dendrite would generate sufficient data to build a training set for a genetic search algorithm and allow constraining of a compartmental model (Keren et al. 2005). Recent numerical simulations have shown that multiple recordings of the membrane potential may be used to accurately constrain compartmental models using a simple gradient decent algorithm, given that enough recording site are available in the training data set (Huys et al. 2006; Gold et al. 2007). Other investigations have extracted salient features from AP trains and used them as training data sets for stochastic search algorithms (Goldman et al. 2001; Golowasch et al. 2002; Prinz et al. 2004; Holmes et al. 2006; Druckmann et al. 2007; Nowotny et al. 2007, Nowotny et al. 2008; Ambros-Ingerson et al. 2008; Günay et al. 2008; Weaver & Wearne, 2008) or to generate a searchable database enabling investigation of the behavior of a given compartmental model under various conditions (Prinz et al. 2003, Prinz et al.2004; Ambros-Ingerson et al. 2008; Günay et al. 2008). These approaches have so far been restricted to the analysis of somatically recorded data, limiting the ability of the modellers to predict dendritic gradients of ion channels.

Currently, state of the art electrophysiology cannot generate the high quality set of simultaneous somatic, dendritic and axonal recordings required for constraining a compartmental model of an entire neurone. A clean set of simultaneous recordings can be obtained with relative ease from two recordings sites, one at the soma and one along the dendrite. It is possible to record from the same neurone through four electrodes, but this has been achieved only rarely (Larkum et al. 2001; Williams, 2004). We have previously shown that a training data set recorded from two locations in the same neurone is less adequate to accurately constrain a full compartmental model for a layer 5 pyramidal neurone (Keren et al. 2005). Can we use this data set to constrain a compartmental model only for the apical dendrite of these neurones? To answer this question, we have now developed a stepwise numerical scheme applying parameter peeling that enables constraining of a compartmental model for one compartment of a more complex neurone. We then designed and performed experiments on the apical dendrite of L5 pyramidal neurones based on the constraints laid out by the simulations. The results of these experiments were analysed using the new numerical approach. This led to an optimized model predicting that the conductance density gradients of voltage-gated K⁺ conductances taper rapidly proximal to the soma, while the density gradient of the voltage-gated Na⁺ conductance tapers slowly along the apical dendrite. The model predicts a mechanism for the back-propagating AP and dendritic Na⁺ spikes in the apical dendrite of L5 pyramidal neurones.

Methods

Slice preparation

Acute brain slices (sagittal, 300 μm thick) were prepared from the somatosensory cortex of 35- to 45-day-old Wistar rats. These were killed by rapid decapitation after anaesthesia with isoflurane (Stuart et al. 1993) and according to the guidelines of the Bar-Ilan University animal welfare committee. Slices were superfused throughout the experiment with oxygenated artificial cerebrospinal fluid (ACSF) containing (mM): 125 NaCl, 15 NaHCO₃, 2.5 KCl, 1.25 NaH₂PO₄, 1 MgCl₂, 2 CaCl₂, 25 glucose (pH 7.4 with 5% CO₂) at 32–34°C. Pyramidal neurones from L5 were visually identified using infrared differential interference contrast (IR-DIC) videomicroscopy (Stuart et al. 1993). The bath solution for current-clamp experiments, in which all voltage-gated Ca²⁺ channels were blocked, contained (mM): 135 NaCl, 15 Hepes, 2.5 KCl, 2 MgCl₂, 1 CoCl₂, 25 glucose (pH 7.4 with NaOH). Bicarbonate and phosphate were removed from the bath solution, since they may precipitate with cobalt. A liquid junction potential of 10 mV was not corrected for. Tetrodotoxin (TTX, Tocris, Bristol, UK) was stored at −20°C as stock solutions in doubly distilled water and added directly to the bath solution to form a final concentration of 200 nM.

Electrophysiology

Whole-cell recordings from the soma and apical dendrite of layer 5 pyramidal neurones were carried out using a Multiclamp-700B amplifier (Axon Instruments, Union City, CA, USA). Voltage was filtered at 10 kHz and sampled at 50 or 20 kHz using Axoclamp9 (Axon Instruments), digitized by a Digidata-1320 interface (Axon Instruments), and stored on the hard disk of a personal computer. Patch pipettes (4–7 MΩ somatic and 7–12 MΩ dendritic) were pulled from thick walled borosilicate glass capillaries (2.0 mm outer diameter, 0.5 mm wall thickness, Hilgenberg, Malsfeld, Germany). The standard pipette solution contained (mM): 125 potassium gluconate, 20 KCl, 10 Hepes, 4 MgATP, 10 sodium phosphocreatin, 0.5 EGTA, 0.3 GTP and 0.2% biocytin (pH 7.2 with KOH). At the end of each experiment, slices were fixed in cold 100 mM phosphate buffer solution (pH 7.4) containing 4% paraformaldehyde. After fixation the slices were incubated for 2 h in avidin-biotinylated horseradish peroxidase (ABC-Elite, Vector-Laboratories, Peterborough, UK) and the stain was developed using 0.015% diaminobenzidine. The stained neurones were digitally traced using a Neurolucida system (MicroBrightField, Williston, VT, USA) and the tracings were converted to NEURON readable code.

Numerical simulations

The compartmental model, the genetic algorithm and the cost function were programmed using NEURON 5.9 (Carnevale & Hines, 2006). Simulations were run on a Linux cluster with 168 CPUs sharing the same network file system (NFS). One of the machines functioned as a master, submitting and managing the jobs using the ParallelContext class of NEURON over a MPICH2 ring spanning the other computers. Ion channel models were implemented using the NMODL extension of NEURON (Carnevale & Hines, 2006). Results were analysed using IgorPro 6.0 (WaveMetrics, Lake Oswego, OR, USA).

Compartmental model

We used our previous model with small modifications and the same assumptions were applied as before (Keren et al. 2005).

• The morphology of the neurone is known.

• The passive membrane parameters are spatially homogeneous.

• The model contains four voltage-gated channels: Na⁺ channel, slow inactivating K⁺ channel (K_s), fast inactivating K⁺ channel (K_f) and an I_h channel.

• The kinetics of the channels are known and are based on experimental recordings.

• Dendritic channel gradients are a continuous function of the distance from the soma.

The full details of the basic model are given in Keren et al. (2005). This model was used for all the simulations described in Figs 1–4. For the analysis of the experimental data presented in Figs 5–12, we modified the functions describing the dendritic gradients of the four voltage-gated channels as reported in Results. The original set of parameters used in the model is listed in Table 1 along with the initial parameter ranges used by the genetic algorithm. The reversal potentials of the voltage-gated conductances were set at 60, −80 and −30 mV for Na⁺, K⁺ and I_h respectively.

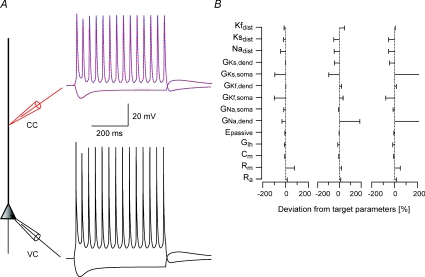
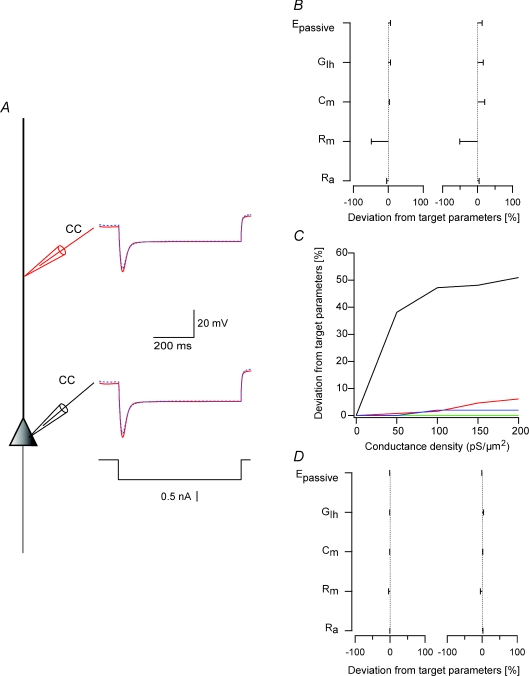
Figure 1. Constraining a model for the apical dendrite of L5 pyramidal neurones in one step results in local minima.

A, schematic drawing of the compartmental model used in the simulations. Somatic current-clamp simulations generated a data set containing both hyperpolarizing and depolarizing membrane potential deflections. Ten 600 ms long square current pulses starting at −500 pA and rising in steps of 200 pA were injected at the soma and the membrane potential changes were recorded at the soma and at 400 μm along the dendrite. The somatic membrane potential traces were then used as somatic voltage-clamp commands (black lines) and the dendritic membrane potential traces as a training data set for the genetic algorithm (red lines). Only two traces of 10 are shown for clarity. The membrane potential traces simulated by the one parameter set constrained using the genetic algorithm are superimposed on the training data set (dashed blue lines). B, deviations of parameter sets from three different runs of the genetic algorithm from the target parameters. The target parameters are listed in Table 1.

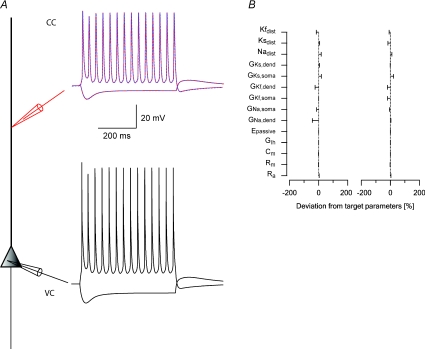
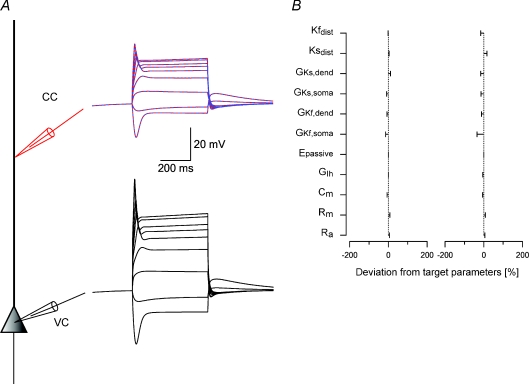
Figure 4. Third stage of the parameter peeling procedure: constraining voltage-gated Na⁺ conductance density gradient.

A, schematic drawing of the compartmental model used in the simulations. Somatic current-clamp simulations generated a data set containing both hyperpolarizing and depolarizing membrane potential deflections. Nine 1000 ms long current square pulses starting at –500 pA and rising in steps of 200 pA were injected at the soma and the membrane potential changes were recorded at the soma and at 400 μm along the dendrite. The somatic membrane potential traces were then used as somatic voltage-clamp commands (black lines) and the dendritic membrane potential traces as a training data set for the genetic algorithm (red lines). Only two traces of nine are shown for clarity. The membrane potential traces simulated by the one parameter set constrained using the genetic algorithm are superimposed on the training data set (dashed blue lines). B, deviations of parameter sets from the target parameters from three different runs of the genetic algorithm. The target parameters are listed in Table 1.

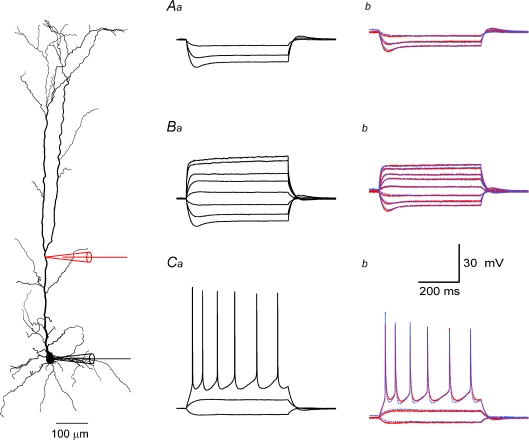
Figure 5. Application of the parameter peeling procedure to recordings from the apical dendrite of L5 pyramidal neurones.

A, constraining passive membrane parameters. Hyperpolarizing membrane potential traces recorded at the soma (a) and at 300 μm along the apical dendrite (b) of the neuron whose reconstruction is shown on the left. Voltage-gated Ca²⁺ conductances were blocked by Co²⁺ and voltage-gated Na⁺ conductances with TTX. In the current-clamp experiment three 800 ms long square current pulses starting at −250 pA and rising in steps of 100 pA were injected at the soma and the membrane potential changes were recorded at the soma and at 300 μm along the dendrite. The colour coding corresponds to the colour of the electrode shown in the neuron reconstruction. The membrane potential traces simulated at the dendrite using the best parameter set obtained by the genetic algorithm are shown as dashed blue lines (b). B, constraining passive membrane parameters and conductance density gradients of voltage-gated K⁺ channels. Hyperpolarizing and depolarizing membrane potential traces recorded at the soma (a) and at 300 μm along the apical dendrite (b) of the neuron whose reconstruction is shown on the left. Voltage-gated Ca²⁺ conductances were blocked by Co²⁺ and voltage-gated Na⁺ conductances by TTX. Ten 800 ms long square current pulses starting at −250 pA and rising in steps of 100 pA were injected at the soma and the membrane potential changes were recorded at the soma and at 300 μm along the dendrite. The colour coding corresponds to the colour of the electrode shown in the neuron reconstruction. The membrane potential traces simulated at the dendrite using the best parameter set obtained by the genetic algorithm are shown as dashed blue lines (b). C, constraining passive membrane parameters and conductance density gradients of voltage-gated K⁺ and Na⁺ channels. Hyperpolarizing and depolarizing membrane potential traces recorded at the soma (a) and at 300 μm along the apical dendrite (b) of the neuron shown on the left. Voltage-gated Ca²⁺ conductances were blocked by Co²⁺. In the current-clamp experiment 10 800 ms long square current pulses starting at −250 pA and rising in steps of 100 pA were injected at the soma and the membrane potential changes were recorded at the soma and at 300 μm along the dendrite. Colour coding corresponds to the colour of the electrode shown on the neuron reconstruction. The membrane potential traces simulated at the dendrite using the best parameter set obtained by the genetic algorithm are shown as dashed blue lines (b). The final parameter set obtained from this optimization is shown in Table 2 (Cell no. 1).

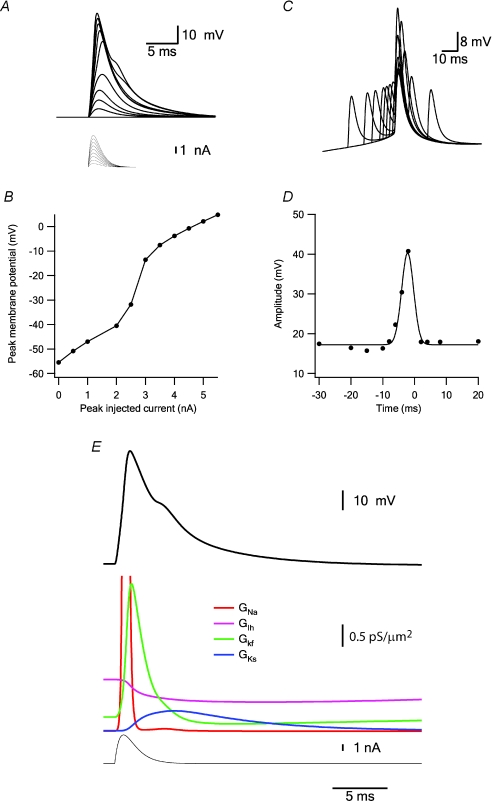
Figure 12. Simulating a fast dendritic Na⁺ spike.

A, changes in the membrane potential (thick lines) simulated 600 μm along the apical dendrite in response to injection of an EPSP-like current via the current-clamp electrode (thin lines). The peak current of the EPSP waveform started at zero and increased in steps of 500 pA. B, plot of the peak membrane potential simulated in A as a function of the maximal current injected during the EPSP-like current injection. C, coincidence between EPSP and back-propagating AP. The soma was voltage-clamped to an experimentally recorded AP. At 600 μm along the apical dendrite a simulated current-clamp electrode injected an EPSP-like current. The timing of the EPSP was varied relative to the back-propagating AP. D, plot of the peak membrane potential simulated in C as a function of the time difference between EPSP-like current injection and the back-propagating AP. The peak of the back-propagating AP was set as time 0. E, simulation of one dendritic Na⁺ spike (thick black line) induced by EPSP-like current injection (thin black line). The activation of the four voltage-gated channels inserted in the model during the spike is shown in colour.

Table 1.

Free parameters of the model used in the simulations in Figs 1–4

Parameter		Target	Lower boundary	Upper boundary
Ra	Ω cm	100	90	250
Rm	Ω cm2	21 000	10 000	60 000
Cm	μF cm−2	1.5	0.5	1.5
GIh	pS μm−2	12	0	50
Epassive	mV	−65	−70	0
GNa,dend	pS μm−2	10	0	100
GNa,soma	pS μm−2	50	0	100
GKf,soma	pS μm−2	65	0	100
GKf,dend	pS μm−2	70	0	100
GKs,soma	pS μm−2	15	0	100
GKs,dend	pS μm−2	90	0	100
Nadist	μm	1 000	0	1000
Ks, dist	μm	900	0	1000
Kf, dist	μm	500	0	1000
GNa,node	pS μm−2	31000	—	—
Nashift,act	mV	−7	—	—
Nashift,inact	mV	−8	—	—
GKf,node	pS μm−2	7 800	—	—
GKs,node	pS μm−2	1 500	—	—

The values of the target data set and the ranges over which the genetic algorithm searched for each parameter are given. The values describing axonal properties do not have parameter search ranges since they were used only to generate a training data set but were not included in the parameter data set constrained by the genetic algorithm. The passive parameters are the membrane resistance (R_m), axial resistance (R_a), the membrane capacitance (C_m) and the passive reversal potential of E_passive. The parameters describing the voltage-gated Na⁺ conductance are the somatic conductance density (G_Na,soma), the nodal conductance density (G_Na,node), the dendritic conductance density (G_Na,dend), the distance along the dendrite over which the conductance density changes from its somatic value to the dendritic value (Na_dist), the shift in the voltage of half activation (Na_shift,act) and the shift in the voltage of half inactivation (Na_shift,inact). The parameters describing the K_f conductance are the somatic conductance density (G_Kf,soma), the nodal conductance density (G_Kf,node), the dendritic conductance density (G_Kf,dend) and the distance along the dendrite over which the conductance density changes from its somatic value to the dendritic value (K_f,dist). The parameters describing the K_s conductance are the somatic conductance density (G_Ks,soma), the nodal conductance density (G_Ks,node), the dendritic conductance density (G_Ks,dend) and the distance along the dendrite over which the conductance density changes from its somatic value to the dendritic value (K_s,dist). The I_h conductance was described just by the conductance density (G_Ih).

Genetic algorithm

A genetic algorithm is an optimization algorithm based on the mechanisms of Darwinian evolution. It uses random mutation, crossover and selection operators to breed better models or solutions (individuals) from an originally random starting population (Mitchell, 1996). In the current study, we used a genetic algorithm similar to those we used previously (Keren et al. 2005; Gurkiewicz & Korngreen, 2007). Briefly, the population was sorted according to the value of the cost function of each individual (eqn (1)) and a new generation was created using selection, crossover, and mutation as operators. Selection used a tournament in which two pairs of individuals were randomly selected and the individual with the better score from each pair was transferred to the next generation. This procedure was repeated N/2 times (where N is the size of the population) until the new population was full. The one exception to this selection process (and later to the crossover and mutation operators) was that the best individual was transferred unchanged to the next generation to prevent genetic drift.

Each pair selected for transfer to the new population was subjected to a one-point crossover operator with a probability of 0.5. After the new population was created each parameter value in the new population was subjected to mutation with a probability of 0.1. The mutation operator performed a substitution of the parameter value with a random value drawn from a flat random number distribution that spanned the entire search space of the parameter. On average, a typical run of the genetic algorithm lasted 2–3 days on our Linux cluster.

The cost function calculated the difference between the target and the test membrane potential traces and summed its mean squares, yielding a cost function value that expresses the distance of the test from the target data set.

(1)

where V represents the target data set and v the membrane potential changes in the test data set, N is the total number of points in each membrane potential trace and M the number of membrane potential sweeps simulated in the model or recorded in the experiment.

Results

Simulated experiments

We have shown that simultaneous recording of the membrane potential at one site on the soma and one on the apical dendrite does not generate a full training data set for the genetic algorithm (Keren et al. 2005). We found, instead, that a full training data set should contain recordings from the axon, as well as soma and apical dendrite, to lead the genetic algorithm closer to the global minimum (Keren et al. 2005). Therefore, the first question we addressed here was: is it possible to use a training data set from a dual simultaneous recording of the membrane potential to constrain a model of only the apical dendrite of L5 neocortical pyramidal neurones?

It was clear from the outset that to use this data set only for the apical dendrite we had to isolate the apical dendrite from the rest of the neurone in the simulations. The general approach we adopted to achieve this was to generate a data set by simulating a dual current-clamp experiment with one electrode located at the soma and one several hundred micrometres away along the apical dendrite using a known parameter set. Square current pulses of varying amplitude were injected via the somatic electrode and the response was recorded in both locations. Instead of using this data as a training data set for the genetic algorithm, we used the somatic membrane potential traces as voltage-clamp commands. Thus, in the simulations used to train the genetic algorithm, the membrane potential at the soma was clamped to the membrane potential values recorded in the simulated experiment. The membrane potential decayed from the soma into the apical dendrite and was recorded by the dendritic current-clamp electrode. A schematic drawing of this procedure is shown in Fig. 1A. It is possible to regard the somatic voltage clamp as a somatic shunt eliminating communication between the axon and the apical dendrite (Rall & Segev, 1985). The genetic algorithm was trained using only the dendritic membrane potential recordings.

This approach eliminated several parameters from the set of parameters originally describing the model. All parameters defining the AP initiation zone in the axon could be discarded, leaving only the passive parameters, the parameters describing the conductance densities at the soma and the parameters describing the conductance distribution along the dendrite. This reduced the original parameter set from 19 to 14 (Table 1). We then tested whether the genetic algorithm could constrain this parameter set using only the single dendritic recording and ran the genetic algorithm 9 times (Fig. 1B). In all cases the genetic algorithm was able to reduce the cost function almost to a perfect fit (Fig. 1A). The fit was equally good for passive traces and for the back-propagating APs (Fig. 1A). However, large deviations of the parameters were observed in all the runs (Fig. 1B), suggesting that the genetic algorithm was unable to reach the target parameter set using only the dendritic membrane potential traces as a training data set.

It is intuitively reasonable that any minimization algorithm functions better on a smaller parameter set. Thus, the trivial approach in many areas is to attempt to reduce the complexity of the problem. In the case of compartmental models it may be possible to define subsets of parameters that can be constrained separately. The passive parameters have been repeatedly and successfully estimated by fitting a compartmental model to small hyperpolarizing membrane potential deflections (Clements & Redman, 1989; Major et al. 1994; Spruston et al. 1994; Stuart & Spruston, 1998; Roth & Häusser, 2001). In the model used here there were five parameters that controlled the response of the membrane potential at negative potentials: C_m, R_m, R_a, E_passive and the conductance density of the cation non-selective current I_h. The target data set was restricted to only membrane potential traces recorded after the injection of a hyperpolarizing current step (Fig. 2A). In over 10 runs the genetic algorithm was able to reduce the cost function almost to zero (Fig. 2A). However, in all simulations the genetic algorithm underestimated the value of R_m by approximately 50% (Fig. 2B). In retrospect, this was hardly a surprise. In addition to passive parameters, the model also contains voltage-gated conductances. While activation threshold of these conductances is ∼20 mV above the resting membrane potential, they do have a small but finite opening probability around the resting membrane potential. Thus, the residual activation of these voltage-gated conductances decreases the apparent R_m, resulting in underestimation of this parameter by the minimization algorithm. In experiments designed specifically to record passive membrane parameters it is possible to block voltage-gated K⁺ conductances by adding Cs⁺ to the whole-cell patch pipette and by adding K⁺ blockers to the bath solution. In the current work we did not wish to block voltage-gated K⁺ conductances. Therefore, we sought a numerical solution to the problem.

Figure 2. First stage of the parameter peeling procedure: constraining passive parameters.

A, schematic drawing of the compartmental model used in the simulations. Somatic current-clamp simulations generated a data set containing hyperpolarizing membrane potential deflections. Five 600 ms long square current pulses starting at −500 pA and rising in steps of 100 pA were injected at the soma and the membrane potential changes were recorded at the soma and at 400 μm along the dendrite. Both somatic and dendritic membrane potential traces were used as a training data set for the genetic algorithm (red lines). Only one trace of five at each recording site is shown for clarity. The membrane potential traces simulated by one parameter set describing passive membrane properties constrained using the genetic algorithm are superimposed on the training data set (dashed blue lines). B, deviations of parameter sets from two different runs of the genetic algorithm from the target parameters. The target parameters are listed in Table 1. C, deviations of each parameter from three different runs of the genetic algorithm from the target parameters when the conductance density of K_s was varied systematically. Substantial error was observed for R_m (black lines) with C_m (red lines), R_a (blue lines) and E_passive (green lines) displaying only small errors. D, deviations of parameter sets from two different runs of the genetic algorithm from the target parameters. The somatic conductance density of K_s was arbitrarily set at 100 pS μm⁻² in these simulations.

We first attempted to estimate the error in the passive parameters when we systematically varied the conductance density of the voltage-gated K⁺ inserted at the soma. Increasing the somatic density of K_s increased the error between the estimated and target value of R_m (Fig. 2B). The deviations of C_m, R_a and E_passive from their target values were less than 10% for all the tested conductance densities of K_s (Fig. 2B). The error in R_m reached an asymptote above 100 pS μm⁻², suggesting that it may be possible to estimate the value of R_m even if the exact value of the conductance density of the voltage-gated K⁺ channels is unknown. We repeated the optimization of the passive parameters when a rough estimate of the K⁺ conductance density was inserted at the soma. Under these conditions, the genetic algorithm constrained the passive parameter set to within 10% of its target values (Fig. 2C). The procedure described in Fig. 2 was not designed to provide an accurate estimate of the passive parameters but, rather, to reduce the error between these parameters and their target values.

Of the 14 parameters that described the full model of the apical dendrite, nine now remained to be constrained. These parameters describe the conductance density distribution of the two voltage-gated K⁺ and Na⁺ conductances. Initially, two options presented themselves. One was to constrain the entire parameter set using the constrained passive parameters to reduce the degrees of freedom for that parameter subset. The other option was to further dissect the remaining parameter set. We have previously shown that it is possible to estimate the local conductance density of voltage-gated K⁺ conductances from membrane rectification following depolarizing steps in current-clamp (Schaefer et al. 2007). These experiments suggested the possibility of constraining only parameters related to voltage-gated K⁺ conductances when the voltage-gated Na⁺ conductance is blocked. We therefore simulated a somatic current-clamp experiment in the same neurone model as before with the voltage-gated Na⁺ conductance density set to zero all over the neurone, thus simulating a complete block of this conductance. We injected several hyperpolarizing and depolarizing current pulses and the response of the membrane was simultaneously recorded at the soma and the dendrite (Fig. 3A). Similarly to the simulations presented in Fig. 1 the somatic membrane potential traces were used as voltage-clamp commands and the genetic algorithm was trained using only the dendritic data set. We allowed the genetic algorithm to change the values of the passive parameters obtained in the previous stage (Fig. 2). However, to prevent these parameters from drifting away from the values obtained in the previous step of the minimization, we set the search ranges for these five parameters to ±25% of the values obtained in the previous optimization stage. Thus, while the genetic algorithm attempted to optimize a problem with 11 parameters, only six of them were allowed to change over a large range. The genetic algorithm was able to provide a very good fit to the target data set (Fig. 3A) and in the two runs presented in Fig. 3B arrived at parameter sets with less than 20% error per parameter (Fig. 3B).

Figure 3. Second stage of the parameter peeling procedure – constraining voltage-gated K⁺ conductance gradients.

A, schematic drawing of the compartmental model used in the simulations. Somatic current clamp simulations generated a data set containing both hyperpolarizing and depolarizing membrane potential deflections. The conductance of the voltage-gated Na⁺ channel was set at zero to simulate complete block of this channel with TTX. Nine 600 ms long square current pulses starting at −500 pA and rising in steps of 200 pA were injected at the soma and the membrane potential changes were recorded at the soma and at 400 μm along the dendrite. The somatic membrane potential traces were then used as somatic voltage-clamp commands (black lines) and the dendritic membrane potential traces as a training data set for the genetic algorithm (red lines). The membrane potential traces simulated by the one parameter set constrained by the genetic algorithm are superimposed on the training data set (dashed blue lines). B, deviations of parameter sets excluding the parameters describing the Na⁺ conductance density from the target parameters from two different runs of the genetic algorithm. The target parameters are listed in Table 1.

In the final stage of the optimization we restricted the search range of the 11 parameters obtained in the preceding step to ±25% of the values obtained in the previous optimization stage, added the three parameters describing the conductance density distribution of the voltage-gated Na⁺ conductance, used the same training data set applied in Fig. 1, and optimized the entire 14 parameter model of the apical dendrite. As observed in the previous optimization steps, the genetic algorithm provided a good fit to the target data set (Fig. 4A) and in the two runs presented in Fig. 3B arrived at parameter sets with less than 20% error per parameter (Fig. 4B). These parameter sets were considerably closer to the target parameter set than the sets obtained when the model was constrained with full parameter ranges (Fig. 1B).

The simulations presented in Figs 2–4 suggested a numerical parameter peeling procedure for constraining a compartmental model of a single dendrite or compartment in a complex model. Three stages apply to the reduced model of an L5 pyramidal neurone used here. In the first stage, the passive parameters were initially fitted. The results of this stage were used to reduce the search range for the passive parameters in the second stage of the optimization. Here the genetic algorithm attempted to constrain a larger parameter set, which included the parameters describing the dendritic distribution of voltage-gated K⁺ channels. The results of the second peeling stage were again used to reduce the search range for the parameters obtained in this stage. In the third and last stage, the parameters describing the dendritic gradient of the voltage-gated Na⁺ channel were added to the parameter set together with the parameters (and reduced search ranges) obtained in the second stage. This three-stage optimization procedure allowed the genetic algorithm to successfully reach the target parameter set with reasonable error. To test the applicability of this peeling procedure to other compartmental models we applied it to another model of an L5 pyramidal neurone (Mainen et al. 1995) and to a model of a CA1 pyramidal neurone (Gasparini et al. 2004). In both cases the peeling procedure performed as well as on the model tested above (see Supplemental figures and tables for a description of these simulations).

Optimizing a model for the apical dendrite of L5 pyramidal neurones

The peeling procedure suggested a simple experimental design that could be applied to the apical dendrite of L5 pyramidal neurones. We simultaneously recorded the membrane potential from the soma and apical dendrite of L5 pyramidal neurones. In the first stage of the experiment, all voltage-gated Ca²⁺ channels were blocked by replacing the Ca²⁺ in the bath solution with Co²⁺. Current steps were injected via the somatic electrode and the membrane potential was recorded by both electrodes. Next, 200 nm TTX were added to the bath solution to block voltage-gated Na⁺ channels and current steps were again injected via the somatic electrode. Following the recordings, all the cells were fixed, stained, traced using Neurolucida, and converted to a code readable by NEURON. This experimental protocol provided an electrophysiological and morphological data set for each neurone that complied with the assumptions made while developing the parameter peeling procedure.

Using this data set we first attempted to constrain the model presented in the previous section. In three data sets tested, this did not result in a good fit (simulations not shown). Therefore, we modified the model using recent experimental findings. It has been shown that the density of the hyperpolarization activated cation non-selective conductance I_h increased along the apical dendrite (Williams & Stuart, 2000; Berger et al. 2001). We extracted the distribution data from the Berger et al. (2001) manuscript and, after some testing, observed it to be best fitted by a sigmoidal function. Therefore, the dendritic conductance density gradient of I_h was set to be sigmoidal in the model. Similar I_h distribution has been previously applied for fitting passive membrane parameters using simultaneous dendritic and somatic recordings (Stuart & Spruston, 1998). The dendritic distribution of voltage-gated K⁺ channels displays an exponential decay along the apical dendrite (Schaefer et al. 2007). These gradients were added to the model. Note that, while the K⁺ gradients were selected to decay exponentially, the initial parameter ranges controlling the slope of the decay were selected to allow almost any shape of the gradient, including a flat one (Table 2). The dendritic Na⁺ conductance density gradient was as in the model in the simulations above, the only change being that the shifts in the activation and inactivation curves, which were restricted to the axon, were introduced as parameters also for the dendritic conductance. All model optimizations described from now on were carried out using the reconstructed morphology of the neurone from which the membrane potential traces were recorded. Prior to using the revised model for the analysis of the experimental traces we generated simulated experiments and applied the parameter peeling procedure to them. In three different runs the genetic algorithm was able to reduce the error in the parameters to less than 20% of the target parameters (simulations not shown).

Table 2.

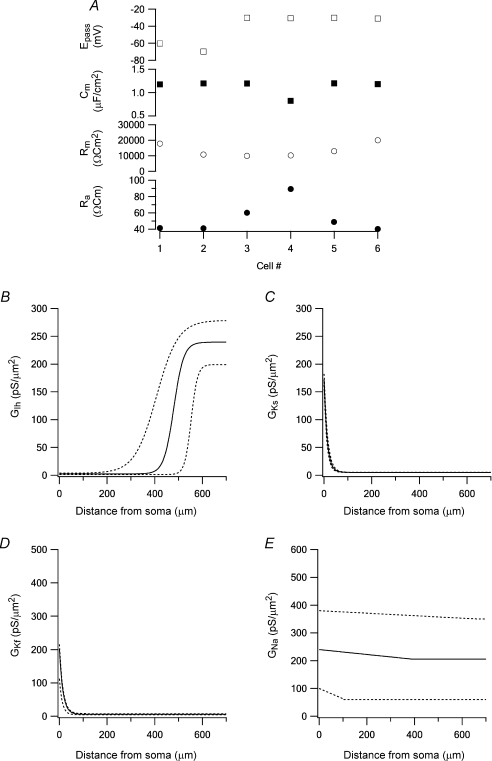
Results of fitting the model to the data

		Lower	Upper	Cell	Cell	Cell	Cell	Cell	Cell
Parameter	Unit	boundary	boundary	no. 1	no. 2	no. 3	no. 4	no. 5	no. 6	Average	STD	CV
Distance	μm			300	380	330	260	240	320	305	51
Ra	Ω cm	0	300	77	73	84	88	83	60	78	10	0.13
Rm	Ω cm2	1000	50 000	15 743	17 118	13 462	10 671	13 064	19 935	14 999	3 294	0.22
Cm	μF cm−2	0.2	3	0.99	1.15	1.19	1.20	1.06	1.19	1.13	0.1	0.07
Epassive	mV	−150	0	−50.2	−64.7	−30.1	−31.8	−32.9	−41.9	−41.9	13.5	0.32
GIh,dend	pS μm−2	0	1000	295	239	237	233	184	180	228	42	0.19
Ih, X1/2	μm	0	1000	464	479	470	403	486	589	482	60.4	0.13
Ih, slope	pS μm−1	−1	0	−0.09	−0.08	−0.08	−0.01	−0.08	−0.06	−0.07	0.03	0.44
GIh,soma	pS μm−2	0	10	1.7	1.3	4.3	3.7	1.0	1.0	2.2	1.4	0.66
GKs,dend	pS μm−2	0	10	5.3	5.4	5.1	5.1	5.3	5.4	5.3	0.1	0.03
Ks,slope	pS μm−1	−1	0	−0.09	−0.08	−0.09	−0.07	−0.09	−0.03	−0.07	0.02	0.30
GKs,soma	pS μm−2	0	1000	218	180	172	153	223	349	216	71	0.33
GKf,dend	pS μm−2	0	100	14	14	6	5	15	17	12	5	0.42
Kf, slope	pS μm−1	−1	0	−0.04	−0.02	−0.08	−0.07	−0.04	−0.06	−0.05	0.02	0.47
GKf,soma	pS μm−2	0	1000	372	467	208	121	365	318	309	125	0.40
GNa,soma	pS μm−2	0	1000	471	46	160	453	137	399	278	185	0.66
GNa,dend	pS μm−2	0	1000	58	106	72	462	149	80	154	154	1.00
Nadist	μm	0	1000	381	303	915	951	838	720	685	278	0.41
Nashift,act	mV	−20	0	−10.6	−14.4	−14.8	−3.8	−15.0	−10.3	−11.5	4.3	0.38
Nashift,inact	mV	−20	0	−6.6	−13.6	−14.7	−0.5	−13.2	−8.9	−9.6	5.4	0.56

Parameter values obtained by constraining the model of the apical dendrite of L5 pyramidal neurones using six experimental data sets. The distance to the dendritic electrode is noted in the top row. The average parameter value, the standard deviation, and the coefficient of variation are presented for each parameter. The dendritic conductance gradient of K_s was calculated using the exponential equation 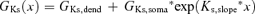(where x stands for the distance from the soma along the apical dendrite). This formula was used also to calculate the dendritic conductance gradient of K_f. The dendritic conductance gradient of I_h was calculated using 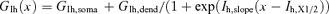. The rest of the parameters have the same meaning and definition as in Table 1.

Figure 5 shows the three stages of the peeling procedure applied to one of the six experimental data sets. In the first stage, only the passive parameters and the conductance density gradient of I_h were constrained using hyperpolarizing membrane potential traces generated by negative current injections (Fig. 5A). In the second stage, search ranges of the parameters constrained in the first stage were shrunk to ±25% of their value, and the genetic algorithm constrained a set of parameters describing the passive, I_h, K_s and K_f dendritic conductance density gradients (Fig. 5B). Finally, in the third stage, search ranges of the parameters constrained in the second stage were shrunk to ±25% of their values, the parameters describing the dendritic conductance density gradient of the voltage-gated Na⁺ conductance were added to the parameter set and the entire set was optimized for the last time. The parameter sets obtained by applying the peeling procedure to recordings from six cells are given in Table 2 and displayed graphically in Fig. 6. In each stage the somatic current-clamp recordings were used in the simulations as voltage-clamp commands and the genetic algorithm was trained using only the dendritic membrane potential. It is important to note that voltage-clamp was not performed in the actual experiments, only in the simulations used to train the genetic algorithm. Using these traces as voltage-clamp commands in an experiment will lead to severe clamp problems due to the lack of space-clamp and proper series resistance compensation.

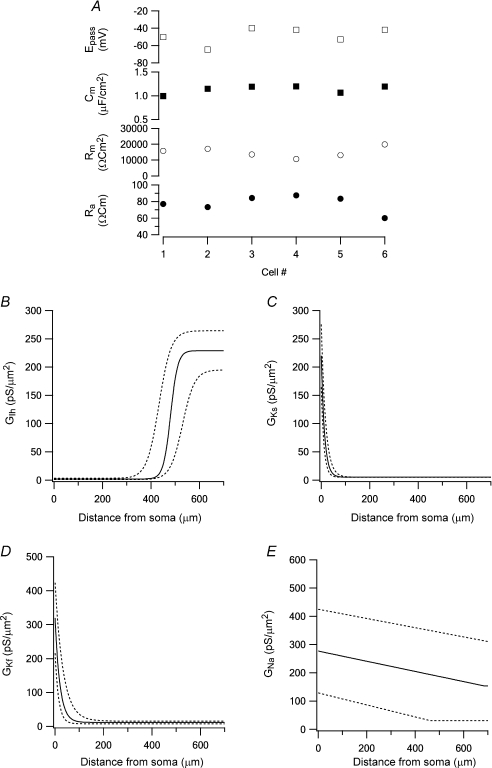
Figure 6. Graphical display of model optimization using several experimental data sets.

A, passive parameters obtained by the peeling procedure in six experiments. B, the average dendritic conductance density of I_h (continuous line). The 95% confidence limits of this average are shown as dotted lines (also in C, D and E). C, the average dendritic conductance density of K_s (continuous line). D, the average dendritic conductance density of K_f (continuous line). E, the average dendritic conductance density of Na⁺ (continuous line).

The values of the passive parameters (Fig. 6A), the dendritic conductance density distribution of K_s (Fig. 6C) and of K_f (Fig. 6D) displayed similar values in all six cells. The gradient of the dendritic distribution of K_s was similar to that we determined recently using a different experimental approach (Schaefer et al. 2007). The density gradient of I_h was also comparable to previous experimental reports (Berger et al. 2001). The dendritic conductance density distribution of I_h showed larger variability in the parameters constrained by the genetic algorithm (Fig. 6B). The largest variability among the six cells optimized in this study was in the dendritic conductance density gradient of the voltage-gated Na⁺ conductance (Fig. 6E). Previous reports suggest that the Na⁺ displays a shallow decrease in conductance density along the apical dendrite of L5 pyramidal neurones (Stuart & Sakmann, 1994) similar to that constrained here.

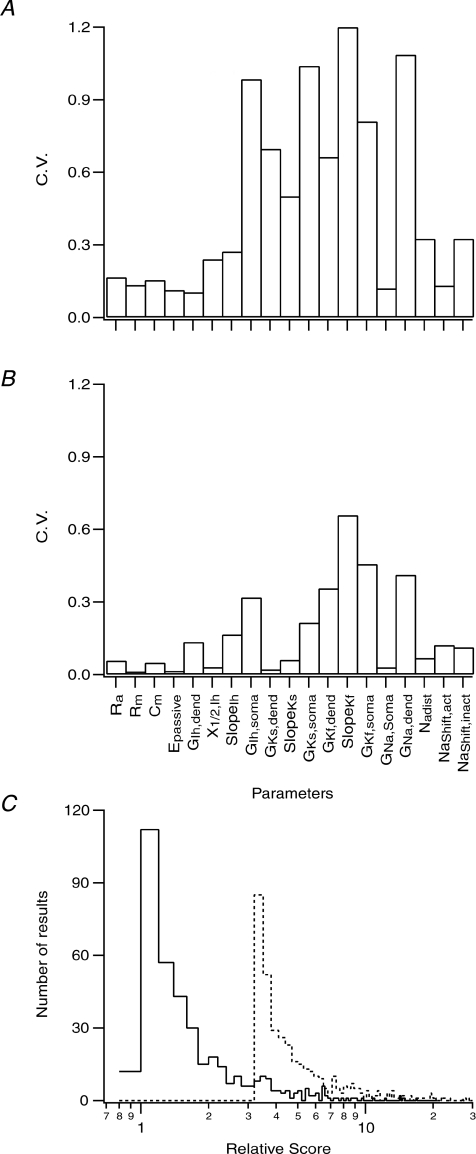
Does the peeling procedure allow the genetic algorithm to reach a global minimum when constraining the compartmental model with experimental data? Obviously, in this case the target parameters are not known, different from constraining the model with simulated data sets. The simulations shown in Figs 1 and 4 indicate the quality of the constrained parameter set. The striking difference between Figs 1B and 4B is the smaller variance in the error between the obtained and target parameter sets after the peeling procedure (Fig. 4) than after a one-step optimization of the entire compartmental model (Fig. 1). We therefore optimized one of the recorded neurones five times using the peeling procedure and five times using a one-step optimization. In each case we calculated the coefficient of variation (CV) for each parameter within the five runs. The CV calculated after one-step optimization was considerably larger for all the parameters of the model (Fig. 7A) than the CV calculated after several runs of the peeling procedure (Fig. 7B). Thus, while we do not know the target parameter set when constraining the model with experimental data, the simulations shown in Fig. 7A and B suggest that the peeling procedure was better at constraining the model than a one-stage optimization.

Figure 7. Smaller parameter variation was obtained using the peeling procedure than when using full model optimization.

A, coefficient of variation (CV) calculated for each parameter in five sets obtained after five optimizations of the model using the training data set recorded from cell no. 1. The optimization was performed in one stage similar to that in Fig. 1 with search ranges given in Table 2. B, coefficient of variation (CV) calculated for each parameter in five sets obtained after five optimizations of the model using the training data set recorded from cell no. 1. The optimization was performed using a peeling procedure like that shown in Figs 2–4. C, semi-logarithmic histograms produced from the cost function calculated from 500 parameter sets generated by randomly modifying all parameters within ±5% of the average values obtained in B. The value of each cost function was calculated using these parameter sets and the distribution of the results was displayed as logarithmic histogram (continuous line). The values of the cost functions were normalized to the cost function calculated using the parameter set that generated B. The same calculation was repeated using the average parameter set used to generate A (dashed line). To allow comparison with the previous calculation the values of the cost function were normalized to the cost function calculated using the parameter set that generated B.

Does the parameter set obtained by the peeling procedure define a more global solution than other possible parameter sets? To investigate this question we generated 500 parameter sets by randomly modifying all parameters within ±5% of the average values obtained in Fig. 7B. The value of each cost function was calculated using these parameter sets and the distribution of the results was displayed as a logarithmic histogram (Fig. 7C). The values of the cost functions were normalized to the value of the cost function calculated using the parameter set used in Fig. 7B. Next, we repeated the calculation using the average parameter set that generated Fig. 7A. For comparison with the previous calculation, the values of the cost function were normalized to the value of the cost function calculated using the parameter set that generated Fig. 7B. The histogram obtained from parameter sets generated from the one-stage optimization calculation was shifted to higher score values than the histogram calculated from parameter sets obtained by the peeling procedure (Fig. 7C). Thus, the one-stage optimization of the model leads the genetic algorithm to a local minimum with a high parameter variance and not to a global minimum.

One assumption here was that the kinetics of the voltage-gated conductances were known. This assumption may potentially distort the optimization of the model by the genetic algorithm. Of the four voltage-gated conductances included in the model, the parameters for the voltage-gated Na⁺ conductance showed the greatest variability (Fig. 6E). We replaced the model of the Na⁺ conductance with an older model of the same conductance (Mainen et al. 1995) and repeated the optimizations. The resulting dendritic conductance density gradient of the voltage-gated Na⁺ conductance still displayed a shallow decrease as a function of distance from the soma (Fig. 8E), but the variability of the parameters describing this gradient was still large between cells. Comparing the results obtained with the alternative model for the Na⁺ conductance to those in Fig. 6 shows a clear decrease in the variability in the parameters describing the dendritic conductance gradients of K_s (Fig. 8C) and K_f (Fig. 8D). This results from our decision to allow parameters from early stages of the peeling procedure to vary by ±25%. This, in turn, lets the genetic algorithm continue fine-tuning parameters without inflating search space. In all six cells, the lowest score function reached by the genetic algorithm was substantially larger when the alternative Na⁺ conductance model was used (4.0 ± 1.8 times larger on average, n= 6), indicating a poorer fit for the model containing the alternative Na⁺ conductance. Finally, we replaced the Na⁺ conductance model with a Markov kinetic scheme (Baranauskas & Martina, 2006) and repeated the simulations. Similar results were obtained with the score function still larger for all cells (data not shown).

Figure 8. Graphical display of model optimization using several experimental data sets and an alternative kinetic model for the voltage-gated Na⁺ conductance.

A, passive parameters obtained by the peeling procedure in six experiments. B, the average dendritic conductance density of I_h (continuous line). Dotted lines give the 95% confidence limits of this average (also in C, D and E). C, the average dendritic conductance density of K_s (continuous line). D, the average dendritic conductance density of K_f (continuous line). E, the average dendritic conductance density of Na⁺ (continuous line). The optimizations were carried out with a different Na⁺ conductance kinetic model from in Fig. 6.

Physiological correlates of the optimized model

Based on the optimizations using the peeling procedure we can now propose a mechanistic description for the back-propagation of the AP in the apical dendrite of L5 pyramidal neurones. Note that this proposed mechanism is based on a reduced model of the apical dendrite of L5 pyramidal neurones. The complex interplay between voltage-gated Ca²⁺ channels and Ca²⁺-dependent K⁺ channels was eliminated by replacing bath Ca²⁺ ions with cobalt ions. That is, the proposed model can provide insight only on the basic mechanism of AP back-propagation involving voltage-gated Na⁺ and K⁺ channels. The conductance density gradients of the two voltage-gated K⁺ channels (Fig. 6C and D) decreased faster than that of the voltage-gated Na⁺ channel (Fig. 6E), possibly making voltage-gated Na⁺ conductance activation the major contributor to the back-propagation of the AP.

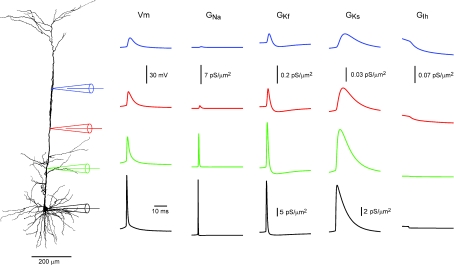
To follow the pattern of conductance activation along the apical dendrite we simulated a voltage-clamp experiment, in which the soma was clamped to the waveform of a somatic AP, and recorded the conductance changes along the apical dendrite (Fig. 9). The largest activation of the two K⁺ conductances was at the soma. This activation became considerably smaller even 200 μm from the soma. Conversely, the Na⁺ conductance was still substantially activated at a distance of 200 μm, the activation only decreasing at 400 μm along the apical dendrite (Fig. 9). The activation of the Na⁺ conductance accounts for the initial rise of membrane potential, while the activation of the K_f conductance follows the initial repolarization stage of the AP. Due to inactivation of K_f, this conductance decreases after the repolarization stage (Fig. 9). This decrease in the K⁺ conductance is offset by the delayed activation of K_s which is active during late repolarization stage and afterhyperpolarization. The model also predicts a decrease in the level of I_h activation due to deactivation especially in the dendrite (Fig. 9). It was not clear from the simulations we performed if or how this change in I_h contributed to AP back-propagation.

Figure 9. Conductance activation during the back-propagating AP according to the optimized model.

In a simulation the somatic membrane potential was clamped to an action potential waveform recorded from cell no. 1 (black dotted lines). The changes in the membrane potential and the conductance of the four voltage-gated channels included in the model are shown at 200, 400 and 600 μm along the apical dendrite. The traces are colour coded according to the colour of the simulated electrodes shown on the left.

The simulations presented in Fig. 9 were carried out with the best parameter set obtained by the peeling procedure using the data set recorded from the neurone whose morphology is displayed in the figure. One may argue that this parameter set represents an unstable state of the model. To address this concern and further investigate the mechanism of AP back-propagation, we generated 200 parameter sets by randomly modifying all parameters within ±5% of the parameter set used to simulate the traces shown in Fig. 9. We repeated the simulations in Fig. 9 using these parameter sets. In each section of the apical dendrite we measured the following: the peak membrane potential during a back-propagating AP; the maximal activation of the K_s, K_f, and Na⁺ conductances; and the value of the I_h conductance at the AP peak. In 43 of 200 simulations the AP did not propagate actively into the apical dendrite. Examination of these simulations revealed a parameter combination containing low Na⁺ conductance and high K⁺ conductances resulting in failure of AP back-propagation. These simulations were removed from the data set given in Fig. 10.

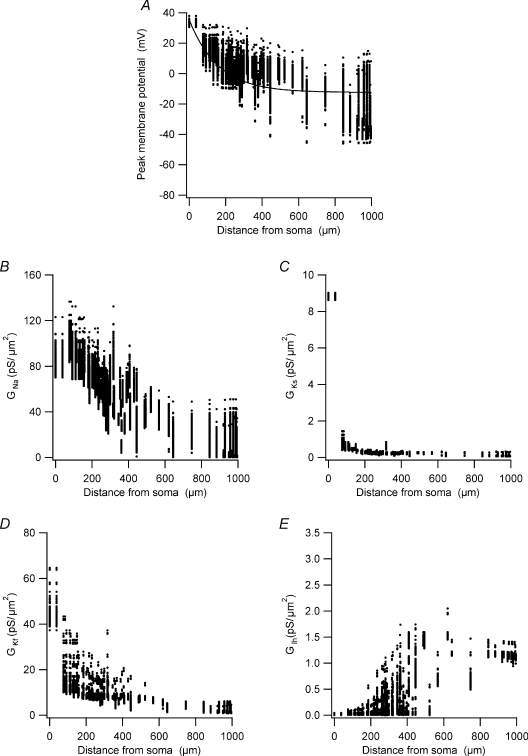
Figure 10. The function of voltage-gated channels during back-propagation of the AP.

A, peak membrane potential during the back-propagating AP simulated in each compartment in the apical dendrite measured in 157 simulations using parameter sets randomly modified within ±5% of the parameter set used to simulate the traces in Fig. 9. The values in B, C, D and E are from the same simulations and the same time points as in A. B, peak voltage-gated Na⁺ conductance activation during the back-propagating AP recorded in each compartment in the apical dendrite. C, peak voltage-gated K_s conductance activation during the back-propagating AP recorded in each compartment in the apical dendrite. D, peak voltage-gated K_f conductance activation during the back-propagating AP recorded in each compartment in the apical dendrite. E, voltage-gated I_h conductance activation during the back-propagating AP recorded in each compartment in the apical dendrite.

The peak amplitude of the membrane potential measured in each section of the reconstructed neurone displayed roughly an exponential decay as a function of distance from the soma (Fig. 10A). This decay in the AP amplitude was correlated with a similar decay in the peak activation of the Na⁺ conductance (Fig. 10B). The peak activation of the K_s conductance was large only at the soma, whereas the peak activation of the K_f conductance gradually decreased from the soma up to approximately 400 μm along the apical dendrite (Fig. 10C). This difference between the two conductances with similar density gradients (Fig. 6) was probably due to the faster activation kinetics of K_f. Thus, trivially, the current model predicts that the peak membrane potential deflection generated by the back-propagating AP in L5 pyramidal neurones is modulated primarily by the Na⁺ and K_f conductances. This suggestion is clearly a rough approximation, since the contribution of K_f and K_s to the shape of the back-propagating AP is complex and dependent on the respective kinetics of these conductances as shown in Fig. 9.

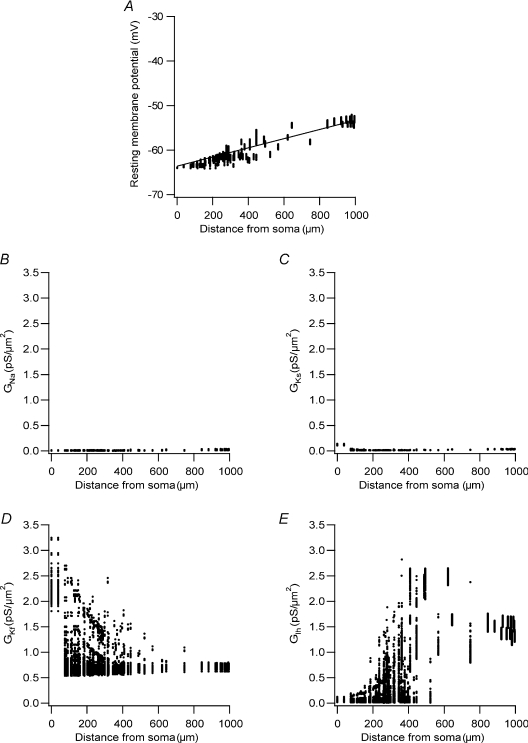
Stuart et al. (1997a) have reported that the resting membrane potential increases linearly along the apical dendrite of L5 pyramidal neurones. Does the constrained model reproduce this physiological property? Using the same set of 200 parameter vectors employed in the simulations above, we simulated the resting state of the neurone and recorded the value of the resting membrane potential and the values of the Na⁺, K_f, K_s and I_h conductances (Fig. 11). Similar to experimental results, the resting membrane potential in all these simulations displayed a shallow linear increase as a function of distance along the apical dendrite (Fig. 11A). The activation of the Na⁺ and K_s conductances near the resting membrane potential was negligible all along the apical dendrite (Fig. 11B and C). As expected from their kinetic properties, both K_f and I_h displayed substantial activation at the resting potential (Fig. 11D and E). Thus, the seemingly linear increase in the resting membrane potential along the apical dendrite is controlled in the model by non-linear density distributions of K_f (Fig. 11D) and I_h (Fig. 11E).

Figure 11. Activation of voltage-gated channels at the resting membrane potential.

A, resting membrane potential simulated in each compartment in the apical dendrite measured in 157 simulations using parameter sets randomly modified within ±5% of the parameter set used to simulate the traces in Fig. 9. The values in B, C, D and E are from the same simulations and the same time points as in A. B, voltage-gated Na⁺ conductance activation at rest in each compartment in the apical dendrite. C, voltage-gated K_s conductance activation at rest in each compartment in the apical dendrite. D, voltage-gated K_f conductance activation at rest in each compartment in the apical dendrite. E, voltage-gated I_h conductance activation at rest in each compartment in the apical dendrite.

Due to the simplifications made to apply the peeling procedure to the experimental results the model cannot generate dendritic Ca²⁺ spikes and does not contain an axonal site for AP initiation. Thus, it is not possible at present to compare the behaviour of the model to many known properties of the apical dendrite of L5 neurones. Luckily, it has been observed that the initial stage of the dendritic Ca²⁺ spike is mediated by a fast dendritic Na⁺ spike (Stuart et al. 1997a; Zhu, 2000; Larkum et al. 2001). To test whether our model can generate dendritic Na⁺ spikes we simulated an experiment in which an EPSP like waveform was injected via a dendritic current-clamp electrode positioned 600 μm along the apical dendrite (Fig. 12A). With low injected current the membrane potential responded linearly as predicted by passive cable theory (Fig. 12B). As the injected current increased, the response of the membrane potential became sharper, reached higher amplitudes than expected from a linear response, and decayed non-exponentially (Fig. 12A and B). Similar results were obtained experimentally (See figures 1 and 2 in Larkum et al. 2001).

Stuart & Häusser (2001) have shown that the amplitude of the back-propagating AP is boosted when it meets synaptic input. We were able to reproduce this experiment using our model (Fig. 12C and D) to simulate fast dendritic Na⁺ spikes similar to those observed experimentally (Fig. 12C) and to calculate a similar coincidence plot between AP and an EPSP (Fig. 12D). Having reproduced the experimental finding, we dissected out the role of the various voltage-gated channels during the initiation of the fast dendritic Na⁺ spike.

Figure 12E shows the membrane potential simulated during a dendritic Na⁺ spike and the time course of activation of the four voltage-gated conductances making up the model. The dendritic Na⁺ spike was initiated by the activation of the voltage-gated Na⁺ conductance followed by activation of two voltage-gated K⁺ conductances in series. After the initial activation of the Na⁺ conductance there was a small resurgent activation of Na⁺ conductance that was responsible for the small bend in the spike waveform. Mechanistically, the resurgent activation of the Na⁺ conductance was due to a window current generated by the activation crossing the inactivation curves.

Discussion

Here we have developed a parameter peeling procedure allowing constraint of a compartmental neurone model for a section of a complex morphology. The procedure was tested on several models of primary CNS neurones. We provide an initial proof of principle that divide and conquer procedures can be used with a high degree of efficacy to constrain a compartmental model for one compartment in a more complex compartmental model. Based on the peeling procedure we designed and performed experiments on the apical dendrite of rat L5 pyramidal neurones. Six data sets recorded from different L5 pyramidal neurones guided the genetic algorithm, using the peeling procedure, to the same region of parameter space. Finally, we used the parameters thus obtained to probe the mechanism of AP back-propagation and dendritic Na⁺ spike initiation.

Simulations

Our parameter peeling procedure allowed us to greatly reduce the variability of the solutions reached by a stochastic optimization algorithm when constraining a compartmental model. For the reduced model of L5 pyramidal neurones we were able to repeatedly arrive at a set of known target parameters using three optimization stages (Figs 2–4). Optimization of another model for L5 pyramidal neurones was achieved using a four-stage optimization that also included voltage-gated Ca²⁺ channels (Supplemental Fig. 2). Thus, we suggest that the peeling procedure will also be effective for further compartmental models. The second stage of the peeling procedure calculates the conductance density gradient of voltage-gated K⁺ channels along the somato-dendritic axis (Fig. 3). This requirement posed a problem for the first stage of the peeling procedure in which the passive membrane parameters were estimated. Thus, the residual activation of the voltage-gated channels, especially that of voltage-gated K⁺ channels, distorts the estimation of R_m (Fig. 2). As this distortion was constant above a given value of the K⁺ conductance density (Fig. 2C), we were able to make a reasonable guess of the passive parameters in the first stage of the peeling procedure.

The second stage of the peeling procedure showed a further improvement for optimizing compartmental models. It was gratifying to learn that, assuming the kinetics of the conductances were known, it was possible to accurately estimate the conductance density of voltage-gated K⁺ conductances from current-clamp recordings showing membrane rectification. During AP firing there is relatively short activation of voltage-gated K⁺ conductances. This limits the information about these conductances in simulated traces containing APs. Blocking APs with TTX allows injection of large amounts of current, leading to a good measure of membrane rectification. We have previously shown that membrane rectification allows extraction of semi-quantitative information on the conductance density at the site of a dendritic current injection (Schaefer et al. 2007). Thus, it may be possible to improve the second stage of the peeling procedure by adding data recorded after current injections at the dendritic site in addition to somatic stimulations.

The third stage of the optimization procedure constrained the dendritic gradient of voltage-gated Na⁺ conductances (Fig. 4). While the first two stages of the peeling procedure may benefit from expanding the training data set by dendritic current injection, this final stage does not. When current is injected via the somatic electrode, the passive decay of the membrane potential and the back-propagating AP both flow from the soma to the dendrite. When current is injected at the dendrite, the passive changes in the membrane potential decay in the forward direction, an AP is generated at the axon initial segment and back-propagates into the dendrite. This bi-directional potential propagation in the dendritic tree is poorly mimicked by voltage-clamping the dendritic recording site to the membrane potential waveform. Indeed, training the genetic algorithm with data generated by dendritic current injections failed to properly constrain the dendritic Na⁺ gradient (simulations not shown).

We have previously suggested an optimization scheme for a full compartmental model of a neurone using multiple voltage recordings from the soma, axon and dendrite as a training data set for the genetic algorithm (Keren et al. 2005). Comparing several cost functions, we concluded that a cost function combining the waveform of the membrane potential, the inter-spike interval and trajectory density is the most suitable for constraining a full compartmental model (Keren et al. 2005). We have shown here that to constrain a model for a single dendrite the point-by-point sum of squares is sufficient as a cost function (eqn (1)), as long as the somatic membrane potential is used as a voltage-clamp command and a parameter peeling procedure is applied. An interesting alternative to the peeling procedure requires the sampling of the membrane potential from many locations along the soma dendrites and axon (Huys et al. 2006). Unfortunately, the application of such massive parallel recordings of the membrane potential requires considerably better voltage-sensitive dyes than we have at present. A partial solution to recording the membrane potential from many locations on the dendritic tree is to optimize the compartmental model using extracellular potentials (Gold et al. 2007). While this approach is highly promising it is sensitive only to suprathreshold changes of the membrane potential and therefore has difficulty optimizing models displaying substantial subthreshold conductance activation, such as I_h.

Other numerical investigations have used a variety of optimization methods to constrain compartmental models. Approaches expanding the range of possible cost functions are the following: calculating the fiducial point of a data set (Ambros-Ingerson et al. 2008); applying multiple objective optimization to even the weight of different parts of the cost function (Druckmann et al. 2007; Druckmann et al. 2008); calculating the cost function from salient features of the recorded membrane potential (Eichler West, 1996; Vanier & Bower, 1999; Goldman et al. 2001; Golowasch et al. 2002; Waters et al. 2005; Achard & De Schutter, 2006; Druckmann et al. 2007, Druckmann et al. 2008; Günay et al. 2008); phase plane transformation of the membrane potential (LeMasson & Maex, 2001; Keren et al. 2005; Nowotny et al. 2008); and inclusion of morphological information in the cost function (Stiefel & Sejnowski, 2007). In addition to genetic algorithms, extremely valuable investigation of the dynamics of compartmental models have used grid searches in databases generated from a large number of simulations (Goldman et al. 2001; Golowasch et al. 2002; Prinz et al. 2003, Prinz et al. 2004; Taylor et al. 2006; Nowotny et al. 2007; Günay et al. 2008). Many of these investigations reveal that similar neuronal physiology may be obtained from diverse parameters. The results presented here suggest that the finding of large parameter manifolds is partly due to optimizing the model using only somatic membrane potential recordings as training data sets.

Experiment

It was important to us to design the numerical peeling procedure using realistic experimental constraints. One critical step in designing the experimental procedure was to assure complete blocking of the channels in each peeling stage. Severe errors may be introduced at various stages of the peeling procedure if the data are contaminated by a conductance that is not completely blocked, since the model assumes it is completely blocked. We chose to use only two blockers of voltage-gated channels, which can be considered relatively clean. For example, the complete replacement of Ca²⁺ with Co²⁺ totally eliminates all currents via voltage-gated Ca²⁺ channels. We resorted to this blocking protocol since even 100 μm Cd²⁺ did not block all the Ca²⁺ current in these neurones (A. Korngreen, unpublished observations). The TTX block of the voltage-gated Na⁺ conductance can also be considered a complete block.

Several experimental protocols may be considered for future refinement of the peeling procedure. First, the initial stage of the procedure may be split into two parts by blocking I_h with ZD7288. This will allow better estimation of both the passive parameters and the dendritic distribution of I_h. Second, as suggested by some of our simulations (Supplemental Fig. 2), it may be possible to extend the peeling procedure to constrain the dendritic conductance gradient of voltage-gated Ca²⁺ channels and thus provide a biophysical mechanism for dendritic Ca²⁺ spikes in L5 pyramidal neurones. Properly constraining the conductance gradient of voltage-gated Ca²⁺ channels may well require blocking the Ca²⁺ activated K⁺ conductances expressed in L5 pyramidal neurones (Kang et al. 1996; Benhassine & Berger, 2005, Benhassine & Berger,2008). To account for the activity of these Ca²⁺ activated conductances, the internal Ca²⁺ concentration in the vicinity of the membrane must be calculated, adding many unknown parameters to the model.

The model used in the initial section underwent several modifications to obtain the best fit with the experimental results. Even in the final version some parameters displayed large variation between cells (Fig. 6 and Table 2), particularly those describing the dendritic density gradient of the voltage-gated Na⁺ conductance (Fig. 6E). Replacing the kinetic scheme describing this conductance did not improve the variance of these parameters between cells. Interestingly, the variance of the entire set of parameters calculated within one cell was smaller than the variance of the same parameter between cells (compare Fig. 7B with Table 2). This inter-cell variability may reflect biological diversity between cortical pyramidal neurones. Alternatively, the inter-cell variability may result from a discrepancy between the kinetics of the conductances used in the model and the true kinetics. Such discrepancy was recently noted in a simulated study comparing the performance of an optimization procedure challenged by surrogate and experimental data (Druckmann et al. 2008). A considerably larger pool of neurones is required to allow a statistical analysis to differentiate between these two options.

While all the above investigations are needed to clearly dissect the origin of cell-to-cell variability, it is tempting to speculate that the variability is indeed of biological origin. This would fit our deterministic view of neuronal and cellular function, that many cellular parameters are constrained by cellular homeostasis to a narrow range, while others are modulated by various factors and external signals. Were this so, there would be less variation than suggested by simulations (Goldman et al. 2001; Golowasch et al. 2002; Prinz et al. 2003, Prinz et al. 2004; Taylor et al. 2006; Günay et al. 2008). Constraining a compartmental model of an invertebrate neurone using experimental traces has produced similar results and hypotheses (Nowotny et al. 2008).

Some of the parameters constrained by the peeling procedure could be compared to previous experimental findings. We have measured the conductance density gradient of the total voltage-gated K⁺ conductance in the apical dendrite of L5 pyramidal neurons (Schaefer et al. 2007). The peeling procedure predicted similar downward gradients for K_f and K_s (Fig. 6). Patch-clamp recordings suggesting that the Na⁺ conductance did not change as a function of distance from the soma provided a lower density estimate than the one constrained by the peeling procedure (Stuart & Sakmann, 1994). These recordings were carried out on P14 rats. Thus, it may be that the higher density obtained by the peeling procedure (Table 2) when fitting data recorded here from P42 rats is due to development. The average passive parameters obtained in this study (Table 2) were similar to parameters constrained by fitting a model to data recorded simultaneously from the soma and apical dendrite (Stuart & Spruston, 1998). Thus, it is possible to predict that the model constrained by the peeling procedure will have similar steady-state and EPSP attenuation to those recorded in the apical dendrite of L5 pyramidal neurons (Stuart & Spruston, 1998; Williams & Stuart, 2000; Berger et al. 2001) and predicted by compartmental modelling (Stuart & Spruston, 1998).

Our model describes only part of the physiology of L5 pyramidal neurones. The assumptions we used to apply the peeling procedure necessitated the use of the somatic membrane potential as voltage-clamp commands isolating the apical dendrite from the axonal AP initiation zone. In addition complete block of all voltage-gated Ca²⁺ channels was required. This enabled us to constrain the model for the apical dendrite and the model could provide a basic quantitative mechanism for the back-propagation of the AP in the apical dendrite and for fast dendritic Na⁺ spikes (Figs 9–12). The model predicted that the back-propagation of the AP in the apical dendrite is mostly achieved by activation of voltage-gated Na⁺ conductances, with a relatively small contribution from voltage-gated K⁺ conductances (Fig. 9). Moreover, the model was able to accurately reproduce the back-propagation of the AP (Fig. 10) and the depolarization of the resting membrane potential along the apical dendrite (Fig. 11). Due to the lack of voltage-gated Ca²⁺ channels it was not possible to simulate a dendritic Ca²⁺ spike. However, we were able to simulate dendritic Na⁺ spikes very similar to those observed experimentally (Stuart et al. 1997a; Zhu, 2000; Larkum et al. 2001). The simulations suggest that the generation of these dendritic Na⁺ spikes is due to the local activation of voltage-gated Na⁺ channels. The prolongation of the spike is mediated by a small resurgent Na⁺ current. These dendritic Na⁺ spikes are important for coincidence detection in the apical dendrite (Stuart & Häusser, 2001) and form the initial stage in the initiation of dendritic Ca²⁺ spikes (Schiller et al. 1997; Stuart et al. 1997b; Larkum et al. 1999a,Larkum et al. 1999b, Larkum et al. 2001; Zhu, 2000).

Outlook

Our study and other recent investigations (Prinz et al. 2003; Druckmann et al. 2007; Gold et al. 2007; Nowotny et al. 2007; Günay et al. 2008; Nowotny et al. 2008) clearly demonstrate the importance of constraining compartmental models using experimental recordings. One conclusion from these investigations is the crucial importance of correct selection of the training data set and the design of the correct cost function to reach verisimilar, and thus physiologically relevant, simulations of neuronal function. Much of the current flourish in the field of automatic construction of compartmental models stems from the rapid increase in computer power and the adaptation of simulation software to parallel computation (Migliore et al. 2006). The computational power available to us will probably continue to increase rapidly. Moreover, modelling of ion channel kinetics will increase in throughput (Willms et al. 1999; Gurkiewicz & Korngreen, 2007; Milescu et al. 2008) and there should be better integration with techniques from bioinformatics (De Schutter, 2008). This will allow investigators to increase the size of training data sets used to constrain compartmental models and to use better cost functions to compare the data with the model, thus permitting mechanistic explanations for many properties of excitable dendrites and of CNS neurones in general.

Supplemental material

Online supplemental material for this paper can be accessed at:

http://jp.physoc.org/cgi/content/full/jphysiol.2008.167130/DC1