Extensions and evaluations of a general quantitative theory of forest structure and dynamics

Abstract

Here, we present the second part of a quantitative theory for the structure and dynamics of forests under demographic and resource steady state. The theory is based on individual-level allometric scaling relations for how trees use resources, fill space, and grow. These scale up to determine emergent properties of diverse forests, including size–frequency distributions, spacing relations, canopy configurations, mortality rates, population dynamics, successional dynamics, and resource flux rates. The theory uniquely makes quantitative predictions for both stand-level scaling exponents and normalizations. We evaluate these predictions by compiling and analyzing macroecological datasets from several tropical forests. The close match between theoretical predictions and data suggests that forests are organized by a set of very general scaling rules. Our mechanistic theory is based on allometric scaling relations, is complementary to “demographic theory,” but is fundamentally different in approach. It provides a quantitative baseline for understanding deviations from predictions due to other factors, including disturbance, variation in branching architecture, asymmetric competition, resource limitation, and other sources of mortality, which are not included in the deliberately simplified theory. The theory should apply to a wide range of forests despite large differences in abiotic environment, species diversity, and taxonomic and functional composition.

Understanding the key forces that shape the structure, function, and dynamics of ecosystems is a fundamental goal of ecology (1–6). Current approaches to plant communities focus on questions such as what allows for species coexistence (7), why tropical sites have more species than temperate ones (8), and what environmental factors determine the structure, dynamics, and species composition of communities (9). Detailed models have been developed to integrate how species-specific traits “scale-up” to influence community and ecosystem dynamics (10, 11).

Here, we present a complementary but alternative approach. We use a few key principles to show how variation in resource supply together with general cross-taxa patterns of plant architecture and growth give rise to predictable emergent patterns of resource use, spatial structure, and demography. In our previous article (12) we incorporated these principles to derive the first part of a general quantitative theory for the structure and dynamics of a single-species stand. In this article we evaluate these predictions, using data from several tropical forests composed of multiple tree species including: (i) a 20-year record from Costa Rica (13); (ii) a 10-year time series from Panama; (iii) a 40-year survey from a Malaysian forest dataset; (iv) and a successional sequence of Costa Rican forests ranging from recently abandoned pasture to mature uncut forests (14) (for methodology and additional detail, see supporting information (SI) Text). We also elaborate and extend the theory to show how the critical assumption of resource and demographic steady state leads to empirically supported predictions for growth, mortality, succession, and whole-stand resource flux.

Our theory, which is an extension of a more general body of theory termed “metabolic scaling theory” (13, 15–19), shows mechanistically how plant growth and allometry influence size distributions and stand dynamics (15, 20–23). It deliberately makes several simplifying assumptions. In particular, the forest (i) can be modeled as a stand with no recruitment limitation, where recruitment begins with seedlings; (ii) is in resource (15) and demographic steady state (24), so that, on average, the total rate of resource use equals the rate of resource supply, birth rates equal death rates, and there is a stable distribution of ages and sizes; (iii) is composed of “allometrically ideal” trees which obey previously derived quarter-power allometric scaling laws (16) that govern how they use resources, occupy space, and grow.

Empirical Results and Theoretical Extensions

Size-Frequency Distributions.

Prediction: Number of stems scales as an inverse square law.

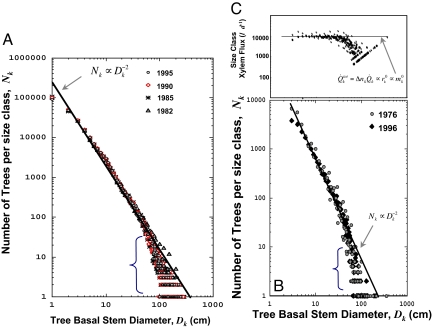
The theory predicts Δn_k ∝ r_k⁻², where Δn_k is the number of trees in the sample plot of standardized area in a given size class or bin, k, and with a stem radius, r_k, between r_k and r_k + Δr_k. With linear binning this gives the continuous frequency distribution, f(r) ≡ dn/dr ∝ r⁻² (see equation 9 and supporting information in ref. 12). As shown in Fig. 1 and Fig. S1, this inverse square law prediction is supported by data from Costa Rica, Malaysia, and Panama. Note that the exponent remains very close to −2 across several decades of time (see Table S1). Therefore, these forests remained close to demographic and resource steady state despite extensive turnover of individuals and substantial changes in species composition (see SI Text). Analysis of a large global dataset, for both temperate and tropical forests, also generally supports the −2 prediction (17, 25). Because stem radii exhibit the predicted scaling with mass, r_k ∝ m_k^3/8 (26, 27), these observations also confirm the predicted scaling of number of stems with mass: f(r) ∝ m^−3/4 (see supporting information in ref. 12). One caveat, discussed below, is that there are deviations from the exact predicted power function (17), especially for the largest trees.

Fig. 1.

Relationship between number of individuals or xylem flux for trees in differing size classes. (A) Size distribution for the 50-ha tropical rain forest on Barro Colorado Island, Panama. Data from surveys in 1982, 1985, 1990, and 1995 are shown. The plotted line has a slope of −2, the value predicted by our model. (B) Size distribution for the ≈16-ha tropical deciduous forest at San Emilio, Guanacaste, Costa Rica. The two forest surveys for 1976 and 1996 are shown. For the 1976 data, the diameter measures were rounded at the time to the nearest 1 cm, which is the likely reason for the observed variation. (C) Approximate invariance of the flux of water through the differing size classes of trees within the San Emilio Forest in 1996. Water flux determined from ref. 15. Note, for both forests, the increasing splay of variation for the largest tree sizes (bracketed regions), which likely reflects sources of mortality in addition to competitive thinning.

Energy Equivalence.

Prediction: The total energy and resource flux of all stems within a size class is independent of plant size when binned linearly with respect to stem radius.

As shown previously, both theoretically (16) and empirically (15, 28), the xylem flux of a tree, Q̇_k, scales as Q̇_k ∝ r _k² ∝ m_k^3/4. When combined with the inverse square law for the number of trees in a bin, Δn_k ∝ r_k⁻² ∝ m_k^−3/4, this predicts that the total resource flux per unit area per size class,

is invariant with respect to tree size. Note that in a continuum notation this invariance is expressed as the energy flux density per unit stem radius, Q̇(r)f(r), being independent of r. If the total xylem flux in a size class is proportional to the metabolic rate of a size class so that, Q_k^Tot ∝ B_k^Tot, then, given Eq. 1, the stand will express energetic equivalence. Fig. 1B shows that this prediction is supported by the data.* Again, however, the very small numbers of trees in the largest size classes result in systematic deviation of large trees from the expected invariance. With this qualification, these findings extend to trees within a stand, the energy equivalence relationship originally shown for different species of animals (29), different species of plants (15), and individual animals within a community (30).

Scaling of Nearest Neighbor Distance.

Prediction: The average distance between individuals within a size class scales linearly with trunk radius.

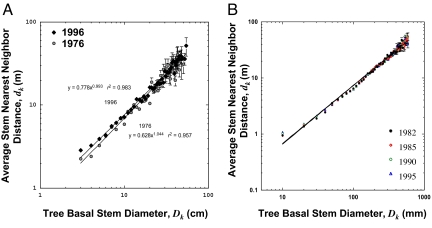
Given the inverse square law, the average distance between trunks of a given size, d_k, is predicted to scale isometrically, between size classes, with stem radius as d_k = c₁r_k. Spatial data from Costa Rica and Panama support this prediction (Fig. 2). Because this relationship has remained unchanged for several decades, despite substantial turnover of individuals, the macroecological size and spatial structure of these forests has essentially remained constant.

Fig. 2.

Nearest neighbor distance, d_k, as a function of diameter size class, D_k; multiple censuses are presented plotted for the forests on Barro Colorado Island (A) and the San Emilio (B). Data are binned at 1-cm increments. 95% confidence intervals for the mean of each size class, k, were calculated, but when sample sizes were large (smaller trees), they were often smaller than the plotted symbol. For each census of each forest ordinary least squares (OLS) regression fits to the data are not statistically different from the predicted value of 1.0, revealing a regular allometric packing rule for how trees fill space to use all available resources.

Spatial Scaling of Canopies.

Prediction: The dimensions and overlaps of tree canopies are governed by the allometry of individual trees and how they fill space within the forest.

Specifically, the theory predicts that canopy radii, r_k^can, and heights, h_k, of individual trees scale as r_k^can ∝ h_k ∝ r_k^2/3. Data from Costa Rica are in good agreement with these predictions (Fig. S2). Additionally, given the predicted scaling of canopy surface area, a_k^can ∝ r_k^4/3 (12), data from another study provides additional support (see figure 1c of ref. 31).^† These allometric scaling relationships for canopies, r_k^can = c₂r_k^2/3, together with the spacing of individuals, d_k = c₁r_k, predict the spacing of canopies, d_k^can = c₁r_k[1 − (r_k̄/r_k)^1/3], where r_k̄ = (2c₂/c₁)³, and c₁ and c₂ are scaling constants reflecting how individuals fill space and the geometry of the canopy, respectively (12). The degree of canopy overlap depends on the values of c₁ and c₂. In general, this predicts that canopy overlap decreases systematically with increasing tree size. Specifically, on average, canopies overlap until r_k > r_k̄, and then those of larger trees are increasingly separated (see equations 10 and 12 in ref. 12). For the Costa Rican forest shown in Fig. 1, c₁ ≈ 70 and c₂ ≈ 95 cm^1/3, so r_k̄ ≈ 30 cm. Thus, the theory predicts, and the data appear to confirm, that in this forest canopies are separated, on average, for trees larger than ≈30 cm in radius and ≈20 m in height. As discussed below, the spatial configuration of canopies will vary among forests, because c₁ and c₂ depend on local conditions, such as rates of resource supply and sizes of the largest trees. Nevertheless, the theory predicts the generic spatial structure shown by Davis and Richards (figure 3 in ref. 12) where canopies of small trees overlap and those of larger trees are increasingly separated.

Stand Dynamics and the Scaling of Mortality Rate.

Prediction: Stand mortality scales approximately as the −2/3 power of stem radius.

Our theoretical framework predicts that mortality and growth are inextricably linked, so it can be extended to predict steady-state stand-level mortality rate as a function of plant size. Mortality rate is defined as

where Δn_k^died is the number of trees in size class, k, that have died in time interval Δt. In steady state, as individuals grow and transition from the kth to the (k + 1)th class, an equal number in the (k + 1)th class must die, so Δn_k^died = Δn_k − Δn_{k + 1}. Thus, μ_k = [(Δn_k − Δn_{k + 1})/Δn_k]/Δt. With substitution, in continuum notation this becomes

This shows explicitly how the mortality rate is determined jointly by the size distribution f(r), which we have shown to originate from competition for resources and resulting space-filling, and the growth rate, dr/dt. Since the number of individuals scales as f(r) ∝ r⁻² this leads to μ = 2d ln r/dt.

Stem radial growth rate, dr/dt, is ultimately governed by metabolic rate (13). We previously derived a general growth equation for animals (18) in terms of mass:

where the parameters ā and b̄ are determined by fundamental biological energetics. Although there are some differences in detail, we assume that a similar equation holds for plants. Since, r = c_mm^3/8 where c_m is a constant, this growth equation can be combined with Eqs. 3 and 4 to give

Here, Ā = (3/4)āc_m^2/3 and B̄ = (3/4)b̄. This shows explicitly how stand-level mortality rate is determined by the fundamental energetic parameters ā and b̄. The growth equation was derived for animals where it gives excellent agreement with data (18, 19). Because of the presence of heartwood, and other nonliving tissues, which do not require energy for maintenance, it may not be strictly valid for plants. However, for trees up to a moderately large size, the first term in Eq. 5 dominates, reflecting the universal role of metabolic rate in fueling growth. So, dm/dt ≈ ām^3/4, which has been shown to be a good quantitative description of plant growth (32, 33) (see also ref. 34).

The growth equation, in terms of stem radius (13), is given by

Deviations are expected for small trees (34), where the exponent for metabolic rate is larger than ¾, leading to an increase >1/3 in the exponent (34). Nonetheless, general support for this prediction is given by Enquist et al. (13) and also by Russo et al. (35) who show that, for 56 New Zealand tree species, the average intraspecific stem growth exponent 0.284 (95% CI = 0.391–0.177) is indistinguishable from the predicted value of 0.333 (but see ref. 31). In a similar manner, the first term also dominates in Eq. 4 and thus, using the above relationships, gives

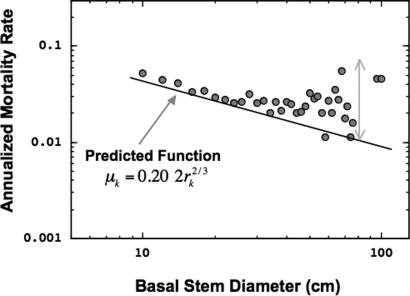
reflecting the primary role of metabolic rate via the coefficient Ā and the value of the exponent −2/3 in setting size-dependent rates of mortality. Consistent with the predictions of Eq. 6, several studies have reported decreasing mortality rates with increasing tree size in both temperate (36) and tropical (31) forests. We provide a more detailed test by measuring mortality rates as a function of tree size from the 1976 and 1996 censuses of the Costa Rican forest. As shown in Fig. 3, the data are in good agreement, but again, as expected, deviations are seen in the largest trees.

Fig. 3.

Relationship between tree size (measured as basal stem diameter, D_k, where D_k = 2r_k) and annualized mortality rate, μ_k, for tagged trees in the San Emilio forest. Size classes are binned at 1-cm resolution. The line, μ_k = D_k^−2/3, is the predicted mortality function based on scaling of growth and the allometric relationship between stem diameter and total biomass for individual trees in this forest (see Eqs. 7 and 8, and the SI Text). Whereas the observed data are generally close to the predicted curve, there is increasing variation and deviation for the largest trees, likely because of noncompetitive sources of mortality not included in the model.

Stand Demography Reflects Metabolic Allocation to Growth.

Prediction: The normalization of the mortality function is given by the energetics of plant growth.

The dominant parameter governing the scaling of stand mortality rate is the quantity Ā = (3/4)āc^2/3. Because the value of ā is determined from basic energetics (18, 33), the growth and mortality functions are, in principle, derivable from fundamental energetic parameters, allowing parameter-free quantitative predictions.

Enquist et al. (13) used the stem growth prediction given by Eq. 6 as a basis to understand variation in growth rates in tropical trees. We use their work to determine A, the normalization of the mortality function. Specifically, Eq. 6 can straightforwardly be solved to yield an equation for the growth of the trunk over any finite period between two sample periods, t to t₀, leading to r(t)^2/3 − r(t₀)^2/3 = (1/3)Ā(t − t₀). For a fixed time interval, t − t₀, a plot of r(t)^2/3 vs. r(t₀)^2/3 should yield an approximate straight line with slope 1, and intercept, I = (1/3)Ā(t − t₀). The value of Ā can be determined from

Growth data for tropical trees in the San Emilio forest in Costa Rica, taken over the time interval t − t₀ (= 20 years), confirmed a slope of approximate unity (13). For 45 species, the average value of the intercept I ≈ 0.68 cm^2/3, thereby predicting, Ā ≈ 0.10 cm^2/3 yr⁻¹ Therefore, in terms of trunk diameter, D = 2r, our predicted mortality function for a forest in steady state is given by μ ≈ 0.20 D^−2/3. This is plotted in Fig. 3 showing good agreement with data up to the largest trees.

Disturbance: Succession and Temporal Dynamics.

Prediction: Even when disturbed from steady state the successional trajectory of a stand is governed by the allometry of growth and mortality.

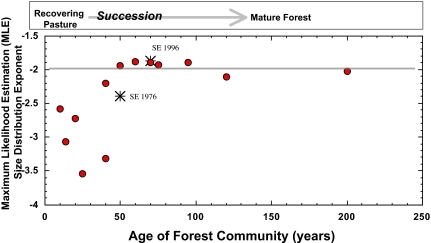
An important implication of our model is that a forest that conspicuously violates the assumption of steady state, because of a major recent disturbance, should deviate substantially from theoretical predictions. Over time, however, as new seedlings are recruited, grow, and fill space to reestablish a steady-state mature forest (3), the size distribution should converge asymptotically on the canonical form, f(r) ∝ r⁻² (see ref. 37). Fig. 4 shows a series of Costa Rican forests in various stages of recovery from disturbance, with steady state reached in ≈50–100 years. These data and previously published data on forest recovery from fire and other disturbances (37) support the predicted return to the inverse square law.

Fig. 4.

Dynamical behavior of the size distribution as a function of age since disturbance for tropical deciduous forests in Guanacaste, Costa Rica., The data are for 13 transects in forests of known and accurately estimated ages (see ref. 14). All forests <100 years are known to be recovering pasture land. The gray line is the exponent predicted once the forest has reached demographic and resource steady state. Plotted is the maximum likelihood estimate (MLE) for the power-law fit to the each of the forests through time. The star symbols are for the undisturbed San Emilio forest (see Figs. 1 and 2). After ≈50–80 years the forests appear to converge around the predicted exponent of −2.

Limiting Resource Supply, Stand Energetics, Biomass, Carbon Flux, and Mortality.

Prediction: The normalization of the size distribution (i.e., the density of similarly sized individuals) and mortality function can be derived from fundamentals of limiting resource supply and plant metabolism.

The size distribution, growth, and mortality of trees arise from the allometry of resource use (15). Given that the metabolic rate of an individual, B = b₀ r², where b₀ is a normalization constant, and the size distribution function, f(r) = c_nr⁻², where c_n is another normalization constant, the total energy use of the stand, per unit area, B_tot, is given by

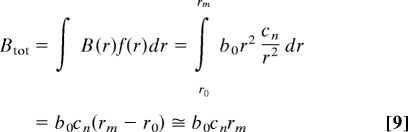where r₀ is the size of the smallest individual and r_m is the size of the largest individual. Eq. 9 shows that if r₀, is much less than r_m, then the total metabolic flux of the stand (carbon, water, etc.) is proportional to the size of the largest tree, r_m. In the case of a discrete distribution, the corresponding whole-community flux B_tot = (K + 1)N_kB_k, where N_k ≡ Δn_k /A_Plot is the population density, A_Plot is the area of the sampled stand, and K is the total number of size classes used to characterize the size distribution. Clearly, the total resource use of the stand, Ṙ_tot, is constrained such that Ṙ_tot ≤ Ṙ. So, at resource steady state, where Ṙ_tot ≈ Ṙ, these relationships lead to a generalized resource-based thinning law for individuals within a stand, which for the cases of discrete and continuous size distributions, respectively, can be written as,

Eq. 10 explicitly predicts that the normalization of the size distribution should increase with increasing rates of limiting resource supply, Ṙ, and decrease with increasing rates of mass-corrected metabolism, b₀ (see SI Text). So, the number of trees in a given size class, k, and the maximum tree size (see SI Text) should increase with Ṙ (38, 39), with additional predictable effects on rates of resource flux, mortality, and turnover of individuals. For example, combining Eqs. 10 and 3 implies that mortality rate, μ, should be directly proportional to rates of limiting resource supply, Ṙ. Several recent field studies appear to support a positive relationship between rates of resource supply and rates of mortality (38–41).

Similarly, our model can be extended to understand how plant metabolism, allometry, and resource supply can influence maximum tree size, total stand biomass, and other ecosystem level processes (see SI Text). For example, the model can be used to “scale up” from individual level metabolism and allometry, showing that total flux of energy, B_tot (and resources such as carbon, water, nutrients), scales nonisometrically with total stand biomass: B_tot = b₀ c_n(5c/3c_nM^Tot)^3/5 (see SI Text).

Discussion

Our model was designed to predict many features of a generic average forest with as few assumptions and parameters as possible. Model predictions of the model are generally well supported by data: the fitted R² values for many relationships are high. We are aware of no other simple analytical model that, with so few starting assumptions, predicts so many features of forest structure and dynamics with such accuracy. Our theory does not, of course, capture all of the variability in quantities such as size-frequency distributions and mortality rates. We point to three patterns of unexplained deviation. First, there are some expected deviations in the smallest trees, which are less numerous and hence further apart in space than predicted by the model (Fig. 2). This discrepancy is likely due to some combination of episodic recruitment resource limitation, (e.g., light), and deviation from predicted scaling of metabolic rate (34). Second, like earlier analyses of plant size-density relationships, the abundance of trees in the largest size classes shows systematic increasing variance in abundance and systematic deviation below the predicted inverse square law distribution. Third and related, the mortality rates of the largest trees also show increasing variance but higher values than the predicted mortality function (Figs. 1 and 4; see also ref. 42). These last two deviations are likely due to violation of the assumption that all mortality is due to competitive thinning. Other sources of mortality, such as herbivory, disease, lightning strikes, and wind damage likely affect most size classes, but their impact on the largest trees is particularly severe (23, 43). These deviations of empirical observations from predictions of the power law model have important implications. In principle, it should be possible to extrapolate from values of the largest trees to predict number of trees and rates of resource flux in smaller size classes as well as integrated whole-stand energy use and biomass (see SI Text). In practice, such extrapolation from the empirically measured numbers and sizes of the largest trees is hazardous and could give seriously incorrect values. The inverse square scaling of number of stems means that the relatively small number of trees in the largest size classes dominate in determining the total resource flux and biomass of a stand. The smaller number of trees in these largest size classes than predicted by the power law model means that extrapolation to smaller size classes or an entire stand will often give misleading predictions.

These observed deviations point to two kinds of important details that will need to be included to produce a more accurate detailed model (see also discussion in ref. 44). First, the model assumes that seedling recruitment is not limiting and is spatially uniform throughout the forest. However, for seedlings and saplings, spatial variation in light, nutrients, water, and locations of other conspecific and heterospecific individuals, and temporal variation in seed rain, germination, and seedling survivorship may be particularly important. Second, our model assumes that all mortality is a consequence of size-based density-dependent competitive thinning and the rate of mortality depends on the rates of plant growth (basically the steady-state assumption). As mentioned above, however, there are other sources of mortality and many of these differentially affect trees of larger size (23, 43). Deviations from model-predicted baselines may allow quantification of density independent and size-selective mortality (see Fig. S3). Additional sources of mortality or limitations to recruitment could be included in the model as additional terms. Indeed, Clark (23) outlines a framework for such a more detailed theory.

Recently, Coomes et al. (45) and Muller-Landau et al. (42) argued that “Demographic Theory” (21, 24, 46) is a better alternative to metabolic scaling theory for understanding size distributions, because there may be deviations from the power-law behavior. We disagree and emphasize three points:

First, our zeroth-order model builds on a rich literature on self-thinning in plant ecology (see refs. 20–23 and references within) by starting from the general principles of metabolism and allometry that are shared across most plants to then predict the primary constraints on stand dynamics. Consequently, it requires no additional fitted parameter values to predict: (i) the allometry of plant growth (33); (ii) the steady-state distribution of tree sizes (Eq. 8); and (iii) the mortality function (Eq. 6). These predictions are possible because metabolism fuels growth and powerfully constrains plant form, which in turn determines the size distribution and scaling of competitive mortality (22, 23). In contrast, “Demographic Theory” does not predict either size-dependent growth or mortality but instead uses these as input parameters to then generate the size distribution. However, since, at steady state, the size distribution must necessarily result from size-dependent growth and mortality (21), “Demographic Theory,” is arguably phenomenological. Although Demographic Theory is complementary to our approach and does provide predictions for the pattern and timescale of how a plant canopy reaches its steady-state structure from a given initial condition (47), it does not provide a clear mechanistic basis for the origin of size distributions.

Second, our framework can reveal the influence of factors in addition to metabolism and allometry, because these will appear as deviations from predictions of our deliberately simplified model. So, for example, deviations from the predicted mortality function may allow mortality to be partitioned between competitive density-dependent and noncompetitive density-independent sources (see ref. 23 and Fig. S3).

Third, our model provides a conceptual foundation that can be fleshed out with additional idiosyncratic detail, as needed, to account for site- or taxon-specific phenomena [such as excessive herbivory (45), disturbances by fire or elephants (42), etc.]. The size-specific deviations in abundance and mortality reported by Muller-Landau et al. (42) and Coomes et al. (45) (and also observed in our analyses here), rather than providing evidence against metabolic theory, instead illustrate the value and promise of a general theory based on fundamental mechanistic features of an idealized forest.

The generality and power of the theory can be attributed to its focus on two fundamental biological phenomena: metabolism and allometry. Together they determine how resources are taken up from the environment, translocated and transformed within the plant, and allocated to survival, growth, and reproduction (48). These processes of individual trees then “scale up” to generate emergent properties of forests, such as size structure, spacing relations, and growth and mortality rates. For example, our theory quantitatively shows how size-specific rates of mortality are mechanistically linked to size-specific rates of metabolism and growth. The effects of additional variables and processes can be included in more detailed models, leading eventually to a conceptually unified and broadly applicable metabolic theory of plant ecology.

Materials and Methods

Long-Term Forest Dynamic Plots.

The Costa Rican forest was censused in 1976 and 1996. Measurements of woody plant basal stem diameter (diameter at breast height, dbh) were recorded within a permanently marked study plot of seasonally dry tropical forest (10°45′ N, 85°30′ W) within sector Santa Rosa, Area de Conservacíon, Guanacaste (ACG), of northwest Costa Rica (49–51). In 1976, S. P. Hubbell mapped all woody plant stems ≥3 cm dbh within a continuous 680 m × 240 m (16.32 ha) area of forest. By using an identical mapping protocol, a second remap of the San Emilio forest was completed between 1995 and 1996 by B. J. Enquist and C. A. F. Enquist (13). In total, 46,833 individuals were surveyed, 26,960 in 1976 and 19,873 in 1996. Together, the two surveys document 20 years of growth and population change within a local community.

The Panamanian Forest, Barro Colorado Island (BCI) was surveyed at ≈5-year intervals starting in 1985. The BCI forest is 50 ha in size and each census includes ≈230,000 individuals. At BCI all stems ≥1 cm dbh were surveyed. Sampling protocols and plot details for this forest are listed in the methods listed in refs. 52–55.

The Malaysian forest was censused in 1947 and 1981, allowing a comparison of size structure over an even longer period (34 years) as reported in Manokaran and Kochummen (56). The Malaysian plot is 2.02 ha in area. During the study period, although many of the study species did not show changes in density, eight of the more common species showed significant changes in dominance during this time period (56).

A description, background, and discussion of the mortality rate and succession data are given in SI Text.

Plant Allometry and Regression Statistics.

The relationship between stem diameter, tree height, and canopy radius was measured for 151 individuals, ranging from saplings to emergent trees, and included 38 of the more dominant species in the forest. Measurements were made by B.J.E. within the San Emilio forest in Guanacaste Costa Rica during the summer of 1999. Height, h_k, was calculated by trigonometry. Canopy radius, r _k^can, was measured from the center of the stem out to an average canopy distance. As there is likely measurement error in both the x and y axes, regression parameters were estimated by using model II or reduced major axis (RMA) regression. For each size distribution, the maximum likelihood estimate (MLE) of the power function exponent was calculated. A detailed description on the MLE for the power function is given in the SI Text.