First-principles design of nanomachines

Abstract

Learning from nature's amazing molecular machines, globular proteins, we present a framework for the predictive design of nanomachines. We show that the crucial ingredients for a chain molecule to behave as a machine are its inherent anisotropy and the coupling between the local Frenet coordinate reference frames of nearby monomers. We demonstrate that, even in the absence of heterogeneity, protein-like behavior is obtained for a simple chain molecule made up of just 30 hard spheres. This chain spontaneously switches between 2 distinct geometries, a single helix and a dual helix, merely because of thermal fluctuations.

Significant advances in laboratory techniques for tailoring and processing materials at the atomic scale have resulted in nanotechnology becoming an increasingly mature field with great promise. One of the exciting goals of the field is the design of powerful machines, such as functional entities that can switch reversibly between distinct geometries (1–4). Such machines would not only be of great use on their own but also could yield novel emergent behavior upon networking them together (5). The existence of life in its myriad forms provides a proof-of-concept of what one might aspire to accomplish with nanotechnology.

Proteins are complex water-soluble chain molecules made up of tens or hundreds of 20 types of naturally occurring amino acids and exhibit conformational switching (6) triggered by influences such as ligand binding. At the nanoscale, thermal fluctuations yield forces with magnitudes comparable with those involved in chemical reactions catalyzed by the proteins (7). How might one design a machine whose functionality is structure based? In its simplest form, we seek an object that takes on just a few distinct geometries in a reproducible manner and is able to switch reversibly between them because of thermal fluctuations. Such a situation would allow external stabilizing influences to favor a given conformation over the others and allow for the development of powerful machines at the nanoscale.

A collection of hard spheres constitutes the simplest model of matter and exhibits both a crystalline phase and a fluid phase on varying the density of spheres (8). A linear chain of hard spheres is the simplest connected object with the fewest constraints and, thus, the greatest flexibility (9). Such a chain, at high temperatures or when there are no interactions promoting compaction, would occupy a random-coil phase in which all self-avoiding conformations are equally likely. This situation is not conducive for machine design. In the presence of intersphere interactions promoting compaction and when there are no frustrating influences from the sphere tethering, one would expect a generic compact phase in which, at least locally, the preferred conformation is that of a face-centered cubic (fcc) lattice. It was conjectured by Kepler, and proven more recently by Hales, that the fcc structure provides for optimal packing of unconstrained spheres (10). There is a high degeneracy of compact conformations with no assurance that any given conformation will be reached from a random coil conformation rapidly and reproducibly. Again, this situation is not conducive for the design of machines.

Of course, what one requires is a phase of matter with much fewer ground-state conformations than either the random-coil or generic compact phase. Additionally, one needs a phase that is in the vicinity of a phase transition (or cross-over for finite size systems) to a distinct phase, because that provides for exquisite sensitivity to the right types of external influences. Our thinking is guided by the liquid crystal phase (8), which is a distinct state of matter that is poised in the vicinity of the liquid phase. This phase is known to be one of the most sensitive phases of matter. The liquid crystal phase opens up because of the anisotropy of the constituent molecules—there is no longer a need for simultaneous ordering in all 3 directions. Rather, one can have translational order in fewer than 3 dimensions along with orientational order. Here, we address the issue of how one might open up a distinct phase with relatively few ground-state conformations in the vicinity of the random-coil phase. Such a phase would then be the analog of a liquid crystal phase but this time for chain molecules.

Armed with insights from the liquid crystal phase and the behavior of proteins, we identify 2 mechanisms for thinning the number of candidate ground-state structures and demonstrate that these are sufficient for the creation of the sought-after behavior. One can define a Frenet reference frame (a local Cartesian coordinate system) at each location of the chain molecule composed of the tangent, the normal, and the binormal as the orthogonal coordinate axes. These coordinate systems play a crucial role in at least 2 ways, as can be readily seen in the protein context: First, the chemistry of hydrogen bonds and other chemical features yield constraints on the relative orientations between the coordinate systems associated with pairs of amino acids in contact; second, the side chains of amino acids are located in a specified direction with respect to these coordinate systems—for example, the amino acid side chains are typically pointed approximately in the outward normal direction. Indeed, both the α-helix and the β-sheet allow for the placement of side chains in a manner that avoids steric clashes.

The first mechanism follows from the observation that a model of a chain composed of spheres is unable to capture the inherent anisotropy induced by the presence of the chain constraint—at each location of the chain, there is a tangent direction defined by the 2 adjacent objects. Thus, the simplest model capturing the correct symmetry is one in which the constituent monomers are no longer isotropic. We therefore allow for the overlap of van der Waals spheres of adjacent monomers along the chain. Such an overlap overtly breaks the isotropy of the spheres and confers uniaxial anisotropy to the chain. In both the emergent building blocks of protein structures, α-helices and β-sheets, nearby segments are placed right up against each other and aligned parallel to each other, reflecting the anisotropy. In a protein, the distance between neighboring C^α atoms is 3.8 Å, requiring that the radius of the backbone of an amino acid be >1.9 Å. This constraint is easily met by considering the van der Waals radii of the constituent atoms. For example, one would estimate (11) that the smallest amino acid, glycine, has a radius >2.4 Å. Second, we study the effect of attaching side chains to the backbone monomer, e.g., in the negative normal direction. The self-avoidance of these side spheres with each other and with the backbone spheres results in an induced coupling between pairs of Frenet frames. Such a coupling is also realized in tube-like or thick polymers (12).

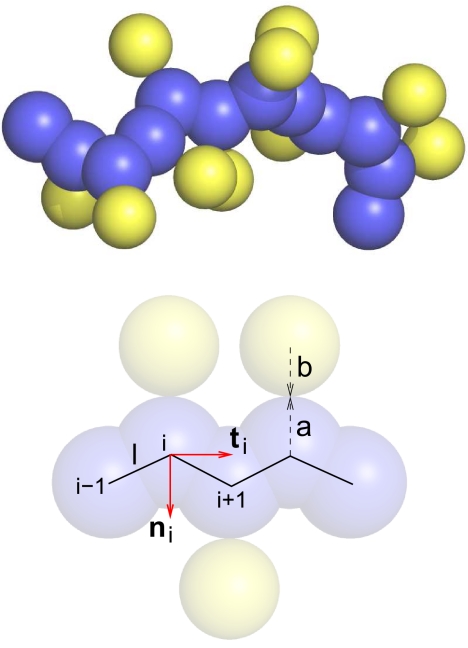
We find that each of these features results in the creation of a distinct intermediate phase for short chains sandwiched between the generic compact phase and the random-coil phase. Furthermore, when the 2 features are combined, the phase is stabilized and occupies a larger region in parameter space. For our simplified model of a chain of backbone spheres (Fig. 1) with a sphere separation along the sequence of 3.8 Å, we have 3 length parameters: the radius a of the backbone spheres, the radius b of the side spheres, and the cut-off scale R_c for the pairwise attractive interaction potential ε/k_B between the backbone spheres (see Materials and Methods). In the absence of side spheres and for nonoverlapping backbone spheres, a ≤ 1.9 Å, there is a cross-over from a random-coil phase (in which the conformations are mostly extended) to a globule phase in which one has compact conformations with no distinct motifs such as helices. The situation becomes qualitatively different upon incorporating 1 or both of the 2 key features.

Fig. 1.

Sketch of the chain molecule. The backbone is modeled as a chain of (dark color) spheres of radius a with a separation along the chain l = 3.8 Å. The nearest-neighbor spheres along the backbone are allowed to overlap with each other, thereby overtly introducing uniaxial anisotropy. t_i and n_i are the tangent and normal vectors assigned to each sphere i, except to those at the ends of the chain. Side spheres (shown in light color) of radius b are attached to the backbone spheres in the negative normal direction. The side spheres are not allowed to overlap with either the backbone spheres or with each other.

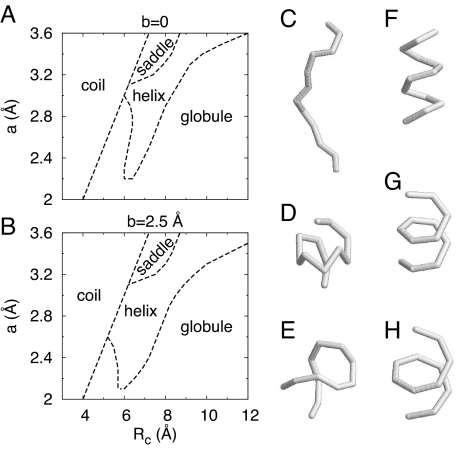
Fig. 2A shows the T = 0 phase diagrams in the a–R_c plane for a N = 12 chain. Distinct phases, corresponding to helical and saddle-like conformations, emerge between the coil and the globular phases analogous to the opening up of a liquid crystal phase between the liquid and crystalline phases for anisotropic molecules (8). The saddle can be thought of as a piece of a dual-helix structure and does develop into a dual helix for longer chains. (The dual helix is distinct from the double helix because the former is a conformation of a single chain, whereas the latter is composed of 2 chains.) These phases have a lower entropy than both the globule and random-coil (swollen) phases but are stabilized by the attractive interaction potential. We also find that the presence of side spheres even without overlap of the backbone spheres induces helical conformations [supporting information (SI) Fig. S1]. This effect is accentuated when both features are present simultaneously (Fig. S2). Interestingly, conformations composed of nearly parallel strands similar to those in β-sheets can be obtained by adding a bending energy into the model (Fig. S3).

Fig. 2.

Phase diagram of chain molecules made up of spheres. (A and B) The phase diagrams at T = 0 in the a–R_c plane for chains of length N = 12 without side spheres (b = 0) and with side spheres (b = 2.5 Å), respectively. The intermediate compact phase arises on the edge of compaction of the chain molecule when R_c becomes sufficiently large to allow the attractive interaction to be effective. The vicinity of this phase to other phases (it is sandwiched between 2 distinct phases) confers sensitivity to structures in the intermediate compact phase. (C–H) Typical ground state conformations: a random coil conformation obtained with R_c < 2a (C), a globule conformation obtained with a = 2.5 Å, R_c = 9 Å (D), a saddle conformation obtained with a = 3.2 Å, R_c = 7 Å (E), several helix conformations with different pitch to radius ratios obtained for a = 2.6 Å, R_c = 6.4 Å (F), a = 3.2 Å, R_c = 8 Å (G), and A = 3.4 Å, R_c = 9 Å (H). The helical and saddle ground-state conformations in the model with no side spheres are retained even when side spheres are present (b = 2.5 Å). However, the side spheres eliminate several random-globule and random-coil conformations, thereby stabilizing the intermediate compact phase.

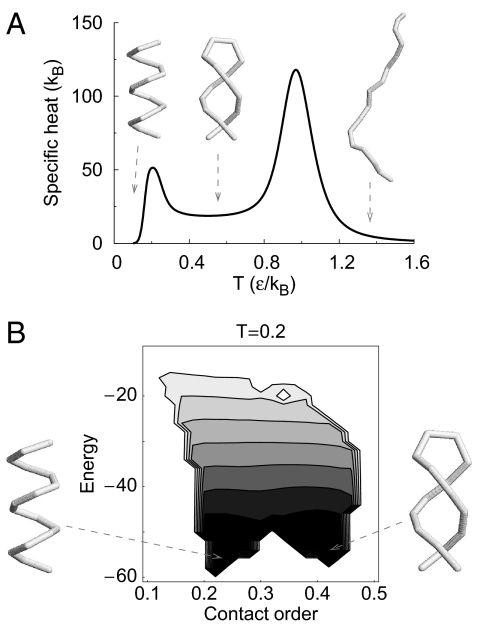
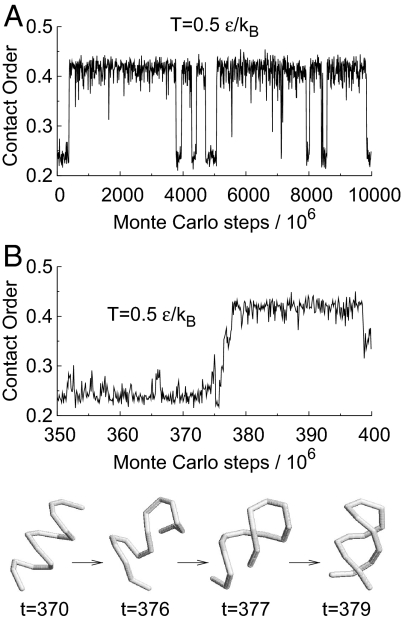
We now consider an even shorter system (N = 16) with an enhanced overlap of the backbone spheres: a = 3.0 Å. The radius of the side sphere is chosen to be b = 2.5 Å, and the range of attraction is now increased to R_c = 7.5 Å. These parameter values yield a helix ground state but are close to a cross-over to the dual-helix state. Fig. 3A shows that the specific heat has 2 peaks corresponding to 2 cross-over temperatures, T₁ ≈ 0.2ε/k_B and T₂ ≈ 0.97ε/k_B. At the lowest temperatures, the helix is the dominant conformation. At intermediate temperatures, one obtains the dual-helix structure, whereas, at higher temperatures, one obtains a random coil. Fig. 3B shows the contour plots of the free energy on the energy–contact order plane at T₁ and exhibits pronounced minima corresponding to the single helix and dual helix. The helix is a bit lower in energy, whereas the dual helix is entropically more favorable. The free-energy barrier for the switching at T₁ is ≈4ε, which is equivalent to the energy required to break 4 contacts. This barrier is significantly higher than k_BT₁, and the 2 helical conformations are each quite stable at this temperature. Quite remarkably, our Monte Carlo (MC) simulations with standard pivot and crankshaft move sets show a dynamical switching between the 2 conformations in a single trajectory at a somewhat higher temperature of T = 0.5ε/k_B. The system is bistable with a rapid switching between distinct conformations (for examples of molecular switches, see refs. 1–4) with little weight for intermediate conformations (Fig. 4). Note that the switching can also be easily effected by means of an external influence that is sensitive to the chain end-to-end distance.

Fig. 3.

Multiple specific heat peaks corresponding to 3 distinct phases. We study a chain of N = 16 with a = 3 Å, b = 2.5 Å, and R_c = 7.5 Å. (A) The temperature dependence of the specific heat indicates 2 peaks—one at T ≈ 0.2 ε/k_B and another at T ≈ 0.97 ε/k_B. The lower temperature peak indicates a cross-over into a single-helix conformation from a dual helix, whereas the peak at the higher temperature indicates a cross-over between the dual helix and the random-coil phases. (B) Contour plot of the effective free energy as a function of energy and contact order (CO) at the lower transition temperature. CO is defined as the sum over sequence separation of all contacts divided by the product of the number of contacts and N. The effective free energy at a given temperature T is determined as ℱ(E, CO) = −k_BT lnP(E, CO), where P(E, CO) is a weighted 2-dimensional histogram for that temperature obtained by using the multiple-histogram method (25). The unweighted histograms at multiple temperatures are collected through parallel tempering (26) MC simulations. The free-energy difference between consecutive contour levels is 4ε. The contour plot shows 2 minima corresponding to the single helix and the dual helix as indicated.

Fig. 4.

Dynamical switching between the single helix and the dual helix. (A) A long MC trajectory, with standard pivot and crankshaft move sets (27), at T = 0.5ε/k_B, shows frequent switches between the single helix (lower contact order) and the dual helix (higher contact order). The chain studied here is the same as in Fig. 3. Both the single and the dual helix have similar energies. (B) Similar to A but for a much smaller window of time steps and with higher resolution, showing a single switch from the single helix to the dual helix. The bottom figures are the snapshots during the switch at times t (in units of 10⁶ steps) as indicated.

It is important to note that the ease with which one obtains this system without any fine-tuning of details is made possible by the existence of the intermediate phase. The conformations in this phase are in the vicinity of the random-coil phase while retaining order because of the proximity of the compact phase. This results in special sensitivity to small perturbations induced, e.g., by thermal fluctuations that, in the example presented here, are responsible for the switching between 2 distinct geometrical shapes. Unlike the random-coil conformations that can switch from one to another easily because of thermal fluctuations, the structures in the intermediate phase exhibit some stability. At the same time, the structures are not so densely compact that they are subject to sluggish dynamics and kinetic inaccessibility characteristic of the glassy phase. These distinct advantages of the intermediate phase have a wider applicability than for chain molecules as evidenced by the sensitive liquid crystal phase sandwiched between the crystalline and liquid phases. In liquid crystals, the anisotropy arises from the asymmetric shape of the constituent molecules, whereas here, the anisotropy is a natural consequence of the chain topology of the molecule. Interestingly, earlier computational studies (13, 14) had found that overlapping adjacent monomers yield helical conformations. Also protein-like folds are adopted by a host of nonbiological polymers (15–21) (see Appendix).

Understanding the properties of matter is greatly simplified upon using the concept of its phases (8). For example, a liquid possesses certain gross properties, such as adopting the shape of the container and its ability to flow, irrespective of its constituent molecules and their underlying chemistry. Globular proteins share a great deal of common characteristics—they are all linear chains of the same 20 aa, and they fold rapidly and reproducibly into their native state structures; these structures are made up of emergent building blocks in the form of helices and almost planar sheets; the total number of distinct folds that proteins adopt is limited in number (22, 23) much as the number of space groups associated with Bravais lattices (8) is 230; proteins are flexible and versatile in their folded state; and proteins have a tendency to aggregate and form amyloid, which in turn, is implicated in debilitating human diseases. These common attributes of proteins suggest that protein structures occupy an intermediate phase of matter (12, 24) that confers on them their many amazing characteristics.

Whitesides wrote (5) that one ought to “take existing nanomachines—those present in the cell—and learn from them. We will undoubtedly be able to extract from these systems concepts and principles that will enable us to make variants of them that will serve our purposes, and others that will have entirely new functions.” The phase of matter so successfully used by nature as the basis of life is ready to be exploited in the laboratory.

Materials and Methods

We consider chains of N hard spheres each of radius a. The beads spacing along the chain is fixed to be l = 3.8 Å. Nonconsecutive spheres are not allowed to overlap, whereas the neighboring spheres along the chain can overlap when a > 1.9 Å. Nonconsecutive spheres interact via a pairwise square-well potential equal to −ε within a contact range R_c. A Frenet frame of reference is assigned to each sphere i, except to those at the ends of the chain. The tangent vector t̂_i in this frame is a unit vector tangential to the circle passing through the centers of beads i − 1, i, and i + 1. The Frenet normal vector n̂_i is an unit vector pointing to the center of this circle. The third vector of the frame is the binormal vector, denoted by b̂_i, and is defined to be the cross-product of the tangent and the normal vectors. A side sphere of radius b is attached to each backbone sphere in the direction opposite to the normal, with the distance between the centers of the backbone sphere and its side-sphere partner equal to a + b. The backbone spheres at the 2 ends of the chain do not have any side spheres attached to them. The role of the side spheres is entirely steric—they are not allowed to overlap with any of the other spheres in the system. The energy of the chain in given conformation can be written as

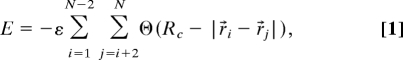where r⃗_i are center positions of the backbone spheres, N is the number of such spheres, and the step function Θ(x) is equal to 1 if x > 0 and 0 otherwise.

We employ a parallel tempering (24) MC scheme for obtaining the ground state as well as other equilibrium characteristics of the system. The simulation entails monitoring 20–30 replicas, each evolving at its own selected temperature T_i. For each replica, the simulation is carried out with the standard pivot and crankshaft move sets (27) and the Metropolis algorithm for move acceptance. In a pivot move, one randomly chooses a sphere i in the chain and rotates the shorter part of the chain (either from 1 through i − 1 or from i + 1 through N, where N is the number of spheres in the chain) by a small angle and about a randomly chosen axis that goes through the ith sphere. In a crankshaft move, 2 spheres i and j are chosen randomly such that ∣i − j∣ < 6, and the spheres between i and j are rotated by a small angle and about the axis that goes through i and j. In both move sets, the rotation angle is randomly drawn from a Gaussian distribution of zero mean and a dispersion of 4°. An attempt to exchange replicas i and j is made every 100 MC steps. The exchange is accepted with a probability equal to p_ij = max{1,exp[k_B⁻¹(T _i⁻¹ − T _j⁻¹)(E_i − E_j)]}, where k_B is the Boltzmann constant, and E_i and E_j are the energies of the replicas at the time of the exchange. The weighted multiple-histogram technique (25) is used to compute the specific heat and the effective free energy.

Appendix: Protein-Like Folds Are Adopted by a Host of Nonbiological Polymers

Poly(diacetylene)s can form multiple-helical superstructures (15) such as double-helical ribbons. Poly(ethylene glycol) (PEG) has been shown to assume a helical conformation in isobutyric acid with a trace amount of water, without which PEG forms a coil configuration (16, 17). PEG also forms helices in isopentanoic and n-propanoic acids but not in isobutanol or 1-butanol (16). In isobutyric acid, PEG forms a mixture of helices and coils, whereas a similar polymer poly(ethy-lene imine) (PEI) merely forms helices. Phenylacetylene oligomers of specific chain lengths (up to 18 units) and containing a tri(ethylene oxide) side-chain segment at each repeat unit have been found to undergo sharp switching between arrays of random coils and arrays of helical conformations upon changing the solvent composition (18). Another interesting example is provided by poly(ethylene oxide) (PEO) dissolved in an electrolyte consisting of a lithium salt (18), LiCF₃SO₃. In the crystalline phase of the system, the PEO chains are helical and form parallel arrays. In the amorphous phase, the arrays dissolve into separate helices. Finally, there are several examples of synthesis of helical polymers that are discussed by Sanda et al. (20) and that include polychloral, polyisocyanates, polyisocyanides, polisilanes, and polycetylenes. Such helical structures can be made to have adjustable geometry and can then used to generate nanocavities of tunable sizes (21). Sanda et al. (20) have recognized that the crucial factor for the synthetic polymers to adopt the helical structures is the steric repulsion between the side chains combined with attraction that is usually provided by hydrogen bonding.