Superconducting characteristics of 4-Å carbon nanotube–zeolite composite

Abstract

We have fabricated nanocomposites consisting of 4-Å carbon nanotubes embedded in the 0.7-nm pores of aluminophosphate-five (AFI) zeolite that display a superconducting specific heat transition at 15 K. MicroRaman spectra of the samples show strong and spatially uniform radial breathing mode (RBM) signals at 510 cm⁻¹ and 550 cm⁻¹, characteristic of the (4, 2) and (5, 0) nanotubes, respectively. The specific heat transition is suppressed at >2 T, with a temperature dependence characteristic of finite-size effects. Comparison with theory shows the behavior to be consistent with that of a type II BCS superconductor, characterized by a coherence length of 14 ± 2 nm and a magnetic penetration length of 1.5 ± 0.7 μm. Four probe and differential resistance measurements have also indicated a superconducting transition initiating at 15 K, but the magnetoresistance data indicate the superconducting network to be inhomogeneous, with a component being susceptible to magnetic fields below 3 T and other parts capable of withstanding a magnetic field of 5 T or beyond.

Superconductivity in carbon nanotubes (CNTs) is a topic of intriguing interest (1–11). While the small-diameter nanotubes are predicted to have enhanced electron-phonon coupling (3)—a key element responsible for nanotube superconductivity– the associated increase in fluctuation effects is unfavorable to the manifestation of a superconducting transition. The possibility of a Peierls transition in thin nanotubes is a further deterrent to superconductivity (12–17). It follows that the existence of coupling between the nanotubes is important to the realization of its superconducting behavior, since the transverse coherence can suppress fluctuations and lower the Peierls transition temperature, thereby making the appearance of a superconducting transition possible. Owing to its ordered and closely-spaced pore structure (with a 13.6-Å center-to-center separation between the 0.7-nm diameter pores), the AFI zeolite (composition: Al₁₂P₁₂O₄₈) with embedded 4-Å carbon nanotubes constitutes an ideal material for the observation of nanotube superconductivity. Indeed, the Meissner effect, a superconducting gap variation as a function of temperature, and the fluctuation supercurrent were observed in these nanocomposites (1), with a transition temperature of 15 K. However, the superconducting resistive transition was not observed.

By increasing the carbon nanotube content with enhanced sample uniformity, we report the carbon nanotube superconducting specific heat transition at 15 K. The specific heat transition is fully suppressed at >2 T. Theory-experiment comparisons show consistent behavior for an inhomogeneous type II superconductor with ≈80 nm clusters of nanotubes weakly linked to form a bulk superconducting composite. Four-terminal resistive data and differential resistivity measurements both show a clear superconducting transition at 15K, but they also point to the existence of a phase incoherent fluctuating superconducting condensate in nanotubes at 5 T or above.

Results

Samples.

AFI zeolite crystals (≈100 μm in diameter and 500 μm long) containing the tripropylamine (TPA) precursor were first heated at 580 °C in 0.7 atm of nitrogen and 0.3 atm of oxygen for 8 h to remove the TPA, and then in 0.7 atm nitrogen and 0.3 atm of ethylene at the same temperature for 8 h. This method of heating is noted to differ from the earlier approach in which the nanotubes were obtained from direct conversion of TPA through heating the crystals in vacuum (18–20). In the present approach, the nanotubes were converted from ethylene instead of the original TPA. As such, the possibility of unintentional nitrogen doping (as TPA contains nitrogen) is minimized. The heated crystals were characterized by Raman spectra (with laser wavelength of 514.5 nm), as shown in Fig. 1. Two peaks, one at 510 cm⁻¹ and one at 550 cm⁻¹, are noted by arrows. They respectively correspond with the (4, 2) and (5, 0) carbon nanotubes' radial breathing modes (RBM) as determined by resonant Raman measurements and first-principles calculations (21). The magnitude of the RBM, relative to the G-band carbon-carbon Raman signal at 1,600 cm⁻¹, is significant as it provides evidence (apart from the ratio of coupling strengths) of the percentage of the carbon in nanotube form. We have done a statistical comparison of the 2 methods of heating. In the inset of Fig. 1, the proportion of the 550 cm⁻¹ peak (delineated by green bars) is seen to be ≈10% of the G-band signal after subtracting the background, significantly higher than the ≈5% average RBM signals observed in the vacuum heat-treated samples (delineated by red bars). The superconductivity is attributed to the (5, 0) carbon nanotubes.

Fig. 1.

Comparison of the Raman spectra for the old (delineated by the red curve) and the current (delineated by the green curve) heating processes. The Raman excitation wavelength is 514.5 nm. The RBM ratio to the G band is nearly doubled for the current process. For clarity, the 2 spectra are vertically displaced from each other. Inset: Proportion of the samples exhibiting the various RBM ratio to the G band.

The sample for the specific heat was prepared by aligning the heated AFI crystals along their c-axis and using GE7031 varnish to glue them together into a 3 × 3 × 0.5 mm platelet, with a total weight of 7.9 mg, in which 5.2 mg was the weight of the crystals. The measurements were carried out by using the standard AC technique (22) where the sample was attached to a suspended sapphire chip with deposited resistive Joule heater. An AuFe/Chromel thermocouple was attached to the chip to measure the temperature modulation of the chip relative to a thermal reservoir. The field dependence of the thermocouple's sensitivity was calibrated very precisely in a subsequent experiment using an Ag calibration sample. To achieve sufficient relative resolution in the measurement of the AC voltage from the thermocouple, a picovolt amplifier, which is free of 1/f noise, in combination with a digital lock-in amplifier was used, and the measurements were performed during slow temperature sweeps of 0.02 K/min at a time constant of 10 s and a modulation frequency of ≈1.5 Hz. The AC measurements were combined with a “long” relaxation technique to achieve an accuracy of the total heat capacity determination of <1%. The contribution of the 2.7 mg of dried varnish was corrected using literature data (23). Measurements were performed in magnetic fields of 0, 0.4, 1, 2, and 5 T, applied both parallel and perpendicular to the c-axis.

Specific Heat Experiments on CNT@AFI.

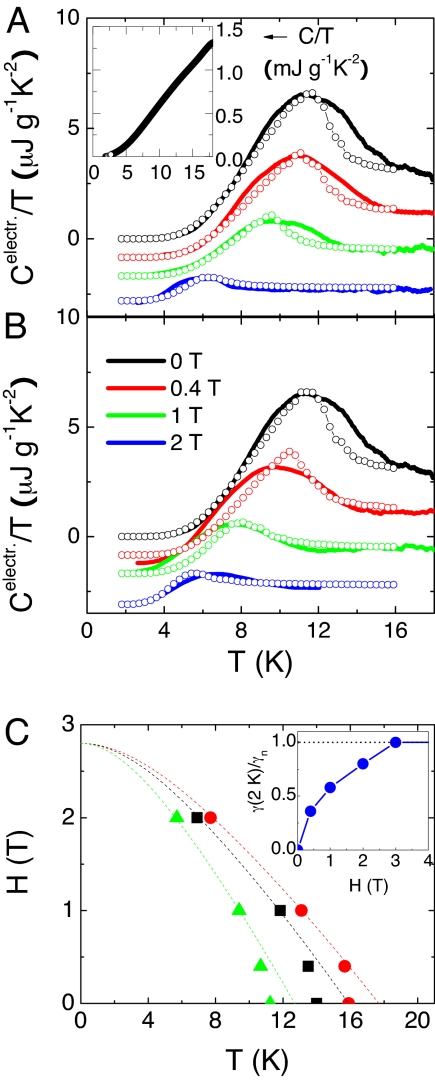
The total specific heat* of the sample C/T, corrected for the GE varnish contribution, is shown in the inset of Fig. 2A. The tiny superconducting transition signal becomes visible only after subtracting the phonon contribution which is dominated by the AFI host, under an applied field of 5 T. We used the data taken at 5 T for this purpose as earlier magnetization measurements (1) suggest that the upper critical field is below 5 T. The resulting C^electr (H)/T data are plotted in Fig. 2A (perpendicular) and 2B (parallel). On a scale that is ≈3 orders of magnitude smaller than the total specific heat, a broad anomaly was visible in zero field with maximum at 12 K and onset at ≈15 K. A magnetic field further broadened the anomaly and shifted it down to lower temperatures. At the lowest temperatures, an exponential increase of the specific heat was observed in zero field which suggests a standard s-wave order parameter. Surprisingly, there was only a very small amount of magnetic anisotropy, a point to be discussed later. We used the criterion that C^electr/T approaches zero at T = 0 for a fully gapped superconductor to estimate the Sommerfeld constant γ_n = 2.2 ± 0.4 mJ/mole of (5, 0) unit cells/K² for the superconducting fraction of the sample*. This value is 370 times smaller than the total specific heat of the AFI crystals at 15 K, and we have used for normalization the number of nanotube unit cells in the total length of the AFI pores in the sample, assuming 100% occupancy. This is certainly not true, but the value allowed us to compare with the BCS prediction, γ_n = (2/3)π ²k_B²N(0), where k_B is Boltzmann's constant, for an estimate of the true filling factor of the pores. Recent calculations (21) suggest a density of states at the Fermi level N(0) = 5/eV/unit cell, implying a theoretical value of γ_n = 23.4 mJ/mole of (5, 0) unit cells/K². This comparison allows us to conclude that 10 ± 2% of the total length of the pores of the AFI crystals were filled with superconducting material. Fig. 2C shows a magnetic phase diagram derived from the specific-heat data in field applied perpendicular to the CNTs. As the transition is broadened by fluctuations, we used three different criteria to trace the upper critical field line, that is, the upper onset of the superconducting transition (highest temperature where the data starts to deviate from γ_n), the midpoint of the broadened specific-heat jump, and the maximum of the specific-heat anomaly. We used the standard model of Werthamer, Helfand, and Hohenberg (WHH model; 24) to extrapolate the upper critical field to H_c2 (0). The 3 curves converge to H_c2 (0) = 2.8 ± 0.4 T. Indeed, at 3 T no more signature of superconductivity was observed in the experiments. The deviation of the data from the model close to T_c(H) is almost certainly related to the presence of strong phase fluctuations, which lower the transition temperature somewhat from the BCS value and broaden the transition. The inset to Fig. 2C shows the normalized magnetic field dependence of the electronic specific heat at 2 K, which also indicates H_c2 (0) ≈3 T. Note that the concave behavior of this quantity is unlikely to be related to the presence of nodes in the order parameter. A linear dependence of the low temperature specific heat for s-wave superconductors is only expected at magnetic fields much smaller than H_c2.

Fig. 2.

Specific heat data of the CNT@AFI sample. Electronic contribution C^electr./T of superconducting nanotubes encaged in the pores of AFI single crystals for magnetic fields applied perpendicular (A) and parallel (B) to the nanotubes. Solid lines represent the data; open circles are theoretical fits with T_c = 15 K and parameter values given in the text. For clarity, the 0.4, 1, and 2 T curves have been shifted downwards by 1.7, 3.4, and 5.1 μJ/g/K², respectively. The data are normalized by the mass of the sample as the total amount of nanotubes in this composite material is unknown (20). Data's error bar is about ± 0.5 μJ/g/K². Inset of (A): Zero field total specific heat of the AFI single crystals with encaged nanotubes in the pores. The Sommerfeld constant of the superconducting contribution is 370 times smaller than the total specific heat at 15 K. (C) Magnetic phase diagram derived from the specific heat (field applied perpendicular to the nanotubes). Because of the fluctuation-induced broadening of the transition, 3 different criteria have been used to trace T_c(H): The upper onset of the transition (red dots), the midpoint of the broadened specific-heat jump (black squares), and the specific-heat maximum (green triangles). The dashed lines are extrapolations toward H_c2 (0) according to a fit with the standard WHH model. Inset: Plot of the normalized low-temperature electronic specific heat at 2 K as a function of the magnetic field.

Theoretical Modeling of the Specific Heat Data.

The peaks are much broader than those observed in bulk superconductors, and there is no significant anisotropy in the data. We attribute both features to the finite size of the superconducting nanotube clusters. To substantiate this attribution and to extract the parameter values relevant to the sample, we used the Bardeen-Cooper-Schrieffer (BCS) specific heat expression (25), with the gap function Δ(T,H) simulated by an anisotropic Ginzburg-Landau (GL) model for finite-sized superconducting clusters (2). Here,

where β = 1/k_BT, E = [ε ² + Δ²]^1/2, g(ε) = N(0)$\sqrt{1+\epsilon /{\epsilon }_{\text{F}}}$, and ε_F is the Fermi energy. By setting [Δ/Δ(0)] = $\sqrt{\langle {\left|\psi \right|}^2/{\left|{\psi }_0\right|}^2\rangle }$, we evaluate the normalized gap function through the ensemble-averaged (denoted by the angular brackets) values of the absolute-value square of the complex GL order parameter ψ. Here, the subscript 0 denotes the value at H, T = 0, and Δ(0) = gk_BT_c with the value of g to be fixed by the low temperature data.

The values of g = 3 ± 0.2 and T_c = 15 ± 1 K can be easily obtained from Monte Carlo simulations (2, 26) on zero-field 〈|ψ²|/|ψ₀|²〉 for a sample of size 6 × 6 × 3 (in units of the zero-temperature coherence length ξ₀, with 3 being along the c-axis direction), with good fits obtained to both the experimental peak height and the observed low temperature behavior as shown by the connected symbols in Figs. 2A and 2B. Here, the theoretical values are normalized to the experimental value of γ_n. It is noted that Δ(0) = 3k_BT_c is larger than the BCS value of Δ(0) = 1.76k_BT_c, but the temperature dependence of the normalized gap is in very good agreement with that obtained earlier via different means (1). For finite magnetic fields, we also obtained very good fits to the data in both orientations without further changes in the parameter values, with dimensionless B̄ = 0.04, 0.1, and 0.2 to correspond with 0.4, 1, and 2 T, respectively. Since B¯ = Bξ₀²/Φ₀ with Φ₀ = hc/2e being the quantum flux, the good agreement between theory and experiment implies ξ₀ = 14 ± 2 nm. As the scaled problem is isotropic in terms of the interactions, ξ₀ is the only coherence length obtainable. The slight difference between the 2 orientations at intermediate fields is due to the shape of the finite-sized sample. We have also used the low temperature asymptotes as an indicator for the fraction ƒ_n(H) of the sample turned to normal by the magnetic field, so that the plotted theory curves represent ƒ_n + (1 − ƒ_n)C_es/(γ_nT). No useful anisotropy information may be obtained from the data, owing to the lack of information on either the actual physical geometry of the nanotube clusters, or the ratio in the coherence lengths along the 2 principal directions^†. From our data fitting, an estimate of zero-temperature H_c ≅ 100 ± 50 G and an effective magnetic penetration length λ ≅ 1.5 ± 0.7 μm were obtained. The values of λ and ξ₀ were noted to be remarkably consistent with those estimated earlier (2).

Electronic Transport Characteristics of CNT@AFI.

As the specific heat was measured with reference to the 5 T values, any superconducting order not quenched at 5 T would not be fully manifested in the data. Transport measurements, however, may yield some information regarding the existence of (fluctuating) superconducting condensate in individual nanotubes beyond 5 T.

To measure the electric transport characteristics, we prepared the sample by selecting an AFI zeolite crystallite (50 × 50 × 300 μm) and using the Focused Ion Beam (FIB, Seiko SMI2050) to delineate a 5-μm slice (see the cartoon inset of Fig. 3) containing nanotubes perpendicular to the slice. To provide electrical contact, 50 nm of Ti and 150 nm of Au were sputtered on the surface of AFI as well as the fresh ends of the single-walled nanotubes (SWNTs). FIB was again used to define the 4-terminal electrode configuration on the AFI surface as shown by the cartoon inset in Fig. 3. The 2 voltage leads in the center were separated by 100 nm. Further annealing in vacuum (10⁻⁶ Torr) at 500–600 °C reduced the contact resistance between SWNTs and Au/Ti. It should be noted that owing to the fact that the nanotubes were situated only ≈10 Å below the AFI surface, sample contact with the electrodes was good, in particular as the AFI surface is imperfect.

Fig. 3.

Resistance plotted as a function of temperature for the 4-terminal sample, measured at 10 nA. The geometry of the sample is illustrated in the cartoon inset, with yellow indicating gold coating and green the AFI crystal surface. The slice between the 2 grooves is 5 μm thick. The enlarged section shows the transition starts at 15 K. Up to 4 T, there is no appreciable change in the R(T) behavior.

Low temperature measurements of resistance vs. temperature were made with a series resistance of less than 15 Ohms. As the AFI zeolite is insulating, the conductance of the sample directly reflects the conductance of the SWNTs.

Fig. 3 shows the resistance measured in the 4-terminal configuration plotted as a function of temperature. It is seen that the transition initiates at 15 K (see the inset showing the enlarged section), with resistance decreasing smoothly toward zero. The resistance vs. temperature behavior was not changed under a 4-T magnetic field (applied perpendicular to the c-axis of the AFI crystal), suggesting the superconducting component, in this case, may consist of thin bundles of coupled nanotubes. Clearly, such a component would not be detectable by specific heat measurements with a quenching field of 4–5 T.

In another sample prepared for 2-terminal measurement (in which the central slice is only 1 μm wide), differential resistivity of the SWNTs array was measured as a function of the bias current.^‡ At 16 K, there was a broad resistivity peak around low current bias, presumably due to electron-electron interaction effects in SWNTs (27). A sudden change occurred at T_c = 15 K with the onset of a dip around the low current bias. In Fig. 4, we show the measured resistivity dip at 14 K (Fig. 4A) and 12K (Fig. 4B). It is seen that as temperature decreased, the depth of the measured resistivity dip increased. At 14 K, there was no magnetoresistance up to 5 T (Fig. 4A), but at 12 K, there was positive magnetoresistance up to 3 T (noted to be consistent with the specific heat data), but beyond which the dip did not change as the field was increased to 5 T (Fig. 4B). The dip disappeared as the temperature was raised to 15 K. These characteristics strongly suggest the superconducting component of the sample to be inhomogeneous, with part of the network susceptible to magnetic effects below 3 T (the part where the nanotubes are coupled through Josephson interaction, with condensation starting at below 14 K) and which can be in series with the other parts (thin bundles or even single nanotubes) capable of withstanding a much higher magnetic field, maybe up to the Pauli limit, whereby the singlet spin pairing is broken, estimated to be 30–40 T. While the Josephson coupled array is detectable by the specific heat, the thin bundle component of the network is only measurable through the transport measurements. Owing to the large sample resistance (on the order of 7 mega Ohms), the R vs. T transition behavior was not seen in the sample with the 2-terminal configuration.

Fig. 4.

Magnetic field dependence of the differential resistivity for the 2-terminal sample. (A) At 14 K, the application of a magnetic field of up to 5 T had no effect on the differential resistivity dip at small bias current. (B) At 12 K, there is clear positive magnetoresistance up to 3 T. A scanning electron microscopy image of the sample is shown in the inset.

Conclusions

In conjunction with the previous Meissner effect data (1), the specific heat and differential resistivity measurements show that nanostructure in the form of thin tubes can induce superconductivity in undoped carbon, which was not previously known to be superconducting. Such superconductivity with 1-D elements displays a qualitatively BCS-type behavior on the scale of 10 nm or more. However, its intrinsic characteristics at the level of individual nanotubes still remain to be further explored^§.