Using an Approximate Bayesian Bootstrap to Multiply Impute Nonignorable Missing Data

Abstract

An Approximate Bayesian Bootstrap (ABB) offers advantages in incorporating appropriate uncertainty when imputing missing data, but most implementations of the ABB have lacked the ability to handle nonignorable missing data where the probability of missingness depends on unobserved values. This paper outlines a strategy for using an ABB to multiply impute nonignorable missing data. The method allows the user to draw inferences and perform sensitivity analyses when the missing data mechanism cannot automatically be assumed to be ignorable. Results from imputing missing values in a longitudinal depression treatment trial as well as a simulation study are presented to demonstrate the method’s performance. We show that a procedure that uses a different type of ABB for each imputed data set accounts for appropriate uncertainty and provides nominal coverage.

1 Introduction

Missing values are a problem in many data sets and are ubiquitous in the social and health sciences. A common and practical method for dealing with missing data is multiple imputation (Rubin 1978, Rubin and Schenker 1986, Rubin 1987, Rubin and Schenker 1991) where the missing values are replaced with two or more plausible values. Most multiple imputation procedures assume that the missing data are ignorable as defined by Rubin (1976) where the probability of missingness depends only on observed values. However, this assumption is questionable in many applications, and even when it is a reasonable assumption, it is important for the analyst to check how sensitive inferences are to different assumptions concerning the missing data mechanism. This paper outlines a strategy for using an Approximate Bayesian Bootstrap to multiply impute nonignorable missing data. The method allows the user to draw inferences and perform sensitivity analyses when the missing data mechanism cannot be assumed to be ignorable. Results from imputing missing values in a longitudinal depression treatment trial as well as a simulation study are presented to demonstrate the method’s performance.

1.1 Background

The properties of missing data methods may depend strongly on the mechanism that led to the missing data. A particularly important question is whether the fact that variables are missing is related to the underlying values of the variables in the data set (Little and Rubin 2002).

Specifically, Rubin (1976) classifies the reasons for missing data as either ignorable or nonignorable. In a data set where variables X are fully observed and variables Y have missing values, the missingness in Y is deemed ignorable if the missing Y values are only randomly different from observed Y values when conditioning on the X values. Nonignorable missingness asserts that even though two observations on Y (one observed, one missing) have the same X values, their Y values are systematically different. Rubin and Schenker (1991) give an example where the missing Y are typically 20 percent larger than observed Y for the same values of X. The role of nonignorability assumptions has been discussed in the context of a variety of applied settings; see, for example, Little and Rubin (2002, chap. 15), Belin et al. (1993), Wachter (1993), Rubin et al. (1995), Schafer and Graham (2002), Demirtas and Schafer (2003).

Imputation is a common and practical method for dealing with missing data where missing values are replaced with plausible values. Simply imputing missing values once, and then proceeding to analyze a data set as if there never were any missing values (or as if the imputed values were the observed values) fails to account for the uncertainty due to the fact that the analyst does not know the values that might have been observed. No matter how successful an imputation procedure has been in eliminating nonresponse bias, it is important to account for this additional uncertainty.

Rubin (1987) proposed handling the uncertainty due to missingness through the use of multiple imputation. Multiple imputation refers to the procedure of replacing each missing value with D ≥ 2 imputed values. Then D imputed data sets are created, each of which can be analyzed using complete data methods. Using rules that combine within-imputation and between-imputation variability (Rubin 1987), inferences are combined across the D imputed data sets to form one inference that properly reflects uncertainty due to nonresponse under that model. However, creating multiple imputations and combining complete-data estimates does not insure that the resulting inferences will be valid. Rubin (1987) defines the conditions that a multiple imputation procedure must meet in order to produce valid inferences and be deemed a proper multiple imputation procedure. To satisfy these conditions, a multiple imputation procedure must provide randomization-valid inferences in the complete data and must represent both the sampling uncertainty in the imputed values and the estimation uncertainty associated with either explicit or implicit unknown parameters.

A hot-deck is an imputation method where missing values (donees) are replaced with observed values from donors deemed exchangeable with the donees. An Approximate Bayesian Bootstrap (ABB) (Rubin and Schenker 1986, Demirtas et al. 2007) is a method for incorporating parameter uncertainty into hot-deck imputation models. Since hot-deck procedures are most tractable when imputing one variable at a time, for the remainder of this paper, define Y to be a single variable with missing values. Y_obs consists of the values of Y that are observed and Y_mis consists of the values of Y that are missing. Let n_obs and n_mis be the number of cases associated with Y_obs and Y_mis respectively. An Ignorable ABB first draws n_obs cases randomly with replacement from Y_obs to create $Y_{\mathit{\text{obs}}}^{*}$. Donors for imputing missing values are then selected from this new set of “observed” cases. For multiple imputation, D bootstrap samples are drawn so that the imputed values are drawn from D different sets of donors.

Rubin and Schenker (1991) discuss how an ABB can be modified to handle nonignorable missing data. Instead of drawing n_obs cases of Y_obs randomly with replacement (i.e. with equal probability), they suggest drawing n_obs cases of Y_obs with probability proportional to $Y_{\mathit{\text{obs}}}^c$ so that the probability of selection for for y_i ∈ Y_obs is

$$\frac{y_i^c}{{\displaystyle {\sum }_{j=1}^{n_{\mathit{\text{obs}}}}{y}_j^c}}.$$ (1.1)

This skews the nonrespondents to have typically larger (when c > 0 and y_j > 0) values of Y than respondents. The methods we present here build on this idea, which Rubin and Schenker (1991) described but did not evaluate in an applied context.

1.2 Motivating Example: The WECare Study

A motivating example is provided by the Women Entering Care (WECare) Study. The WECare Study investigated depression outcomes during a 12-month period in which 267 low-income mostly minority women in the sub-urban Washington, DC area were treated for depression. The participants were randomly assigned to one of three groups: Medication, Cognitive Behavioral Therapy (CBT), or care-as-usual, which consisted of a referral to a community provider. Depression was measured every month for the first six months and every other month for the rest of the study through a phone interview using the Hamilton Depression Rating Scale (HDRS).

Information on ethnicity, income, number of children, insurance, and education was collected during the screening and the baseline interviews. All screening and baseline data were complete except for income, with 10 participants missing data on income. After baseline, the percentage of missing interviews ranged between 24% and 38% across months.

Outcomes for the first six months of the study were reported by Miranda et al. (2003). In that paper, the primary research question was whether the Medication and CBT treatment groups had better depression outcomes as compared to the care-as-usual group. To answer this question, the data were analyzed on an intent-to-treat basis using a random intercept and slope regression model which controlled for ethnicity and baseline depression. Results from the complete-case analysis showed that both the Medication intervention (p < 0.001) and the CBT intervention (p = 0.006) reduced depression symptoms more than the care-as-usual community referral.

1.3 Research Overview

The outline for the rest of this paper is as follows. Section 2 gives more detail on implementing a nonignorable ABB and describes the imputation method we will use to investigate the performance of the nonignorable ABB. Section 3 describes an experiment to evaluate our methods using data from the WECare study and presents the results from the experiment. In Section 4 we further evaluate our methods using simulated data. Section 5 provides guidelines for implementing our methods and discussion.

2 Methods

In this section we briefly describe the hot-deck imputation method of Siddique and Belin (2008) that we will use to implement the nonignorable ABB. A nonignorable ABB can be used with most hot-deck imputation techniques, but we use this method because it allows us to clearly observe how the size of the donor pool alters the effectiveness of the nonignorable ABB. We then discuss methods for implementing a nonignorable ABB that go beyond previously described strategies.

2.1 Hot-Deck Multiple Imputation Using Distance-Based Donor Selection

In order to implement a nonignorable ABB we use predictive mean matching (Little 1988, Schenker and Taylor 1996) in a hot-deck described by Siddique and Belin (2008). In predictive mean matching, values Y_obs are regressed on a set of observed variables, say X. Then, using the regression parameters calculated on the observed data, predicted values Ŷ are calculated for all Y. Finally, Y_mis values are imputed using Y_obs values whose predicted Ŷ values are similar.

Siddique and Belin (2008) describe a distance-based donor selection approach with an ABB where donors are selected with probability inversely proportional to their distance from the donee. Let Y be the target variable to be imputed and X the predictive mean matching covariates. Using only those rows (cases) where Y is observed, perform the ABB by drawing n_obs rows with replacement. Let w_j, j = 1,…, n_obs designate the number of times the row belonging to y_j ∈ Y_obs was chosen with replacement in the ABB. Let W represent a diagonal matrix of w_j values. The formula for calculating the predicted values is Ŷ = X B̂ where B̂ = (X^TW X)⁻¹ X^TWY_obs. For a given donee, let $D_{0i}^k$ be the distance between donee 0 and donor i, where the distance is the absolute difference in predicted values raised to a power k with a non-zero offset to avoid complexities posed by zero distances. That is,

$$D_{0i}^k={(|{\widehat{y}}_0-{\widehat{y}}_i|+\delta )}^k,$$ (2.1)

where

$$\delta =\text{min}|{\widehat{y}}_0-{\widehat{y}}_i|\text{for all}i=1,\cdots ,n_{\mathit{\text{obs}}}\text{where}{\widehat{y}}_0\ne {\widehat{y}}_i.$$

In settings where no two cases i and j have Ŷ_i = Ŷ_j (i.e., when no two individuals have the same pattern of observed covariates or identical predicted values), then the Δ offset term can be dropped (although retaining it in the procedure is apt to have little practical consequence).

Using the distance defined in Equation 2.1, the donor i selection probability $l_i^k$ (Ŷ₀) for donee 0 is

$$l_i^k({\widehat{y}}_0)=\frac{\frac{1}{D_{0i}^k}{w}_i}{{\displaystyle {\sum }_{j=1}^{n_{\mathit{\text{obs}}}}\frac{1}{D_{0_j}^k}{w}_j}}.$$ (2.2)

Equation 2.2 ensures that

$${\displaystyle \sum _{i=1}^{n_{\mathit{\text{obs}}}}{l}_i^k({\widehat{y}}_0)=1}$$

and that given observed donor values Y_donor = (Y₁,…, Y_nobs) and selection probabilities $l_{\text{donor}}^k({\widehat{y}}_0)=(l_1^k({\widehat{y}}_0),\cdots ,l_{n_{\mathit{\text{obs}}}}^k({\widehat{y}}_0))$, the expected value of the imputation for donee 0 is

$$E(y_0|Y_{\text{donor}},l_{\text{donor}}^k({\widehat{y}}_o))={\displaystyle \sum _{i=1}^{n_{\mathit{\text{obs}}}}{l}_i^k({\widehat{y}}_0)Y_i}$$

With this approach, donors closest to the donee have greatest probability of selection, but all donors are eligible and have some non-zero selecion probability. The exponent k in Equation 2.1 is a closeness parameter, which adjusts the probability of selection assigned to the closest donors. As k → ∞ this procedure amounts to a nearest-neighbor hot-deck where the donor whose predicted mean is closest to the donee is always chosen. Conversely, when k equals 0, each donor has equal probability of selection, which is equivalent to a simple random hot-deck. In practice, a value of k somewhere between these two extremes is chosen by the imputer. Siddique and Belin (2008) considered an example where a closeness parameter value around 3 appeared to be reasonable to favor nearby donors while allowing donor probabilities to decline smoothly as a function of distance.

In addition to adjusting the probability of selection assigned to the closest donors, the closeness parameter also has an impact on the bias and variance of the imputed values. Small values of the closeness parameter imply lower variance (averaging over more donors) but presumably higher bias (since it may not be plausible to assume that all donors are equally good matches).

When covariates in the predictive mean matching models have missing values, starting values are introduced. Then, once all variables have been imputed once, they are re-imputed, this time replacing starting values with imputed values. This procedure is iterated until convergence diagnostics are achieved (Siddique and Belin 2008). Siddique and Belin (2008) showed in one setting that 10 iterations of the hot-deck procedure produced estimates that were not significantly different from estimates resulting from iterating the procedure until more formal convergence diagnostics were satisfied.

Multiple imputation is incorporated into the method to reflect the uncertainty of the imputations by performing the procedure D times to create D complete data sets. Each data set is analyzed separately, and inferences are combined using the rules described by Rubin (1987).

2.2 Implementing a Nonignorable Approximate Bayesian Bootstrap

In addition to the nonignorable ABB proposed by Rubin and Schenker (1991) where n_obs cases of Y_obs are drawn with probability proportional to $Y_{\mathit{\text{obs}}}^c$, we consider a number of variations on this idea. ABBs where values of Y_obs are drawn with probability proportional to $Y_{\mathit{\text{obs}}}^c$ where c = −1, 1, 2, and 3, are referred to as an “Inverse-to-size ABB,” “Proportional-to-size ABB,” “Proportional-to-size-squared ABB,” and “Proportional-to-size-cubed ABB” respectively. We also propose a nonignorable ABB where n_obs cases of Y_obs are drawn with probability proportional to [|Y_obs – Q_p(Y_obs)|]^c where the notation Q_p(Y_obs) represents the pth quantile of Y_obs. For example, when p = 2 so that Q_p(Y_obs) is the median of the observed Y values, the implication of drawing with probability proportional to the distance from the median is to favor values for the non-respondents with either larger or smaller values than respondents with the same set of covariates (when c < 0). We refer to this approach as a “U-Shaped ABB” because observations in the extremes of the distribution of Y_obs have greater weight than observations in between that are close to the specified quantile

In a variation of this idea with p = 1, we refer to the ABB that centers the donor sizes around the 1st quantile as a “Fishhook ABB,” because this ABB mostly favors large values but retains a U-shaped pattern featuring a slight upturn in the weight given to the smallest observed values.

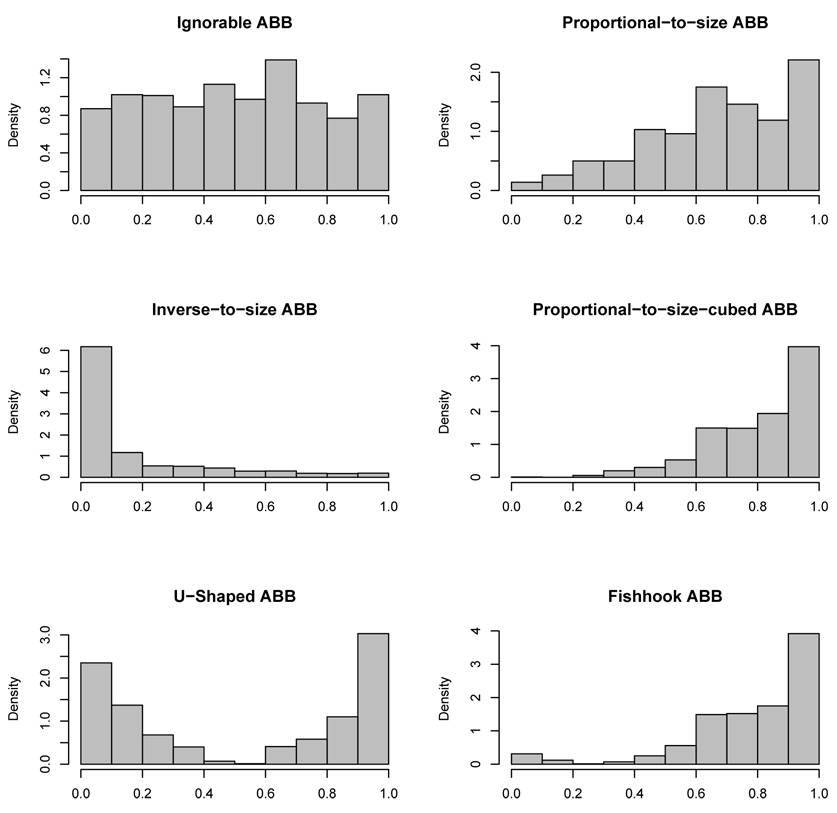
Figure 1 displays histograms of n = 1000 simulated observations from a uniform distribution after the observations have been weighted by six different ABB types. The Ignorable ABB places equal weight on each observation and as a result, the histogram is relatively flat. The Proportional-to-size and Proportional-to-size-cubed ABBs place more weight on larger values while the Inverse-to-size ABB places more weight on the smaller values. The U-Shaped ABB is symmetric, and places almost no weight in the middle of the distribution. The Fishhook ABB mostly favors the larger values, but also places some weight on the smaller values in the distribution.

Figure 1.

Histograms of n = 1000 observations simulated from a uniform distribution that have been weighted by six different ABB types that place weight on a value based on its size.

The histograms in Figure 1 can be considered prior distributions on the donor selection probabilities. The Ignorable ABB is akin to a flat prior, and gives each donor equal prior probability of selection. The other ABB types are informative priors, and give more or less weight to a donor based on the donor size. We will see in Sections 3 and 4 that inferences from the WECare study and the simulation study are affected by the choice of ABB.

For all nonignorable ABBs described above, when values of Y_obs are less than or equal to 0, the values of Y_obs need to be transformed to ensure that the selection probabilities in the nonignorable ABB are positive and (in the case where Y_obs are drawn with probability proportional to $Y_{\mathit{\text{obs}}}^c$, c > 0) that the selection probability for y_i ∈ Y_obs is greater than the selection probability for y_j ∈ Y_obs when y_i > y_j. Define α and β to be the smallest and second smallest values of Y_obs respectively where α ≠ β. Transform y_i ∈ Y_obs using y_i + |α| + |α – β|. Then Equation 1.1 is rewritten as

$$\frac{{(y_i+|\alpha |+|\alpha -\beta |)}^c}{{\displaystyle {\sum }_{j=1}^{n_{\mathit{\text{obs}}}}{(y_j+|\alpha |+|\alpha -\beta |)}^c}}.$$ (2.3)

This transformation is used only for calculating the selection probabilities. The original values of Y_obs are used for imputation.

3 Experiment Based on Motivating Example

Siddique and Belin (2008) describe an experiment they used to evaluate their imputation methods using the WECare data. They imputed the WECare data many different ways using different choices for closeness parameter, different choices for the order in which variables were imputed, different choices for the number of iterations and different choices for starting values when covariates in their imputation models had missing values. In every scenario, five imputations were made for every missing value, and each treatment group was imputed separately. They then investigated how these different factors in their imputation procedure affected inferences from the WECare data.

We performed a similar experiment with the WECare data, holding fixed the variable order, the method for introducing starting values, and the number of iterations but this time adding seven different choices for ABB. We used closeness parameter values equal to the integers between 0 and 10 and starting values based on mean imputation. To accommodate longitudinal outcomes, variables were imputed in a sequence from the earliest to latest time points, and 10 iterations of the entire sequence were performed.

When imputing and analyzing the WECare data, we restricted our attention to the depression outcomes that were analyzed in Miranda et al. (2003), variables used as covariates in final analyses, and a set of additional variables used in the imputation models because they were judged to be potentially associated with the analysis variables. Table 1 lists variables that were used in imputation and analysis models and also indicates the percentage of missing values.

Table 1.

WECare Variables Under Study.

Variable Name	For Imputation or Analysis?	Missing Values?	Variable Type
Baseline HDRS	Both	0%	Scaled
Month 1 HDRS	Both	25%	Scaled
Month 2 HDRS	Both	24%	Scaled
Month 3 HDRS	Both	30%	Scaled
Month 4 HDRS	Both	34%	Scaled
Month 5 HDRS	Both	38%	Scaled
Month 6 HDRS	Both	30%	Scaled
Month 8 HDRS	Imputation	33%	Scaled
Month 10 HDRS	Imputation	34%	Scaled
Month 12 HDRS	Imputation	24%	Scaled
Ethnicity	Both	0%	Nominal
Income	Imputation	4%	Continuous
Education	Imputation	0%	Ordinal
Number of Children	Imputation	0%	Continuous
Received 9 Weeks of Meds	Imputation	0%	Binary
Number of CBT Sessions	Imputation	0%	Continuous
Insurance Status	Imputation	0%	Nominal

Four important targets of inference from the model used by Miranda et al. (2003) are the intercepts and slopes of the Medication treatment group and the CBT treatment group, reflecting the average HDRS score and the change in HDRS scores over time for the two active interventions. Here, for brevity, we focus our attention on the slope of the Medication treatment group to illustrate the impact of different factors in the imputation procedure.

Each of the nonignorable ABBs favor donors based on their size. In the context of this experiment using the WECare data, the “size” of a donor refers to its depression score or income in dollars depending on the variable being imputed (HDRS score or income), adjusted accordingly using Equation 2.3. Donors whose size is large have high incomes or are depressed (high HDRS scores). Donors whose size is small have low incomes or are less depressed (low HDRS scores).

In this experiment, we implemented several ABBs in order to investigate whether inferences from the WECare analysis were sensitive to assumptions concerning the missing data mechanism. Bootstrap samples were drawn in the following alternative ways:

1. An Ignorable ABB that treats donors as a priori equally likely

2. An Inverse-to-size ABB where donors are drawn with probability proportional to the inverse of the donor size

3. A Proportional-to-size ABB where donors are drawn with probability proportional to the donor size

4. A Proportional-to-size-cubed ABB where donors are drawn with probability proportional to the cube of the donor size

5. A U-Shaped ABB where donors are drawn with probability proportional to the square of the donor size centered around its median

6. A Fishhook ABB where donors are drawn with probability proportional to the square of the donor size centered around its 1st quantile

7. A Mixture ABB where a different ABB is implemented for each of the 5 imputed data sets. For this experiment, the following ABBs were used

   1. An Inverse-to-size ABB (c=−1)
   2. An Ignorable ABB (c=0)
   3. A Proportional-to-size ABB (c=1)
   4. A Proportional-to-size-squared ABB (c=2)
   5. A Proportional-to-size-cubed ABB (c=3)

Each version of the ABB corresponds to an implied process that could be envisioned as different explanations for nonresponse. The U-Shaped ABB is a plausible missing data mechanism for a depression treatment trial where participants often refuse to respond because they are either: (1) healthy and feel no need to participate in the study, or (2) too depressed to go through with the interview. Our motivation for considering a Fishhook ABB is to favor larger values in a manner that might be expected to incorporate somewhat more uncertainty in parameter estimates than a Proportional-to-size ABB.

The motivation for the Mixture ABB approach which uses a different type of ABB for each imputed data set is to provide estimates that incorporate a range of possible nonignorability scenarios. In addition to the intuitive appeal of averaging over the uncertainty about the degree of nonignorability, we will see in the next section that this approach provides better coverage than the other ABB approaches.

With eleven choices for closeness parameter value and 7 different ABB strategies, there are 77 possible combinations. We performed four replicates for each combination. We then analyzed the WECare data using a random intercept and slope model for longitudinal outcomes focusing on the parameter estimate of the slope of the Medication intervention. We evaluated main effects and 2-way interactions of the experimental factors in a regression framework with the slope of the medication intervention as the dependent variable in the regression. Across experimental conditions, we analyzed relative differences in the slopes using a regression model incorporating factors in the experiment.

3.1 Results

3.1.1 Descriptive Summary

Table 2 provides estimates, standard errors, and p values of the WECare Medication slopes by ABB type based on one replication with a closeness parameter equal to 2. As discussed in Section 1.1, an Inverse-to-size ABB has the effect of favoring smaller imputed values. With the WECare data, this assumption resulted in stronger Medication effects as compared to a Medication effect using an Ignorable ABB. Conversely, the Proportional-to-size ABB and the Proportional-to-size-cubed ABB favor larger imputed values. With the WECare data, the use of these ABBs resulted in a weaker Medication effect as compared to Medication effects under an ignorable assumption. Especially since there are more missing values at later time points, imputations favoring smaller values result in a steeper downward slope while imputations favoring larger values result in a flatter slope. Still, all of the results for procedures (1)–(4) remained statistically significant at conventional significance levels.

Table 2.

Table of Medication Intervention Slopes by ABB Type based on one replication with a closeness parameter value of 2.

Procedure	ABB Type	Estimate	Std. Error	t value	Pr(> |t|)
(1)	Ignorable ABB	−2.18	0.47	−4.66	<0.0001
(2)	Inverse-to-size ABB	−2.79	0.48	−5.86	<0.0001
(3)	Proportional-to-size ABB	−1.83	0.45	−4.05	0.0002
(4)	Proportional-to-size-cubed ABB	−1.42	0.43	−3.30	0.0012
(5)	U-Shaped ABB	−1.22	0.74	−1.65	0.1319
(6)	Fishhook ABB	−1.34	0.52	−2.61	0.0141
(7)	Mixture ABB	−2.13	0.70	−3.04	0.0156

The results from the U-Shaped ABB and the Fishhook ABB both induced considerably flatter slope estimates and considerable larger standard errors. We had anticipated that these approaches would result in parameter estimates approximately equal to those using a Ignorable ABB, but with larger standard errors. Instead, the U-Shaped ABB and Fishhook ABB appear to have favored smaller donors at the beginning of the study and larger donors later on in the study. As a result, the Medication treatment effects are smallest using a U-Shaped or Fishhook ABB than any other ABB. However, as expected, the U-Shaped ABB and the Fishhook ABB did provide increased uncertainty in the form of larger standard errors of parameter estimates as compared to the Ignorable ABB. The slope remained significant at the 0.05 level with the Fishhook ABB but not with the U-Shaped ABB.

The Mixture ABB provides a point estimate similar to that of an Ignorable ABB but an estimated standard error that is nearly 50% larger than the Ignorable ABB. The departure of the slope estimate from that of the Proportional-to-size ABB reflects the fact that the impact of nonignorability assumptions on the slopes in not purely an additive function of the index c, and the larger standard error reflects that we are incorporating a range of nonignorability scenarios into our inference.

3.1.2 Regression Analysis Summary

As discussed above, parameter estimates from analyzing the WECare data were regressed on factors from the imputation models. Table 3 lists the coefficients from the regression predicting the slope of the Medication intervention. The model included main effects, a quadratic effect for the closeness variable, and all two-way interactions among closeness parameter and ABB type. The reference group in this model reflects a closeness parameter equal to 5 and an Ignorable ABB.

Table 3.

Table of regression coefficients from the model predicting the slope of the Medication treatment from the WECare data.

Variable	Estimate	Std. Error	t value	Pr(> |t|)
INTERCEPT	−1.916	0.020	−96.47	<0.0001
CLOSE	0.003	0.005	0.51	0.6101
CLOSE2	−0.002	0.001	−1.77	0.0772
Inverse-to-size ABB	−0.744	0.030	−24.84	<0.0001
Proportional-to-size ABB	0.104	0.030	3.46	0.0006
Proportional-to-size-cubed ABB	0.416	0.030	13.90	<0.0001
U-Shaped ABB	0.723	0.030	24.15	<0.0001
Fishhook ABB	0.528	0.030	17.64	<0.0001
Mixture ABB	−0.154	0.030	−5.15	<0.0001
CLOSE*Inverse-to-size ABB	0.033	0.009	3.47	0.0006
CLOSE*Proportional-to-size ABB	0.002	0.009	0.21	0.8318
CLOSE*Proportional-to-size-cubed ABB	−0.021	0.009	−2.26	0.0244
CLOSE*U-Shaped ABB	0.006	0.009	0.60	0.5464
CLOSE*Fishhook ABB	−0.015	0.009	−1.59	0.1125
CLOSE*Mixture ABB	0.000	0.009	0.00	0.9977

The Medication slope associated with this reference group is equal to −1.92. All of the indicators for type of nonignorable ABB have coefficients that imply significant differences from the Ignorable ABB. As was seen in Table 2, nonignorability assumptions that favor donors with larger values reduce the effect of the Medication intervention, while the assumption that favors donors with smaller values increases the effect of the Medication intervention. The effects of the U-Shaped and Fishhook ABBs were very large and produced much flatter slope estimates (i.e., smaller estimated treatment effects).

The effect of the Mixture ABB was small in magnitude and was in the direction corresponding to a larger treatment effect. At first glance, the direction of the Mixture ABB coefficient was surprising, since the “middle” ABB in the Mixture approach, with c = 1, is an Proportional-to-size ABB. However, looking at the other coefficients in the regression, it can be seen that the magnitude of the Inverse-to-size ABB is much greater than that of the Proportional-to-size ABB or the Proportional-to-size-cubed ABB. For the Mixture approach, which uses a different ABB for each data set, it seems that the Inverse-to-size ABB data set provided an estimate that the other ABBs did not completely cancel out.

Both closeness and quadratic closeness were significant in the model, replicating the results in Siddique and Belin (2008) in which both coefficients for closeness parameter were significant and the effect of the closeness parameter was most pronounced among small closeness parameter values.

Two of the interactions of the closeness parameter with the nonignorable ABB variables were also significant. Smaller values of the closeness parameter are associated with greater impact of the nonignorable assumptions. The reason for this is that the smaller the closeness parameter, the larger the available donor pool. While nearby donors using an Ignorable ABB might not be very different from nearby donors using a nonignorable ABB, farther away donors (which have low probability of selection when the closeness parameter is large) can be quite different under the two ignorability assumptions.

4 Simulation Study

An advantage of working in an applied context such as the WECare study is the realistic nature of the data, but a disadvantage is that true parameter values are not known. Using simulated data with nonignorable missing values, we evaluated how the choice of ABB and the choice of closeness parameter affect the bias, variance, and mean squared error (MSE), of the post-multiple-imputation mean and the coverage rate of the nominal 95% confidence interval of the post-multiple-imputation mean. Siddique and Belin (2008) reported on a simulation study with ignorable missing data. In this paper we only consider scenarios with nonignorable missing data.

4.1 Setup

Building on an example in Little and Rubin (2002, p.23), trivariate observations {(y_i1, y_i2, u_i), i = 1,…, 100} on (Y₁, Y₂, U) were generated as follows:

$$\begin{array}{ccc}{z}_{i1}=\sqrt{0.125}\ast x_{i1}\hfill & z_{i2}=\sqrt{0.5}\ast x_{i2}\hfill & z_{i3}=2\ast z_{i1}+z_{i2}\hfill \\ y_{i1}=1+z_{i1}\hfill & y_{i2}=\mathit{\text{exp}}(z_{i3})\hfill & u_i=b\ast z_{i3}+c\ast x_{i3}\hfill \end{array}$$ (4.1)

where {(x_i1, x_i2, x_i3), i = 1,…, n} are independent standard normal deviates. The hypothetical complete data set consists of observations {(y_i1, y_i2), i = 1,…, n}, which have a bivariate normal-lognormal distribution (the marginal distribution of Y₁ is normal, the marginal distribution of Y₂ is lognormal) with means (1.0, 1.65), variances (0.13, 4.67) and correlation 0.54. The observed (incomplete) data are {(y_i1, y_i2), i = 1,…, n}, where the values {y_i1} of Y₁ are all observed, but some values {y_i2} of Y₂ are missing. The latent variable U determines missingness of Y₂. Here, an expected rate of 50% missingness on Y₂ is generated by making y_i2 missing when u_i > 0.

The variable b in Equation 4.1 governs the missing data mechanism. When b = 0, the missing data are ignorable. When b ≠ 0, the missing data are nonignorable. We generated simulated data with 50% nonignorable missingness by setting b = 2, $c=\sqrt{5}$, and y_i2 missing when u_i > 0. As a result, the larger values of Y₂ tended to be missing.

We simulated data with 100 observations and 50% missingness. Predictive mean matching is based in part on a traditional normal-theory linear regression model to obtain predicted values. Sensitivity to violations in that model was investigated by simulating lognormal data. One thousand replications for the above scenario were simulated. Multiple imputation was performed with five multiply imputed data sets using the methods described in Section 2. In particular, the data were imputed with closeness parameters values equal to the integers between 0 and 10 using an ABB. We evaluated the bias, variance, and MSE of the post-multiple-imputation mean of Y₂ as well as the coverage rate of its nominal 95% interval estimate.

In addition to an Ignorable ABB, we investigated the effectiveness of using an ABB to impute nonignorable missing data by using three different ABB approaches that favor larger donors. These three ABBs were an attempt to account for uncertainty due to nonignorability when missing values are thought to be larger than observed values even after controlling for observed values.

The first approach was a Proportional-to-size-squared ABB, where “size” refers to the observed values of Y₂. The second nonignorable ABB approach was a Mixture ABB. We chose the same five ABBs that were used in the WECare experiment (Inverse-to-size, Ignorable, Proportional-to-size, Proportional-to-size-squared, Proportional-to-size-cubed). The third approach was the Fishhook ABB. We hypothesized that this approach would provide estimates similar to the Proportional-to-size-squared approach but with better coverage since the Fishhook ABB incorporates more uncertainty than the Proportional-to-size squared ABB by adding weight to small donors.

This simulation design represents a challenging scenario for hot-deck imputation. A continuous, skewed target variable where the missing values occur disproportionately in the tail of the distribution implies that there will sometimes be few nearby donors. The investigation aimed to study statistical properties (bias, variance, MSE, and coverage) of hot-deck imputation with distance-based donor selection as a function of the value of the closeness parameter and the ABB type for nonignorable missing data.

4.2 Results

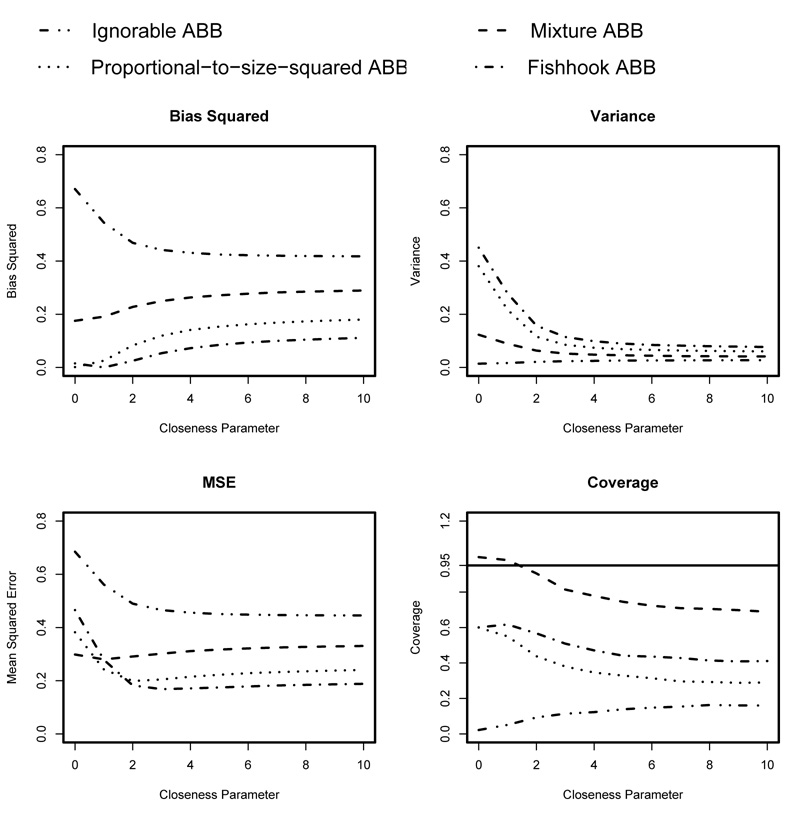
Figure 2 plots the results of our simulations (in terms of bias, variance, MSE, and coverage) under the four different ABBs. Looking first at the lines corresponding to an Ignorable ABB, bias (squared) decreases and variance increases as the closeness parameter increases. This result was also seen with simulated ignorable missing data in Siddique and Belin (2008). Still, even with large closeness parameter values, there is substantial bias leading to large mean squared errors and poor coverage. The reason for the substantial bias is due to the nonignorability of the data, where missingness on Y₂ depends on Y₂ itself. Matching on Y₁ does not provide suitable donors for the missing values since their missingness does not depend on Y₁ (matching on Y₁ does help since the two variables are correlated, but substantial bias remains). Also, there is little variablity in the resulting estimates. Since the missing-data mechanism implies that larger values of the target variable tend to be missing, the donor pool is not heterogenous and the resulting variability is limited. Because the variability of the post-imputation-mean is so small compared to the bias, the MSE is determined primarily by its bias component. Coverage is poor, never going above 20%. The results from a complete-case analysis (not shown) are similar to the results in Figure 2 that correspond to a closeness parameter value of 0 with an Ignorable ABB but the complete-case analysis featured worse coverage (although estimates from both analyses were far from achieving nominal coverage levels).

Figure 2.

Plots of the bias squared, variance, MSE, and coverage rate of the nominal 95% confidence interval for the post-multiple-imputation mean from simulated data with nonignorable missing values with 50% missingness and n = 100. The four lines represent: an Ignorable ABB, a Proportional-to-size-squared ABB, a Mixture ABB, and a Fishhook ABB. While the bias decreases with increases in the closeness parameter for an Ignorable ABB, it increases for the other ABBs. Closeness parameter has little effect on variance under an Ignorable ABB or a Mixture ABB, but has an impact under an Proportional-to-size-squared ABB or a Fishhook ABB. The Mixture ABB provides superior coverage as compared to the other ABBs.

Compared to the results from using the Ignorable ABB, the Proportional-to-size-squared ABB produces less bias and smaller MSE. Interestingly, greater values of the closeness parameter value are associated with greater bias and smaller variance. This is different from the Ignorable ABB, where the bias is lower and variance is greater for larger values of the closeness parameter. The Proportional-to-size-squared ABB shows better coverage than an Ignorable ABB, but still well below the nominal coverage target. Unlike the Ignorable ABB, greater values of the closeness parameter are associated with worse coverage for the Proportional-to-size-squared ABB.

A similar phenomenon was observed when evaluating the factors used to impute the WECare data in Section 3. There were significant interactions with the closeness parameter and the variables indicating a nonignorable ABB. The reason for this is that a larger value of the closeness parameter effectively shrinks the size of the donor pool, thereby reducing the capacity of the ABB to reflect the nonignorability in the simulation scenarios.

As hypothesized, the Fishhook ABB gives results similar to the Proportional-to-size-squared ABB but with better coverage. However the difference in coverage between the Fishhook ABB and the Proportional-to-size-squared ABB is not substantial and coverage is still well below the nominal 95% level.

The bias, variance, and MSE values from the Mixture ABB are somewhere between those of the Ignorable ABB and the Proportional-to-size-squared ABB. This is not surprising since the “middle” ABB value in the Mixture ABB is a Proportional-to-size ABB. However, the benefit of the Mixture ABB reveals itself when examining coverage. Incorporating the additional uncertainty in the choice of ABB results in coverage that reaches the nominal 95% level for closeness parameters between 0 and 1, approaches the 95% level for closeness parameter values up to 2, and considerably outperforms the other three ABB types for all values of the closeness parameter.

5 Implementation Guidelines and Discussion

The use of a nonignorable ABB was effective in our simulations for reducing bias and MSE and improving coverage in the presence of nonignorable missing data as compared to an Ignorable ABB. In the WECare experiment, the nonignorable ABB provided inferences different from those using an Ignorable ABB. However, not all the ABBs we investigated performed equally well.

In particular, strategies that used the same ABB type for each imputed data set provided poor coverage in the simulation study. Since missing data mechanisms are unknown in practice, an imputer has little information on hand when determining what type of nonignorable ABB to choose. As a result, it is not surprising that committing to only one ABB type provides overly precise estimates.

Similarly, care should be taken to avoid strong nonignorablilty assumptions which can also result in overly precise parameter estimates and poor coverage. For example, consider an ABB that chooses donors with probability proportional to the donor size raised to the power 100. Then the sample of donors will consist of only the donor with the largest value in the data set for all multiply imputed data sets. This is the equivalent of single imputation and will result in no between-imputation variability, leading to unduly precise estimates. For these reasons, we do not recommend using the same ABB type for each imputed data set.

Instead, our recommendation is to use a Mixture ABB approach where a different type of ABB is used for each imputed data set. The WECare experiment and the simulation study both gave evidence that this approach appears to account for appropriate uncertainty and provide nominal coverage. The performance of the Mixture ABB approach was even more impressive considering that the simulation design featured a difficult scenario for hot-deck imputation. As was seen in both the WECare experiment and the simulation study, large closeness parameter values reduce the effectiveness of the nonignorable ABB. For this reason, we recommend using a large donor pool when implementing the Mixture ABB. In the hot-deck approach of Siddique and Belin (2008), this corresponds to using a closeness parameter value in the range of 1 to 2.

The Mixture ABB procedure can be altered depending on what is perceived as the reasons for missingness. For example, if the imputer believes that the larger values tend to be missing, but still wishes to incorporate uncertainty regarding nonignorability, then a Mixture ABB can be chosen that is centered around an ABB that favors larger donors. This strategy is similar to the approach used in the WECare experiment and the simulation study, where Inverse-to-size, Ignorable, Proportional-to-size, Proportional-to-size-squared, and Proportional-to-size-cubed ABBs were used.

A Mixture ABB that is centered around an Ignorable ABB (e.g. Inverse-to-size-squared, Inverse-to-size, Ignorable, Proportional-to-size, Proportional-to-size-squared) is apt to provide inferences similar to an Ignorable ABB, but with larger standard errors that presumably account for the uncertainly regarding the missing data mechanism. The U-Shaped and Fishhook ABBs can also be incorporated into a Mixture ABB along with other ABBs if the imputer believes that these ABBs represent plausible missing data mechanisms.

A nonignorable ABB is a very general procedure and can be incorporated into most hot-deck procedures, not just the procedure described here. Depending on the goals of the imputer, a nonignorable ABB can be used to provide a single inference that does not assume ignorability and/or to check the sensitivity of inferences to different ignorability assumptions.

A desirable approach has been outlined by Daniels and Hogan (2008), namely 1) explore the sensitivity of inferences to unverifiable missing data assumptions, 2) characterize the uncertainty about these assumptions, and 3) incorporate subjective beliefs about the distribution of missing responses. We see connections between these goals and the use of nonignorable ABBs. Specifically, by analyzing data using several different ABBs, the analyst can explore the sensitivity of inferences to different missing data assumptions. Use of the mixture ABB approach allows the analyst to characterize uncertainty about ABB assumptions. And the choice of the ABB itself, whether it favors small or larger donors incorporates subjective beliefs about why values are missing. Without the benefit of external sources of information to anchor the degree of nonignorability, there is inevitably some subjectivity in such approaches, and there is a lingering challenge regarding how to relate statements about subjective uncertainty in a convincing manner to the coverage properties of interval estimates. We see this as area worthy of further methodological development. But akin to sensitivity analyses in causal-inference settings (Cornfield et al. 1959, Rosenbaum 2002), quantification of the degree of sensitivity in significance tests for quantities of interest can provide valuable insights to help further scientific understanding.