Positive association between cognitive ability and cortical thickness in a representative US sample of healthy 6 to 18 year-olds

Abstract

Neuroimaging studies, using various modalities, have evidenced a link between the general intelligence factor (g) and regional brain function and structure in several multimodal association areas. While in the last few years, developments in computational neuroanatomy have made possible the in vivo quantification of cortical thickness, the relationship between cortical thickness and psychometric intelligence has been little studied. Recently, cortical thickness estimations have been improved by the use of an iterative hemisphere-specific template registration algorithm which provides a better between-subject alignment of brain surfaces. Using this improvement, we aimed to further characterize brain regions where cortical thickness was associated with cognitive ability differences and to test the hypothesis that these regions are mostly located in multimodal association areas. We report associations between a general cognitive ability factor (as an estimate of g) derived from the four subtests of the Wechsler Abbreviated Scale of Intelligence and cortical thickness adjusted for age, gender, and scanner in a large sample of healthy children and adolescents (ages 6-18, N=216) representative of the US population. Significant positive associations were evidenced between the cognitive ability factor and cortical thickness in most multimodal association areas. Results are consistent with a distributed model of intelligence.

Introduction

A number of reports have shown that scores on various tests of intelligence and cognitive ability are correlated with regional brain structure and function (Colom et al., 2006; Deary et al., 2006; Duncan et al., 2000; Gray et al., 2003; Jung and Haier, 2007; Schmithorst and Holland, 2006). A recent review and meta-analysis, suggested that a distributed network of multimodal association areas consisting of the dorsolateral prefrontal cortex (DLPF), the inferior and superior parietal lobule, the anterior cingulate cortex (ACC) and parts of the temporal and occipital lobes, seems to be highly correlated structurally, functionally and/or biochemically to general intellectual abilities (Jung and Haier, 2007). This resulted in the proposal of a Parieto-Frontal Integration Theory (P-FIT) (Jung and Haier, 2007). According to the P-FIT, sensory information is first processed by temporal and occipital areas for subsequent integration and abstraction in parietal areas. Problem evaluation is then implemented by the prefrontal cortex and response selection mediated via the anterior cingulate.

Some of the structural imaging data that has served to develop the P-FIT model stems from work conducted using Voxel-Based Morphometry (VBM); a brain imaging analysis method that essentially produces, for each subject, concentration maps representing tissue proportion in local neighbourhoods. More specifically, to each voxel (ie data point in a subject's brain) becomes attached a value representing a distance-weighted estimation of the proportion of a tissue of interest (eg gray matter) that is present in its vicinity. These VBM-produced concentration maps can be influenced by a multitude of factors (Ashburner and Friston, 2001). For instance, in the cortex, VBM-related associations with gray matter concentration for a given region can be due, among other things, to differences in gray matter volume, shape of cortical folding, and/or misalignment of cortical gyri between subjects. Even if it were possible to ascertain that VBM-related gray matter associations were due exclusively to differences in cortical volume, this would still not disambiguate cortical surface-related from cortical thickness-related volume differences.

Developments in computational neuroanatomy have now made possible MRI-based quantification of cortical thickness. (Duncan et al., 2004; Fischl and Dale, 2000; Kim et al., 2005; Kriegeskorte and Goebel, 2001; MacDonald et al., 2000; Mangin et al., 2004; Thompson et al., 2004; Tohka et al., 2004). In contrast to VBM, MRI-based cortical thickness quantification follows cortical folding patterns and captures the distance between white matter surface and pial gray matter surface, producing scalar values measured in millimeters throughout the cerebrum. It has been shown to be sensitive to differences in cortical thickness as small as 0.29 mm between groups with 100 subjects or more (Lerch and Evans, 2005). Not only can cortical thickness quantification allow the examination of associations between variables of interest and regional cortical thickness, but it also can provide a measure of the size of an effect in millimeters of cortical thickness per unit of variable of interest. Importantly, cortical thickness has been shown to be an index of normal brain development (O'Donnell et al., 2005; Shaw et al., 2008; Sowell et al., 2004).

Using fully automated measures of cortical thickness by Constrained Laplacian Anatomic Segmentation using Proximity (CLASP), Shaw et al. (2006) investigated, in collaboration with our lab at the Montreal Neurological Institute (MNI), the relationship between IQ and regional cortical thickness using selected subtests from age-appropriate Wechsler intelligence scales (Wechsler, 1989, 1991, 1997). A main finding was that individuals having an estimated IQ in the superior range (ie >121) had a generally thicker cortex (primarily in frontal areas) during their late childhood to early adulthood (ie between 8.6 to 29 years of age) than subjects with a lower IQ. However, the pattern was reversed for early childhood (ie between 3.8 and 8.4 years of age) as high IQ was associated with a thinner cortex in the same areas.

Recently, an iterative hemisphere-specific template registration algorithm that provides an improved between-subject alignment of brain surfaces, when compared with the one used for the Shaw et al. (2006) study, was developed and implemented as a new step in cortical thickness estimation using CLASP (Lyttelton et al., 2007).

As the association between regional cortical thickness and psychometric intelligence has been little studied, we aimed to examine this relationship in a new sample of children and adolescents using the recently developed template registration algorithm. Our aims were to further characterize and identify brain areas where cortical thickness was associated with cognitive performance and to determine whether such areas were compatible with the recently proposed P-FIT (Jung and Haier, 2007). In order to do this, data were obtained from the Pediatric MRI Data Repository (database version 2.0) created by the NIH MRI Study of Normal Brain Development. This is a multi-site, longitudinal study of typically developing children, from ages newborn through young adulthood, conducted by the Brain Development Cooperative Group and supported by the National Institute of Child Health and Human Development, the National Institute on Drug Abuse, the National Institute of Mental Health, and the National Institute of Neurological Disorders and Stroke (Contract #s N01-HD02-3343, N01-MH9-0002, and N01-NS-9-2314, -2315, -2316, -2317, -2319 and -2320). A listing of the participating sites and of the study investigators can be found at http://www.bic.mni.mcgill.ca/nihpd/info/participating_centers.html. The NIH Pediatric MRI study was organized around two “objectives”, corresponding to two age groups, the largest being Objective 1, comprised of subjects aged between 4:6 to 18:3 years at Visit 1 (ie time 1). Only data from Objective 1, Visit 1, were used here.

Experimental Procedures

Sampling and recruitment

The population-based sampling method implemented in the NIH Pediatric MRI study was used to minimize biases that can be present in samples of convenience in order to maximize the generalizability of the data collected. Based on available US Census 2000 data, a representative healthy sample of 433 subjects was recruited into objective-1 of the NIHPD study at 6 pediatric study centers: Children's Hospital—Boston, Children's Hospital Medical Center—Cincinnati, University of Texas Houston Medical School—Houston, UCLA Neuropsychiatric Institute and Hospital—Los Angeles, Children's Hospital of Philadelphia—Philadelphia, and Washington University—St. Louis. A sampling plan for each pediatric center was developed from the Census data so as to allow neighborhood demographic variables to be estimated for corresponding zip codes (so called geocoding). This allowed targeted recruitment and comparison to the general population by reference to geocoded census data. Recruitment was monitored continuously in order to assure that the sample recruited across all pediatric centers was demographically representative on the basis of variables that included age, gender, ethnicity, and socioeconomic status. Once specific demographic target goals were reached, enrollment ‘cells’ were closed. As this study aimed at recruiting healthy subjects, exclusion criteria included (but were not limited to) prior history of most Axis I psychiatric disorders, neurological, or other medical illness with CNS implications (eg malignancy, systemic rheumatologic illness, diabetes), an IQ < 70, intra-uterine exposure to substances known or highly suspected to alter brain structure or function, and prior family history (first degree relative) of inherited neurological disorder or other inherited illness with CNS implications. For a more extensive description of sampling procedures, see (Evans and Brain Development Cooperative Group, 2006). All data were transferred electronically to the data coordinating center at the Montreal Neurological Institute, and entered into a MYSQL database that allowed full interrogation of the data (Evans and Brain Development Cooperative Group, 2006).

Psychometric Measures

Extensive batteries of behavioral measures were obtained from recruited subjects on the day of or within a few days of scanning -- for a thorough description, see (Evans and Brain Development Cooperative Group, 2006). The principal intelligence measure used here was the Wechsler Abbreviated Scale of Intelligence (WASI) (Wechsler, 1999) administered to children ages 6 and older. Thus, the same test was used to measure intelligence across the age range analyzed in this paper. The WASI includes vocabulary, similarities, matrix reasoning, and block design subtests. Subtest Tscores were subjected to a principal component analysis (unrotated method of extraction) to derive a measure of their shared variance as an estimate of general cognitive ability for each subject. Scree plot analysis and the eigenvalues-greater-than-1 rule both indicated that there was a single component and that it accounted for about 48.6% of the total variance in test performance. Scores on this first unrotated component were saved as standardized scores with a mean of 0 and a standard deviation of 1. Although we used principal components analysis, we adopt the much-used convention of naming the first unrotated principal component, the general cognitive factor derived from the four subtests.

It could be argued that IQ scores could have been used as a measure of general cognitive ability instead of a general cognitive factor. While IQ provides perhaps a fair estimate of ‘average’ cognitive ability, a derived general factor is a more optimal measure of general intelligence (Carroll, 1993; Colom et al., 2006; Johnson et al., 2004; Johnson et al., 2008; Neisser et al., 1996; Plomin and Spinath, 2002). This being said, it is noteworthy that the general cognitive factor derived here was very highly correlated with WASI Full Scale IQ (r = 0.99, p<0.001).

MRI Acquisition Protocol

A 3D T1-weighted (T1W) Spoiled Gradient Recalled (SPGR) echo sequence was obtained with 1mm isotropic data acquired sagittally from the entire head. Slice thickness of ∼1.5mm was allowed for GE scanners due to their limit of 124 slices. In addition, T2-weighted (T2W) and proton density weighted (PDW) images were acquired using a 2D multi-slice (2mm) dual echo fast spin echo (FSE) sequence. Total acquisition time was ∼25 minutes and was often repeated when indicated by the scanner-side quality control process. Some subjects were unable to tolerate this procedure and received a fallback protocol that consisted of shorter 2D acquisitions with slice thicknesses of 3mm (Evans and Brain Development Cooperative Group, 2006).

MR Image Processing

All MR images were submitted to the CIVET pipeline (version 1.1.9) (http://wiki.bic.mni.mcgill.ca/index.php/CIVET) developed at the MNI for fully automated structural image analysis (Ad-Dab'bagh et al., 2006). The main pipeline processing steps include:

1. Linearly register native (ie original) MR images to standardized MNI-Talairach space based on the ICBM152 data set (Collins et al., 1994; Mazziotta et al., 1995; Talairach and Tournoux, 1988). This step is implemented in order to account for gross volume differences between subjects.

2. Correct for intensity non-uniformity artifacts using N3 (Sled et al., 1998). These artifacts are introduced by the scanner and need to be removed to minimize, in the current context, biases in estimating gray matter boundaries.

3. Classify the image into white matter (WM), gray matter (GM), cerebrospinal fluid (CSF) and background using a neural net classifier (INSECT) (Zijdenbos et al., 2002).

4. Fit images with a deformable mesh model to extract 2-dimensional inner (WM/GM interface) and outer (pial) cortical surfaces for each hemisphere with the 3^rd edition of CLASP. This produces high-resolution hemispheric surfaces with 81924 polygons each (40962 vertices (ie cortical points) per hemisphere) (Kabani et al., 2001; Kim et al., 2005; Lyttelton et al., 2007; MacDonald et al., 2000). This step places 40962 cortical points on each hemisphere for each subject.

5. Register both cortical surfaces for each hemisphere non-linearly to a high resolution average surface template generated from the ICBM152 data set in order to establish inter-subject correspondence of the cortical points (Grabner et al., 2006; Lyttelton et al., 2007; Mazziotta et al., 1995).

6. Apply a reverse of the linear transformation performed on the images of each subject to allow cortical thickness estimations to be made at each cortical point in the native space of the magnetic resonance image (Ad-Dab'bagh et al., 2005). This avoids having cortical thickness estimations biased by the scaling factor introduced by the linear transformations (ie step 1) applied to each subject's brain.

7. Calculate cortical thickness at each cortical point using the ^tlink metric (Lerch and Evans, 2005) and blur each subject's cortical thickness map using a 20-millimeter full width at half maximum surface-based diffusion smoothing kernel (a necessary step to impose a normal distribution to corticometric data and to increase signal to noise ratio) (Chung et al., 2001).

Subjects with imaging and cognitive data

Of the 433 subjects recruited, 392 had MRI acquisitions that passed raw imaging data quality control (QC). Of these 392 subjects, 33 were under 6 years of age and had no WASI evaluations. Due to the sensitivity of post-acquisition processing methods that produce corticometric measures on the native MR images, all subjects with fallback acquisition protocols, whether for T1W or T2W/PDW spectra, were excluded from the present study. More specifically, of the remaining 359 subjects with the full complement of MRI and behavioral data, 107 had T1W and/or T2W/PD fallback protocols and so 252 subjects were retained. Finally, a visual QC (blinded as to the IQ of the subjects) of the native cortical thickness images of each subject was implemented to make sure that there were no important aberrations in cortical thickness estimations for a given subject. 36 subjects had problems with their cortical thickness maps (eg in some cases, gyri were fused together or parts of the frontal lobe were truncated) and were eliminated from further analysis, leaving a final size sample of 216 subjects. For a comparison of demographic and IQ characteristics between the Objective 1 visit 1 sample and the analyzed sample, see Table 1.

Table 1.

Demographic and WASI Full Scale IQ (FSIQ) characteristics of original sample and of analyzed sample

	Objective 1 visit 1 Sample	Accepted Sample	Statistics
	n=433	n=216
Age (yrs)	10.4±3.8	12.1±3.5	t = 5.51, p < 0.001
Proportion of males	48%	46%	χ2 = 0.17, p =.68
Proportion with low/medium/high adjusted SES*	22.9%/41.6%/35.5%	22.6%/40.6%/36.4%	χ2 = 0.0071, p >.99
WASI-FSIQ**	110.7±12.5**	111.0±11.3	t = 0.30, p =0.77
Proportion of Whites/African Americans/Other	78.9%/9.2%/11.9%	76.4%/8.3%/15.3%	χ2 = 1.48, p =.48

When appropriate, means ± standard deviations are provided

^*Based on the US Departement of Housing and Urban Development method for comparing family income levels as a function of regional costs of living

^**WASI IQ data available for only 380 subjects out of 433 that were initially recruited

^***The ‘Other’ category includes American Indian, Alaskan Native, Asian, Native Hawaiian or Other Pacific Islander, and those for which ethnicity or race was not provided or for which parents came from different racial or ethnic background.

Statistical Analyses

Statistical analyses were implemented using SurfStat, a statistical toolbox (Worsley et al., 2004) created for MATLAB 7 (The MathWorks, Inc.) by Dr. Keith Worsley (http://www.math.mcgill.ca/keith/surfstat/) at the MNI. Each subject's absolute native-space cortical thickness was linearly regressed against the general cognitive ability factor at each cortical point after accounting for the effects of gender, age, and MRI scanners from the six sites. In order to take into account previously reported quadratic and cubic effects of age on cortical thickness (Shaw et al., 2008), simple linear, quadratic, and cubic models were tested for the age term. As quadratic and cubic models did not provide a significantly better fit with the data, a simple first order linear model was retained. Although handedness was initially included as a regressor, it was found to add nothing to the model and so was discarded. This is in part explained by the fact that only 9.7% of the current sample was non right-handed and that between 31% and 54% of non right-handed individuals (ie mixed, ambidextrous, or left-handed) are known to have the same pattern of hemispheric dominance as right-handers (Isaacs et al., 2006). This would lead to an expectation of only about 10 to 14 subjects in our sample of 216 having right-hemispheric dominance.

In summary, the following model was fitted to each one of the 81924 cortical points:

$$\text{Y}\sim {\text{b}}_0+{\text{b}}_1\text{CF}+{\text{b}}_2\text{Age}+{\text{b}}_3\text{Gender}+{\text{b}}_4\text{Scanner}+\mathrm{\epsilon }$$

where:

• Y = Cortical Thickness

• CF = Cognitive Factor

• b₀ = Y intercept

• b₁ to b₄ = regression coefficients for effects of the different regressors

• ε = error term

For each cortical point, the coefficient of the CF regressor, b₁, was estimated and a resultant t-test value calculated, thereby producing a 3D t-statistic map. A t-statistic threshold of statistical significance was established, taking into account multiple comparisons via the False Discovery Rate (FDR) method (Benjamini and Hochberg, 1995; Genovese et al., 2002). The FDR value is the expected proportion of false positives among all cortical points where the t-value is above the selected threshold. Thus, setting the threshold to an FDR of 0.05 implies that it is expected that 5% of all cortical points having a t-value above threshold, are false positives. For the purpose of visualization, resultant thresholded t-value Pearson correlation maps were projected on an average surface template generated from the ICBM152 data set.

In addition to examining results for the whole sample, the cohort was split into two equal subgroups of 108 subjects each in order to see whether or not the same areas were associated with intelligence differences in both young children and adolescents. After generating results for the entire selected sample (n=216), analyses were performed separately for young children (age range: 6 to 11.9 years) and adolescents (age range: 12 to 18:3 years). A ‘Group by CF’ interaction term (ie b₅Group*CF) was added to the model in order to make a formal statistical comparison between the groups. The interaction was evaluated at each cortical point to identify regions where the association between cortical thickness and intelligence was significantly stronger in adolescents than in young children, and vice versa. This being done, the overall effect of age was estimated on the whole sample by replacing the ‘Group by CF’ interaction term by an ‘Age by CF’ interaction term (ie b₅Age*CF).

Results

Except for mean age, no statistically significant demographic differences were evidenced between the full NIH Pediatric MRI sample and the analyzed subjects (for whom WASI IQ data, good raw scan data, and good cortical thickness estimations were available) (see Table 1). The greater mean age for the analyzed sample is mostly due to excluding children below age 6 (ie the lower age limit of the WASI).

Regression of cortical thickness against the general cognitive factor at each cortical point —while controlling for age, gender, and scanner — revealed a positive association between cortical thickness and the general cognitive factor in several areas distributed throughout the brain. Statistically significant foci were largely localized in multimodal association areas and, while tending to be symmetrical, were slightly more extensive on the left hemisphere (see Figure 1 and Table 2). Correlations in statistically significant foci were in the modest to moderate range (0.15 to 0.32) (see Figure 1).

Figure 1.

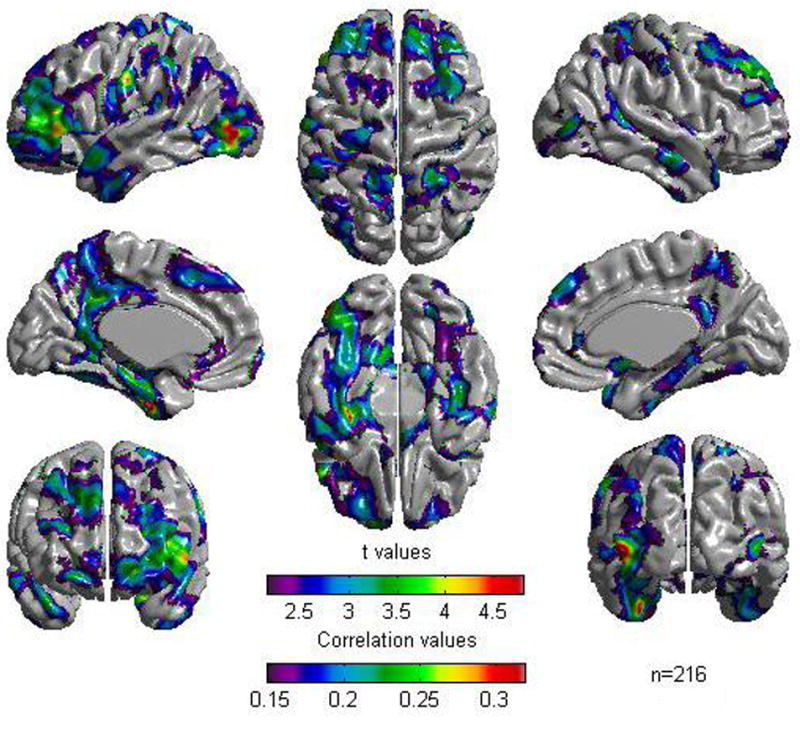
Results of Cortical Thickness regressed against the cognitive factor for the whole sample of 216 subjects. A False Discovery Rate threshold of 0.05 is used to control for multiple comparisons. Colors, representing Pearson correlations as well as Student t values, are superimposed on left and right lateral average surface templates generated from the ICBM152 data set. Results are corrected for gender, age, and scanner.

Table 2.

Cortical point coordinates within areas of association between cortical thickness and general cognitive ability for the whole sample (FDR threshold = 0.05)

Brodmann Area	Region Name	X, Y, Z Coordinates in MNI space
Left Frontal
BA 4	Dorsal Precentral gyrus	-31, -19, 73
BA 6	Superior frontal gyrus	-21, 16, 63
BA 6	Ventral Precentral gyrus	-60, 0, 23
BA 8	Medial frontal gyrus	-4, 44, 47
BA 9	Middle frontal gyrus	-26, 51, 31
BA 10	Middle frontal gyrus	-18, 66, -5
BA 45	Inferior frontal gyrus	-55, 28, 4
BA 46	Middle frontal gyrus	-43, 45, 21
BA 47	Inferior frontal gyrus	-50, 39, -3
Right Frontal
BA 4	Dorsal precentral gyrus	44, -13, 63
BA 6	Superior frontal gyrus	22, 16, 63
BA 8	Medial frontal gyrus	4, 42, 49
BA 9	Superior frontal gyrus	13, 46, 40
BA 10	Middle frontal gyrus	14, 63, -9
BA 46	Middle frontal gyrus	46, 42, 21
Left Parietal
BA 1, 2, 3 *	Postcentral gyrus	-62, -11, 35
BA 7	Precuneus	-6, -65, 52
BA 39	Angular gyrus	-47, 62, 47
BA 40	Supramarginal gyrus	-64, -45, 27
Right Parietal
BA 1, 2, 3 *	Postcentral gyrus	58, -17, 48
BA 7	Precuneus	4, -54, 59
BA 7	Superior parietal lobule	17, -47, 72
BA 39	Angular gyrus	31, -62, 53
Left Temporal
BA 20	Inferior temporal gyrus	-55, -8, -39
BA 21	Middle temporal gyrus	-60, 1, -27
BA 22	Wernicke's area	-65, -43, 20
BA 28	Parahippocampal gyrus	-25, -10, -35
BA 36	Lingual gyrus	-17, -48, -9
BA 36	Medial occipito-temporal gyrus	-28, -50, -18
BA 37	Lateral occipito-temporal gyrus	-47, -47, -14
BA 38	Temporal pole	-48, 17, -27
BA 41	Planum temporale	-37, -30, 16
Right Temporal
BA 20	Inferior temporal gyrus	53, -7, -40
BA 21	Middle temporal gyrus	63, -7, -22
BA 28	Parahippocampal gyrus	22, -23, -27
BA 36	Medial occipito-temporal gyrus	29, -52, -18
BA 38	Temporal pole	47, 19, -26
Left Occipital
BA 18	Lateral occipital gyrus	-36, -92, -1
BA 19	Lateral occipital gyrus	-48, -82, 2
Right Occipital
BA 18	Lateral occipital gyrus	32, -94, -6
BA 19	Lateral occipital gyrus	50, -75, 7
Left Cingulate
BA 23, 26, 29, 30, 31 *	Posterior cingulate gyrus	-6, -42, 33
BA 24, 33 *	Anterior cingulate gyrus	-4, 38, 6
Right Cingulate
BA 23, 26, 29, 30, 31 *	Posterior cingulate gyrus	3, -47, 27
BA 24, 33 *	Anterior cingulate gyrus	4, 38, 5
BA 25	Subcallosal area	2, 8, -9

^*These BA could not be distinguished from each other

Stratifying the sample into a subgroup of young children (mean IQ = 111.7, SD = 11.3) and a subgroup of adolescents (mean IQ = 110.3, SD = 11.4), revealed a similar picture to the one obtained with the whole sample for the group of adolescents but, as would be expected due to decreased power, with less extensive areas of association between cortical thickness and the general cognitive factor (see Figure 2 and Table 3). For the group of young children, no association was found between cortical thickness and the general cognitive factor under the FDR threshold of 0.05. However, relaxing the threshold to 0.2, revealed a similar picture (see figure 3 and Table 4) to the one obtained for adolescents. In both groups, the most consistent areas of association between cortical thickness and the general cognitive factor were in lateral prefrontal, occipital extrastriate, and parahippocampal areas. In statistically significant foci, correlations ranged between .25 and .44 for adolescents and between .2 and .33 for young children. Examination of the regressor coefficients of the ‘Group by CF’ and ‘Age by CF’ terms revealed no statistically significant group or age effects on the associations between cortical thickness and the cognitive ability factor. This remained the case for all cortical points even after relaxing the threshold to an FDR value of 0.5.

Figure 2.

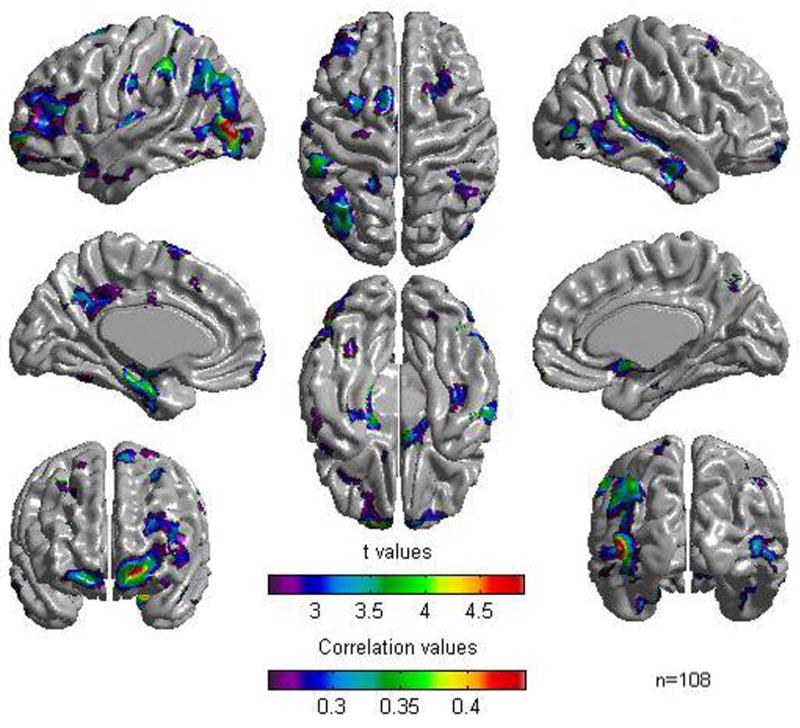
Results of Cortical Thickness regressed against the cognitive factor for the sample of adolescents (n = 108). A False Discovery Rate threshold of 0.05 is used to control for multiple comparisons. Colors, representing Pearson correlations as well as Student t values, are superimposed on left and right lateral average surface templates generated from the ICBM152 data set. Results are corrected for gender, age, and scanner.

Table 3.

Cortical point coordinates within areas of association between cortical thickness and general cognitive ability for the subgroup of adolescents (FDR threshold = 0.05)

Brodmann Area	Region Name	X, Y, Z Coordinates in MNI space
Left Frontal
BA 4	Dorsal Precentral gyrus	-30, -15, 73
BA 6	Superior frontal gyrus	-8, 6, 71
BA 6	Middle frontal gyrus	-37, 4, 40
BA 9	Middle frontal gyrus	-26, 53, 26
BA 10	Middle frontal gyrus	-18, 66, -5
BA 45	Inferior frontal gyrus	-52, 35, 4
BA 46	Middle frontal gyrus	-45, 42, 19
Right Frontal
BA 6	Superior frontal gyrus	-45, 42, 19
BA 10	Superior frontal gyrus	28, 62, -11
Left Parietal
BA 1, 2, 3 *	Postcentral gyrus	-61, -13, 34
BA 7	Precuneus	-65, -55, 39
BA 39	Angular gyrus	-47, 61, 46
BA 40	Supramarginal gyrus	-60, -37, 46
Right Parietal
BA 1, 2, 3 *	Postcentral gyrus	59, -16, 41
BA 7	Precuneus	4, -54, 59
BA 7	Superior parietal lobule	17, -47, 72
BA 39	Angular gyrus	31, -62, 53
Left Temporal
BA 21	Middle temporal gyrus	-60, 1, -27
BA 22	Wernicke's area	-45, -54, 29
BA 28	Parahippocampal gyrus	-23, -11, -35
BA 36	Medial occipito-temporal gyrus	-28, -50, -18
BA 38	Temporal pole	-49, 16, -26
Right Temporal
BA 20	Inferior temporal gyrus	56, -12, -31
BA 21	Middle temporal gyrus	64, -10, -20
BA 36	Medial occipito-temporal gyrus	39, -20, -31
Left Occipital
BA 18	Lateral occipital gyrus	-37, -90, 0
BA 19	Lateral occipital gyrus	-48, -82, 2
Right Occipital
BA 18	Lateral occipital gyrus	33, -93, -6
BA 19	Lateral occipital gyrus	50, -78, 3
Left Cingulate
BA 23, 26, 29, 30, 31 *	Posterior cingulate gyrus	-3, -48, 30
Right Cingulate
BA 24, 33 *	Anterior cingulate gyrus	4, 38, 6
BA 25	Subcallosal area	3, 11, -9

^*These BA could not be distinguished from each other

Figure 3.

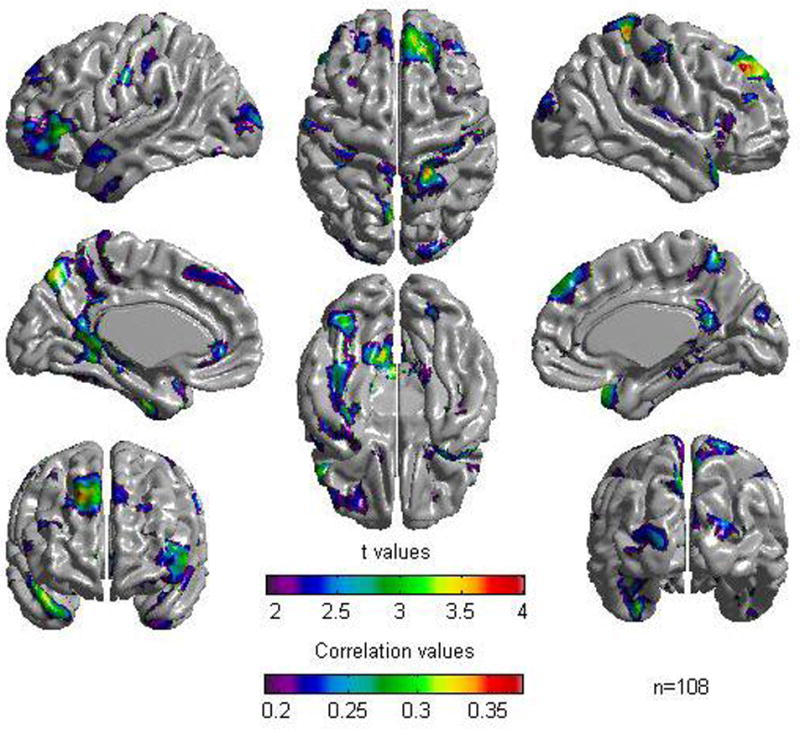
Results of Cortical Thickness regressed against the cognitive factor for the sample of young children (n = 108). A False Discovery Rate threshold of 0.2 is used to control for multiple comparisons. Colors, representing Pearson correlations as well as Student t values, are superimposed on left and right lateral average surface templates generated from the ICBM152 data set. Results are corrected for gender, age, and scanner.

Table 4.

Cortical point coordinates within areas of association between cortical thickness and general cognitive ability for the subgroup of young children (FDR threshold = 0.2)

Brodmann Area	Region Name	X, Y, Z Coordinates in MNI space
Left Frontal
BA 4	Dorsal Precentral gyrus	-34, -31, 73
BA 6	Ventral Precentral gyrus	-56, -2, 27
BA 8	Medial frontal gyrus	-4, 42, 47
BA 9*	Middle frontal gyrus	-26, 47, 37
BA 45*	Inferior frontal gyrus	-54, 36, -2
BA 46*	Middle frontal gyrus	-40, 71, 8
BA 47*	Inferior frontal gyrus	-51, 37, -10
Right Frontal
BA 8	Medial frontal gyrus	5, 51, 41
BA 9*	Superior frontal gyrus	15, 45, 44
BA 46	Middle frontal gyrus	41, 42, 24
Left Parietal
BA 1, 2, 3 *	Postcentral gyrus	-62, -11, 39
BA 7	Precuneus	-6, -66, 54
BA 40	Supramarginal gyrus	-64, -46, 26
Right Parietal
BA 1, 2, 3 *	Postcentral gyrus	56, -17, 48
BA 7	Precuneus	12, -59, 58
Left Temporal
BA 20	Inferior temporal gyrus	-51, -6, -35
BA 22	Wernicke's area	-63, -48, 27
BA 28	Parahippocampal gyrus	-28, -15, -32
BA 36	Lingual gyrus	-16, -48, -8
BA 36	Medial occipito-temporal gyrus	-30, -45, -19
BA 37	Lateral occipito-temporal gyrus	-47, -41, -19
BA 38	Temporal pole	-38, 6, -42
BA 41	Planum temporale	-43, -33, 20
Right Temporal
BA 20	Inferior temporal gyrus	44, -11, -41
BA 21	Middle temporal gyrus	66, -11, -16
BA 36	Medial occipito-temporal gyrus	42, -24, -22
BA 38	Temporal pole	45, 19, -29
Left Occipital
BA 18	Lateral occipital gyrus	-31, -94, 3
BA 19	Lateral occipital gyrus	-33, -91, 15
Right Occipital
BA 18	Lateral occipital gyrus	28, -93, 20
BA 19	Lateral occipital gyrus	24, -98, 10
Left Cingulate
BA 23, 26, 29, 30, 31 *	Posterior cingulate gyrus	-11, -42, 34
BA 24, 33 *	Anterior cingulate gyrus	-5, 40, 4
Right Cingulate
BA 23, 26, 29, 30, 31 *	Posterior cingulate gyrus	3, -47, 27
BA 24, 33 *	Anterior cingulate gyrus	4, 38, 5

^*These BA could not be distinguished from each other

Discussion

Positive bilateral associations between cortical thickness and a general cognitive factor derived from the four WASI subtests were detected in many areas of the frontal, parietal, temporal, and occipital lobes for a large, representative sample of the US population between 6 and 18:3 years of age. Regions with the greatest relationship between cortical thickness and a general cognitive factor were observed in multimodal association areas. Young children (ie 6 to 11.9 year-olds) and adolescents (ie 12 to 18:3 year-olds) exhibited associations in the same areas and no statistically significant differences were observed between them.

Overall, results are consistent with distributed models of intelligence like the P-FIT (Jung and Haier, 2007). Our results, however, include more brain regions than highlighted by the P-FIT and place greater importance on medial structures than the P-FIT model does. Indeed, while absent from the P-FIT, the precuneus (part of the medial parietal lobe), the posterior cingulate, the dorsomedial prefrontal cortex, as well as the lingual and parahippocampal gyri, have all been identified here as being associated, bilaterally, with the general cognitive factor. Importantly, these are all known to be areas where information from different parts of the brain converges for high-level processing and have been shown to be involved with cognitive performance (Cavanna and Trimble, 2006; Eisenberg et al., 2005; Geake and Hansen, 2005; Gong et al., 2005; Haier et al., 2004; Hulshoff Pol et al., 2006; Shaw et al., 2006; Stoitsis et al., 2008; Westlye et al., 2008). While they are good candidates as modulators of general intelligence, these regions generally reached here lower levels of statistical significance than the regions highlighted by the P-FIT. It could be speculated that this reflects a genuine but relatively weaker association with intelligence than the P-FIT regions, making them less consistently detected across studies and leading to their exclusion from the P-FIT.

Observing a decrease in statistical significance in both children and adolescents, when compared with the group as a whole, could be attributed to several factors. However, in both subsamples, this decrease is most likely due to reduced statistical power due to dividing the sample in two. The relative greater decrease observed for the subsample of young children (ie 6 to 11.9 years of age) may have been due to the difficulty that many of them may have had with being immobile for a prolonged period of time in a scanner (Evans and Brain Development Cooperative Group, 2006). Indeed, micromovements, which may not have been sufficient to grossly distort the image and result in rejection as part of the quality control procedures, may have nonetheless induced a slight blurring effect on the white/gray matter interface and lead to a deterioration in the precision of cortical thickness estimations. Alternatively, it could be speculated that the association between cortical thickness and the cognitive ability factor is weaker or less homogeneous in young children in that age group, leading to a decrease in statistical significance.

Generally, current results support findings from the Shaw et al. study (2006) in terms of brain regions involved with intelligence differences (Shaw et al., 2006). In that previous study, while associations were predominantly in the prefrontal cortex, they also included significant areas of the parietal lobe and small areas of the occipital and temporal lobes. Here, we confirm and extend these findings, using the same FDR threshold as that used by the Shaw et al. study (2006), to encompass most if not all known cortical association areas. Such a finding is meaningful as these areas are specifically those known to be 1) involved in the processing of multimodal information converging from various regions of the brain, 2) those most likely to lead to post-lesional cognitive deficits and 3) the ones that have most frequently been theorized to be linked to intelligence differences (Jung and Haier, 2007). While finding an extension of the areas involved when compared with those reported in the Shaw et al. study may be due to important differences in the sample selection process, it is most likely due to improved surface alignment within CLASP (Lyttelton et al., 2007).

A strength of the current study is the use of a relatively large representative sample of the US population with ages ranging from 6 to 18:3 years. As the cost of scanning a large sample of subjects and as the methodological complications of recruiting one that is representative of a general population are both generally prohibitive, most imaging studies have been limited to recruiting relatively small samples of convenience. Another strength of the current study is the reliance on a single IQ test (ie the WASI) across the entire age range analyzed. The earlier study (Shaw et al., 2006) relied on measures that differed among the subjects studied (different number of subtests administered as well as different tests). While the use of a general cognitive factor derived from four disparate mental tests is also a strength here, a limitation is that this general factor was derived from a relatively small group of tests.

Being correlational in nature, the results presented here are bound by the usual limitations associated with such data. For instance, finding associations between a general cognitive ability factor and a distributed network does not necessarily imply an involvement of the whole network in cognitive ability differences. Indeed, it is possible to imagine a mechanism influencing cortical thickness throughout a given network but with only a subset of this network being responsible for intelligence differences. As the same mechanism would influence cortical thickness throughout the network, and assuming the existence of an association between cortical thickness and intelligence, cortical thickness estimations in components of this network would correlate with each other as well as with intelligence. Yet, only cortical thickness in the subset of this network responsible for intelligence differences would really be of importance. This being said, finding a correlation between cortical thickness and a general cognitive ability factor preferentially distributed in known multimodal association areas is pleasing to the mind and suggests that links between mental ability and cortical thickness in these areas are not simply inconsequential findings.

In summary, using the recently developed cortical thickness metric with improved between-subject alignment of brain surfaces, regional cortical thickness in multimodal association areas was found to be positively associated with a general cognitive factor. While previous studies have shown an involvement of cortical association areas, it is the first time that an association between a general cognitive ability factor and essentially all cortical association areas is evidenced in the same study. Results further suggest that similar areas of the cortex are related to intelligence differences in both children and adolescents. Results exhibit a good level of generalizability as they have been evidenced on a relatively large representative healthy young sample of the US population. As a next step, it would be informative to conduct the same analyses on a sample of individuals that spans the whole adult age range. Also, it is noteworthy that cortical thickness is not, on its own, sufficient to describe all aspects of cortical shape. Cortical surface area, cortical complexity (or gyrification), and cortical volume complete the corticometric measurements that are possible and would further add to the characterization of cortical shape associations with intelligence. We are currently in the process of implementing some such analyses.

Appendix A. Brain Development Cooperative Group

Key personnel from the six pediatric study centers are as follows: Children's Hospital Medical Center of Cincinnati, Principal Investigator William S. Ball, M.D., Investigators Anna Weber Byars, Ph.D., Mark Schapiro, M.D., Wendy Bommer, R.N., April Carr, B.S., April German, B.A., Scott Dunn, R.T.; Children's Hospital Boston, Principal Investigator Michael J. Rivkin, M.D., Investigators Deborah Waber, Ph.D., Robert Mulkern, Ph.D., Sridhar Vajapeyam, Ph.D., Abigail Chiverton, B.A., Peter Davis, B.S., Julie Koo, B.S., Jacki Marmor, M.A., Christine Mrakotsky, Ph.D., M.A., Richard Robertson, M.D., Gloria McAnulty, Ph.D; University of Texas Health Science Center at Houston, Principal Investigators Michael E. Brandt, Ph.D., Jack M. Fletcher, Ph.D., Larry A. Kramer, M.D., Investigators Grace Yang, M.Ed., Cara McCormack, B.S., Kathleen M. Hebert, M.A., Hilda Volero, M.D.; Washington University in St. Louis, Principal Investigators Kelly Botteron, M.D., Robert C. McKinstry, M.D., Ph.D., Investigators William Warren, Tomoyuki Nishino, M.S., C. Robert Almli, Ph.D., Richard Todd, Ph.D., M.D., John Constantino, M.D.; University of California Los Angeles, Principal Investigator James T. McCracken, M.D., Investigators Jennifer Levitt, M.D., Jeffrey Alger, Ph.D., Joseph O'Neil, Ph.D., Arthur Toga, Ph.D., Robert Asarnow, Ph.D., David Fadale, B.A., Laura Heinichen, B.A., Cedric Ireland B.A.; Children's Hospital of Philadelphia, Principal Investigators Dah-Jyuu Wang, Ph.D. and Edward Moss, Ph.D., Investigators Robert A. Zimmerman, M.D., and Research Staff Brooke Bintliff, B.S., Ruth Bradford, Janice Newman, M.B.A. The Principal Investigator of the data coordinating center at McGill University is Alan C. Evans, Ph.D., Investigators Rozalia Arnaoutelis, B.S., G. Bruce Pike, Ph.D., D. Louis Collins, Ph.D., Gabriel Leonard, Ph.D., Tomas Paus, M.D., Alex Zijdenbos, Ph.D., and Research Staff Samir Das, B.S., Vladimir Fonov, Ph.D., Luke Fu, B.S., Jonathan Harlap, Ilana Leppert, B.E., Denise Milovan, M.A., Dario Vins, B.C.,, and at Georgetown University, Thomas Zeffiro, M.D., Ph.D. and John Van Meter, Ph.D. Ph.D. Investigators at the Neurostatistics Laboratory, Harvard University/McLean Hospital, Nicholas Lange, Sc.D., and Michael P. Froimowitz, M.S., work with data coordinating center staff and all other team members on biostatistical study design and data analyses. The Principal Investigator of the Clinical Coordinating Center at Washington University is Kelly Botteron, M.D., Investigators C. Robert Almli Ph.D., Cheryl Rainey, B.S., Stan Henderson M.S., Tomoyuki Nishino, M.S., William Warren, Jennifer L. Edwards M.SW., Diane Dubois R.N., Karla Smith, Tish Singer and Aaron A. Wilber, M.S. The Principal Investigator of the Diffusion Tensor Processing Center at the National Institutes of Health is Carlo Pierpaoli, MD, Ph.D., Investigators Peter J. Basser, Ph.D., Lin-Ching Chang, Sc.D., Chen Guan Koay, Ph.D. and Lindsay Walker, M.S. The Principal Collaborators at the National Institutes of Health are Lisa Freund, Ph.D. (NICHD), Judith Rumsey, Ph.D. (NIMH), Lauren Baskir, Ph.D. (NIMH), Laurence Stanford, PhD. (NIDA), Karen Sirocco, Ph.D. (NIDA) and from NINDS, Katrina Gwinn-Hardy, M.D., and Giovanna Spinella, M.D. The Principal Investigator of the Spectroscopy Processing Center at the University of California Los Angeles is James T. McCracken, M.D., Investigators Jeffry R. Alger, Ph.D., Jennifer Levitt, M.D., Joseph O'Neill, Ph.D.