Abstract
The concept of assumption adequacy averaging is introduced as a technique to develop more robust methods that incorporate assessments of assumption adequacy into the analysis. The concept is illustrated by using it to develop a method that averages results from the t-test and nonparametric rank-sum test with weights obtained from using the Shapiro-Wilk test to test the assumption of normality. Through this averaging process, the proposed method is able to rely more heavily on the statistical test that the data suggests is superior for each individual gene. Subsequently, this method developed by assumption adequacy averaging outperforms its two component methods (the t-test and rank-sum test) in a series of traditional and bootstrap-based simulation studies. The proposed method showed greater concordance in gene selection across two studies of gene expression in acute myeloid leukemia than did the t-test or rank-sum test. An R routine to implement the method is available upon request.
Keywords: Gene expression data analysis, microarray data, assumption assessment, assumption adequacy averaging, empirical Bayes
1. Introduction
Microarray technology enables researchers to simultaneously measure the messenger RNA expression of thousands of genes. A common objective of a microarray study is to identify genes that are differentially expressed (DE), i.e. have unequal mean or median expression across two or more groups. One basic approach to identifying DE genes is to apply a classical statistical method such as the t-test to the data for each gene and then adjust for multiple testing by estimating or controlling a multiple-testing error rate (Pounds 2006) such as the false discovery rate (Benjamini and Hochberg 1995) or empirical Bayes posterior (EBP; Efron et al., 2001) probability that the null hypothesis is true. A number of additional approaches that pool information across genes have also been developed in recent years. Some of these methods are reviewed by Allison et al. (2005) and Pounds et al. (2007).
One issue that has not been thoroughly examined to date is that of assumption adequacy. In applications involving only a few variables, it is accepted practice to assess the adequacy of the assumptions of possible methods to guide which methods to perform. For example, the t-test assumes that data values within each group are independently and identically distributed observations from a normal distribution. This assumption could be assessed using the procedure of Shapiro and Wilk (1965), which is commonly referred to as the Shapiro-Wilk test. If the assumption is violated, the data analyst might explore other possibilities, such as data transformations or use of the nonparametric Wilcoxon (1945) rank-sum test. The analysis of microarray data could reasonably be improved by formally assessing the adequacy of the assumptions of various methods under consideration. However, due to the large amount of data, it is infeasible to perform assumption adequacy analyses for microarray applications unless the process is automated in a reasonable way. Subsequently, assumption adequacy analyses are not routinely performed in the analysis of microarray data.
Therefore, we propose the concept of assumption adequacy averaging (AAA) as a technique to develop more robust methods of analysis that incorporate automated assessments of assumption adequacy into the analysis. Briefly, this method-development technique requires the investigator to select some competing analysis methods and describe an algorithm to use the results of assumption-adequacy testing to choose among those methods in a simpler setting. The technique utilizes empirical Bayesian principles described by Efron et al. (2001) and Pounds and Morris (2003) to develop a method that averages the results from competing methods with weights determined by tests of assumption adequacy. We use AAA to develop a method that combines results from the classical t-test and rank-sum tests with weights determined by using the Shapiro-Wilk test to assess the normality assumption.
The paper is organized as follows: Section 2 describes the AAA concept in general. Section 3 proves some desirable properties of AAA procedures. Section 4 uses AAA to develop a new analysis method. Section 5 presents the results of traditional simulations, bootstrap-based simulations using modified real data sets, and an example application. Section 6 includes discussion and concluding remarks.
2. THE GENERAL CONCEPT OF ASSUMPTION ADEQUACY AVERAGING
We propose AAA as a concept to develop more robust methods of analysis by combining the results of several methods with weights determined by a formal assessment of assumption adequacy. In general, AAA requires specification of competing methods of analysis, methods to assess the assumption(s) of one or more of these competing methods, and an algorithm that specifies which of the competing methods are preferred given the results of the assumption-adequacy testing. Additionally, AAA requires a method to compute empirical Bayes posterior (EBP) probabilities for the results of each competing method and the results of assumption-adequacy testing.
We now introduce some notation to more specifically describe the AAA concept in the simple case of developing a technique to average the results of two competing methods. We briefly describe the concept in more generality later. Suppose that we seek to test G hypotheses (one for each of G genes) of the form H0: θg = 0, g = 1,…, G. Suppose there are two methods,  1 and
1 and  2 that could be used to perform these tests. When used to perform each test,
2 that could be used to perform these tests. When used to perform each test,  1 produces a set of p-values
, one p-value per hypothesis (or gene in a microarray study). Similarly, the method
1 produces a set of p-values
, one p-value per hypothesis (or gene in a microarray study). Similarly, the method  2 produces a set of p-values
, one p-value per hypothesis.
2 produces a set of p-values
, one p-value per hypothesis.
Additionally, suppose that there exists a test 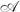 that tests G hypotheses of the form H0: Ag = 1, g = 1, …, G, where Ag = 1 (Ag = 0) indicates that a specific assumption of
that tests G hypotheses of the form H0: Ag = 1, g = 1, …, G, where Ag = 1 (Ag = 0) indicates that a specific assumption of  1 is (not) satisfied for gene g. Let Pa = {Pa1, Pa2, …, PaG} represent the set of p-values computed by
1 is (not) satisfied for gene g. Let Pa = {Pa1, Pa2, …, PaG} represent the set of p-values computed by 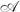 . Furthermore, suppose that given the true value of Ag, one can derive a reasonable decision rule
. Furthermore, suppose that given the true value of Ag, one can derive a reasonable decision rule 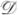 to choose a preferred method to test H0: θg = 0. In particular, let
to choose a preferred method to test H0: θg = 0. In particular, let 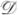 (Ag) = 1 if Ag = 1 and
(Ag) = 1 if Ag = 1 and 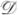 (Ag) = 2 if Ag = 0 so that
(Ag) = 2 if Ag = 0 so that 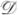 indicates whether method 1 or method 2 is preferred.
indicates whether method 1 or method 2 is preferred.
Now, let 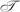 represent a method that estimates the empirical Bayes posterior (EBP) probability that each null hypothesis is true from a set of p-values. Pounds and Morris (2003) describe such a method. Their method fits a beta-uniform mixture (BUM) model to the p-values and then estimates the EBP for a specific p-value p as the ratio of the proportion of the density that is attributable to a uniform distribution to the value of the fitted model’s PDF at p. Allison et al. (2002) also describe a method to fit similar and more elaborate models to p-values to compute multiple-testing error metrics.
represent a method that estimates the empirical Bayes posterior (EBP) probability that each null hypothesis is true from a set of p-values. Pounds and Morris (2003) describe such a method. Their method fits a beta-uniform mixture (BUM) model to the p-values and then estimates the EBP for a specific p-value p as the ratio of the proportion of the density that is attributable to a uniform distribution to the value of the fitted model’s PDF at p. Allison et al. (2002) also describe a method to fit similar and more elaborate models to p-values to compute multiple-testing error metrics.
Let
, and
be the EBP estimates computed from P1, P2, and Pa, respectively. Clearly,
can be interpreted as EBP(Ag = 1), g = 1, …, G. Additionally, in light of the decision rule,
can be interpreted as EBP(θg = 0|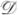 (Ag)=1) = EBP(θg = 0|Ag=1) and
can be interpreted as EBP(θg = 0|
(Ag)=1) = EBP(θg = 0|Ag=1) and
can be interpreted as EBP(θg = 0| 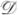 (Ag)=2) = EBP(θg = 0|Ag=0). From the law of total probabilities, we have
(Ag)=2) = EBP(θg = 0|Ag=0). From the law of total probabilities, we have
| (1) |
as an estimate of the probability that θg = 0. Of interest, this estimate accounts for an assessment of the assumption for gene g. Then, each hypothesis g with EBP(θg = 0) less than a specified threshold τ is rejected.
In general, for each gene g, an AAA procedure computes a set of p-values using each of a set of component methods  1, …,
1, …,  k. It then applies assumption assessment methods
k. It then applies assumption assessment methods 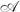 1, …,
1, …, 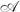 r to the data for each gene to obtain a set of p-values from each of these methods. A p-value modeling tool
r to the data for each gene to obtain a set of p-values from each of these methods. A p-value modeling tool 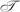 is used to compute EBP estimates for each set of p-values obtained from
is used to compute EBP estimates for each set of p-values obtained from  1, …,
1, …,  k and
k and 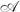 1, …,
1, …, 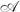 r. Standard probability laws, EBP estimates from application of
r. Standard probability laws, EBP estimates from application of 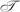 to the p-values of
to the p-values of 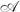 1, …,
1, …, 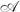 r, and a method-selection rule
r, and a method-selection rule 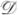 based on the validity of the assumptions of
based on the validity of the assumptions of  1, …,
1, …,  k are used to determine weights
. The weights satisfy the constraints
for g = 1, …, G and j = 1, …, k and
for each g. Then, a final EBP estimate
is determined for each g. The hypothesis θg = 0 is rejected for each g with
less than a pre-specified threshold τ.
k are used to determine weights
. The weights satisfy the constraints
for g = 1, …, G and j = 1, …, k and
for each g. Then, a final EBP estimate
is determined for each g. The hypothesis θg = 0 is rejected for each g with
less than a pre-specified threshold τ.
3. SOME ROBUSTNESS PROPERTIES OF AAA METHODS
The AAA concept provides a framework to develop a method that builds upon the strengths of its component methods in a reasonable way. Here, we describe some statistical properties of an AAA method relative to the properties of its component methods.
3.1 AAA Methods Identify All Genes Found by Each Component Method
First, we note that any gene declared significant with EBP < τ by each component method of an AAA method will also be declared significant with EBP < τ by the AAA method. By definition, any gene g such that for all j will also satisfy . If each value in a weighted average is less than τ, then the average must be less than τ as well. Thus, the AAA method will have greater statistical power than the approach of selecting genes that are significant by each of its component methods. This property has some important practical implications, because the latter approach is commonly applied in practice (see Ross et al 2004, for example). In particular, the AAA method will not miss any gene that is detected by each of its component methods when all methods are applied with the same EBP threshold τ.
3.2 AAA Methods Give Little Weight to Methods with Clear Evidence of Assumption Violation
Secondly, we note that a well-constructed AAA method will not heavily weight the results of a method with clear evidence of violation assumption. If multiple genes show strong evidence of assumption violation, then the assumption assessment methods will obtain p-value distributions that are dense near 0 and the genes with strong evidence of violation assumption will have a small EBP that the assumption is satisfied. The small EBPs will translate into small weights for the results of tests with violated assumptions. Subsequently, the AAA procedure will rely most heavily on the method that appears to have the most reasonable assumptions. Thus, in applications in which one component method is clearly preferred, the AAA method should perform similarly to that of the preferred component method. We have observed this trend in the simulation studies that we report below. We are currently exploring how to more precisely describe this property with greater theoretical rigor.
3.3 Large Sample Properties of AAA Methods
Third, an AAA method will have good large sample properties if its component methods and the assumption assessment methods have good large sample properties. If the assumption assessment methods maintain their level (i.e. the p-value distribution is indeed uniform when the null hypothesis of the test is satisfied) and the power for a test of arbitrarily small level approaches 1, then for each gene, the weight for the “best” component method (according to the method selection rule) will approach 1 as the sample size becomes infinite. This can be seen in that the p-value distribution of the assumption assessment will approach a mixture with point mass at 0 (power of 1 for arbitrarily small level for “alternative” genes) and a uniform distribution (the “null” genes). In such case, the estimate of the EBP that the assumption is satisfied approaches 1 for p > 0 and 0 for p = 0. Similarly, if the component methods have power that approaches 1 for arbitrarily small levels and maintain their level, then the EBP from the component methods will approach 0 for true null hypotheses and 1 for other hypotheses. Thus, the final AAA EBP estimates will approach 0 for true null hypotheses and 1 for other hypotheses. This property is also observed in our simulation studies. Rigorous proofs of such properties for specific AAA methods require detailed consideration of the specific assumptions and properties of each component method and each assumption assessment method.
4. USING AAA TO DEVELOP A ROBUST METHOD FOR TWO-GROUP COMPARISONS
We now utilize the AAA principle to develop a robust method to perform a two-group comparison. We will use the t-test and rank-sum tests as component methods because their statistical properties and underlying assumptions are well-understood. Each of these tests has desirable statistical properties when their underlying assumptions are satisfied. Using the notation of section 2, the t-test is component method  1 and the rank-sum test (Wilcoxon 1945) is component method
1 and the rank-sum test (Wilcoxon 1945) is component method  2.
2.
We propose that the Shapiro-Wilk test (Shapiro and Wilk 1965) be the method 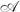 utilized for assumption assessment. The Shapiro-Wilk test is “generally regarded as the most powerful statistical test of normality” (Mason et al. 1989, p. 534) and thus used to assess the normality assumption of the t-test. For this method, we first apply the Shapiro-Wilk test to the combined residuals of the log-signals for each gene. We combine residuals across the groups to increase the statistical power of the Shapiro-Wilk test under the assumption that the two distributions differ only in terms of a location parameter. The assumption could be relaxed to assuming the two distributions are members of the same location-scale family by scaling the residuals of each group prior to applying the Shapi-ro-Wilk test.
utilized for assumption assessment. The Shapiro-Wilk test is “generally regarded as the most powerful statistical test of normality” (Mason et al. 1989, p. 534) and thus used to assess the normality assumption of the t-test. For this method, we first apply the Shapiro-Wilk test to the combined residuals of the log-signals for each gene. We combine residuals across the groups to increase the statistical power of the Shapiro-Wilk test under the assumption that the two distributions differ only in terms of a location parameter. The assumption could be relaxed to assuming the two distributions are members of the same location-scale family by scaling the residuals of each group prior to applying the Shapi-ro-Wilk test.
Now, our decision rule 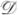 to select between the t-test (
to select between the t-test ( 1) and the rank-sum test (
1) and the rank-sum test ( 2) is simple. We select the t-test (
2) is simple. We select the t-test ( 1) for each gene g such that the normality assumption Ag is satisfied (i.e. Ag = 1) because the t-test is uniformly most powerful when its assumptions are satisfied. Otherwise, we select the rank-sum test (
1) for each gene g such that the normality assumption Ag is satisfied (i.e. Ag = 1) because the t-test is uniformly most powerful when its assumptions are satisfied. Otherwise, we select the rank-sum test ( 2) because it is a nonparametric method.
2) because it is a nonparametric method.
We use the BUM model described by Pounds and Morris (2003) as our p-value modeling tool 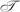 . Thus, we fit the BUM model to the p-values P1, P2, and Pa, from the t-test, rank-sum test, and Shapiro-Wilk test, respectively. The fitted models provide empirical Bayes posterior (EBP) probability estimates B1, B2, and Ba, from the same tests, respectively. We note that other methods could be used as the p-value modeling tool
. Thus, we fit the BUM model to the p-values P1, P2, and Pa, from the t-test, rank-sum test, and Shapiro-Wilk test, respectively. The fitted models provide empirical Bayes posterior (EBP) probability estimates B1, B2, and Ba, from the same tests, respectively. We note that other methods could be used as the p-value modeling tool 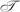 to compute the EBP from the p-value distribution (Allison et al. 2002; Liao et al. 2004; Pounds and Cheng 2004; Cheng et al. 2004).
to compute the EBP from the p-value distribution (Allison et al. 2002; Liao et al. 2004; Pounds and Cheng 2004; Cheng et al. 2004).
Now, using the decision rule 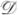 , we loosely interpret
as the EBP that gene g is not differentially expressed given that the log-signals of gene g are normally distributed, i.e., EBP(θg = 0 | Ag = 1). Similarly,
is interpreted as EBP(θg = 0 | Ag = 0). Finally,
is interpreted as EBP(Ag = 1) and thus
is taken as EBP(Ag = 0). Now, equation (1) can be used to compute EBP(θg = 0). For this specific AAA method, the final EBP estimate can be expressed as
, we loosely interpret
as the EBP that gene g is not differentially expressed given that the log-signals of gene g are normally distributed, i.e., EBP(θg = 0 | Ag = 1). Similarly,
is interpreted as EBP(θg = 0 | Ag = 0). Finally,
is interpreted as EBP(Ag = 1) and thus
is taken as EBP(Ag = 0). Now, equation (1) can be used to compute EBP(θg = 0). For this specific AAA method, the final EBP estimate can be expressed as
| (2) |
where “g is not DE” denotes “gene g is not differentially expressed” and “g is normal” denotes “the expression of gene g is normally distributed.” Subsequently, for gene g, the weights are and . After the EBPs are computed as described above, each gene g with an EBP less than a preselected τ is reported as significant.
This method has some appealing characteristics. It automatically incorporates an assessment of the assumption of normality and weighs the results of two alternative methods based on that assessment. The results of the rank-sum test are most heavily weighed for genes with strong evidence of non-normal distribution as measured by EBP(g is normal). Similarly, the results of the t-test are most heavily weighed for genes with little evidence that the normality assumption of the t-test is violated. Thus, the AAA method places most weight on the procedure that the data suggest should be preferred.
5.0 SIMULATION STUDIES AND AN EXAMPLE APPLICATION
We study the performance of this AAA method in a traditional simulation study and a simulation performed by selecting bootstrap samples from a modified data set of gene expression in acute myeloid leukemia. Thus, the primary objective of our simulation study is to describe the performance of the proposed procedure relative to that of the t-test and rank-sum test. We compared the procedures in terms of the actual FDR incurred and the average power (average statistical power across tests with a false null, Gadbury et al. 2003; Pounds and Cheng 2005) across all genes that are truly differentially expressed. In each simulation, we used τ = 0.10 as a threshold for the null EBP estimate to declare a result significant.
5.1 Traditional Simulation Studies
In each traditional simulation, we generated data for G = 1,000 genes in each subject. We let a proportion η of 1,000 genes have normally distributed log-signals with variance 1 in both groups and let the remaining proportion of 1−η genes have a Cauchy distribution with scale 1 in both groups. For each subject, the log-signals were independently generated. We added an effect size of δ to a proportion 1−π of the genes, with equal representation among genes with normal and Cauchy distributions. After the data was generated, we computed EBP(g is DE|t-test) and EBP(g is DE|rank-sum test) as described above, and also determined EBP(g is DE) according to our equation. For each method, we inferred gene g to be differentially expressed if the EBP of differential expression was greater than 0.90 with the intent to keep the FDR below 0.10 (see supplementary materials for details on the relationship between the EBP and FDR). We studied a collection of 100 settings that varied according to the number n of subjects in each group, the effect size δ, the proportion η and the proportion π. Each setting was studied in a set of 100 independent realizations.
In each simulation, all three methods kept the FDR well below the desired threshold of 0.10 (Supplementary Materials, Table S1). The highest observed FDR was 0.078, which was incurred by the t-test in the simulation with 50% of genes differentially expressed with an effect size of 1.0, 90% of genes with normally distributed signals, and per-group sample size of 5.
The average power of the proposed method compared quite favorably against that of the t-test and rank-sum test in each simulation (Table S1). The estimated power of the proposed method was greater than or equal to that of the t-test in 69 of 80 simulations with π < 1 (some genes are differentially expressed). The estimated average power of the t-test never exceeded that of the proposed method by more than 0.0028. In several cases, the average power of the proposed method was much greater than that of the t-test. In one simulation, the estimated average power of the proposed method exceeded that of the t-test by 0.8965. Additionally, the estimated average power of the proposed method was greater than or equal to that of the rank-sum test in 55 of 80 simulations with π < 1 and the estimated power of the rank-sum test never exceeded that of the proposed method by more than 0.034. The average power of the proposed method exceeded that of the rank-sum test by 0.0607 in one simulation. Furthermore, as proven in section 3.1, the proposed method did not have lower average power than both of the other methods in any simulation.
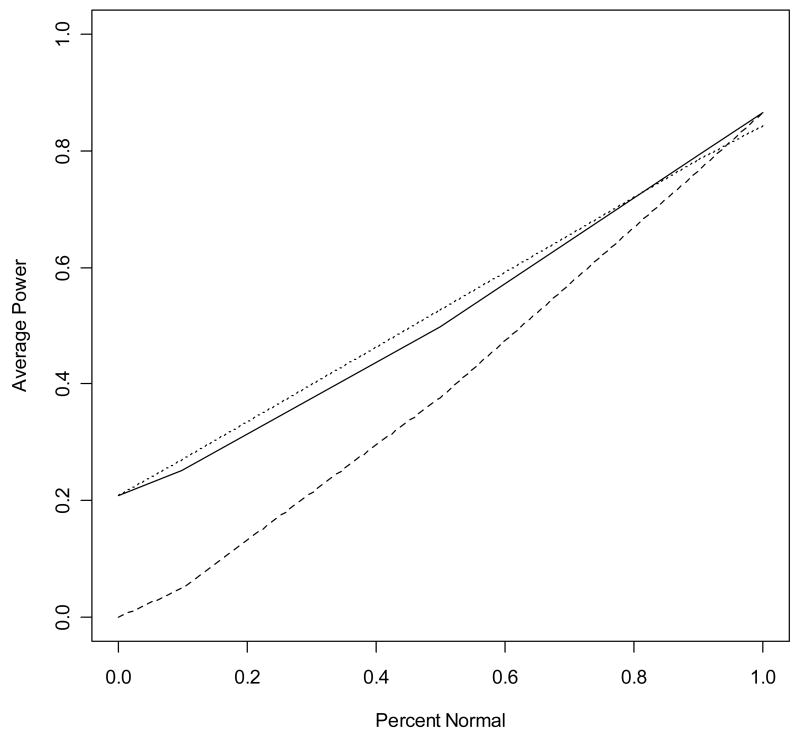
We noted an interesting trend in average power as a function of the proportion η of genes with normally distributed signals (Figure 1 and Table S1). For η = 0 and n = 10, 25, or 100, the power of the proposed method is very similar to that of the rank-sum test. For η = 0 and per-group sample sizes as small as 10, the Shapiro-Wilk test is adequately powered so that the average EBP(g is normal) is less than 0.10 (Table S1). As η increases, so does the average power of each method. Additionally, as η increases, the power of the proposed method appears to approach that of the t-test from above. Furthermore, for sufficiently large η, the average power of the t-test exceeds that of the rank-sum test because the t-test is uniformly most powerful for normally distributed data (Casella and Berger 1990).
Fig. 1.
Trend in average power as a function of η. The above plot gives the average power for the t-test (dashed line), the proposed method (solid line), and the rank-sum test (dotted line) observed in the set of simulations with 50% of genes differentially expressed with effect size 1.0 and sample size of 25.
Subsequently, the proposed method has the greatest average power for most simulations with η = 0.9 (Table S1). For η = 1, the average power of the proposed method is nearly identical to that of the t-test, which is uniformly most powerful in such settings. For η = 1, the BUM model usually fits a uniform distribution to the p-values from the Shaprio-Wilk test and hence the proposed method computes EBP(g is normal) = 1 for all genes and gives the same results as the t-test.
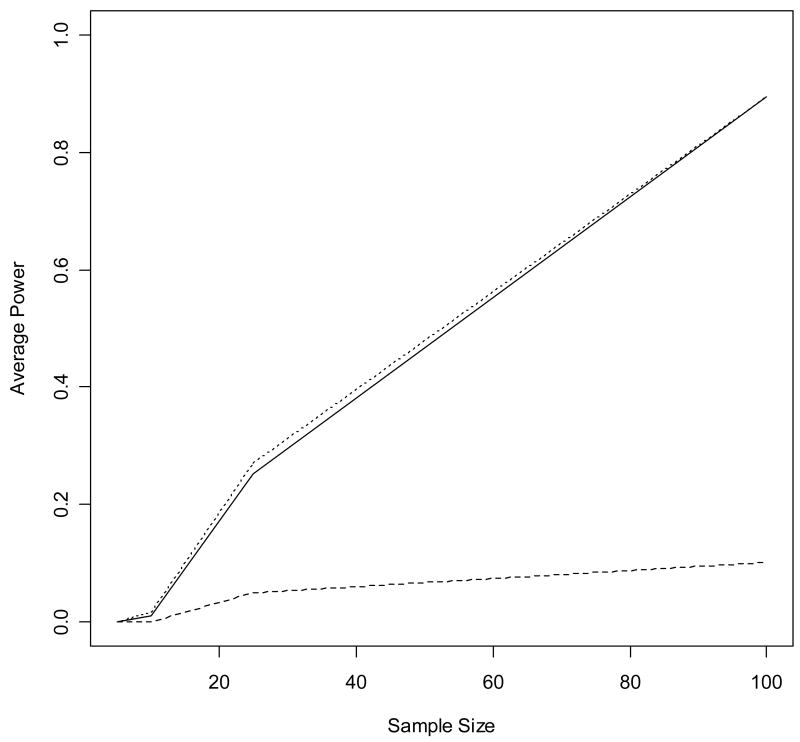
The simulation results illustrate the properties of AAA methods described in section 3. As proven in section 3.1, the average power of the proposed method was greater than at least one of the component methods in each simulation. Additionally, consistent with the arguments of section 3.2, the average power of the proposed method is similar to the rank-sum test for small η (the preferred test when few genes are normally distributed) and similar to the t-test for η near 1 (the preferred test when all or most genes are normally distributed). Finally, the large sample properties described in section 3.3 are observed when examining the average power of the proposed method and the two component methods as a function of increasing sample size (Figure 2, Table S1).
Figure 2.
Trend in average power as a function of sample size. The above plot gives the average power for the t-test (dashed line), the proposed method (solid line), and the rank-sum test (dotted line) observed in the set of simulations with 50% of genes differentially expressed with effect size 1.0 and 10% of genes normally distributed. In this case, the rank-sum method is preferred because few genes satisfy the normality assumption of the t-test. The average power of the proposed AAA method approaches that of the rank-sum test as the sample size increases, consistent with the property described in section 3.3.
5.2 Bootstrap Simulation Studies
We also study the performance of the proposed method using a bootstrap-based simulation similar to that of Pounds and Cheng (2006). We perform the bootstrap-based simulations using data from a study of gene expression in pediatric acute myeloid leukemia conducted at St. Jude Children’s Research Hospital (Ross et al. 2004). In these bootstrap-based simulations, we compare the profiles of subjects with the t(8;21) subtype to those of subjects with the MLL subtype. We used shift and scale transformations to obtain modified data sets for purposes of our bootstrap simulation. We note that shift and scale transformations maintain the Pearson and Spearman measures of inter-gene correlations. Additionally, shift and scale transformations do not change whether the signals are normally distributed. We generated five data sets for our bootstrap study: (1) all genes have equal mean and variance of expression in the two groups, (2) the mean of 10% of genes differ by ½ of a standard deviation, (3) the mean of 50% of genes differ by ½ of a standard deviation, (4) the mean of 10% of genes differ by 1 standard deviation and (5) the mean of 50% of genes differ by 1 standard deviation. We performed bootstrap simulations with n = 5 or n = 10 subjects from each group. Each bootstrap simulation was performed with 100 replicates. The 3 methods were applied in the same way as in the traditional simulation.
The results of the bootstrap simulation study are summarized in Table 1. In each simulation, all methods kept the FDR below 0.10 as desired. In most of these simulations, all 3 methods had very low power due to small sample size and small effect size. In the simulation with effect size of 1 and per-group sample size of 10, the average power estimates of the t-test, rank-sum test, and the proposed method were 0.3633, 0.3613, and 0.3696, respectively. In each simulation with some differential expression, the proposed method had greater estimated average power than at least one of the other two methods. Furthermore, the best average power did not exceed the average power of the proposed method by more than 0.006 in any simulation.
Table 1.
Results of bootstrap-based simulations.
| Setting | t-EBP | rs-EBP | Proposed Method | |||||
|---|---|---|---|---|---|---|---|---|
| n | π | δ | FDR | Power | FDR | Power | FDR | Power |
| 5 | 1 | n/a | 0.01000 | n/a | 0.00000 | n/a | 0.00000 | n/a |
| 10 | 1 | n/a | 0.06000 | n/a | 0.06000 | n/a | 0.05000 | n/a |
| 5 | 0.5 | 0.5 | 0.01644 | 0.00012 | 0.00000 | 0.00000 | 0.00500 | 0.00000 |
| 5 | 0.5 | 1.0 | 0.02692 | 0.00024 | 0.00000 | 0.00000 | 0.00250 | 0.00003 |
| 5 | 0.9 | 0.5 | 0.01534 | 0.00011 | 0.00000 | 0.00000 | 0.00400 | 0.00000 |
| 5 | 0.9 | 1.0 | 0.03078 | 0.01175 | 0.00252 | 0.00416 | 0.02110 | 0.00597 |
| 10 | 0.5 | 0.5 | 0.04541 | 0.00256 | 0.05651 | 0.00417 | 0.05466 | 0.00371 |
| 10 | 0.5 | 1.0 | 0.02302 | 0.02900 | 0.03792 | 0.02799 | 0.02934 | 0.02821 |
| 10 | 0.9 | 0.5 | 0.01704 | 0.00371 | 0.03316 | 0.00670 | 0.02822 | 0.00547 |
| 10 | 0.9 | 1.0 | 0.03061 | 0.36630 | 0.04093 | 0.36127 | 0.03653 | 0.36955 |
5.3 Concordance of Two Leukemia Studies
Ross et al. (2004) used Affymetrix arrays to obtain gene expression profiles of pediactric acute myeloid leukemia and Bullinger et al. (2004) used cDNA arrays developed at Stanford to generate expression profiles of acute myeloid leukemia in adults. One question of interest is to identify genes that show similar patterns of expression across disease subtypes in both pediatrics and adults. We were interested in whether the proposed AAA method would find more genes that show significant patterns of expression in the t(8;21) subgroup relative to subjects with a translocation involving 11q23 (MLL) in both adults and children than either the t-test or rank-sum test alone. Data sets from both studies are publicly available.
Bullinger et al (2004) profiled expression in 10 MLL and 10 t(8;21) subjects while Ross et al (2004) profiled expression in 23 MLL and 32 t(8;21) subjects. The arrays used by Ross et al (2004) included 1,318 probe sets with a UniGene annotation found in the study of Bullinger et al (2004). The arrays of Bullinger et al. (2004) included 1,038 probes with a UniGene annotation found in the study of Ross et al. (2004). There were 1,702 pairs of probe sets with a probe from each study annotated to the same UniGene ID.
We applied the t-test and rank-sum test to each data set to compare the median expression of the t(8;21) subtype to that of the MLL subtype. We used the BUM model to compute the EBP for each analysis and considered a probe sets with EBP(g is DE) ≥ 0.90 to be significant. Additionally, we applied the proposed method to the data from each study. For each pair of analyses, we determined the number of pairs that were significant and showed the same direction in both analyses. The results are reported in Table 2.
Table 2.
Concordance of results by study and method(s) of analysis. The first item of each entry gives the number of probe sets that are overexpressed in t(8;21) relative to MLL and are significant at EBP(g is DE) ≥ 0.90 in both studies when the indicated methods are applied. The second item of each entry gives the number of probe sets that are underexpressed in t(8;21) relative to MLL and are significant at EBP(g is DE) ≥ 0.90 in both studies when the indicated methods are applied. For example, when St. Jude data is analyzed with the t-test and Stanford data is analyzed with the rank-sum test, there are 32 probe sets that are significant with EBP(g is DE) ≥ 0.90 and overexpressed in t(8;21) in both studies and 41 probe sets that are significant with EBP(g is DE) ≥ 0.10 and underexpressed in t(8;21) in both studies.
| Study | St. Jude | Stanford | |||||
|---|---|---|---|---|---|---|---|
| Method | t-test | rank-sum | proposed | t-test | rank-sum | proposed | |
| St. Jude | t-test | (195, 166) | |||||
| rank-sum | (185, 161) | (248, 225) | |||||
| proposed | (187, 162) | (223, 211) | (225, 212) | ||||
|
| |||||||
| Stanford | t-test | (52, 42) | (55, 44) | (55, 44) | (78, 71) | ||
| rank-sum | (32, 41) | (35, 43) | (35, 43) | (53, 40) | (60, 48) | ||
| proposed | (50, 39) | (53, 42) | (53, 42) | (76, 56) | (53, 41) | (76, 57) | |
The proposed method found more significant probe sets than the t-test for the study of Ross et al. (2004) and more significant probe sets than the rank-sum test for the study of Bullinger et al. (2004). Thus, as in the simulations reported above, the proposed method did not show the lowest power in either of the two studies. Additionally, within each study, the proposed method showed greater concordance with the t-test and the rank-sum test than the later two methods showed with one another. Finally, the proposed method showed higher total concordance across the two studies than either the t-test or the rank-sum test. These observations suggest that the proposed method is identifying genes in a more statistically robust and powerful manner than either the t-test or rank-sum test.
6. Discussion
We introduced the principle of empirical Bayes AAA to develop a robust procedure that capitalizes on the respective strengths of the t-test and rank-sum test. The proposed procedure performed very well in traditional and bootstrap simulation studies. The simulation studies support our assertion that AAA improves the robustness of the overall analysis by placing greater emphasis on the test that should be more reliable for specific genes.
The principle of AAA can be applied to other settings as well. In experiments that compare the expression of k>2 groups, one-way ANOVA and the Kruskal-Wallis (1952) test could be used in place of the t-test and rank-sum test respectively. The principle could also be used to develop a method that weights the results of equal and unequal variance t-tests according to the results a test of equal variances. In exploring the association of censored survival time with expression, we could use proportional hazards regression (Cox 1972) as a parametric test for this type of association, the procedure of Jung et al. (2005) as a nonparametric test for this type of association, and use a test of the proportional hazards assumption to obtain the assumption adequacy weights. We plan to explore these extensions of empirical Bayes AAA in the near future.
The proposed method incorporates gene-specific assessments of assumption adequacy into the analysis. However, the assumptions used to compute the EBPs still need to be assessed. In this work, we applied the BUM model to the p-values to compute the EBPs. The fit of the BUM model to the p-values should be assessed using quantile-quantile plots (Pounds and Morris 2003; Pounds 2006). If quantile-quantile plots indicate a lack-of-fit, then one may want to use other methods (Allison et al. 2002; Pounds and Cheng 2004; Liao et al. 2004; Cheng et al. 2004) to compute the EBP. We did not incorporate an assessment of fit of the BUM model into our simulation studies because it would be difficult to automate this process in a simulation. However, this should be easily done in practice because it would involve examining only 3 quantile-quantile plots. In practice, including an assessment of p-value model fit should further improve the performance of empirical Bayes AAA.
The AAA concept is distinct from other statistical methods or concepts that are similar in spirit. AAA differs from Bayesian or information-theoretic model averaging (Burnham and Anderson 2002). In model averaging, the robustness is achieved by averaging across models that differ in their parametric form or the set of covariates they include. AAA allows one to average results from parametric and nonparametric hypothesis tests that assess the validity of the assumptions of the parametric test. Additionally, AAA is distinct from Bayesian sensitivity analysis. Bayesian sensitivity analysis explores the influence of the prior on the posterior and the resulting inference. In AAA, no prior is specified, only specific procedures are selected for testing assumptions and the hypotheses of primary interest.
The AAA concept may also provide an approach to determine a course of action for some difficult model-selection problems that arise in practice. For example, models with quite different forms may have similar values of the information criteria such as Akaike’s (1973) information criterion, the Bayes information criterion (Schwartz 1978), or the deviance information criterion (Spiegelhalter et al. 2002). In such cases, an approach based on the AAA concept may help to resolve the situation. Future research may provide some guidance on how to apply the AAA principle in such problems.
It would be interesting to compare the performance of AAA methods to that of methods that use shrinkage utilize shrinkage-based variance estimators, i.e. methods that borrow information across genes to stabilize gene-specific variance estimates of t-type or F-type statistics. Some leading researchers have suggested that some form of shrinkage should be used in most applications in practice (Allison et al. 2006). To our knowledge, no simulations have been performed to explore the performance of shrinkage-based methods in settings that violate the normality assumption. The computation burden of such simulations may be reduced by using analytical formula for constants used by some shrinkage-based methods (Pounds 2007). It would be interesting to generate data from variety of distributions in these simulation studies, such as skewed distributions and t-distributions with varying degrees of freedom.
It would be interesting to explore ways to use AAA concepts to improve the robustness of methods that The shrinkage-based methods make differing assumptions regarding the variance of gene expression within experimental groups. For example, Cui et al. (2005) assume that gene-specific variances arise from a common hyper-distribution that does not depend on mean expression of individual genes while Jain et al. (2003) assume that the variance of gene expression is a function of mean expression. These two methods make very different assumptions regarding expression variance. Developing procedures to test such assumptions would be valuable to the field (Pounds et al. 2007). It would be interesting to consider how to use tests of shrinkage assumptions to combine these methods into an AAA procedure. One challenge in applying the AAA concept in this way would be to accommodate assumptions regarding the entire set of genes. In this paper, we have proposed a way to apply the AAA concept in a gene-specific manner. Thus, it is not immediately clear how to implement the AAA concept when procedures make different assumptions about the entire set of genes.
There are several open questions regarding AAA procedures. One question is the selection of the procedure to test assumption adequacy. For example, and Wilk (1965) describe or cite several methods for testing the goodness-of-fit of an assumed distribution. Based on the recommendation of Mason et al. (1989), we selected the procedure of Shapiro and Wilk (1965) for this application. The Shapiro-Wilk procedure compares the observed order statistics to the expected values of the order statistics and derives the null distribution of the test statistic by assuming that all data values are iid observations from a normal distribution. Other tests of distributional fit are designed to test the fit of other distributions. In choosing the assumption-testing procedure, it is important to consider the level and power of the various choices. These questions would also be important in choosing the procedures to test the hypothesis of primary interest (e.g. equal mean or median expression). Another question is how the components of and the overall AAA procedure perform in the context of gene-gene correlations that are common in microarray data.
There are some other interesting questions worthy of additional research. One is how to best perform follow-up pairwise comparisons after rejecting the null hypothesis that 3 or more groups have equal mean or median expression. Another question is how to develop a procedure that would use t-distributions with varying degrees of freedom to model the expression values within each experimental group. Such a procedure may perform well in the simulation studies of this paper because the Cauchy and normal distribution are t-distributions with 1 and infinite degrees of freedom, respectively.
Supplementary Material
Acknowledgments
We gratefully acknowledge funding from the American Syrian Lebanese Associated Charities (ALSAC), and NIH grants CA021765-27 and CA115422-01A1.
Footnotes
Supplementary materials for this article are available at the journal website.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Akaike H. Information theory as an extension of the maximum likelihood principle. In: Petrov BN, Csaki F, editors. Second International Symposium on Information Theory. Akademiai Kiado; Budapest: 1973. pp. 267–281. [Google Scholar]
- Allison DB, Gadbury GL, Heo M, Fernandez JR, Lee C-K, Prolla TA, Weindruch R. A mixture model approach for the analysis of microarray gene expression data. Computational Statistics and Data Analysis. 2002;39:1–20. [Google Scholar]
- Allison DB, Cui X, Page GP, Sabripour M. Microarray data analysis: from disarray to consolidation and consensus. Nature Reviews. 2006;7:55–65. doi: 10.1038/nrg1749. [DOI] [PubMed] [Google Scholar]
- Benjamini Y, Hochberg Y. Controlling the false discovery rate: a practical and powerful approach to multiple testing. J Roy Statist Soc B. 1995;57:289–300. [Google Scholar]
- Bullinger L, Dohner K, Bair E, Frohling S, Schlenk RF, Tibshirani R, Dohner H, Pollack JR. Use of Gene-Expression Profiling to Identify Prognostic Subclasses in Adult Acute Myeloid Leukemia. The New England Journal of Medicine. 2004;350:1605 – 1616. doi: 10.1056/NEJMoa031046. [DOI] [PubMed] [Google Scholar]
- Burnham KP, Anderson DR. Model Selection and Multimodel Inference. 2. Springer; New York: 2002. [Google Scholar]
- Cheng C, Pounds S. A Review of FDR Methods for Microarray Data Analysis. Bioinformation. 2007;1:436–446. doi: 10.6026/97320630001436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng C, Pounds S, Boyett JM, Pei D, Kou M-L, Roussel MF. Significance Threshold Selection Criteria for Massive Multiple Comparisons with Applications to DNA Microarray Experiments. Statistical Applications in Genetics and Molecular Biology. 2004;3:36. doi: 10.2202/1544-6115.1064. [DOI] [PubMed] [Google Scholar]
- Cox DR. Regression Models and Life Tables (with Discussion) Journal of the Royal Statistical Society B. 1972;34:187–220. [Google Scholar]
- Cui X, Hwang JT, Qiu J, Blades NJ, Churchill GA. Improved statistical tests for differential gene expression by shrinking variance components estimates. Biostatistics. 2005;6:59–75. doi: 10.1093/biostatistics/kxh018. [DOI] [PubMed] [Google Scholar]
- Efron B, Tibshirani R, Storey JD, Tusher V. Empirical Bayes analysis of a Microarray experiment. J Am Stat Assoc. 2001;96:1151–1160. [Google Scholar]
- Gadbury GL, Page GP, Edwards J, Kayo T, Prolla TA, Weindruch R, Permana PA, Mountz JD, Allison DB. Power and Sample Size Estimation in High Dimensional Biology. Statistical Methods in Medical Research. 2004;14:325–338. [Google Scholar]
- Jung SH, Owzar K, George SL. A multiple testing procedure to associate gene expression levels with survival. Statist Med. 2005;24:3077–3088. doi: 10.1002/sim.2179. [DOI] [PubMed] [Google Scholar]
- Kruskal W, Wallis W. Use of ranks in one-criterion variance analysis. J Am Stat Assoc. 1952;53:814–861. [Google Scholar]
- Liao JG, Lin Y, Selvanayagam ZE, Shih WJ. A mixture model for estimating the local false discovery rate in DNA Microarray analysis. Bioinformatics. 2004;20:2694–2701. doi: 10.1093/bioinformatics/bth310. [DOI] [PubMed] [Google Scholar]
- Mason RL, Gunst RF, Hess JL. Statistical Design and Analysis of Experiments. New York: John Wiley and Sons; 1989. [Google Scholar]
- Pounds S. Estimation and control of multiple testing error rates for the analysis of microarray data. Briefings in Bioinformatics. 2006;7:25–36. doi: 10.1093/bib/bbk002. [DOI] [PubMed] [Google Scholar]
- Pounds S, Morris S. Estimating the occurrence of false positives and false negatives in microarray studies by approximating and partitioning the empirical distribution of p-values. Bioinformatics. 2003;19:1236–1242. doi: 10.1093/bioinformatics/btg148. [DOI] [PubMed] [Google Scholar]
- Pounds S, Cheng C. Improving false discovery rate estimation. Bioinformatics. 2004;20:1737–1745. doi: 10.1093/bioinformatics/bth160. [DOI] [PubMed] [Google Scholar]
- Pounds S, Cheng C. Sample size determination for the false discovery rate. Bioinformatics. 2005;21:4263–4271. doi: 10.1093/bioinformatics/bti699. [DOI] [PubMed] [Google Scholar]
- Pounds S, Cheng C, Onar A. Statistical Inference for Microarray Studies. In: Balding DJ, Cannings C, Bishop M, editors. The Handbook of Statistical Genetics. 3. Wiley: New York; 2007. [Google Scholar]
- Pounds S. Computational Enhancement of a Shrinkage-Based ANOVA F-test Proposed for Differential Gene Expression Analysis. Biostatistics. 2007;8:505–506. [Google Scholar]
- Ross ME, Mahfouz R, Liu HC, Zhou X, Song G, Shurtleff S, Pounds S, Cheng C, Ma J, Ribiero RC, Rubnitz JE, Girtman K, Williams WK, Raimondi SC, Liang DC, Shih LY, Pui C-H, Downing JR. Gene expression profiling of pediatric acute myleogenous leukemia. Blood. 2004;104:3679–3687. doi: 10.1182/blood-2004-03-1154. [DOI] [PubMed] [Google Scholar]
- Schwartz G. Estimating the dimension of a model. Annals of Statistics. 1978;6:461–464. [Google Scholar]
- Shapiro SS, Wilk MB. An analysis of variance test for normality (complete samples) Biometrika. 1965;52:591–611. [Google Scholar]
- Spiegelhalter DJ, Best NG, Carlin BP, van der Linde A. Bayesian measures of model complexity and fit. J Royal Stat Soc B. 2002;64:583–639. [Google Scholar]
- Wilcoxon F. Individual comparisons by ranking methods. Biometrika. 1945;1:80–83. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.