A charge coupled device camera with electron decelerator for intermediate voltage electron microscopy

Abstract

Electron microscopists are increasingly turning to intermediate voltage electron microscopes (IVEMs) operating at 300–400 kV for a wide range of studies. They are also increasingly taking advantage of slow-scan charge coupled device (CCD) cameras, which have become widely used on electron microscopes. Under some conditions, CCDs provide an improvement in data quality over photographic film, as well as the many advantages of direct digital readout. However, CCD performance is seriously degraded on IVEMs compared to the more conventional 100 kV microscopes. In order to increase the efficiency and quality of data recording on IVEMs, we have developed a CCD camera system in which the electrons are decelerated to below 100 kV before impacting the camera, resulting in greatly improved performance in both signal quality and resolution compared to other CCDs used in electron microscopy. These improvements will allow high-quality image and diffraction data to be collected directly with the CCD, enabling improvements in data collection for applications including high-resolution electron crystallography, single particle reconstruction of protein structures, tomographic studies of cell ultrastructure, and remote microscope operation. This approach will enable us to use even larger format CCD chips that are being developed with smaller pixels.

INTRODUCTION

It has long been recognized that there are numerous benefits to raising the accelerating voltage in an electron microscope. As the voltage increases, both elastic and inelastic scattering cross sections decrease, so that thicker specimens can be used. This is of particular importance with frozen-hydrated preparations of large molecules and protein complexes, and with specimens studied by tomography for three-dimensional visualization. Also, the single-scattering approximations that are fundamental to much of the image interpretation and processing improve with increasing voltage, so that the data are a better representation of the specimen. The envelope function for temporal coherence improves, so it is easier to routinely obtain high resolution. The depth of field is larger, so the area of a tilted specimen that is close to focus is larger. The diffraction-limited spot size is smaller, so spot-scan imaging can be done with a smaller illumination spot. Focus ramp correction with spot-scan imaging¹ can then better ensure that the entire image of a tilted crystal will be at essentially the same focus. The gun brightness is higher, providing an improvement in coherence and∕or exposure time. Each of these factors provides a small increment, and taken together the difference is quite substantial. It is indeed this combination of factors that is driving microscope manufacturers to improve intermediate and high voltage microscopes, and the voltage of what is considered the “routine” microscope continues to increase.

Slow-scan charge coupled device (CCD) cameras are now standard equipment on high-end microscopes, and they have completely replaced photographic film for data collection in some laboratories. Particularly with 100 kV microscopes, experience suggests that some CCDs are at least as good as film even for low-dose microscopy of proteins.² However, virtually all of the quantitative analyses of CCD performance at 300 kV and above demonstrate that the quality of data collected with the CCD is compromised at the higher voltages. Two different effects contribute to the decrease in performance. First, the point spread function is broadened by scattering (lateral straggling) of the electrons within the scintillator and its support. Second, the signal produced by each electron is not the same, adding a significant noise component. These problems may be the principal disadvantage of IVEMs. Given the number of advantages of high voltage, though, it is apparent that the IVEM will more and more be the instrument of choice for structural studies.

In many fields, resolution limits are being pushed back by technical improvements that allow finer detail in more complex structures to be studied. Electron crystallography of proteins, single particle analysis, and tomography have all seen significant advances in the past few years. In each of these cases, improvements in resolution require significant increases in the amount of data recorded. This increase, in turn, generates a need for all aspects of the microscopy—especially data recording—to increase in efficiency. Application of direct digital readout is one of the most sought-after improvements in the field. However, especially in biology, there are presently only a few circumstances where the available CCD cameras provide sufficient performance to be preferred over conventional photographic film. In electron crystallography, diffraction patterns are now usually recorded on a CCD, which yields better data quality than film.³ Data sets of several hundred diffraction patterns have consequently become the standard for work such as electron diffraction of protein crystals.⁴ However, the available CCD array sizes are not large enough for imaging many of these crystals. Images of crystals that have been recorded on film are often digitized in arrays of at least 5000×5000 pixels, even up to 10 000 pixels on edge, in order to obtain an adequate signal-to-noise ratio. While the 4k (i.e., 4096×4096 pixels) CCD cameras that have recently become available bring us closer to the minimum size, the performance at 300–400 kV is degraded to the point where the effective array size is far smaller than is required. In general, one can expect that presently available CCD cameras will record in a single frame only about 10% of the area that would be imaged on photographic film at the same resolution.

Similarly, in single particle work, the desired data set size for high resolution often requires on the order of hundreds to thousands of films. Use of a CCD increases the number of images that need to be recorded by a significant factor, and thus is, so far, not a universally appealing alternative for high-resolution work. A much more significant problem, which arises when working at voltages much above 100 kV, is that the quality of the images recorded on the CCD is worse than on film even when adjustments are made for the differences in detector resolution. Since it is the signal-to-noise ratio in the image that ultimately limits the resolution, we cannot afford to compromise quality for ease of collecting the data.

In the case of tomography, this compromise has been easier to justify, since the CCD is so intimately involved with the microscope operation, the number of images in a single data set exceeds the capacity of any film camera, and digitizing images on film would introduce an additional problem of rotational image registration. Thus, most tomographic data are currently recorded on CCDs.

A number of software projects have developed control systems for automated, or semiautomated, microscope operation and data recording, both for single particle work⁵ and for tomography.⁶ This approach will be essential for collecting the large amounts of data needed for high-resolution, single particle studies. However, the bottleneck is the recording medium: film is still generally considered the best medium for recording high-resolution images with the 300–400 kV microscopes. Development of a better camera for the higher voltage range will allow realization of the full potential of EM automation.

The performance problems encountered in using a CCD on an IVEM have been well documented in the literature. A number of papers have compared the expected or experimentally measured modulation transfer function (MTF) and point spread function (PSF) at different voltages, and compared the PSF with the size of the CCD pixels, which in the current generation of devices is usually 15–24 μm. Most of these reports also include evaluation of the detective quantum efficiency (DQE). In all cases, the performance by essentially any criterion is significantly worse at the higher voltages. Daberkow et al.^{7, 8} presented calculations and measurements that show a drastic falloff in the DQE on going from 100 to 300 kV. To some extent, the DQE loss can be avoided with a thick scintillator, but only at the cost of a rather wide PSF. For example, the PSF is predicted to be wider than 60 μm for any condition that provides a DQE of over 0.5 at 300 kV. Faruqi et al.⁹ used a thicker scintillator to improve sensitivity, but obtained a PSF well over 50 μm (full width at half maximum) even at 120 kV. de Ruijter¹⁰ and Meyer and Kirkland¹¹ compared 100 and 300 kV operation, showing a loss of about a factor of 2 in MTF at the higher voltage, and both reports also provide good discussions of noise sources that have made some MTF measurements appear anomalously favorable. The main problem is that a substantial amount of noise is generated within the scintillator, arising from the wide pulse height distribution of photons per incident electron. This noise occurs after signal damping by the early component of the MTF, adding to the amplitude of the power spectrum at high spatial frequencies so that the spectrum is not reflective of the full system MTF. MTF measurements based only on the Fourier transform or autocorrelation of the image will thus be biased toward high values by this noise source. Results presented by Sherman et al.¹² are among the most favorable for IVEM applications, but still show a strong loss of both signal and signal-to-noise ratio (SNR) at high resolution, compared to film. Measurements by Booth et al.¹³ produced a favorable comparison of a CCD and film under certain conditions. Our own experience with a CCD optimized for working at 400 kV included quantitative comparisons of images of purple membrane and other specimens on film and on the CCD. Data recorded on film were of substantially better quality than that recorded with the CCD,³ and evaluation of the camera performance showed disappointing values for both the MTF and DQE.

Substantial improvements have been made in CCD cameras since the earlier measurements, though, particularly in the fiber optic coupling and scintillator deposition. Still, there is tremendous room for improvement in the 300 kV range. This point is illustrated by measurements of MTF and DQE on a Gatan UltraScan CCD camera¹⁴ with two scintillators of different thicknesses. At 300 kV, the MTF at half-Nyquist frequency is about 0.1 for the thicker scintillator, and 0.2 for the thinner one. With both scintillators, the DQE is below 0.1 at half the Nyquist frequency. The DQE of the thinner scintillator improves to about 0.5 when the electron energy is reduced to 40–60 keV, reflecting the significant degradation of performance at higher energies.

Alternative approaches exist for reducing the loss of SNR due to backscatter and electron straggling. A thick scintillator coupled to the CCD via a reducing fiber optic taper improves the match between the PSF in the scintillator and the CCD pixel size. Faruqi and Andrews¹⁵ have employed tapered fiber optics with about a 1.7 demagnification factor, which provides a good match at around 120 kV. However, the largest commercially available high-resolution taper, with diameter of 200 mm, only provides a 2× increase in effective pixel size over existing 1:1-coupled CCDs, not nearly as large as the ratio of the 300 kV PSF to the CCD pixel size. That approach can be extended by grinding the edges of the taper square and tiling multiple sensors and their fiber optics together. While this is an expensive approach, it has been used for detectors in x-ray crystallography. Further extension to formats larger than 4000×4000 would be extremely costly.

Another alternative approach makes use of a self-supporting transmission scintillator coupled by a folded lens optic to the CCD. Special consideration must be given to ensure adequate conversion efficiency (e.g., the use of a back-thinned CCD and a high numerical aperture lens), and to minimize electron backscatter. Preliminary measurements on such a camera, the Gatan UltraCam,¹⁴ show a significant improvement over more conventional arrangements (Brent Baily, personal communication), but it is clear that further improvements would be of great benefit.

Alternative detector technologies offer a great deal of promise. For example, large-pixel, silicon-based detectors are under development for high energy physics experiments and for x-ray crystallography, and have also been tested for electron microscopy.¹⁶ These devices provide a single-electron signal that is well above the noise background, so that the SNR is extremely high. The dynamic range can be well above 10⁶. However, the experimental analyses show that the point spread function in silicon is substantially larger than in the more dense scintillators, and that the effective MTF and DQE suffer the same problems as CCDs at higher voltages. As is the case with CCDs, efforts to construct larger arrays with these detectors include building devices with smaller pixels as well as tiling together arrays with a small number of pixels. The experimental results on electron microscopes indicate that reducing the pixel size to less than the current of 50–150 μm size will be counterproductive with accelerating voltages much above 100 kV. These hybrid detectors may eventually offer better performance than CCDs, especially when they operate in an electron counting mode with exceptionally low noise. There is also the possibility to replace the silicon with a denser material that would stop the electrons more efficiently.

Another form of pixel detector is based on monolithic, complementary metal-oxide semiconductor technology, as opposed to the “bump-bonded” fabrication used to make the silicon pixel detectors. These devices use an active layer only a few microns thick and may work substantially better at higher voltages. Simulations suggest, however, that backscattering from the silicon substrate will still seriously limit the DQE. Experimental tests of the first devices on electron microscopes showed a promising SNR and fair MTF but did not explicitly address the question of DQE.¹⁷

While it does seem likely that CCDs will eventually be superseded by other readout technology, we have chosen first to adapt existing CCD technology that can produce clear improvements on a much shorter time scale at far less cost. Here, we describe an adaptation of the CCD camera that takes advantage of all of the features of the IVEM in interactions of the beam with the specimen, but overcome all of the limitations of the CCD with high voltage electrons. This development will make CCD cameras far more functional in many biological applications. The benefits will not be limited to low-dose biological work, although this is where the most dramatic improvements should be seen. This work also establishes the feasibility of combining our approach with the newer detector technologies.

CAMERA DESIGN

The essential feature that distinguishes this approach is that the electrons are decelerated by passing through a retarding electrostatic potential before they reach the scintillator. This approach, in principle, can provide the same performance on a 300 kV microscope as has been achieved at 100 kV, and even better performance when the electron energy is brought below 100 keV. As discussed above, the two main problems with operating at higher voltages are the increased width of the PSF and noise introduced by the wide pulse height spectrum produced at high voltages. Mounting the CCD on an electron decelerator overcomes both of these problems. We can obtain more signal than currently available at 300–400 kV, with a point spread function in the scintillator smaller than the CCD pixel size and a pulse height spectrum that is narrower as well.

Computer simulations have been highly informative in investigating the spatial distribution of light produced in a scintillator. We have used Monte Carlo simulation programs¹⁸ to model electron scattering in various potential scintillators at a range of voltages. Figure 1 shows Monte Carlo calculations of electron trajectories for 60 and 300 kV electrons in a phosphor scintillator on glass fiber optics. The scintillator is coated with a thin (3 μm) protective layer. Although this is not meant to be an exact representation of the situation, it will be readily apparent that even a 25 μm thick scintillator absorbs rather little of the 300 keV electron energy. The 300 keV electrons scatter within the scintillator over a range corresponding to several CCD pixels (15–24 μm pixel spacing), but an even greater contribution to the width of the point spread function is generated by electrons that travel through the scintillator into the fiber optic and then back up into the scintillator. As many as 15%–20% of the incident electrons scatter back into the scintillator, often at distances of 10 pixels or more from the incident site. On the other hand, the stopping power for electrons with energy slightly below 100 kV is such that all electrons can be stopped within a thin layer of the scintillator, with lateral spreading of less than a pixel even with the smaller (∼15 μm) pixels on the current large-format CCD chips. Figure 1c shows the dependence of PSF on incident energy, based on these Monte Carlo calculations. The dramatic improvement in the PSF as the energy decreases is the basis for our proposal to float the CCD to a high voltage, in order to provide a good match between the PSF of the scintillator and the CCD pixel size.

Figure 1.

Monte Carlo calculations of (a) 60 keV and (b) 300 keV electron trajectories in a 25 μm thick phosphor scintillator mounted on fiber optics and covered with a 3 μm metallization and protective layer. These layers are indicated by the dashed lines. Because of the lower density and atomic number of the fiber optics, the range of the electrons is much larger than in the scintillator. (c) Predicted width of the point spread function estimated from simulations at various accelerating voltages.

The CCD decelerator

A block diagram of the basic design of the decelerator-CCD camera is shown in Fig. 2a. The CCD chip and fiber-optic-coupled scintillator are mounted at the end of an inverted accelerator tube (National Electrostatics Corp.). The package is contained in a pressure vessel that uses SF₆ at 80 psi as the high voltage insulator. All of the camera control electronics are mounted within this tank adjacent to the CCD, and power to run the system is brought in with the high voltage. A small 250 kV power supply (Gamma High Voltage, Inc., model RR250.2) provides the voltage, which is brought in through a feedthrough in the high voltage tank below the microscope’s viewing chamber. A transformer between the high voltage generator and the tank adds the 110 V power to run the camera.

Figure 2.

(a) Block diagram of the CCD decelerator system. (b) Cross section through the system, showing arrangement of the decelerator stack, CCD and electronics in the HV tank, and the electron beam path.

Figure 2b shows a more detailed schematic of the decelerator. The system has been designed to fit on JEOL 300 and 400 kV microscopes. The high voltage tank fits in the space under the film camera. The CCD is mounted slightly off axis because of the presence of two large structural beams at the back of this space. The camera is an early version of the Gatan UltraScan camera which supports a 4096×4096 CCD chip from Fairchild Imaging. An enclosure containing the electronics (camera control electronics, amplifier, analog to digital converter, etc.) is mounted inside the pressurized SF₆ tank. Optoelectronic isolators and fiber optics incorporating standard interfaces to conventional Firewire computer interconnects carry the CCD control and output signals. A nonconductive coolant, circulated through an external heat exchanger, is used to dissipate heat generated by the electronics and the Peltier cooler. In the present implementation, the CCD is cooled to about −10 °C, limited by the lead x-ray shielding between the vacuum section and the cooled baseplate. The fiber optic and coolant lines run along the decelerator electrodes inside the SF₆ tank, to minimize effects of field gradients and the danger of arcing.

High voltage discharges pose a serious threat to the CCD and associated electronics. Discharges within the SF₆ tank are easily avoided by conservative design. The multistep decelerator above the CCD and generous space between the tank and the elements at high voltage minimize the risk of a discharge in the vacuum. The drift tube between the decelerator section and the CCD chip is designed to provide substantial protection from the intense, high frequency electromagnetic fields that could be generated with a discharge. Shielding and isolation in all power and electronics lines reduce the danger that the effects of a discharge would penetrate into the electronics section.

The electron optical properties of the decelerator were analyzed to ensure that image distortions, which are common in electrostatic systems, would not pose a limitation. Using the program SIMION (Scientific Instrument Services, Inc.), which was also used to analyze field gradients within the system, we made ray-tracing calculations to predict these distortions. The distortions increase rapidly with the ratio of initial and final electron energy and with distance from the optical axis. Under all conditions expected for operation, though, they are a small fraction of the CCD size. Similar distortions are routinely characterized and corrected in images of two-dimensional protein crystals.¹⁹ Thus, we expected that the distortions of the electrostatic system could easily be characterized and computationally removed simply by interpolation. Experimental characterization and correction of distortions are described below.

The magnification of the electrostatic lens was also predicted by the ray-tracing simulations, and the calculations agree well with the experimental observations. The magnification change induced by the decelerating potential under all anticipated operating conditions is between a factor of 1.0 and 1.25. We note that the fringing field at the bottom of the decelerator tube, where the electrons have the lowest energy, acts as a converging optical element to reduce the geometrical magnification. Since we operate primarily in the region where the magnification is nearly independent of the decelerator voltage [see Fig. 3b below], the stability and ripple of the high voltage supply are not at all an issue.

Figure 3.

(a) Images of a grating replica taken with the microscope set at 250 kV and the decelerator at (left to right): 0, 100, and 200 kV. There is an increase in magnification of about 20% with the 200 kV potential, as predicted, and some distortions are detectable by sighting along the grating lines. Contrast has been adjusted for uniform appearance. (b) Magnification of image on CCD as a function of the net incident electron energy. Curves are shown for four series of measurements, starting from 200, 230, 250, and 300 kV, and decelerating the beam by up to 220 kV. The “net energy” is corrected for the calibrations of the power supplies (see text). (c) System gain (arbitrary scale) as a function of incident voltage for the decelerator camera with a thin (triangles) or thick (circles) phosphor. The gain is corrected for changes in magnification, and the net energy is corrected for the voltage calibration errors.

EXPERIMENTAL CAMERA PERFORMANCE

The prototype camera has been mounted and tested on JEOL 3000, 3100, and 4000 electron microscopes, with two different scintillators. Several standard test specimens have been used in recording data on the camera, including a grating replica, ordinary carbon films, PtC-coated holey films and a protein crystal, bacteriorhodopsin. Using a number of different criteria and tests, we have characterized the camera performance with the microscope high voltage between 200 and 300 kV and the decelerating voltage in the range of 0–250 kV. The most significant finding is that the camera performs properly when floated to the high voltage. The initial tests have confirmed that there are no fundamental flaws in the concept and that the camera performance is substantially improved by decelerating the beam. Results of some of these tests are represented in Figs. 3456789.

Figure 4.

(a) Line scans across an image of the edge of the electron microscope’s beam stop, with the accelerating voltage set to 300 or to 220 kV and the beam decelerated as indicated. (b) MTF curves derived from the beam stop images.

Figure 5.

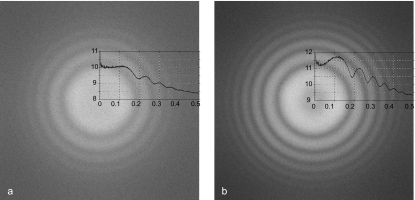
Fourier transforms of carbon film images recorded with the microscope at 300 kV and the decelerator set to (a) 0 kV and (b) 250 kV. The magnification at the CCD was 75 000×, and the Nyquist frequency corresponds to 1∕(4 Å). The nominal microscope magnification was changed from 25 to 20 000× to account for the increase in magnification as the deceleration voltage increases, and to maintain the same exposure at the level of the specimen or detector. The images were gain normalized with reference images recorded at the corresponding voltages. The improvement in clarity of the Thon rings, which arise from the focus-dependent phase contrast transfer function, is an illustration of the improvement in DQE, or SNR. Curves were obtained from rotationally averaged transforms.

Figure 6.

DQE measurements with the decelerator-CCD system. (a) A series of measurements of DQE vs spatial frequency with various microscope and decelerator voltage combinations. The corrected net voltage difference is given. (b) A summary of the DQE dependence on voltage, for two spatial frequencies; the upper curves (each curve representing a different microscope voltage) are for low frequencies, around 0.05 Nyquist, while the lower curves are for half-Nyquist frequency (0.25 on the graph at the left). The essential point is that the DQE improves from 0.08 at 300 kV to 0.4—i.e., by a factor of 5—at the midfrequencies, and a factor of 2 at the low frequencies.

Figure 7.

Characterization of distortions. (a) Array of illumination spots made by stepping the beam in small increments through a two-dimensional lattice. The microscope was set to 245 kV, the decelerator to 200 kV. (b) Representation of displacements of the spots from ideal lattice positions as determined by program QUADSERCH (Ref. ¹⁹). Line segments correspond to ten times the actual displacement. (c) Image after correction for displacements using program CCUNBEND. (d) Fourier transform of the original image; diffraction spots are spread over many pixels, even at low spatial frequencies. (e) Fourier transform after correction; diffraction spots are concentrated essentially to a single pixel and extend to the edge of the transform.

Figure 8.

Representation of the SNR for diffraction spots in the Fourier transform of an image of bR, a two-dimensional protein crystal. The image was taken with the microscope set to 245 kV and the decelerator to 200 kV, with a nominal magnification of 12 000×. The edge of the transform corresponds to a resolution of 7 Å. The size of each circle reflects the IQ (Ref. ¹⁹) for each spot. The IQ is a measure of the signal-to-noise ratio calculated as 1+INT (8*B∕A) where A is the spot amplitude and B the local background. An IQ of 1 indicates a peak-to-background ratio greater than 7, while a ratio between 1 and 1.33 gives an IQ of 8. Circle sizes are shown at the lower left. Excellent SNR is obtained essentially out to the edge of the transform.

Figure 9.

Images of a typical plastic-embedded and stained cell section. The sample was decorated with 5 nm diameter gold beads, which would be used as fiducial markers in aligning a tomographic series of images. Each image shows an area comprising 3400×3400 pixels out of the original 4096×4096 pixel image. The microscope was set at 300 kV, the decelerator at [(a)–(c)] 250 kV or [(d)–(f)] 0 kV. Nominal microscope magnification was [(a)–(c)] 20 000× or [(d)–(f)] 25 000×, giving a final magnification of 75 000× for both conditions. Exposures at the CCD were [(a) and (d)] 2 electrons∕pixel [(b) and (e)] 8 electrons∕pixel, and [(c) and (f)] and 32 electrons∕pixel. The insets in each image show the same set of gold beads. Contrast has been adjusted for uniform appearance of the images.

Figure 3a shows a set of images of a grating replica that were recorded with increasing decelerator voltage. These images illustrate that the deceleration principle is useful over a wide range of voltages. With no deceleration voltage, a small part of the image was blocked by an off-axis shield just below the microscope’s film camera. As the decelerating voltage increases up to about 140 kV, the magnification increases enough so that the image fills the CCD. As the net voltage decreases below about 60 kV, the image is slightly demagnified, and distortions become quite evident. However, the image is still quite stable, and the results show that we could, with an appropriate scintillator, operate the decelerator in a mode that would use an incident energy of some tens of keV.

Figure 3b shows the variation in magnification with decelerating voltage. Equivalent measurements were obtained with images of the grating as in Fig. 3a and images of the microscope’s beam stop. Several series of images starting with the microscope set to different voltages and increasing the deceleration voltage revealed a small miscalibration of both the microscope voltage, in the 200–250 kV range, and the decelerator power supply. It appears that the microscope voltage is about 5% higher, and the decelerator about 5% lower, than the nominal values in this range. The magnification in Fig. 3b is plotted against the actual net incident beam energy. With the microscope set at 250 kV and the decelerator at 200 kV, the true beam energy is about 70 keV. This is, of course, a minor technical point that has no impact on the system performance.

The way in which the image amplitude varies with the incident electron energy indicates whether the scintillator thickness is a good match to the expected operating conditions. Figure 3c shows the measured signal level with varying deceleration voltage, for a constant beam intensity, for the thinner scintillator that we have used for most work with the decelerator system. The response curves show an increase in signal as the beam energy increases up to the point where the electrons begin to pass through the scintillator into the substrate and then a subsequent falloff. The optimum operating voltage should be close to the peak, as this point produces the greatest light output and avoids much of the noise contribution that arises from the variation in conversion when the electron energy is not all absorbed in the scintillator. There is still a small signal even with the microscope is set to 200 kV and the decelerator is set to 190 kV, again indicating the presence of some voltage calibration errors, since the coatings on the scintillator prevent penetration of electrons with energy less than about 20 keV.

Various criteria have been used in testing the camera performance. Both the noise performance and resolution are of principal interest. As a measure of resolution, the line spread function, which gives the MTF, can be easily measured with the image of a straight edge such as the beam stop. The effect on image SNR is described by the frequency-dependent DQE,¹⁰ which can be derived from the MTF and noise power spectrum (NPS) of a blank image with no specimen in place as DQE(D,s)=MTF²(s)∕[NPS(D,s)∕D], where s is the spatial frequency and D is the exposure in electrons per pixel.^{11, 14}

Figure 4a shows line scans across such an edge with net incident energies of 300, 220, 120, and 30 keV. The improvement in sharpness of the edge image with decreasing energy is clear. The MTFs derived from these images are shown in Fig. 4b, illustrating the corresponding improvement with the greater amount of deceleration.

A substantial improvement in the DQE with increasing deceleration has also been documented, which is the result of the decreased noise level in the images, combined with the MTF improvement. The decrease in noise level is illustrated in Figs. 5a, 5b, which are Fourier transforms of carbon film images taken with the microscope at 250 kV and the decelerator at 0 and 220 kV, respectively. A dominant feature of these figures is the “Thon rings” that arise from modulation of the specimen scattering factor by the defocus-dependent contrast transfer function of the microscope. The improvement in clarity of the Thon rings with the beam decelerated is rather dramatic and represents a significant decrease in the noise level in the image.

Quantitative measurements of the DQE are shown in Fig. 6. At 300 kV, the curves correspond well to other published measurements that typically show a DQE near 0.1 at half-Nyquist frequency.^{8, 11} As the incident energy of the electrons decreases, the DQE improves dramatically, reaching its highest values around 40–50 keV. As the energy decreases below 40 keV, the signal amplitude falls rapidly, resulting in substantially lower DQE. As seen in Fig. 6b, which shows the DQE at two spatial frequencies as a function of net energy, the peak is fairly narrow but represents an improvement of a factor of close to 5 at half the Nyquist frequency, and over two at the lowest frequencies.

The image distortions were initially characterized with the use of a spot-scan image formed as an array of small illumination spots on a regular lattice. The standard software of the MRC image processing package²⁰ was used first to identify the position of each spot in the image and its displacement from the ideal lattice defined by the least distorted region near the center of the image, and then to define a function by which the distortions could be computationally corrected.¹⁹ Figure 7 shows images of the original spot-scan array, the distortion field derived from displacements of each spot from its ideal position, and the image that results from correcting for this distortion by “unbending” the image using a function based on the distortion field. Image distortions cause blurring of diffraction spots in the Fourier transforms of crystals, limiting the resolution to which data can be extracted from the transform. Figures 7d, 7e illustrate the degree of blurring in the transform of the original image and the improvement to very sharp spots after distortion correction.

The largest displacements in this example are as much as 250 pixels. While it would be preferable to avoid such distortions, it is important to demonstrate that even these larger distortions can be computationally corrected and do not limit the system performance. In fact, the distortions have already been substantially reduced. These images were obtained with an early version of the drift tube above the CCD. This version had a square cross section, which caused distortion of the fringing fields below the decelerator tube. The image distortions from the fringing field were reduced by about a factor of 5 when the drift tube cross section was made round. On the other hand, we can expect that the distortions will be larger when the system is operated under conditions that involve a greater degree of deceleration.

In order to demonstrate that the system is now useful for recording images of biological materials under low-dose conditions, and to test the procedures for correcting electron optical distortions, we recorded a set of images of purple membrane (bacteriorhodopsin, bR). The images were recorded at a magnification of 43 000 on the CCD, which produces a pixel size of 3.5 Å. The exposure was about 15 e∕Ų, with the microscope at 245 kV and the decelerator at 0 or 200 kV.

Due to the combination of electron optical and crystal distortions, the diffraction spots from the raw images are spread over a rather large number of pixels. After 2 cycles of unbending, the diffraction spots are sharpened essentially to a single pixel. A representation of the SNR for each spot after correction is shown in Fig. 8. Three of the images recorded under these conditions were processed, each giving similar results. The phase residuals for these images with respect to a reference data set for bR were less than 10° out to 8 Å resolution, further indicating the high quality of the data. A map of the structure computed from the data in these images is shown as an inset in Fig. 8 and matches the known structure very well. This procedure illustrates that the distortions are not a limitation in extracting data from the image of a crystal.

As an illustration of the improvement in visibility of specimen features with the system, Fig. 9 shows a set of images of a conventionally prepared cell section decorated with gold beads as would be used in electron tomography. These images were recorded at different exposure levels, with the decelerator providing a net electron energy of 300 or 50 keV. In principle, the resolution of a tomographic reconstruction improves as the number of images in the tilt series increases. However, for sensitive (e.g., unstained, frozen-hydrated) biological structures, only a limited exposure can be given to the specimen before serious radiation damage limits the results. One of the limiting factors in distributing this exposure among a large number of images is that positions of the gold beads must often be identified for alignment of the images. These results suggest that the beads could be identified at an exposure at least a factor of 4 lower with the decelerator, so that the number of images could be increased by a factor of 4. This would be a significant factor in improving the quality of cellular tomography.

DISCUSSION

The results with the bR images illustrate that data can be recovered to very near the Nyquist limit with good SNR. Electron microscopists working on single particle reconstruction of proteins generally oversample images by a factor of 2 or more in order to avoid loss of Fourier amplitudes with the many operations that are necessary for image scaling, alignment, and other processing steps. Each interpolation decreases the amplitudes in the high frequency region of the transform, and oversampling avoids much of this loss. On the other hand, images of crystals recorded on film are often digitized such that the desired resolution is just below the Nyquist limit.¹⁹ While interpolation, such as used in the distortion correction, decrease the amplitudes in this case as well, it does not degrade the SNR, which has been recognized as a more important criterion. Many microscopists have become resigned to the fact that it is necessary to work at a magnification high enough that the target resolution corresponds to half the Nyquist frequency, or even lower, when recording data on a CCD camera at 300 kV, even though this requires using at least twice the magnification and recording less than a quarter of the area that is theoretically possible. The ability to use the full frequency spectrum with our camera provides an important increase in image area compared to other cameras on IVEMs.

It is clear that there is a great deal of room for improving the scintillator and the coupling to the CCD chip. We note that, according to the interpretation of the Monte Carlo simulations presented in Fig. 1c, the point spread function (and thus the MTF) should continue to improve as the electron energy decreases. However, experimental results (not shown) corresponding to those presented in Fig. 4 show that the MTF improves as the incident energy decreases to around to around 100 keV with very little improvement beyond, even to 40 keV. It appears that we have reached the limits imposed by the structure of the phosphor, e.g., light scattering from the phosphor grains, as well as effects of local shear in the fiber optics and the conductive and protective coatings applied to the scintillator. Use of an optically clear scintillator would avoid the first problem. The metallization layer on the scintillator could be made thinner, but since it provides protection as part of the Faraday shield for the CCD chip, it needs to retain sufficient conductivity. A major improvement should be obtained by carefully matching the thickness of these layers to the operating voltage.

The ability to work at a low incident voltage also raises the possibility of depositing the scintillator directly onto the CCD, avoiding problems with the fiber optics that include the bonding process, loss of light, and the increasingly close match of the fiber size with the reduced CCD pixel size. We would need to ensure that x rays produced in the scintillator do not degrade the image quality, but we expect that this will be not a limitation at voltages around 30 kV.

Because the trend in large-format CCDs is clearly in the direction of smaller pixels, and because these offer advantages in speed and noise performance, it will be important to explore the limits of our approach. CCDs with 8000 to 10 000 pixels on edge are now becoming available, but these have pixel sizes of 9–11 μm. It is our belief that the decelerator is the best approach to take full advantage of this new technology.

With either larger camera formats or a higher decelerating voltage, the image distortions may become a significant problem. A simple solution to this problem would be to add a weak lens with a magnification of a few times at the bottom of the decelerator so that the beam passing through the electrostatic field would maintain a small diameter that would avoid distortions. The beam would then be spread by the magnification lens to fill the CCD.

CONCLUSION

Operating a CCD camera with an incident beam energy below 100 keV was predicted to yield significant improvements over energies in the 300 keV range. We have demonstrated the feasibility of decelerating the electrons in an IVEM and realizing these improvements. The DQE at half-Nyquist frequency is increased by a factor of 5, and we can record data with good SNR out to near the Nyquist limit. This system paves the way for use of larger format CCD chips with smaller pixels that are now becoming available for building a system that will satisfy essentially all of the needs of electron microscopists in replacing photographic film for data recording.