Problems detecting density-dependent diversification on phylogenies

While various sources of evidence suggest that speciation and perhaps also extinction rates decline as a clade diversifies (summarized in McPeek 2008; Rabosky & Lovette 2008a), estimates of these rates from molecular phylogenies were for a long time limited to constant-rates processes (Nee et al. 1994; Nee 2001; Ricklefs 2007). The difficulty of fitting more advanced models of diversification to phylogenies is largely due to the fact that molecular phylogenies only provide information about the evolutionary history of the species that exist at present: they are pruned of all extinct species. If extinct species are observed (as is the case in palaeontological studies of fossil data), it is not particularly difficult to determine whether the number of species arising in a time window is related to the number of existing species in that time window. If only a phylogeny of present-day species is available, even structurally simple time or density dependence is hard to detect, primarily because a phylogeny provides no direct information about the number of species throughout history.

Given the mathematical difficulty of treating density-dependent branching processes in retrospect, it is interesting that Rabosky & Lovette (2008a) claim to present evidence for density-dependent diversification in North American Dendroica warblers. They avoid mathematical complexity by a rather peculiar assumption: that the speciation rate depends on the number of species present (at some time t) in the reconstructed phylogeny, instead of the number of species actually present in nature at the time.

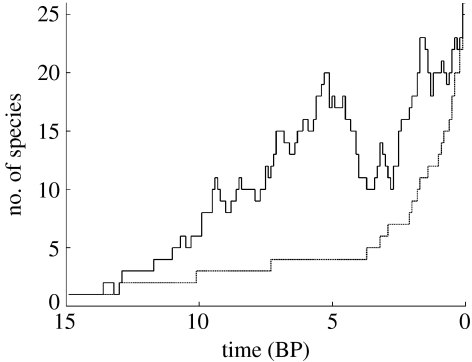
The number of species present in the reconstructed phylogeny N_t is lower than the actual number of species in nature n_t, unless there is no extinction at all; if extinctions occur, N_t only approaches n_t over time, to become equal just before the present (figure 1). To illustrate this, let us consider the phylogeny of mammals, which has only just over 20 lineages crossing the Cretaceous–Tertiary border (Bininda-Emonds et al. 2007), while there probably existed hundreds of mammal species at that time. It does not make sense to estimate density dependence of the speciation rate from the 20 or so species that happen to have extant descendants. Statistically, n_t and N_t will be correlated, but the correlation may be poor, especially near the base of the phylogeny where their discrepancy may be very large, as in the mammal example. Of particular interest here is that the correlation between n_t and N_t is especially weak if speciation rates are density dependent. In that case, n_t is approximately constant except during the early history of the process, while N_t always increases over time.

Figure 1.

Actual number of species (n_t, solid line) in a clade and the number of lineages (N_t, dotted line) in a perfectly reconstructed phylogeny of the 25 species that exist at present. The clade was simulated with a speciation rate of 0.5 and an extinction rate of 0.45 over time 15.

Figure 1 illustrates the discrepancy between N_t and n_t for a constant-rates birth–death process: actual and reconstructed numbers of lineages are moderately correlated (r²=0.59), but that correlation is largely due to the rapid rise in the number of lineages close to the present. For much of its early history, N_t is a very poor predictor of n_t. Thus, analysing density dependence using N_t is only a very coarse approximation.

Rabosky & Lovette (2008b) wrote that their approach ‘extends the birth–death model that has been used previously for inference on diversification rates’. In fact, while they explicitly considered extinction rates in an earlier paper, they neglected extinction here (which greatly reduces computational complexity) for two reasons. First, if the rate of diversification appears to slow down on reconstructed phylogenies, this can be explained by a decreasing speciation rate, but not by an increasing extinction rate. Second, constant high extinction rates would erase signs of changing speciation rates (Rabosky & Lovette 2008b), and since the Dendroica phylogeny suggests a decline in speciation rate, there is little reason—they argue—to expect high extinction rates. However, if speciation is density dependent as Rabosky and Lovette claim, the concave shape of their lineages-through-time plot may be due to density dependency, so that extinction may still have been a frequent phenomenon. Consequently, there is little reason to assume that N_t is a good predictor of n_t, and it should not be used to base inferences on without accounting (statistically) for this uncertainty.

In addition, by greatly reducing model complexity, neglecting extinction artificially reduces confidence intervals around parameters. A simpler example may be appropriate to understand this: if we assume diversification is a pure birth process, we obtain a much narrower confidence interval around the rate of speciation in Dendroica than we would have obtained assuming a birth–death process. Essentially, that is because the outcome of a birth–death process is more variable and less predictable. (In particular, if extinction does not take place, N_t always equals n_t.) Similarly, a density-dependent birth–death process is more variable than a density-dependent pure birth process. Neglecting extinction confounds model comparison, by setting one of the model parameters (the extinction rate) to zero, with a zero confidence interval around it, and without penalizing the model likelihood.

The approach to detect density-dependent diversification by Rabosky & Lovette (2008a) is currently too simple, primarily owing to the odd assumption that ancient speciation rates were determined only by those species that happen to have extant descendants. The idea, however, is sufficiently important to merit attempts to overcome these shortcomings. Certainly, the present comment should not be interpreted as suggesting that the frequent signs of initial rapid lineage splitting (McPeek 2008; Rabosky & Lovette 2008a) need no explanation. Considering also the evidence from palaeontological literature, it is both important and interesting to investigate whether speciation rates are density dependent, and if so, in what way. Several studies have shown that even moderate background extinction rates erase signs of early radiations on reconstructed phylogenies (Weir 2006; Phillimore & Price 2008; Rabosky & Lovette 2008b). How, then, can frequent signs of early radiations be explained? Rabosky & Lovette (2008a) suggest that background extinction rates have been low, but the fossil record shows that background extinction rates are not, generally, low. It seems that ecological models of speciation and extinction offer interesting alternative explanations for this pattern (Gavrilets & Vose 2005; McPeek 2008).