Effects of the nucleoid protein HU on the structure, flexibility, and ring-closure properties of DNA deduced from Monte-Carlo simulations

Abstract

The histone-like heat unstable HU protein plays a key role in the organization and regulation of the Escherichia coli genome. The non-specific nature of HU binding to DNA complicates analysis of the mechanism by which the protein contributes to the looping of DNA. Conventional models of the looping of HU-bound duplexes attribute the changes in biophysical properties of DNA brought about by the random binding of protein to changes in the effective parameters of an ideal helical wormlike chain. Here we introduce a novel Monte-Carlo approach to study the effects of non-specific HU binding on the configurational properties of DNA directly. We randomly decorate segments of an ideal double-helical DNA with HU molecules that induce the bends and other structural distortions of the double helix found in currently available X-ray structures. We find that the presence of HU at levels approximating those found in the cell reduces the persistence length by roughly threefold compared to that of naked DNA. The binding of protein has particularly striking effects on the cyclization properties of short duplexes, altering the dependence of ring closure on chain length in a way that cannot be mimicked by a simple wormlike model and accumulating at higher than expected levels on successfully closed chains. Moreover, the uptake of protein on small minicircles depends upon chain length, taking advantage of the HU-induced deformations of DNA structure to facilitate ligation. Circular duplexes with bound HU show a much greater propensity than protein-free DNA to exist as negatively supercoiled topoisomers, suggesting a potential role of HU in organizing the bacterial nucleoid. The local bending and undertwisting of DNA by HU, in combination with the number of bound proteins, provide a structural rationale for the condensation of DNA and the observed expression levels of reporter genes in vivo.

Introduction

Making sense of gene expression in living bacteria requires understanding of the looping properties of DNA in crowded, multi-component systems. The observed expression levels of reporter genes reflect not only the sequence-dependent mechanical properties of DNA but also the structure and flexibility of the mediating repressor proteins, the presence of other molecules bound to DNA, and the available space in the cellular environment. For example, deletion of the histone-like heat unstable (HU) nucleoid protein from E. coli drastically alters the chain-length dependent pattern of repression of the lac operon [1, 2], even though the operon contains no known HU-binding sites. The presence of HU, a non-specific dimeric protein that introduces sharp bends and localized untwisting in double-helical DNA [3–5], appears to stabilize functional repression loops as small as ~65 bp (where loop size refers to the center-to-center spacing of lac operator sites engineered on DNA). Moreover, DNA chain length has little or no effect on repression in the lac system, other than the periodic modulation expected from the torsional alignment of DNA with the Lac repressor protein [1, 2, 6–10].

Theories conventionally used to interpret DNA loop formation and stability ignore the complexity of the double-helical structure, including details of nucleotide conformation, which may influence loop configuration. In addition, the effects on looping of structural distortions, such as those imparted by the random binding of proteins like HU on DNA, are typically subsumed in the parameters of a simplified model, e.g., the bending and twisting moduli and the double-helical repeat of a naturally straight, DNA isotropic elastic rod. Interpretation of the in-vivo expression profiles of proteins regulated by the lac protein-DNA assembly on the basis of such a model may be misleading. For example, the longer period and smaller amplitude of the oscillation of gene expression with the distance between lac operator sites compared to the chain-length dependent properties of similar pieces of DNA in solution [1, 2, 6, 7], suggests an order-of-magnitude reduction in the persistence length, a decrease in the torsional modulus, and an increase in the double-helical repeat of the protein-bound molecule. The key role of HU in DNA looping and gene expression [1, 2] is lost in such models.

Meaningful interpretation of the ways in which HU and other molecular agents contribute to the in-vivo looping properties of DNA requires a model that conforms more closely and in an identifiable manner with the structural and deformational characteristics of the protein-bound duplex [3]. Such a model should account equally well for the effects of random, non-specific HU binding on both the end-to-end extension [11–13] and the cyclization properties [14, 15] of long, linear DNA molecules. Models employed to date to treat the persistence length of protein-bound DNA [16, 17], however, do not address the effects of protein on DNA looping or cyclization, and published studies of HU-induced DNA looping [1, 6, 7, 18] do not consider the effects of protein on the properties of linear DNA. Moreover, none of these treatments incorporates the unique features of HU-bound DNA revealed in high-resolution crystal complexes [3–5], such as the ~120° overall bending of DNA, concentrated at two base-pair steps, and the untwisting of base pairs along the length of the duplex (see Table S1 in Supplementary Materials for complete details of the deformations of base-pair steps in currently available structures).

The DNA sequences crystallized in the presence of HU include mismatched and unpaired nucleotides specifically designed to enhance sharp bending. The effects of HU on DNA extension [11, 13] and ring closure [14, 15], when incorporated in an appropriate model, can provide insight into the extent to which such kinks might persist when the protein binds ordinary intact sequences. The persistence length of DNA extracted from atomic force microscopy (AFM) images obtained in the presence of dilute amounts of HU (one HU per ~100 bp) drops to roughly half that found for DNA without bound proteins. By contrast, at high concentrations, where HU covers DNA completely, the protein assembles into a rigid, superhelical filament on DNA with a persistence length several times that of naked DNA [11]. HU molecules ‘localized’ at designed binding sites in labeled oligonucleotide duplexes appear to bend DNA in solution to the same extent as the crystallized DNA-bound protein; distances extracted from fluorescence resonance energy measurements of an HU-bound 55-mer correspond to a bend angle of 148° [13]. The degree of bending per dimeric protein, however, decreases at higher HU concentrations [12, 13]. The presence of HU also stimulates the rate of DNA cyclization and enhances the enzymatic closure of short (78–126 bp) chain fragments that would otherwise remain linear [14, 15]. The levels of HU used to effect circularization, e.g., 7 HU dimers per 99-bp cyclized DNA fragment [14], are much higher than those found in vivo. For example, the ~30,000 HU dimers present during the exponential growth phase of E. coli [19] correspond to roughly one dimer per 150 bp of the 4.6× 10⁶-bp genome [20].

Extrapolation of the structural features of in-vivo LacR-mediated DNA looping (and in-vivo DNA cyclization in general) is a challenging problem, requiring (i) accurate models of the sequence-dependent structure and deformability of DNA, (ii) theoretical understanding of how local structural features of DNA are revealed in its global configurational properties, and (iii) efficient numerical methods for treating the statistical mechanics of supercoiled DNA with variable numbers of bound proteins. Here as a first step in the analysis of such looping, we investigate the effects of HU on the configurational properties of short fragments of ideal B DNA. We treat the double helix at the level of base-pair steps, using elastic potentials that account for variability in the intrinsic structure and elastic moduli of individual base-pair steps, including those bound to HU. We omit explicit terms that take account of long-range protein-protein interactions and DNA electrostatic repulsion. We introduce a new sampling technique to model the non-specific binding of HU (or any other such molecule) to DNA and use a recently developed fast Monte-Carlo approach [21] to generate three-dimensional structures of protein-bound DNA. We first examine the effects of bound HU on the global configuration of linear DNA, including the distribution of end-to-end distances and orientations of terminal base pairs. We also compute the persistence length of DNA from the chain configurations sampled at the same low levels of HU binding and determine the J factor, the well-known measure of DNA cyclization [22], from the fraction of spatial arrangements that satisfy the restrictions on end-to-end displacement and base-pair orientation required for ring closure. We show that the presence of HU alters the dependence of J on chain length in a way that cannot be mimicked by the elastic parameters of a simple wormlike chain. We study the effects of HU concentration, i.e., binding probability, on both the average dimensions and cyclization efficiencies of linear DNA over a broad range of chain lengths. We allow for flexibility in the HU·DNA complex consistent with the variability of DNA in known high-resolution, protein-bound structures [3] and consider the effects of lesser bending deduced from some fluorescence studies [12, 13]. Finally, we examine the number of bound HU molecules in the cyclized molecules and the effects of bound protein on the distribution of DNA topoisomers.

Results

HU-bound DNA sample

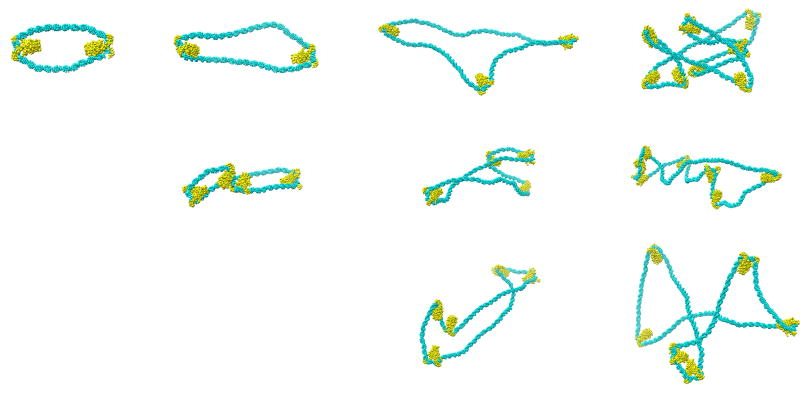
The set of representative chain configurations in Figure 1 illustrates how the random binding of HU to a 126-bp ideal DNA duplex transforms a smoothly deformed, relatively stiff polymer into what appears to be a highly flexible chain molecule. The series of images — with HU distributed such that there is, on average, one protein per 100 bp (w_HU=1.15 × 10⁻²) and DNA modeled as a sequence of ‘ideal’ B-type steps (see Methods for terminology and computational treatment) — bears a striking resemblance to the configurations of HU-DNA complexes detected in AFM images collected under similar binding conditions [11], i.e., the computer-generated structures exhibit the same degree of bending seen in DNA fragments of comparable length within the 1000-bp HU-bound chains studied experimentally. The proportion of HU in the illustrated examples (3 protein-free configurations, 5 with one HU, 3 with two HU’s, 1 with three HU’s) corresponds to the distribution of bound molecules found in a simulated ensemble of 10¹⁰ configurations with the aforementioned binding ratio (Table 1). The persistence length of HU-bound DNA derived from this configurational sample (138 Å) falls short of the value (240 Å) deduced from the observed end-to-end distances and contour lengths of 1000-bp HU-bound DNA molecules [11]. The analysis of experimental data, however, assumes that the DNA is an ideal, two-dimensional elastic rod subject to small isotropic bending fluctuations [23]. Differences in assumed vs. simulated chain properties, such as the tenfold reduction in the average cosine of the angle between terminal base pairs in the computer-generated sample compared to the expected behavior of ideal DNA, may contribute to the differences in persistence length. Furthermore, the fraction of protein bound to the imaged DNA molecules may not necessarily correspond to the concentration of HU in the solution used in sample preparation. The computed persistence length increases at lower levels of HU binding (see below) as well as under lesser degrees of protein-induced DNA bending. For example, modeled HU-induced bends of 80–92°, obtained by a 2/3 reduction in the bending angles at all protein-bound steps and randomly placed every 100 bp along DNA, lead to a persistence length to 230 Å.

Figure 1.

Representative configurations of a 126-bp ideal B-DNA duplex in the presence of HU. The proportion of HU in the illustrated examples (3 protein-free configurations, 5 with one HU, 3 with two HU’s, 1 with three HU’s) corresponds to the distribution of bound molecules found in a simulated ensemble of 10¹⁰ configurations with the dimeric protein randomly distributed such that there is one HU per 100 bp of DNA (w_HU = 1.15×10⁻²). The double helix is assumed to be naturally straight in its equilibrium rest state, inextensible, and capable of isotropic bending and independent twisting at the base-pair level. The assumed twisting and bending fluctuations are consistent with experimental properties of mixed-sequence DNA, i.e., 10.5 bp per helical turn and a persistence length of ~500 Å. The HU-bound DNA steps are constructed from the sets of base-pair step parameters found in known high-resolution structures [3–5]. The DNA pathway is generated from Monte-Carlo sampled base-pair step parameters using the 3DNA software package [54]. Protein coordinates are obtained by superposition of DNA from the appropriate crystal structure on the simulated pathway. Images are rendered with Chimera [60].

Table 1.

Protein populations, as a function of simulated binding level w_HU and chain length N, on short open and closed HU-bound DNA chains.^†

DNA chain	wHU	N (bp)	0 HU	1 HU	2 HU	≥3 HU
Linear	5.35 × 10−3	126	0.546	0.354	0.089	0.011
		210	0.347	0.395	0.194	0.064
	1.15 × 10−2	126	0.277	0.412	0.236	0.075
		210	0.105	0.274	0.312	0.309
	2.70 × 10−2	126	0.049	0.212	0.347	0.392
		210	0.005	0.038	0.124	0.833
Circular	5.35 × 10−3	126	0	0.002	0.897	0.101
		210	0.004	0.041	0.615	0.340
	1.15 × 10−2	126	0	0.002	0.730	0.268
		210	0	0.005	0.301	0.694
	2.70 × 10−2	126	0	0	0.326	0.674
		210	0	0	0.037	0.963

^†HU binding probabilities, w_HU=5.35 × 10⁻³, 1.15 × 10⁻², or 2.70 × 10⁻² , correspond respectively to one bound protein per 200, 100, or 50 bp in the simulated ensemble of open chain configurations (note the larger HU binding fraction in closed molecules). Dominant HU-DNA stoichiometric ratios are highlighted in boldface.

Even though the HU-bound steps are restricted to the narrow range of states found in the four known crystal structures [3] (see Table S1 and Figure 8 in Methods), the presence of the modeled protein dramatically broadens the range of accessible configurations compared to that of a pure DNA of the same chain length. The likelihood of end-to-end contact increases with the number of bound HU molecules, as both the peak in the radial density distribution (Figure 2) and the normalized mean chain extension 〈r 〉/L₀, where r is the end-to-end distance and L₀ the contour length, become progressively smaller (Table 2). The introduction of modeled protein concomitantly perturbs the orientation of terminal base pairs. Whereas the ends of the 126-bp protein-free DNA tend to be aligned in a more parallel than antiparallel fashion, with the cosine of the angle γ between the normals of terminal base pairs nearly four times more likely to be positive than negative, the ends of chains of the same length with a single bound HU molecule are more apt to be antiparallel rather than parallel (Table 2). These orientational propensities, a measure of the bending angle of the DNA as a whole, become less pronounced as additional proteins bind to the 126-bp duplex. By contrast, the twisting correlation between terminal base pairs found in protein-free DNA, i.e., the tendency of the end-to-end twist τ to fall in the range 0–90°, diminishes abruptly with the binding of a single HU molecule (Table 2). The distribution of τ in the latter chains is nearly uniform (data not shown).

Figure 2.

Distributions of the end-to-end distances r for a series of 126-bp HU-bound DNA molecules with specfic numbers of randomly placed proteins. Distances, obtained from Monte-Carlo sampling, are expressed in terms of relative chain extension, r/L₀, where L₀ is the contour length of the fully extended molecule (3.4×126 = 428.4 bp). Bin width Δr is set to 5 Å and W(r) is normalized such that the total probability is unity.

Table 2.

Average end-to-end properties, as a function of chain length and binding stoichiometry, of short, linear, HU-bound DNA chains.^†

Property	N (bp)	0 HU	1 HU	2 HU	≥3 HU
	126	0.868	0.627	0.518	0.445
〈r〈/L0	210	0.795	0.600	0.507	0.424
	126	0.077	0.162	0.163	0.154
(〈r2〈 − 〈r〈2)1/2/L0	210	0.111	0.166	0.162	0.150
	126	0.803:0.197	0.339:0.661	0.588:0.412	0.460:0.540
cosγ >0:cosγ<0	210	0.667:0.333	0.413:0.587	0.546:0.454	0.487:0.513
	126	0.899:0.101	0.544:0.456	0.486:0.514	0.486:0.514
τ <90° : τ > 90°	210	0.755:0.245	0.522:0.478	0.486:0.514	0.496:0.514

^†HU binding probability, w_HU=1.15 × 10⁻² , corresponds to one protein per 100 bp of simulated DNA. End-to-end distances r are reported with respect to the contour length L₀=3.4N of the fully extended molecule of chain length N. See text for definitions of (γ,τ) orientation angles.

As expected for polymeric molecules [24], the distribution of configurational states broadens with increase in chain length. This broadening is illustrated by the wider dispersion of end-to-end distances and the increased proportion of chains with terminal base pairs aligned in parallel vs. antiparallel arrangements (compare corresponding values of the normalized dispersion, (〈r²〉 − 〈r〉²)^1/2/L₀, and the bending and twisting ratios, cos γ > 0 : cos γ < 0 and τ < 90°:τ > 90°, for 126- and 210-bp chains with the same number of HU molecules under identical binding conditions in Table 2). The degree of broadening, however, depends upon the presence or absence of protein. The relative chain extension also depends on protein number and tends to decrease with increase in chain length. The effect of protein binding on chain cyclization is not obvious from these data.

Longer chains naturally incorporate more HU molecules under the chosen binding conditions, altering the fraction of sampled chains with a particular number (0, 1, 2, 3, etc.) of bound protein molecules (see Table 1). The distribution of chains with a given number of bound HU molecules consequently depends upon HU concentration. For example, doubling the binding fraction of HU to one per 50 bp (w_HU=2.70×10⁻²) decreases the fraction of linear 126-bp chains with 0 or 1 HU and increases the fraction with ≥2 HU compared to chains with one HU bound per 100 bp (see Table 1). Conversely, decreasing the HU binding fraction to one per 200 bp (w_HU=5.35×10⁻³) increases the fraction of protein-free linear DNA molecules.

Cyclization of HU-bound DNA

The random binding of HU has striking effects on the cyclization properties of the short duplexes described above and the average number of bound protein molecules. Binding at the level of one HU per 100 bp (w_HU=1.15×10⁻²) increases the J factor of the 126-bp chain by four orders of magnitude and that of the 210-bp chain by two orders of magnitude over the cyclization propensities of ideal, protein-free DNA molecules of the same length. Moreover, in contrast to the naked duplex, which cyclizes roughly an order of magnitude more easily at the longer chain length, the J factor of the shorter HU-bound chain is of the same order of magnitude as that of the longer molecule. The average HU spacing, i.e., one HU per 100 bp, used to generate these findings, refers to the probability w_HU of one HU dimer binding, on average, every 100 bp of linear unconstrained DNA. As will become apparent below, the average number of HU molecules bound to the cyclic DNA species collected under these conditions is quite different.

Figure 3 presents the full chain-length dependence of the J factors for both ideal, protein-free DNA molecules and DNA chains with non-specific HU binding (at an average level of one HU per 100 bp). The intrinsic properties of the ideal duplex limit the values of N over which the two J factors can be compared, i.e., it is not practical to sample a stiff, naturally straight ideal duplex shorter than 90 bp. The chain length of HU-bound DNA most readily cyclized is substantially shorter than the optimum chain length of naked DNA rings, i.e., the maximum in J for the modeled protein-bound duplex occurs in chains of 75 bp whereas that of the ideal, protein-free chain occurs at 483 bp, a value close to the familiar multiple of three times the persistence length [21]. The phasing and amplitude of oscillations in J also decrease much more rapidly, with increasing chain length, in HU-bound than in pure DNA minicircles; the amplitude in log J varies from 1.0 to 0.04 in HU-bound chains of 90–290 bp compared to values between 1.1 and 0.3 for naked duplexes over the same range of N. Although the distances between successive peaks or valleys in the plots of J vs. N are comparable in HU-bound and naked chains (10–11 bp), the locations of these points differ, i.e., the most probable chain lengths of cyclic HU-bound DNA molecules are typically 3–4 bp longer than those of protein-free minicircles.

Figure 3.

Monte-Carlo estimates of the chain-length dependence of the J factor, i.e., cyclization propensity, of free and HU-bound DNA. Configurations of HU-bound circles are generated such that there is one HU dimer binding, on average, every 100 bp of DNA (w_HU = 1.15 × 10⁻²) in the simulated ensemble of (open and closed) configurations. DNA and protein are modeled as in Figure 1. Inset shows the dependence of J on N when configurations with protein-protein, protein-DNA and DNA-DNA overlaps are excluded in small minicircles.

Consideration of DNA and protein steric contacts alters the predicted cyclization propensities of the modeled HU-bound duplexes (inset to Figure 3). The effects are most striking at chains lengths where cyclization is less likely, i.e., out-of-phase values of N where there is a local dip in J. As shown below, these hard-to-form minicircles bind more HU proteins on average than closed duplexes that are 5–6 bp longer or shorter. The order-of-magnitude difference in the J factor in the very shortest (91 bp) out-of-phase minicircle reflects the difficulty of fitting multiple proteins on such a DNA (the proteins lie inside the DNA minicircle in relatively close contact with one another). The fraction of unacceptable closed configurations becomes significant at longer chains lengths where the cumulative fluctuations of local DNA structure become significant. Roughly a third of the cyclic HU-bound structures exhibit some sort of self-contact at the longest chain lengths considered here (315 bp), reducing the cyclization factor by ~0.2. The decrease in log J is less than 0.1 in chains shorter than 200 bp (other than the out-of-phases cases noted above).

Population of HU in simulated minicircles

Despite the assumed binding probability of one HU per 100 bp, nearly three quarters of the successfully closed, 126-bp molecules contain two bound proteins, with either 3 or 4 bound proteins in the remaining examples (Table 1), i.e., an average of 2.4 bound proteins per closed DNA molecule. In other words, the number of bound HU molecules on the closed 126-mer is nearly double the expected number of HU molecules in a randomly sampled DNA chain. The number of HU proteins associated with the 210-bp minicircles formed under the same binding conditions also exceeds the average number of bound proteins in all simulated structures, i.e., 3.3 bound HU per closed 210-mer compared to 2.0 proteins on average in the complete ensemble. Although the fraction of chains binding 2 HU molecules is similar in rings vs. all 210-mers, most of the closed molecules form in the presence of 3 or more HU and many of the unconstrained chains contain 0 or 1 HU (Table 1). The ratio of the average number of HU proteins in a closed duplex compared to the average number in the complete ensemble of simulated DNA molecules decreases in longer minicircles (Figure 4).

Figure 4.

Average number of HU molecules, as a function of chain length N, on successfully cyclized DNA chains (dashed curve) compared to the simulated degree of binding in the ensembles of all (linear and cyclic) HU-bound chains of the same N (solid line). See legend to Figure 3 for computational details.

The number of HU molecules in successfully closed duplexes exhibits a periodic dependence on chain length. There are fewer proteins bound to minicircles of chain lengths corresponding to local peaks in the plot of J vs. N and more HU molecules associated with minicircles in valleys (compare the out-of-phase sinusoidal variation of HU build-up with N in Figure 4 with the plot of J vs. N in Figure 3). The minicircles in the former cases bind 2–3 HU molecules depending on chain length, whereas those in the latter cases bind 3 or more proteins. Furthermore, the HU populations change abruptly with increase in N, particularly at short chain lengths. Small populations of minicircles with 5 or 6 bound HU accumulate with increase of chain length (data not shown).

HU positioning in open and closed molecules

The placement of proteins on the simulated HU-bound DNA molecules is approximately uniform although the half-chain sampling technique introduces a slight build-up of protein at the ends and centers of open duplexes, i.e., DNA molecules with no constraints on the placement and orientation of chain ends. The build-up of HU occurs at all chain lengths, with more pronounced effects found in longer molecules (see Figure S1 in the Supplementary Materials for the simulated placement of HU for 10⁸ random half-chain combinations of 126- and 210-bp open chains at three levels of HU binding). The build-up at the start of the segment is natural (not an artifact) and explained by the fact that there is never an occupied site that excludes the placement of protein at the first m binding sites on DNA, with m = 14 for HU. The build-up in the middle and the far end of the chain is avoided by extending the chain by m phantom base pairs (see Methods). There is less than a 10% difference in the number of proteins bound at the center compared to other locations on the simulated chains. Such differences are inconsequential on the logarithmic scale used to assess ring closure.

The configuration of the protein-bound duplex and the intrinsic stiffness of the intervening DNA determine the number and positions of bound proteins on the cyclized molecules (Figure 5). The proteins tend to be evenly spaced along shorter minicircles, with segments of unbound DNA straightened at higher levels of protein binding (note the ‘oval’ configuration of a 126-bp minicircle with relatively straight segments of DNA between the two bound proteins). The proteins often lie at the tips of hairpin loops and in semicircular fragments of longer chains. Many of the 210-bp rings adopt ‘figure-8’ arrangements with one or two HU molecules bound in each half of the closed structure. Longer closed chains of 420 and 630 bp assume open, plectonemic arrangements with proteins bound to interwound interior segments and end loops as well as collapsed, multi-lobed states with HU bound at the ends of hairpin loops. Some of the latter structures, e.g., the 630-bp protein-bound configuration shown in the top right corner of Figure 4, incorporate a regular serpentine-like fold of the sort thought to nucleate the rodlike condensates formed in the presence of HU [25].

Figure 5.

Representative computer-generated images of successfully closed HU-bound DNA minicircles of different chain lengths (126, 210, 420, 630 bp). Images in the first, second, and third rows illustrate examples of molecules with excess link ΔLk of 0, −1, and −2, respectively. Molecules are generated and constructed under conditions described in Figures 1 and 3.

Topological properties of cyclized HU-bound DNA

The minicircles of HU-bound DNA occur in several topological states, or topoisomers, with different values of the excess link, ΔLk, or the difference in the linking number of the closed DNA compared to that of a relaxed, protein-free molecule. If HU associates with DNA prior to cyclization, the binding will influence the resulting distribution of topoisomers found at any given chain length, with the general result of broadening the range of topological states (Figure 6). Whereas most of the protein-bound minicircles associated with local peaks in the J factor have zero excess link (ΔLk =0), most of those associated with the intervening valleys have negative excess link (ΔLk =−1). By contrast, virtually all naked DNA minicircles have zero excess link over the corresponding range of chain lengths and as predicted by theory [26], show no directional preference when occasionally supercoiled (see below). The reported variation of ΔLk for HU-bound DNA in the figure spans a slightly different range of chain lengths (126–252 bp), although of the same width, as that for naked DNA (189–315 bp).

Figure 6.

Distribution of the linking-number deficit ΔLk, as function of chain length N, (a) in successfully closed HU-bound DNA molecules free of self-contact compared to (b) ideal, protein- and contact-free minicircles of comparable lengths. See inset and legend to Figure 3 for computational details.

Inspection of the data shows that HU binds at different levels in supercoiled and relaxed structures: the relaxed structures tend to bind fewer proteins (2–3 on average depending upon chain length) and the supercoiled structures more HU molecules (3 or more on average), cf. Figures 4 and 6a. As the HU-bound minicircles increase in size beyond the chain lengths where the J factor locally peaks, the average number of HU molecules on the closed duplexes increases, cf. Figures 3 and 6a. Furthermore, the topoisomer distribution shifts abruptly 2–3 bp beyond each peak in the J-factor profile from a population of rings with ΔLk zero in almost every simulated configuration to one where nearly every successfully closed structure has a linking number difference of −1. The peaks in the average number of bound proteins and the local minima in the J factor lie another 2–3 bp beyond this transition point. The topoisomer distribution changes gradually with further increase in minicircle length, returning the protein-bound DNA rings to a homogenous population of relaxed ΔLk = 0 topoisomers.

As shown in Figure 6, the variation of ΔLk with chain length in the HU-bound minicircles is completely different from that in ideal DNA. Most of the short, protein-free minicircles occur in a single topoisomeric form with ΔLk = 0. Chains that differ in length by roughly a half turn from an integral multiple of the double-helical repeat, however, also adopt states where ΔLk = ±1. The proportion of rings in the latter states increases with chain length, ranging from 0.28 in minicircles of 194 and 205 bp (~18.5 and 19.5 helical turns) to 0.35–0.38 in closed molecules of 299 and 310 bp (~28.5 and 29.5 helical turns). Thus circular duplexes with bound HU are much more likely than naked DNA to exist as diverse topoisomers, particularly as negatively supercoiled forms. The experimental observation of such broadening in the population of topoisomers would be conventionally interpreted in terms of a decrease in the effective twist modulus of the protein-bound minicircles compared to that of protein-free DNA. Here we know that the DNA has the same elastic properties in the two types of molecules and that the changes in ΔLk reflect the distortions of DNA imposed by the HU protein.

Concentration effects

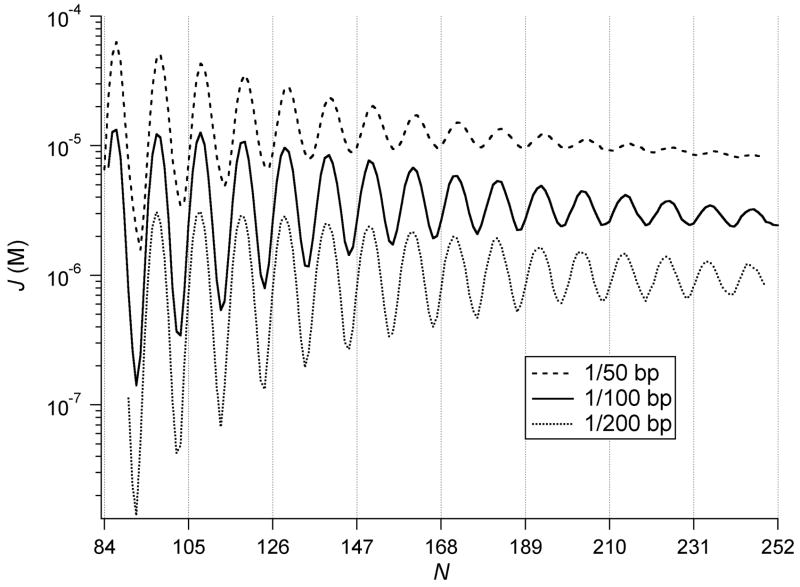
A twofold change in the protein-binding levels has more than a twofold effect on the computed ring-closure propensities (Figure 7). Doubling the simulated fraction of bound HU increases the J factor, dampens the amplitude of oscillations in J, and shifts the local maxima and minima in J to longer chain lengths, i.e., from N to N+1 for each protein-doubling event. The combined effects enhance the J factor by as much as an order-of-magnitude, particularly at the lower range of N considered here. The minicircles formed at higher concentrations have a greater number of bound proteins than rings of the corresponding size formed at lower binding levels (Table 1). The number of proteins on the minicircles always exceeds the simulated binding levels, and, remarkably, there are only a few minicircles with less than two bound HU molecules, even at the lowest binding levels. Added protein broadens the range of chain lengths over which the minicircles adopt a particular linking number, e.g., the Lk=15 topoisomer persists at appreciable levels (10%) in minicircles of 155–171 bp when the simulated protein-binding levels are high (w_HU=2.70 × 10⁻²) but in minicircles of 155–167 bp when the binding probability is low (w_HU=5.35 × 10⁻³). As a result, the range of topoisomers found at a given chain length is broadened with the addition of HU, e.g., minicircles of 206 bp form topoisomers with Lk of 18, 19, or 20 when w_HU=2.70 × 10⁻² but only Lk 18 or 19 when w_HU=5.35 × 10⁻³.

Figure 7.

Effect of simulated levels of HU binding on the chain-length dependence of the J factor. HU binding probabilities w_HU (5.35 × 10⁻³, 1.15 × 10⁻², 2.70 × 10⁻²) correspond respectively to one protein bound on average every 200, 100, or 50 bp of DNA in the full ensemble of (open and closed) configurations.

Higher levels of HU binding lower the persistence length. For example, the values of a extracted from the product of generator matrices P_N obtained in simulations of a 210-bp DNA with HU molecules randomly positioned every 200, 100, and 50 base pairs are 218, 142, and 76 Å, respectively. (Note the slight increase in a when the persistence length is extracted from the longer 210-bp chain compared to the value of 138 Å obtained from simulations of a 126-bp DNA subject to the same HU concentration.) Given the random placement of protein on DNA in the simulations, the nonlinear response of chain extension to binding levels must reflect the unique local structure of HU-bound DNA rather than the cooperative binding effects thought to give rise to the concentration dependence of the efficiency of fluorescence resonance energy transfer of HU-bound oligomers [13].

Effective elastic moduli of HU-bound DNA

The complex dependence of the J factor on chain length points to some of the potential problems associated with interpreting the global properties of a real protein-bound duplex in terms an oversimplified model. The effective (averaged) parameters of an ideal isotropic elastic chain fitted to the simulated HU-bound DNA data depend not only on protein concentration but also on chain length (Table 3). The ideal models also fail to account for the 3–4-bp phase shift in the peaks and valleys in J of the protein-bound duplex compared to naked DNA. Here we fit the J factors of simulated ideal chains of 126–147 and 230–251 bp to the data reported above for HU-bound duplexes by shifting the test points by an appropriate increment in N. Although the HU-decorated chain may appear to be more flexible than a naked DNA molecule of the same length in terms of the fitted elastic parameters, the protein-free segments have the same flexibility in the two cases. The apparent fluctuations in dimeric structure yield elastic constants comparable to values reported in previous analyses of the in-vivo looping properties of DNA [18, 27], e.g., the apparent persistence length a= Δs/(〈 Δθ₁〉^eff)², derived from the effective room-temperature fluctuations in bending 〈 Δθ₁〉^eff=〈 Δθ₂〉^eff, drops by a factor of four and the global torsional constant C=k_BT/(〈 Δθ₃ 〉^eff)², extracted from the apparent variation in the twist angle 〈 Δθ₃ 〉^eff, is slightly reduced when HU is spaced on average every 100 bp base pairs along the simulated duplex. Surprisingly, the apparent deformability depends upon chain length. That is, no single elastic model fits the two ranges of protein-bound DNA J factors considered here. Furthermore, whereas the apparent bending constant decreases with uptake of HU, the twisting constant increases. Ideal chains governed by bending constants as low as those needed to match the J factors obtained in the presence of 1 HU per 50 bp, where a ≈ 72–78 bp, have the same apparent twisting stiffness as protein-free DNA. The variety of configurations accessible to such easily bent chains overcomes the apparent twisting penalty associated with ring closure.

Table 3.

Effective parameters of an ideal elastic model fitted to the simulated ring-closure properties of DNA cyclized in the presence of HU.^†

					〈ÆLogJ〉
wHU	N (bp)	${\theta }_3^{\mathit{eff}}$ (°)	〈Æθ1〉eff (°)	〈Æθ3〉eff (°)	126–147	210–231
	130–151	34.3	11.95	4.09	0.04	0.10
2.7 × 10−2	214–235	34.3	12.40	4.09	0.20	0.06
	129–150	34.3	9.98	4.39	0.01	0.21
1.15 × 10−2	213–234	34.3	9.76	4.39	0.12	0.01
	129–150	34.3	8.19	5.27	0.01	0.21
5.35 × 10−3	213–234	34.3	7.62	5.68	0.30	0.03

^†HU binding probabilities w_HU = 2.7×10⁻², 1.15×10⁻², and 5.35×10⁻³ correspond respectively to one bound protein per 50, 100, or 200 bp in simulated, protein-bound minicircles, and elastic parameters ${\theta }_3^{\mathit{eff}}$, 〈Æθ₁〉^eff=〈Æθ₂〉^eff, and 〈Æθ₃〉^eff to the effective helical twist angle, the room-temperature fluctuations in the bending angles that raise the elastic energy by kT/2 , and the corresponding room-temperature fluctuations in the twist angle of the fitted elastic chains. 〈ΔlogJ〉 is the root-mean-square deviation of the logarithm of the J factors of elastic chains of 126–147 or 210–231 bp compared to the values simulated for HU-bound duplexes of length N at the given value of w_HU

Degree of protein-induced bending

The ring-closure profiles of the HU-bound duplexes also reflect the degree of protein-induced DNA deformation. For example, the partial straightening of DNA brought about by the uniform decrease in tilt and roll (θ₁,θ₂) at the base-pair steps in known crystal complexes leads to a reduction in the J factor. The 2/3 decrease in dimeric bending introduced above to increase the persistence length of DNA with one HU bound per 100 bp lowers J by 1–3 orders of magnitude in chains of 105–126 bp, concomitantly enhancing the amplitude of oscillations of J vs. N and making the cyclization of chains with ‘out-of-phase’ ends more difficult. The ease of ring formation, nevertheless, exceeds that of DNA in the absence of protein. The lesser distortions of the protein-bound DNA — with net bending angles of 80°, 85°, 89°, and 92° for ‘opened’ models constructed from the four HU-bound structures detailed in Tables S1-(a–d) (Supplementary Materials) — increase the number of proteins on closed DNA. In contrast to the X-ray-modeled HU-DNA system where two HU molecules bind on average to 108 and 119-bp minicircles, there are 3–4 proteins on the corresponding 109 and 120-bp minicircles formed under less severe bending conditions, i.e., in chains subject to the same (w_HU=1.15 × 10⁻²) binding probability and of lengths at comparable peaks in the variation of J with N but with different protein-induced structures. The ‘out-of-phase’ minicircles formed in the presence of the ‘opened’ complexes behave more like ideal DNA in assuming a mix of topoisomers, e.g., a 0.61:0.39 ratio of Lk 11 and 12 in 125-bp rings collected from 4 × 10¹² configurations. Thus, the number of bound proteins and the topology of DNA show a chain-length dependence analogous to that found with the crystallographically modeled protein.

Discussion

New insights into protein-mediated DNA cyclization

The explicit treatment of double-helical structure, including protein-induced deformations of DNA, in simulations of long protein-bound duplexes provides new insight into how the non-specific binding of architectural proteins like the E. coli HU protein stabilize DNA looping. While it has long been appreciated that the bending of DNA by proteins enhances chain cyclization [28], the structural role of non-specific binding on DNA ring closure and/or loop formation has remained elusive. Now we see that the non-specificity of binding allows proteins or other ligands to accumulate at different levels in closed chains of specific length N. Indeed, we find that HU is preferentially found in closed over open DNA structures (Table 1). That is, successfully closed DNA minicircles contain more HU dimers on average than the complete ensemble of sampled protein-bound structures, even though the HU binding affinity, i.e., the probability of binding at a given location on DNA, is assumed to be independent of substrate configuration.

Such information goes beyond the conventional picture of non-specific DNA-ligand interactions [29], which focuses on the possible arrangements of a fixed number of ligands on a DNA chain rather than the variable composition of ligands on different chains and the effect of ligand binding on global chain configuration (Figure 1). The higher levels of HU on the DNA minicircles treated here provide a new structural perspective on the increased binding affinity of HU [30] to 222-bp circular vs. linear duplexes in solution. Even though we impose no added benefit to HU binding curved over straight DNA, more HU accumulates on average on covalently closed than linear chains (Figure 5). The local binding event has an unexpected global effect that persists in minicircles at all three concentration ranges considered. One interpretation of these findings is that DNA molecules with higher HU content are more likely to cyclize. Although the present calculations do not directly address the question of whether HU preferentially binds cyclic over linear substrates, our results suggest this to be the case. In particular, the difference 〈ΔU〉 in the average elastic energy of short circular and linear DNA molecules of the same length, i.e., 〈ΔU〉= 〈U_circle〉−〈U_linear〉, depends upon the number of bound proteins. For example, the average elastic energy of a 126-bp circle exceeds that of the linear chain by 17.5 kT, but the difference drops to 9.9 kT in chains of the same length with one bound HU and 2.9 kT in chains with two HU molecules. In other words, the more HU is bound, the lower the energy difference is between the circular and linear forms (with the same HU number). Thus, HU will preferentially bind to circular DNA as opposed to linear DNA, because the binding to circular DNA is associated with a decrease in the average DNA elastic energy, whereas the binding to the linear form is not. As noted above, these preferences assume that the HU-DNA binding energy is independent of whether the DNA is closed or open.

The multiple bound proteins counterbalance the bending stress on cyclic DNA, allowing the intervening, protein-free segments to straighten to their intrinsic form and thereby reduce the total free energy of the system. All previous thinking about the enhanced binding of HU to circular over linear DNA has focused on the advantages of nucleotide deformation in the circular form and the apparent thermodynamic differences in the association of a single protein on open versus closed DNA. The possibility that the number of bound proteins might differ in the two classes of molecules has never been considered. The structural information gleaned from our work reveals this surprising possibility. Similar mechanisms may contribute to the preferential association of other proteins that severely deform DNA, e.g., the TATA-box binding protein [31] and the integration host factor [32], with cyclic over linear molecules.

DNA molecules of only slightly different chain lengths bind very different numbers of proteins when closed in the presence of HU (Figure 4). This variation in protein-binding levels underlies the approximate independence of DNA ring closure on N found in the present simulations (Figure 3). The DNA chains that are more likely to cyclize, i.e., chains of length corresponding to local maxima in the computed dependence of the J factor on N, tend to bind 2–3 HU molecules on average and the chains that are less likely to cyclize bind an average of three or more proteins. In contrast to naked DNA, where base pairs must twist in order to bring the ends of the duplex in register for ligation, duplexes cyclized in the presence of HU simply bind additional protein. Any apparent changes in the properties of DNA reflect the composite distortions of HU-bound base-pair steps. Not only is DNA sharply bent by HU, many of the steps in contact with protein are under-twisted compared to the usual ~34.3° helical twist, i.e., 10.5-bp helical repeat, of B DNA in solution. The base pairs at the sites of sharpest bending are also severely sheared, thereby dislocating the double-helical axis [33].

The number of proteins on the closed molecules determines DNA topology. Whereas the duplexes with fewer bound HU molecules are torsionally relaxed (ΔLk=0), the minicircles 5–6 bp longer with more bound proteins are negatively supercoiled (ΔLk=−1). That is, minicircles of HU-bound DNA alternate between topological states, with HU binding preferentially to relaxed or supercoiled substrates depending upon chain length (Figure 6). The preferential inducement of negatively supercoiled states reflects the undertwisting of DNA by HU found in high-resolution structures. Of course, proteins do not necessarily remain on the DNA once it is cyclized, but the protein-induced changes in linking number persist. The effects of HU on DNA topology also make clear why the protein preferentially binds supercoiled over relaxed DNA [34], i.e., HU fits naturally both at the ends of hairpin loops and within interwound segments of supercoiled configurations (Figure 5).

Less severely deformed HU-bound DNA fragments have a less pronounced effect on ring-closure propensities, but the proteins show the same tendency to bind at very different levels and change the superhelical state upon slight variation in DNA chain length. Thus, the protein-induced structure of DNA underlies the complete ring-closure profile, determining both the phasing and the chain-length dependent magnitude and oscillations in the J factor. The experimentally observed variation in these quantities can accordingly serve as indicators of protein-induced DNA deformation.

The fraction of closed molecules of a given chain length with a given number of bound proteins depends on simulated binding conditions. The proportion of minicircles complexed to HU decreases with a decrease in binding probability. The magnitude of the J factor and the amplitude of the oscillations in J consequently depend upon protein concentration. Conditions that favor the binding of greater numbers of protein molecules increase the J factor and dampen the oscillations in J with N at shorter chain lengths (Figure 7).

‘Realistic’ vs. conventional modeling of protein-bound DNA

The ability to account precisely for the proteins on closed minicircles is one of the principal advantages of a ‘structural’ approach in deciphering the cyclization and looping properties of DNA. Such treatment offers physical insight into gene regulatory phenomena not possible from conventional elastic treatments of DNA. As emphasized here, the cyclization propensities of DNA in the presence of HU reflect both the deformations of DNA by protein and the number of proteins bound to a circular duplex. Ideal models of DNA fail to account for the full chain-length dependence of the J factors of HU-bound duplexes and, instead, yields unrealistically small elastic constants (Table 3). Moreover, such models attribute the computed dampening of the oscillations in the J factor with increase of N to a chain-length dependent decrease in the bending and/or torsional modulus of DNA rather than to the uptake of HU binding sites. Ideal elastic models of DNA do not anticipate the structural irregularities in DNA brought about by protein binding. Indeed, the classical twisted wormlike theory of DNA [35] assumes a much more limited range of DNA deformation than found in the presence of HU.

Our direct structural approach also provides insights into the effects of HU binding on the configurational properties of linear DNA (Figure 2, Table 2). The random placement of protein-deformed segments on DNA at levels bracketing the cellular content of HU lowers the persistence length of an ideal B-like duplex by a factor of approximately three (2.2 for chains with HU-DNA segments like those found in high-resolution crystal complexes [3–5] every 200 bp and 3.4 for chains with such segments every 100 bp). Although the computed decrease in chain extension is roughly comparable to that deduced from AFM images collected under similar binding conditions [11], other structural features could contribute to the reported values. Both protein-induced bending and protein-induced deformability affect DNA chain extension [36]. Given the approximations used in extracting the persistence length and in determining the net bending of HU-bound DNA in solution [11–13], it is difficult to separate the relative effects of HU-induced bending and deformability on the persistence length from the present calculations. Nevertheless, the base-pair level modeling of HU-bound duplexes shows that the limited fluctuations of the crystalline protein-DNA complex, when randomly placed along the double helix, is sufficient to account for the macromolecular flexibility observed at low levels of HU binding [11].

Changes in intrinsic structure and deformability that decrease the persistence length tend to enhance the J factor. Unfortunately, the only available measurements of HU-induced DNA cyclization [14, 15] are, at best, semi-quantitative, e.g., HU stimulates the cyclization of rings as short as 78 bp and increases the proportion of closed structures in longer chains that cyclize in the absence of HU. Other factors not considered here, such as the coupling of bending and twisting in known DNA structures [21] and the sequence-dependent deformability of DNA [37], may also increase the J factor. The fit of computation to the concentration and chain-length dependence of the cyclization tendencies of different types of DNA sequences could help to decipher the HU-induced changes in DNA structure and deformability.

Implications for DNA looping

The dimeric model of DNA employed here shows promise for deciphering the mechanism of in-vivo looping at a structural level. The cyclization properties of HU-bound DNA mimic the apparent independence of gene expression on chain length in living cells [1, 2, 9], i.e., the simulated cost of ring closure shows the same relative insensitivity to chain length as the observed expression levels of reporter genes. The low amplitude of the oscillations in the computed J factors and the substantially reduced values of the persistence length of the HU-bound duplexes also mimic the apparently low cost of constraining very short HU-bound DNA fragments into looped configurations. Analysis of the complex, chain-length dependent expression of genes controlled by the Lac repressor protein (LacR) in terms of conventional elastic models of DNA [18, 27] suggests the presence of different types of DNA looping and/or significant distortions of the LacR tetramer from its crystalline V-shaped conformation [38] to a linear, extended form in vivo. The structure and precise placement of HU and other key nucleoid proteins on DNA undoubtedly play important roles in determining both the configurations and the populations of the LacR-mediated loops formed in the cell and detected in gene expression studies.

Methods

DNA model

We make use of a dimeric representation of DNA that incorporates the known effects of base sequence on the intrinsic structure and deformability of the constituent dinucleotide steps [39]. The base pairs are represented by rectangular slabs and the configuration of a DNA segment of N+1 base pairs, i.e., N base-pair steps, is specified by giving, for 1 ≤ n ≤ N+1, both the location r_n of the center of the slab that represents the n^th base pair and a right-handed orthonormal frame $({\mathbf{d}}_n^1,{\mathbf{d}}_n^2,{\mathbf{d}}_n^3)$ that is embedded in the base pair [40]. The arrangement of each base-pair is described by six independent step parameters —three angular variables (θ₁,θ₂,θ₃) called tilt, roll, and twist and three variables (θ₄,θ₅,θ₆) called shift, slide, and rise with dimensions of distance [41]. The values of these parameters are defined by a matrix-based scheme [42–44] that allows for the characterization of base-pair arrangements in known structures and the precise reconstruction of models from these values. The configuration of the n^th base-pair step is denoted by the vector, Θ_n, with components ${\theta }_i^n(i=1-6)$ corresponding to the instantaneous values of the parameters at the given step.

The elastic energy U of a configuration of the segment is the sum, over n, of the energy of interaction Ψ_n of the n^th and (n+1)^th base pair, $U={\displaystyle \sum _{n=1}^N}{\psi }_n$. Here Ψ_n is a function of the relative orientation and displacement of the (n+1)^th base pair with respect to the n^th base pair. The function Ψ_n depends on the chemical composition of the n^th and (n+1)^th base pairs but is assumed, for simplicity, to be independent of the composition of all other base pairs. The known complementarity of Watson-Crick base pairs, i.e., the specific association of A·T and G·C, and the antiparallel directions of the sugar-phosphate chains place restrictions on the Ψ_n. That is, step parameters are defined such that tilt and shift (,θ₁,θ₄) change signs in complementary strands [41], and the potential Ψ_n (XZ) of dimer step XZ determines that of its complement X′Z′ [40].

In order to focus on the role of protein as well as to compare our work with earlier treatments of DNA ring closure in the absence of proteins [35, 45–47], we assume that the potential governing the fluctuations of DNA base-pair steps is uniform, i.e., independent of sequence:

$$\psi =\frac{1}{2}\sum _{i=1}^6{f}_{ij}({\theta }_i-{\theta }_i^0)({\theta }_j-{\theta }_j^0).$$ (1)

Here the ${\theta }_i^0$ are the values of the step parameters of the minimum-energy reference state, the θ_i are the corresponding values of the instantaneous configurational state stored in θ, and the f_ij are stiffness constants. Although the form the equation allows us to incorporate features of DNA, such as intrinsic curvature or enhanced pyrimidine-purine deformability, thought to be responsible for the unexpected ease of cyclization of some sequences [21, 48, 49], we assume, for simplicity, that the potential follows that of an ideal elastic rod. Thus, the step parameters vary independently of one another, i.e., f_ij = 0 (i ≠ j), the bending is isotropic (f₁₁ = f₂₂), and the DNA is naturally straight and unsheared in its equilibrium rest state, with an intrinsic B-type helical repeat of 10.5 bp per turn and a pitch of 35.7 Å, i.e., ${\theta }_1^0={\theta }_2^0=0,{\theta }_3^0\approx 34.3°,{\theta }_4^0={\theta }_5^0=0,{\theta }_6^0=3.4\acute{\text{Z}}$. Deformations in rotational parameters are chosen such that the limiting persistence length of the protein-free fragments is ~500 Å (f₁₁ = f₂₂ = kT/4.84² deg²) and the twisting of base-pair steps is slightly more restricted than the bending (f₃₃/f₂₂ = 1.4). Translational parameters are held near their intrinsic values (f₄₄ = f₅₅ = f₆₆= 50kT/²) so that the chain is effectively inextensible [21].

Chain model/dimensions

Base-pair level models are constructed from serial products of generator matrices A_n that incorporate the displacement vectors r_n and the rotation matrices T_n that relate coordinate frames on successive base pairs (n, n+1): A_1:N = A₁A₂…A_N−1A_N, where

$${\mathbf{A}}_n=\left[\begin{array}{cc}{\mathbf{T}}_n& {\mathbf{r}}_n\\ \mathbf{0}& 1\end{array}\right]\text{and}{\mathbf{A}}_{1:N}=\left[\begin{array}{cc}{\mathbf{T}}_{1:N}& {\mathbf{r}}_{1:N}\\ \mathbf{0}& 1\end{array}\right].$$ (2)

The dependence of T_n and r_n on the θ_n follows the aforementioned matrix-based scheme [42–44], in which the angular step parameters are defined in terms of a sequence of symmetric Euler rotations and the translational components are expressed in the ‘middle’ base-pair frame corresponding to the axis positions generated by half the rotational operation that brings adjacent base-pair frames into coincidence. The presence of bound protein is modeled by replacement of the appropriate set of base-pair step matrices by a new matrix A^protein, which is the product of generator matrices constructed from the step parameters of DNA in the given complex. If the length of the bound region is m base-pair steps, this matrix can be written as ${\mathbf{A}}_{1:m}^{\text{protein}}$. Values needed to evaluate chain cyclization — (i) the end-to-end vector r_1:N+1, (ii) the cosine of the angleγ between the normals of terminal base pairs, and (iii) the twisting of terminal base pairs — are extracted from A_1:N+1 as described elsewhere [21]. Also as described there, a joining step N+1 is included in the cyclization calculation to test for terminal base-pair overlap, but this step is subsequently removed and circles are exactly closed by a step c connecting the N^th to the first base pair, i.e., A_1:N A_c = I, where I is the identity matrix, for calculation of topological properties.

Configurational sampling

Representative configurations of chain molecules are obtained by direct Monte-Carlo enumeration, as in previous work [21]. To sample the probability density function for each base-pair step, we modify a standard Gaussian random-number generator [50] and collect a Boltzmann distribution of states without the necessity of using the Metropolis method [51]. This approach, which we term Gaussian sampling, is superior to the Metropolis method in that it is computationally more efficient and does not suffer from correlations between sample points or incomplete coverage of phase space.

J factor

The J factor depends on the fraction M_c/M of configurations that meet the selected chain-closure criteria, namely the product of probability densities [52] that (i) the end-to-end vector r is null W(r=0), (ii) the normals are aligned, i.e., the cosine of the angle between the normals of terminal base pairs is unity, given that the vector r is null Γ_r (cosγ=1), and (iii) the end-to-end twist is zero, given that the normals are aligned and the vector r is null Φ_r,_{cos γ}(τ=0). This product is approximated by choosing three corresponding bounds: (i) the magnitude of r being less than r₀; (ii) the cosine of the angle γ between the normals of terminal base pairs being greater than 1−Γ₀; and (iii) the magnitude of the end-to-end twist being less than τ₀. Thus, the J factor is given by

$$J=\frac{4\pi }{N_{\text{A}}}W(\mid \mathbf{r}\mid \le r_0){\mathrm{\Gamma }}_r(cos\gamma \ge 1-{\mathrm{\Gamma }}_0){\mathrm{\Phi }}_{r,cos\gamma }(\tau \le {\tau }_0)=\frac{1}{K}\frac{M_c}{M},$$ (3)

where $K=2N_{\text{A}}{r}_0^3{\mathrm{\Gamma }}_0{\tau }_0/3$, N_A is Avogadro’s number, M_c is the number of configurations that satisfy the three closure constraints, and M is the total sample size. The bounds used here —r₀ = 10, Γ₀ = 0.02, τ₀=11.5° (cosτ₀ =1−0.02 = 0.98) — are very restrictive, constraining the trace of A_1:N to values very close to 3 and the radial bound to distances no more than 5% of the contour length of the sampled DNA chains. Previous work [21] has shown that such bounds yield the most accurate results for M_c ≥ 1000, i.e., at least 1000 closed configurations can be found in the simulation with the chosen bounds. As outlined below, we also discard configurations with long-range base-pair overlap, protein-DNA overlap, and protein-protein overlap.

Since DNA segments shorter than a persistence length are stiff and the probability that a randomly generated configuration satisfies all three ring-closure criteria is very small, we use a modified half-chain pairwise-combination technique in order to enhance the sampling. Our approach combines the classic half-chain sampling technique introduced by Alexandrowicz [53] with a novel approach that combines only the pairs of half-segments that satisfy the desired end-to-end spacing of the full-length molecule [21]. Rather than generate the configurations of a DNA with N base pairs, we divide the chain into two equal (or nearly equal) pieces and sample L configurations of each half-chain segment separately. By taking all pairwise combinations of both halves we can theoretically achieve L² configurations of the full-length chain.^† In order to reduce the number of unnecessary half-chain combinations, we join only those pairs of segments that have a good chance of satisfying the end-to-end ring-closure criteria. This essential component of the method reduces the number of combinations performed to the order of millions, which is in the neighborhood of the number of half-chains generated. The algorithm keeps track of transformed values of the end-to-end vectors of the first and second half-segments, and combines only those for which the radial overlap condition is approximately satisfied. With this approach, the calculation time runs approximately linearly with L, although we evaluate the possibility of ring closure in all L² samples.

Random protein binding

Conformational sampling that accounts for the non-specific binding of proteins like HU, is achieved by introducing an appropriate set of protein-bound DNA step parameters (and associated generator matrices) at random sites along the chain. Placing a protein-bound dimer at step n requires substitution of the next m base-pair steps with the step parameters in the bound duplex. The minimum spacing between proteins is thus equal to the length m of the bound segment (also referred to as the binding-site length), although certain spacings may be excluded by steric contacts between neighboring or more distantly bound proteins. The probability w that a site is occupied depends upon the concentration of free protein c, its DNA-association constant, and the concentration of DNA base pairs. To generate an equilibrium distribution of bound proteins, the DNA is examined one base pair at a time in random order, and a decision is made at each step whether or not to place the protein with probability w. If the protein is placed, the next m sites are automatically filled (because they are part of the binding site) and the decision-making process is resumed at the next untested base pair. In order to avoid the build-up of proteins in the middle of the chain, where the DNA is split, we extend the half chains by m phantom base pairs and then remove protein that binds beyond the real chain. Although this approach ignores the kinetics of binding, e.g., the preferred configurations to which proteins bind, the time of occupancy at a given site, etc., the process generates the random placement on DNA expected of a non-specific binding protein.

In order to achieve compatibility with the pairwise combination of half-chains, the protein is placed on the first L half-chain samples at positions 1 through the center step q. The last m of these positions overlap the half-chain split point. Any two half chains can be combined as long as the protein placement matches at the split point, i.e., the three-dimensional structure of protein-bound DNA is preserved. In order to ensure a proper sample size, the number of second half-segments for each possible overlap of protein with the split point must be the same and equal to the number of first half-segments. The resulting number of total full configurations considered thus remains L², as in the case of protein-free DNA [21], although the algorithm is slowed down by a factor of approximately m, the length of the protein-binding site.

Protein model

Models of HU-bound DNA are constructed from the base-pair step parameters of DNA fragments that have been co-crystallized with the homodimeric HU homolog from the cyanobacterium Anabaena PCC7120 (PDB IDs: 1P51a, 1P51b, 1P71 and 1P78) [3]. Each structure is reduced to 15 base pairs, including the central T·T mismatch and the Watson-Crick pairs that flank unpaired thymines, and the step parameters (m=14) are extracted using the program 3DNA [54]. Less strongly deformed duplexes are generated by uniform reduction of the bending angles (θ₁,θ₂) at all steps in these structures.

The proteins can be bound relative to either strand of DNA, yielding eight different HU-DNA configurations for each position of bound HU (Figure 8). The change of strand is achieved by placing the m step parameters, 1 < μ < m, for the bound region in reverse order, each with the opposite tilt and shift, i.e., the θ^μ associated with second-strand binding is given by the θ^m−μ−1 associated with first-strand binding, except for ${\theta }_1^{\mu }=-{\theta }_1^{m-\mu +1}$ and ${\theta }_4^{\mu }=-{\theta }_4^{m-\mu +1}$. One of the possible configurations is chosen at random with equal probability every time a protein is successfully placed on the DNA. The two types of strand binding are considered separate types of binding modes, and hence the running time is slowed by a factor of two by the generation of second half segments with both types of binding modes, each having m positions overlapping the midpoint where segments are split.

Figure 8.

Molecular schematic illustrating the flexibility allowed HU-bound DNA sites in the present simulations. Virtual-bond representations of the eight sampled DNA configurations from the four currently known crystal complexes [3] are compared with the deformed (cyan) double-helical pathway of DNA in a representative complex (1P71, top). The sets of virtual bonds (bottom) connect the centers of successive base-pair ‘blocks’ in the central, protein-bound 15-bp fragment in each structure. The thick black lines highlight the virtual bonds common to the two images. The yellow ribbon denotes the dimeric protein. Images are rendered with Chimera [60].

Long-range contacts

The ensemble of HU-bound DNA structures obtained with the above procedure does not take account of DNA and protein steric interactions. In order to test how such long-range contacts affect the J factor, we examine the pairwise distances between base-pair centers and protein atoms in representative structures, rejecting configurations with steric overlap from both a ‘full’ ensemble of generated chains and the successfully closed structures. In particular, we discard configurations in which (i) the center-to-center distance between sequentially distant base-pairs (separated by more than 20 bp along the DNA contour) is less than 20 Å, (ii) the distance between any pair of atoms on bound HU molecules (one atom taken from each protein) is less than 2 Å, and (iii) the distance between any atom of protein is less than 5 Å from the center of a DNA base-pair, to which it does not bind. In view of the approximations used to estimate ring closure, we also omit consideration of any ‘end-to-end’ contacts between the centers of the 10 bp on either end of the DNA.

To simplify the calculations, we test for steric contacts in the closed molecules only. In order to check this approximation, we estimate the fraction of protein-DNA contacts in the full configurational ensemble of an HU-decorated 315-bp duplex, a chain long enough to encounter such interactions, from random combinations of protein-bound DNA half-chains. We find that ~84% of 100,000 such combinations are contact-free when HU binds at a level of 1 HU per 100 bp and that 65% of the closed configurations in the full configurational ensemble are contact-free under the same conditions. That is, self-contact is much more significant in the closed than in the open chains. Because the number of closed configurations is always much less than the total sample size, e.g., O(10³) closed configurations out of a total of 10¹² total configurations generated from 10⁶ half-chains, corrections of the J factor in terms of the contacts of closed chains are thus valid at 315 bp and all shorter chain lengths. Only the J factors in the inset of Figure 3 take account of long-range contacts.

Topological properties

Closed configurations are classified in terms of the linking number Lk, which is computed using a discretization of a Gauss integral [55] over two polygonal curves, C and $C\ll :Lk=2{\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{j=1}^N}L{k}_{ij}$. Here C is the curve connecting the centers of base pairs, C≪ the curve connecting the ends of the short axes, i.e., ${\mathbf{r}}_{1:n}^{\ll }={\mathbf{r}}_{1:n}+{\mathbf{d}}_n^1$, and LK_ij the contribution to Lk from segments ${\mathbf{s}}_m^k$ between corresponding points on the two curves, i.e., ${\mathbf{s}}_m^k={\mathbf{r}}_k^{\ll }-{\mathbf{r}}_m$, where m is j−1 or j and k is i−1 or i. As show elsewhere [55], the value of Lk_ij can be expressed as a combination of four dihedral angles,

$$L{k}_{ij}=\frac{1}{4\pi }\left[\mu ({\mathbf{t}}_i,{\mathbf{d}}_{j-1}^{i-1}{\mathbf{t}}_j)-\mu ({\mathbf{t}}_i,{\mathbf{d}}_{j-1}^i{\mathbf{t}}_j)-\mu ({\mathbf{t}}_i,{\mathbf{d}}_j^{i-1}{\mathbf{t}}_j)+\mu ({\mathbf{t}}_i,{\mathbf{d}}_{j-1}^i{\mathbf{t}}_j)\right],$$ (4)

where

$$cos\mu ({\mathbf{t}}_i,{\mathbf{d}}_m^k,{\mathbf{t}}_j)=\frac{[{\mathbf{t}}_i\times {\mathbf{d}}_m^k]·[{\mathbf{d}}_m^k\times {\mathbf{t}}_j]}{\mid {\mathbf{t}}_i\times {\mathbf{d}}_m^k\mid \mid {\mathbf{d}}_m^k\times {\mathbf{t}}_j\mid }$$ (5)

and the sign of μ is equal to that of $\mid {\mathbf{t}}_i\times {\mathbf{t}}_j\mid ·{\mathbf{d}}_m^k$.

Effective elastic chain

We relate the effects of simulated HU binding to the elastic parameters of a naturally straight isotropic chains by comparing the J factors for a series of such chains with the values determined for protein-bound DNA. We extract the J factors as a function of the bending and twisting moduli, from configurational ensembles (10¹⁰ states) generated for each choice of variables. Because the elastic model cannot account for the observed phase shifting of J induced by HU binding, we must fit the ideal chains against HU-DNA data collected at slightly different lengths. The protein, however, does not appear to alter the 10.5-bp helical repeat of DNA. We therefore generate J factors for ideal chains of 126–147 and 210–231 bp and fit the peaks and valleys in these data to the closest corresponding points of HU-bound duplexes. The best-fit parameters for each range of chain lengths are obtained by minimization of the mean-squared error in log J over two helical turns and are reported as effective local bending and twisting fluctuations, i.e., 〈Δθ₁〉^eff = 〈Δθ₂〉^eff and 〈Δθ₃〉^eff. In practice, a close match of the peaks and the valleys in the variation of J vs. N for protein-bound data requires a set of ~10 different elastic-chain simulations. We perform six such series of calculations to obtain the data in Table 3.

Persistence length

The persistence length a, a measure of the distance over which the direction of the DNA is maintained [56], is computed, following Flory [57], from the projection of the mean end-to-end vector at infinite chain length, 〈r_∞ 〉 along the initial direction of the chain, i.e., a=〈r_∞ 〉i˛ r₁/|r₁|. We take advantage of the independence of dimeric chain units and determine 〈r〉 from the product P_N= 〈A₁〉 〈A₂〉 K 〈A_N−1〉 〈A_N〉 of average generator matrices 〈A_n〉 [58, 59]. The components of 〈r〉, which accumulate in the far right column of P_N, approach limiting values with increasing N, owing to the non-orthogonality of each 〈T〉 matrix of the flexible duplex [36]. Thus the persistence length of DNA can be obtained by calculating the limiting value of the [3,4] matrix element of P_N:

$$a=\underset{N\to \infty }{lim}\left[\begin{array}{cccc}0& 0& 1& 0\end{array}\right]\acute{\text{Z}}{\mathbf{P}}_N\acute{\text{Z}}\left[\begin{array}{c}0\\ 0\\ 0\\ 1\end{array}\right].$$ (6)

The contribution of protein-bound DNA steps is considered by first evaluating the serial product ${\mathbf{A}}_{1:m}^{\text{protein}}$ of the generator matrices associated with the base-pair steps in each of the protein-bound fragments and determining the average product for the protein-bound steps 〈A^protein〉 over the assumed set of models, e.g., the average product 〈A^HU〉 is evaluated over the 14 base-pair steps in each HU-DNA model and then averaged over the eight different models. The segment of protein-bound DNA is then interspersed in all possible helical settings on DNA. For example, if the DNA is treated as a homopolymer, 〈A^protein〉 is pre-and postmultiplied by products of the average DNA generator matrix 〈A^DNA〉, yielding the generator matrix of a longer fragment that spans an integral multiple of the double-helical repeat h. An average generator matrix 〈A^P+DNA〉 is then determined for the protein-bound DNA steps in all settings on the longer fragment, e.g.,

$$\langle {\mathbf{A}}^{\text{P}+\text{DNA}}\rangle =\sum _{n=0}^{s-m}{\langle {\mathbf{A}}^{\text{DNA}}\rangle }^{s-m-n}\langle {\mathbf{A}}^{\text{protein}}\rangle {\langle {\mathbf{A}}^{\text{DNA}}\rangle }^n/(s-m).$$ (7)

Here s, the number of base pairs in the extended fragment, exceeds the length m of the DNA that is in contact with protein and the quotient s/h is an integer.

If we assume the random incorporation of protein-bound fragments in the DNA, the persistence length reduces to a sum of two limiting products, weighted by the fraction w of protein-bound regions and each spanning the same length of DNA:

$$a=\underset{N\to \infty }{lim}\left[\begin{array}{cccc}0& 0& 1& 0\end{array}\right]\left[w{\mathbf{P}}_N^{\text{P}+\text{DNA}}+(1-w){\mathbf{P}}_N^{\text{DNA}}\right]\left[\begin{array}{c}0\\ 0\\ 0\\ 1\end{array}\right],$$ (8)

a form familiar in the theory of random copolymers [24]. Here ${\mathbf{P}}_N^{\text{P}+\text{DNA}}={\langle {\mathbf{A}}^{\text{P}+\text{DNA}}\rangle }^N$ and ${\mathbf{P}}_N^{\text{DNA}}={\langle {\mathbf{A}}^{\text{DNA}}\rangle }^{sN}$.

Simulations

Enhancements in sampling and larger amounts of memory allow the calculation of the J factor for naked DNA with more precision than previously reported [21], i.e., with sufficient numbers of configurational examples that meet the more restrictive bounds for ring-closure described above. Computations of J involving HU rarely take more than 4 hours on inexpensive AMD computers, but the most accurate calculations of J for naked DNA can take up to 48 hours and several gigabytes of RAM.