Effects of Written Informed Consent Requirements on HIV Testing Rates: Evidence From a Natural Experiment

Abstract

Objectives. I evaluated the effects of written informed consent requirements on HIV testing rates in New York State to determine whether such consent creates barriers that discourage HIV testing.

Methods. New York streamlined its HIV testing consent procedures on June 1, 2005. If written informed consent creates barriers to HIV testing, then New York's streamlining exercise should have reduced such barriers and increased HIV testing rates. I used logistic regression to estimate the effects of New York's policy change.

Results. New York's streamlined consent procedures led to a 31.4% (95% confidence interval [CI] = 20.9%, 41.9%) increase in the state's HIV testing rate. In absolute terms, 7% of the state's population had been tested for HIV in the preceding 6 months under the streamlined procedures, whereas only 5.3% would have been tested under the original procedures. These estimates imply that the streamlined consent procedures accounted for approximately 328 000 additional HIV tests in the 6 months after the policy change.

Conclusions. Written informed consent requirements are a substantial barrier to HIV testing in the United States.There may be a trade-off between efforts to increase HIV testing rates and efforts to improve patient awareness.

In 2006, the Centers for Disease Control and Prevention (CDC) endorsed a shift from targeted HIV testing of high-risk groups to broad-based screening of the general population.¹ The CDC called for opt-out HIV screening of all patients in health care settings and argued that written informed consent procedures that are separate and distinct from general consent to medical treatment procedures should not be required for HIV testing.¹ The CDC recommendations reflect concerns that HIV testing rates are too low in the United States because a large number of people do not learn about their infection until it is too late for treatment to be effective.

Opt-out screening has increased testing rates in other settings, including genitourinary clinics in the United Kingdom, and there is little doubt that it would increase HIV testing in the general population.^2,3 The effect of informed consent regulations on HIV testing rates is less clear. The CDC claims that such regulations create administrative and social barriers that discourage HIV testing.¹ There is also some evidence that written informed consent regulations represent a legal impediment to the implementation of opt-out testing.⁴ Such concerns might also explain the CDC's advocacy of informed consent repeal.

Critics of the recommendations argue that separate informed consent promotes important ethical and clinical objectives in public health policy and that removing informed consent regulations could lead to a more coercive HIV testing environment.^5–8 In summarizing the controversy, Bayer and Fairchild argued that the CDC's informed consent recommendations signal an end to the practice of HIV exceptionalism, which leads the medical establishment to approach HIV/AIDS issues differently than it approaches other health conditions.⁹

It is difficult to estimate the effects of informed consent regulations on HIV testing rates because variations in state consent requirements may be correlated with state-level characteristics that themselves predict testing rates; that is, state populations are not randomly assigned to different informed consent policies. Zetola et al. reported the best evidence to date. They found that monthly testing rates increased from 13.5 to 17.9 HIV tests per 1000 patients in a set of institutions in San Francisco after that city's department of public health eliminated written informed consent requirements.⁵ However, the Zetola et al. study lacked a comparison group, which would have alleviated concerns that the increases observed were associated with underlying trends and changes in HIV testing that occurred in the same time frame as the San Francisco policy change.

In addition, Zetola et al. relied on administrative data, for which observations were conditional on patients' visits to particular institutions. It is possible that HIV testing rates among patients who visited these institutions were different than testing rates in the general population. As a result of such problems, it is difficult to generalize the effects of the San Francisco policy change on HIV testing rates in particular institutions to testing rates in the general population.

A careful decision on whether to repeal or maintain written informed consent requirements in HIV testing depends on estimates of the effects of the regulations in terms of both testing rates and the physical and psychological risks to patient well-being. It also requires normative judgments regarding the relative importance of these effects in terms of public welfare.¹⁰ In this study, I investigated the CDC's claim that informed consent regulations lead to reductions in HIV testing rates. I used data from the Behavioral Risk Factor Surveillance System (BRFSS) to examine HIV testing rates in New York State and a set of comparison states before and after the introduction of streamlined HIV test consent procedures in New York. The policy change in New York generated a natural experiment that helps address many of the challenges associated with evaluating the effects of consent procedures on testing rates.

METHODS

New York State streamlined its HIV test consent procedures on June 1, 2005 (copies of the old and new consent forms are available on request from the author). The state now uses a consent form that encompasses consent to several HIV-related procedures, including HIV antibody testing, resistance testing, viral load testing, and incidence testing.¹¹ The new form replaces pretest counseling procedures with an informational section that patients are encouraged to review and keep for future reference. Documentation supporting the change explains that the new consent form provides “the basic information that someone would need to know to make a decision about being tested in simple, easy-to-follow language.”¹²

If written informed consent requirements decrease HIV testing rates, as the CDC claims, then New York's streamlining exercise should have increased HIV testing by lowering these barriers. In the natural experiment I describe, New York State contained the “treated” population. In principle, any state that did not introduce streamlined consent procedures during the study period would represent a good comparison population in this context. A stable HIV-test consent requirement is the key feature of a good comparison population in this context.

I imposed an even stronger criterion, using as a comparison group a set of states that do not require any form of HIV test–specific written informed consent. I used this set of states (and the District of Columbia) because the possibility of unmeasured streamlining of the consent environment in these states seemed unlikely given that they do not require HIV-specific consent. The comparison group was made up of Alaska, Arkansas, the District of Columbia, Idaho, Indiana, Iowa, Mississippi, Missouri, Montana, New Hampshire, New Jersey, New Mexico, North Carolina, North Dakota, Oklahoma, South Carolina, South Dakota, Tennessee, Texas, Utah, and Virginia.

Behavioral Risk Factor Surveillance System Data

I used 2004, 2005, and 2006 data from the BRFSS, which is an ongoing cross-sectional telephone survey of the adult household population conducted throughout the calendar year by state health departments with technical assistance from the CDC. BRFSS data are collected in the 50 states, the District of Columbia, Puerto Rico, the US Virgin Islands, and Guam. With the exception of the 3 territories, a disproportionate stratified sample design is used in selecting BRFSS state-level samples. I limited my analysis to observations drawn from New York State and the comparison states described earlier. The BRFSS has been described in further detail elsewhere.¹³

Measuring HIV Testing

BRFSS respondents who have been tested for HIV are asked the following question: “Not including blood donations, in what month and year was your last HIV test?” The testing years observed in the present data ranged from 1985 to 2006. Research on medical testing usually defines a testing rate with reference to a time period that is sufficiently large to yield precise measures and sufficiently small to evaluate trends and changes. For instance, some researchers use a 1-year testing window, which defines a testing rate as the percentage of people in the population tested in the 12 months preceding a particular date.

Smaller window sizes are desirable for evaluating the effects of different events on testing rates. For example, 1-day or 1-week windows that define a rate as the percentage of people tested on a single day or within a given week might allow researchers to evaluate short-, medium-, and long-term implications of different changes in policies or other environmental factors relevant to a particular health outcome. However, these smaller windows would require extremely large sample sizes to produce accurate estimates.

I employed a 6-month HIV testing rate, defining a variable taking a value of 1 if respondents had been tested for HIV during the 6 months preceding their interview date and a value of 0 otherwise. Respondents who had never been tested for HIV were coded as 0 because they had not been tested in the preceding 6 months. I also assumed that respondents who reported having been tested for HIV but did not report a test date had not recently been tested. These respondents were coded as 0 as well. When I reestimated the models excluding these respondents, the results were almost identical.

Treatment Status

Respondents' treatment status was defined according to the state and month in which they were observed. Here “treatment” refers to the HIV testing environment. Observations drawn from the New York State population before June 1, 2005, provided pretreatment information about the subsequently treated population, whereas observations taken after this date provided posttreatment information. Observations from comparison states before and after June 1, 2005, provided information on the untreated comparison population.

Of the overall sample of 314 393 respondents, 14 646 respondents were New York State residents (6864 from the pretreatment period and 7782 from the posttreatment period), and 299 747 were residents of comparison group states (140 906 from pretreatment months and 158 841 from posttreatment months). The number of respondents in each interview month was quite consistent over time. On average, there were 8326 comparison group observations per month and 407 New York State observations per month.

Statistical Model

I used data from the pretreatment and posttreatment periods in the New York State and comparison state populations to estimate logistic regression models of the probability that a respondent had been tested for HIV in the 6 months preceding his or her interview date. In these models, the estimated treatment effect was the between-group difference in pretreatment and posttreatment differences in testing behavior (i.e., the estimated treatment effect was the difference between the posttreatment change in testing rates in New York and the posttreatment change in testing rates in the comparison states after other model covariates had been taken into account). Researchers often refer to such models as difference-in-differences estimators.

I estimated different specifications of the basic model, controlling for year, state, and linear and nonlinear trends to account for unmeasured influences on HIV testing rates in the treated and comparison populations over time. (When I repeated the analysis with controls for age, race, education, health insurance status, binding medical costs, and HIV risk behaviors, the estimated treatment effects did not change.)

Treatment Window

As mentioned, the dependent variable was coded 1 if respondents had been tested for HIV in the 6 months preceding their interview date. In the case of some observations, the 6-month dependent variable window straddled the pretreatment and posttreatment periods. This straddling, if ignored, could have attenuated estimates of the treatment effect. I used 2 strategies to account for the windowing problem in the data.

The first strategy accounted for the 6-month window in the dependent variable by weighting each respondent's treatment indicator by the proportion of months in the respondent's window that fell after the introduction of the consent form. The weighting procedure assigned respondents interviewed 1, 2, 3, 4, and 5 months after the introduction of the consent form a weighted treatment variable equal to one sixth, two sixths, three sixths, four sixths, and five sixths, respectively. All respondents interviewed 6 or more months after the consent form change were assigned a weighted treatment variable equal to 1, and all respondents interviewed before the consent form change were assigned a weighted treatment indicator equal to 0. The main drawback of this approach is that there is no way to know whether the weighting procedure accurately accounts for the attenuation caused by the treatment window.

The second strategy excluded respondents who had been interviewed within the first 6 months after the consent form change. As a result, the dependent variable did not straddle the pretreatment and posttreatment periods for any of the remaining respondents. One drawback of this approach is that the remaining posttreatment respondents were all interviewed in 2006, making it impossible to include a full set of calendar year effects in the model. Excluding the window respondents also reduced the sample size. In practice, these 2 methods yielded nearly identical results.

Sociodemographic Covariates

HIV testing rates may vary with sociodemographic characteristics; however, because of the nature of this study's sample and intervention, such covariates were unimportant with respect to estimating the effects of the streamlined consent form on overall HIV testing rates. That is, the design of the BRFSS implies that a respondent's interview month is statistically independent of her or his demographic characteristics. Given that treatment assignment was a function of interview date and state of residence, the survey design also implies that respondents' demographic characteristics were not correlated with their treatment status and that estimated treatment effects were unbiased in the absence of controls for these covariates.

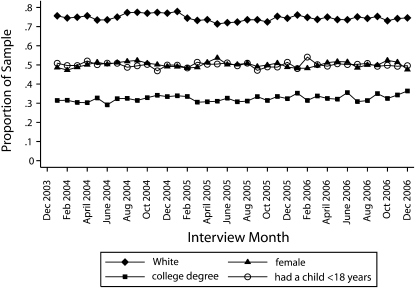
Figure 1 supports the assertion that respondents' demographic characteristics did not change over time. The lines plot the mean value of 4 sample sociodemographic characteristics by interview month. These plots provide some evidence that change in the demographic composition of the sample is not an important source of bias in this study. There is no discernible trend in the percentage of the sample that was White, female, or college educated or had a child younger than 18 years. These results hold for other demographic characteristics as well and lend credibility to the assumption that interview month, and therefore treatment assignment, was independent of demographic traits.

FIGURE 1.

Sample demographic characteristics, by interview month: Behavioral Risk Factor Surveillance System, 2004–2006.

RESULTS

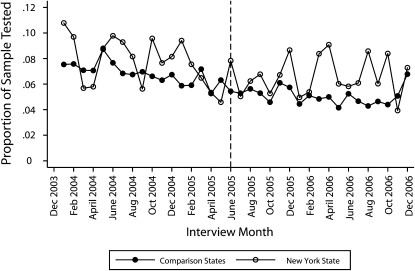
Figure 2 plots the means of the 6-month HIV testing indicator, by interview month, for the comparison states and New York State. The vertical reference line indicates the introduction of the streamlined consent form in New York State. Testing rates were more volatile in New York State than they were in the comparison states because the New York rates were based on a smaller number of observations. This volatility made it difficult to clearly identify differences in the 2 trends. Nevertheless, the New York State testing incidence seemed to follow the basic downward trend of the comparison states in the pretreatment months, and the gap between the testing rates in the 2 groups seemed to increase in the posttreatment months.

FIGURE 2.

Proportions of the sample tested for HIV in the preceding 6 months in New York State and comparison states, by interview month: Behavioral Risk Factor Surveillance System, 2004–2006.

Note. The vertical dotted line indicates the introduction of the streamlined consent form in New York State.

I used logistic regression models to smooth the volatility in the HIV testing rate trends and to summarize and quantify the effects of the policy change on HIV testing rates. To account for potential correlation between respondents interviewed in the same state, I calculated robust standard errors clustered at the state level.^14,15 I used Stata SE 10 (StataCorp LP, College Station, TX) to estimate the models. In Table 1, I report unstandardized logistic regression coefficients and standard errors estimated from models that accounted for linear trends, New York–specific linear trends, state effects, year effects, and New York–specific 5th-order polynomial trends. I used the weighted treatment procedure to estimate models 1 through 4 and excluded the window observations to estimate models 5 through 8. The results were very stable across these different specifications, although the 5th-order polynomial trend models produced noisier estimates.

TABLE 1.

Estimated Logit Coefficients From Weighted Treatment Models (n = 314 393) and Models Excluding Window Observations (n = 251 950): Behavioral Risk Factor Surveillance System, 2004–2006

	Weighted Treatment Models				Models Excluding Window Observations
	Model 1, Coefficient (SE)	Model 2, Coefficient (SE)	Model 3, Coefficient (SE)	Model 4, Coefficient (SE)	Model 5, Coefficient (SE)	Model 6, Coefficient (SE)	Model 7, Coefficient (SE)	Model 8, Coefficient (SE)
Weighted posttreatment	−0.0426 (0.0386)	−0.0647 (0.0419)	−0.0637 (0.0433)	0.1659 (0.1501)
Posttreatment					−0.0889 (0.0760)	−0.1173 (0.0868)	−0.1119 (0.0887)	−0.1288 (0.4366)
New York	0.1366 (0.0456)	0.1869 (0.0471)	−0.9312 (0.0294)	−0.4908 (0.1202)	0.1393 (0.0438)	0.2000 (0.0507)	−0.8925 (0.0318)	−0.3256 (0.1752)
New York × weighted posttreatment	0.1856 (0.0389)	0.2918 (0.0371)	0.2911 (0.0430)	0.6466 (0.1658)
New York × posttreatment					0.1885 (0.0455)	0.3357 (0.0868)	0.3303 (0.0887)	1.3172 (0.4366)
Year 2005	−0.1547 (0.0484)	−0.1557 (0.0485)	−0.1583 (0.0482)	0.0085 (0.0540)
Year 2006	−0.2069 (0.0876)	−0.2072 (0.0877)	−0.2117 (0.0863)	−0.0463 (0.0709)
Time	−0.0064 (0.0038)	−0.0053 (0.0038)	−0.0052 (0.0038)	0.0585 (0.0591)	−0.0124 (0.0027)	−0.0110 (0.0032)	−0.0113 (0.0033)	0.1067 (0.0955)
Time2				−0.0129 (0.0078)				−0.0237 (0.0156)
Time3				0.0009 (0.0005)				0.0018 (0.0010)
Time4				0.0000 (0.0000)				−0.0001 (0.0000)
Time5				0.0000 (0.0000)				0.0000 (0.0000)
New York × time		−0.0053 (0.0019)	−0.0052 (0.0020)	−0.3480 (0.0538)		−0.0069 (0.0032)	−0.0066 (0.0033)	−0.4747 (0.0955)
New York × time2				0.0672 (0.0075)				0.0962 (0.0156)
New York × time3				−0.0050 (0.0005)				−0.0074 (0.0010)
New York × time4				0.0002 (0.0000)				0.0002 (0.0000)
New York × time5				0.0000 (0.0000)				0.0000 (0.0000)
Constant	−2.5181 (0.0407)	−2.5283 (0.0423)	−1.4109 (0.0369)	−1.4573 (0.1301)	−2.4993 (0.0473)	−2.5112 (0.0507)	−1.4186 (0.0318)	−1.5390 (0.1752)

Note. Time was measured in months subsequent to January 2004. Models 3, 4, 7, and 8 include state fixed effects.

I used the coefficients from the models to estimate the percentage of New York State residents aged 18 to 64 years who were tested for HIV in the 6 months prior to January 2006 under the streamlined consent procedures and under the original consent procedures. (I estimated the effect at month 25, which was January 2006, because that was the first posttreatment month falling outside the 6-month HIV testing window.) The estimated testing rate in New York under streamlined informed consent was the predicted testing probability at month 25 (January 2006) with the New York indicator, the posttreatment indicator, and the New York by treatment interaction all set to 1. The counterfactual testing rate was the predicted testing probability under the same conditions but with the New York by treatment interaction set to 0. The counterfactual testing rate was an estimate of the testing rate that would have prevailed if New York had not streamlined its written informed consent procedures.

I multiplied the predicted probabilities by 100 and report the results as the percentage of the population tested. Table 2 displays estimated testing rates under the streamlined and counterfactual scenarios along with estimates of the absolute and percentage differences between the 2 rates.

TABLE 2.

Effects of Streamlined Consent Procedures on HIV Testing Rates: Behavioral Risk Factor Surveillance System, 2004–2006

	Estimated Testing Rate Under Streamlined Consent Procedures	Estimated Testing Rate Under Original Consent Procedures	Absolute Change in Testing Rate (95% CI)	Percentage Change in Testing Rate (95% CI)
Weighted treatment models
Base + year	6.9	5.8	1.1 (0.7, 1.5)	19.0 (10.5, 27.5)
Base + year + New York trends	7.0	5.3	1.7 (1.3, 2.1)	31.5 (22.5, 40.6)
Base + year + state + New York trends	7.0	5.3	1.7 (1.2, 2.1)	31.4 (20.9, 41.9)
Base + year + state + New York polynomial	6.8	3.7	3.1 (−0.9, 7.1)	87.5 (27.3, 147.8)
Models excluding window observations
Base	7.1	6.0	1.1 (0.7, 1.6)	19.3 (9.3, 29.3)
Base + differential trends	7.3	5.3	2.0 (1.1, 2.8)	37.0 (14.9, 59.0)
Base + state + differential trends	7.3	5.4	1.9 (1.1, 2.8)	36.3 (13.9, 58.7)
Base + state + polynomial	6.9	1.9	4.7 (3.2, 6.3)	255.2 (−43.1, 553.6)

Note. CI = confidence interval. The testing rate is the percentage of the population tested for HIV in the preceding 6 months. Predicted probabilities from the logit models were multiplied by 100 to calculate testing rates. Only estimated treatment effects are reported. The models used to generate the estimates in the bottom panel did not contain year fixed effects because excluding all of the respondents interviewed in the treatment window meant that all posttreatment respondents were interviewed in 2006.

The results presented in the third row of the top panel in Table 2 accounted for differential linear trends and year and state effects. Under the streamlined consent procedures, this model showed that approximately 7% of New York State residents aged 18–64 years had been tested for HIV in the 6 months prior to January 2006. The counterfactual estimate implies that only about 5.3% of the same population would have been tested if the streamlined procedures had not been implemented. This means that, after state effects, year effects, and the New York–specific time trend had been taken into account, the streamlined consent procedures increased the testing rate by about 1.7 percentage points (95% confidence interval [CI] = 1.2, 2.1). This translated to a 31.4% (95% CI = 20.9%, 41.9%) relative increase in the HIV testing rate in New York State.

Another way of measuring the size of the barrier imposed by written informed consent regulation is to compute the number of “extra” people tested under the streamlined procedures. To this end, the US Census Bureau estimated that 19 281 988 people aged 18–64 years resided in New York State in 2006. The change in testing rates, combined with this population estimate, implies that the streamlined consent procedures accounted for approximately 328 000 additional HIV tests in the 6 months after the policy change.

DISCUSSION

My results suggest that streamlining the written informed consent process increased HIV testing rates in New York State by a substantial margin. In fact, given that New York State streamlined but did not remove its written informed consent requirements, it is possible that the effects reported here represent lower-bound estimates of the impact of totally abolishing such requirements. The estimates I report are comparable in magnitude to those reported by Zetola et al.⁵ They found a 33% increase in testing rates at a set of San Francisco hospitals; I found a 31% increase in testing rates in the New York State population. The evidence in combination provides support for the CDC's claim that informed consent is a barrier to HIV testing.

The main threat to the validity of this study is the possibility that unmeasured differences in HIV testing incentives in New York and the comparison states may have been correlated with the change in the written informed consent policy. Including flexible trends and fixed effects in regression models is a way of addressing this concern, but estimates may still be biased if these flexible specifications do not adequately approximate the effects of any unmeasured factors. A related threat to the interpretation of the estimates reported here is the possibility that other programmatic changes occurred in New York at the same time as the change in informed consent policy. Such a scenario would make it difficult to separate the effects of the 2 concurrent changes in HIV testing policy.

The quality of the BRFSS sample may also be a concern. A telephone-based sampling frame is used in the BRFSS, which could generate biased estimates of the impact of informed consent regulations on HIV testing rates if people who do not have a telephone are more or less influenced by such regulations than are people who do have a telephone. Despite this possibility, the BRFSS provides the best data available for studying the effects of informed consent requirements on HIV testing rates because its observations are not conditional on the use of particular health services and because it contains a set of questions that allow comparisons of HIV testing rates across states and over time.

I did not assess the effects of written informed consent regulations on the number of infections identified. Streamlining informed consent seems to increase the number of people tested for HIV, but my data do not reveal how many of these newly tested people are actually infected with HIV. My results also raise questions about the provider and patient behaviors that underlie HIV testing rates. Neither the data nor the models explained whether informed consent regulations lower HIV testing rates by making providers less likely to recommend HIV tests to patients or by discouraging patients from accepting or requesting HIV tests.

It is important as well to recognize that testing rates are not the only outcome relevant to HIV testing policy. Informed consent regulations may fulfill an ethical purpose that justifies reductions in HIV testing rates. They may also improve outcomes by preparing patients for test results both medically and socially. There is a need for further research on the effects of informed consent regulations on these issues.