Effective population size and the rate and pattern of nucleotide substitutions

Abstract

Both the overall rate of nucleotide substitution and the relative proportions of synonymous and non-synonymous substitutions are predicted to vary between species that differ in effective population size (N_e). Our understanding of the genetic processes underlying these lineage-specific differences in molecular evolution is still developing. Empirical analyses indicate that variation in substitution rates and patterns caused by differences in N_e is often substantial, however, and must be accounted for in analyses of molecular evolution.

1. Introduction

Nucleotide sequence data have been a great boon for the study of evolution. DNA sequences bring all organisms into the fold of comparative analyses, allowing us to jointly reconstruct the evolutionary histories of taxa that differ enormously in morphology and lifestyle. But while DNA is universal, its tempo and mode of evolution are not. It has become increasingly clear that the way in which a species' DNA evolves is affected by numerous aspects of its biology (e.g. Welch et al. 2008). One such aspect is effective population size (N_e), which is predicted to affect species' molecular evolution at many levels, from numbers of segregating nucleotide polymorphisms (Petit & Barbadilla 2008) to genome size and complexity (Lynch & Conery 2003; Hershberg et al. 2007). In this short review, however, I will focus on another level of molecular evolution affected by N_e: nucleotide substitutions. In particular, I will discuss how both the overall rate of nucleotide substitution and the ratio of non-synonymous to synonymous substitutions are likely to vary in lineages that differ in N_e.

2. What is effective population size?

The simplest scenario under which change in allele frequencies can be studied is the Wright–Fisher model, which consists of a population of constant size N diploid individuals, with discrete generations, random mating and binomial distribution of offspring number per parent. In reality, all natural populations will deviate from the Wright–Fisher model in numerous ways. Wright therefore developed the concept of the effective population size, or N_e, which is the size of an idealized population that would experience the same effects of random sampling of alleles as the real population under consideration (Wright 1931; see also Charlesworth (2009) for a comprehensive review of subsequent theoretical developments).

The list of demographic or genetic factors expected to reduce N_e relative to N is long, and includes common phenomena such as skewed sex ratios, non-random mating, variance in reproductive success, fluctuations in census population size, some forms of population subdivision, and linkage between loci under selection (Charlesworth 2009). Even closely related species that vary in one or more of these traits may therefore have substantially different effective population sizes.

3. Why should a species' N_e affect its evolution?

N_e reflects the balance of power between selection and drift: in small populations, drift plays a greater role and selection (both positive and negative) is correspondingly less efficacious. A mutation is effectively neutral when the magnitude of its selective coefficient is less than or equal to the inverse of the effective population size (Kimura 1983), so as N_e decreases, mutations of larger and larger effects behave as neutral. In species with small N_e, therefore, increasing numbers of slightly deleterious mutations may drift to fixation rather than being removed by purifying selection, increasing the substitution rate for this class of mutations. By contrast, more slightly advantageous mutations are likely to be lost due to drift rather than being fixed by positive selection, decreasing the substitution rate for this second class of mutations in species with small N_e.

If advantageous mutations are rare, while a substantial proportion of mutations are slightly deleterious, then we should be able to detect an increase in overall substitution rate in lineages with small N_e compared with those with larger N_e (all else, including mutation rates, being equal). If we make the further assumption that non-synonymous mutations are more likely to be slightly deleterious than synonymous mutations, many of which are probably neutral (but see Chamary et al. 2006), the ratio of non-synonymous to synonymous substitution rates (ω) should also be greater in lineages with small N_e (Ohta 1992).

4. How great should the effect be?

The magnitude of the effect of a change in N_e on nucleotide substitutions is determined by the distribution of selective effects of mutations. To illustrate this, consider two lineages with different effective population sizes, the larger N_eL and the smaller N_eS. If we assume that advantageous mutations are rare and most of the mutations that go to fixation are slightly deleterious, then the difference in substitution rate between these lineages will be largely determined by the proportion of mutations that have selective coefficients between 1/N_eL and 1/N_eS (figure 1). This proportion, in turn, is determined by the distribution of selective effects.

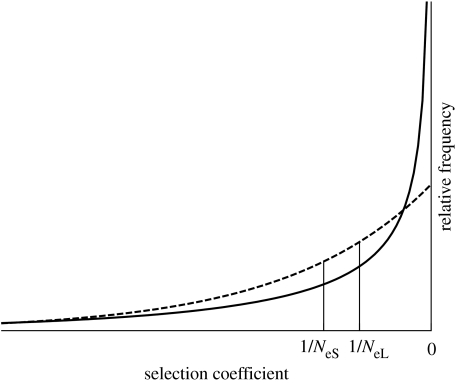
Figure 1.

The distributions of fitness effects modelled by Ohta (1977) (exponential or gamma with β=1, dashed curve) and Kimura (1979) (gamma with β=0.5, solid curve). In a small population, with effective population size N_eS, mutations with selection coefficients between 1/N_eS and zero will be effectively neutral. Fewer mutations, those with selection coefficients between 1/N_eL and zero, will be effectively neutral in a larger population with N_eL. The proportion of mutations that have selective coefficients between 1/N_eS and 1/N_eL will be greater under a gamma distribution of fitness effects with β=1 than with β=0.5 for most regions of parameter space.

Ohta (1977) assumed that the distribution of selection coefficients for new mutations was exponential. Under this distribution, and given a realistic mean strength of selection, a substantial proportion of mutations have fitness effects of the order of 1/N_e for many natural populations, and the effect of a change in population size on the rate of molecular evolution is expected to be quite large. This model was modified by Kimura (1979) who proposed that negative selection coefficients followed a more leptokurtic distribution. For a given strength of selection, fewer mutations will typically fall in the range from 1/N_eL to 1/N_eS under this distribution, and so the difference in substitution rate between lineages with different N_e will also be less, although a negative correlation between N_e and fixation rate is still predicted.

Neither of these distributions were chosen on the basis of biological data (Gillespie 1991), but a number of empirical estimates of the distribution of fitness effects of deleterious mutations have recently been made. Results vary between datasets and between taxa, with the estimated distributions including normal (Nielsen & Yang 2003), lognormal (Loewe & Charlesworth 2006) and strongly leptokurtic gamma distributions (Keightley & Eyre-Walker 2007) (figure 2). These estimates are based on the data from relatively few species, but indicate that the distribution of mutant effects is likely to vary between taxa. Adding further complexity, recent experimental work has suggested that a species' distribution of fitness effects is dynamic, and may change as organismal fitness and/or effective population size change (Silander et al. 2007).

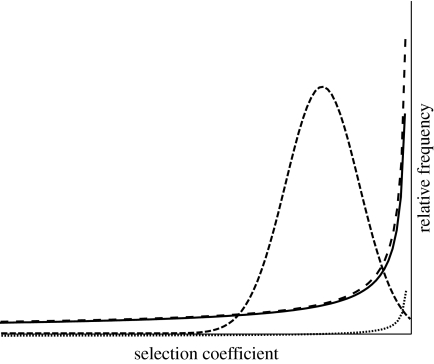
Figure 2.

Example distributions of fitness effects estimated from different datasets, including lognormal for Drosophila miranda and Drosophila pseudoobscura (Loewe & Charlesworth 2006; dotted curve), strongly leptokurtic gamma for Drosophila melanogaster (solid curve) and human (spaced dashed curve) nuclear genes (Keightley & Eyre-Walker 2007), and normal for primate mitochondrial genes (Nielsen & Yang 2003; closed dashed curve).

The prediction of increased rate of evolution in species with small N_e relies on the assumption that advantageous mutations are rare: positive selection is less efficacious in small populations, so fixation of advantageous mutations will be reduced rather than increased in species with low N_e. Slightly advantageous mutations are in fact likely to be relatively common (Charlesworth & Eyre-Walker 2007), but theoretical work that incorporates positive selection on such mutations shows that a negative correlation between overall rate of substitution and effective population size is still predicted (Ohta 1992). More problematically, some studies have suggested that, far from being rare, strongly advantageous mutations may comprise a substantial proportion of those mutations that contribute to substitution in humans and Drosophila (Eyre-Walker 2006), and this may further weaken the inverse relationship between N_e and substitution rate.

5. What do the data say?

An increase in either overall substitution rate or ω in taxa with long-term low N_e has been shown for a broad range of species. For example, island endemic animal species, which are likely to experience a reduction in N_e compared with their mainland relatives due to both the bottleneck during island colonization and long-term restriction in range size, show significantly increased ω values (Woolfit & Bromham 2005). Endosymbiotic bacteria and fungi, which live within invertebrate hosts and undergo severe bottlenecks with each transmission to the next host generation, have higher substitution rates and values of ω than their free-living relatives (Woolfit & Bromham 2003; Moran et al. 2008). Also, hominids have higher values of ω, genome-wide, than other mammalian lineages with larger N_e (Kosiol et al. 2008).

We see the same patterns repeated across genomic regions that differ in N_e. Genes in regions of low recombination have reduced N_e due to Hill–Robertson interference, in which linkage between weakly selected loci reduces the efficacy of selection at any one locus (Hill & Robertson 1966); such genes show increased values of ω (Haddrill et al. 2007) and reduced fixation of beneficial mutations (Presgraves 2005).

By contrast, Charlesworth & Eyre-Walker (2007) have shown that lineages which have undergone an expansion in N_e may experience a transient, though potentially substantial, increase in substitution rate before the rate of evolution decreases to below the level it was before the increase in N_e. This temporary increase in substitution rate is due to the fixation by positive selection of slightly advantageous mutations that had previously been effectively neutral. They tested for such an effect in sequences from taxa that had probably undergone population expansion after colonizing the mainland from an island and found a significant increase in ω, supporting their prediction. Furthermore, Bachtrog (2008) recently analysed divergence data from 91 genes in two species of Drosophila that differ substantially in N_e, and found no evidence that N_e is a major determinant of the rate of adaptive evolution for these data, possibly due to recent changes in N_e or differences in the distribution of fitness effects of mutations between taxa.

6. What next?

It is clear that N_e may have substantial effects on the rates and patterns of nucleotide substitution, but predicting the precise form of those effects is far from simple. Nonetheless, some obvious implications for evolutionary analyses can be extrapolated from these results. For example, as even closely related species may differ substantially in N_e (e.g. Ramos-Onsins et al. 2004), assuming that changes in evolutionary rate along lineages are rare, is unlikely to be an appropriate model for estimating divergence dates. Similarly, when performing comparative analyses of selection in different lineages or genes, the possibility that variation in ω is due to differences in N_e must be considered alongside selective explanations.

To move beyond these caveats and begin to incorporate N_e into analyses of molecular evolution more quantitatively, we must obtain better estimates of the effective population sizes and distributions of fitness effects of both deleterious and advantageous mutations for many more taxa. Such analyses require substantial amounts of sequence data. Next-generation sequencing technology is making this increasingly tractable, although the effort involved in both sample collection and computational analysis of the data is likely to remain substantial. The return on investment would be great, however, as estimates of these parameters are essential not only to fully understand this major driver of molecular rate variation, but to answer questions in a host of other evolutionary fields ranging from conservation biology to quantitative genetics (Keightley & Eyre-Walker 2007).