Propagating Waves of Activity in the Neocortex: What They Are, What They Do

Abstract

The development of voltage-sensitive dyes (VSD) and fast optical imaging techniques have brought us a new tool for examining spatiotemporal patterns of population neuronal activity in the neocortex. Propagating waves have been observed during almost every type of cortical processing examined by VSD imaging or electrode arrays. These waves provide subthreshold depolarization to individual neurons and increase their spiking probability. Therefore, the propagation of the waves sets up a spatiotemporal framework for increased excitability in neuronal populations, which can help to determine when and where the neurons are likely to fire. In this review, first discussed is propagating waves observed in various systems and possible mechanisms for generating and sustaining these waves. Then discussed are wave dynamics as an emergent behavior of the population activity that can, in turn, influence the activity of individual neurons. The functions of spontaneous and sensory-evoked waves remain to be explored. An important next step will be to examine the interaction between dynamics of propagating waves and functions in the cortex, and to verify if cortical processing can be modified when these waves are altered.

Imagine that you could visualize neuronal population activity in the cortex. What would you see when a sensory perception is forming, when a motor program is being planned and executed, or when a thought is being conceived? Most likely, you would see wavelike activity propagating within and between cortical areas. Some 60 years ago, Sir Charles Sherrington pictured just this scenario: “Imagine activity in [the brain] is shown by little points of light. Of these some stationary, flash rhythmically, faster or slower. Others are traveling points, streaming in serial trains at various speeds. The rhythmic stationary lights lie at the nodes. The nodes are both goals whither converge, and junctions whence diverge, the lines of traveling lights.” Such propagating waves reflect the organization of neuronal activity, within which millions of neurons work together to carry out a function. Thanks to the development of voltage-sensitive dyes (VSD) and optical imaging techniques, led by the groups of Larry Cohen, Amiram Grinvald, and others, Sherrington’s dream has become a reality. Propagating waves, fast and slow, have been observed during almost every type of cortical processing examined by VSD imaging or electrode arrays.

In this review, we will only discuss propagating waves in the neocortex, but not review the large literature of propagating waves in developing nervous systems (Katz and Shatz 1996; Wong 1999; Momose-Sato and others 2007) or of slower waves mediated by calcium transients and/or glial mechanisms (Haydon 2001; Webb and Miller 2003).

The propagating waves observed in VSD imaging are a manifestation of depolarization of the neuronal membrane. Each neuron may only depolarize by 5 to 10 mV from resting potential, but with increased probability of firing action potentials (Fig. 1). The propagation of these waves is generated by successive depolarization of neuronal populations, much like a “stadium wave” during a sport event by successive groups of spectators briefly standing and raising their arms. During a stadium wave, each individual is only required to rise slightly after the person immediately next to him/her and does not have to fully stand up to participate in this mass phenomenon. Similarly in the cortex, mild depolarization during the wave increases the chance of spiking in the population and these spikes will in turn depolarize more postsynaptic neurons in the neighboring area to sustain the wave propagation.

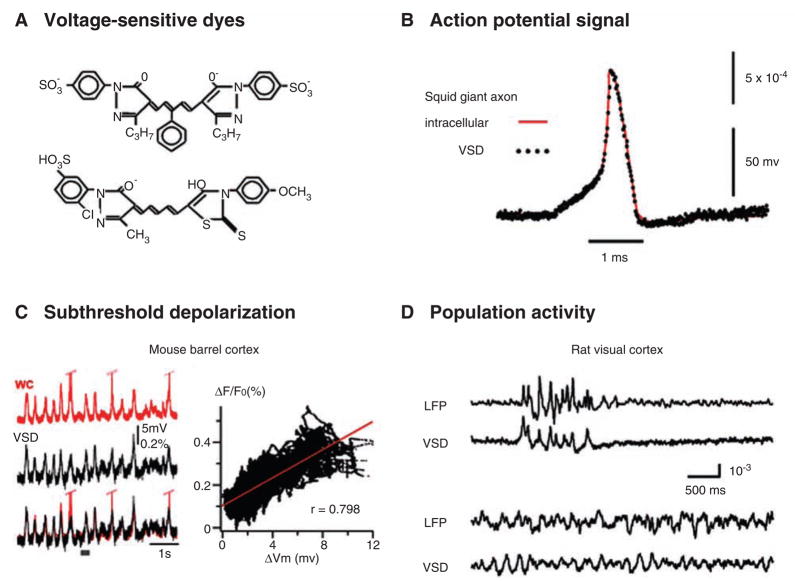
Fig. 1.

(A) Structural formula of commonly used voltage-sensitive dyes (VSD). (Top) RH482 (also known as NK3630), an absorption dye used for imaging neuronal activity in brain slices. (Bottom) RH1691, a fluorescent dye commonly used for imaging cortex in vivo. It is one of newly developed “blue” dyes, and it has small pulsation artifacts for imaging cortex in vivo (Shoham and others 1999). (Structural formulae for more dyes can be found at: http://square.umin.ac.jp/optical/optical/dye.html.) (B) Simultaneous VSD (dots) and intracellular (line) recordings from a squid giant axon. The axon is stained with an absorption dye. The two signals follow each other precisely, providing the first evidence that dye signal is membrane potential dependent. Note that although the linearity and temporal response of the dye signal are excellent, the amplitude of the dye signal is small, only about 0.1% change from the resting light level per 100 mV changes in membrane potential. (Reprint from Ross and others 1977, with permission from Springer.) (C, left) Simultaneous recordings of intra-cellular potential (whole-cell patch, red) from one cortical neuron and VSD signal (black) from the surrounding population of neurons. The cortex is stained with RH1691. Under anesthesia, cortical neurons undergo synchronized up and down states. The subthreshold membrane potential fluctuations are closely correlated with the VSD signal, but the spikes on individual neurons were not correlated with large deflections of the VSD signal. (C, right) The VSD signal is plotted against membrane potential changes, demonstrating a linear relationship. (Modified from Ferezou and others 2006, with permission from Elsevier.) (D) Simultaneous local field potential (LFP) and VSD recordings from the rat visual cortex, demonstrating the sensitivity of VSD imaging compared to that of LFP (microelectroencephalography). The top two traces show synchronized bursting activity recorded under 1.5% isoflurane anesthesia. The correlation is high between LFP and VSD signals. The bottom two traces were recorded later under lower anesthesia level. Both LFP and VSD signals show sleep-like oscillations but the correlation remains low. The poor correlation is unlikely attributed to the baseline noise, because the baseline noise of the analogous recording under higher anesthesia is low. (Reprint from Lippert and others 2007, with permission from the American Physiological Society.)

Propagating waves may contribute to cortical function in a number of ways. First, waves provide a background depolarization to a selected cortical region. In such a region, depolarized neurons have increased firing probability and higher synaptic transmission efficacy, in comparison with the neurons outside of the region. Thus the spatiotemporal patterns of the waves could determine when and where neurons are most likely to fire and fire synchronously. Second, a sensory-evoked wave propagating to a larger area would increase the sensitivity/network gain for incoming stimulation. In this sense, the evoked wave generates an unintentional focus of attention in the sensory cortex. Third, propagating waves associated with an oscillation can organize spatial phase distributions in a population of neurons. For example, rotating waves such as spirals can work as a population oscillator to periodically depolarize an area without any cellular pacemaker.

A propagating wave is an emergent behavior of underlying neuronal interactions. Therefore, understanding interactions between individual neurons may not be sufficient for understanding waves, as understanding interactions between single air molecules is not sufficient for understanding turbulence. To extend this analogy, methods and tools of fluid dynamics have brought additional helps for understanding waves (Senseman and Robbins 1999; Schiff and others 2007). On the other hand, wave-to-wave interactions may generate top-down influences to the interactions between individual neurons. For example, during plane waves associated with carbachol-induced 10-Hz oscillations, neighboring oscillating neurons are nearly synchronized with a small phase gradient of (~0.05 pi per 100 μm). However, when two plane waves interact to generate a spiral wave, near the spiral phase singularity the phase gradient becomes much larger, approaching infinity (Huang and others 2004).

Visualization of Neuronal Propagating Waves

Neuronal propagating waves have mostly been observed by VSD imaging, an optical method of measuring neuronal transmembrane potential. The VSD is a type of molecule that binds to the neuronal membrane and reports changes in membrane potential by shifting absorbance or fluorescence spectra. Since pioneering work published about 40 years ago (Cohen and others 1968), the technique has developed into a powerful tool for studying neuronal activity (Grinvald and Hildesheim 2004).

The dye signal has an excellent linearity within a membrane potential range of more than ±300 mV and a very fast (<1 μsec) response time (Fig. 1; Ross and others 1977). When imaging cortical tissue, the sensitivity of VSD recording is comparable with that of local field potential recordings (Fig. 1). Subthreshold depolarizing/hyperpolarizing potentials of neurons in the population are the main contributors to the VSD signal. The contribution of each neuron to the signal is a product of the area of stained membrane times the changes in membrane potential. Spikes from individual neurons cannot be seen, because they are sparse in the population and have very short duration (~1 msec), so that their contribution is much less than that of the long and overlapping subthreshold potentials (Petersen, Hahn, and others 2003). To record the contribution of individual neurons to the wave, one would require either stain-isolated cells (Zecevic 1996) or use confocal or two-photon techniques that can distinguish dye signals from individual neurons (Yuste 2005). Unfortunately, two-photon techniques are not yet sensitive enough to detect the VSD signal of spikes. The current techniques with population staining can only reach a spatial resolution of 100 × 100 × 100 μm³ for each pixel, as they are limited by light scattering of the tissue. This volume contains about 50 to 100 neuronal soma and dendrites and axons from hundreds of other neurons.

Mechanisms for Generating and Sustaining Waves

What are the mechanisms for a neuronal population to sustain its mildly depolarized state? If we assume that mild depolarization does not propagate from neuron to neuron through extrasynaptic transmission, spikes would be the only means for sustaining depolarization of the system. Therefore, if a population can maintain the same number of spikes over time, the depolarization would be sustained. This does not seem to be a problem for cortical networks. Neurons in cortical local circuits are extensively interconnected, with a typical pyramidal cell making connection to 3% of its neighbors or ~1500 postsynaptic neurons within a 1-mm range (Douglas and others 2004). In a simplified picture, if a spike can increase the firing probability by 1:1500 in its postsynaptic population, one spike in the system should be able to generate another spike and the activity would be sustained. Therefore, when the averaged spike-to-excitatory postsynaptic potential transition exceeds a certain threshold, the system may converge into a “network attractor” to sustain the wave. Intracellular recordings in vivo have demonstrated such a scenario, where neocortical neurons receive an intense synaptic bombardment from other neurons, resulting in a depolarized state around −60 mV, the up state (Destexhe and others 2003).

Ermentrout and Kleinfeld (2001) proposed three mechanisms for wave propagation in the nervous system (Fig. 2): 1) A single oscillator directly excites neighboring cortical areas with different time delays, resulting in a fictive propagating wave (Fig. 2A). 2) The propagating of the wave originates from a chain of successively activated neurons (Fig. 2B). In cortical networks, each neuron makes distributed excitatory connections to its neighboring neurons. The pacemaker initiates an excitation on the neurons directly connected to it and these neurons will subsequently activate the neurons they innervate, resulting in a regenerative wave propagating from the pacemaker to neighboring areas. This type of wave is also known as a “propagating pulse,” which may underlie epileptiform waves and sensory evoked waves in the cortex. 3) Coupled local oscillators generate wave propagation due to phase delay between individual oscillators (Fig. 2C). In the cortex, individual neurons and neuronal clusters can become local oscillators and the oscillating phases among the local oscillators can be interrelated. In general, stronger coupling between local oscillators would result in smaller phase differences and faster velocity; weaker coupling would result in larger phase gaps, slower velocity, or broken waves. In a system with coupled oscillators, waves can travel back and forth like water waves in a pond. Coupled oscillators in the cortex can generate complex spatiotemporal patterns such as plane, spiral, and irregular waves (Prechtl and others 1997; Lam and others 2000; Huang and others 2004; Bai and others 2006).

Fig. 2.

Mechanisms for generating and sustaining propagating waves in space. Open circles indicate excitable but not necessarily oscillatory neurons or neuronal tissue, and circles with ~ indicate local oscillators with frequency ν. For simplicity, in A–C only one-dimensional models are shown. (A) The fictitious wave motion is generated from a single generator that drives adjacent regions of cortex through increasing time delays of τ_D. ΔΨ = phase difference between neighboring units. (B) Wave motion originates from the transmission of an excitatory pulse along a network of cortical neurons. The propagation delay between neurons is τ_D. (C) Wave motion originates as a phase lag between neighboring neuronal oscillators. Function Γ determines the spatial phase shift, the isolated frequency, and the interactions. (D) Population interactions can generate spatial phase distribution (right) and the propagating direction (arrows) without any cellular pacemakers as that in A–C. As emergent properties of the spiral wave, oscillations (bottom) are generated by the rotation of the wave. At different locations (1 and 2) there is a phase lag due to the wave rotation. (A–C are modified from Ermentrout and Kleinfeld 2001, with permission from Elsevier.)

Network interactions provide a fourth mechanism for generating and sustaining propagating waves (Fig. 2D). For example, in an excitable medium, one stimulus can only generate a nonoscillatory propagating pulse. However, when two pulses interact at a certain timing and angle, a spiral wave is generated and the spiral phase singularity will become an engine to oscillation and rotating waves (Huang and others 2004). The entire system will be rhythmically activated by the rotating waves without any cellular pacemaker (Fig. 2D). This mechanism differs from the first three mechanisms in the sense that the mechanism is top-down, or an emergent property of the network exerts its influence to govern the activity of individual neurons.

Propagating Waves in Cortical Local Circuits In Vitro

The majority of cortical connections are local. For example, neurons in visual cortex receive no more than 1% to 2% synaptic inputs from the lateral geniculate nucleus (Douglas and others 2004). Thus one would expect that most cortical dynamics have an intrinsic cortical origin. Studying wave patterns in brain slices can provide basic information on propagation and sustaining of the activity in cortex.

Propagating pulse

When GABAergic local inhibitory circuits are blocked (by bicuculline or picrotoxin) in the cortex, local excitatory activity can become regenerative and propagate to a large area (Chervin and others 1988). This activity is referred to as “epileptiform spikes” by physiologists and “propagating pulses” in the computational field (Fig. 2; Golomb and Ermentrout 2002). Epileptiform spikes/propagating pulses have been observed extensively in various brain structures (Grinvald and others 1994; Chervin and others 1988; Albowitz and Kuhnt 1995; Golomb and Amitai 1997; Demir and others 1998; Tsau and others 1998). The propagation is mediated mainly by α-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid (AMPA) receptor-mediated fast glutamate excitation in the synapses (Golomb and Amitai 1997). The propagating velocity of the pulses is about 140 mm/sec in hippocampal slices (Miles and others 1988) and from 80 mm/sec (Chervin and others 1988) to 130 mm/sec (Wu and others 2001) in neocortical slices. The propagating velocity of the pulse is faster compared with that of the phase wave of oscillatory events.

Phase waves and coupled oscillators

Two types of spatiotemporal patterns are observed in oscillatory waves in cortex. One is referred to as “one-cycle-one-wave,” that is, there is a clear correlation between the oscillation at each location and waves distributed in space; each oscillation cycle measured at a given location is associated to a propagating wave swapping through that location (Wu and others 1999; Bao and Wu 2003; Huang and others 2004). The other type does not have a clear correlation between oscillations and waves; usually many oscillation cycles are enveloped into one propagating wave (Wu and others 2001).

The one-cycle-one-wave pattern is observed in many oscillations around 10 Hz. In cortical slices, these oscillations can be developed when N-methyl-D-aspartate (NMDA) receptor-mediated excitation is largely enhanced (Anderson and others 1986; Silva and others 1991) or when the tissue is bathed with carbachol and bicuculline (Lukatch and MacIver 1997). For coronal slices, during these oscillations the cortical circuits are synchronized in the vertical direction (pia-white matter direction) and the phase gradient is distributed in the horizontal (laminar) direction, thus making quasi one-dimensional propagation (Fig. 3). The starting point of each oscillation cycle, or the location with the earliest phase in the oscillation, is also the initiation site of a wave of activation. As shown in Figure 3B, waves are often initiated from two locations and collide when the two waves meet, after collision the waves are annihilated.

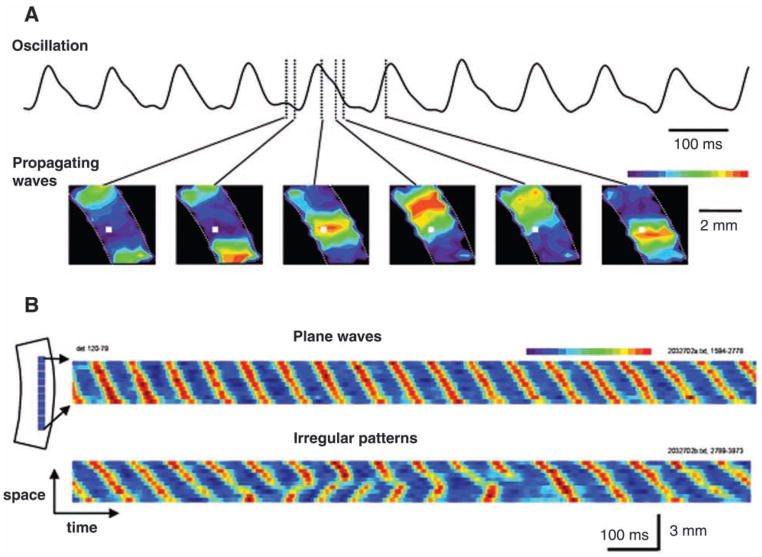
Fig. 3.

Oscillation and propagating wave in neocortical slices. The slices develop spontaneous oscillations of ~10 Hz when perfused with carbachol (100 μM) and bicuculline (10 μM). (A, top) The voltage-sensitive dyes (VSD) signal of the oscillation recorded by an optical detector (white square in the bottom images). (A, bottom) Snap shots of the VSD signals taken at different phases of an oscillation cycle as marked on the top trace. The pseudocolor images are converted from the amplitude of the VSD signals on many detectors in the field of view using a linear color scale (peak = red, baseline = blue, top right of the images). The white broken lines in the images mark the boundary of the cortical area of the slice. During each cycle of the oscillation, a propagating wave started from the bottom of the slice and propagated to the top end. This one-cycle-one-wave pattern is observed in all oscillation cycles. (B) A “space-time” map showing wave-to-wave interactions during the 10-Hz oscillations. The space-time map was made from VSD signals on one row of detectors horizontally arranged in cortical layers II–III (left schematic diagram, 10 detector, ~3 mm wide). During an epoch of spontaneous oscillations, at the beginning the waves initiated on the upper side of the slice and propagated downward (top, plane waves); later the top-down wave was interacted with a new wave initiated from the lower end of the slice (bottom, irregular patterns). (Modified from Bao and Wu 2003, with permission from the American Physiological Society.)

In tangential slices (sectioned parallel to cortical lamina), such oscillations develop into two-dimensional waves. The interactions between wave fronts become more complicated with various waveforms, such as plane waves, ring waves, spiral waves, and irregular waves (Huang and others 2004). Spiral waves can evolve from a traveling wave front with a free end (Winfree 2001); the free end will bend itself and the curvature dependence of the velocity of the wave front can maintain spiral wave propagation. Figure 4 shows how a spiral wave can be generated from two wave interactions. Before spiral waves occur, there is an ongoing ring wave. At one point, the ring wave splits into two wave fronts, and these two fronts collide to create a free end, which evolves into a spiral wave (Fig. 4).

Fig. 4.

Wave-to-wave interactions in two dimensions. Wave-to-wave interactions caused rotating spiral waves. The preparation is a 6 × 6-mm² patch from rat visual cortex (top left, schematic diagram), also known as a tangential cortical slice. (Top) The voltage-sensitive dyes (VSD) signal of the oscillation induced by carbachol and bicuculline. (Bottom) The images are made from five consecutive oscillation cycles marked by the line under the top trace; each row of images is from one of the cycles. The first two rows of images show that the wave started from a pacemaker at the bottom of the imaging field and propagated upward in a “ring wave” pattern. During the third cycle, the ring wave was broken up into two wave fronts and the two fronts collided (third row, marked by the arrow). A rotating spiral wave was generated afterward with a wave front. In the fourth and fifth rows, this spiral wave front started to rotate in the field of view and continued rotating for the next 20 to 30 cycles (not shown).

Eight types of oscillatory activities in rodent neocortical or hippocampal slices have been reported and six of them have been examined by voltage sensitive dye imaging or multiple electrodes (Table 1). The spatiotemporal patterns of these oscillations reflect the coupling strength between local oscillators. One type of the oscillations, type II in Table 1, was synchronized over space and did not appear as propagating waves (Mann and others 2005), suggesting that coupling between local oscillators is very strong. Some other types have one-cycle-one-wave patterns, i.e., types I (Wu and others 1999), III (Bao and Wu 2003; Huang and others 2004) and V (Kim and others 1995), indicating that the entire tissue oscillated in the same frequency, but weaker coupling allows phase lag between spatially distributed local oscillators. The coupling between local areas is often broken, causing complex wave patterns (Figs. 3, 4). With even weaker coupling, (VIII of Table 1), local oscillations with different frequencies can coexist and each cycle of the oscillation is initiated at a new location (Bai and others 2006). The weakest coupling between local oscillators is seen in the type IV in Table 1, which do not have a one-cycle-one-wave pattern. The oscillation can be seen in local field potential recordings, with a frequency of 40–80 Hz, but in VSD imaging only one depolarization wave propagates slowly, enveloping many cycles of oscillations (Wu and others 2001).

Table 1.

Reported Oscillations in Brain Slices

Conditions	Frequency	Brain Area	Duration
I Zero or low Mg2+	7–10 Hz	Hippocampusa, cortexb	Long episodes
II Carbachol/kainate	~40 Hz	Hippocampusc, cortexd	Continuous
III Carbachol/bicuculline	4–15 Hz	Cortexe	Long episodes
IV Evoked in normal ACSF	20–80 Hz	Cortexf	Short episodes
V Spontaneous	6–10 Hz	Thalamusg	Short episodes
VI Tonic stimulation	~40 Hz	Hippocampush	Short episodes
VII Transient K+ elevation	50–80 Hz	Hippocampusi	Long episodes
VIII Pretreated with choline and evoked in normal ACSF	~25 Hz	Cortex j	Short episodes

Note: ACSF = artificial cerebrospinal fluid.

^aAnderson and others 1986.

^bSilva and others 1991.

^cFisahn and others 1998.

^dBuhl and others 1998.

^eLukatch and MacIver 1997.

^fLuhmann and Prince 1990; Metherate and Cruikshank 1999.

^gKim and others 1995.

^hWhittington and others 1995.

ⁱTowers and others 2002.

^jBai and others 2006.

Propagating Waves In Vivo during Sensory Processing

In olfactory, visual, somatosensory, auditory, and motor cortices, VSD imaging or electrode arrays have revealed evoked propagating waves manifested during sensory/motor processes and during spontaneous events.

Propagating Waves in Olfactory System

Walter Freeman and colleagues found complex spatiotemporal dynamics in rabbit olfactory bulb (Freeman 1978; Eeckman and Freeman 1990). Using local field potential electrode arrays they observed propagating waves in the olfactory bulb and higher cortices related to olfaction. Odor-specific wave patterns were reported when the animal was performing odor-discrimination tasks; however, the changes were subtle and require extensive data processing.

Propagating waves were later observed in salamander olfactory bulb by Lawrence Cohen and colleagues using VSD imaging (Orbach and Cohen 1983). Cohen’s group further examined propagating waves in turtle olfactory bulb during oscillations evoked by olfactory stimulation. They found that sniffing an odor induced three oscillations at different locations of the turtle olfactory bulb (Lam and others 2000). These oscillations manifested as propagating waves in a pattern of one-cycle-one-wave (Fig. 5). The three oscillations originated at different locations of the bulb and they interacted in a complex way (Zochowski and Cohen 2005). When consecutive odor stimulations were presented, two of the oscillations were depressed in response to the second stimulation even if a new odorant was presented. The third oscillation was enhanced if the odorant was the same but suppressed if the odorant was new (Zochowski and Cohen 2005). These findings suggest that the oscillations and propagating waves may carry information about previous olfactory experience.

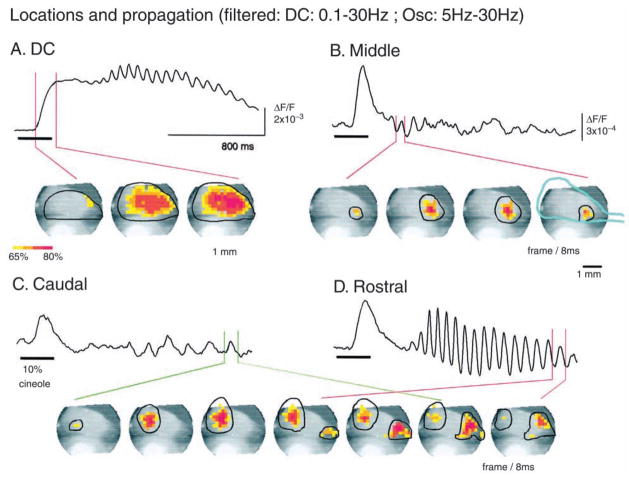
Fig. 5.

Four propagating components in turtle olfactory bulb with odor stimulus. (A) The DC component propagating from rostral to almost the entire bulb. (B–D) Three oscillatory components with different initiation loci, different propagation direction, and ranges (labeled by line circles). The center of the middle oscillation (B) remained relatively fixed. (Reprinted from Lam and others 2000, with permission from the Society for Neuroscience.)

Propagating waves were also found in the olfactory system of terrestrial gastropod mollusks (snails and slugs). Gelperin and Tank (1990) identified a 0.5-Hz oscillation in the procerebral lobe of garden slug Limax maximus. The oscillations occur spontaneously as propagating waves traveling across the entire procerebral lobe. Odorant stimulations transiently switch propagating waves into standing oscillations, suggesting global spatiotemporal patterns play a role in olfactory processing (Delaney and others 1994).

The olfactory bulb is organized with glomeruli structures. A propagating wave sweeping across many glomeruli may contribute to the integration of an odor that activates many glomeruli. Although extensive attempts have been made to find correlation between wave patterns and patterns of odorants, such an exclusive correlation has not been found. The functional roles of the waves in olfactory system remain to be explored.

Propagating Waves in the Visual System

Orbach and others (1985) observed that a single diffused flash to the eye could activate a large area in rat visual cortex by using VSD imaging. This large area could not be explained by light scattering of the dye signal in the cortical tissue. Later in a seminal work, Grinvald and colleagues examined the spreading of cortical activity in macaque primary visual cortex (Grinvald and others 1994; Arieli and others 1995). They surprisingly found that even a small visual stimulus (1° × 1°) evoked cortical activity spreading to a large area of 6 × 6 mm². The neuronal activity first initiated from the retinotopic representation in V1, and then propagated to a large area of the primary visual cortex. In recent years, similar visually evoked propagating waves were reported in studies in cats, monkeys, ferrets, and rodents (Sharon and Grinvald 2002; Slovin and others 2002; Jancke and others 2004; Chen and others 2006; Roland and others 2006; Benucci and others 2007; Lippert and others 2007; Sharon and others 2007; Xu and others 2007). Although the spatiotemporal pattern and velocity vary in different reports, the common features of the evoked propagating wave are that it is initiated from the retinotopic representation of the primary visual cortex and spreads to a large area. The propagating velocity of these waves is fast, about 0.1 to 0.25 m/sec and the duration of the waves is 50 to 400 msec (Grinvald and others 1994; Slovin and others 2002; Roland and others 2006; Sharon and others 2007; Xu and others 2007). Evoked propagating waves in the visual cortex suggest a distributed processing of visual information in the primary visual cortex.

Anisotropy in propagation is a distinct feature in visually evoked waves. Grinvald and others (1994) reported a large anisotropy of the spreading near the monkey V1/V2 border. Xu and others (2007) further examined wave propagation between rat visual areas. They found that the evoked wave propagated fast in the V1 and then slowed down at the V1/V2 border, causing “wave compression.” A new wave, the “reflective wave,” was initiated after the compression and propagated into both directions, backward into V1 and forward into V2 (Fig. 6). The reflective wave may have a functional significance because it depolarizes V1 and V2 simultaneously and may facilitate the synaptic transmissions between the two areas. The distinct pattern of compression and reflection in the evoked waves is not seen in spontaneous waves (up-down states or sleeplike waves) in the same cortical area (Xu and others 2007), suggesting that it is governed by mechanisms related to the visual processing or sensory-evoked unintentional attention. Reflective waves from higher visual areas were also observed about 200 to 400 msec after the onset of the visual stimulus, which may contribute to the top-down feedback during visual processing (Roland and others 2006).

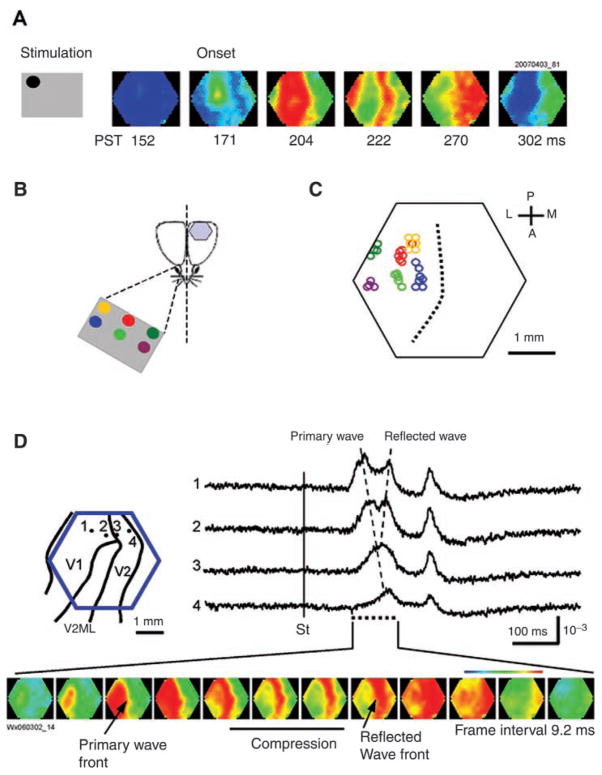
Fig. 6.

Evoked waves in visual cortex. (A) Visually evoked wave. The visual stimulus is a drifting grating within a small field of 6° in size. The left gray box shows the visual field and location of the stimulation (details in B). The visual stimulus evoked a wave propagating in V1 and toward V2. The six snapshots on the right are selected at the six stages of the propagating wave: from left, before onset, onset of primary wave, onset of wave compression, full compression, reflection, and the end of the primary/reflection wave complex. The number under each image is the poststimulus time (PST) in milliseconds. (B) Schematic diagram of the visual stimulation. The stimuli were projected onto a screen of 10 × 7 inches placed at 20 cm in front of the animal’s contralateral eye. The retinotopic map was made by presenting the drifting pattern (6° in size) at six locations on the screen (colored dots). (C) Retinotopic map in V1. Each circle represents the location of the response onset. The color of the circles represents the location of the visual stimulation in the field of view. The approximate coordinates of the stimulation sites are (in degrees from the center): yellow (−19, 11); red (0, 11); dark green (19, 11); blue (−19, 0); light green (0, 0); and purple (19, 0). All the data are from the same animal. The broken line marks the approximate position of V1/V2 border. (D, left) Schematic drawing of the imaging field (blue hexagon) overlying the map of the visual areas. Four optical detectors, 1–4, were selected and their signal traces are shown on the right. (D, right) Optical signals of visually evoked activity from four detectors (1–4). The onset of the visual stimulus is marked by the vertical line (St). The peak of the evoked activity occurred sequentially from detector 1 to 4, indicating a propagating wave (primary wave) from V1 to V2 (left broken line). A reflected wave can be seen starting from detector 3 and propagating backward to detector 1 (right broken line). The two waves can be clearly seen in the bottom images. (Bottom) Twelve images are selected from the initial response (time marked by the doted line under the traces). The first image was taken when the evoked primary wave first appeared in the V1 monocular area, approximately 104 msec after the grating started to drift. (Modified from Xu and others 2007, with permission from Elsevier.)

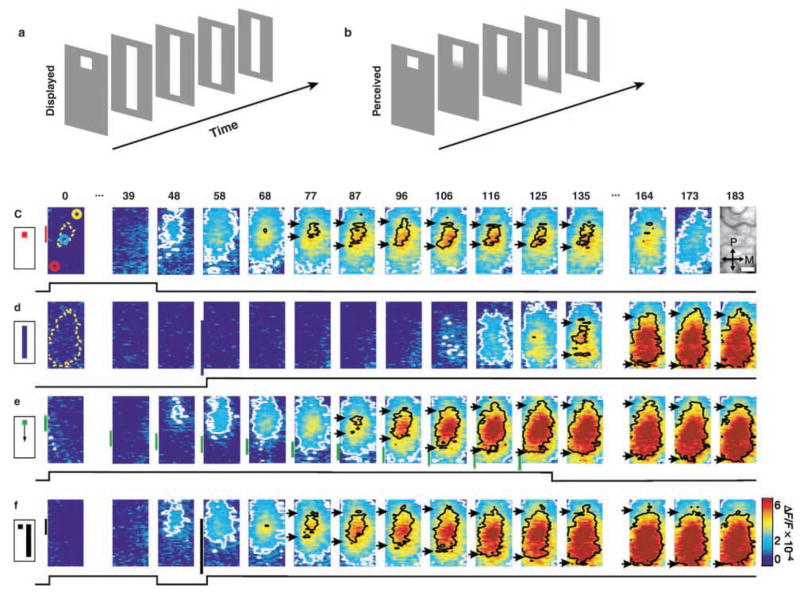
The correlation between visual stimulus patterns and wave patterns remains elusive. Chen and others (2006) showed that visual stimulus evoked a wave propagating to an 8 × 8 mm2 region of monkey V1, regardless the type of stimulus. Although different stimuli (size of the drifting pattern, stationary objects, flash, etc.) can cause various spiking patterns in neighboring neurons, wave patterns appear similar (Chen and others 2006; Roland and others 2006; Xu and others 2007). The wave may provide a correlated depolarization of the population whereas individual neurons in the population may respond differently. Jancke and others (2004) showed that nonmoving stimuli presenting with special sequence could induce indistinguishable wave patterns as that evoked by a real motion stimulus (Fig. 7), suggesting that propagating waves may involve in the perception of line-motion illusion.

Fig. 7.

Propagating waves may contribute to the perception of visual illusion. Cortical representations of stationary, moving, and illusory moving stimuli. The line-motion illusion. (a) Square (“cue”) presented before a bar stimulus. (b) Subjects report illusory line drawing. (c–f) Patterns of evoked cortical activity as a function of time. Yellow dotted contours approximate retinotopic representation of the stimuli; white contours delimit low-amplitude activity (significance level, P < 0.05). The cortical area imaged is shown at upper right. Scale bar, 1 mm. P = posterior; M = medial. Green vertical lines in e indicate estimated position of the stimuli along posterior–anterior axis. Time in milliseconds after stimulus onset is shown at the top. Stimulation time is shown at the bottom of each row. Color scale indicates averaged fractional changes in fluorescence intensity (F/F). Stimuli: c = flashed small square; d = flashed bar; e = moving small square (32° s-1); f = line-motion paradigm. A total of 22 repetitions were averaged. (Reprinted from Jancke and others 2004, with permission from Nature.)

Benucci and others (2007) have observed orientation/retinotopic maps and propagating waves with different stimuli. Using an ingenious method of Fourier transformation of visually evoked VSD signals, they measured the amplitude and spatial phase distribution of the evoked activity with respect to the parameters of the visual stimulus. The propagating wave was described as the spatial distribution of phase delay in response to the stimulus.

More complex spatiotemporal patterns were observed in turtle visual cortex. Prechtl and others (1997) found spontaneous and evoked propagating waves with multiple frequency domains. Visually evoked high-frequency oscillations (10–20 Hz) distributed spatiotemporally as plane, spiral-like waves, and more complex patterns. The evoked waves started at the entrance of the fibers to the lateral visual area and propagated with the front orthogonal to the direction of the fibers. These complex wave patterns, comparable with the wave patterns observed in brain slices, suggest that coupled cortical oscillators may be involved in visual processing.

Propagating Waves in Rodent Barrel Cortex

Rodent whisker/barrel system is a classical example of columnar structure of the cortex (Woolsey and Van der Loos 1970). However, the cortical area activated by a single whisker stimulation (whisker functional representation, WFR) is much larger than a single whisker barrel. Intrinsic optical imaging revealed that stimulating one whisker could activate a large portion of the posteromedial barrel subfield (PMBSF). For WFRs located near the primary somatosensory cortex (SI) border, activation even propagated crossed the SI and reached the border of primary auditory cortex (reviewed by Frostig 2006; Petersen 2007).

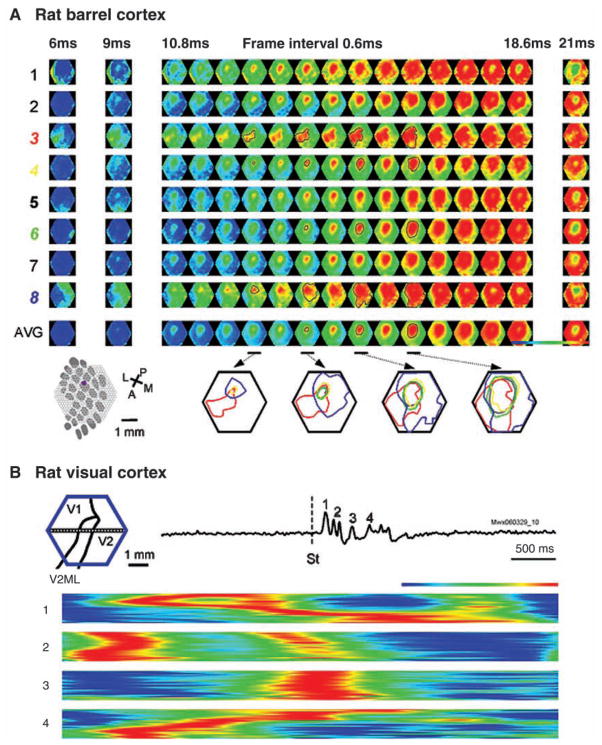
Using VSD imaging, London and others (1989) reported that stimulating a single whisker evoked VSD signal in an area larger than the corresponding cortical barrel. This observation was later confirmed by other VSD imaging studies (Kleinfeld and Delaney 1996; Derdikman and others 2003; Petersen, Grinvald, and others 2003, Petersen, Hahn, and others 2003; Civillico and Contreras 2005; Ferezou and others 2006; Lippert and others 2007). VSD imaging has a submillisecond temporal resolution and clearly demonstrated that the large WFR is caused by a propagating wave, starting from the corresponding barrel and quickly spreading to a large portion of the primary somatosensory cortex within a duration of 15 to 50 msec. Whisker-evoked propagating waves are much faster than those seen in the visual cortex and have large trial-to-trial variations (Fig. 8; Lippert and others 2007).

Fig. 8.

Variations in propagating direction and velocity. (A) Variations of evoked waves in rat barrel cortex. Eight trials (rows 1–8) are shown with identical whisker deflection. The bottom images (AVG) are averaged from 105 trials from the same animal. (Bottom row, left) Schematic diagram of the barrel pattern and the imaging field. (Bottom row, right) The contour lines show the isolevels of the relative amplitude of the population membrane potentials. The different colors indicate different trials. Each of the four maps then consists of contour lines superimposed from trials 3 (red), 4 (yellow), 6 (green), and 8 (blue), along with contour lines from the averaged data (gray). Responses in some trials (4, 6) are similar to the average (gray), whereas in some trials (3, 8) propagating direction and velocity are very different. (Modified from Lippert and others 2007, with permission from the American Physiological Society.) (B) Variations of evoked waves in rat visual cortex. (Top image) Schematic drawing of the imaging field (blue hexagon) overlying the map of the visual areas. A horizontal row of detectors is selected to make space-time map in the bottom images. (Top) A visual stimulus evoked a primary wave (1) and a number of secondary waves (2–4). (Bottom) 1, the primary forward/reflex wave complex with compressions as seen in Figure 6D. 2–4, secondary waves following the primary wave, showing variations in propagating velocity and direction. In particular, there is a wave collision in the first part of wave 2, and in wave 3 there is a wave split; wave 4 is much slower than the others. Note that only the primary wave shows a compression/reflection pattern.

Surprisingly, the activity evoked by deflecting a single whisker is not limited in the barrel cortex; it can also activate other cortical areas. Ferezou and others (2007) have reported fast propagating waves in both barrel cortex and whisker motor cortex. The evoked wave first initiated from primary whisker barrel and propagated in the barrel cortex, subsequently another wave started from the whisker motor cortex. The spread of sensory response to motor cortex was dynamically regulated by behavior and correlated with the generation of sensory-evoked whisker movement (Ferezou and others 2007). Takagaki and others (2008) reported whisker evoked waves initiated from the corresponding barrel, to propagate beyond the barrel cortex into the parietal association area and then entering the primary visual cortex (V1). Similarly, if a visual stimulus is presented, the evoked wave will propagate conversely from the V1 through the parietal association area into the barrel cortex (Takagaki and others 2008). Although the function of long-range propagation remains elusive, one might expect that with larger cortical areas examined by imaging, propagating waves evoked by sensory stimulus might be found to excite multiple cortical areas.

Waves in Auditory Cortex

Several studies using VSD imaging found propagating waves in auditory cortex of guinea pigs (Song and others 2006; Nishimura and others 2007). With pure tone stimulation, lower frequencies activated the rostral primary auditory cortex, whereas higher frequencies activated the caudal part, in agreement with the tonotopic map. The wave was initiated at the dorsal site and filled a narrow dorsal-ventral strip along the isofrequency axis within ~10 msec. Later the wave also spread in the rostral-caudal directions to a large portion of the imaging field (3 × 3 mm²). Electrode arrays implanted in cat auditory cortex also revealed evoked fast propagating waves (Witte and others 2007). Propagating patterns are in general the same as those in visual and barrel cortices.

Waves in Motor Cortex

Rubino and others (2006) have described propagating waves in monkey motor cortex accompanying 10- to 45-Hz oscillations during motor preparation. These waves propagated at a velocity of ~160 mm/sec in a one-cycle-one-wave pattern across the motor cortex. Interestingly, they found that information regarding movement preparation and execution was carried by the latency and amplitude of the evoked waves at a time when the field phase-locked with respect to the target onset, suggesting that propagation of the oscillation is relevant to cortical information transfer during movement preparation and execution (Rubino and others 2006).

Spontaneous Waves

The cortex is continuously active even in the absence of sensory inputs (during anesthesia, sleep, and quiet wakefulness). In the cortex neuronal membrane potential undergoes a spontaneous transition between up and down states (Steriade and others 1993; Lampl and others 1999; Petersen, Hahn, and others 2003; Shu and others 2003). At the network level, neurons in the up state are synchronized by recurrent synaptic inputs from the surrounding neuronal network. The population activity during the up state manifests as propagating waves (Petersen, Hahn, and others 2003; Ferezou and others 2007; Xu and others 2007). Spontaneous waves in cortex reflect organized, large-scale intrinsic cortical population activity, which may play an important role in cortical processing.

Arieli and others (1995) found that cortical spontaneous events in cat visual cortex correlated over large areas but not homogenously. Later Xu and others (2007) showed that spontaneous activity in rat visual cortex initiated from various locations and propagated with different velocity and directions (Fig. 8B). In sensorimotor cortex, Ferezou and others (2007) found diverse patterns of spontaneous activity propagating across cortex in both anesthetized and awaked mice. Takagaki and others (2008) showed that spontaneous waves propagate in parietal association area with a preferred direction, along the visual and somatosensory cross-modal axis.

Spontaneous waves interact with evoked cortical activity. Arieli and others (1996) found that in cat visual cortex about 80% of the variance in the evoked responses can be attributed to the spontaneous activity occurring at the same time of the stimulus. Evoked responses in single trials could be predicted by linear summation of the deterministic response and the preceding spontaneous ongoing activity. In rodent barrel cortex, spontaneous activity inhibited the sensory responses evoked by whisker deflection (Petersen, Hahn, and others 2003). If a whisker stimulus occurs at the peak of a spontaneous event, the evoked response is reduced (Ferezou and others 2007). The large trial-to-trial variability of sensory-evoked postsynaptic potentials and action potentials might be caused by the interaction of spontaneous activity and evoked activity (Fig. 8A).

The spatiotemporal pattern of spontaneous events often resembles those evoked by sensory stimuli. Petersen, Hahn, and others (2003) found the spontaneous activity in barrel cortex was either localized to an area of a barrel column or occurred as waves propagating into a large area. In visual cortex, spontaneous population activity is organized into patterns similar to orientation columns (Kenet and others 2003).

Propagating Waves versus Functional Maps

At first glance, the observation of propagating waves during cortical processing contradicts the concept of topographical arrangement of cortical functions. The concept of topographic maps was introduced very early by evoked potentials (Woolsey and others 1942) and later developed into the concept of cortical columns (Powell and Mountcastle 1959; Hubel and Wiesel 1962). In the visual system, ocular dominance columns, orientation columns, and other functional structures emerge in the visual cortex and can be identified by electrophysiology and intrinsic optical imaging. Given that these columns are a robust phenomenon under these other experimental conditions, why do we observe something different with VSD imaging? This disagreement may be explained in several aspects.

First, propagating waves are initiated from the site of thalamic afferents and propagate to surrounding areas (Figs. 6A, 8A). Thus, functional maps on cortex can be obtained with VSD imaging by labeling the wave initiation sites under different stimuli. This is true in visual (Xu and others 2007), barrel (Ferezou and others 2007; Lippert and others 2007), and auditory cortices (Song and others 2006).

Second, functional maps in intrinsic imaging are usually generated by differential images, that is, images recorded under one stimulus condition are subtracted by that of another stimulus condition. Propagating waves, in contrast, are seen on single presentations of the stimulus. If multiple trials of VSD data are properly averaged, and differential imaging is applied, functional maps can also be generated (Fig. 6B, C). Cortical activity comprises activity of cortical origin and activity that is driven by the thalamus. Maps and other static functional organizations are more relevant to the thalamic driven activity, whereas propagating waves are more related to the dynamics originating in the cortex. Arieli and others (1996) reported that 85% of the variations in the visually evoked activity are of cortical origin. Averaging triggered by stimulus will emphasize thalamic driven components while removing the dynamical components that are not correlated to the stimulus (Arieli and others 1996; Xu and others 2007).

The third issue is the signal amplitude and threshold for mapping. Functional maps usually plot amplitude distribution over area, emphasizing amplitude information while disregarding temporal development of the activity. On the other hand, propagating waves emphasize the time course for the activity to emerge at a given location, with less emphasis on the signal amplitude. Benucci and others (2007) observed maps of orientation preference and retinotopy by measuring the amplitude of the second harmonic (VSD signals oscillating at twice of the modulation frequency), while at the same time observing propagating waves by measuring the phase of the second harmonic. In both visual and auditory cortex, signal amplitude is highest at the center of the cortical retinotopic/whisker representation and lower in other areas the activity spreads to (Grinvald and others 1994; Frostig 2006; Takagaki and others 2008). When a high threshold is used to process the imaging, a retinotopic or a whisker barrel map can be obtained; by lowering the threshold, one can obtain a larger active area extending to a large fraction of primary visual or the barrel cortex (Grinvald and others 1994; Slovin and others 2002; Roland and others 2006; Sharon and others 2007).

The fourth issue is the nonlinear relationship between stimulus intensity and spatial distribution of evoked cortical activity. Petersen, Grinvald, and others (2003) showed that small stimulus to the whisker only causes localized response around the corresponding barrel (localized at the map structure), but stronger stimulus causes a propagating wave spreading in a large area in layers II–III.

Future Studies

Although almost every sensory cortical process examined by VSD imaging or electrode arrays has revealed propagating waves, the connection between the spatiotemporal pattern and the function of the cortex is still missing. During sensory-evoked waves in rodent barrel cortex, neurons outside the correspondent barrel are depolarized to 5 to 10 mV from resting with an elevated spiking rate (Moore and Nelson 1998; Zhu and Connors 1999; Petersen, Hahn, and others 2003). In the visual cortex, the wave significantly increases the firing rate outside the corresponding retinotopic site (Eriksson and Roland 2006; Roland and others 2006), and similar facilitation of spiking may also happen in other cortices during sensory processing. However, it remains to be explored whether such effects contribute to cortical processing and not an epiphenomenon.

Future studies are needed to test if evoked waves are necessary for a cortical function. A direct test would be to apply cortical microstimulation at the specific timing and location, and to examine if the stimulus can disturb the wave patterns and alter the cortical function in a congruent manner. To understand how a wave is involved in a sensory function, one would examine the correlation between patterns of stimulation and evoked waves. Such correlation may reside in the fine structures of the waves that have much lower amplitude than the waves we observed, so high dynamic range imaging devices for resolving fractional light changes of 10⁻⁴ may be essential for these studies. Interactions between propagating waves and anatomical/functional domains would be an interesting topic as well. Waves may change speed or direction when passing orientation columns, area borders, or other functional domains identified by fast Fourier transform intrinsic imaging (Kalatsky and Stryker 2003).

Conclusions: A Tool for Examining Cortical “Swarm Intelligence”?

Waves in the cortex are an emergent behavior of millions to billions of cortical neurons. Individual neurons involved in the wave may have neither control of the global spatiotemporal patterns nor knowledge of the patterns they are generating. The scenario is analogous to the construction of a “cathedral” mound by a termite colony. Although such a cathedral mound has important functions for the survival of the colony, none of the individuals in the colony knows the architectural design of the mound. Individual animals only follow local rules of interaction among fellows to carry soil and deposit it on the mound, bit by bit. Similarly, wave patterns may be highly organized but do not need a conductor or a cellular organizer. Models with identical neurons and defined local rules are fully capable of generating spiral and other wave patterns (Wilson and Cowan 1972, 1973; Pinto and Ermentrout 2001; Huang and others 2004). Following this line of thought, one may speculate that large-scale cortical neuronal events such as a sensory perception, thought, and planning of movements may also be emergent behaviors of the cortex without explicit “super neurons” to organize the overall activity. Although studying individual neurons and interactions among them provide the basic information on which the emergent functions are based, studying wave patterns, as examining the macrostructure of a termite mound, may provide an approach to understand the “swarm intelligence” of cortical neurons.