Methods for aligning and for averaging 3D volumes with missing data

Abstract

The visibility and resolution of a tomographic reconstruction containing multiple copies of discrete particles can be enhanced by averaging subtomograms after they are corrected aligned. However, the “missing wedge” in electron tomography can easily lead to erroneous alignment. We have explored a Fourier space cross-correlation method with a proper weighting scheme to align and average different sets of volumetric data, each of which has different missing data due to the limited specimen tilts. This approach depends neither on a preexisting template, nor an exact knowledge of the geometry, orientation, or amount of the missing data. This paper introduces a procedure where the missing data might be gradually “filled in” by consecutively aligning and averaging volumes with different orientations of their missing data. We have validated these techniques by a set of simulated data with various symmetries and extent of missing data. We have also successfully applied these procedures to experimental cryo-electron tomographic data (Chang et al., 2007; Schmid et al., 2006).

Introduction

After completing a tomographic reconstruction, it is often feasible and desirable to align and average similar objects that occur in the reconstructed volume. Cryo-electron tomograms that contain multiple copies of discrete macromolecular assemblies can be used to develop such a 3D average. For the case where the composition is known and 3D models are created or are available, as described below, for use as templates, procedures have been developed and applied to do this. However, there are circumstances where the size, shape and/or symmetry of the objects are not known a priori, and it would be advantageous to have a method that does not need a starting template. Such a method would involve all-vs.-all comparisons of the 3D objects against each other, the criterion for choosing both the correct orientation and the best-matching pairs of particles usually being the cross-correlation peak height. Therefore the critical requirement for such a method to work is that 3D volumes extracted from the tomogram must be able to be aligned properly to each other. This study investigates the effect of symmetry, relative orientations and completeness of the data in Fourier space on the feasibility of aligning objects to each other. This method has been applied to classify, align and average subvolumes that turned out to be icosahedral particles which varied in size (Schmid et al., 2006).

Because a tilt angle range of ±90° cannot be achieved in the electron microscope, central sections in Fourier space for tilts higher than 60-70° are missing, leading to the problem commonly referred to as the “missing wedge” in Fourier space (Hoppe and Hegerl, 1980). After extraction of 3D subvolumes from the tomogram and before applying any rotations, the orientations of the missing wedges in Fourier space are identical for each particle/volume. However, the orientations of the particles themselves are unknown with respect to each other and must be searched for in 3D rotation space. Because of the effect of the missing wedge, the cross-correlation map may merely lead to the alignment of the two missing wedges to each other, which is certainly not correct. This problem is not as severe in cases where an isotropic starting template is used for 3D alignment (Walz et al., 1997), although accounting for the missing wedge in the data to be aligned is still important (Frangakis et al., 2002). Here “isotropic” is used to refer to a template whose resolution is similar in all directions. The template may be based on a higher resolution structure (Bohm et al., 2000; Frangakis et al., 2002), a rotational (usually cylindrical) average of the particles (Beck et al., 2004; Zanetti et al., 2006; Zhu et al., 2006), a simple object like a cylinder (Nickell et al., 2007), or on an arbitrarily chosen example from the data set (Murphy et al., 2006). The starting orientation may also be estimated (Forster et al., 2005). However, in the case of the carboxysome, for instance, it was not possible to postulate any starting model, because the size and symmetry of the particle were not known a priori. The method described here is applicable without the use of a preexisting model of the computationally extracted subvolume from the tomogram and thus can be a general solution to post-tomographic averaging.

In addition, the proper scaling of these aligned 3D volumes during averaging should also take into account the fact that some data from the aligned particles is missing. In real space, the missing data is convoluted with the genuine data, but in Fourier space, they are separable. A weighting scheme is proposed for 3D volume averaging.

Examples used

To illustrate and test this method, we are using simulated data at known orientations with varying amounts of missing data. Our purpose is to specifically investigate the effect that the size of the missing data wedge, the starting orientations of the particles and the symmetry have on structure alignment for tomography.

Our data includes an icosahedral herpesvirus pentonless nucleocapsid map (EMD-1305) (Chang et al., 2007), a d7 symmetry GroEL map (EMD-1080)(Ludtke et al., 2001), and a c1 symmetry ribosome map (EMD-1003)(Gabashvili et al., 2000). These test cases represent macromolecular complexes with different symmetries. All were low-pass filtered to 40Å nominal resolution. The herpes capsid map was 90³ pixels at 16.2Å/pixel. The GroEL map was resampled to 44³ pixels at 6.1Å/pixel, and the ribosome map was resampled to 32³ pixels at 5.9Å/pixel. Four orientations of the GroEL and ribosome were used (three mutually perpendicular orientations, and one at 50°). For the herpes case, two views, a 5-fold along z and a 3-fold along z, were tested.

We then created missing wedges in the Fourier transforms of these 3D maps, centered about the z axis for each orientation of the maps, varying from 0 to 50% missing data, equivalent to tilt series of ±90° (0% missing data) down to ±45° (50% missing data).

The alignment problem and our solution

As one of a pair of 3D volumes represented in Fourier space, both containing a missing wedge, is rotated against the other in the orientation cross-correlation search, and one volume is multiplied by the complex conjugate of the other, zeros are generated. They occur when the missing-data region for one of the particles is multiplied by data or zeros in the other particle and vice versa, and the number of such zeros changes at each rotation angle in the search. This is shown schematically in Figure 1. The fraction of zero data has a profound effect on the peak height of a correlation map as shown in Figure 2. If we renormalize the cross-correlation peak at each orientation by a factor of 1/(fraction of the non-zero data), we restore the relative peak height to approximately the value it had with no missing data (Figure 2). Of course, the result of the correction depends on what data was zeroed, which will vary depending on the starting orientations of the particles. This is illustrated in Figure 3 and analyzed further in the Discussion, but Figure 2 suggests that the volume-fraction of non-zero data appears to be an acceptable approximation. It also has the advantage that it is a quick and easy calculation to perform.

Figure 1.

Cartoon showing the relationships of the missing wedges of two particles in Fourier space. Before the orientation search (top row), the missing wedges are aligned with maximum overlap. As one particle is rotated with respect to the other (bottom row), zeros in either Fourier transform will yield zeros in the complex product.

Figure 2.

The dotted line shows the averaged correlation peak for the herpes capsid in both starting orientations as a function of missing data when the missing data is not taken into account. The peak height is diminished with increasing amount of missing wedge data. The solid line shows the averaged correlation with our compensation for the missing data. The compensation is not perfect but reduces the effect of the missing wedge to a large extent.

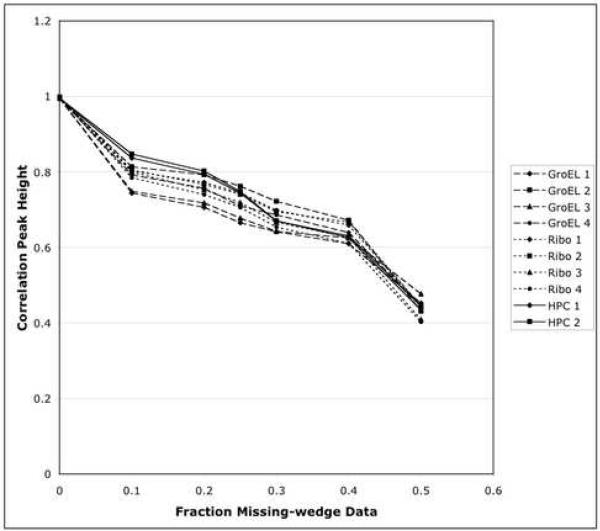
Figure 3.

Plot of cross-correlation peak height as a function of fraction of missing data, as in Figure 2, except that all the data used for this study is plotted separately, including all four starting orientations of GroEL (dashed lines with different symbols), all four orientations of the ribosome (dotted lines with different symbols), and both orientations of the icosahedral capsid (solid lines with different symbols).

Averaging in Fourier Space

Our approach was simply to amplitude-weight the amplitude sum for the real and imaginary parts of the Fourier voxels when averaging two or more rotationally and translationally aligned 3D volumes together.

$$A_t=\frac{1}{{\mathit{amp}}_t}\underset{i}{\Sigma }{A_i}^{\ast }{\mathit{amp}}_i$$

and

$$B_t=\frac{1}{{\mathit{amp}}_t}\underset{i}{\Sigma }{B_i}^{\ast }{\mathit{amp}}_i$$

for the real and imaginary terms, respectively.

Weak or zero amplitudes for a voxel in any particle will contribute less to the weighted average for that voxel; conversely, equal amplitudes will contribute equally. One could explicitly determine how many particle images contribute to a voxel (Walz et al., 1997). However, to do this they applied a matrix transformation to each of the raw 2D particle images in each tilt view according to their respective orientations, then a new 3D volume was computed from the re-oriented 2D particle images. However, our method of averaging automatically takes into account the weighting due to missing vs. non-missing data

Results

There is a detrimental effect of the missing wedge in the alignment of two particles with different orientations, which is mitigated by our compensation detailed above. We searched for the orientation of one map against its rotated version with the same missing wedge amount, using a search step of 5° (for the virus capsid) or 10° (for GroEL and ribosome).

The icosahedral case

For the icosahedral case, to rotate our 3-fold orientation to the 5-fold, the correct solution is <37.72°, 18°, −18°> or one rotated by 120°. The Euler angles that yielded the highest cross-correlation values are shown in Table I.

Table I.

Results of orientation search of herpesvirus pentonless capsid map with 3-fold vertical against map with 5-fold vertical, with different amounts of missing data in each map.

Fraction missing	Tilt Series equivalent	Ignoring effect of missing wedge	Accounting for missing wedge
.00	±90.0°	40, 20, −20	40, 20, −20
.05	±85.5°	40, 20, −20	40, 20, −20
.10	±81.0°	40, 20, −20	40, 20, −20
.15	±76.5°	40, 20, −20	40, 20, −20
.20	±72.0°	40, 20, −20	35, −105, 125
.25	±67.5°	5, 20, −20	40, 15, −15
.30	±63.0°	5, 15, −15	35, 20, −20
.35	±58.5°	5, 15, −15	35, 20, −20
.40	±54.0°	5, 15, −15	40, 20, −20
.45	±49.5°	5, 15, −15	15, 75, −90
.50	±45.0°	5, 15, −15	10, −60, 50

With no compensation for the missing wedge, the point at which the correct alignment is lost in the cross-correlation search occurs at 25% missing data, equivalent to a tilt series of ±67.5°. With larger missing data, corresponding to lower tilt angle sampling during data collection, the correct orientation does not appear within the 10 highest values (not shown). Our compensation, on the other hand, fails only for a tilt series of less than ±49.5°, and even then, the correct orientation is still within the 10 highest peaks (not shown). The alignments shown are accurate to within the search step size (5°). This simulates the result of a coarse search, which could be refined to yield a more nearly correct orientation with a finer step size near this orientation.

GroEL and Ribosome Cases

In the case of lower symmetry, the alignments were found to be less sensitive to the missing wedge (Table II and Supplemental Material), though most searches failed to find a correct orientation when the missing wedge was 50% (equivalent to a ±45° tilt series). However, for some starting orientations of the GroEL particles (Table II), the search without compensation failed for fractions of the missing wedge which are relevant to real-world situations (±63°). Our compensation was able to find an orientation within 10° of the true orientation in this case.

Table II.

Results of orientation search of GroEL map with 7-fold vertical against map with 7-fold horizonal^*, with different amounts of missing data in each map.

Fraction missing	Tilt Series equivalent	Ignoring effect of missing wedge	Accounting for missing wedge
.00	±90.0°	90, −180, 180	90, −180, 180
.10	±81.0°	90, −180, 180	90, −180, 130
.20	±72.0°	90, −180, 280	90, 0, 0
.25	±67.5°	90, −180, 280	90, −170, 10
.30	±63.0°	0, 0, 90	80, 0, −150
.40	±54.0°	0, 0, 90	80, 170, −40
.50	±45.0°	10, 0, −180	20, 40, −60

^*orientation searches for 5 other different pairs of starting orientations of GroEL, and results for all 6 ribosome orientation searches, are in Supplementary Data

Averaging of aligned particles

Figure 4a-d shows the rotated and aligned GroEL particles. The distortions due to the different orientations of the missing wedge are obvious. Figure 4e shows the real-space average of the 4 particles. The residual anisotropic distribution of amplitudes in Fourier space is convoluted into this average, and the average lacks the symmetry of the starting model. Our amplitude-weighted amplitude summation in Fourier space (Figure 4f) minimizes this anisotropy.

Figure 4.

Averaging particles with missing data.

(a-d) particles with missing wedges of 40% along their original z axes, as described in the text, but here (b), (c) and (d) are rotated correctly with respect to (a). (e), particles (a-d) averaged in real space. (f) particles (a-d) averaging with amplitude weighting in Fourier space as described in the text.

Discussion

A major issue impacting the general applicability of our approach is whether the cross-correlation peak heights properly track with the missing volume. In Figure 3, the correlation peak height is plotted against the fraction of missing wedge data for all the molecules in every orientation used in this study. In this plot, the herpesvirus icosahedral capsid, the GroEL d7-symmetry particle and the asymmetric ribosome are denoted with solid, dotted and dashed lines, respectively, and the different starting orientations of the particles have different symbols. All the plots reveal a decrease in peak height as the fraction of missing data increases. It should be noted that even for a missing wedge of, for example, only 20%, for some orientations during an orientation search, the data missing from one or the other subvolume would double that value, to 40%. The solid lines representing herpesvirus capsid have very similar falloffs in their two extreme orientations (5-fold along z and 3-fold along z). Similarly, the dotted lines for the 4 orientations of the ribosome closely follow each other. This indicates the roughly isotropic nature of the power spectrum for these two cases. For the GroEL (dashed lines), the anisotropy is more pronounced, and the lines are more separated. However, even in this case, for extremely different orientations (mutually perpendicular), the maximum difference in peak height for a particular fraction of missing data is less than 10%. This is much smaller than the potential error of up to 50% seen in this plot and in Figure 2 if the missing wedge is not compensated at all. Indeed, in the case of the particle at 50° (dashed line, circle symbol), the line is intermediate between the extremes. This suggests that aligning, averaging and refining the alignment of enough particles with different orientations will lead to convergence of this process, as we observed previously (Schmid et al., 2006).

Somewhat surprisingly, we found that in general the orientation search involving lower symmetry particles like GroEL and ribosomes were less sensitive to the missing wedge. In real space, this can be expressed in terms of the probability of chance (but incorrect) overlap of density features. The reason may lie more in the morphology of different specimens than in their symmetry per se. The herpesvirus capsid has three types of morphological units (hexons) per asymmetric unit that can give chance coincidences of superposition for this roughly spherical particle. They could be wrongly chosen (Table I) as being the best in orientation searches that did not properly compensate for the missing wedge because of the effect shown schematically in Figure 1 and quantitatively in Figure 2. The objects of lower symmetry may also have less shape similarity in their asymmetric units, and thus display a characteristic density pattern (and thus the corresponding amplitudes and phases in Fourier space) which make them more distinctive for a correct orientation identification with any reasonable cross-correlation result. However, chance superposition of densities can still occur, and lead to wrong orientations, even for particles such as GroEL. In this case the missing wedge compensation would help finding the correct orientation.

Our consecutive and iterative procedure involves averaging the best-correlating pairs of volumes, then searching with this average against the remaining particles and other independent averages. This procedure, which was followed in our classification, alignment and averaging of the carboxysome (Schmid et al., 2006), would gradually fill in the missing wedge as more and more particles are included in the average, and the amount of compensation would consequently become smaller. It should be emphasized that it is important to properly weight the particle averages (Figure 4), emphasizing the same point as Figure 4 of (Walz et al., 1997), especially at the early stages when there are only a few particles in the average.

It should also be mentioned that the “missing wedge” is not strictly empty. We used the IMOD (Kremer et al., 1996) reconstruction package, which employs back projection to calculate the reconstruction for tomography of the carboxysomes (Schmid et al., 2006) so the Fourier space volume occupied by the missing wedge is relatively empty to start with. However, spherical masking of some kind is essential to prevent orientation-dependent artifacts from the “corners” of the rotated cubic volumes. The non-linear operations of masking or other filters that might be applied to the 3D subvolumes before mutual alignment can cause Fourier space components to “leak” into the missing wedge volume.

Therefore a threshold is used to define what constitutes a “zero” amplitude in the complex product. The threshold depends on the scaling and normalization of the maps and any filtering applied to the volumes, and it should be adjusted so that a search which covers the entire volume of rotation space leads to a reasonable ratio between the largest and the smallest number of non-zeros, which corresponds, respectively, to the biggest and smallest overlap of the missing wedges. For a tilt series of ±72° this ratio should be about 1.33. A tilt series of ±60° would have a ratio of about 2.0. The threshold for normalized maps ranges up to 0.001. Finally, it should be noted that there is “missing data” between every image in a tilt series beyond a certain resolution because of the tilt interval (usually 1-2°, in addition to the more obvious “missing wedge”. Usually, the resolution is purposely limited to avoid dealing with this issue, but our compensation would consider this kind of “missing data” the same as it does the missing wedge.

Different weighting schemes have been used to account for the missing wedge. In one, (Frangakis et al., 2002), the weight is taken to be the product of the standard deviations of the two maps to be compared. It should be pointed out that the total power (intensity) in the complex product of the two maps is exactly equivalent to the product of the standard deviations of the two maps when the “intersecting area” (the volume for which there is data in both maps) is taken into account. This equivalence can be rationalized as follows.

Every Fourier component naturally gives rise to a cosine wave in the image. The standard deviation of a cosine wave is Amp*sin(45°). Its variance is Amp²/2. So the variance in real (or in this case cross-correlation) space is proportional to Intensity (or in this case the complex product) for that Fourier component. Since all Fourier terms are independent, any equivalent total sum of intensities (whichever Fourier terms they come from, except the F000 term) would give rise to the same variance in the image(s).

Since our method is exploring all orientations (the correct one and all possible incorrect ones), the power in the complex product would fluctuate accordingly. What is incontrovertible, however, is that the missing wedge (zero) in the Fourier transform of either map would produce a zero in the complex product. Thus to correct for the missing wedges per se, we have chosen to “count” the zeros.

Our approach is much simpler than dealing with the standard deviations in the two maps. One would have to generate the standard deviation of the “intersecting volume” for both subvolumes, where each subvolume starts out having a missing wedge that is increased by the missing wedge from the other volume. This is not a trivial calculation, and it must be repeated for both maps for each step in the orientation search of one volume with respect to the other. In our approach, the simplicity of counting the zeros (or rather the “non-zeros”) is that it automatically defines the proper intersecting volume of the cross-correlation complex product.

Conclusion

A tomographic reconstruction of the contents of a cell, for instance, will contain an unknown number of unknown macromolecular assemblies. If 3D models of all the expected assemblies are not available (Bohm et al., 2000), it will be difficult to classify, align and average the different objects present in the tomographic volume using template-based schemes. The significance of our approach is that it can provide an averaged model or models not biased in any way, because it aligns and averages the 3D volumes directly to each other. Finally, this approach has been demonstrated to be robust and practical in our studies of the carboxysome and herpesvirus capsid tomograms.

The software is available at http://ncmi.bcm.edu