Catalytic Mechanism and Performance of Computationally Designed Enzymes for Kemp Elimination

Abstract

A series of enzymes for Kemp elimination of 5-nitrobenzisoxazole have been recently designed and tested. In conjunction with the design process, extensive computational analyses were carried out to evaluate the potential performance of four of the designs, as presented here. The enzyme-catalyzed reactions were modeled using mixed quantum and molecular mechanics (QM/MM) calculations in the context of Monte Carlo (MC) statistical mechanics simulations. Free energy perturbation (FEP) calculations were used to characterize the free-energy surfaces for the catalyzed reactions as well as for reference processes in water. The simulations yielded detailed information about the catalytic mechanisms, activation barriers, and structural evolution of the active sites over the course of the reactions. The catalytic mechanism for the designed enzymes KE07, KE10(V131N), and KE15 was found to be concerted with proton transfer generally more advanced in the transition state than breaking of the isoxazolyl N-O bond. On the basis of the free-energy results, all three enzymes were anticipated to be active. Ideas for further improvement of the enzyme designs also emerged. On the technical side, the synergy of parallel QM/MM and experimental efforts in the design of artificial enzymes is well illustrated.

Introduction

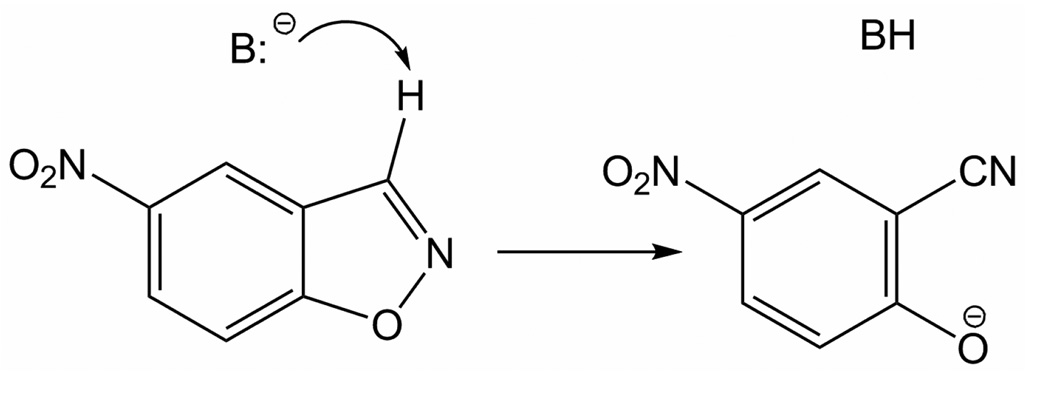
Theoretical and experimental efforts are being directed towards the design of artificial enzymes.^1–11 The challenge is great in trying to approach the performance of biological catalysts in view of their specificity and high activity under mild conditions.¹² It is, therefore, inviting to mimic strategies that Nature employs and, especially, to apply them in the design of catalysts for important organic reactions that Nature seems to have overlooked. In the course of this pursuit, an efficient enzyme design protocol has been recently reported¹¹ and it was employed to design artificial enzymes for the Kemp elimination¹³ of 5-nitrobenzisoxazole (Scheme 1).¹ Designed enzymes were synthesized and tested experimentally, and yielded k_cat/k_uncat values in the 10² – 10⁵ range; subsequent in vitro evolution of one of the designs provided a greater than 200-fold increase in k_cat/K_M and a maximal k_cat/k_uncat of 1.2 × 10⁶. The simplicity of the Kemp elimination and its sensitivity to medium effects have made it the target for numerous prior efforts at catalyst discovery, as summarized elsewhere.^14a So far, catalytic antibodies have been the only alternatives to achieve rate accelerations in the million-fold range.^14b

Scheme 1.

Kemp elimination of 5-nitrobenzisoxazole.

Desirable features in the design of catalysts for the Kemp elimination have been elucidated previously with the aid of ab initio quantum mechanical calculations.¹⁵ The primary requirement is a catalytic base for the proton abstraction. For this role, Röthlisberger et al. chose Asp, Glu or an unprotonated His;¹ the His can also be coupled with an Asp or Glu in a catalytic dyad, which allows tuning of the pK_a and, thus, protonation state of the His. An additional feature explored in some enzyme designs was the inclusion of residues with side-chain groups capable of hydrogen bonding to the isoxazolyl oxygen atom of the substrate, specifically, Ser, Lys, and Tyr. The intention was to stabilize the evolving phenolate ion or even to protonate it in a relatively hydrophobic active site. Finally, residues were added to form π-stacking interactions with the substrate. Their intended tasks were to orient properly the substrate and catalytic base and to stabilize the evolving negative charge through π-delocalization or polarization. The remainder of the enzyme needs to provide an orientational match for projection of the side chains in the designed active sites; TIM barrels emerged as the preferred scaffolds.¹

So far, direct information on the catalytic mechanism for these enzymes is lacking. Base-catalyzed Kemp eliminations in aqueous solution are well established as E2 reactions with concerted proton transfer and N-O bond cleavage.¹³ The product 2-cyano-4-nitrophenolate ion is stable in water with a pK_a of 4.1 for its conjugate acid.^13a Fundamental mechanistic questions are whether this concerted pathway is also followed in the designed enzymes and the details of the involvement of active-site residues. A mechanistic spectrum can be imagined depending on the order of proton transfer, N-O bond cleavage, and possible protonation of the phenolate or isoxazole. Formation of an intermediate from the initial proton transfer is certainly a possibility.¹³ Indeed, variation of the catalytic residues could lead to multiple mechanisms ranging from base-catalyzed to acid-catalyzed.¹⁵ It is also not known how the positions and conformations of the residues in the active sites evolve during the reactions, and whether they actually perform the desired catalytic functions. The locations and possible participation of water molecules are additional points to address.

The present quantum and molecular mechanics (QM/MM) investigations are directed at elucidating these issues, providing deeper understanding of the enzyme structure-function relationships, and giving guidance for further rational enzyme design and optimization of catalytic performance. Specifically, Kemp eliminations of 5-nitrobenzisoxazole catalyzed by four designed enzymes in explicit water were investigated using QM/MM Monte Carlo (MC) and free energy perturbation (FEP) methodologies. The mechanistic details and energetics of the enzymatic reactions are elucidated, and comparison is made to results for the reference reaction in water.

Methods

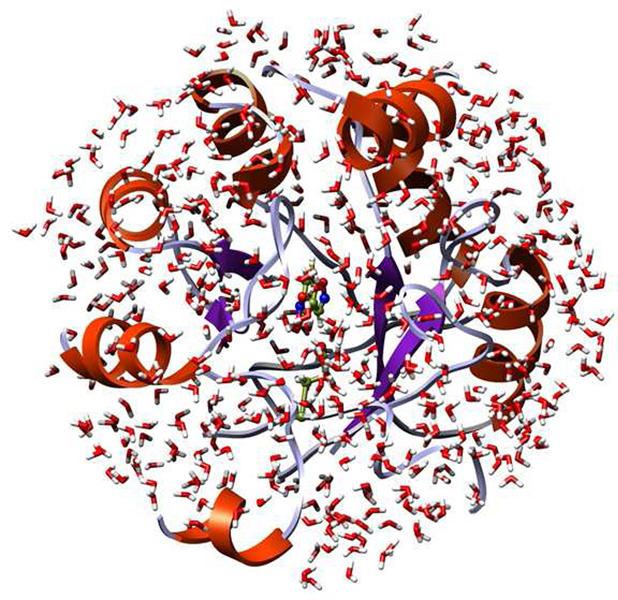
Initial coordinates for all proteins were obtained from the model building of Röthlisberger et al. using the Rosetta program.¹ In preparation for the MC simulations, the complexes with 5-nitrobenzisoxazole were truncated such that only protein residues with any atom within ca. 15 Å of the substrate were retained. For the four cases, 188–253 residues were retained out of a total of 247 or 253. The overall charge was set to zero via neutralization of residues remote from the active site. The substrate was initially positioned with the hydrogen on C3 oriented towards the putative base, as in the original design.¹ A short, 50-step conjugate gradient relaxation was performed for each system. Subsequently, a 20-Å cap containing TIP4P water molecules¹⁶ was centered on the substrate, and ca. 500 water molecules remained after removal of ones with their oxygen atom within 2.5 Å of any non-hydrogen atom of the complex. Figure 1 illustrates a system prepared in this way.

Figure 1.

A truncated protein-substrate complex with ca. 500 TIP4P water molecules; the QM-region (dark green) consists of the side chain of the catalytic base and the substrate. The nearest ca. 200 residues of the protein and the solvent form the MM-region.

Initial simulations for the systems were carried out using QM/MM/MC statistical mechanics calculations, as implemented in the MCPRO program.¹⁷ Technically similar studies of reactions catalyzed by macrophomate synthase and fatty acid amide hydrolase have been previously reported.^{18, 19a} The simulations consisted of 5 × 10⁶ configurations of solvent equilibration, 10 × 10⁶ configurations of full equilibration, and 35 × 10⁶ configurations of averaging at 25 °C. The protein backbone was held fixed, while the side chains, substrate and water were sampled. All degrees of freedom for the substrate were variable, bond angles and dihedral angles were sampled for the side chains, and the TIP4P water molecules could translate and rotate. The final configurations were then used as starting points for the mechanistic investigations. Some MC simulations were carried out with the protein backbone sampled using a concerted rotation algorithm;²⁰ however, this resulted in rmsd’s of only ca. 0.15 Å from the starting backbone structure.

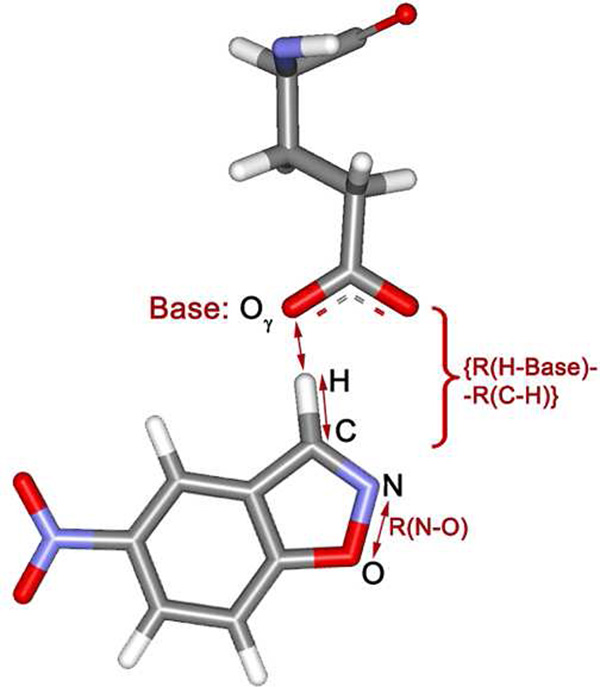
Potential of mean force (PMF) calculations were carried out for the Kemp eliminations by perturbing along reaction coordinates using MC/FEP calculations. Two distances were chosen as reaction coordinates in all cases, and two-dimensional free-energy maps were created. The increment between simulations was 0.04 Å for preliminary scanning, and 0.02 Å for refinement near stationary points. Double-wide sampling was used so two free-energy changes were obtained for each window by incrementing in both the forward and reverse directions. One reaction coordinate was the length of the breaking C-N bond. The reaction coordinate for the hydrogen transfer was chosen as the difference between the lengths of the forming and breaking bonds to the hydrogen, {R(H-Base) − R(C-H)}, where the sum, {R(H-Base) + R(C-H)}, was fixed at the value obtained in the initial QM/MM MC simulation (Figure 2). The combined reaction coordinate for hydrogen transfer reduces the dimensionality for creation of the free-energy surfaces from three to two. The approach has been previously validated; it was shown that the error for the barrier to hydrogen transfer thus obtained is insignificant.¹⁹ In addition, for the hydrogen transfers, the quadrature method of Tubert-Brohman et al.^19a was also followed whereby the free energy changes are fit by cubic polynomials using free-energy derivatives obtained from only five windows of double-wide sampling (i.e., ten free energy changes in all). Analytical integration then yields the free energy profile. This approach was shown to introduce errors in the activation barrier of no greater than 0.5 kcal/mol versus conventional results using 25–30 windows.^19a In the present case, this treatment for hydrogen transfers reduced the computational effort from roughly 36,000 to 7,200 hours for construction of each two-dimensional free energy surface on 3-GHz Pentium processors.

Figure 2.

Choices for the reaction coordinates: R(N-O) and {R(H-Base) − R(C-H)}. An oxygen atom of the ionized Glu plays the role of the base in this case.

In the QM/MM implementation, the energy of the QM region was computed using the PDDG/PM3 semiempirical molecular orbital method.²¹ PDDG/PM3 has been extensively tested for gas-phase structures and energetics,²¹ and it has performed well in QM/MM/MC studies for numerous pericyclic,²² substitution,²³ and elimination reactions in solution.^19b,24,25 Notably, the previous study of Kemp eliminations of benzisoxazole-3-carboxylates yielded free energies of activation within 2–3 kcal/mol of experimental data in water and methanol, and revealed the importance of ion-pairing in aprotic media.²⁵ In the present study, the QM-region consisted of the substrate, 5-nitrobenzisoxazole, and the side chain of the putative base, Glu or Asp (Figure 1). The linking hydrogen atom for the side chain was made coincident with C_α of the basic residue.^18,19a The energy of the QM region was computed for every attempted move of the solute, i.e., every 10 configurations. The rest of the system was treated using the OPSL-AA force field.²⁶ To compute the electrostatic part of the interaction energy between the QM and MM regions, CM3P atomic charges were used for the QM atoms and the MM charges for the MM atoms.²⁷ The CM3P charges were unscaled as the QM region had a net charge of −1 for all cases examined here.²⁸ Interactions were truncated using a 10-Å residue-based cutoff based on distances between non-hydrogen atoms. Each FEP window entailed 5 × 10⁶ configurations of solvent equilibration, 10 × 10⁶ configurations of full equilibration, and 25 × 10⁶ configurations of averaging. At each point on the free energy surface, configurations from the Monte Carlo runs were saved. They are used to analyze and illustrate the structural variations along the reaction paths.

Results

The naming of the enzymes is adopted from Röthlisberger et al;¹ KE07, KE10(V131N), KE15, and KE16 are the artificial enzymes considered here. The experimental kinetic parameters and the choices for the catalytically important residues are listed in Table 1. KE10 in reference ¹ is the Asn131Val variant of the enzyme studied here; it is more active than KE10(V131N) with a k_cat/K_M of 51.6 ± 4.0 s⁻¹M⁻¹.¹ In all cases, Glu or Asp is the catalytic base and a Trp or Tyr is used for π-interactions; three of the designs include a Lys or Asn to hydrogen bond with the isoxazolyl oxygen of the substrate and possibly stabilize the evolving phenolate ion. The present computations were completed before the experimental kinetic parameters were available.

TABLE 1.

Observed Kinetic Parameters and Computed Geometrical Parameters (Å) and Free Energy of Activation (kcal/mol) for the Four Designed Enzymes

design	PDB code	key residuesa	kcat,b s−1	kcat/KM,b s−1M−1	{R(H-base)+ R(C-H)}	R(N-O) in TS	ΔG‡
KE07	1thf	E101, K222, W50	0.018±0.001	12.2±0.1	2.86	1.74	8.1
KE10 (V131N)	1a53	E178, N131, W210	NDc	3.68±0.32	2.78	1.71	13.5
KE16	1thf	D48, K201, Y126	0.006±0.001	13.4±1.4	2.80	NDc	NDc
KE15	1thf	D48, None, Y126	0.022±0.003	35.1±4.8	2.94	1.78	12.3

^aThe key residues are specified in the following order: catalytic base, hydrogen-bond donor, π-stacking residue.

^bFrom Ref. 1

^cNot determined; see text.

KE07

KE07 is one of the earliest designs that was found to be active. Though the present calculations were initiated from the structure generated with Rosetta, a crystal structure, 2rkx in the RCSB Protein Data Bank, was subsequently obtained for it and found to be very close to the computational design.¹ KE07 is based on a TIM-barrel protein fold; the natural enzyme is an imidazoleglycerolphosphate synthase from thermotoga maritima and a crystal structure at 1.45-Å resolution is available in the Protein Data Bank (code: 1thf).²⁹ Glu was incorporated in the binding cavity of the 1thf structure as residue 101 to serve as the catalytic base. Lys222 was provided as the potential hydrogen-bond donor for the isoxazolyl oxygen, and Trp50 was included for π-stacking with the substrate.¹

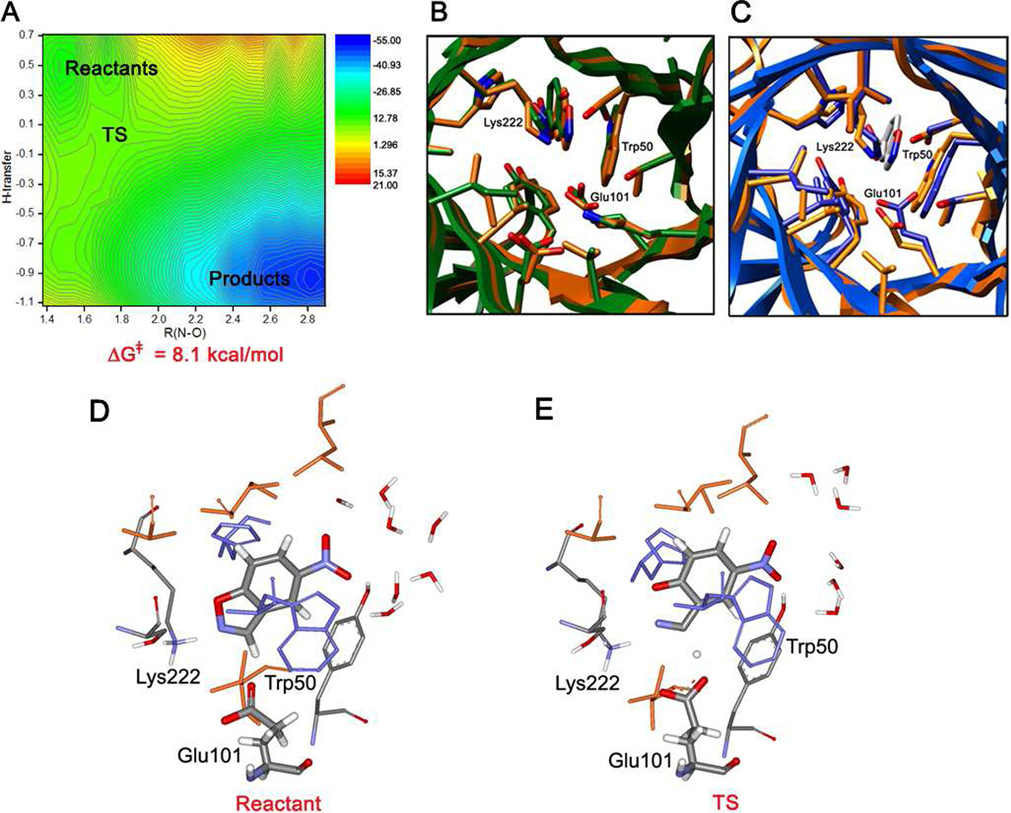
The complex of the protein with the substrate was relaxed in the QM/MM/MC simulations in TIP4P water. Further, using R(N-O) and {R(H-O_γGlu)-R(C-H)} as the two reaction coordinates, a free energy surface for the catalyzed reaction was obtained from FEP calculations. The results are summarized in Figure 3. The two-dimensional map is shown in Figure 3A. Representative configurations corresponding to the stationary points on the surface are shown in Figures 3B–F. From the free-energy map, the reaction is found to follow a single-step, concerted mechanism. However, the reaction pathway is asymmetric; the hydrogen transfer from the substrate to Glu101 is significantly advanced before the N-O bond opening is triggered. At the transition state, TS, the N-O bond has lengthened to 1.74 Å (Table 1); the corresponding computed value for the Kemp decarboxylation of benzisoxazole-3-carboxylate in water was 1.75 Å.²⁵ The prior gas-phase quantum mechanical studies of the elimination reaction of 5-nitrobenzisoxazole with acetate ion also found a relatively early transition state with R(N-O) = 1.81 Ǻ at the B3LYP/6-31+G(d) level.¹⁵

Figure 3.

KE07: (a) Computed two-dimensional free energy map for the catalyzed Kemp elimination. (b) Overlay of the Rosetta designed structure (green) and the QM/MM/MC relaxed structure (orange) for the enzyme-substrate complex. (c) Overlay of the X-ray structure (blue) and QM/MM/MC relaxed structure (orange). (d) Configuration of the binding site with the substrate bound at the end of the QM/MM/MC run for the reactant state. (e) A configuration of the transition state from the QM/MM/MC FEP simulations.

Figures 3b–d show the structure of the initial complex of KE07 with 5-nitrobenzisoxazole, as obtained from the QM/MM/MC relaxation of the structure from Rosetta. In Figures 3b and 3c, it is overlaid with the starting structure from Rosetta and with the crystal structure of KE07,¹ which lacks the substrate. The positioning and conformations of the ligand and the side chains are very similar in both cases. The agreement between the designed and crystallographic results for the backbone is striking; it validates the enzyme design protocol, which is based on point mutations in existing protein folds.¹ Overall, the structural consistency in Figures 3b and 3c supports the utility of both the QM/MM/MC and Rosetta methodologies.

Figure 3d further illustrates the active site in the reactant state at the end of the QM/MM/MC equilibration. In this initial complex, the substrate is in close contact with the catalytic base, Glu101, with R(H-O_Glu101) = 1.65 Å and {R(H-O) + R{C-H)} = 2.86 Å. However, Lys222 forms a hydrogen-bond with the isoxazolyl nitrogen rather than the oxygen, R(H_Lys-N) = 2.26 Å. The orientation of Lys222 is supported by the nearby Ser48, as Lys222 also participates in a hydrogen bond with the oxygen atom of its hydroxyl group. The π-stacking interaction with Trp50 is present, though Trp50 is somewhat tilted away from the substrate and interacts primarily with the substrate’s six-membered ring. No water molecules are found in the active site in the MC simulations. However, the nitro group of the substrate points outward towards the solvent and forms several hydrogen bonds with water molecules. Overall, the interactions found in the binding site at the reactant geometry from the MC simulations are consistent with the desired design¹ with the exception of the detail for Lys222.

Similarly, Figure 3e illustrates a typical configuration from the FEP calculations near the transition state. The transferring H is approximately half-way between the donor and the acceptor, and the N-O bond is stretched to 1.74 Å. Trp50 is π-stacking well with the six-membered ring portion of the substrate. The hydrogen-bond length between an ammonium hydrogen of Lys222 and the isoxazolyl N, 2.25 Å, is still shorter than the distance to the isoxazolyl oxygen, 3.46 Å. This configuration is promoted by the persistent hydrogen bond between Lys222 and the hydroxyl group of Ser48. The contact between Lys222 and the isoxazolyl N may contribute to the observed asymmetry of the reaction mechanism, in which the hydrogen transfer progresses significantly before the N-O bond lengthens. N-O bond cleavage would presumably be better promoted by stabilization of the forming charge on the oxygen. Water remains excluded from the active site in spite of the charge redistribution. In comparing Figure 3d and 3e, it is also noted that catalysis might be improved in a design in which the carboxylate oxygen in the reactant state was better oriented to receive the proton on a syn lone-pair to achieve the stable Z-carboxylic acid conformation.^15a Furthermore, it would be preferable to have the carboxylate group rotated such as to minimize the electrostatic repulsion between the oxygen that does not receive the proton and the isoxazolyl nitrogen (cf. Figure 3 in reference 15b).

For the structure of the product (not illustrated), the positioning of the side chains of KE07 is very similar to that for the transition state according to the FEP calculations. The N-O bond opening and hydrogen transfer are complete, and finally the hydrogen bond with the ammonium group of Lys222 is shifted from the isoxazolyl N to O in response to the charge concentration on the oxygen.

The difference in free energy between the transition state and reactant geometries corresponds to the free energy of activation, ΔG^‡, which is directly related to the rate of the catalyzed reaction, k_cat. From the two-dimensional map in Figure 3a, the computed ΔG^‡ for KE07 is 8.1 kcal/mol; the estimated uncertainty is less than ±1 kcal/mol based on the fluctuations in the averages for the individual FEP windows. As presented below, the corresponding, computed ΔG^‡ for the reference reaction in water with hydroxide ion as the base is 19.8 kcal/mol. Thus, the enzymatic environment is predicted to provide strong catalysis. This assumes that formation of the enzyme-substrate complex is not highly unfavorable, which seems unlikely based on the computed structures, as in Figures 3b–d. The catalytic efficiency, k_cat/K_M, has not been computed owing to the technical challenges for K_M, which requires computation of the absolute free energy of binding for the substrate. However, the computed ΔG^‡ and the one that can be derived from the observed k_cat can be compared. Assuming first-order kinetics for conversion of the enzyme-substrate complex to the product, the observed k_cat of 0.018 s⁻¹ (Table 1) corresponds to a ΔG^‡ of 17.1 kcal/mol. Thus, the computations over-estimated the catalytic prowess of the enzyme, though they clearly made the correct qualitative prediction that KE07 would be a good catalyst for the Kemp elimination. The observed k_cat/k_uncat turned out to be 1.6 × 10⁴.¹ There may be multiple contributors to the discrepancy between the computed ΔG^‡ and the one estimated from the observed k_cat; candidates include the lack of backbone sampling, which may cause the initial state to be too constrained, and standard issues with the QM/MM calculations such as the accuracy of the semiempirical QM and the lack of instantaneous polarization in the MM. Though the present approach has worked well for several solution-phase elimination reactions,^19b,24,25 the enzymatic environment provides greater challenges for configurational sampling and proper representation and treatment of the electrostatic interactions.

KE10(V131N)

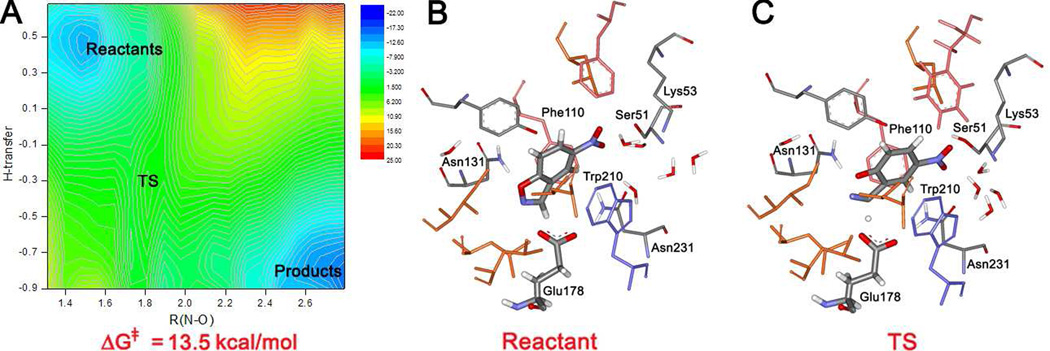
Results are collected for the KE10 variant in Table 1 and Figure 4. The modeling again started from the structure generated with Rosetta. No crystal structures are available for comparison in this and the remaining cases. The design is based on the 1a53 crystal structure for indole-3-glycerolphosphate synthase from sulfolobus solfataricus, which also belongs to the TIM-barrel family.³⁰ In this design, Glu178 is the intended base. It is paired with Asn231 through a hydrogen bond, which promotes proper positioning with respect to the binding cavity and the substrate, though it is expected to weaken the basicity of Glu178. From the initial QM/MM/MC relaxation, the hydrogen-bond contact between the substrate and Glu178 is tight, {R(H-O)+R(C-H)} = 2.78 Å (Figure 4b), and the orientation of the carboxylate group relative to the substrate is ideal.¹⁵ Additionally, a long hydrogen bond is found between the isoxazolyl oxygen of the substrate and the amino group of Asn131 with R(O-HN) = 2.80 Å; we consider strong hydrogen bonds to have R(O-H) or R(N-H) below 2.5 Å. Thus, Asn131 provides some hydrogen-bond donating potential for the evolving phenolate oxygen. Trp210 was included to π-stack with the substrate, and it is positioned in front in Figure 4b. In addition, Phe110 is seen to sandwich the substrate from the back. Both residues are more proximal to the six-membered ring of the substrate than the isoxazole ring. Thus, Phe110 and Trp210 form a slot for the substrate and the catalytic base is well-positioned at the opening at one end of the slot. This critical region of the binding site is densely packed and no water molecules enter it during the MC runs. At the opposite end of the substrate, the nitro group is less solvent-exposed than for KE07; two hydrogen bonds are found between a nitro oxygen and the side-chain functional groups of Ser51 and Lys53 as well as a hydrogen bond with a water molecule.

Figure 4.

KE10(V131N): (a) Computed two-dimensional free energy map for the catalyzed Kemp elimination. (b) Configuration of the binding site with the substrate bound at the end of the QM/MM/MC run for the reactant state. (c) A configuration of the transition state from the QM/MM/MC FEP simulations.

The free-energy map from the MC/FEP simulations for the Kemp elimination catalyzed by KE10(V131N) is shown in Figure 4a. Since the catalytic strategy is similar for KE10 and KE07, it is not surprising that the mechanistic details and free-energy maps are also similar. The reaction proceeds via a concerted mechanism, which is more synchronous than for KE07. As illustrated in Figure 4c, all residues play the desired roles. The Glu178-Asn231 catalytic pair functions properly: the abstracted hydrogen smoothly transfers from the substrate to Glu178 and the hydrogen bond between Glu178 and Asn231 lengthens simultaneously; R(O-HN) averages 1.75, 1.85, and 2.10 Å for the reactant, TS, and product, respectively. Furthermore, the hydrogen bond between the isoxazolyl oxygen and the NH₂ in the side chain of Asn131 shortens as the negative charge increases on the oxygen in progressing to the transition state; R(O-HN) is 2.05 Å in the reactants and 1.92 Å in the TS. Notably, this contact becomes less tight in the product, R(O-HN) = 2.93 Å, owing to geometrical constraints in the binding site that emerge upon fully opening the N-O bond. So, the stabilization provided by Asn131 appears to be greatest for the transition state. This effect, the lack of a proximal ion-pairing partner for the product state, and the stabilization of Glu178 by Asn231 in the reactant state likely contribute to the fact that the computed overall ΔG for the catalytic step with KE10(V131N) is significantly less exergonic than for KE07 (−4.5 vs. −36.3 kcal/mol). In view of this, it would not be surprising if product inhibition is reduced with KE10(V131N). Furthermore, based on the proton-transfer coordinates, the transition state occurs significantly earlier for KE07 than the KE10 variant (Figure 3a and Figure 4a), which may again reflect the greater exergonicity with KE07 and lessened basicity of Glu178.

The computed ΔG^‡ for the reaction with KE10(V131N) from the FEP calculations is 13.5 kcal/mol, which is 5.4 kcal/mol higher than for KE07, but still comfortably lower than for the reference hydroxide-catalyzed reaction. The experimental value of k_cat for KE10(V131N) was not determined; however, k_cat/K_M was found to be a factor of 3.3 lower than for KE07 (Table 1). The present QM/MM MC simulations predict the k_cat ratio to be even smaller, so it is possible that the K_M is smaller with KE10(V131N), i.e., it has better substrate binding. This seems plausible as the substrate in KE10 is less solvent-exposed and more engulfed by the protein including the Phe110-substrate-Trp210 stacking. In any event, the MC/FEP results were correct in predicting that KE10(V131N) would be a successful catalyst for the Kemp elimination, though likely less active than KE07.

KE16

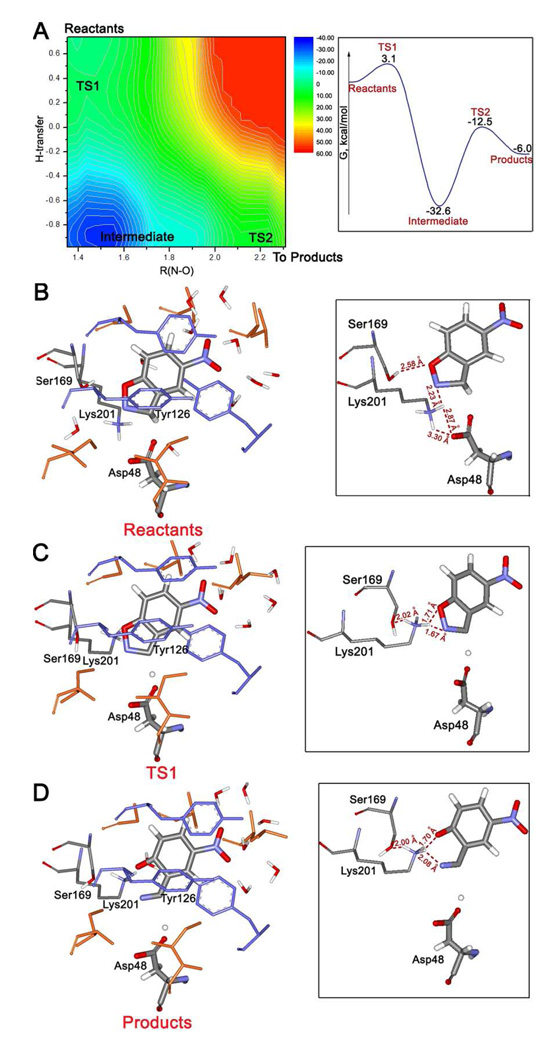
Figure 5 summarizes the results of QM/MM MC simulations for KE16, another artificial enzyme based on the 1thf TIM-barrel protein fold. In comparison to KE07, which used Glu101 as the catalytic base, the base for KE16, Asp48, was installed earlier in the sequence. Lys201 is now introduced to form a hydrogen bond to oxazolyl oxygen of the substrate. Ser169 is another important residue, which can form a hydrogen bond to the ammonium group of Lys201, and Tyr126 is the residue included for π-stacking with the substrate (Figure 5b). There are also additional tyrosines in the binding site, forming parallel and perpendicular π-interactions with Tyr126. The initial QM/MM/MC relaxation of KE16 revealed a design issue, as highlighted in Figure 5b and the inset. Specifically, Lys201 appears to not be functioning as desired; in the reactant state, it participates in a hydrogen bond with the carboxyl group of the catalytic base, Asp48, as well as one with the isoxazolyl nitrogen of the substrate. When the substrate is removed from the binding site and a full QM/MM/MC relaxation is performed on the apo protein, a tight salt bridge between Asp48 and Lys201 arises. This is troublesome since, upon binding, the substrate has to compete with Lys201 for hydrogen-bonding to Asp48. Furthermore, depending on the hydrophobicity of the binding site, full hydrogen transfer might occur yielding the catalytically disabled protonated Asp48 and deprotonated Lys201. Thus, there is uncertainty concerning the protonation states of Asp48 and Lys201 for both the apo protein and substrate-bound complex.

Figure 5.

KE16: (a) computed free-energy data for the catalyzed Kemp elimination, and illustrative QM/MM/MC structures for (b) the reactants, (c) transition state TS1, and (d) the products.

In the event, the QM/MM FEP MC simulations were carried out for KE16 assuming that Asp48 is deprotonated and Lys201 is protonated in the reactant state. Figure 5a shows the FEP map for the Kemp elimination. A different surface is found; instead of a concerted mechanism as in the other cases, the reaction follows a step-wise pathway. The first step is proton abstraction from the substrate with a low barrier, ΔG^‡ = 3.1 kcal/mol. Deprotonated Asp48 can be viewed as ‘hot’ and the transition state (Figure 5c) and the resultant isoxazolyl anion are stabilized by ion-pairing and hydrogen bonds between the ammonium group of Lys201 and both the isoxazolyl nitrogen and oxygen. Further stabilization comes from Lys201 also acting as a hydrogen bond donor to the hydroxyl group of Ser169. The intermediate is in a deep free energy well, in which the proton has transferred, but the N-O bond is still intact. The reaction is completed via ring opening of the isoxazolyl anion through TS2 to yield the product. Overall, the mechanism can be classified as a conjugate E1cB process. The FEP calculations for the second step just used the N-O distance as the reaction coordinate. The two-dimensional free-energy surface in Figure 5a only extends to an N-O distance of 2.3 Å; however, the overall profile is projected in one dimension in the inset. In the product state (Figure 5d), Lys210 has shifted so that its ammonium group is hydrogen-bonded to the phenolate oxygen.

The facile proton transfer from the substrate to Asp48 is the rate-determining step; the elimination step has a high barrier in view of the stability of the intermediate, but TS2 still ends up below the reactant state in free energy. The intermediate is the most stable species in this reaction route and the enzyme efficiency could be adversely affected by trapping in this state. Additional uncertainty arises from again noting that the starting point was deprotonated Asp48 and protonated Lys201. It may be that the true rate-determining step is achievement of this state from the corresponding doubly unionized one. Though in principle this could be addressed by FEP calculations for the Asp to Lys proton transfer, in practice, the results for such processes where two ions are created from two neutral species are prone to large uncertainties associated with the accompanying large changes in the electrostatics, their sensitivity to choices made for the protonation states of all other ionizable residues, and the treatment of long-range interactions. Thus, given the uncertainties, comparisons between the computed activation barrier for the Kemp elimination step and the observed k_cat are unwarranted.

In summary, the computational results indicated that pursuit of KE16 was risky. Experimentally, it turned out that catalytic activity was observed for this design;¹ however, the k_cat and k_cat/k_uncat were only 0.006 s⁻¹ and 5.2 × 10³. The computations suggest that improvement could be sought by repositioning the hydrogen-bond donor so that it is less likely to stabilize the base, Asp48, and more likely to hydrogen bond with the incipient phenolate oxygen.

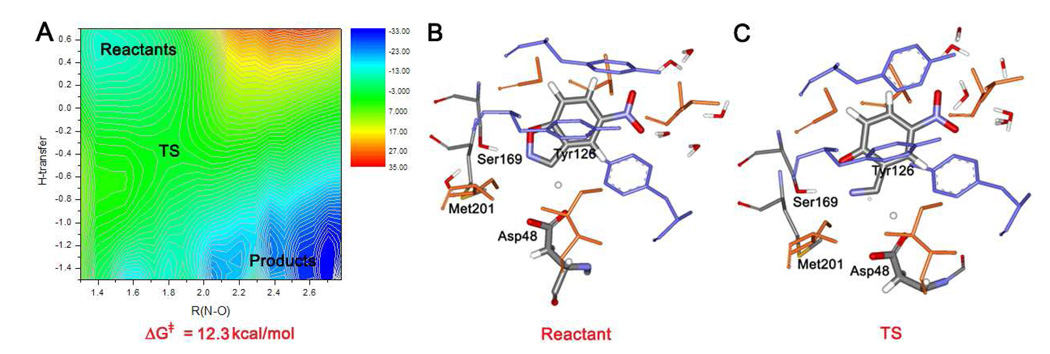
KE15

The repositioning of the hydrogen-bond donor was partially reflected in KE15 (Figure 6). This 1thf-based design is very similar to KE16; Asp48 is retained as the base, but Lys201 is replaced with Met. This eliminates the potentially disadvantageous Asp-Lys interaction, but Met201 does not allow for electrostatic stabilization of the emerging phenolate ion. Met201 is buried in the wall of the binding pocket and it is expected to play no direct role in the reaction (Figure 6b). Stabilization of the reactant complex by π-interactions is achieved by a cluster of tyrosine residues, especially Tyr126 in this design. The QM/MM/MC simulations indicate that Ser169 now plays a more active role. Though it was not designated as the hydrogen-bond donor,¹ the simulations find that it does donate a hydrogen bond to the substrate in the reactant (Figure 6b), transition (Figure 6c), and product states.

Figure 6.

KE15: (a) Computed two-dimensional free energy map for the catalyzed Kemp elimination. (b) Configuration of the binding site with the substrate bound at the end of the QM/MM/MC run for the reactant state. (c) A configuration of the transition state from the QM/MM/MC FEP simulations.

The free energy map for the Kemp elimination catalyzed by KE15 is similar to those for KE07 and KE10 (Figure 6a). The reaction again proceeds via a concerted mechanism with relatively synchronous proton transfer and N-O bond opening as for KE10. In Figures 6b and 6c, the key residues are seen to deliver the desired interactions in the binding site. The orientation of the carboxylate group of Asp48 with the substrate is good, and Ser169 forms a bifurcated hydrogen bond with both the isoxazolyl N and O of the substrate in the reactant and transition states. It shifts to hydrogen bond only to the phenolate oxygen in the product (not illustrated).

The computed free energy of activation is 12.3 kcal/mol, while the observed k_cat of 0.022 s⁻¹ (Table 1) corresponds to a ΔG^‡ of 17.0 kcal/mol. Since the FEP calculations revealed the normal concerted mechanism for KE15 with an activation free energy significantly below the reference value of 19.8 kcal/mol, it was anticipated that KE15 should be a viable catalyst for the Kemp elimination. With a k_cat/k_uncat of 1.9 × 10⁴ and k_cat/K_M of 35.1 M⁻¹s⁻¹, its proficiency is very similar to that of KE07. In view of the complexity of the systems and limitations of the QM/MM methodology, the agreement between the computed and observed activation barriers is encouraging. However, it is emphasized that the comparison of the computed results for the catalyzed and uncatalyzed processes is what is most important for catalyst design.

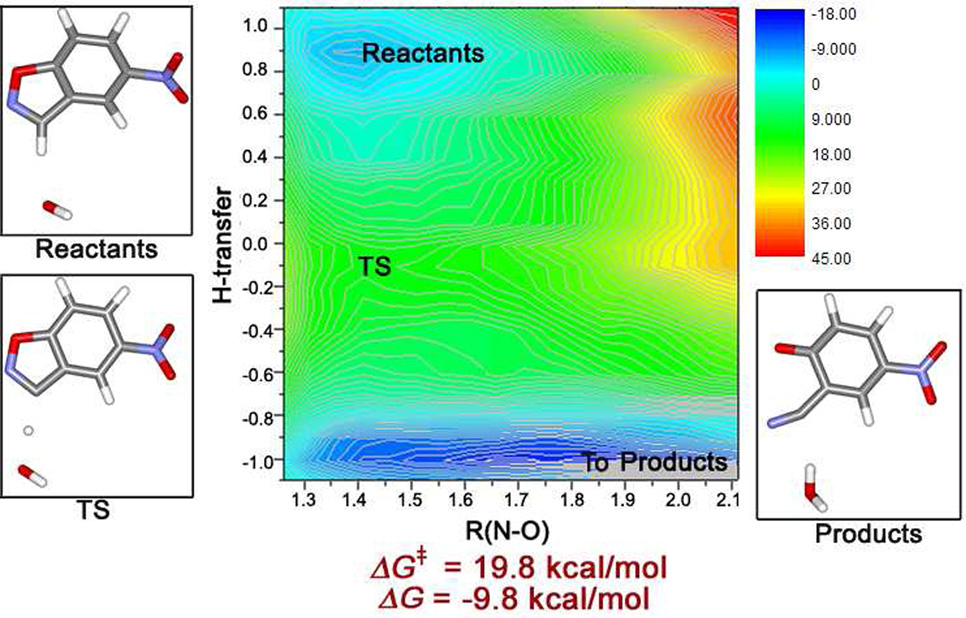
Reference reaction in water

In order to assess the catalytic effect, the Kemp elimination reaction was also modeled in aqueous solution. An immediate issue arose concerning the choice of base. Kemp and Casey did provide experimental free energies of activation for the reaction of 5-nitrobenzisoxazole with hydroxide ion, trimethylamine, and water as the base.^13b Initially, it was decided to make the comparisons with the fastest process, hydroxide catalysis. Thus, the same procedure was followed as for the enzymatic reactions with the substrate and base being equilibrated in contact. The simulations were performed for the reacting system, OH⁻ plus the substrate, in a periodic box containing 395 TIP4P water molecules in the isothermal-isobaric ensemble at 25 °C and 1 atm. The key results of the FEP calculations are summarized in Figure 7. The mechanism of the hydroxide-catalyzed reaction in water is not significantly different from the one in the designed enzymes. The process remains concerted. It is relatively asynchoronous with proton transfer more advanced in the transition state than N-O bond lengthening; however, the free-energy map is quite flat in the vicinity of the transition state. The process is certainly a classic E2 elimination, as demonstrated by Kemp and co-workers.¹³ The computed free energy of activation is 19.8 kcal/mol, again with an estimated uncertainty of less than ± 1 kcal/mol. This result is in respectable agreement with the experimental value of 16.0 kcal/mol at 30 °C.^13b The reaction is also computed to be significantly exergonic with a ΔG of −9.8 kcal/mol, which is qualitatively consistent with the observed exothermicities of Kemp eliminations in water.¹³ In this case, the {R(H-base) + R(C-H)} distance was fixed at 3.12 Ǻ after the equilibration period. This is 0.2–0.3 Ǻ greater than for the enzymatic reactions (Table 1). Though simple correlation of this distance and the barrier heights is not found here, it is reasonable that compression of this distance by the enzymes assists catalysis.

Figure 7.

Computed two-dimensional free energy map for the Kemp elimination catalyzed by hydroxide ion in aqueous solution. The QM region consisted of hydroxide ion plus the substrate; 395 TIP4P water molecules comprised the MM region.

The salient point in the present context is that the computed activation barriers near 10 kcal/mol for the reactions catalyzed by the enzymes KE07, KE10(V103N), and KE15 are significantly smaller than the barrier of 19.8 kcal/mol computed for the reference reaction catalyzed by hydroxide ion. The difference is particularly impressive given that hydroxide ion is a much stronger base in water than carboxylate ions. Thus, confidence was high that the designed enzymes would be catalytic. The situation for KE16 was unclear in view of the uncertainties associated with the Asp48-Lys201 pair. Finally, as an alternative comparison point, the reaction in water between free glutamate as the base and 5-nitrobenzisoxazole was also examined with the FEP calculations. The process was found to be concerted and asynchronous with a free energy of activation of 30.2 kcal/mol and {R(H-base) + R(C-H)} increased to 3.20 Ǻ. Clearly, the carboxylate ion is much better stabilized in water compared to the active sites of the designed enzymes making it a much poorer base.

Conclusions

QM/MM/MC/FEP investigations for Kemp eliminations of 5-nitrobenzisoxazole catalyzed by four computationally designed enzymes were carried out. The catalytic mechanisms and functionality of the key residues in the active sites were elucidated. In comparison to results for reference reactions in water, it was expected that three of the four enzymes should be catalytic and a confident prediction could not be made for the fourth design, KE16. All four designed enzymes turned out to be catalytic with k_cat/K_M values falling in a relatively narrow range (Table 1) and with k_cat/k_uncat values of 10³ – 10⁴ for KE07, KE15, and KE16.¹ The catalytic mechanism for KE07, KE10(V103N), and KE15 was computed to be concerted with proton transfer generally more advanced in the transition state than breaking of the isoxazolyl N-O bond. The same is true for the reference reactions in water catalyzed by hydroxide ion or glutamate, so no new intermediates are formed in the enzymatic processes. Hence, no new chemistry is introduced in the designed enzymes in contrast to many highly proficient enzymes;³¹ the catalytic effect mainly comes from the specific microenvironment in the binding sites, especially desolvation of the catalytic base.^14,15 If the mechanism can not be altered, then improved enzyme designs for the Kemp elimination should focus on further increasing the basicity of the catalytic base, optimizing the mutual orientation of the base and substrate for the proton transfer, and better positioning of hydrogen-bond donating groups to interact with the isoxazolyl N and O in the transition state.