Non-ossicular signal transmission in human middle ears: Experimental assessment of the “acoustic route” with perforated tympanic membranes

Abstract

Direct acoustic stimulation of the cochlea by the sound-pressure difference between the oval and round windows (called the “acoustic route”) has been thought to contribute to hearing in some pathological conditions, along with the normally dominant “ossicular route.” To determine the efficacy of this acoustic route and its constituent mechanisms in human ears, sound pressures were measured at three locations in cadaveric temporal bones [with intact and perforated tympanic membranes (TMs)]: (1) in the external ear canal lateral to the TM, P_TM; (2) in the tympanic cavity lateral to the oval window, P_OW; and (3) near the round window, P_RW. Sound transmission via the acoustic route is described by two concatenated processes: (1) coupling of sound pressure from ear canal to middle-ear cavity, H_PCAV≡P_CAV/P_TM, where P_CAV represents the middle-ear cavity pressure, and (2) sound-pressure difference between the windows, H_WPD≡(P_OW−P_RW)/P_CAV. Results show that: H_PCAV depends on perforation size but not perforation location; H_WPD depends on neither perforation size nor location. The results (1) provide a description of the window pressures based on measurements, (2) refute the common otological view that TM perforation location affects the “relative phase of the pressures at the oval and round windows,” and (3) show with an intact ossicular chain that acoustic-route transmission is substantially below ossicular-route transmission except for low frequencies with large perforations. Thus, hearing loss from TM perforations results primarily from reduction in sound coupling via the ossicular route. Some features of the frequency dependence of H_PCAV and H_WPD can be interpreted in terms of a structure-based lumped-element acoustic model of the perforation and middle-ear cavities.

I. INTRODUCTION

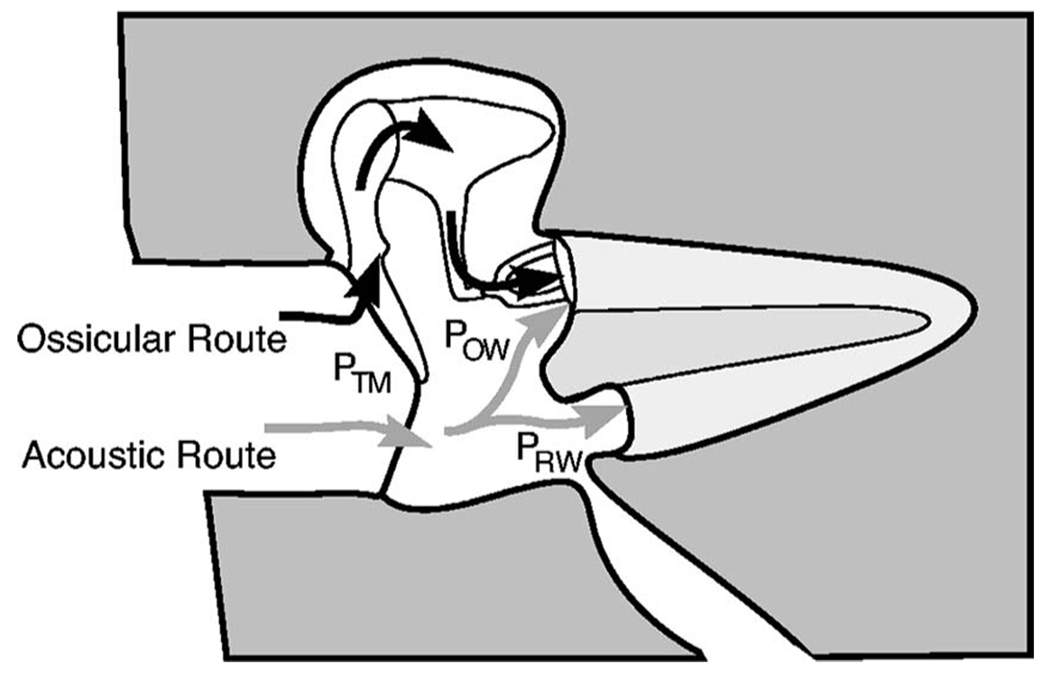
Because the cochlea responds to the pressure difference between the oval and round windows (Voss et al., 1996), it is useful to understand how these “window pressures” are generated in both normal and pathological ears. In normal ears, the net window pressure difference is dominated by the sound pressure delivered to the oval window via the ossicular system, a mechanism referred to as the “ossicular route” by Peake et al. (1992). Via the ossicular route, a cochlear window-pressure difference is generated by motion of the tympanic membrane (TM), malleus, incus, and stapes driven by the pressure difference across the TM. In addition to driving the ossicular system, TM motion generates a sound-pressure field in the middle-ear cavity, which for most of the audio frequency range is approximately uniform throughout the cavity (e.g., Lynch, 1981; Voss, 1998). Thus, the sound pressures at the adjacent oval and round windows, P_OW and P_RW, are nearly equal; the relatively small pressure difference ΔP_win=P_OW−P_RW adds to the ossicular-route stimulus to the cochlea. Consistent with Peake et al. (1992), we refer to the mechanism that drives the cochlea through ΔP_win as the “acoustic route” (Fig. 1).

FIG. 1.

Schematic representation of two routes for sound transmission to the cochlea. Sound pressure at the TM, P_TM, is transmitted to the cochlea through both “ossicular” and “acoustic” routes. In the ossicular route, P_TM acts through the coupled motion of the TM, malleus, incus and stapes and produces a pressure P_ossicular at the stapes footplate. In the acoustic route, P_TM produces a sound-pressure difference P_OW−P_RW=ΔP_win between the oval and round windows. The net stimulus to the cochlea is the sum of pressures transmitted via the two mechanisms: P_ossicular+ΔP_win. For low frequencies the acoustic-route stimulus ΔP_win is expected to be small relative to P_OW, as the oval and round windows are separated by only about 4 mm while the wavelength of sound at 100 Hz is about 3.5 m. In fact, the acoustically coupled stimulus ΔP_win is generally only 0.01–0.001 of the ossicularly coupled stimulus. Thus, pathologies that interrupt the ossicular route cause large (40–60 dB) hearing losses. Figure modified from Merchant et al. (1997b).

In a normal ear the contribution of the acoustic route is insignificant compared to the ossicular route, but the acoustic route can become important when ossicular transmission is decreased (Békésy, 1947; Schmitt, 1958; Peake et al., 1992; Merchant et al., 1997a). Perforation of the TM decreases ossicular-route transmission and purportedly increases acoustic-route transmission. The primary goals of this work are: (1) To describe the acoustic-route transmission systematically and the effect of TM perforations on it; (2) To assess the characteristics of the mechanisms involved in the acoustic route; and (3) To identify conditions in which the acoustic route plays a significant role in hearing.

The effect of TM perforations on the acoustic route has been discussed in the literature, but no systematic measurements have been reported. Békésy (1947) reported measurements of the pressure difference between the oval and round windows at six frequencies in one temporal-bone preparation without a TM. In Peake et al. (1992) these measurements are used with a middle-ear model to predict hearing loss with a total perforation (i.e., TM removed). The model predicts that with the elimination of ossicular coupling, the acoustic route provides hearing levels of 40–60 dB, from 250 to 3000 Hz, consistent with clinically observed hearing loss.

With TM perforations, a popular idea is that a perforation’s location in the TM affects the sound pressures at the oval and round windows. Schmitt (1958) introduced the idea that differences in both the magnitude and phase angles of the sound pressures at the two windows are important. Sub-sequently, a view developed that a perforation directly lateral to the round window affects the pressures acting on the oval and round windows differently from a perforation at other (e.g., more anterior) locations (e.g., Pickles, 1987; pp. 60, 61; Glasscock and Shambaugh, 1990, p. 314; Schuknecht, 1993, p. 196). Specifically, this view assumes that the sound pressure at the round window “cancels” the pressure at the oval window more with posterior-inferior perforations than with perforations at other locations.

Recent work that describes total middle-ear sound transmission in the presence of TM perforations includes: (1) Input impedance and ossicular-motion measurements from temporal-bone preparations with controlled, experimentally produced TM perforations (Voss et al., 2001b); (2) An analog-circuit model that describes mathematically the effects of TM perforations on total middle-ear sound transmission (Voss et al., 2001c); (3) Clinical measurements that are consistent with the temporal-bone experimental and theoretical work (Mehta et al., 2006). Collectively, this work describes and explains hearing loss resulting from a TM perforation as:

1. Frequency dependent with the largest loss occurring at the lowest frequencies

2. Increasing with perforation size

3. Depending on the volume of the middle-ear and mastoid air space with larger losses in ears with smaller volumes

4. Not varying significantly with location of the perforation in the TM

Here we present measurements [from the same preparations reported in Voss et al. (2001b, c)] of sound pressures outside the cochlear windows and describe how these pressures influence sound transmission in the presence of TM perforations. These measurements and analyses place constraints on sound transmission with perforations. Specifically, the importance of the acoustic route relative to the ossicular route is quantified, and the acoustic route’s dependences on perforation location, size, and sound frequency are determined.

II. ANALYTICAL APPROACH

To describe sound transmission via the acoustic route, we follow the approach of Békésy (1947) and define the effective acoustic-route (AR) transfer function H_AR as the ratio of the pressure difference between the oval and round windows to the pressure in the external ear canal at the TM

$$H_{\text{AR}}\equiv \frac{P_{\text{OW}}-P_{\text{RW}}}{P_{\text{TM}}},$$ (1)

where P_OW is the pressure within the middle-ear cavity adjacent to the oval window, P_RW is the pressure within the middle ear adjacent to the round window, and P_TM is the pressure within the ear canal adjacent to the TM. In order to represent the acoustic mechanisms involved (with TM perforations ), we express H_AR in terms of two factors: the middle-ear-cavity-pressure transfer function H_PCAV and the window-pressure-difference transfer function H_WPD,

$$H_{\text{AR}}\equiv \frac{P_{\text{OW}}-P_{\text{RW}}}{P_{\text{TM}}}=\frac{P_{\text{CAV}}}{\underset{H_{P_{\text{CAV}}}}{\underbrace{P_{\text{TM}}}}}\frac{P_{\text{OW}}-P_{\text{RE}}}{\underset{H_{\text{WPD}}}{\underbrace{P_{\text{CAV}}}}}=H_{P_{\text{CAV}}}{H}_{\text{WPD},}$$ (2)

where P_CAV is the sound pressure within the middle-ear air space. Note that in general P_CAV depends on location in the middle-ear cavity; we address this dependence below. The first factor, H_PCAV, is a measure of the acoustic processes that couple sound pressure in the ear canal to the middle-ear cavity; the second factor, H_WPD, is determined by the acoustic processes that produce spatial variations within the cavity. In the absence of a detailed model for the acoustic processes, it is conceivable that H_PCAV and H_WPD depend on both location and size of perforations and on frequency.

III. METHODS

A. Transfer function calculations

We use measurements of the oval- and round-window pressures, P_OW and P_RW, and the ear-canal pressure P_EC transformed to pressure at the TM P_TM (Voss et al., 2001b), to calculate the factors of the acoustic route. The middle-ear-cavity-pressure transfer function, H_PCAV, is calculated from our pressure measurements as

$$H_{P_{\text{CAV}}}\equiv \frac{P_{\text{CAV}}}{P_{\text{TM}}}\approx \frac{P_{\text{OW}}}{P_{\text{TM}}},$$ (3)

where we assume that the cavity pressure P_CAV is nearly uniform throughout the cavity and therefore can be approximated in this ratio by the pressure measured near the oval window, P_OW (or equally well by P_RW). The approximation P_CAV≈P_OW is reasonable for frequencies for which the dimensions of the middle-ear cavity are much smaller than the wavelength of sound; i.e., up to about 4000 Hz, where the wavelength (≈9 cm) is about ten times the largest cavity dimension. An experimental test of this simplification showed that even near a TM perforation the pressure within the middle-ear cavity is nearly constant in space (Voss, 1998, Fig. 2–Fig 7, p. 69).

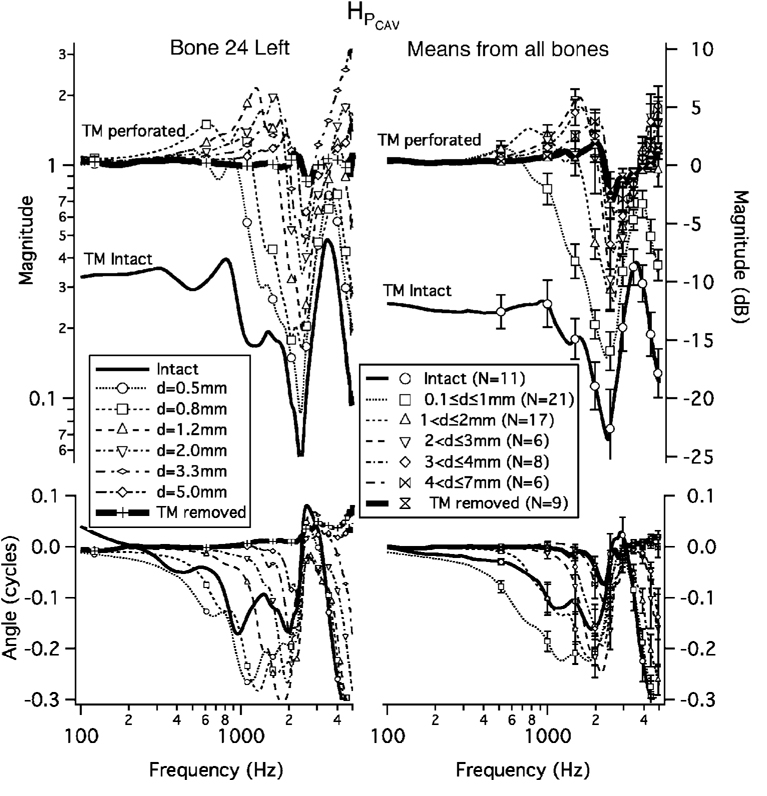
FIG. 2.

Measurements of the middle-ear-cavity pressure transfer function H_PCAV =P_OW/P_TM with an intact TM and with perforations of increasing diameter. Symbols are spaced by 20 data points. (There are no symbols for the intact case.) Left panel: Bone 24L. Right panel: Means and standard errors from all measurements. Upper: Magnitude. The two vertical coordinate systems are equivalent; on the left “Magnitude,” is the |H_PCAV| and on the right “Magnitude(dB)” =20 log₁₀ “Magnitude.” Lower: Angle.

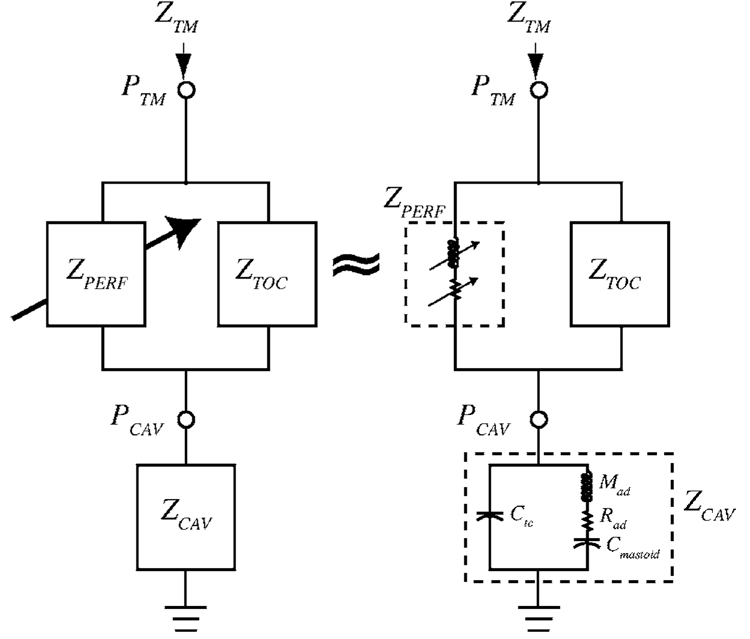
FIG. 7.

Analog electric-circuit model of the human middle ear with a TM perforation. Voltages are analogous to sound pressures. The impedance of the TM loaded by the ossicular chain is represented by Z_TOC. The perforation is represented as the impedance Z_PERF; the impedance of the middle-ear cavities is represented as Z_CAV; P_TM is the sound pressure at the TM; P_CAV is the sound pressure in the middle-ear cavity; Z_TM is the input impedance in the ear canal at the TM. Arrows on circuit components indicate changes with perforation size. Left: General topology [as developed in Voss et al. (2001c)]. Right: Representation by ideal elements that represent the impedances ZPERF [see Voss et al. (2001c) for detailed description] and Z_CAV [see Voss et al. (2000) and Stepp and Voss (2005) for detailed description] C_tc represents the acoustic compliance of the tympanic cavity; M_ad represents the acoustic mass of the aditus; R_ad represents the resistance of the aditus; C_mastoid represents the compliance of the antrum and mastoid space.

The window-pressure-difference transfer function H_WPD is computed from measurements as

$$H_{\text{WPD}}\approx \frac{P_{\text{OW}}-P_{\text{RW}}}{P_{\text{OW}}}=1-\frac{P_{\text{RW}}}{P_{\text{OW}}}$$ (4)

The acoustic-route transfer function H_AR (Eq. (2)) is the product of the factors H_PCAV and H_WPD

$$H_{\text{AR}}=\frac{P_{\text{OW}}}{\underset{H_{P_{\text{CAV}}}}{\underbrace{P_{\text{TM}}}}}\underset{H_{\text{WPD}}}{\underbrace{(1-\frac{P_{\text{RW}}}{P_{\text{OW}}})}}$$ (5)

B. Experimental overview

Acoustic measurements of middle-ear cavity pressures at the oval and round windows and lateral to the tympanic membrane (TM) were made in cadaveric temporal bones with both intact and perforated TMs. The prepared bones were 11 of the ears for which intact TM results are presented in Voss et al. (2000) and for which stapes velocity and impedance at the TM were measured with perforations (Voss et al., 2001a), (b); most of the measurement techniques are described in detail in Voss et al. (2000, 2001a, b). Additional methods are described here.

Measurements were made on fresh temporal bones for which no evidence of otologic disease was found either in medical records or in oto-microscopic examination. In each case, the bony ear canal was drilled away to expose the TM, and a brass ring was cemented to the bony rim around the TM to allow repeatable coupling and uncoupling of the sound source and calibrated microphone to the ear. Two calibrated probe microphones were introduced into the middle-ear cavity with one probe-tube tip adjacent to the oval window and the other to the round window. In each ear, perforations of different sizes and locations were made with an otosurgical Argon laser, as described by Voss et al. (2001a, b); generally, a small perforation was made and then perforations of increasing size were centered at the same location [see Fig. 1 of Voss et al. (2001b)]. The ear-canal pressure P_EC was measured about 3 mm from the TM and these measurements were transformed to approximate the pressure at the TM P_TM by modeling the remaining bony ear canal as a uniform cylindrical tube (Voss et al., 2001b, p. 1434).

In these preparations, measurements were also made of stapes velocity and acoustic impedance (Voss et al. 2000, 2001a, b, c); some of these results will be useful here in interpretation of the acoustic mechanisms.

C. Measurement of the oval- and round-window pressures

1. Placement of the oval- and round-window probe-tube microphones in the temporal-bone preparation

Probe-tube microphones sensed the sound pressure outside each cochlear window. In each case, the probe-tube microphone consisted of a Knowles hearing aid microphone coupled to a 33-mm-long steel tube with an inner diameter of 0.8 mm and an outer diameter of 1.1 mm; the distal open end of each probe tube was positioned near the appropriate cochlear window. Each probe microphone was attached to the temporal bone as follows. First, a guide tube (inner diameter 1.2 mm), through which the probe tube could slide, was carefully positioned and glued to the temporal bone. The guide tube provided a straight, repeatable path for the probe tube to reach its window. Next, under the view of a dissecting microscope, the open end of the probe tube was inserted through the guide tube until it was as close as possible to its window (0.5–2 mm). Finally, with the position of the probe tube set within the guide tube, a rubber “o-ring” around the probe tube was positioned to “stop” the probe at the proximal end of the guide tube so that the probe tube was held at this location. This arrangement made it convenient to remove the probe-tube microphone assemblies for repeated calibrations throughout an experiment. The distal openings of the probe tubes were at the posterior-most edge of the footplate (oval window) and lateral to the round window.

2. Calibration of the probe-tube microphones

Each probe-tube microphone (one for measurements at the round window and one for measurements at the oval window) was calibrated by coupling it to the sound source and calibrated microphone assembly that was used to generate and measure sound stimuli in the ear canal (Voss et al., 2000); we refer to this calibrated microphone as the “ear-canal microphone” and the calibration procedure to determine the microphone sensitivity in terms of microphone voltage per sound pressure sensed is described in detail by Voss et al. (2000). Each of the two window probe-tube microphones was calibrated relative to the calibrated ear-canal microphone. Together, the tip of each probe-tube microphone was placed within 1 mm of the calibrated ear-canal microphone within a short cylindrical cavity (Voss et al., 2000). Sound stimuli were generated within the cavity and the sound pressure was assumed equal at the ear-canal microphone and the orifice of the probe-tube microphone; the simultaneous responses of each probe-tube microphone and the calibrated ear-canal microphone were used to determine the sensitivity of each probe-tube microphone. This procedure was followed to determine the calibrations for both microphones—specifically—the transfer functions $P_{\text{OW}}^{\text{mic}}/V_{\text{OW}}^{\text{mic}}\text{and}{P}_{\text{RW}}^{\text{mic}}/R_{\text{RW}}^{\text{mic}}$ , which represent the ratios of sound pressure at the oval and round windows to the oval-window and round-window probe-microphone output voltages, respectively.

3. Do the probe-tube microphones measure the pressures at the probe tips?

As the microphones were coupled to the windows via 33-mm-long probe tubes, it is possible that they could sense sound from locations other than the probe tip. To test this possibility, with the microphone coupled to the temporal bone, we measured the microphone output with the probe tube open and also with the window end of the probe tube plugged with cotton. For most frequencies, the output with the probe tube open was at least 40 dB greater (and always at least 20 dB greater) than with the probe tube plugged with cotton (Voss, 1998, Fig. 3-2, p. 112). We concluded that the microphones’ outputs are determined by the sound pressure at the probe-tube tip.

FIG. 3.

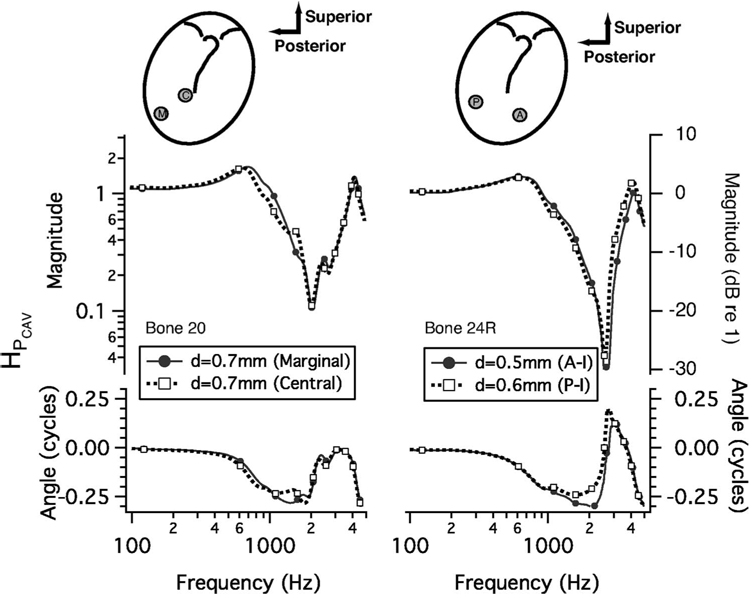
Comparisons of H_PCAV with a perforation at one of two locations. Cartoons at the top portray the TM with manubrium of the malleus as seen from the external ear canal. Patches made of cigarette paper were applied to close a perforation of the TM so that measurements represent the effect of only one perforation. Measurements (not shown here) with a patch in place demonstrate that the response with the patch was similar to the response with the TM intact (Voss et al., 2001a). Left panel: A perforation in either the marginal (M) or central (C) part of the posterior-inferior quadrant. Right panel: A perforation in either the posterior-inferior (P) or anterior-inferior (A) quadrants. Symbols are at every 20th data point. Upper: Magnitude. The vertical coordinate systems are equivalent, with the scale on the left the pressure ratio and the scale on the right the ratio in dB. Lower: Angle.

4. Errors in relative calibration between the oval- and round-window microphones

The absolute calibration of the oval- and round-window microphones is not critical for our interest in the window-pressure differences, but consistency in the relative calibrations between the oval- and round-window microphones is crucial in determining precisely the pressure difference between the windows

$$P_{\text{OW}}-P_{\text{RW}}=P_{\text{OW}}(1-\frac{P_{\text{RW}}}{P_{\text{OW}}}).$$ (6)

As |P_RW/P_OW|≈1, changes in the relative sensitivity of the microphone pair $(P_{\text{RW}}^{\text{mic}}/V_{\text{RW}}^{\text{mic}}/P_{\text{OW}}^{\text{mic}}/V_{\text{OW}}^{\text{mic}})$, which produce small changes in the inferred P_OW and P_RW, may have big effects on the inferred pressure difference. However, small changes that are common to the calibration ratios for both microphones will have equally small effects on the pressure difference; these changes are “divided out” in the ratio P_RW/P_OW and contribute only a small percentage to P_OW in Eq. (6) (Voss, 1995).

To detect small changes in the relative calibration (e.g., from moisture in a probe tube), the calibration procedure (Sec. III C 2) was repeated several times during each experiment. We use variation in the relative calibration $P_{\text{OW}}^{\text{mic}}/V_{\text{OW}}^{\text{mic}}/P_{\text{RW}}^{\text{mic}}/V_{\text{RW,}}^{\text{mic}}$, over repeated measurements, to estimate the range of error in the measurement of P_RW/P_OW.

The process of coupling the probe microphones to the sound-source assembly used for calibrations seemed to be the major source of variability in the calibration. When a probe-tube microphone was attached to the sound-source assembly and left undisturbed, repeated measurements made over several hours showed changes that were less than 0.05 dB in magnitude and 0.001 cycles in angle. In contrast, when the sound-source assembly was moved, and the coupler that attached it to a probe tube was removed and then replaced, the changes in the measured absolute calibrations increased to about 1 dB in magnitude. However, the relative calibration of the two microphones was more stable as it was possible to calibrate both probe-tube microphones, one at a time, without moving the sound source or coupler. Thus, while the absolute calibration of the two microphones changed by 1 dB from calibration to calibration, the relative calibration between the two microphones varied less.

Repeated calibrations among the 11 experiments had different levels of variability. In three of the 11 experiments (bones 23, 22 Right, and 8), the relative calibrations of the oval- and round-window microphones varied by more than 1 dB in magnitude and 0.01 cycles in angle. We considered this level of uncertainty in the calibrations unacceptable for computation of the window-pressure difference (Sec. III C 5). However, in the remaining eight experiments, the relative calibrations of the oval- and round-window microphones varied up to only 0.25 dB¹ in magnitude and 0.005 cycles in angle. Thus, we focus our attention on the results from the subset of eight bones with smaller variability in the ratio between the oval- and round-window microphone calibrations. In one of the eight bones (bone 18), there was a dramatic change (2–3 dB) in the round-window microphone calibration midway through the experiment. It is not clear what happened to the microphone; measurements made after the change are not included here.

5. Inaccuracies in the calculations of P_RW/P_OW, H_WPD, and H_AR

Changes in the relative calibration between the microphones limit the accuracy of calculations of H_AR and H_WPD. In this section, we estimate limits for accurate calculation of these quantities, based on our estimate of ranges of ±0.25 dB in magnitude and ±0.005 cycles in angle.

First consider how a variation of ±0.25 dB in magnitude and ±0.005 cycles in angle affects the ratio P_RW/P_OW when P_RW≈P_OW. A 0.25 dB change in magnitude in either P_OW or P_RW corresponds to a factor of 1.03. Thus, if the pressures are equal (i.e., P_RW=P_OW), the measurement of the magnitude |P_RW/P_OW| could range from 0.97 to 1.03, and the angle measurement could range from −0.005 to 0.005 cycles when the actual angle ∠(P_RW/P_OW)=0. Next, consider how a relative variation of ±0.25 dB in magnitude and ±0.005 cycles in angle affects the measured H_WPD=(1−P_RW/P_OW) (Eq. (4)), when P_RW=P_OW. With P_RW/P_OW=1.03∠0.005, |H_WPD| is 0.04 instead of zero. Small errors in magnitude can introduce variation in the angle ∠(H_WPD) of ±0.5 cycles because the calculation of H_WPD depends on a difference that can have a negative or positive sign depending on the relative values of |P_RW| and |P_OW|; thus, we have chosen to ignore ∠(H_WPD) because of possibly large errors.

Finally, consider how the relative changes of ±0.25 dB and ±0.005 cycles in P_RW and P_OW affect the acoustic-route transfer function H_AR. If we assume that measurement errors in the ratio P_OW/P_TM (i.e., H_PCAV) are negligible, then (from Eq. (5)), errors in |H_AR| are equal to errors in |H_WPD| multiplied by the factor |P_OW/P_TM|. Thus, when the calculated |H_AR|∠0.04|P_OW/P_TM|, H_AR may be strongly influenced by relative microphone calibration changes. We define a boundary at |H_AR|=0.04|P_OW/P_TM| and refer to this as the “edge of inaccuracy in the measurement of |H_AR|.” As discussed above in relation to ∠(H_WPD), when |H_AR| ∠0.04|P_OW/P_TM| our measurements of angle ∠H_AR contain uncertainties of up to ±0.5 cycles.

Table I summarizes the uncertainties and their influence on our ability to measure the quantities P_RW/P_OW, H_WPD and H_AR. In the results that follow, we plot all of our magnitude measurements, but we indicate the edge of inaccuracy based on Table I.

Table I.

Measurement uncertainties or edge of inaccuracy for calculation of P_RW/P_OW, H_WPD and H_AR, based on the assumption that relative errors in the measurements of the oval- and round-window sound pressures are less than ±0.25 dB in magnitude and ±0.005 cycles in angle

Calculated quantity	Measurement uncertainty or edge of inaccuracy
|PRW/POW|	Uncertainty ±0.03
∠ |PRW/POW|	Uncertainty ±0.005 cycles
|HWPD|	Edge of inaccuracy: 0.04
|HWPD|	Uncertainty ±0.50 cycles
|HAR|	Edge of inaccuracy: 0.04 $\left|\frac{P_{\text{OW}}}{P_{\text{TM}}}\right|$
∠HAR	Uncertainty ±0.50 cycles

D. Statistical tests to compare two groups of data

We use a statistical test to determine the significance of differences between different populations within our data. Specifically, to test the null hypothesis that two means are from the same population, we compute the probability (p) that a given pair of means could differ by as much as the data show, given the null hypothesis. In particular, we test to determine the p values associated with the means for |P_RW/P_OW|, ∠(P_RW/P_OW), |H_WPD|, and |H_AR| when there are (1) different sized perforations and (2) perforations at different TM locations.

Since the sample sizes used to compute the means are small (range N=2 to N=16), we compute the corresponding p values using a bootstrap permutation test (Efron and Tibshirani, 1993); this method makes no assumption about the probability distribution. The probability that the two means are equal depends on the fraction of the permutations in which the difference between the means of the two permutated test populations are greater than or equal to the difference between the actual means. Further details of our application of this permutation test can be found in Voss (1998).

IV. RESULTS

A. Organization

Each of three sections presents results from our measurements of sound transmission via the acoustic route: (1) the middle-ear-cavity transfer function H_PCAV =P_OW/P_TM; (2) the ratio between the oval- and round-window pressures P_RW/P_OW and the window-pressure-difference transfer function magnitude |H_WPD|= |1−P_RW/P_OW|; (3) the acousticroute transfer function H_AR=| (P_OW−P_RW)/P_TM|. For each of these the effects of both perforation size and location are examined. In general, we present results from one of our preparations (bone 24L) as an example and mean measurements across all preparations when appropriate. [Results from each preparation are in Voss (1998).]

B. Middle-ear-cavity-pressure transfer function: H_PCAV

1. H_PCAV measurements with an intact tympanic membrane

Measured middle-ear-cavity-pressure transfer functions are presented in Fig. 2 with TM perforation sizes varying from zero (intact) to total (TM removed) for the example bone (24L) and for mean measurements from 11 ears. Both the individual measurements (on bone 24L) and the mean measurements are representative of all measurements of H_PCAV on the 11 preparations.

With the TM intact, at low frequencies (i.e., ∠1000 Hz) |H_PCAV| is roughly independent of frequency at about −10±1 dB on bone 24L (Fig. 2) and across the 11 preparations ranges from −6.6 to −21.1 dB at 488 Hz (mean −12.7 dB and standard deviation 4.8 dB). In the 1000–3000 Hz range, |H_PCAV| has a sharp minimum: across the 11 preparations this magnitude minimum ranges from −20.5 to −39.2 dB (mean −30.5 dB and standard deviation 6 dB) and the frequency of the minimum ranges from 928 to 2686 Hz (mean 2151 Hz and standard deviation 531 Hz). In some preparations, at a lower frequency, a peak in magnitude occurs such as that near 800 Hz in Fig. 2 (upper, left); in other preparations there is no peak in this region. In all preparations, there is a sharp maximum in |H_PCAV| at a frequency above the sharp minimum described above; across the 11 preparations this maximum occurs between 2612 and 4785 Hz (mean 3650 Hz and standard deviation 564 Hz) and has a value that ranges from −10.3 to −0.8 dB (mean −4.5 dB and standard deviation 2.7 dB).

The angle ∠H_PCAV is about zero at the lowest frequencies (∠200 Hz) with the TM intact,² indicating that the cavity and ear-canal pressures are in phase. As frequency increases toward the frequency of the minimum in |H_PCAV|, ∠H_PCAV decreases so that the middle-ear cavity pressure lags the ear-canal pressure by up to 0.3 cycles. At the frequency of the sharp minimum in |H_PCAV|, ∠H_PCAV increases rapidly toward a value between 0 and 0.1 cycles. As frequency increases further, ∠H_PCAV decreases rapidly in the 3000–4000 Hz range of the local maximum in |H_PCAV|.

In summary, with the TM intact, for frequencies from 100 to 5000 Hz, H_PCAV shows behavior consistent with a system with at least two resonances, represented by a midfrequency sharp minimum in magnitude and a higher frequency sharp maximum in magnitude.

2. H_PCAV with a tympanic-membrane perforation

In additional to the plots in Fig. 2, the features described here of H_PCAV with a perforated TM are summarized in Table II for all 11 preparations and all perforation sizes. At the lowest frequencies H_PCAV (with a TM perforation) is approximately one (i.e., magnitude=0 dB and angle=0) (Fig. 2); physically, the perforation acts as an acoustic short circuit between the ear canal and middle-ear cavity, making the pressures equal. As frequency increases above 300 Hz, |H_PCAV| peaks above 0 dB (i.e., the middle-ear cavity pressure is greater than the ear-canal pressure); the frequency of this peak increases systematically with perforation diameter. Above the frequency of the peak, |H_PCAV| has a sharp minimum (near 2000 Hz); the frequency of this minimum appears to be the same as seen with the TM intact, independent of perforation diameter; |H_PCAV| at the minimum increases with perforation size increases. At higher frequencies, the location of the sharp maximum in |H_PCAV| that occurs with the TM intact increases somewhat in frequency and magnitude with increasing perforation diameter.

Table II.

Features of H_PCAV discussed in the text for each preparation. The columns labeled “Bone” and “Perf. Diam” indicate the preparation number and the state of the TM as intact, removed, or by the diameter of the perforation; the column labeled |H_PCAV| Max(0.5–2.8 kHz) indicates the magnitude and frequency location of the local maximum that occurs between 0.5 and 2.8 kHz; the column labeled |H_PCAV|Min (0.9–3.3 kHz) indicates the magnitude and frequency location of the local minimum that occurs between 0.9 and 3.2 kHz; the column labeled |H_PCAV| Max(>2.5 kHz) indicates the magnitude and frequency location of the local maximum at a frequency greater than 2.5 kHz; the column labeled ∠H_PCAV (0.2–2.7 kHz) indicates the lowest frequency at which the angle ∠H_PCAV decreases from greater than to less than −0.03 cycles; the column labeled |Z_TM|Min (0.5–3.0 kHz) indicates the frequency of the local minimum that occurs between 0.5 and 3.0 kHz in the magnitude of the impedance measured in the ear canal at the tympanic membrane. Entries for which the feature does not exist in the data are indicated by DNE (does not exist). The entry “noisy” indicates the measurement was too noisy to identify the extremum. The entry “NA” indicates the measurement was not available.

Middle-ear cavity transfer function HPCAV (f ,d) Measures of salient features
Preparation		|HPCAV| Max 0.5–2.8 kHz		|HPCAV| Min 0.8–3.2 kHz		|HPCAV| Max >2.5 kHz		∠HPCAV0.2–2.7 kHz	|ZTM| Min 0.5–3.0 kHz
Bone No.	Perf. Diam. (mm)	Mag. (dB)	fmax (kHz)	Mag. (dB)	fmin(kHz)	Mag. (dB)	fmax (kHz)	lowest f for ∠=−0.03 (kHz)	fmin (kHz)
8	Intact	DNE	DNE	−39.2	2.39	−6.0	4.79	DNE	0.98
	0.5	−1.5	1.00	−34.0	2.32	−2.5	5.37	DNE	1.03
	0.7	1.8	1.05	−30.3	2.39	0.2	4.93	0.37	1.07
	1.1	7.40	1.12	−28.9	2.39	5.3	5.96	0.59	1.17
	1.6	8.5	1.27	−23.2	2.39	9.4	6.15	0.66	1.34
	2.4	9.8	1.39	−21.7	2.39	11.4	6.54	0.76	1.44
	3.2	12.3	1.56	−21.9	2.37	11.7	7.28	0.98	1.61
	Removed	10.3	2.00	−15.5	2.47	11.1	8.33	1.10	1.96
9	Intact	DNE	DNE	−26.1	0.93	−0.8	2.61	DNE	0.98
	0.1	DNE	DNE	−23.5	0.85	0.2	2.56	DNE	0.93
	1.1	6.3	0.54	−17.4	0.81	7.2	2.91	0.39	0.56
	1.9	6.3	0.71	−11.9	0.93	7.1	3.39	0.59	0.73
	3.3	4.4	0.90	−7.7	1.17	4.5	4.00	0.76	0.98
	Removed	DNE	DNE	−0.2	1.00	1.4	4.32	DNE	0.98
13	Intact	DNE	DNE	−34.4	1.37	−2.0	3.44	DNE	1.86
	0.5	DNE	DNE	−28.5	1.32	−3.0	3.44	DNE	0.73
	0.8	6.9	0.61	−24.0	1.37	−1.7	3.56	0.39	0.73
	1.4	7.9	0.76	−23.4	1.25	3.7	3.59	0.56	0.81
	1.8	9.3	0.90	−21.1	1.29	3.7	3.98	0.71	0.98
	Removed	3.2	1.27	−3.2	1.49	DNE	DNE	1.22	1.37
18	Intact	DNE	DNE	−35.4	2.44	−10.3	3.22	DNE	NA
	0.4	DNE	DNE	−25.4	2.25	−7.2	3.17	DNE	NA
	0.5	3.6	0.59	−22.1	2.25	−3.6	3.20	0.24	NA
	1.0	7.8	0.88	−16.6	2.22	0.0	3.37	0.59	NA
	1.7	6.6	1.10	−15.3	2.22	7.5	3.59	0.81	NA
	2.3	5.8	1.20	−9.4	2.29	8.0	3.71	0.93	NA
	3.0	5.1	1.34	−7.0	2.37	10.3	4.00	1.15	NA
	Removed	4.2	2.12	0.0	2.69	16.3	4.98	2.00	NA
19	Intact	DNE	DNE	−25.8	2.10	−4.1	3.44	DNE	2.49
	0.6	4.5	0.85	−16.2	2.25	1.0	3.76	0.59	0.88
	1.3	6.4	1.07	−12.2	1.95	5.5	3.96	0.83	1.10
	1.9	5.6	1.34	−10.2	1.98	7.9	4.15	1.00	1.42
	2.6	6.2	1.44	−8.2	2.03	10.8	4.44	1.12	1.46
	Removed	4.7	1.76	−2.8	2.29	31.2	6.01	1.73	1.98
20	Intact	DNE	DNE	−28.2	2.15	−3.7	4.08	DNE	1.90
	0.7	4.6	0.71	−19.6	2.10	2.9	4.27	0.46	0.81
	0.7	4.4	0.66	−19.1	2.10	2.7	4.22	0.42	0.73
	1.0	5.4	0.83	−13.2	2.69	4.4	4.37	0.63	0.85
	1.7	5.5	1.17	−9.9	2.59	8.2	4.71	0.90	1.59
	3.0	6.3	1.56	−8.1	2.64	12.6	5.42	1.15	1.61
	4.0	5.5	1.64	−6.4	2.61	17.2	5.93	1.29	1.73
	5.0	4.2	1.64	−5.9	2.66	20.0	6.13	1.37	1.81
	Removed	2.6	2.27	−2.2	2.66	29.5	7.47	2.22	2.22
22L	Intact	DNE	DNE	−20.5	2.32	−2.8	3.59	DNE	2.29
	0.6	1.3	0.93	−17.5	2.15	1.7	3.74	0.24	0.93
	1.2	5.4	1.05	−15.3	2.20	5.6	4.03	0.61	1.10
	2.0	7.1	1.37	−10.8	2.34	7.5	4.25	1.17	1.59
	3.3	7.8	1.71	−7.9	2.39	8.7	4.61	1.44	1.81
	5.0	7.0	1.86	−5.1	2.39	11.2	5.35	1.73	1.98
	Removed	4.5	2.12	−3.0	2.61	9.9	5.91	2.03	2.20
22R	Intact	DNE	DNE	−29.0	2.69	−5.8	3.66	DNE	1.76
	0.6	0.9	1.27	−25.5	2.69	−1.0	3.76	0.37	1.27
	1.3	7.7	1.46	−22.7	2.69	6.8	4.03	0.76	1.47
	2.3	11.8	1.68	−18.4	2.69	11.4	4.37	1.34	1.76
	3.3	12.1	1.95	−14.4	2.69	15.1	4.96	1.73	2.03
	6.8	8.6	2.20	−9.8	2.81	Noisy	Noisy	2.10	2.37
	Removed	2.4	2.20	−4.7	2.83	Noisy	Noisy	1.15	2.37
23	Intact	DNE	DNE	−29.0	2.69	−5.1	3.59	DNE	1.88
	0.8	DNE	DNE	−25.5	2.69	−0.4	3.71	0.29	1.71
	1.0	2.6	1.51	−22.7	2.69	1.6	3.83	0.56	1.73
	2.0	8.6	1.83	−18.4	2.69	6.1	4.03	0.98	1.86
	3.0	10.3	2.03	−14.4	2.69	7.5	4.27	1.44	2.03
	4.0	10.4	2.20	−9.8	2.81	7.8	4.54	1.73	2.15
	5.0	5.7	2.37	−4.7	2.83	Noisy	Noisy	2.27	2.54
	Removed	DNE	DNE	−2.3	3.15	Noisy	Noisy	DNE	2.81
24L	Intact	DNE	DNE	−25.7	2.37	−6.4	3.49	DNE	1.86
	0.5	0.6	0.88	−21.3	2.37	−2.5	3.52	0.27	0.95
	0.8	3.3	1.00	−15.8	2.39	−2.0	3.83	0.46	1.03
	1.2	6.7	1.25	−14.2	2.42	2.0	4.10	0.78	1.29
	2.0	6.1	1.64	−9.3	2.42	5.4	4.47	1.20	1.59
	3.3	4.1	1.83	−6.7	2.49	10.6	4.98	1.44	1.98
	5.0	2.7	1.96	−4.3	2.47	15.5	6.18	1.89	1.98
	Removed	1.1	2.17	−1.7	2.64	22.3	7.67	DNE	2.10
24R	Intact	DNE	DNE	−32.8	2.54	−2.2	4.22	DNE	2.88
	0.5	2.6	0.73	−30.7	2.61	0.3	4.22	0.37	0.83
	0.6	2.3	0.73	−27.7	2.61	2.0	4.13	0.37	0.78
	1.3	5.5	1.44	−19.5	2.54	7.2	4.56	0.98	1.54
	2.3	8.5	1.81	−14.0	2.61	10.9	5.20	1.71	1.81
	4.0	10.0	2.10	−11.3	2.61	11.0	5.79	1.73	2.10
	5.0	8.7	2.25	−7.1	2.61	15.0	6.37	1.98	2.22
	Removed	4.1	2.79	−1.3	2.49	21.9	8.03	2.71	2.61

The angle ∠H_PCAV (with the TM perforated) is near zero at the lowest frequencies. As frequency increases, ∠H_PCAV decreases; the frequency at which the angle decrease begins increases as perforation diameter increases. For both the intact and perforated conditions, ∠H_PCAV increases rapidly at the frequency for which |H_PCAV| is a minimum, and ∠H_PCAV again decreases rapidly near the frequency of the local maximum in |H_PCAV|.

In summary, perforations have dramatic effects on the middle-ear-cavity transfer function H_PCAV and increase its magnitude relative to the intact case. For the lowest frequencies, all perforation sizes used equalize the ear-canal and middle-ear-cavity pressures so that H_PCAV≈1. Perforations introduce a resonance at which the cavity pressure magnitude exceeds the ear-canal pressure magnitude by up to 10 dB; the resulting local maximum in |H_PCAV| occurs between 0.5 and 2.8 kHz, and in each preparation the frequency of the maximum increases as perforation diameter increases. A minimum in |H_PCAV| occurs above the frequency of this first peak (in the 1000–3000 Hz range); the frequency of the minimum for each preparation appears to be independent of the TM condition (i.e., intact, various perforation sizes, or TM removed), and the minimum |H_PCAV| increases with increasing perforation diameter. A second peak occurs at a frequency above the frequency of this minimum, and the frequency of this peak increases with increasing perforation diameter. These trends occur in each preparation (Table II).

3. Effects of perforation location on H_PCAV

To test for effects of perforation location on H_PCAV, we measured H_PCAV in two preparations [discussed in Voss et al. (2001a) (bones 20, 24 Right)], in each of which measurements were made with a perforation at either of two locations. Voss et al. (2001a) demonstrated that patching small perforations (diameter less than 1 mm) with cigarette paper (moistened with saline) returns the middle-ear response (stapes velocity) to that with an intact TM, thus allowing comparison of responses with one perforation size at different locations.

Figure 3 compares the effects of perforations at two locations on H_PCAV for these two cases. In each case, the difference in H_PCAV (magnitude and angle) between the two perforation locations is small compared to the large variation with frequency; thus, H_PCAV appears to be independent of a perforation’s location for the comparisons (a) marginal versus central (Fig. 3, left column) and (b) anterior-inferior versus posterior-inferior (Fig. 3, right column). The slight differences in H_PCAV in the two locations could result from small differences in the perforation size or changes in H_PCAV from intact to patched TM. These results extend the conclusion of Voss et al. (2001a) that the effects of a TM perforation on the middle-ear’s response to sound do not depend on the perforation’s location in the TM.

C. Window-pressure-difference transfer function: H_WPD

Measurements of the pressure ratio P_RW/P_OW and the calculated transfer function H_WPD=1−P_RW/P_OW were analyzed for the subset of eight ears in which the probe-tube microphone calibrations were least variable (Sec. III C 4). Figure 4 plots P_RW/P_OW and |H_WPD|= |1−P_RW/P_OW| from one preparation (bone 24L); these plots are representative of the results from the other seven bones, as described below. Mean results across ears are not displayed, as inter-ear differences in the frequencies of magnitude maxima and minima result in means that are not representative of the shape of individual measurements; instead, features of these transfer functions in the eight preparations are presented in Table III.

FIG. 4.

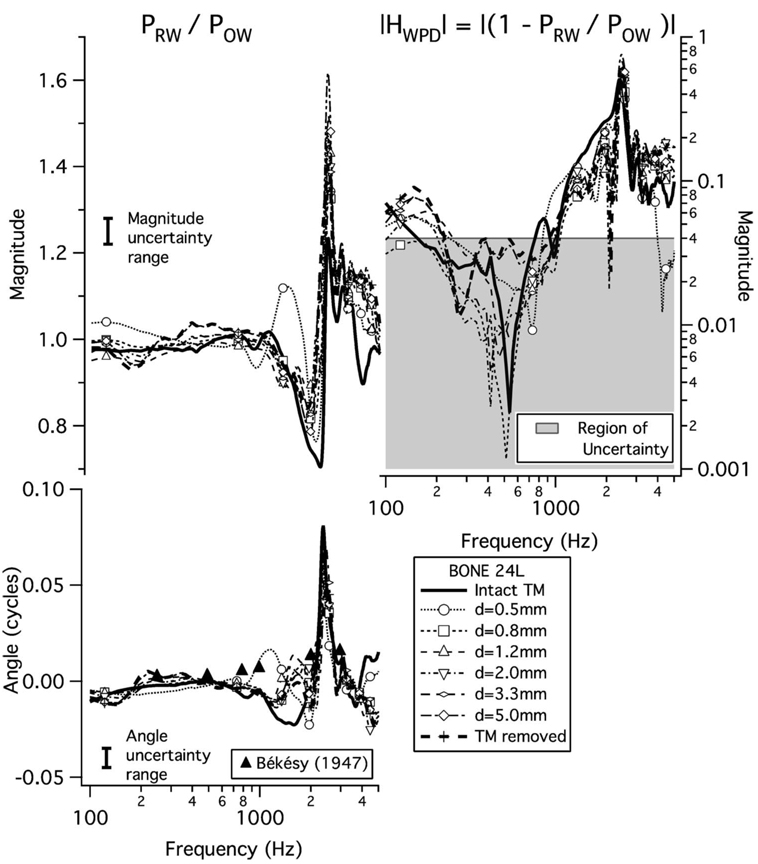
Example results from bone 24L yielding the window pressure difference transfer ratio H_WPD. The parameter is perforation size; symbols are plotted at every 20th data point. Left: P_RW/P_OW. The vertical bars labeled “Magnitude uncertainty range” and “Angle uncertainty range” indicate the range within which results are not distinguishable with our estimate of measurement error. The magnitude range is 0.06, corresponding to our error estimate of ±0.25 dB, and the angle range is 0.01 cycles, corresponding to our error estimate of ±0.005 cycles. In the lower plot, the filled triangles indicate angle-difference measurements from Békésy (1947) between the oval- and round-window pressures at six frequencies in one temporal bone with the TM removed. Right: |H_WPD|= |1−P_RW/P_OW| calculated from data on left. Points below 0.04 (gray shaded region) may have sizable errors (see Sec. III C 4).

Table III.

Features of H_WPD discussed in the text for each measurement. The columns labeled “Bone” and “Perf. Diam” indicate the preparation number and the state of the TM as intact, removed, or by the diameter in mm of the perforation; the column labeled $\left|\frac{P_{\text{RW}}}{P_{\text{OW}}}\right|$ (max) indicates the magnitude and frequency location of the maximum; the column labeled $\angle \frac{P_{\text{RW}}}{P_{\text{OW}}}$ (max) indicates the angle and frequency location of the maximum in angle; the column labeled $\left|\frac{P_{\text{RW}}}{P_{\text{OW}}}\right|$ (min) indicates the magnitude and frequency location of the minimum; the column labeled |H_WPD| (max) indicates the magnitude and frequency location of the maximum; the column labeled |Z_CAV| indicates the frequencies of the maximum and minimum in |Z_CAV| for each preparation, as reported in Voss et al. (2001c). The entry “NA” indicates the measurement was not available

Measures of salient features related to HWPD
Preparation		$\left|\frac{P_{\text{RW}}}{P_{\text{OW}}}\right|$ (max)		$\angle \frac{P_{\text{RW}}}{P_{\text{OW}}}$ (max)		$\left|\frac{P_{\text{RW}}}{P_{\text{OW}}}\right|$ (min)		|HWPD| (max)		|ZCAV|
Bone No.	Perf. Diam. (mm)	Mag.	fmax (kHz)	Angle (cycles)	f_max(kHz)	Mag.	fmin(kHz)	Mag.	fmax(kHz)	fZmax (kHz)	fZmin (kHz)
9	Intact	NA	NA	NA	NA	NA	NA	NA	NA	2.08	0.98
	0.1	1.1	0.95	0.02	0.83	1.0	0.78	0.2	0.85
	1.1	1.1	0.85	0.03	0.81	0.9	0.71	0.2	0.81
	1.9	1.2	0.95	0.05	0.90	0.9	0.85	0.3	0.90
	3.3	1.1	1.20	0.04	1.12	0.9	1.03	0.2	1.12
13	Intact	1.4	1.29	0.10	1.37	0.8	1.29	0.7	1.42	2.67	1.32
	0.5	1.3	1.15	0.06	1.32	0.9	1.15	0.4	1.39
	0.8	1.7	1.27	0.12	1.39	0.8	1.27	0.9	1.46
	1.4	1.7	1.12	0.14	1.20	0.7	1.12	1.1	1.25
	1.8	1.9	1.17	0.17	1.27	0.6	1.17	1.3	1.29
	Removed	1.3	1.32	0.07	1.42	0.8	1.32	0.5	1.44
18	Intact	1.4	2.49	0.09	2.42	0.79	2.29	0.6	2.44	NA	NA
	0.4	1.3	2.44	0.06	2.22	0.86	2.05	0.4	2.32
	0.5	1.4	2.37	0.07	2.20	0.84	2.05	0.5	2.27
	1.0	1.3	2.42	0.07	2.17	0.80	2.03	0.4	2.25
19	Intact	1.2	2.7	0.05	2.08	0.9	1.90	0.28	2.12	2.93	1.98
	0.6	1.3	2.4	0.05	1.98	0.9	1.61	0.30	2.37
	1.3	1.2	2.4	0.06	1.90	0.9	1.66	0.42	1.93
	1.9	1.2	2.4	0.07	1.88	0.9	1.66	0.43	1.93
	2.6	1.2	2.4	0.07	1.88	0.9	1.64	0.45	1.93
	Removed	1.2	2.4	0.04	2.05	0.9	1.90	0.25	2.03
20	Intact	1.1	2.34	0.01	2.12	0.9	2.05	0.1	2.08	3.66	2.22
	0.7	1.1	2.42	0.02	2.05	0.9	2.00	0.2	2.03
	0.7	1.1	3.00	0.02	2.05	0.9	1.95	0.1	2.00
	1.0	1.1	2.95	0.03	2.61	0.9	1.90	0.2	2.61
	1.7	1.1	2.95	0.03	2.56	0.9	1.86	0.2	2.56
	3.0	1.1	2.95	0.04	2.54	0.9	1.86	0.3	2.56
	4.0	1.1	2.93	0.04	2.54	0.9	1.83	0.3	2.56
	5.0	1.1	2.95	0.04	2.54	0.9	2.00	0.3	2.56
	Removed	1.1	2.95	0.04	2.54	1.0	2.05	0.3	2.54
22L	Intact	1.5	2.44	0.08	2.29	0.8	2.10	0.7	2.37	3.37	2.20
	0.6	1.4	2.44	0.04	2.27	0.8	2.05	0.4	2.42
	1.2	1.7	2.42	0.09	2.25	0.7	2.05	0.8	2.37
	2.0	1.7	2.44	0.09	2.29	0.8	2.03	0.9	2.39
	3.3	1.7	2.44	0.09	2.32	0.8	2.00	0.9	2.42
	5.0	1.7	2.44	0.09	2.29	0.8	1.95	0.9	2.39
	Removed	1.6	2.44	0.07	2.34	0.8	1.93	0.7	2.42
24L	Intact	1.2	2.47	0.08	2.37	0.7	2.22	0.5	2.39	2.98	2.10
	0.5	1.5	2.44	0.07	2.34	0.8	2.10	0.6	2.42
	0.8	1.4	2.49	0.05	2.42	0.8	2.00	0.5	2.49
	1.2	1.5	2.49	0.07	2.39	0.9	2.03	0.7	2.47
	2.0	1.5	2.49	0.07	2.42	0.8	1.83	0.6	2.47
	3.3	1.4	2.51	0.07	2.44	0.8	2.00	0.6	2.49
	5.0	1.6	2.47	0.06	2.37	0.8	1.93	0.8	2.44
	Removed	1.4	2.49	0.05	2.49	0.8	1.88	0.5	2.49
24R	Intact	2.0	2.83	0.23	2.73	0.3	2.69	1.5	2.78	4.00	2.61
	0.5	1.9	2.81	0.36	2.71	0.5	2.64	2.2	2.76
	0.6	1.7	2.76	0.18	2.64	0.8	1.93	1.4	2.71
	1.3	1.8	2.93	0.37	2.71	0.1	2.76	1.2	2.67
	2.3	1.8	2.93	0.35	2.69	0.6	2.76	1.6	2.66
	4.0	1.9	2.93	0.43	2.71	0.1	2.73	1.2	2.64
	5.0	1.8	2.93	0.34	2.69	0.0	2.71	1.1	2.93
	Removed	1.5	2.93	0.38	2.69	0.1	2.73	1.1	2.69

1. Frequency dependence

In all eight preparations, at the lower frequencies (i.e., less than 1000 Hz), the magnitude |P_RW/P_OW|≈1 and the angle ∠(P_RW/P_OW)≈0, indicating that P_RW≈P_OW; these features appear for both the intact TM cases and all perforation sizes, and are apparent in the example bone 24L in Fig. 4 (left). Above 1000 Hz, a frequency region exists where |P_RW/P_OW| exhibits a minimum with a magnitude less than 1 and at a higher frequency a maximum with a magnitude greater than 1; for example, in bone 24L with an intact TM, the magnitude minimum is about 0.7 at 2200 Hz and the magnitude maximum is about 1.2 at 2500 Hz (Fig. 4, left). In the frequency range of these extrema there is a sharp increase in ∠(P_RW/P_OW) to a peak and a steep decrease to near 0 cycles; in bone 24L, the peak in angle is about 0.08 cycles at about 2400 Hz. These features in data for bone 24L occur across all preparations. In each ear, for all TM conditions, between about 1000 and 3000 Hz, the ratio exhibits a local magnitude minimum adjacent to a local magnitude maximum, with an increase and decrease in angle. Although this pattern is seen in all ears, there are inter-ear variations in size and frequency of peaks (Table III).

Although at most frequencies P_RW and P_OW are roughly equal, between 1000 and 3000 Hz |P_RW| and |P_OW| have large derivatives with respect to frequency, and the biggest differences between P_RW and P_OW occur at the frequencies where |P_RW| and |P_OW| change rapidly (i.e., near 2500 Hz). All measurements show that in the frequency region of steep change a decrease in |P_RW| occurs in a slightly lower frequency range than the decrease in |P_OW|. This “frequency shift” produces the pattern of the local minimum in the pressure ratio |P_RW/P_OW| at a frequency just below a local maximum in |P_RW/P_OW|. The consistency of this behavior suggests that the dominant mechanism(s) is the same in all preparations. Possibilities for this mechanism(s) are proposed in Sec. V C.

In Sec. III C 4 we suggest that errors in the measurements of the oval- and round-window pressures lead to uncertainties of ±0.25 dB in magnitude and ±0.005 cycles in angle for the calculation of P_RW/P_OW. The corresponding “uncertainty ranges” of ±0.03 in magnitude (assuming P_RW ≈P_OW) and ±0.005 cycles in angle are indicated by a bracket in each plot of Fig. 4 (left). At a given frequency, measurements that are within the span of this bar may not represent a real difference. Therefore, differences between perforation conditions that are smaller than a factor of 0.06 in magnitude and 0.01 cycles in angle are considered not detectably different. Most of the measurements of magnitudes and angles of P_RW/P_OW are within the uncertainty estimate, so the small differences with perforation size may not reflect real differences. Measurements outside this uncertainty estimate, such as those from bone 24L between 1000 and 3000 Hz for all perforation sizes, are presumed to be significant.

Next, we consider the window-pressure-difference transfer function H_WPD (Fig. 4, right). This transfer function is simply related to the pressure ratio: H_WPD=1−(P_RW/P_OW). Thus, when P_RW/P_OW≈1, the magnitude |H_WPD|≪1 and the angle ∠H_WPD can be very sensitive to small changes in magnitude.

Most of the |H_WPD| results increase with frequency above 800 Hz to a local maximum between 1000 and 3000 Hz. This local maximum is a consequence of the local maximum of the pressure ratio |P_RW/P_OW|. However, below 800 Hz, 0.97≤ |P_RW/P_OW|≤1.03, such that |H_WPD|<0.04, and we cannot reliably determine |H_WPD|.

2. Effects of perforation size on |H_WPD|

For a given frequency below 1000 Hz, variations in bone 24L (Fig. 4) and the other seven preparations (Voss, 1998, page 251) do not seem to be systematically related to perforation size. The variability may result from small errors in our pressure measurements when P_OW≈P_RW, as the estimate of the lower limit for which we can accurately measure |H_WPD| is 0.04 (Sec. III C 4), which is indicated on the plot in Fig. 4 (right). Our calculations of |H_WPD| below about 1000 Hz are in the “region of uncertainty.” Data in this region are shown because their coherence across measurements in this region indicates that the main trends may be representative even at levels below |H_WPD|=0.04.

To compare results across ears and perforation size we systematically sort P_RW/P_OW and H_WPD results into seven groups differing in TM condition (defined in the legend of Fig. 2), and we compute the means within each of the seven groups for the three quantities |P_RW/P_OW|, ∠(P_RW/P_OW) and |H_WPD|. To determine if the differences between these means are significant, at each of six frequencies (125, 250, 500, 1000, 2000, and 4000 Hz) we use the “resampling-permutation” methodology described in Sec. III D to compute p values for differences between each group’s mean relative to all other measurements.

Tests between all combinations of seven TM conditions at six frequencies and for three quantities yield a total of 378 p values, which are all reported in Voss (1998). Almost all of the computed p values for all three quantities (|P_RW/P_OW| ,∠(P_RW/P_OW), |H_WPD|) are such that p≫0.05, indicating that the differences between the means are not significant. There are comparisons for which p<0.05, but these do not suggest any trends with perforation size. For example, there are four comparisons (of a total of 126 comparisons) for |P_RW/P_OW| for which p<0.05; two of these occur at 125 Hz and the other two at 250 Hz, both frequencies where the uncertainties limit the measurements. Similarly, occasional values where p<0.05 occur in the calculations for ∠(P_RW/P_OW) at the lower frequencies. However, there are no cases where p<0.05 for |H_WPD|. Thus, in general, we conclude that our results for |P_RW/P_OW|, ∠(P_RW/P_OW), and |H_WPD| do not demonstrate dependence on perforation size for any frequency range.

3. Effects of perforation location on H_WPD

We compare the effects of perforation location (i.e., anterior-inferior versus posterior-inferior) on the quantities |P_RW/P_OW|, ∠(P_RW/P_OW), and |H_WPD| in a similar manner to our comparison of perforation size (Sec. IV C 2). First, we form three perforation-size categories: (1) 0.1≤ d≤1 mm; (2) 1<d≤2 mm; and (3) 2<d≤4 mm. Next, within each size category, means are computed separately (at six frequencies ) for |P_RW/P_OW|, ∠(P_RW/P_OW), and |H_WPD| from perforations in the anterior-inferior quadrant and posterior-inferior quadrant. These means are then tested to determine if the differences between the two locations are significant.

The resulting p values for the perforation-location dependence of |P_RW/P_OW|, ∠(P_RW/P_OW), and |H_WPD| do not show systematic dependences of H_WPD on perforation location. For 51 of the 54, p>0.05; the remaining three comparisons, where p<0.05, do not suggest any trends. For example, for the diameter range 1<d≤2 mm, there is a possible location dependence for ∠(P_RW/P_OW) between anterior and posterior perforations for the frequencies 500 and 1000 Hz. However, this dependence is not seen for smaller or larger perforations at these frequencies. In general, the results do not indicate a perforation-location dependence of any of the three quantities |P_RW/P_OW|, ∠(P_RW/P_OW), and |H_WPD|.

D. Effects of tympanic-membrane perforations on net sound transmission via the acoustic route: |H_AR|

1. Measurements of |H_AR|

The acoustic-route transfer function |H_AR| is plotted in Fig. 5 for the example bone (24L) [and in Voss (1998) for all eight bones]. The lower plots in Fig. 5 (corresponding to the TM intact, removed, and with six perforation sizes) show that, below 1000 Hz, the measurements of |H_AR| are often in the “region of uncertainty,” which is based on relative errors in the measurement of P_OW and P_RW. Thus, some of these low-frequency measurements of |H_AR| are likely to be influenced by measurement errors.

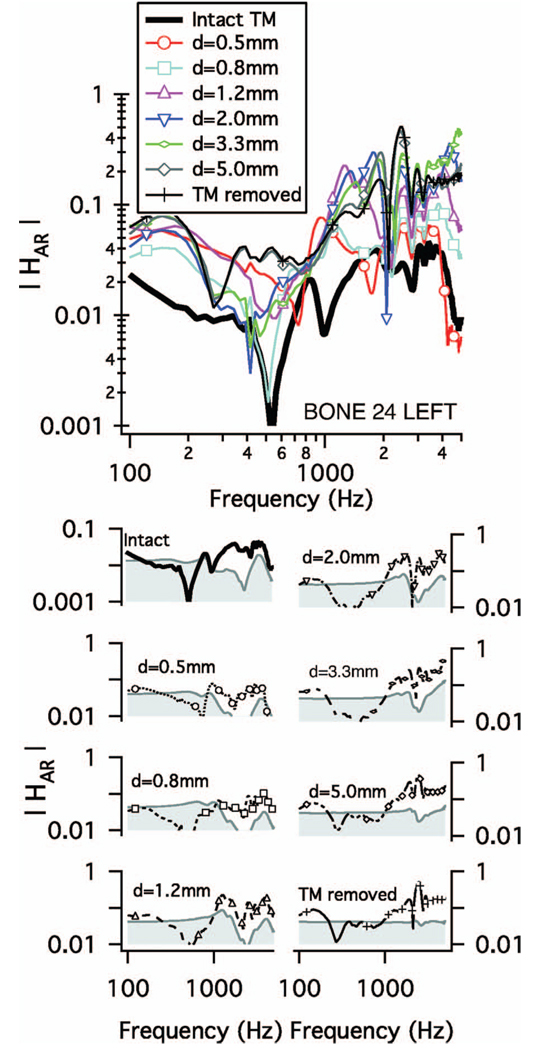
FIG. 5.

Acoustic-route transmission magnitude |H_AR|. Upper: |H_AR| for bone 24L. The parameter is perforation size as indicated in the legend. Symbols indicate every 20th data point. Lower: |H_AR| for each TM condition with our estimate of measurement “region of uncertainty,” which is shaded in gray. For each case, the upper limit of this region is 0.04|H_PCAV| (Table I)where the |H_PCAV| (Fig. 2) corresponds to the relevant TM condition. Note that the displayed y-axis range differs between the intact and perforated TM cases to accommodate differences in |H_PCAV|.

2. Effect of perforation size on |H_AR|

Figure 5 shows two general trends that occur across the preparations with perforation size as a parameter. First, with an intact TM |H_AR| is generally less than |H_AR| with a perforation; the increase in |H_AR| with a perforation is a consequence of the perforation-induced increase in |H_PCAV| as seen in Fig. 2. Second, for frequencies above about 1000 Hz, the perforation size influences |H_AR| in a manner similar to |H_PCAV| (see Fig. 2): at most frequencies, |H_AR| increases with perforation size, with the largest increase associated with the change from less than 1 mm to more than 1 mm in perforation diameter. These trends are apparent in the means of all |H_AR| measurements, grouped by perforation size (Fig. 6).

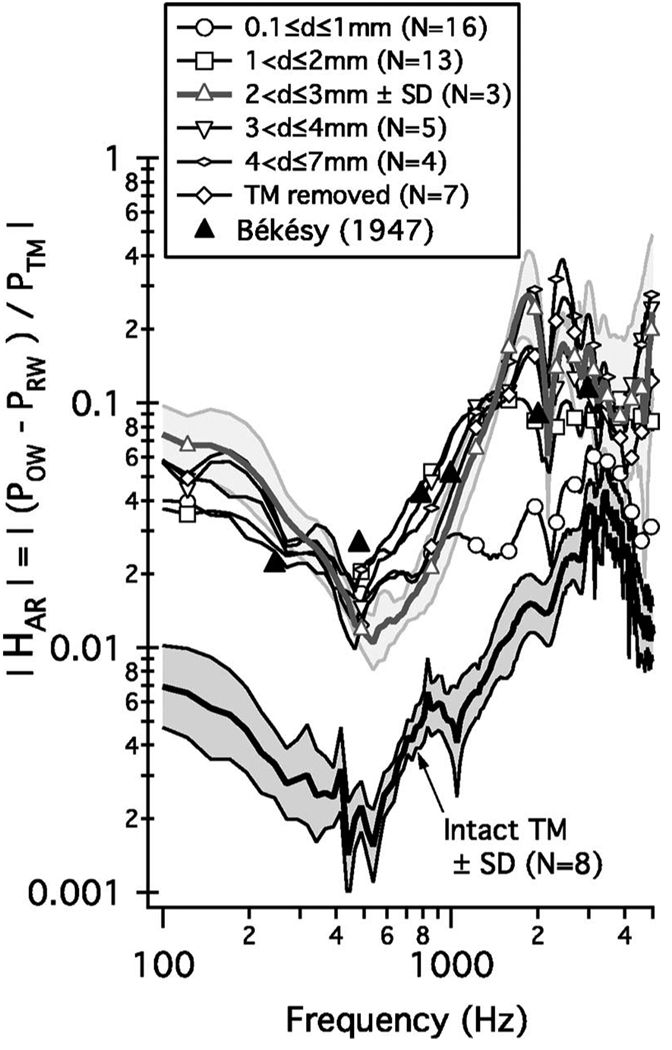
FIG. 6.

Mean acoustic-route transfer function magnitude |H_AR| computed in the logarithmic domain for the indicated TM conditions. The standard errors for the intact TM and perforation-diameter range 2<d≤3 mm are indicated by the shaded regions. The standard errors for all other groups are about the same or smaller than those for 2<d≤3 mm. Symbols indicate every 20th data point. The six black triangles indicate measurements from Békésy (1947) of the window pressure difference from one temporal bone with the TM removed. Below 1000 Hz, values may be influenced by relative errors in the measurement of the oval- and round-window pressures; for these lower frequencies the plotted curves can be considered an upper bound on |H_AR|.

We performed a probabilistic analysis to determine whether the differences between the means of the seven different groups plotted in Fig. 6 are significant. Using the “resampling-permutation” methodology (Sec. III D), we computed null-hypothesis probabilities p for each |H_AR| mean measurement relative to the six other mean measurements. The resulting probabilities that test for significance of differences in the means of |H_AR| are summarized here. Generally, the results are consistent with the qualitative impression given by Fig. 6. In particular, the differences between |H_AR| with an intact TM and |H_AR| with a TM perforation of any size are highly significant (p≪0.05) for nearly all perforation sizes at nearly all tested frequencies. At frequencies below 1000 Hz, there are no significant differences (p <0.05) between perforations of different sizes; either there are no true differences or our analysis is limited by inaccuracy in measuring the small pressure difference at these lower frequencies. Above 1000 Hz, there is evidence of significant differences in |H_AR| between the larger and smaller perforations: for example, at 2000 Hz there are significant differences between 15 of the 16 comparisons for size categories up to 3 mm diameters. There are not systematic trends at the other tested frequencies (1000 and 4000 Hz), and comparisons at 2000 Hz are not significant for comparisons among size pairs for which both are greater than 3 mm in diameter.

3. Effect of perforation location on |H_AR|

We compare the effects of perforation location on the |H_AR| in a similar manner to our comparison of perforation size performed above for P_RW/P_OW and H_WPD (Section IV C 2). Again, we compare perforations in the anterior-inferior quadrant to those in the posterior-inferior quadrant. First, we form three perforation-size categories: (1) 0.1≤d ≤1 mm; (2) 1<d≤2 mm; and (3) 2<d≤4 mm. All perforations such that 0.1≤d≤4 mm are placed into the appropriate category. Next, within each size category, means are computed separately for |H_AR| from perforations in the anterior-inferior quadrant and posterior-inferior quadrant. These means are then tested to determine if their differences are significant. There is no evidence of any perforation-location dependence for |H_AR|, as for all tests p>0.20.

V. DISCUSSION

A. Summary of measurements and their limitations

We have represented the acoustic-route transfer function H_AR=(P_OW−P_RW)/P_TM as the product of two transfer functions: the cavity-pressure transfer function (H_PCAV) and the window-pressure difference transfer function (H_WPD); i.e., H_AR=H_PCAVH_WPD. Here we summarize our conclusions regarding the effects of perforation location and size on these transfer functions.

The measurements show that H_PCAV depends on perforation size and not perforation location. In contrast, measurements of H_WPD do not show dependence on (1) whether the TM is intact or perforated, (2) perforation size, or (3) perforation location. Below 1000 Hz, the measurement accuracy for H_WPD and H_AR may be degraded by errors in the measurement of P_OW−P_RW (Sec. III C 4), but the measurements provide an upper limit for |H_WPD|.

B. Acoustic mechanisms that determine H_PCAV

An analog circuit model representing the acoustic interactions in middle ears with a TM perforation is shown on the left side of Fig. 7. The topology of this model requires that the volume velocity into the cavity is the sum of the volume velocities of the TM and of air through the perforation. Z_PERF and Z_CAV are represented on the right side of Fig. 7 by simple connections of ideal elements based on structural features of the perforation and cavities, and acoustic theory, as detailed in other work (Voss et al., 2000, 2001c; Stepp and Voss, 2005). This model topology is used here to consider mechanisms that might influence H_PCAV.

With this model (Fig. 7, left) we can relate impedance and pressure quantities that we have measured, specifically the circuit configuration requires that

$$H_{P_{\text{CAV}}}\equiv \frac{P_{\text{CAV}}}{P_{\text{TM}}}=\frac{Z_{\text{CAV}}}{Z_{\text{TM}}},$$ (7)

where Z_CAV is the impedance of the middle-ear cavities and Z_TM is the input impedance at the tympanic membrane.

Equation (7) suggests that, if |Z_CAV| varies gradually with frequency, then a local maximum in |H_PCAV| might occur at a local minimum in |Z_TM|. This relationship is tested in Fig. 8 (left) with independent measurements of |H_PCAV| (reported here) and |Z_TM| [reported in Voss et al. (2001c)]. The scatter plot demonstrates that the frequency of the local minimum in the magnitude of the input impedance at the TM Z_TM correlates well with the frequency of the local maximum in |H_PCAV|. Note that variations in each ear are a result of changes in perforation size, which alter both coordinates. Thus, the low-frequency (0.5–2.8 kHz) maximum in |H_PCAV| depends on features of both the cavities and the perforation (as Z_TM depends on both quantities).

FIG. 8.

Scatter plots that connect frequencies of extrema of |H_PCAV| and frequencies of extrema in the magnitudes of the middle-ear input impedance |Z_TM| and the middle-ear cavity impedance |Z_CAV|. (Impedance measurements were reported in Voss et al. (2001c).) In each plot points are shown for all measurements including several perforation sizes (see legends for numbers) and all preparations. Bone 18 is omitted because impedance measurements do not exist for that preparation. The straight lines in each plot represent the relationship y (ordinate)=x (abscissa). Left: the frequency of the maximum in |H_PCAV| versus the frequency of the minimum of |Z_TM|. Right: The frequency of the minimum in |H_PCAV| versus the frequency of the minimum of the impedance of the middle-ear cavity |Z_CAV|. N.B. The horizontal coordinate for all points in a given ear is the same, because Z_CAV was measured in only one condition—i.e., with the TM removed.

Similarly, the model suggests that the frequency of the minimum in the cavities’ impedance magnitude |Z_CAV| [reported in Voss et al. (2000) and Voss et al. (2001c)] might occur at the same frequency as the minimum in |H_PCAV|. This relationship is tested in Fig. 8 (right) with independent measurements of |H_PCAV| and |Z_CAV| [reported in Voss et al. (2000)]. The scatter plot demonstrates that the frequency of the local minimum in the cavities’ impedance magnitude |Z_CAV| correlates well with the frequency of the local minimum in |H_PCAV|. Thus, the minimum in |H_PCAV| (0.9–2.7 kHz) depends primarily on features of the middle-ear cavities, consistent with the observation that the minimum frequency appears to be independent of perforation diameter.

The more detailed model in Fig. 7 (right) provides representations for the model impedances Z_PERF and Z_CAV (Fig. 7, left) (Voss et al., 2000, 2001c). The perforation is represented by a combination of mass and resistive components that depend on frequency and perforation size (Voss et al., 2001c); except for the very smallest perforations and the lowest frequencies (diameters less than 1 mm and frequencies less than 300 Hz), the perforation’s impedance is mass dominated such that the impedance magnitude |Z_PERF| generally can be represented as

$$Z_{\text{PERF}}\approx j\omega M_{\text{PERF},}$$ (8)

where ω=2πf with f frequency and M_PERF the equivalent acoustic mass of the perforation. We note that |Z_PERF| increases with frequency for a constant diameter and decreases with larger perforation diameters for a constant frequency [see Fig. 3 of Voss et al. (2001c)]. The model representation for the middle-ear cavities includes two volume-velocity paths: (1) the tympanic-cavity air space, represented by a compliance, and (2) the aditus-ad-antrum leading to the antrum and mastoid-cell network represented by a series mass and resistance leading to a compliance. [This model representation is detailed in Voss et al. (2000) and Stepp and Voss (2005)]. For low frequencies³

$$Z_{\text{CAV}}\approx \frac{1}{j\omega C_{\text{CAV}}},$$ (9)

where C_CAV is a compliance that is proportional to the cavities’ equivalent volume. The mass of the perforation and the compliance of the middle-ear cavities produce a series resonance (i.e., Z_PERF+Z_CAV=0) such that |H_PCAV| is a maximum at

$$f_{\text{max}}=\frac{1}{2\pi C_{\text{CAV}}{M}_{\text{PERF}}},$$ (10)

where f_max increases with increasing perforation diameter because M_PERF decreases with increasing perforation diameter. This dependence is qualitatively consistent with the observation that the frequency of the maximum in |H_PCAV| increases with increasing perforation diameter (Table II). Thus, the model predicts that the frequency of the maximum in |H_PCAV| is effectively determined by the dimensions of the perforation and the volume of the middle-ear air space.

For each ear, the frequency of the minimum in |H_PCAV| changes moderately with perforation size and is correlated with a feature of Z_CAV (Fig. 8, right). The model for Z_CAV (Fig. 7, right) has a minimum in Z_CAV that occurs at the frequency of the series resonance between the mass of the aditus (M_ad) and the compliance of the air in the antrum and mastoid (C_mastoid) (Voss et al., 2000; Stepp and Voss, 2005) such that the frequency of the minimum in |Z_CAV| occurs at

$$f_{\text{min}}=\frac{1}{2\pi C_{\text{mastoid}}{M}_{\text{ad}}}.$$ (11)

Thus, the model predicts that the frequency of the minimum in |H_PCAV| is effectively determined by the resonance between the mass that represents the aditus ad antrum and the compliance that is determined by the volume of the antrum and mastoid air space. This dependence is consistent with the observation that the frequency of the minimum in |H_PCAV| does not depend on perforation size (Table II). We note that there is substantial variation in f_min among preparations, which appears to result from intra-ear structural variations in the aditus, antrum, and mastoid.

Our H_PCAV results can be compared to finite-element (FE) model predictions from Gan et al. (2006). The FE model pressures that determine H_PCAV are plotted in Fig. 4 of Gan et al. (2006) for an intact TM and in Fig. 6–Fig 8 of Gan et al. (2006) for small TM perforations; the comments here focus on the model predictions corresponding to pressures 2 mm from the umbo and within the middle-ear cavity. The FE model results are consistent with our measurements in that the model pressures at both the oval and round windows are nearly identical, making the calculation of H_PCAV essentially independent of the location of measurement of middle-ear pressure. For an intact TM, FE model results of Gan et al. (2006) differ from both our measurements and our lumped-element model at frequencies below 1000 Hz. Both the lumped-element model of Fig. 7 and measurements of H_PCAV on 11 ears with intact TMs [Fig. 2 here and Appendix G of Voss (1998)] show that the magnitude |H_PCAV| is relatively independent of frequency for low frequencies (typically below 500–1000 Hz) with a corresponding angle ∠H_PCAV that is nearly zero; Fig. 4 of Gan et al. (2006) shows low-frequency FE model predictions that result in |H_PCAV| systematically increasing with frequency and ∠H_PCAV systematically decreasing with frequency. For a perforated TM, the FE model results [Fig. 6–Fig 8 of Gan et al. (2006)] are similar to both our measurements and our lumped-element model at all frequencies; specifically, magnitude |H_PCAV| is approximately 1 for low frequencies (typically below 1000 Hz) with a corresponding angle ∠H_PCAV that is nearly zero, consistent with the mechanisms described in detail by Voss et al. (2001c) for how a perforation affects the pressure difference across the TM.

C. Acoustic mechanisms that determine H_WPD

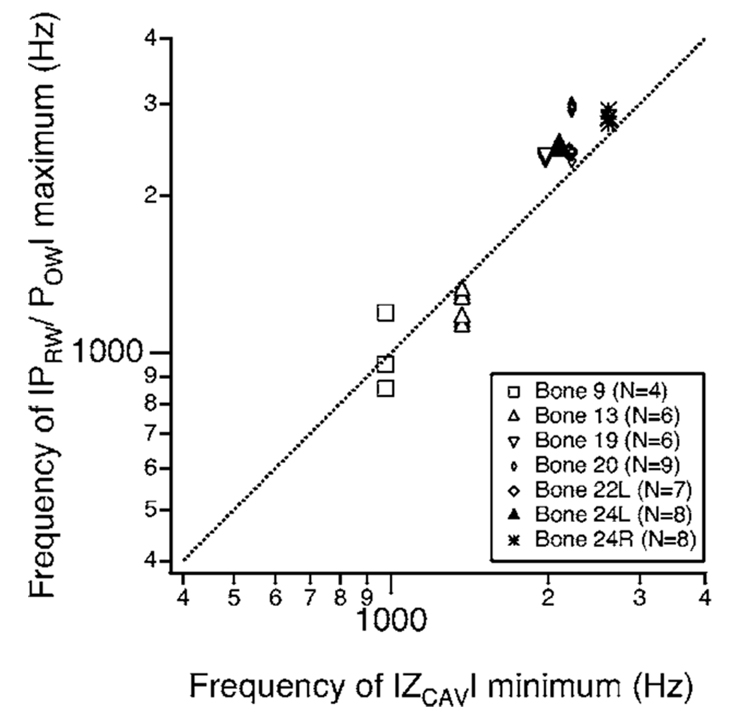
The quantities P_OW, P_RW, and H_WPD are not represented by the lumped-element model of Fig. 7, as the model assumes a uniform middle-ear-cavity pressure. However, we can suggest a mechanism that relates |P_RW/P_OW| to the middle-ear cavities. The results show a consistent peak in |P_RW/P_OW| at a frequency that varies among preparations between 800 and 3000 Hz but in a given preparation is independent of perforation size. The lack of dependence on perforation size suggests that this peak is related to the structure of the middle-ear cavities. The frequency of the peak in |P_RW/P_OW| and the frequency of the minimum in |Z_CAV| are closely correlated (Fig. 9). At the frequency of the minimum in |Z_CAV|, one might expect a maximum in volume velocity (and particle velocity) entering the aditus from the tympanic cavity. This velocity maximum might produce a relatively large spatial derivative in pressure⁴ in the region of the windows and therefore an increased difference between P_RW and P_OW. Thus, a feature of the middle-ear cavity structure might determine the peak frequency of |P_RW/P_OW|.

FIG. 9.

Scatter plot that connects the window-pressure ratio to features of the middle-ear cavity. Plotted is the frequency of the magnitude maximum in |P_RW/P_OW| versus the frequency of the minimum of the middle-ear cavity impedance |Z_CAV|. (Impedance measurements were reported in Voss et al. (2001c).) In many cases points from different perforations on the same preparation (bone) are identical and so it is not possible to distinguish all of the plotted points. Data are included only from ears in which variability in P_RW/P_OW calibrations were small; Bone 18 does not appear as impedance measurements are not available.

In the future, finite-element models might provide additional insight into the relationship between P_OW and P_RW. The plots and text in Gan et al. (2006) are consistent with small differences between P_OW and P_RW.

D. Effects of reduced middle-ear air space

Measurements in Stepp and Voss (2005) demonstrate that reduction of the mastoid portion of the cadaver ears influences middle-ear acoustics. The measurements presented here were made on bones that were removed with a circular saw (Schuknecht, 1968) such that much of the mastoid air-cell network was removed. The demonstrable effects of this loss of mastoid air cells are a decrease in total middle-ear air-space volume and removal of highly individualistic resonances in the cavity impedance at frequencies above 1000 Hz (Stepp and Voss, 2005). These results suggest that, if the acoustic-route measurements reported here had been made on ears with intact mastoid spaces, changes would be:

1. Greater inter-ear variability in H_PCAV as a result of inter-specimen structural variations of mastoid air spaces; specifically, the frequencies and values of the extrema in H_PCAV at higher frequencies (i.e., f>1000 Hz) would be altered.

2. Larger changes between the intact and the perforated |H_PCAV|, especially at the lower frequencies (f<1000 Hz) where the acoustics are compliance dominated. Specifically, the larger cavity volumes would lead to smaller low frequency |H_PCAV| with an intact TM, whereas a perforation would still make H_PCAV≈1 for the lower frequencies.

3. As H_WPD is apparently determined by the acoustic configuration of the middle-ear cavities, it seems likely that H_WPD would also have different features with intact cavities.

E. Conditions in which the acoustic route may be important for hearing with tympanic-membrane perforations

1. Overview

As discussed in the Introduction, when an ear is normal, the ossicular route is the dominant mechanism for sound transmission to the cochlea, and transmission via the acoustic route is negligibly small. Figure 6 demonstrates that sound transmission via the acoustic route increases when the TM is perforated. Here, we look for situations in ears with perforations in which the acoustic route becomes significant.

Voss et al. (2001b) present measurements of the middle-ear transfer function V_S /P_TM (stapes velocity per pressure at the TM) made with both intact and perforated TMs. These measures are assumed to include transmission via both the ossicular and acoustic routes:

$$\frac{V_S^{\text{total}}}{P_{\text{TM}}}=\frac{V_S^{\text{acoustic}}}{P_{\text{TM}}}+\frac{V_S^{\text{ossicular}}}{P_{\text{TM}}}.$$ (12)

In this section, we use our measurements of the acoustic-route transfer function H_AR to compute an upper bound for the acoustic-route transmission $|V_S^{\text{acoustic}}/P_{\text{TM}}|$. We then compare this upper bound with our measurements of $|V_S^{\text{total}}/P_{\text{TM}}|$ (Voss et al., 2001b) in order to determine the importance of the acoustic-route component in the total transmission.

2. Comparison of acoustic route transmission to normal middle-ear transmission

In this section, we compare the total middle-ear transmission to the acoustic-route transmission for ears with either intact or missing TMs.

The stapes velocity per pressure at the TM that results from the pressure difference at the oval and round windows, $V_S^{\text{acoustic}}/P_{\text{TM}}$, can be expressed in terms of three quantities: the pressure measurements at the oval and round windows, the stapes-cochlea acoustic impedance Z_SC, and the area of the stapes footplate A_S

$$\frac{V_s^{\text{acoustic}}}{P_{\text{TM}}}=\frac{P_{\text{OW}}-P_{\text{RW}}}{P_{\text{TM}}{Z}_{\text{SC}}{A}_s}=\frac{H_{\text{AR}}}{Z_{\text{SC}}{A}_s}.$$ (13)

Here we use the average Z_SC measured in cadaveric temporal bones by Merchant et al. (1996) and the average A_S =3.2 mm² reported by Wever and Lawrence (1954, p. 417).

Equation (13) was used to compute the mean $\left|V_S^{\text{acoustic}}\right|/P_{\text{TM}}$for both the TM intact and TM removed cases (two lower curves in the top plot of Fig. 10); these curves are upper bounds for middle-ear sound transmission with either the TM intact or removed. The magnitude is larger with TM removed because |H_AR| is larger (see Fig. 5). Higher in the top plot (Fig. 10) is the mean measured total middle-ear sound transmission $|V_S^{\text{total}}/P_{\text{TM}}|$ from Fig. 4 of Voss et al. (2000). The magnitude of the total transmission relative to the acoustic-route transmission (in the lower plot of Fig. 10) describes the importance of the acoustic route in sound transmission to the cochlea. With an intact TM, the total stapes velocity is 100–3000 times (i.e., 40–70 dB) greater than the upper bound on the acoustic-route stapes velocity (Fig. 10, lower). Thus, when the TM and ossicular chain are normal, transmission via the acoustic route is negligibly small relative to the ossicular route.

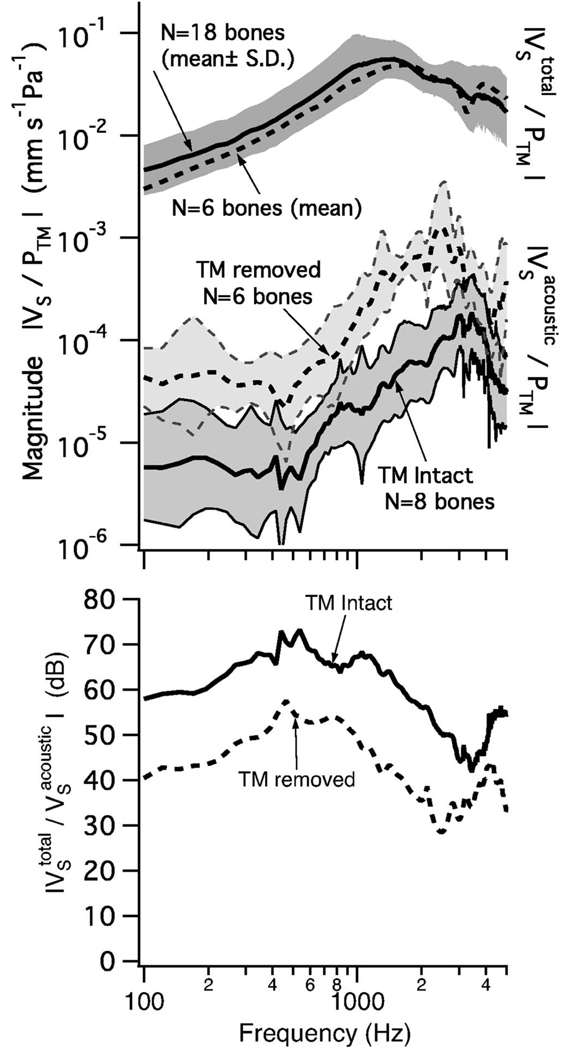
FIG. 10.

Results relevant to the possible impact of acoustic coupling. Upper: Eq. (13) was used to compute the mean $\left|V_S^{\text{acoustic}}\right|/P_{\text{TM}}$for both the TM intact and TM removed cases (two lower curves in the top plot). For comparison the upper curve shows the average measured total middle-ear transmission $|V_S^{\text{total}}/P_{\text{TM}}|.\left|V_S^{\text{total}}{P}_{\text{TM}}\right|$was measured with the laser-Doppler system on bones with an intact TM. The mean±the standard deviation (S.D.), associated with 18 bones, comes from Voss et al. (2000), (Fig. 4). The mean of N=6 normal bones (dashed line upper) is from the six bones used to calculate the acoustic-route stapes velocity with the TM removed (dashed line lower), where $\left|V_S^{\text{acoustic}}\right|/P_{\text{TM}}|$is calculated from Eq. (13) using the mean H_AR for the normal and the TM removed conditions. (The closeness of these two upper curves indicates that the smaller group was similar to the larger group in making comparisons with the N=6 TM removed group.) The standard deviations are shaded and account for variation in both (1) the H_AR measurements made here and (2) the Z_SC measurements made by Merchant et al. (1996). Lower: Curves show the dB differences between each of the two acoustic-route transmissions and the total transmission curve (from the top plot). The vertical coordinate here represents the hearing loss resulting from loss of ossicular coupling for either TM condition.

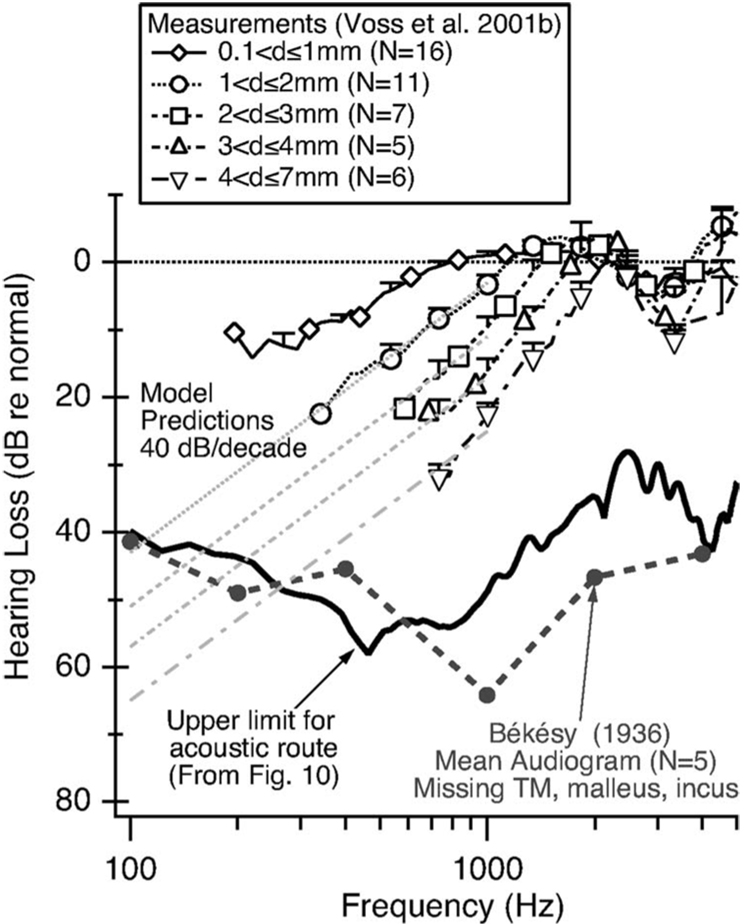
The measurements of H_AR allow us to calculate an upper bound for hearing loss with the TM removed; measurements of stapes velocity under this condition are not available because the stapes motion was below the noise floor of the measurement system. H_AR for the TM-removed condition is similar to that with TM perforations (Fig. 6). When the TM is removed (or perforated) the upper bound on transmission via the acoustic route $V_S^{\text{acoustic}}/P_{\text{TM}}$ increases (Fig. 10) and the total transmission $V_S^{\text{total}}/P_{\text{TM}}$decreases (not shown), with specific decreases dependent on the perforation size (Voss et al. 2001b). When the decrease in $V_S^{\text{total}}/P_{\text{TM}}$is substantial (e.g., with larger perforations), the acoustic-route transmission could make significant contributions to the total transmission and thus determine the hearing loss. This upper hearing-loss limit is equivalent to the ratio between total sound transmission in the intact condition ($V_S^{\text{total}}/P_{\text{TM}}$with an intact TM) and the upper bound on the acoustic-route sound transmission in the TM removed condition ($V_S^{\text{acoustic}}/P_{\text{TM}}$ with the TM removed). This estimate of an upper limit for loss with TM perforations is included in the lower part of Fig. 10. The limit is between 40 and 60 dB at frequencies up to 2000 Hz, and from 2000 to 4000 Hz between 30 and 40 dB. These limits are comparable to the 45–65 dB hearing losses that Békésy (1936) reported in patients with missing TMs, mallei, and incudes (Békésy, 1936; Peake et al., 1992).

Figure 11 compares total transmission loss with different sized TM perforations (Voss et al., 2001a, b) to an estimated upper limit for transmission loss that is determined by the acoustic route. At most frequencies, even with perforations, the measured stapes-velocity (V_S) losses are above the limit set by the acoustic route, indicating that the ossicular route dominates the stapes-velocity measurements. However, the plotted upper limit for the “acoustic-route” suggests that the acoustic route may limit the loss at the lowest frequencies, especially for the larger perforations, where the measured losses begin to approach the acoustic-route limit. The measured losses are limited at the lowest frequencies by the noise floor for stapes velocity, but models of middle-ear sound transmission with perforations predict that the low-frequency losses increase as frequency decreases (Voss et al., 2001c); for perforations greater than about 1 mm in diameter, the model predicts that changes in the pressure difference across the TM dominate the total loss in the ossicular route and that at low frequencies these losses increase with decreasing frequency at 40 dB/ decade. These predictions are included on the plot in Fig. 11, showing that the acoustic route could contribute substantially with the larger perforations at the lowest frequencies (e.g., less than 500 Hz).

FIG. 11.

“Hearing loss” (based on stapes-velocity V_S measurements in cadaveric temporal bones) resulting from perforations in the tympanic membrane. The upper five lines are mean measured loss in total transmission for five categories of perforation size (Voss et al., 2001a, b). The curve labeled “Upper-limit for acoustic-route” is the transmission loss that would result if the acoustic route were dominant (from the “TM removed” curve in the lower plot of Fig. 10). Measurement of loss at the lower frequencies was not possible because the measurements were indistinguishable from noise. However, the model prediction for the loss increases at 40 dB/decade for low frequencies (Voss et al., 2001c) as indicated by the straight gray lines for four perforation sizes. Also plotted is the mean audiogram collected by Békésy (1936); (1960 p. 105) on five subjects with missing TM, malleus, incus and stapes. The similarity of the two lower curves is consistent with the hypothesis that the acoustic route is the dominant path for sound transmission in these ears.

Figure 11 also plots the mean audiogram measured by Békésy (1936) on five ears missing the TM, malleus, incus, and stapes. In these ears, it seems that the acoustic route could be responsible for hearing. That is, the measured hearing loss is comparable to the upper limit for the acoustic route for frequencies less than 4000 Hz. Thus, this audiogram is consistent with the hypothesis that hearing in this condition is determined by the acoustic route⁵ (Peake et al., 1992; Mehta et al., 2006).

VI. CONCLUSIONS

Middle-ear sound transmission with perforated tympanic membranes is dominated by sound transmission via the ossicular system (ossicular route) for most perforation sizes; the acoustic route dominates when the TM is missing. Direct acoustic stimulation of the cochlear windows (acoustic route) provides a significant amount of sound transmission only at the lowest frequencies with a condition approaching total removal of the tympanic membrane. Sound transmission via the acoustic route is independent of perforation location but does depend on perforation size. These variations of sound transmission via the acoustic route result entirely from changes in transmission of sound from the ear canal to the middle-ear cavity, measured here as H_PCAV. In fact, the dependence of the window-pressure ratio P_RW/P_OW and the window-pressure difference H_WPD on the pressure in the middle-ear cavity appear independent of (1) the presence of a tympanic-membrane perforation, (2) perforation size, and (3) perforation location. In other words, the relative magnitudes and angles of the pressures just outside the oval and round windows are unaffected by any tympanic-membrane perforation. The results (1) refute the common clinical view (described in the Introduction) that perforation location affects the relative phase of the sound pressures at the oval and round windows, and (2) provides the most complete existing description of the window pressure ratio P_RW/P_OW based on experimental data.