Enumerating the decomposable neighbours of a decomposable graph under a simple perturbation scheme

Abstract

Given a decomposable graph, we characterize and enumerate the set of pairs of vertices whose connection or disconnection results in a new graph that is also decomposable. We discuss the relevance of this results to Markov chain Monte Carlo methods that sample or optimize over the space of decomposable graphical models according to probabilities determined by a posterior distribution given observed multivariate data.

1 Introduction

The flexibility and tractability of decomposable graphical models make them an attractive option for fitting to a broad array of complex multivariate data types. Commonly, the Markov, or conditional independence, graph of the graphical model is regarded as unknown, and is an objective of inference, along with parameters of the joint probability distribution of the data. This is the setting, of joint structural and parametric inference, that is considered here. [6] developed a penalized likelihood approach to graphical model estimation that they implemented in the BIFROST program, which used a deterministic search method to find an optimal model. Other authors have used random methods to optimize the model, or sample from well fitting models, in effect implementing Metropolis-Hastings [10, 5] or simulated annealing [8] samplers for the posterior probability distribution on decomposable graphical models corresponding to the penalized likelihood. [4] developed such methods for Gaussian models, while [13] and [12] applied this approach to modelling discrete distributions for allelic association between genetic loci in the same genomic region. The programs developed for this latter application can also be used to estimate a graphical model for general finite valued multivariate data. More recent work in graphical model estimation includes [7] and [2]. Common algorithmic elements in these approaches are, given a decomposable graphical model with Markov graph G, to propose a new graph G′ by either adding or deleting an edge, checking that the G′ is decomposable, calculating its likelihood and prior probability, and hence either accepting or rejecting the proposal as appropriate according to the posterior probabilities. Implemented naively, checking for decomposability of G′, using a maximum cardinality search [11] for example, will take time of order |V | + |E| where V and E are respectively the vertex and edge sets of G. Calculating the likelihood and prior of G′ directly is also a substantial computation of order |V |. However, [4] showed that establishing the decomposability of G′, given the decomposability of G, could be done in close to constant time when the perturbations involve either adding or deleting an edge and, moreover, that the difference in likelihood and prior between G and G′ depends only on local differences that can be evaluated in time independent of the size of the graph. These results allow much faster sampling and optimization methods even for moderately large graphs. For example, the HapGraph program [12] for estimating graphical models for allelic association between genetic loci has been changed to use Giudici and Green’s method and so works in reasonable time for several thousand variables.

However, for very large graphs the probability that the addition or deletion of a randomly proposed edge results in a decomposable graph becomes vanishingly small. Intuitively, for the relatively sparse graphical models often seen in practice, we would expect the number of allowable changes to be approximately linear in the size of the graph, whereas the number of all pairs is quadratic. Thus, as the size of the problem increases, any rejection algorithm becomes very inefficient. Recent advances in technology, particularly in molecular biology, allow simultaneous measurement of hundreds of thousands of variables in a single assay, so, in this field at least, this low acceptance rate is a real obstacle to the use of graphical model based inference.

This problem could be avoided by characterizing and enumerating the set of pairs of vertices whose connection or disconnection results in a decomposable model, and then sampling a proposed perturbation with uniform probability from this set. Identifying the pairs whose disconnection results in a decomposable graph is easily done using Giudici and Green’s result, and we illustrate this below. Identifying pairs which can be connected while preserving decomposability is more involved, but we develop here a framework that allows this and again provide an illustrative example.

2 Definitions and preliminary results

We begin by reviewing some definitions and standard properties of decomposable graphs and junction trees. A complete treatment of the topic is given by [9].

Consider a graph G = G(V,E) with vertices V and edges E. A subset of vertices U ⊆ V defines an induced subgraph of G which contains all the vertices U and any edges in E that connect vertices in U. A subgraph induced by U ⊆ V is complete if all pairs of vertices in U are connected in G. A clique is a complete subgraph that is maximal, that is, it is not a subgraph of any other complete subgraph.

Definition 1

A graph G is decomposable if and only if the set of cliques of G can be ordered as (C₁,C₂, …,C_c) so that for each i = 1, 2,…, c − 1

$$if{S}_i=C_i\cap \underset{j=i+1}{\overset{c}{\cup }}{C}_j\mathit{then}{S}_i\subset C_k\mathit{for}\mathit{some}k>i.$$ (1)

This is called the running intersection property. Note that decomposable graphs are also known as triangulated or chordal graphs and that the running intersection property is equivalent to the requirement that every cycle of length 4 or more in G is chorded. The sets S₁,…S_c−1 are called the separators of the graph. The set of cliques {C₁, …C_c} and the collection of separators {S₁, …S_c−1} are uniquely determined from the structure of G, however, there may be many orderings that have the running intersection property. The cliques of G are distinct sets, but the separators are generally not all distinct. Let S_[1], …S_[s] be the distinct sets contained in the collection of separators.

Definition 2

The junction graph of a decomposable graph has nodes {C₁, …,C_c} and every pair of nodes is connected. Each link is associated with the intersection of the two cliques that it connects.

Note that for clarity we will reserve the terms vertices and edges for the elements of G, and call those of the junction graph and its subgraphs nodes and links.

Definition 3

Let J be any spanning tree of the junction graph. J has the junction property if for any two cliques C and D of G, every node on the unique path between C and D in J contains C ∩ D. In this case J is said to be a junction tree.

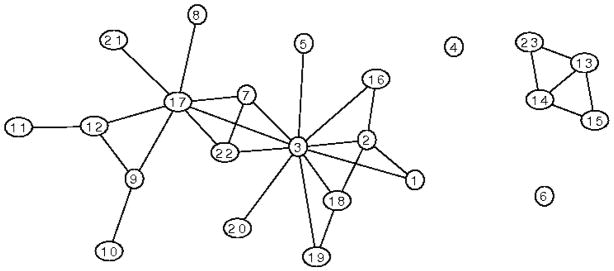
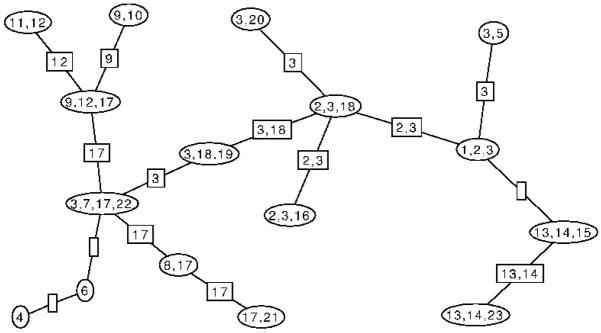
For illustration, Figure 1 gives an example of a decomposable graph while Figure 2 shows one of its possible junction trees. Some authors first partition a graph into its disjoint components before making a junction tree for each component, combining the result into a junction forest. The above definition, however, will allow us to state results more simply without having to make special provision for nodes in separate components. In effect, we have taken a conventional junction forest and connected it into a tree by adding links between the components. Each of these new links will be associated with the empty set and have zero weight. Clearly, this tree has the junction property. Results for junction forests can easily be recovered from the results we present below for junction trees. A junction tree for G will exist if and only if G is decomposable, and algorithms such as the maximal cardinality search of [11] allow a junction tree representation to be found in time of order |V | + |E|. The collection of clique intersections associated with the c − 1 links of any junction tree of G is equal to the collection of separators of G. The junction property ensures that the subgraph of a junction tree induced by the set of cliques that contain any set U ⊆ V is a single connected tree.

Figure 1.

A decomposable graph containing 23 vertices in 4 disjoint components.

Figure 2.

One possible junction tree for the graph shown in Figure 1. The 16 cliques are the vertices of the junction tree and are shown as ovals. The 15 clique separators are represented by the edges of the graph and each edge is associated with the intersection of its incident vertices. These intersections are shown as rectangles. Note that some of these intersections are empty.

3 Enumerating allowable perturbations

[3] and [4] gave efficient methods for checking that G′ is decomposable, given that G is, when the perturbation scheme involves respectively disconnecting or connecting a random pair of vertices. Using our definition of a junction tree, we can restate their results as follows.

• Removing an edge (x, y) from G will result in a decomposable graph if and only if x and y are contained in exactly one clique.

• Adding an edge (x, y) to G will result in a decomposable graph if and only if x and y are unconnected and contained in cliques that are adjacent in some junction tree of G.

Thus, enumerating the disconnectible pairs of vertices is easy to do. Having found the cliques of G, we simply visit each in turn and count the number of edges that appear only in that clique. If C is the unique clique containing (x, y), we say that the disconnection of (x, y) is allowed by C.

Characterizing connectible pairs of vertices, however, is more complicated. If we keep track of the junction tree J representing our incumbent graph in the course of a sampling scheme, it is not enough to check the links of J to see whether x and y are in adjacent cliques. We also have to, in effect, consider all possible junction trees equivalent to J. To achieve this we first show that the set of connectible pairs can be partitioned over the distinct separators of G. We then give a method for identifying the pairs corresponding to each distinct separator.

Let x and y be unconnected vertices of decomposable G whose connection results in a new decomposable graph G′. Giudici and Green’s condition ensures that G must have cliques C_x∋ x and C_y ∋ y that are linked in some junction tree J of G. Let S = C_x ∩ C_y be the intersection associated with the link. Under this assumption the two following results hold.

Proposition 4

There are no cliques $C_x^{\prime }\ni x$ and $C_y^{\prime }\ni y$ with either $C_x^{\prime }\ne C_x$ or $C_y^{\prime }\ne C_x$ that are adjacent in J.

Proof

Assume for the sake of contradiction that such $C_x^{\prime }$ and $C_y^{\prime }$ do exist. By the junction property there is a path from $C_x^{\prime }$ to C_x in J through nodes that all contain x, and similarly one from $C_y^{\prime }$ to C_y through nodes containing y. Since C_x and C_y are not both equal to $C_x^{\prime }$ and $C_y^{\prime }$, at least one of these paths has length greater than 0. Also, since x and y are not connected they cannot appear in the same clique so these paths do not intersect. Thus, since C_x and C_y are adjacent, a link between $C_x^{\prime }$ and $C_y^{\prime }$ creates a cycle of at least 3 nodes violating J’s tree property.

Proposition 5

Let $C_x^{\prime }\ni x$ and $C_y^{\prime }\ni y$ be cliques of G that are adjacent in some junction tree J′ ≠ J. Let $S^{\prime }=C_x^{\prime }\cap C_y^{\prime }$. Then S′ = S.

Proof

Consider the positions of $C_x^{\prime }$ and $C_y^{\prime }$ in J. Again we construct the unique path in J from $C_x^{\prime }$ to C_x, C_x to C_y and C_y to $C_y^{\prime }$, although it is possible now that $C_x^{\prime }=C_x$ and $C_y^{\prime }=C_y$ in which case the path has length 1. By the junction property S′ must be contained in each node along the path, and in particular S′ ⊆ C_x and S′ ⊆ C_y. Hence S′ ⊆ C_x ∩ C_y = S. By similarly considering the path from C_x to C_y in J′ we also have that S ⊆ S′, and so S′ = S.

These two results immediately give us the following.

Theorem 6

The set of all possible connectible pairs of vertices of a decomposable graph G can be partitioned according to the distinct separators of G. The subset of connectible pairs for a particular distinct separator S are those that appear in cliques adjacent in some junction tree and whose intersection is equal to S. We say that these pairs are allowed by S.

Let T_S be the subtree of J induced by the cliques that contain the distinct separator S. The junction property ensures that T_S is a single connected subtree. For example, Figure 3 shows T_{3}, the subtree of the junction tree in Figure 2 defined by the separator {3}. Then, let F_S be the forest obtained from T_S by deleting all the links associated with S. For example, Figure 4 shows the forest obtained by deleting links associated with the separator {3} from T_{3}. If we now reconnect the subtrees of F_S by inserting copies of the separator S to make a new tree $T_S^{\prime }$ say, and then replace T_S in J by $T_S^{\prime }$ to make a new spanning tree J′, J′ will also be a junction tree of G because it spans all the cliques of G and has the same collection of separators associated with the links. Moreover, since F_S contains the only cliques of G that contain S, this represents all the ways in which the edges associated with S can be rearranged to make a new junction tree. We can then characterize the pairs allowed by S as follows.

Figure 3.

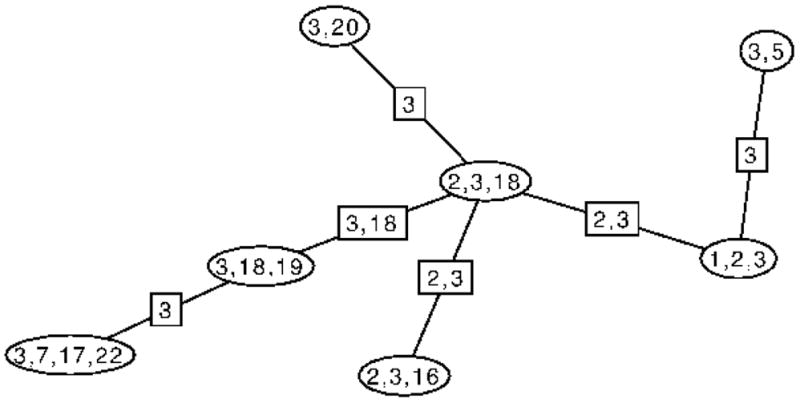
T_{3}, the connected subtree of the junction graph shown in Figure 2 induced by the cliques that contain the separator {3}.

Figure 4.

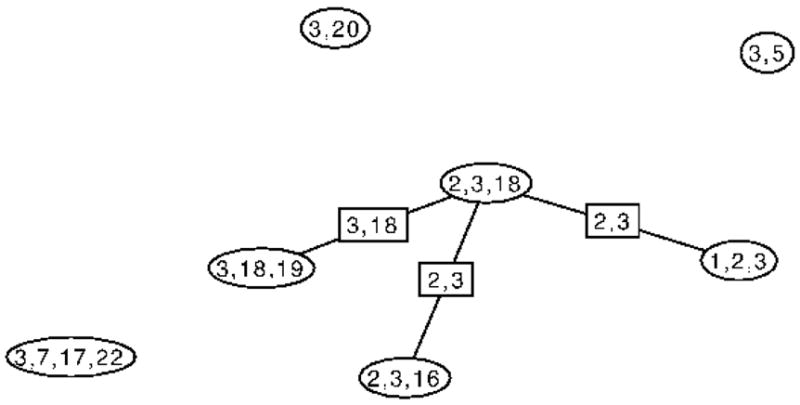
F_{3}, the forest obtained by from the tree shown in Figure 3 by deleting edges associated with the separator {3}.

Theorem 7

A connection (x, y) is allowed by a distinct separator S if and only if x ∉ S, y ∉ S and x and y are in cliques that are nodes of different subtrees of F_S.

Proof

We have established that the set of equivalent junction trees consists precisely of those obtained by inserting links associated with S into the gaps in F_S so as to form a tree. Then by Theorem 6, we only have to look at the cliques (A ∪ S,B ∪ S) at either end of those links associated with S, and by Giudici and Green’s result S allows connecting (x, y) if and only if x ∈ A and y ∈ B or vice versa.

4 Method summary

It is already established that the set of disconnectible pairs of G can be partitioned among the cliques of G [4]. Theorem 6 now establishes a corresponding result for the connectible pairs: that they can be partitioned among the distinct separators of G. However, not all the edges in any given clique are disconnectible, only those that appear in no other cliques. The junction property makes this easy to check: if a pair of vertices (x, y) contained in clique C is also contained in another clique, they must appear in a neighbour of C in the junction tree, thus only the neighbours of C in J need to be checked. Let the number of pairs of disconnectible vertices allowed by C be β(C). Theorem 7 allows us to similarly find the disconnectible pairs allowed by any distinct separator S. These are pairs of vertices that do not appear in S and which do not appear in cliques in the same subtree of F_S. If we let m_S be the number of times a distinct separator S appears in the collection of all separators {S₁, …, S_c−1}, since F_S is obtained by deleting m_s links from T_S, it must comprise m_S + 1 subtrees. Let A_j be the union of the sets of vertices in the cliques of the jth subtree of F_S. Let a_j = |A_j − S|, or a_j = |A_j | − |S| since S must be contained in each A_j, and let $b={\sum }_{i=j}^{m_S+1}{a}_j$. The number of connectible pairs allowed by S must therefore be

$$\alpha (S)=\frac{1}{2}\sum _{j=1}^{m_S+1}{a}_j(b-a_j)$$

Hence, an outline of a method to enumerate the neighbourhood of a decomposable graph G is as follows:

• Given a decomposable graph G find any junction tree representation J.

• For each clique C_i of G:

  • – For each pair of vertices (x, y) in C_i check that {x, y} is not a subset of any neighbouring clique of C_i in J.

  • – β(C_i) is the number of such pairs.

• The number of disconnectible edges in G is Σ_i β(C_i).

• For each distinct separator S_[i] of G:

  • – Identify T_S[i] the connected subtree of J induced by the cliques containing S_[i].

  • – Find J_S[i] by deleting from T_S[i] the links corresponding to the separator S_[i].

  • – Calculate a_j for each of the m_S + 1 components of F_S[i].

  • – Hence find α(S_[i]) = 1/2Σ_j a_j(b − a_j).

• The number of connectible edges in G is Σ_i α(S_[i])

5 Illustration

As most of the above steps are either standard, such as finding a junction tree, or straightforward, such as checking that edges appear in only 1 clique, we illustrate only the novel enumeration of connectible edges. As an example, consider enumerating the connectible edges allowed in the graph in Figure 1 by the separator {3}. The forest, F_{3}, shown in Figure 4 has 4 components. The vertices in the cliques in each component, excluding vertex 3 are {20}, {7, 17, 22}, {5} and {1, 2, 16, 18, 19}. Any pair of vertices selected from any two of these sets are connectible making

$$\alpha (\{3\})=\frac{1}{2}(1\times 9+3\times 7+1\times 9+5\times 5)=32$$

connections allowed by separator {3}. Note that the result of connecting the vertices 16 and 18 that appear in cliques in Figure 4 is also a decomposable graph, however, this is allowed by the separator {2, 3}, not by {3}, so we do not count this possibility at this stage.

The other distinct separators are dealt with in the same way and the final results are presented in Table 2 which enumerates all the pairs of vertices in Figure 1 whose connection makes a new decomposable graph. Table 1 shows an enumeration of the edges in Figure 1 that are disconnectible. Of the ²³C₂ = 253 possible pairs only 26 + 169 = 195 can be changed to give a new decomposable graph.

Table 2.

An enumeration of the connectible pairs for the graph in Figure 1.

Distinct separator S	ms	Variables in cliques of components of Fs	Sizes	α (S)
∅	4	{4} {6} {13, 14, 15, 23}	1, 1, 4, 17	111
		{1, 2, 3, 5, 7, 8, 9, 10, 11, 12, 16, 17, 18, 19, 20, 21, 22}
{13, 14}	1	{15} {23}	1,1	1
{3}	3	{20} {5} {7, 17, 22} {1, 2, 16, 18, 19}	1, 1, 3, 5	32
{2,3}	2	{1} {16} {18}	1,1,1	3
{3,18}	1	{2} {19}	1, 1	1
{9}	1	{10} {12, 17}	1,2	2
{12}	1	{11} {9, 17}	1,2	2
{17}	3	{8} {21} {9, 12} {3, 7, 22}	1, 1, 2, 3	17

Total number of connectible pairs 169

Table 1.

An enumeration of the disconnectible pairs for the graph in Figure 1.

Clique C	Edges only in C	Count
{4}	-	0
{6}	-	0
{13,14,15}	(13,15) (14,15)	2
{13,14,23}	(13,23) (14,23)	2
{3,5}	(3,5)	1
{1,2,3}	(1,2) (1,3)	2
{2,3,18}	(2,18)	1
{2,3,16}	(2,16) (3,16)	2
{3,20}	(3, 20)	1
{3,18,19}	(3,19) (18,19)	2
{17,21}	(17,21)	1
{8, 17}	(8,17)	1
{9,10}	(9,10)	1
{11,12}	(11,12)	1
{9,12,17}	(9,12) (9,17) (12,17)	3
{3,7,17,22}	(3,7) (3,17) (3,2) (7,17) (7,22) (17,22)	6

Total number of disconnectible pairs 26

6 Discussion

As noted above, a junction tree for a decomposable G can be found in time of order |V | + |E|. Letting n = |V|, this is at worst O(n²), and for the sparser graphs likely to be encountered in model estimation is closer to linear in n. As we build the junction tree, J, we can, at no extra cost, note for any distinct separator S_[i] a clique in which it is contained. Thus, by searching out from that clique we can find T_S[i] in time proportional to the number of nodes in T_S[i]. Since J can have at most n vertices, finding all the T_S[i] can be done in at most O(n²) time. While it is possible to construct examples where this bound is attained, for graphs encountered in model estimation actual performance is again likely to be far faster. Given T_S[i], with appropriate indexing of vertices, J_S[i] and α(S_[i]) can be found in O(n) time. Hence, overall, enumerating the connectible vertex pairs by our method allows an O(n²) worst case implementation.

The method previously described by [1] also solves this problem in O(n²) time and is in many ways similar. It too, in essence, relies on an understanding of the result of [4] when stated as: two unconnected vertices of G are connectible if and only if they are contained in cliques that are adjacent in some junction tree J of G. In order to exploit this they require two auxiliary data structures that are both of order O(n²) in size. One of these, the clique graph, can be thought of as the union of all possible junction trees of G. It is here that our method has a significant advantage as it requires only a single, arbitrary, junction tree representation J of G. As J is of O(n) size this represents a considerable saving of space. Moreover, as [4] showed, if G is updated to a decomposable G′ by either the connection or disconnection of a pair of vertices, the corresponding junction tree J′ can be found from J in O(1) time. The update will depend on the context, but involves changes to 4 cliques or separators where a change may be the addition or deletion of the clique or separator. This compares very favourably with the O(n²) method for correspondingly updating the clique graph given by [1].

Furthermore, adjustments to the probability of G to obtain that of proposed G′ requires only the calculation of the clique marginals of the same 4 cliques or separators which is again quick and independent of the size of the graph. We also note that this does not require construction of G′ so that both the proposal and acceptance/rejection steps of the Metropolis sampling process can be carried out using only the junction tree representation.

If we accept a proposal G′, we could, at worst, then enumerate the allowable perturbations anew and select another random update. However, the structure of the junction tree enables the new enumeration to be made as a modification of the previous. Once more, counting the number of allowable disconnections is easy. We simply decrease the count by the number allowed in any clique removed, and increase by the number in any clique created.

When a link of J, associated with separator S, is added or removed, this will affect not only T_S but also T_U for any other separator U ⊂ S, so we need to track the partial ordering of the distinct separators defined by inclusion. The junction property can again help here as it ensures that if U ⊂ S then T_S is a connected subgraph of F_U. Thus, the effect of changes to T_S on F_U, and hence the number of connections allowed by U, can be evaluated by searching in J starting at the changed link S and ending when, in each direction, a link associated with U is found.

There remains some challenge in developing specific algorithms and data structures to implement efficiently the methods outlined above. However, it is clear that the junction tree has very strong properties that can be exploited to make this possible.