In Silico and in Vitro Modeling of Hepatocyte Drug Transport Processes: Importance of ABCC2 Expression Levels in the Disposition of Carboxydichlorofluroscein

Abstract

The impact of transport proteins in the disposition of chemicals is becoming increasingly evident. Alteration in disposition can cause altered pharmacokinetic and pharmacodynamic parameters, potentially leading to reduced efficacy or overt toxicity. We have developed a quantitative in silico model, based upon literature and experimentally derived data, to model the disposition of carboxydichlorofluroscein (CDF), a substrate for the SLCO1A/B and ABCC subfamilies of transporters. Kinetic parameters generated by the in silico model closely match both literature and experimentally derived kinetic values, allowing this model to be used for the examination of transporter action in primary rat hepatocytes. In particular, we show that the in silico model is suited to the rapid, accurate determination of K_i values, using 3-[[3-[2-(7-chloroquinolin-2-yl)vinyl]phenyl]-(2-dimethylcarbamoylethylsulfanyl)methylsulfanyl] propionic acid (MK571) as a prototypical pan-ABCC inhibitor. In vitro-derived data are often used to predict in vivo response, and we have examined how differences in protein expression levels between these systems may affect chemical disposition. We show that ABCC2 and ABCC3 are overexpressed in sandwich culture hepatocytes by 3.5- and 2.3-fold, respectively, at the protein level. Correction for this in markedly different disposition of CDF, with the area under the concentration versus time curve and C_max of intracellular CDF increasing by 365 and 160%, respectively. Finally, using kinetic simulations we show that ABCC2 represents a fragile node within this pathway, with alterations in ABCC2 having the most prominent effects on both the K_m and V_max through the pathway. This is the first demonstration of the utility of modeling approaches to estimate the impact of drug transport processes on chemical disposition.

In recent years there has been increasing interest in the role of drug transport proteins and, more specifically, how these proteins affect the disposition, efficacy, and toxicity of xenobiotics (Glavinas et al., 2004; Oswald et al., 2007). In parallel with the phase I and II metabolic enzymes, the drug transporter system has evolved to be able to handle the complex chemical set to which humans are exposed (Dean et al., 2001; Hagenbuch and Meier, 2004). In common with drug-metabolizing enzymes, drug transporter proteins tend to have wide, overlapping substrate specificities and variable, inducible expression in target tissues, allowing the most efficient response to chemical insult; indeed, transcriptional control of drug transporter proteins is under the control of the same nuclear receptors that regulate drug-metabolizing enzyme levels (Staudinger et al., 2003; Plant, 2004; Klaassen and Slitt, 2005). This control system means that drug transport proteins tend to be expressed at different levels in different tissues and that this expression level will alter in response to cellular conditions. Examples of this can be seen in pathological conditions such as cancer, in which transporter proteins are often overexpressed in tumors (Glavinas et al., 2004), or in normal tissue after chemical exposure (Nishimura et al., 2006), both of which can result in decreased chemical access and loss of pharmacological efficacy. Another area of interest, but an area that is poorly studied at present, is the expression of drug transport proteins in in vitro systems, with recent work focusing on the characterization of drug transport levels in vitro for several systems (Hilgendorf et al., 2007; Bow et al., 2008; Nishimura and Naito, 2008). However, to date the impact of this on the total transport capacity of cells has not been examined nor has how this altered transporter expression relative to in vivo levels could contribute to the sometimes poor predictive power for such in vitro screens.

In common with drug-metabolizing enzymes, many drug transporters show promiscuity in their substrate binding profile, and this has complicated the development of probe substrates. However, several fluorescent probes are now emerging that are diagnostic for the activity of groups of transporters, including rhodamine-123 (SLCO1A, ABCG, and ABCC subfamilies) (Katayama et al., 2007; Perrière et al., 2007) and carboxydichlorofluorescein (SLCO1A and ABCC subfamilies) (Sun et al., 2001; Zamek-Gliszczynski et al., 2003; Lengyel et al., 2008), allowing the establishment of kinetic parameters of drug transport for many model substrates (Zamek-Gliszczynski et al., 2003; Pratt et al., 2006).

Such a data-rich environment is thus open to in silico modeling of transport processes, allowing estimations of the biological importance of these processes, and the predictive nature of in vitro systems with respect to compound disposition. Such systems modeling has traditionally followed either a top-down or bottom-up approach; in the former, all data at one (or more) biological level are incorporated into a comprehensive model, whereas bottom-up modeling focuses on a single aspect in detail. Top-down modeling has had considerable success in less complex organisms such as bacteria or yeast (Beste et al., 2007), but models in higher eukaryotes tend to be descriptive rather than quantitative in nature (Oda et al., 2005). To achieve quantitative models of higher organisms bottom-up approaches have been more usually applied, including the examination of membrane transport processes at both the theoretical (Ofer et al., 2006; Bartholomé et al., 2007) and practical (Sun and Pang, 2008; Sun et al., 2008) level. Such work demonstrates the potential of this approach to examine the impact of drug transporter expression on the life cycle of compounds within cells.

Using a bottom-up systems biology approach, we have created the first model of a complete transport process in primary rat hepatocytes, including both apical and basolateral transport. Using this model, we show that ABCC2 levels are a fragile node controlling the disposition of the tool substrate carboxydichlorofluroscein (CDF) and that the alteration in ABCC2 expression between in vitro and in vivo has a significant impact on CDF flux through hepatocytes.

Materials and Methods

Primary Rat Hepatocyte Culture. Freshly isolated rat liver was obtained in ice-cold saline from Han-Wistar rats of approximately 300 g in weight; only male rat livers were used to mitigate the known variation in expression of drug transporter proteins between the sexes (Lu and Klaassen, 2008). Primary hepatocytes were isolated using a modification of the protocol of Seglen (Seglen and Jervell, 1969), followed by enrichment of live cells using Percoll gradient centrifugation.

Primary rat hepatocytes were plated in collagen-coated six-well plates at a 1.5 × 10⁶ cells per well and overlaid with Matrigel (BD Biosciences, Oxford, UK) to form a sandwich culture. Cells were culture in Williams' E medium, supplemented with 100 U/ml penicillin, 100 μg/ml streptomycin, 0.17 μM insulin, 0.03 μM dexamethasone, 50 μg/ml gentamicin, and 1% (v/v) 1 M HEPES.

Carboxydichlorofluroscein Diacetate Assay. CDFDA is a nonfluorescent chemical that can passively diffuse into cells, with a logP = 2.8. Once within cells, it is converted by intracellular esterases to the metabolite CDF, which is a fluorescent substrate for ABCC transporters (Zamek-Gliszczynski et al., 2003).

Medium was aspirated from cells, and they were washed with HBSS. This wash was repeated, and the cells were returned to the incubator for 10 min and covered in HBSS. After removal of the HBSS, the appropriate working solution of CDFDA was added to the cells, or vehicle control (0.1% dimethyl sulfoxide), and cells incubated at 37°C as required. Cells were washed three times with HBSS, and an image was taken at 10× magnification using an Axiovert 200 microscope (Carl Zeiss GmbH, Jena, Germany). During imaging, cells were exposed to an excitation wavelength of 480 nm using an FITC filter for 2 s, followed by quantitation at 530 nm using Axiovert 4.5 software suite (Carl Zeiss GmbH).

Transcript Level Measurement. Primers and 5-carboxytetramethylrhodamine/5-carboxyfluorescein dual-labeled probe specific for ABCC2, ABCC3, SLCO1A1, SLCO1A4, SLCO1B2, and 18s were designed using the Primer Express software (Applied Biosystems, Warrington, UK) and were purchased from MWG (Milton Keynes, UK).

Primary rat hepatocytes were plated in collagen-coated six-well plates at a concentration of 1.5 × 10⁶ cells per well and overlaid with Matrigel (BD Biosciences) to form a sandwich culture. Cells were culture in Williams' E medium, supplemented with 100 U/ml penicillin, 100 μg/ml streptomycin, 0.17 μM insulin, 0.03 μM dexamethasone, 50 μg/ml gentamicin, and 1% (v/v) 1 M HEPES. At specified time points, total RNA was isolated from quadruplicate samples using the RNeasy Mini kit (QIAGEN, Dorking, Surrey, UK) and was quantified using a Nanodrop Agilent 2100 Bioanalyzer (Agilent Technologies, Santa Clara, CA).

Total RNA was treated with RNase-free DNase (Promega, Southampton, UK) to remove genomic contamination. Reverse transcription was primed with random hexamers and carried out by SuperScript II (Invitrogen, Paisley, UK) as per the manufacturer's instructions. To ensure that DNase-treated samples were free from genomic contamination, a reverse transcriptase– control (lacking enzyme) was carried out for every RNA sample. cDNA generated from 50 ng (all transporters) or 50 pg (18S rRNA) of total RNA was amplified using TaqMan Universal PCR Master Mix (ABI Biosystems, Foster City, CA) with 400 nM primers and 200 nM fluorogenic probe in a total reaction volume of 25 μl. Quantitative PCR reactions were run on the ABI7000 SDS instrument (ABI Biosystems), and quantitation was carried out using the ABI proprietary software against a standard curve generated from human genomic DNA (Promega, Madison, WI).

Protein Level Measurement. Primary rat hepatocytes were plated in collagen-coated six-well plates at a concentration of 1.5 × 10⁶ cells per well and overlaid with Matrigel (BD Biosciences) to form a sandwich culture. Cells were culture in Williams' E medium, supplemented with 100 U/ml penicillin, 100 μg/ml streptomycin, 0.17 μM insulin, 0.03 μM dexamethasone, 50 μg/ml gentamicin, and 1% (v/v) 1 M HEPES. At specified time points, total protein was extracted in radioimmunoprecipitation assay buffer (1× phosphate-buffered saline, 1% Nonidet P-40, 0.5% sodium deoxycholate, 0.1% SDS, and protease inhibitor cocktail), and membrane fraction was derived by differential centrifugation.

Total (5 μg/lane) or membrane (5 μg/lane) protein extracts were resolved on 12% SDS-polyacrylamide gels and then transferred electrophoretically to Hybond ECL nitrocellulose membranes (GE Healthcare, Little Chalfont, Buckinghamshire, UK). Membranes were blocked (1 h) in 5% fat-free dried milk and then probed with primary antibodies against rat ABCC2/ABCC3 (Autogen Bioclear, Calne, Wilts, UK), followed by anti-rabbit IgG (Autogen Bioclear). Bound antibodies were visualized using enhanced chemiluminescence reagents according to the manufacturer's instructions (GE Healthcare). Immunoblots were also probed with an antibody against β-actin to ensure even loading per lane (data not shown).

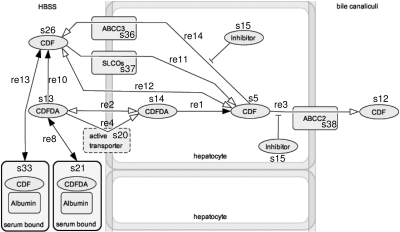
In Silico Model Generation and Simulation. In silico models were generated using CellDesigner version 3.5.2 (Systems Biology Institute, http://celldesigner.org/index.html), a graphical front-end for creating process diagrams of biochemical networks in systems biology markup language (SBML) (Hucka et al., 2003). Each individual chemical or protein is identified as a species (s1... sn), whereas interactions between species are identified as reactions (r1..rn). For each reaction, a kinetic term can be included, detailing the mathematics underlying the interaction of the species. Derivation of kinetic constants for the reactions studied within the network as presented in Table 1, with the total model, as SBML script, being available as supplemental data. Simulations of created networks are then undertaken using the Jarnac Simulation Service version 2.26b, accessed through the Systems Biology Workbench module (Deckard et al., 2006).

TABLE 1.

Reaction constants and their derivations for use during in silico modeling

Reaction	Kinetic Parameters of Reaction	Source of Data
r1	Hydrolysis of CDFDA (s14) to CDF (s5) within the cell	Zamek-Gliszczynski et al., 2003
	Sandwich culture of primary rat hepatocytes: all CDFDA was converted to CDF within 10 s. Presume this is 20 half-lives; therefore, t1/2 = 0.5 s.
	For a first-order reaction, t1/2 = ln2/k. Therefore, k = 0.693/0.5 = 1.39 s-1.
r2	Passive diffusion of CDFDA (s13) into the cell.	Zamek-Gliszczynski et al., 2003
	Uptake clearance of 10, 100, and 500 μM CDFDA into rat hepatocytes = 4.9, 687, and 3374 μl/min/mg protein, respectively.
	Assume to be a reversible first-order process, so rate = k[s]. Therefore, k ≈ 6.8 min-1.
r3	Efflux of CDF (s12) via Abcc2 into the bile canaliculi.	Pratt et al., 2006 and experimentally derived
	Abcc2 overexpression in human embryonic kidney cells: KM = 18.9 ± 2 μM and Vmax = 95.5 ± 14.8 pmol/min/mg protein.
	Sandwich culture of primary rat hepatocytes: MK571 IC50 value at 10 μM CDFDA = 1.9 ± 3.7 μM.
r4	Uptake of CDFDA (s13) into the cell via active transport.	Zamek-Gliszczynski et al., 2003; Wu and Benet, 2005
	Because CDFDA is a very lipid-soluble molecule, the presence of active transport into the cell will be minimal and transport is unaltered by temperature. Discounted in the model.
r8	Binding of CDFDA (s13) to extracellular proteins.	Zamek-Gliszczynski et al., 2003
	In vivo CDFDA is 22% protein-bound. The model simulates the in vitro assay and because hepatocytes were dosed with CDFDA in HBSS, containing no extracellular protein, this figure will be zero.
	Discounted in the model.
r10	Conversion of CDFDA (s13) to CDF (s26) outside of the cell.	Zamek-Gliszczynski et al., 2003
	In phosphate-buffered saline, t1/2 = 7.6 ± 0.1 h-1. For a first-order reaction, t1/2 = ln2/k. Therefore, k = 0.693/456 = 0.00152 min-1
r11	Uptake of CDF (s26) into the cell via active transport.	Zamek-Gliszczynski et al., 2003
	Sandwich culture of primary rat hepatocytes: uptake clearance of CDF into rat hepatocytes = 1.9 ± 0.1 μl/min/mg protein and was inhibited by low temperature (10 μM dose).
	Uptake was saturable with and inhibited by substrates of organic anion-transporting polypeptides, e.g., taurocholate and rifampicin.
	KM of 22 ± 10 μM and Vmax = 97 ± 9 pmol/min/mg protein.
r12	Passive diffusion of CDF (s26) into the cell.	Zamek-Gliszczynski et al., 2003 and experimentally derived
	Sandwich culture of primary rat hepatocytes: uptake inhibited by low temperature so mainly transporter-mediated. Octanol/water coefficient demonstrates no evidence for partition into lipid membranes.
	Discounted in the model.
r13	Binding of CDF (s26) to extracellular proteins.	Zamek-Gliszczynski et al., 2003
	In vivo CDF is 20% protein-bound. The model simulates the in vitro assay and as hepatocytes were cultured in HBSS, containing no extracellular protein, this figure will be zero.
	Discounted in the model.
r14	Efflux of CDF (26) across the sinusoidal membrane via Abcc3.	Zamek-Gliszczynski et al., 2003 and experimentally derived
	Sandwich culture of primary rat hepatocytes: rate of efflux is approximately a quarter of efflux via Abcc2.
	Vmax ≈ 24 pmol/min/mg protein and KM ≈ 20 μM.
	Sandwich culture of primary rat hepatocytes: MK571 IC50 value at 10 μM CDFDA = 1.9 ± 3.7 μM.

Results

Generation of in Silico Model of CDF Transport in Primary Rat Hepatocytes. To generate a comprehensive model of CDFDA/CDF flux in primary rat hepatocytes, it was first necessary to generate a qualitative model of interactions that occurs, or may possibly occur, upon which kinetic parameters can be built. Figure 1 shows the initial model generated from known interactions of CDFDA and CDF with cellular systems.

Fig. 1.

Generated in silico model for CDFDA/CDF transport in cells. The generated model is based upon known and presumed interactions of CDFDA and CDF with hepatocytes and was generated using CellDesigner version 3.5.2 (Systems Biology Institute, http://celldesigner.org/index.html). Each individual chemical or protein is identified as a species (s1... sn), whereas interactions between species are identified as reactions (r1..rn). The kinetic terms and their associated constants that underlie the model are provided in Table 1.

After construction of the qualitative model, a kinetic equation was added for each reaction, and populated kinetic data from either literature sources or experimentally derived data; these parameters, along with their literature source, are provided as supplemental data. The complete SBML-script for the generated model is provided as supplemental data.

Using the Jarnac Simulation Service, each individual reaction was tested in isolation to ensure that they produced the inputted kinetic parameters correctly (data not shown). Following this approach, the total pathway was simulated under basal conditions, producing an overall V_max = 98 ± 3 pmol/min/mg and K_m = 46 ± 6 μM for the pathway. Levels of individual species within the system over time are shown in Fig. 2A.

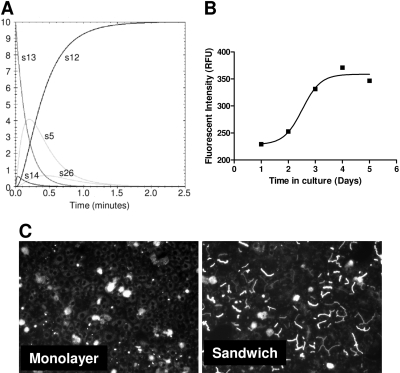
Fig. 2.

Bile canaliculi formation reaches an optimum after 4 days of sandwich culture. A, using the generated in silico model, with all parameters as described in Table 1, CDFDA/CDF levels were simulated for a period of 3 min by using a starting concentration of 10 μM CDFDA in HBSS. The levels of the major species are shown. B, rat hepatocytes were plated on day 0 and sandwich cultured over the following 5 days. On each day, cells were washed in HBSS and dosed with 10 μM CDFDA (0.1% dimethyl sulfoxide) before being incubated for 30 min at 37°C, 5% CO₂, and then fluorescent intensity measured. C, fluorescent images of sandwich- and monolayer-primary rat hepatocytes after 4 days in culture and 30 min subsequent to 10 mM CDFDA challenge. Images are taken at 10× magnification with an Axiovert 100 microscope with the integral digital camera through an FITC filter (485 nm).

For any generated model to be of use, it must closely model the in vitro, and potentially in vivo, situation. To assess this, we next compared in silico-generated flux parameters with those derived from sandwich cultures of primary rat hepatocytes. Figure 2B shows efflux of CDF reaches a maximum after 4 days in sandwich culture, which is concordant with the formation of functioning bile canaliculi within the sandwich cultures (Fig. 2C). In comparison, monolayer-cultured hepatocytes do not form canaliculi correctly, as evidenced by their lack of CDF efflux after 4 days in culture (Fig. 2C); indeed, no efflux is seen up to 6 days in culture (data not shown).

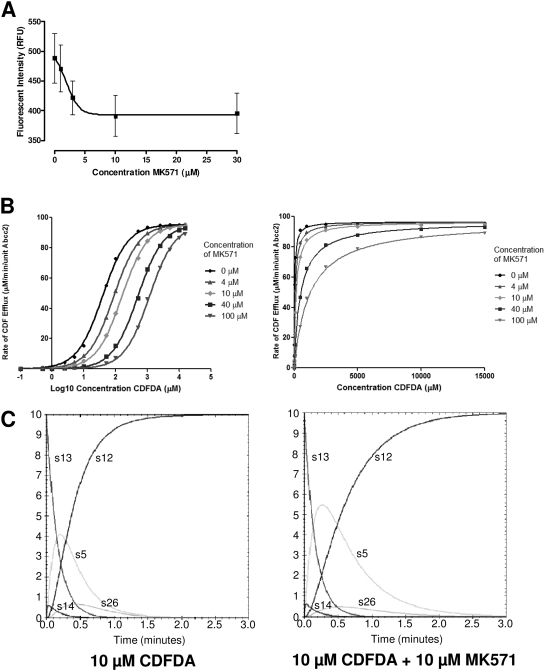
After construction of the in silico model, and its validation against in vitro data, we wanted to examine whether the model could simulate pharmacological modulation of the pathway. Thus, we used MK571, a potent pan-ABCC inhibitor (Gekeler et al., 1995): Exposure of sandwich cultures of primary rat hepatocytes to MK571 results in a derived IC₅₀ value of 1.9 ± 3.7 μM (Fig. 3A), and this was used in subsequent in silico simulations, presuming that MK571 had similar characteristics against both ABCC2 and ABCC3. Because the IC₅₀ value is dependent on the concentration of substrate, it is often more useful to derive a K_i value for an inhibitor, because this is substrate concentration-independent. In silico simulation allows a much more rapid determination of K_i; the derived Schild plot is presented in Fig. 3B, showing a right shift characteristic of competitive inhibition, whereas analysis of the Michaelis-Menten plot (Fig. 3B) allows the derivation of K_i = 3.5 ± 0.1 μM. From these derived data, it is possible to predict the effect of inhibitor of all species within the network, as seen in Fig. 3C. Addition of 10 μM MK571 results in a slowing of flux through the system, resulting in increased levels of intracellular CDF, producing an increase in AUC of s5 (intracellular CDF) of 503%, with a concomitant increase in C_max by 179%.

Fig. 3.

Simulation of competitive inhibition. A, rat hepatocytes were sandwich-cultured for 4 days after plating (where cells were plated on day 0) and dosed with 10 μM CDFDA and 0 to 30 μM MK571, and then they were incubated for 25 min at 37°C, 5% CO₂. Fluorescent intensity was measured using an Axiovert 100 microscope with FITC filter (485 nm) and supplied software. Data were fitted using nonlinear regression analysis (IC₅₀ = 1.9 ± 3.7 μM; n = 3; error bars are S.E.M.). B, using the generated in silico model, with all parameters as described in Table 1, CDFDA/CDF levels were simulated for a period of 3 min using a starting concentration of 0.1 to 15,000 μM CDFDA in HBSS. The concentration of inhibitor was increased from 0 to 100 μM, and the rate of CDF accumulation in the bile canaliculi was measured over 3 min. Data were analyzed by Schild and Michaelis-Menten kinetics. C, kinetic parameters for each of the major CDFDA/CDF species are shown for 10 μM CDFDA and 0 μM (left) and 10 μM (right) MK571 and map to those shown in Fig. 1.

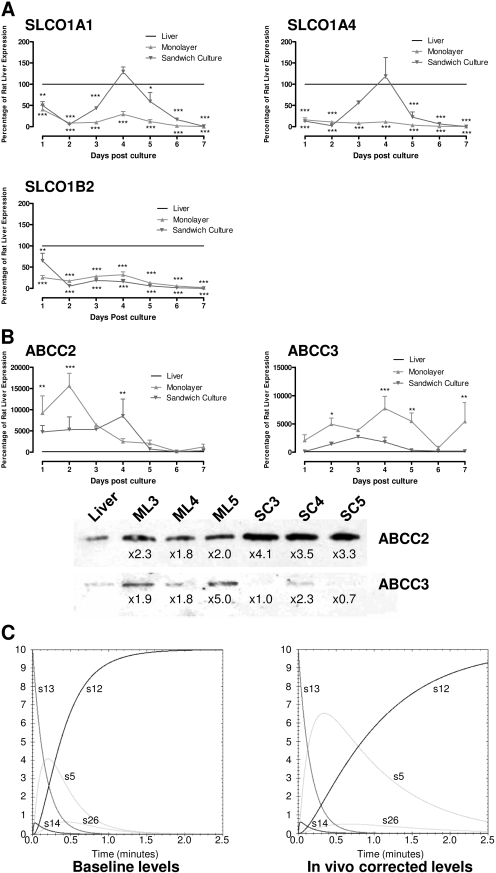
Drug Transport Protein Levels Differ Significantly between Primary Cells in Vitro and in Vivo. One potential use of in silico modeling is to simulate, and understand, differences between in vitro and in vivo systems, allowing more accurate extrapolation of data from initial screens to preclinical testing. To examine how differences in expression levels of drug transport proteins could affect the disposition of chemicals in these two systems, we next measured levels of all influx (Fig. 4A) and efflux (Fig. 4B) transporters implicated in CDF transport within primary rat hepatocytes at the transcript level.

Fig. 4.

Variation in drug transporter expression during time in culture affects in vitro-in vivo correlation. Rat hepatocytes were cultured for 7 days (where cells were plated on day 0) in either monolayer (▾) or sandwich culture (▴) conformation. Samples of cells were taken each day for analysis by reverse transcriptase-PCR of the expression of the influx transporters SLCO1A1, 1A4, and 1B2 (A) and the efflux transporters ABCC2 and C3 (B). Data are expressed as a percentage of the level in rat liver (100%, —), with RNA isolated from the fresh rat livers subsequently used to prepare hepatocytes cultures. Data were analyzed by two-way analysis of variance with Bonferroni post hoc test and show where expression in hepatocytes is significantly different from liver expression (***, p < 0.001; n = 3; error bars are S.E.M.; where no error bars are observed, they are contained within the limits of the data point). Protein levels of ABCC2 and C3 were also measured by Western blot after 3, 4, and 5 days of culture and compared with the level from fresh rat livers subsequently used to prepare hepatocytes cultures (B). Finally, in silico modeling was used to compare how altered protein levels of ABCC2 and C3 might affect disposition of CDFDA/CDF in 4-day sandwich cultures (baseline levels) versus in vivo-corrected levels (C). Kinetic parameters for each of the major CDFDA/CDF species are shown and map to those shown in Fig. 1.

In general, influx transporter levels seem suppressed in the sandwich culture system, with transcript levels below 100% of levels in the freshly excised liver used to prepare the cultures. However, after 4 days of culture, when in vitro experiments are routinely undertaken, SLCO1A1 and SLCO1A4 transcript levels peak to approximate in vivo levels, being 129 and 119%, respectively, whereas SLCO1B2 transcript levels are within an order of magnitude of the in vivo transcript levels, being 15% (Fig. 4A). By comparison, ABCC2 and ABCC3 transcript levels in the sandwich culture system are significantly higher than in vivo levels for the first 6 days of culture, with levels being 8524 and 1807% of in vivo transcript levels, respectively, after 4 days of sandwich culture. As changes in transcript levels do not always correlate to the protein level, we next assessed the level of these two transporters throughout the culture period via Western blotting, revealing a 4.1- and 2.6-fold variability in ABCC2 and ABCC3 expression levels, respectively, between 3 and 6 days in culture compared with freshly isolated rat liver, which was subsequently used to prepare hepatocytes for the culture experiments (Fig. 4B). This variability is significantly larger for ABCC2 than ABCC3, and on day 4 of culture when in vitro experiments are routinely undertaken ABCC2 protein levels are 3.5-fold higher than those observed in vivo, whereas ABCC3 protein levels are only 2.3-fold higher. As stated above, correct localization of drug transporters is as important as their physical presence; hence, it is pertinent to note that these protein levels were derived from membrane fraction and not total protein and thus should reflect active protein. These large deviations in transcript levels compared with in vivo rat liver suggest that they may affect the disposition of chemicals transported by these ABCC proteins. To examine this, in silico simulations were undertaken using both the base model, which correlates well with the in vitro sandwich culture, and a model adjusted for the lower levels of ABCC2 and ABCC3 in fresh rat liver.

Kinetic simulations of the network using protein levels from either fresh rat liver or hepatocytes sandwich cultured for 4 days demonstrated the impact of the alteration of efflux transporter levels described above. Examining the net movement through the pathway (from CDFDA in HBSS to CDF in bile canaliculi) produces a V_max value of 97.6 ± 3 pmol/min/mg, which is reduced to 28 ± 0.2 pmol/min/mg when protein levels are adjusted to the lower transporter levels seen in freshly isolated rat liver. In addition, because the ratio of ABCC2/ABCC3 expression is also altered, this affects the K_m value of the network, decreasing it from 47.5 ± 6.5 to 27.6 ± 1 μM; taken together, this modeled decrease in V_max and K_m in freshly isolated rat liver relative to in vitro is suggestive of overprediction of flux through the pathway in the in vitro system compared with the in vivo situation. In addition to alterations in flux through the entire network, changes in the levels of individual species can be identified between the two simulations (Fig. 4C); intracellular levels of CDF (s5) are particularly affected, resulting in a predicted increase in AUC and C_max by 365 and 160%, respectively, for the in vivo simulation compared with baseline in vitro simulation.

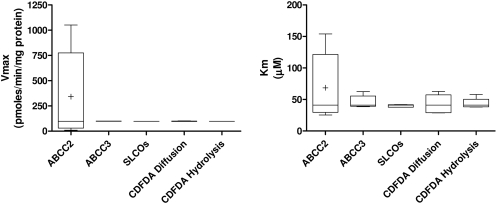
ABCC2 Acts as a Fragile Node in the Disposition of CDF within Cells. As demonstrated above, alteration of protein levels within the network can both dramatically alter the total flux through the pathway and the kinetic profile of individual chemical species. However, the impact of altering the levels of each node on flux through the total pathway is variable; robust nodes refer to those proteins where alteration of their expression levels has little impact on either the total flux through the pathway or the kinetic profile of individual chemical species. By comparison, a fragile node refers to a protein within a network for which even small alterations in expression levels can have significant impact on the pathway, altering both the total flux through the pathway and the kinetic profile of individual chemical species. Determination of robust or fragile nodes in a network is an important step in understanding the functioning of the network, including the controlling reactions within that network. We have examined this phenomenon in the generated in silico model through sequential alteration of each of the nodes of the network. Figure 5 shows the variability in V_max and K_m of the total pathway when each node is altered one order of magnitude either side of unity. Of the nodes examined altering ABCC2 had the largest impact on total pathway flux, altering V_max and K_m values by 2004 and 170%, respectively.

Fig. 5.

ABCC2 expression represents a fragile node in CDF disposition within primary rat hepatocytes. Levels of each node was altered sequentially to 0.1, 05, 1, 5, and 10 units, relative to baseline model, within the in silico model, and CDFDA/CDF levels were simulated for a period of 3 min using a starting concentration of 0.1 to 2500 μM CDFDA in HBSS. The impact of these changes on V_max and K_m are shown.

Discussion

Herein, we report the generation of an in silico model capable of simulating the flux of a compound through a cellular system. Several attempts have been made to use in silico models to examine biological processes, ranging from top-down qualitative models of entire networks (Oda et al., 2005), to theoretical analyses of individual biological processes (Schmierer et al., 2008). In the latter category, several attempts have been made to examine drug transport processes (Ofer et al., 2006; Sun et al., 2008; Sun and Pang, 2008), and the current work adds to this field. The work of Ofer et al. (2006) examined ABCB1-mediated transport of flavonoids, looking at movement across a single membrane, whereas Sun and colleagues (Sun et al., 2008; Sun and Pang, 2008) developed a quaternary model to examine movement across both apical and basolateral membranes in a polarized Caco2 cell system. The approach presented herein has two major differences from these other approaches. First, the use of specialized, but freely available, modeling software removes much of the complication associated with the mathematics of modeling networks. Because the model calculates the total flux through the network based upon each individual step, a researcher need only concentrate on deriving data for each step, generally simple enzyme kinetics equations, as opposed to the complete network. In addition, where data are sparse, assumptions can be made or multiple steps combined to provide the “best-case” scenario: Such an approach is thus much more user-friendly to researcher in general. Second, the modular approach of the system presented herein means that it is relatively easy to alter individual processes, or to introduce more processes as they are identified, and study their impact upon the network. This can be of use to enlarge or refine a network when more data are determined, or to examine the role of individual nodes within the network. The latter scenario is of particular importance with regard to understanding differences between biological systems (e.g., species differences, in vitro versus in vivo or normal versus pathophysiological tissue), an area of intense interest for both the understanding of basic biological processes and the correct prediction of drug action in cells. The data presented herein show that even altering two nodes within a network (the amounts of ABCC2 and ABCC3) can highlight potentially dramatic effect on the flow through the network, altering both total flux and also the disposition of individual species.

The choice of CDFDA/CDF as a investigative tool has two distinct advantages: first, the conversion between nonfluorescent and fluorescent chemicals produces an ideal tool set for examining multiple steps within the network. As such, CDFDA/CDF is ideal for increasing our understanding of the interrelationship between multiple factors (e.g., influx/efflux transporters, metabolism, sequestration) within a cell, which will be applicable for all chemical interactions within cellular networks. Second, the interaction of other novel chemicals with this network can be easily examined through their competition with CDFDA/CDF without the need to develop novel analytical methodologies. In addition, as the generated model is presented through an easy-to-use front-end, it is possible to run multiple scenarios to estimate the impact of variability within the parameters, allowing, for example, the extrapolation of data from in vitro to in vivo. An important part of any in silico model is its validation through comparison of the kinetic parameters derived from the simulation with those produced experimentally using sandwich culture of primary rat hepatocytes. Zamek-Gliszczynski et al. (2003) derived V_max and K_m values of 97 ± 9 pmol/min/mg and 22 ± 10 mM for CDF transport within sandwich cultures of primary rat hepatocytes. It is notable that the in vitro- and in silico-derived values for V_max are within the errors of measurement, suggesting that this component has been well modeled. In comparison, the K_m value is higher in the in silico system compared with the in vitro measurement of Zamek-Gliszczynski et al. (2003). This variance may be explained by two different scenarios. First, it is possible that there is an error in the model, resulting in an overestimation of the “negative K_m” for ABCC3-mediated efflux of CDF through the apical membrane. Second, it is possible that temporal differences when transport studies were undertaken might affect the overall flux. As can be seen from Fig. 4, ABCC2 protein levels remain relatively constant, albeit overexpressed, in sandwich cultures from day 3 to 5; in contrast, ABCC3 levels vary significantly. Hence, differences in time of culture between the in silico model presented herein and the in vitro model of Zamek-Gliszczynski may result in different ABCC3 levels, which would affect the K_m of the overall pathway. Data on the total flux through the pathway within our system would support the latter hypothesis, because derived K_m values are more consistent with the in silico model then than the Zamek-Gliszczynski values (data not shown).

The utility of the in silico system is further shown by its ability to generate inhibition constants. Whereas inhibition is often quoted as an IC₅₀ value, the usefulness of this is questionable because it is dependent upon not only the inhibitor but also the concentration of the substrate used to measure the IC₅₀ value. A more generally applicable value is the inhibition constant, K_i, which is substrate concentration-independent. However, derivation of a K_i value is time-consuming and expensive because it requires the generation of IC₅₀ curves over a wide range of substrate concentrations to allow the derivation of a dose ratio, from which the K_i value can be derived. From a single piece of experimental data, the IC₅₀ value of MK571 at 10 μM CDFDA, it is possible to run simulations across a range of both inhibitor and substrate concentrations and derive the K_i value. The K_i value for MK571 generated for the in silico system (3.5 ± 0.1 μM) agrees very well with previously published, experimentally derived K_i values for MK571 (Paul et al., 1996). Such an approach has two important advantages: First, derivation of a K_i value in silico is rapid, and as demonstrated herein, provides a good estimation of K_i compared with in vitro-derived values. This means that the generated data are robust enough to be used to assess the properties of novel chemicals, and to plan in vitro experiments based upon this value, producing a significant increase in workflow efficiency. Second, because the derived K_i is dependent upon multiple simulations across a range of both substrate and inhibitor concentrations, its derivation is relatively robust, meaning it can be used to confirm in vitro experiments. From the data shown in Fig. 3A, it is clear that the derivation of the IC₅₀ value is not 100% robust because the data points used are suboptimal. However, because of the multiple simulations involved in K_i determination, these errors are minimized, resulting in a value that closely agrees with an in vitro-derived K_i value (Paul et al., 1996). In addition, in silico simulation could in fact be used to guide the concentrations used for in vitro determination of IC₅₀ values, through the running of multiple simulations spanning a range of potential IC₅₀ values, allowing the determination of what experimental points are based suited to ensure an accurate determination of the IC₅₀ value in vitro.

As the amount of data concerning drug transporter expression and activity increases, it is important to be able to place this in a biological context. For example, much information exists on the expression of drug transporters from both the SLCO and ABC families in several different cellular models (Hilgendorf et al., 2007; Bow et al., 2008; Nishimura and Naito, 2008), with such data being used to infer in vitro-in vivo correlations in transporter function. However, to increase the utility of such correlations two improvements would be useful. First, the expression data, which are usually captured at the transcript level, must be confirmed in terms of correctly localized, functional protein. Second, the impact of altering expression of a single transporter on chemical flux through a pathway must be estimated; it is probable that some transporters have significantly more impact on pathway flux, representing fragile nodes within the system.

One important factor of in silico modeling is the ability to derive information on intermediate species within the pathway and not just the proximate product that is measured within the in vitro system. This utility of this can be clearly seen through the simulations of altered protein levels and pharmacological inhibitors, whereby the biggest impact is on the AUC and C_max of an intermediate species, intracellular CDF. It is easy to envisage where such information could be of importance, because it is often these intermediates that either exhibit pharmacological or toxicological activity. Alterations in the levels of either of these factors could significantly alter the safety/efficacy profile of the compound. A central driver at the discovery/development borderline is the ability to accurately extrapolate data from in vitro screens to preclinical, and indeed clinical, scenarios. It can be seen that the model herein begins to address the variance seen between in vitro and in vivo generated data, allowing for correction of differences in protein expression. In addition to the production of correction factors to allow improved extrapolation from in vitro to in vivo the use of in silico modeling allows the testing of nodes within a network to identify those that are fragile; these nodes may represent important points for intervention as they will have the most profound impact on flux through the pathway. One possibility for such intervention is the identification of the proteins, the levels of which should be altered in vitro to achieve a desired impact on a biological process; this could be the manipulation of cell lines to be more similar to in vivo, either normal or a pathological tissue state, or the deliberate compromising of cells so that they act as more sensitive markers of toxicity. An alternate use of fragile nodes is the identification/refinement of therapeutic targets, whereby only those targets most likely to produce the desired biological effect when manipulated pharmacologically are pursued.

In summary, through the use of both literature-based and experimentally derived data, we have been able to construct an in silico model of the disposition of a chemical through a rat hepatocytes. Furthermore, we have produced the first data to show the utility of such systems in being able to both understand and mimic differences between in vitro and in vivo.