Ultrasound attenuation estimation using backscattered echoes from multiple sources

Abstract

The objective of this study was to devise an algorithm that can accurately estimate the attenuation along the propagation path (i.e., the total attenuation) from backscattered echoes. It was shown that the downshift in the center frequency of the backscattered ultrasound echoes compared to echoes obtained in a water bath was calculated to have the form Δf=mf_o+b after normalizing with respect to the source bandwidth where m depends on the correlation length, b depends on the total attenuation, and f_o is the center frequency of the source as measured from a reference echo. Therefore, the total attenuation can be determined independent of the scatterer correlation length by measuring the downshift in center frequency from multiple sources (i.e., different f_o) and fitting a line to the measured shifts versus f_o. The intercept of the line gives the total attenuation along the propagation path. The calculations were verified using computer simulations of five spherically focused sources with 50% bandwidths and center frequencies of 6, 8, 10, 12, and 14 MHz. The simulated tissue had Gaussian scattering structures with effective radii of 25 μm placed at a density of 250∕mm³. The attenuation of the tissue was varied from 0.1 to 0.9 dB∕cm-MHz. The error in the attenuation along the propagation path ranged from −3.5±14.7% for a tissue attenuation of 0.1 dB∕cm-MHz to −7.0±3.1% for a tissue attenuation of 0.9 dB∕cm-MHz demonstrating that the attenuation along the propagation path could be accurately determined using backscattered echoes from multiple sources using the derived algorithm.

INTRODUCTION

In recent years, there has been an explosion of new applications for medical ultrasound. These applications range from ultrasound therapy to tissue characterization. Ultrasound therapy often involves thermal ablation where tissue necrosis is induced by elevated temperatures during ultrasound exposure (Foley et al., 2004; Hynynen, 1997; Lizzi et al., 1992; Otsuka et al., 2005; Souchon et al., 2003; Takegami et al., 2005; Wu et al., 2004). However, ultrasound has also been used for removing tissue in a controlled manner (Parsons et al., 2006; Xu et al., 2005; Xu et al., 2004), gene transfection (Christiansen et al., 2003; Duvshani-Eshet and Machluf, 2005; Feril et al., 2005; Frenkel et al., 2002; Liang et al., 2004; Manome et al., 2005; Ogawa et al., 2002; Wei et al., 2004; Zarnitsyn and Prausnitz, 2004), localized drug delivery (Shortencarier et al., 2004; van Wamel et al., 2004), and the acceleration of thrombolysis (Everbach and Francis, 2000). In tissue characterization, backscattered ultrasound echoes have been used to estimate the characteristic scatterer correlation length for tissue microstructure (Insana and Hall, 1990; Insana et al., 1990; Lizzi et al., 1997; Lizzi et al., 1983; Oelze et al., 2004; Oelze and Zachary, 2006) as well as to estimate tissue displacement∕stiffness after using acoustic radiation force (ARFI) to push the tissue (Fahey et al., 2005; Fahey et al., 2004; Hsu et al., 2007; Nightingale et al., 2002).

In all of these applications, an accurate estimate of attenuation along the propagation path could improve the clinical utility of the technique. For the therapy applications, knowing the attenuation would improve therapy planning by allowing for an estimate of ultrasound fields at the sight of the therapy prior to initializing the therapy. When performing ARFI, an estimate of attenuation along the propagation path would allow for an estimate of the radiation force pushing the tissue to be determined, allowing for the stiffness of the tissue to be quantified. Also, when estimating the scatterer correlation length, an accurate estimate of the frequency dependence of total attenuation along the propagation path is critical in order to compensate for the spectral changes due to attenuation prior to estimating the scatterer correlation length.

Despite these benefits, an accurate estimation of total attenuation along the propagation path from backscattered ultrasound echoes has remained an elusive goal for many years. The challenge results from both attenuation and scatterer correlation length modifying the backscattered power spectrum (Bigelow et al., 2005; Insana et al., 1990). Some previous approaches have included quantifying the attenuation based on changes in the backscattered intensity with depth (He and Greenleaf, 1986; Tu et al., 2006), estimating the local attenuation of the tissues along the propagation path and then summing these attenuations to obtain estimates of total attenuation (Lizzi et al., 1992; Sidney, 1997), estimating the attenuation by comparing the echoes at two different frequencies assuming a coarse model for scattering (Lu et al., 1995), and simultaneously estimating the scatterer correlation length and attenuation along the propagation path from backscattered ultrasound echoes (Bigelow and O’Brien, 2005a; Bigelow and O’Brien, 2005b; Bigelow et al., 2005). However, these approaches have many deficiencies. The estimates based on changes in backscatter intensity assume that the tissue along the propagation path is homogeneous. Summing multiple estimates of local attenuation to obtain an estimate of total attenuation is highly computationally intensive and prone to errors as the errors can accumulate with increasing tissue depth. Lastly, simultaneously estimating both scatterer size and total attenuation results in poor precision and is highly dependent on an accurate model for the tissue scattering structure prior to obtaining the estimate. Therefore, a new algorithm is needed if attenuation along the propagation path is to be accurately estimated.

In this paper, a new algorithm for estimating the attenuation along the propagation path is derived. It combines backscattered echoes from multiple sources. Unlike the previous approach based on changes in backscattered intensity, the proposed algorithm does not assume that the tissue is homogeneous along the propagation path. Also, unlike the previous approach that sums estimates of local attenuation resulting in cumulative errors and high computational demands, the new algorithm estimates the attenuation based on the echoes received from a single region of the tissue. Last, unlike the previous algorithms that attempt to find the total attenuation and correlation length simultaneously, the proposed algorithm has only a weak dependence on the scattering structure of the tissue. After deriving the new algorithm, the performance of the algorithm is validated using computer simulations where the attenuation of the tissue is varied from 0.1 to 0.9 dB∕cm–MHz.

DERIVATION OF ALGORITHM

The backscattered power spectrum received by an ultrasound source from a random distribution of weak scatterers at the focus that satisfy the Born approximation is given by (Bigelow and O’Brien, 2004b)

$$E\left[{\mid V_{\mathrm{scat}}\left(f\right)\mid }^2\right]\propto \frac{k^4{\mid V_{\text{plane}}\left(f\right)\mid }^2}{A_{\mathrm{comp}}\left(f\right)}{F}_{\gamma }(f,a_{\mathrm{eff}}),$$ (1)

where k is the wave number. Also, V_plane(f) is the voltage spectrum that would be returned from a rigid plane placed at the focal plane in a water bath and is obtained independently to calibrate the echoes from the tissue. F_γ(f,a_eff) is the form factor describing the correlation function for the tissue and depends on both frequency and the effective scatterer size, a_eff, of the tissue. A_comp(f) is a generalized attenuation-compensation function that accounts for focusing, local attenuation, and total attenuation and is given by (Bigelow and O’Brien, 2004b)

$$A_{\mathrm{comp}}=\frac{e^{4{\alpha }_{\mathrm{tot}}{z}_T}}{{\int }_{-L∕2}^{L∕2}d{s}_z\left(g_{\mathrm{win}}\left(s_z\right)e^{-4s_z^2∕w_z^2}{e}^{4{\alpha }_{\mathrm{loc}}{s}_z}\right)},$$ (2)

where α_tot is the total attenuation along the propagation path from the source to the focus and is the parameter being estimated by the algorithm developed in this paper. For inhomogeneous propagation paths, α_tot is the effective attenuation weighted by the attenuation of each tissue along the path and the path length in each tissue. Therefore, Eqs. 1, 2 are equally valid for inhomogeneous tissues. Also, z_T is the distance from the aperture plane to the focal plane for the transducer, L is the length of the windowing function, g_win, in millimeters that is used to gate the backscattered waveform, and α_loc is the local attenuation in the focal region. w_z is the effective Gaussian depth of focus that results from approximating the field in the focal region with a Gaussian function and can be used to quantify the ultrasound field for both spherically focused and array sources. w_z depends linearly on wavelength and is given by w_z=6.01λ(f#)² for an ideal spherically focused source where f# is the f-number of the source (Bigelow and O’Brien, 2004b).

The value for w_z for a focused ultrasound source can be determined experimentally prior to imaging the tissue by obtaining echoes from a rigid plane scanned through the focal region in a water bath (Bigelow and O’Brien, 2004a). Furthermore, an earlier paper demonstrated that

$${\alpha }_{\mathrm{loc}}\equiv \sqrt{({\alpha }_{\text{high}}^2+{\alpha }_{\text{low}}^2)∕2}$$ (3)

is a good choice for α_loc when there is uncertainty in the value of local attenuation where α_high and α_low are the largest and smallest attenuation values expected for the tissue (Bigelow and O’Brien, 2006). Therefore, the impact of local attenuation and focusing can be removed by dividing E[∣V_scat(f)∣²] by ${\int }_{-L∕2}^{L∕2}d{s}_z\left(g_{\mathrm{win}}\left(s_z\right)e^{4s_z^2∕w_z^2}{e}^{4{\alpha }_{\mathrm{loc}}{s}_z}\right)$ after obtaining echoes from the region of interest, yielding

$$E{\left[{\mid V_{\mathrm{scat}}\left(f\right)\mid }^2\right]}_{\text{compensated}}\propto k^4{\mid V_{\text{plane}}\left(f\right)\mid }^2{e}^{-4{\alpha }_{\mathrm{tot}}{z}_T}{F}_{\gamma }(f,{\alpha }_{\mathrm{eff}}).$$ (4)

A similar expression to Eq. 4 can also be found after removing the focusing∕diffraction effects for array sources. If we then split the attenuation term into a forward propagating contribution (i.e., prior to scattering), z_T+, and a backward propagating contribution (i.e., after scattering), z_T−, Eq. 4 becomes

$$E{\left[{\mid V_{\mathrm{scat}}\left(f\right)\mid }^2\right]}_{\text{compensated}}\propto k^4{\mid V_{\text{plane}}\left(f\right)\mid }^2{e}^{-2{\alpha }_{\mathrm{tot}}{z}_{T+}}{F}_{\gamma }(f,a_{\mathrm{eff}})e^{-2{\alpha }_{\mathrm{tot}}{z}_{T-}}.$$ (5)

This split is necessary because some modifications of the spectrum due to attenuation occur prior to scattering and some occur after.

Equation 5 can be simplified further if we assume that the backscattered spectrum is approximately Gaussian such that

$$k^4{\mid V_{\text{plane}}\left(f\right)\mid }^2\propto \exp (-\frac{{(f-f_o)}^2}{2{\sigma }_{\omega }^2}),$$ (6)

and we assume that the correlation function for the tissue has the form

$$F_{\gamma }(f,a_{\mathrm{eff}})\propto e^{-A{f}^n}$$ (7)

at least over a frequency range of interest. Equation 7 has been used as a general form for several form factors, including Gaussian and spherical shell, in the past (Bigelow et al., 2005). In this equation, A is a constant that depends on a_eff as well as the correlation function while n gives the frequency dependence of the correlation function. n∼2 for most form factors. Based on these approximations and assuming that α_tot=α_of (i.e., strictly linear dependence on frequency), Eq. 5 can be written as

$$E{\left[{\mid V_{\mathrm{scat}}\left(f\right)\mid }^2\right]}_{\text{compensated}}\propto \exp (-\frac{{(f-f_o)}^2}{2{\sigma }_{\omega }^2}-2{\alpha }_{o}f{z}_{T+}-A{f}^n-2{\alpha }_{o}f{z}_{T-}).$$ (8)

Therefore, the impact of total attenuation and scattering can be considered as a series of Gaussian transformations on a Gaussian function. A linear dependence on frequency may limit the usefulness of the derived algorithm in some applications. However, over a sufficiently small bandwidth, the power-law frequency dependence of some tissues can be approximated as α_of+α_b (Jongen et al., 1986). The complete impact of this approximation when the tissue has a strong power-law dependence will be investigated in detail in the future.

The first Gaussian transformation corresponding to the propagation prior to scattering can be simplified to yield

$$\exp (-\frac{{(f-f_o)}^2}{2{\sigma }_{\omega }^2}-2z_{T+}{\alpha }_{o}f)=\exp [-\left(\frac{{[f-(f_o-2z_T{\alpha }_o{\sigma }_{\omega }^2)]}^2+4z_T{\alpha }_o{\sigma }_{\omega }^2{f}_o-{\left(2z_T{\alpha }_o{\sigma }_{\omega }^2\right)}^2}{2{\sigma }_{\omega }^2}\right)].$$ (9)

Therefore, the expected backscattered power spectrum can be written as

$$E{\left[{\mid V_{\mathrm{scat}}\left(f\right)\mid }^2\right]}_{\text{compensated}}\propto \exp (-\frac{{(f-{\tilde{f}}_o)}^2}{2{\sigma }_{\omega }^2}-A{f}^n-2{\alpha }_{o}f{z}_{T-}),$$ (10)

where the terms independent of frequency are absorbed by the proportionality and ${\tilde{f}}_o=f_o-2z_T{\alpha }_o{\sigma }_{\omega }^2$. Hence, the attenuation due to forward propagation only modifies the center frequency of the power spectrum. The second transformation corresponding to scattering can also be simplified while neglecting higher order terms and assuming n<3, as was done in an earlier publication, yielding (Bigelow et al., 2005)

$$E{\left[{\mid V_{\mathrm{scat}}\left(f\right)\mid }^2\right]}_{\text{compensated}}\propto \exp (-\frac{{(f-{\tilde{f}}_o^{\prime })}^2}{2{\tilde{\sigma }}_{\omega }^2}-2{\alpha }_{o}f{z}_{T-}),$$ (11)

where ${\tilde{f}}_o^{\prime }={\tilde{f}}_o-{\tilde{\sigma }}_{\omega }^{2}An{\tilde{f}}_o^{n-1}$ and ${\tilde{\sigma }}_{\omega }^2={[1∕{\sigma }_{\omega }^2+An(n-1){\tilde{f}}_o^{n-2}]}^{-1}$. Therefore, scattering modifies both the center frequency and the bandwidth of the power spectrum. The last Gaussian transformation corresponding to back propagation can then be simplified similar to the first propagation corresponding to forward propagation to yield

$$E{\left[{\mid V_{\mathrm{scat}}\left(f\right)\mid }^2\right]}_{\text{compensated}}\propto \exp (-\frac{{[f-({\tilde{f}}_o^{\prime }-2z_T{\alpha }_o{\tilde{\sigma }}_{\omega }^3)]}^2}{2{\tilde{\sigma }}_{\omega }^2})=\exp (-\frac{{(f-{\tilde{f}}_o^{″})}^2}{2{\tilde{\sigma }}_{\omega }^2}).$$ (12)

Therefore, attenuation due to back propagation also only modifies the center frequency of the power spectrum. Only this time, it is the center frequency after scattering from the tissue.

Based on the Gaussian transformations corresponding to forward propagation, scattering, and back propagation, the change in center frequency of the spectrum scattered from the tissue as compared to the center frequency of the reference spectrum obtained from a rigid plane at the focus is given by

$$f_o-{\tilde{f}}_o^{″}=4z_T{\alpha }_o\left(\frac{{\sigma }_{\omega }^2+{\tilde{\sigma }}_{\omega }^2}{2}\right)+{\tilde{\sigma }}_{\omega }^{2}An{(f_o-2z_T{\alpha }_o{\sigma }_{\omega }^2)}^{n-1}.$$ (13)

Equation 13 can be further simplified by assuming that n∼2, yielding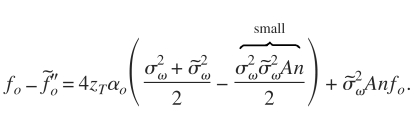

  (14)

However, ${\sigma }_{\omega }^2{\tilde{\sigma }}_{\omega }^{2}An∕2$ is typically much smaller than $({\sigma }_{\omega }^2+{\tilde{\sigma }}_{\omega }^2)∕2$ for diffuse scattering. Therefore, Eq. 14 is approximately given by

$$f_o-{\tilde{f}}_o^{″}\cong 4z_T{\alpha }_o\left(\frac{{\sigma }_{\omega }^2+{\tilde{\sigma }}_{\omega }^2}{2}\right)+{\tilde{\sigma }}_{\omega }^{2}An{f}_o.$$ (15)

In Eq. 15, the downshift in center frequency is linearly dependent on the center frequency, f_o, of the reference spectrum k⁴∣V_plane(f)∣². Also, the intercept of this line only depends on the attenuation along the propagation path, z_Tα_o, the bandwidth of the backscattered spectrum from the tissue, ${\tilde{\sigma }}_{\omega }^2$, and the bandwidth of the reference spectrum ${\sigma }_{\omega }^2$. It does not depend on the form or size of the scattering structures. Therefore, the attenuation along the propagation path can be determined regardless of the scattering structure in the region of interest by scanning the same tissue region by multiple sources with different center frequencies (i.e., f_o’s) and measuring the downshift in center frequency normalized with respect to the average bandwidth, as given by

$$\Delta f_{\mathrm{norm}}=\frac{f_o-{\tilde{f}}_o^{″}}{\left(\frac{{\sigma }_{\omega }^2+{\tilde{\sigma }}_{\omega }^2}{2}\right)}\cong 4z_T{\alpha }_o+\frac{{\tilde{\sigma }}_{\omega }^{2}An}{\left(\frac{{\sigma }_{\omega }^2+{\tilde{\sigma }}_{\omega }^2}{2}\right)}{f}_o$$ (16)

for each source. Fitting a line to Δf_norm vs f_o and finding the intercept of that line yields the attenuation along the propagation path. Theoretically, Eq. 16 will yield the effective attenuation along the propagation path even for inhomogeneous tissues while only requiring echoes from a specific region of interest.

COMPUTER SIMULATIONS

Simulation parameters

The algorithm was verified by simulating the echo waveforms corresponding to five spherically focused ultrasound sources exposing exactly the same homogeneous attenuating half-spaces. The sources had focal lengths of 5 cm and f-numbers of 4. The center frequencies of the sources were 6, 8, 10, 12, and 14 MHz, and each source had a −3 dB bandwidth of 50%. The sound speed of the half-spaces was 1540 m∕s, and the attenuation of the half-spaces was varied from 0.1 to 0.9 dB∕cm-MHz in order to assess the dependence of the algorithm on attenuation. The attenuation dependence is critical when verifying the performance of the algorithm because an earlier algorithm also based on Gaussian approximations of the spectrum failed to give accurate attenuation estimates for attenuation values greater than 0.05 dB∕cm MHz for tissue depths of ∼5 cm (Bigelow et al., 2005). The scattering structures within each half-space had Gaussian correlation functions (i.e., form factor of F_γ(f,a_eff)=exp[−0.827(ka_eff)²]) with an a_eff of 25 μm and were positioned at a density of 250∕mm³ (approximately five scatterers per resolution cell for a 14 MHz transducer). Echoes were generated for 1000 random scatterer distributions for each value of half-space attenuation.

Estimates for E[∣V_scat(f)∣²]_compensated from each source were obtained by first windowing the simulated echoes in the time domain by a rectangular windowing function. A rectangular windowing function was selected because it yielded the best performance when compensating the backscattered power spectrum for windowing, focusing, and local attenuation (Bigelow and O’Brien, 2006). After windowing the echoes in the time domain, the power spectrum was found for each gated window, and a set of independent spectra (number in set varied from 5 to 100) was averaged together to yield ten estimates E[∣V_scat(f)∣²]_windowed. Depending on the number of spectra, not all 1000 echoes were used in the estimate. The broadening of the spectra by windowing was then reduced by

$$E\left[{\mid V_{\mathrm{scat}}\left(f\right)\mid }^2\right]\cong E{\left[{\mid V_{\mathrm{scat}}\left(f\right)\mid }^2\right]}_{\text{windowed}}\exp (-\frac{{(f-{\tilde{f}}_a)}^2{\sigma }_g^2}{2({\tilde{\sigma }}_a^2+{\sigma }_g^2){\tilde{\sigma }}_a^2}),$$ (17)

as has been described previously (Bigelow and O’Brien, 2005b). In Eq. 17, ${\tilde{f}}_a$ and ${\tilde{\sigma }}_a$ are the approximate values for the spectral peak frequency and Gaussian bandwidth of the backscattered power spectrum (i.e., $E{\left[{\mid V_{\mathrm{scat}}\left(f\right)\mid }^2\right]}_{\text{windowed}}\propto \exp (-{(f-{\tilde{f}}_a)}^2∕2{\tilde{\sigma }}_a^2)$) and ${\sigma }_g^2$ is the bandwidth found by fitting a Gaussian function to the magnitude squared of the Fourier transform of the rectangular windowing function. E[∣V_scat(f)∣²] was then divided by ${\int }_{-L∕2}^{L∕2}d{s}_z(g_{\mathrm{win}}\left(s_z\right)e^{-4s_z^2∕w_z^2}\times e^{4{\alpha }_{\mathrm{loc}}{s}_z})$, where α_loc=0.64 dB∕cm MHz, as given by Eq. 3 with α_high and α_low equal to 0.9 and 0.1 dB∕cm MHz, respectively, to yield an estimate of E[∣V_scat(f)∣²]_compensated.

Once E[∣V_scat(f)∣²]_compensated was determined, estimates for ${\tilde{f}}_o^{″}$ and ${\tilde{\sigma }}_{\omega }^2$ were obtained for each source by fitting a Gaussian function to the power spectrum using frequencies in the −20 dB bandwidth of the backscattered power spectrum. While noise was not considered in this preliminary analysis, we anticipate that the main impact of noise will be to reduce the frequency range used to fit the Gaussian to the power spectra and hence should not significantly impact our results. Also, f_o and ${\sigma }_{\omega }^2$ were found for each source by fitting a Gaussian function to the backscattered power spectrum of the echo from a rigid plane placed at the focal plane. From these quantities,

$$\xi \left(f_o\right)=\frac{2(f_o-{\tilde{f}}_o^{″})}{4z_T({\sigma }_{\omega }^2+{\tilde{\sigma }}_{\omega }^2)}\cong {\alpha }_o+(\cdots )f_o$$ (18)

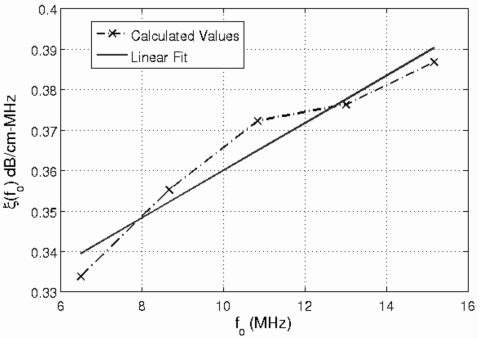
was calculated for each source. A linear fit to ξ(f_o) vs f_o for the different sources yields an estimate for the slope of the attenuation along the propagation path. As an example, Fig. 1 shows a plot of ξ(f_o) in dB∕cm- MHz vs f_o for the five different sources used in the simulations with the corresponding linear fit. The attenuation for half-space was 0.3 dB∕cm MHz, and this example was obtained using 25 independent rf echoes and a window length of 4.36 mm (i.e., 17λ).

Figure 1.

A sample plot of ξ(f_o) in dB∕cm-MHz vs f_o for the five different sources used in the simulations with the corresponding linear fit. This example is for a half-space attenuation of 0.3 dB∕cm-MHz and was obtained using 25 independent rf echoes and a rectangular gating window length of 4.36 mm (i.e., 17λ).

Simulation results: Dependence on window length and number of rf echoes

Prior to assessing the algorithm dependence on attenuation, we needed to determine the optimal window length and the number of independent rf echoes needed to obtain reasonable estimates of attenuation. The algorithm assumes that the tissue is locally homogeneous in a small region about the focus. Therefore, the window length equates to the depth while the number of rf echoes along with the beam width at the focus relates to the width of the required homogeneous region. Ideally, this region should be as small as possible.

In order to assess the dependence on window length, the length of the rectangular window used to gate the time domain waveforms was varied from 9λ to 33λ (2.31–8.47 mm) in steps of 4λ, where λ corresponds to the wavelength in the tissue at 6 MHz, the smallest source frequency used in the simulations. The same rectangular window length (i.e., 2.31 mm for the smallest window) was used for all five sources even though the length corresponded to a larger number of wavelengths for the higher frequency sources. Therefore, the size of the homogeneous region along the beam axis was set by the wavelength of the lowest frequency source. In future studies, we anticipate this size to scale with frequency. The attenuation of the half-space for this simulation was 0.3 dB∕cm-MHz, and 100 independent echoes were used when estimating the power spectrum.

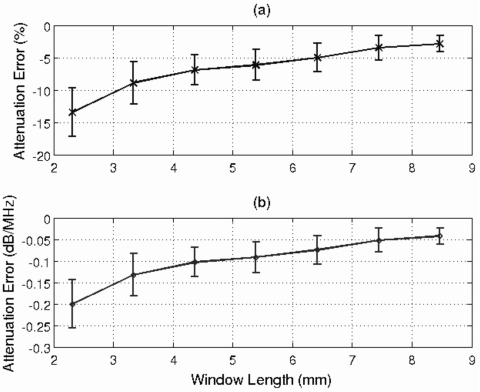
Figure 2a shows the mean and standard deviation of the percentage error in the attenuation slope estimate, α_o, as a function of window length, while Fig. 2b shows the mean and standard deviation of the error in α_oz_T as a function of window length. The multiplication by z_T removes the influence of propagation depth when quantifying the error in the attenuation estimate. The error in the attenuation estimate is reduced as the window length is increased. However, the improvement is minimal for window lengths greater than 4.36 mm (i.e., 17λ). Therefore, a window length of 17λ was considered to be adequate and was used for the remainder of the simulations.

Figure 2.

Plot of mean and standard deviation of error in attenuation slope in (a) percent and in (b) dB∕MHz vs the rectangular window length used to gate the time domain waveforms in millimeters. The attenuation of the half-space for this simulation was 0.3 dB∕cm-MHz, and 100 independent echoes were used when estimating the power spectrum.

After determining an adequate window length, the next step was to find the number of independent rf echoes needed to obtain a reasonable estimate of attenuation. Therefore, the number of echoes used to obtain the estimates was set to 5, 10, 25, 50, 75, and 100. Once again, the attenuation of the half-space for this simulation was 0.3 dB∕cm-MHz, and a window length of 4.36 mm was used to gate the time domain waveforms. The mean and standard deviation of the error in the attenuation estimate versus the number of echoes used to obtain the estimate is shown in Fig. 3.

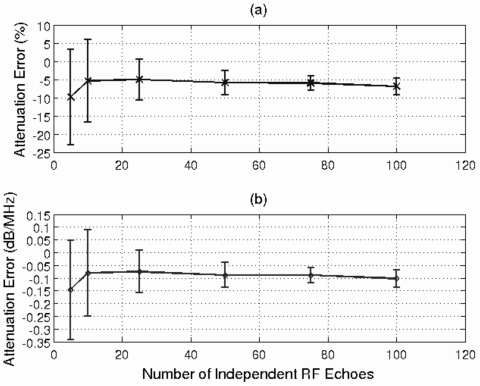
Figure 3.

Plot of mean and standard deviation of error in attenuation slope in (a) percent and in (b) dB∕MHz vs the number of rf echoes used to obtain the estimates. The attenuation of the half-space for this simulation was 0.3 dB∕cm-MHz, and a window length of 4.36 mm (i.e., 17λ) was used to gate the time domain waveforms.

Once again, the error is plotted as both a percentage error [Fig. 3a] as well as the error in α_oz_T [Fig. 3b]. Initially, as we go from five to ten echoes, both the mean and standard deviation of the error improve. For a larger number of echoes, the error in the mean remains relatively constant, but the precision of the estimates improves as the number of echoes increases. The improvement in precision is not significant when more than 25 echoes are used in the estimate. Therefore 25 echoes were considered adequate to obtain a reasonable estimate of total attenuation.

Simulation results: Dependence on half-space attenuation

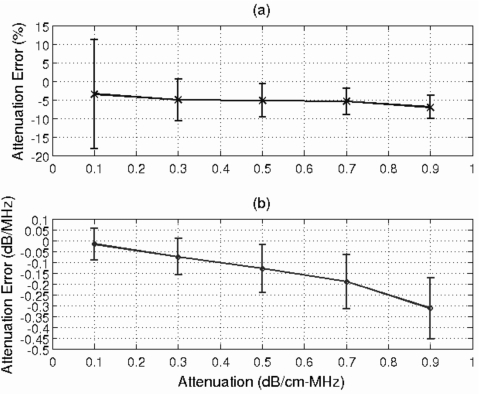
After determining adequate values for window length and the number of rf echoes, the next step was to evaluate the dependence of the algorithm on half-space attenuation. Figure 4a shows the mean and standard deviation of the percentage error in the attenuation slope estimate, α_o, while Fig. 4b shows the mean and standard deviation of the error in α_oz_T for half-space attenuations of 0.1 to 0.9 dB∕cm-MHz. The results were obtained using 25 independent rf echoes and a window length of 4.36 mm (i.e., 17λ). The percentage error [Fig. 4a] ranges from −3.5±14.7% for a tissue attenuation of 0.1 dB∕cm-MHz to −7.0±3.1% for a tissue attenuation of 0.9 dB∕cm-MHz, demonstrating that the attenuation along the propagation path could be accurately determined using the derived algorithm even for large attenuation values. The precision of the α_oz_T estimate is also very good, varying from 0.07 to 0.14 dB∕MHz as the half-space attenuation increases [Fig. 4b]. The mean error of α_oz_T degrades as the attenuation of the half-space increases, but since the percentage error remains approximately −5%, the degradation is due to the ∼−5% bias contributing more significantly at the higher attenuation values.

Figure 4.

Plot of mean and standard deviation of error in attenuation slope in (a) percent and in (b) dB∕MHz vs the attenuation of the half-space. The window length used in this simulation was 4.36 mm to gate the time domain waveforms, and 25 independent echoes were used when estimating the power spectrum.

DISCUSSION

In this paper, we demonstrated that the slope of the attenuation along the propagation path, α_o, can be determined by scanning the region of interest using multiple transducers. The algorithm only assumes that the attenuation along the propagation path has a linear dependence on frequency and that the spectrum transmitted by the ultrasound source, either array or spherically focused, is approximately Gaussian. The downshift in center frequency when comparing the backscattered spectrum to the echo from a reference spectrum was shown to have the form Δf=mf_o+b after normalizing with respect the the source bandwidth where m depends on correlation length and b depends on α_o. Hence, the intercept of this line can be used to find α_o independent of the frequency dependence of the scattering. This algorithm could lead to significant advances in ultrasound tissue characterization and ultrasound therapy planning since attenuation along the propagation path is a critical parameter in both applications. This algorithm is different from previously proposed algorithms in that it can find the attenuation along the propagation path from echoes from a single region of interest rather than require attenuation estimates along the entire propagation path. The algorithm is also not strongly dependent on the scattering properties in the region of interest. Therefore, errors in the modeling of the sources of ultrasound scattering should not impact the attenuation estimates. The algorithm also does not assume that the tissue along the propagation path is homogeneous, allowing for clinical implementation using real tissues.

While the performance of the developed algorithm looks very promising, the performance could be significantly improved if the source of the ∼−5% bias could be determined. One possibility that was considered is that the bias results from the assumption that ${\sigma }_{\omega }^2{\tilde{\sigma }}_{\omega }^{2}An∕2$ is typically much smaller than $({\sigma }_{\omega }^2+{\tilde{\sigma }}_{\omega }^2)∕2$ from the derivation of Eq. 15. However, a more rigorous mathematical analysis revealed that a violation of this assumption would result in a slight overestimation of the attenuation, whereas the simulations demonstrate a slight underestimation. Therefore, the source of the underestimation is not clear at this time. Additional computer simulations and phantom experiments will provide more insights as the investigation is continued in the future.

While the ∼−5% bias should be investigated further and possibly removed, the algorithm still has significant clinical utility even with this bias. Therefore, the algorithm is almost ready for clinical implementation. The main hurdle that remains is that the accuracy and precision of the algorithm should be verified experimentally. The experiments should include both phantom experiments as well as ex vivo tissue experiments. Also, when implementing the algorithm using array sources, calibrating the sources to determine the values of f_o using a planar boundary might be challenging and, other calibration techniques might need to be explored. Overall, the algorithm has great potential clinically and could greatly improve many different emerging clinical ultrasound applications.