Abstract
Human ventilation at rest exhibits complexity and chaos. The aim of this study was to determine whether suprapontine interferences with the automatic breathing control could contribute to ventilatory chaos. We conducted a post-hoc analysis of a previous study performed in awake volunteers exhibiting cortical pre-motor potentials during inspiratory loading. In 8 subjects, flow was recorded at rest, while breathing against inspiratory threshold loads (median 21.5 cmH2O) and resistive loads (50 cmH2O/L/s) loads, and while inhaling 7%CO2–93%O2. Chaos was identified through noise titration (noise limit, NL) and the sensitivity to initial conditions was assessed through the largest Lyapunov exponent (LLE). Breath-by-breath variability was evaluated using the coefficient of variation of several ventilatory variables. Chaos was consistently present in ventilatory flow recordings, but mechanical loading did not alter NL, LLE, or variability. In contrast, CO2 altered chaos and reduced variability. In conclusion, inspiratory loading —and any resultant respiratory-related cortical activity— were not associated with changes in ventilatory chaos in this study, arguing against suprapontine contributions to ventilatory complexity.
Keywords: chaos, respiratory control, inspiratory loading
1. Introduction
Lung ventilation depends on the alternation between inspiratory and expiratory gas flow. In humans, this process seems periodic. In fact, it is not. Rather, the dynamics of ventilatory flow exhibit complexity and have the mathematical features of chaos (Wysocki et al., 2006; Fiamma et al., 2007a; Fiamma et al., 2007b). This behaviour is similar to the behaviour of other human physiological processes, such as the heart rhythm (Poon and Merrill, 1997) and the electroencephalographic activity of the brain (Iasemidis et al., 2005). In mathematical terms, this indicates that the trajectory of ventilatory flow is bounded and depends on deterministic processes, but is unpredictable in the long term and sensitive to the initial conditions.
Chaos is altered in biological systems in response to physiological stimulation or disease. For example, cardiac chaos decreases during congestive heart failure (Poon and Merrill, 1997). Changes in the chaotic behaviour of electroencephalographic activity occur prior to the onset of overt clinical seizures (Iasemidis et al., 2005). Stimulating breathing with carbon dioxide increases the sensitivity of ventilatory flow to initial conditions as well as its unpredictability (Fiamma et al., 2007b). In patients with respiratory failure, ventilatory chaos increases when coordination between the patient’s breathing efforts and the respiratory assist device improves (Mangin et al., 2008). Characterising ventilatory chaos is thus of physiological interest as well as clinical importance.
Nevertheless, the physiological basis of the chaotic dynamics of ventilatory flow is not well understood. In addition to the intrinsic properties of the central respiratory pattern generators within the brainstem, the presence and/or intensity of ventilatory chaos may depend on one or more additional factors. These would include: the mechanical properties of the respiratory system, afferent information from mechanoreceptors, chemoreceptor reflexes, and suprapontine or behavioural influences. Several reports point to the automatic ventilatory command —produced by the activity of brainstem rhythmogenetic neurones—, possibly modulated by vagal afferents, as the main source of ventilatory chaos in mammals (Sammon and Bruce, 1991; Del Negro et al., 2002; Fiamma et al., 2007b). By failing to detect ventilatory chaos in patients undergoing passive mechanical ventilation, Mangin et al. (Mangin et al., 2008) provided a strong argument against the contribution of the mechanical properties of the respiratory system. The information available on the potential effects on ventilatory chaos of suprapontine volitional or behavioural factors (which are particularly abundant in humans) is somewhat contradictory and difficult to reconcile. Voluntary control of breathing abolished ventilatory chaos (Fortrat et al., 1997). Such a result suggests that cortical influences would tend to decrease chaos. The decrease in ventilatory chaos during slow wave sleep (as compared to wakefulness, (Burioka et al., 2002) and its increase in patients with panic-anxiety disorders (Yeragani et al., 2002) suggest the opposite.
It has recently been shown that in awake normal humans the pre-motor cerebral cortex is activated by the application of inspiratory resistive or threshold loads (Raux et al., 2007). The presence of cortical pre-motor activity during loaded breathing, that is neither voluntary nor necessarily conscious, provides an opportunity to examine the influence of suprapontine behavioural factors on ventilation during wakefulness. The objective of this study was therefore to assess the effect of inspiratory resistive and threshold loading on the chaotic dynamics of breathing. We hypothesized that any changes that occurred compared to unloaded breathing would reflect the behavioural cortical pre-motor influence on ventilatory control. To test this hypothesis, we analyzed the ventilatory flow dynamics of the subjects who participated in the previously published study of Raux et al. (2007) mentioned earlier.
2. Methods
2.1 Subjects
This study was carried out on the ventilatory flow signals recorded previously by Raux et al. (2007) during their initial description of respiratory pre-motor potentials associated with inspiratory loading. The experimental protocol received appropriate legal and ethical clearance (Comité Consultatif de Protection des Personnes se prêtant à des Recherches Biomédicales, Pitié-Salpêtrière, Paris, France) and the participants gave written informed consent. The methods have been previously described in detail (Raux et al., 2007). Briefly, ten subjects participated in the study (age 19–34 years, three men, body mass index 21.5 ± 2.2 kgm2). They received detailed information about the methods used but were naive concerning the purpose of the study and had not previously participated in respiratory physiology experiments. All were healthy with no prior history of respiratory or neurological disease, other significant medical illness, or medication use.
2.2 Equipment and procedures
Subjects sat in a comfortable chair with full support of the head, neck and back. For the purpose of recording pre-motor potentials as previously reported, subcutaneous needle electrodes were inserted into the scalp and surface electrodes were attached to the earlobes (see (Raux et al., 2007). Periodically, subjects were asked to perform stereotyped hand movements (finger snapping). They watched a movie —the same movie for all subjects, that they all had already seen— on a computer monitor during the whole experiment, while wearing headphones to exclude auditory cues and extraneous noise.
The experimental protocol included two sets of measurements. In the first one, the subjects wore a nose clip and breathed through a mouthpiece attached to a low dead space linear pneumotachometer (3700A series, Hans Rudolph, Kansas City, MO, USA, dead space 14 ml, flow resistance 0.02 to 0.04 cmH2O.l.s−1) connected to a differential pressure transducer (DP-45–18; ± 2 cm H2O, Validyne, Northridge, CA, USA). The flow signal was digitized at 2 kHz (Chart v5.2, ADInstruments, Sydney, Australia) and stored on a personal computer for off-line analysis. Inspiration was loaded by attaching either a 50 cm H2O.l−1.s−1 linear resistor or a threshold loading device (Spring-to-Stretch®,Threshold Inspiratory Muscle Trainer, Model #730, Health Scan Products, Cedar Grove, NJ, USA) to the inspiratory port of a medium two-way non-rebreathing valve (2600 series, Hans Rudolph, Kansas City, MO, USA) placed in series with the pneumotachometer. The median value of the threshold load was 21.5 cmH2O (interquartile range, 19–25). End-tidal CO2 was measured from a side port of the mouthpiece using an infrared CO2 gas analyser (IR 1505, Servomex, Plaine Saint Denis, France).
In the second set of measurements, a low resistance pneumotachometer linear over the experimental range of flow (MLT 1000 l, ADInstruments, Sydney, Australia; dead space 350 ml, flow resistance 0.002 cmH2O.1−1.s−1) replaced the low dead space pneumotachometer. It was connected in series to a large two-way non-rebreathing valve (2700 series; Hans Rudolph, Kansas City, MO, USA). The inspiratory port was used for the breathing of a gas mixture of 7% CO2 and 93% O2.
The two sets of measurements were performed in random order. One set consisted of: 1) a control period of quiet breathing, 2) inspiratory threshold loading, 3) a 15 min rest period following disconnection from the respiratory apparatus, and 4) inspiratory resistive loading. The other set of measurements consisted of: 1) an additional control period of quiet room air breathing, 2) breathing a gas mixture of 7% CO2 and 93% O2, and 3) a 15 min rest period following disconnection from the respiratory apparatus. In each condition, 5–10 min were allowed for stabilization of the respiratory pattern before recording. Of note, the subjects did not receive any instruction regarding their ventilatory pattern.
Only unfragmented continuous recordings of the flow signal were retained for analysis. The duration was 6–10 minutes for the assessment of the effect of mechanical loading and 4–7 minutes for CO2 stimulated breathing.
2.3 Data analysis
2.3.1 Breath-by-breath variability
A specific routine developed with Matlab™, V.7.0.1 R14 (MathWorks Inc, Natick, MA, USA) permitted the calculation for each ventilatory cycle of tidal volume (VT), total respiratory cycle time (TT), inspiratory time (TI), expiratory time (TE), mean inspiratory flow (VT/TI), inspiratory duty cycle (TI/TT), and minute ventilation (V′I). The breath-by-breath variability was expressed in terms of the coefficient of variation (standard deviation/mean) for each of these parameters.
2.3.2 Non-linear analysis and assessment of chaos
The non-linear analysis of ventilatory flow was performed as previously described in humans by our group (Wysocki et al., 2006; Fiamma et al., 2007a; Fiamma et al., 2007b; Mangin et al., 2008). A detailed description of the methods is provided in Wysocki et al., (Wysocki et al., 2006).
Detection of chaos
For each recording, the frequency content of the flow signal was described using a 1024 point fast Fourier transform function (Hamming window, no overlap, zero values removed). The digitized files were then subsampled at 5 Hz (Dataplore™, Datan, Teltow, Germany), a frequency always greater than the Nyquist frequency and previously shown to yield the best results for the detection of chaos in ventilatory flow using the noise titration technique (Wysocki et al., 2006). We used the latter because of its robustness and specificity to detect chaos in short and noisy time series (Poon and Barahona, 2001). In brief, noise titration begins with the generation of several Volterra-Wiener-Korenberg series. They are generated with different degrees of non-linearity (d) and embedding dimensions, Kappa (K), to produce a family of linear and non-linear polynomial autoregressive models. The models are then compared and the null hypothesis (linearity) is tested against the alternate hypothesis (non-linearity) using parametric (F-test) and non-parametric (Whitney–Mann) statistics (Barahona and Poon, 1996). If the null hypothesis is rejected, white noise of incrementally increasing standard deviation is added to the time-series until the null hypothesis can no longer be rejected. This defines a “noise limit” (NL) which, when above 0, indicates chaos and provides an estimate of its intensity. When the noise limit is equal to 0 or when no non-linearity is detected, the presence of chaos cannot be ascertained. We performed the noise titration technique using a specific routine developed for Matlab™, V.6.5 R13 (MathWorks Inc, Natick, MA, USA) according to a trial-and-error process including the testing of K values of 4 to 6 and of non-linear degrees of 3 to 5. We retained the highest value for each condition.
Sensitivity to the initial conditions
In order to assess the sensitivity of the ventilatory flow to initial conditions (that also reflects its instability), we calculated the largest Lyapunov exponent (LLE). To this aim, we determined the Lyapunov spectrum (Dataplore™ Software Package, Datan, Teltow, Germany) using the polynomial interpolation approach described by Briggs (Briggs, 1990).
2.4 Statistical analysis
The distribution of the values obtained for each test condition was first tested for normality using the Kolmogorov-Smirnov test. Since all distributions were found to be normal, the results were expressed as the mean ± standard deviation (SD). The effects of inspiratory loading on ventilatory variability and chaos were assessed in comparison with the control situation using an analysis of variance for repeated measures, with a subject factor and the breathing condition as the between-subject factor (control, resistive loading, threshold loading). Since we did not use the same pneumotachometer (low resistance instead of low dead space) and non-rebreathing valve to assess the effects of CO2, we did not include this data in the same analysis of variance. Instead, ventilatory variability and chaos were assessed in comparison with the corresponding control condition using Student’s paired t-test (Prism™4.01, Graphpad Software, San Diego, CA, USA). Differences were considered significant when the risk P of a type I error was less than 0.05.
3. Results
Of the ten subjects studied by Raux et al. (Raux et al., 2007), two were excluded from the present analysis. One was omitted because the ventilatory pattern changed dramatically for unknown reasons during threshold loading. The other was excluded because the recording of the control condition before mechanical loading was segmented into several epochs of short duration. Among the eight remaining subjects, one did not participate in the hypercapnic challenge.
3.1 Breath-by-breath variability
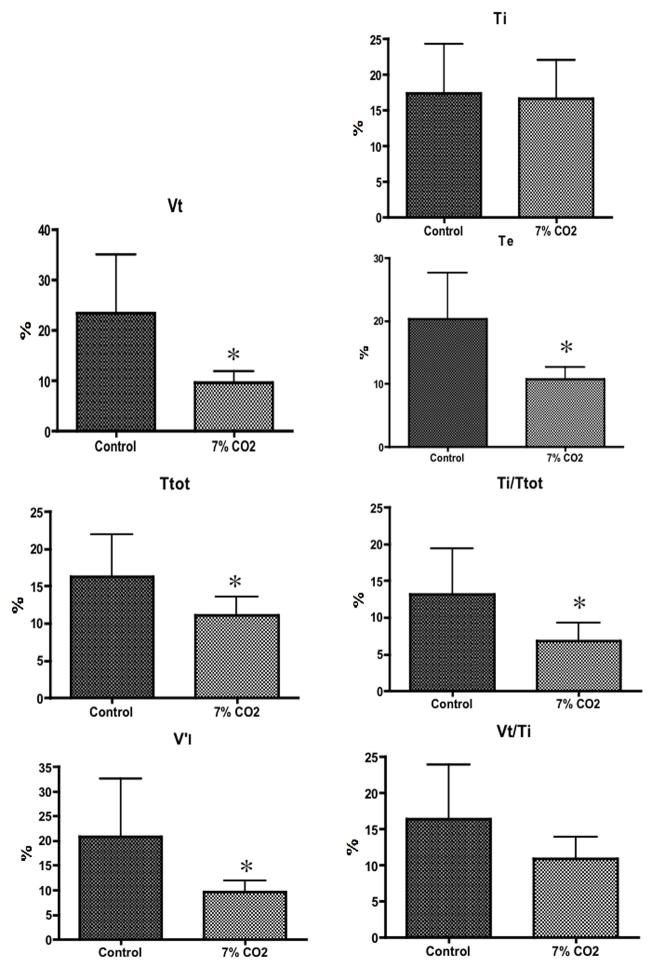
According to the analysis of variance, the coefficient of variation for the pattern of breathing variables measured were not altered by inspiratory threshold or resistive loading compared to the control condition (F values ranged from 1.320 to 1.936, P values varied between 0.0992 and 0.2984) (Fig. 1). Of note, end tidal PCO2 did not change during mechanical loading (Raux et al., 2007). In contrast, CO2 stimulated breathing reduced the coefficient of variation for VT (p=0.0155), TT (p=0.0480), TE (p=0.0157), TI/TT (p=0.0238), and V′I (p=0.0444). The coefficient of variation of TI (p=0.8267) and of VT/TI (p=0.0883) did not change (Fig. 2).
Figure 1.
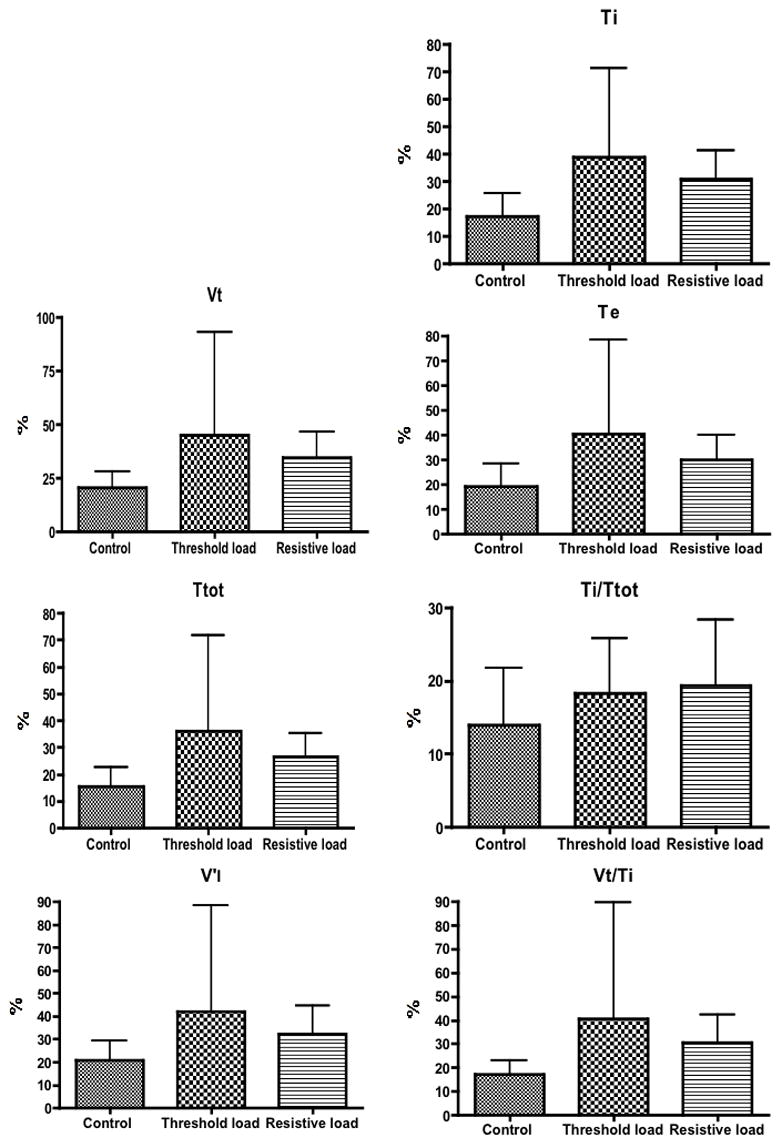
Mean value of coefficient of variation ± SD for tidal volume (VT), total cycle time (TT), inspiratory time (TI), expiratory time (TE), mean inspiratory flow (VT/TI), duty cycle (TI/TT) and minute ventilation during mechanical loading. There was no significant difference between the three conditions.
Figure 2.
Mean value of coefficient of variation ± SD for tidal volume (VT), total cycle time (T TOT), inspiratory time (TI), expiratory time (TE), mean inspiratory flow (VT/TI), duty cycle (TI/TT) and minute ventilation during CO2 breathing. * indicates a significant difference in comparison to the control condition.
3.2 Non-linear analysis of ventilatory flow
3.2.1 Noise titration (Fig. 3)
Figure 3.
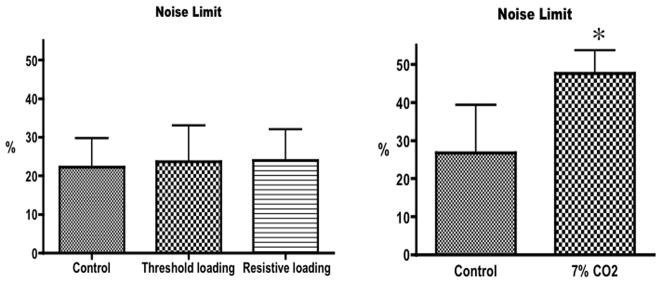
Left panel: mean value ± SD of the noise limit during unloaded breathing (control), threshold loading and resistive loading. There was no significant difference between the three conditions (ANOVA, p=0.87). Right panel: mean value ± SD of the noise limit during room air breathing (control) and breathing a gas mixture of 7%CO2–93%O2 (7%CO2). * indicates a significant difference (t-test, p=0.0108).
The noise limit was above zero for all test conditions in all subjects. The noise limit was 22.25 ± 7.52% during the control condition and was not altered by inspiratory threshold (23.63 ± 9.41%) or resistive loading (24.00 ± 8.09%) (F2,7 = 0.1395, p=0.8710). During CO2breathing, however, the noise limit increased significantly from 26.71±12.66 to 47.57 ± 6.13% (p=0.0108).
3.2.2 Lyapunov exponents (Fig. 4)
Figure 4.
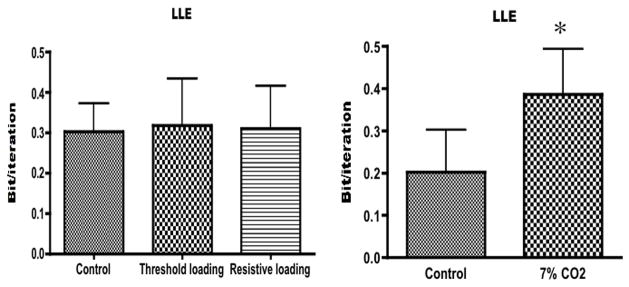
Left panel: mean value ± SD of the largest Lyapunov exponent (LLE) during unloaded breathing (control), threshold loading and resistive loading. There was no significant difference between the three conditions (ANOVA, p=0.9502). Right panel: mean value ± SD of the largest Lyapunov exponent during room air breathing (control) and breathing a gas mixture of 7%CO2–93%O2 (7%CO2). *indicates a significant difference (t-test, p=0.0009
In all test conditions for all subjects, at least one of the Lyapunov exponents was positive, at least one was negative, and their sum was always negative, a pattern compatible with the presence of chaos. LLE did not change with mechanical loading, amounting to 0.3026 ± 0.0694 bit/it during the control condition compared with 0.3190 ± 0.1138 bit/it and 0.3090 ± 0.1073 bit/it during threshold and resistive loading, respectively (F2,7 = 0.05123, p=0.9502). In contrast, LLE increased during CO2 breathing from 0.2025 ± 0.09981 bi/it to 0.3866 ± 0.11074 bit/it (p=0.0009).
4. Discussion
This study shows that sustained high-level inspiratory mechanical loading does not modify the chaotic dynamics of ventilatory flow in awake humans. Given the cortical activity elicited by inspiratory mechanical loading (Raux et al., 2007), our observations suggest that modulation of the automatic drive to breathe through behavioural suprapontine pathways has little effect, if any, on ventilatory chaos.
4.1 Methodological considerations
Chaos detection
How to best identify chaos in short and noisy time series remains a matter of debate, a detailed discussion of which would be beyond the scope of this article. Rather than other methods, we used the noise titration technique since it has been previously validated in this type of experimental setting (Poon and Barahona, 2001). It is also in keeping with our previous work (Wysocki et al., 2006; Fiamma et al., 2007a; Fiamma et al., 2007b; Mangin et al., 2008), allowing for more meaningful comparison of findings amongst studies. In this view, the results observed with CO2 in the present study are reassuring. They derive from the post-hoc treatment of a ventilatory signal gathered from a purpose entirely unrelated with chaos analysis. Yet they are closely similar to those described in a completely separate set of experiments designed specifically to study chaos (Fiamma et al., 2007b). However, the values for LLE obtained during the control periods are higher than those we reported previously (see, in particular Fiamma et al., 2007b), possibly in line with differences in the experimental setting and protocol.
Worthy of emphasis, the noise titration approach has the major advantage to be robust to measurement noise because it uses the noise itself to detect (titrate) chaos. In contrast, LLE estimates obtained by traditional approaches such as the Briggs method (Briggs, 1990) are highly sensitive to noise. It has been shown (Poon and Barahona, 2001) that the noise limit (NL) correlates with the LLE of the equivalent noise-free dynamics. In this regard, the similar behaviour of NL and LLE in our study (Fig. 3 and Fig. 4, respectively) is reassuring.
Finally, it should be noted that the noise titration is a sufficient proof of chaos when the studied system is “autonomous”, namely not driven by dynamic noise (Poon and Barahona, 2001; see also Lei and Meng, 2008). However, stochastic inputs (or “dynamic noise”, as opposed to “additive noise”) can lead to a positive noise limit even when the original non-linear system itself is non-chaotic. This situation is denominated “stochastic chaos” by some, in contrast to “deterministic chaos”. There is currently no available technique to readily distinguish these two situations, including noise titration that will provide a NL value above zero in both cases. In the specific case of ventilation, the dynamics of the respiratory pattern depend critically on the intrinsic properties the respiratory rhythm generator (Del Negro et al., 2002; Rachmuth and Poon, 2008) as well as the time-dependent modulation of the pontomedullary respiratory neuronal networks by chemical and vagal afferent feedbacks (Sammon and Bruce, 1991; Young et al., 2003; Fiamma et al., 2007a). Thus, it seems reasonable to assume that the underlying process is primarily deterministic, although it could be influenced secondarily by dynamic random noise through interaction with other physiologic (non-respiratory related) processes. However, from a physiological standpoint, it is immaterial whether the chaos present in a biological system is purely deterministic or whether it is generated by the interaction of a nonlinear system with dynamic noise. Therefore, when the noise limit does not change from a control state to a test state (as it is the case during mechanical inspiratory loading in this study), then it is reasonable to conclude that the non-linear process that contribute to the generation of the chaos has not changed, be this chaos entirely deterministic or partly stochastic. In other words, the lack of change in NL after inspiratory loading in our study indicates that inspiratory loading in itself does not interfere with the process (and dynamic noise, if any) that produces ventilatory chaos.
Breathing route
Mouth breathing, used in this study, influences the breathing pattern (Perez and Tobin, 1985; Fiamma et al., 2007a; Rameckers et al., 2007), but it does not stamp out ventilatory chaos (Wysocki et al., 2006; Fiamma et al., 2007a). In addition, the breathing route was the same for all the experimental conditions in the present study. As a result, the influence of mouth breathing should not be an issue in the interpretation of the present results, where what matters is the comparison of sequential situations.
Study power
The lack of an effect of mechanical loading on respiratory variability and chaos could be attributed to insufficient power, because of the small size of the study population. We have no means to rule out this possibility. However, it should be emphasized that CO2 stimulated breathing produced highly significant changes in respiratory variability (Fig. 2) and chaos (increased noise limit, increased LLE), in keeping with previous reports (Suyama et al., 2003; Fiamma et al., 2007b). This indicates that if insufficient power due to the small sample size masked the true impact of inspiratory loading on chaos, this impact would have to be modest and of a far lesser magnitude than seen with CO2 breathing.
4.2 Comparison with available data
4.2.1 Breath-by-breath variability
The effects of sustained loading on breath-by-breath variability have been evaluated using resistive (3 to 6 cmH2O/L/s) and elastic (~10 cmH2O/L) loads (Daubenspeck, 1981; Brack et al., 1998). To the best of our knowledge, the effect of inspiratory threshold loading on respiratory pattern variability has not been previously reported. Resistive loading (~3 cmH2O/L/s) decreased the standard deviation of respiratory frequency, V′I, VT, VT/TI and TE (Daubenspeck, 1981; Brack et al., 1998) as well as the coefficient of variation of respiratory frequency, VT, TI and V′I (Brack et al., 1998). In contrast, a larger resistive load (6 cmH2O/L/s) increased the standard deviation of V′I, VT, TI and TE., but did not affect the corresponding coefficients of variation (Brack et al., 1998). Elastic loading did not change ventilatory variability (Daubenspeck, 1981). Taken together, these results suggest that small inspiratory loads can decrease ventilatory variability, whereas with larger loads it can be increased or remain unchanged. This was the case for the extremely high resistance used in our study. This was also true for threshold loading, the magnitude of which was also considerable.
4.2.2 Chaotic dynamics of ventilation
By virtue of the noise titration technique, our study demonstrates that the dynamics of breathing remain chaotic during mechanical loading. This information is new. It contradicts the prediction made by Thibault et al. (Thibault et al., 2004) from a model analysis that stated that very high resistive loads (80 cmH2O/L/s) would render breathing non-chaotic (negative LLE). Of note, Thibault et al (2004) modelled and measured a decrease in LLE with increasing levels of resistive loadings (3.6, 5.8, and 8.8 cmH2O/L/s). Curiously, a secondary rise in LLE occurred at 13.1 cmH2O/L/s. Larger loads were not tested. Specific studies would be needed to determine whether the discrepancies between our approach and that of Thibault et al. (2004) are real, and the possible reasons for this.
4.3 Physiological significance of the results
How suprapontine factors affect ventilatory chaos has seemingly never been specifically examined, but indirect information does exist. In a study of the effects of breathing on the non-linear dynamics of heart rate variability in humans, Fortrat et al. (1997) noted that the underlying ventilatory dynamics present during volitional breathing (which depends on activation of well-identified structures residing predominantly in the primary motor cortex, e.g.(Colebatch et al., 1991) were not chaotic. These findings appear to indicate that volitional breathing abolishes ventilatory chaos. However, the approach used by Fortrat et al. (1997) to characterize ventilatory complexity in humans led these authors to doubt the chaotic nature of spontaneous resting breathing, which is contradictory with more extensive recent data (Wysocki et al., 2006; Fiamma et al., 2007a; Fiamma et al., 2007b). Furthermore, other circumstances where suprapontine influence on ventilation may be altered have been shown to increase ventilatory complexity. For example, ventilatory complexity is less marked during slow-wave sleep (Burioka et al., 2001; Sako et al., 2001; Burioka et al., 2003), where by definition the suprapontine influence on respiration is minimal. The corollary of this observation is that wakefulness increases complexity. Ventilatory complexity is also increased in panic-anxiety disorders (Yeragani et al., 2002). Pre-frontal cortical abnormalities (Berkowitz et al., 2007) have been noted in such individuals, which might be expected to alter the nature and/or extent of suprapontine control over breathing behaviour. Reliably interpreting the above results remains difficult, however, in the absence of objective documentation of suprapontine involvement, or lack thereof. The circumstances involved are themselves inherently complex, potentially impacting on the control of breathing at multiple sites and/or through varied mechanisms.
The recordings analyzed in the present study were obtained under conditions (i.e., inspiratory loading) during which respiratory-related cortical activity was unambiguously demonstrated by the presence of inspiratory pre-motor potentials (Raux et al., 2007). This activity arises from a well-defined cortical structure, namely the pre-motor cortex (and likely the supplementary motor area as well, Ball et al., 1999; Raux et al., 2007). Breathing against a sustained mechanical load induced a suprapontine response that was of a behavioural rather than volitional nature (the subjects were not asked to voluntarily modify their breathing pattern, as in the study by Fortrat et al., 1997). The cortical activation was specific for the respiratory stimulus, rather than “global”, as in the case of the influence of wakefulness or panic-anxiety disorders on ventilation. Our results demonstrate that inspiratory loading has no appreciable effect on the chaotic dynamics of ventilation. By extension, any respiratory-related activity of the cerebral cortex evoked by inspiratory loading can also be said to have no effect on the chaotic dynamics of ventilation. Of importance, inspiratory mechanical loading is often not associated with increased ventilatory drive, as assessed by the measurement of airway occlusion pressure, for instance (Lopata et al., 1983; Ramonatxo et al., 1991; Clague et al., 1992; Locher et al., 2006).
In conclusion, the available data can be summarized as follows. Conditions that increase respiratory neural drive or responsiveness, such as hypercapnia, wakefulness (compared to sleep, (Douglas et al., 1982), and panic-anxiety disorders -often associated with abnormal CO2 sensitivity (Klein, 1993) - also enhance the intensity of ventilatory chaos (Sako et al., 2001; Burioka et al., 2002; Fiamma et al., 2007b). Conversely, circumstances in which respiratory neural drive is not markedly affected, such as mechanical loading (Lopata et al., 1983; Ramonatxo et al., 1991; Clague et al., 1992; Locher et al., 2006), do not change the chaotic dynamics of ventilation even though the influence of suprapontine factors on breathing control can be demonstrated (this study). Conditions that decrease respiratory neural drive, such as sleep (Douglas et al., 1982), also reduce the intensity of ventilatory chaos (Sako et al., 2001; Burioka et al., 2002). Finally, situations that totally disrupt the automatic command, like volitional breathing, abolish ventilatory chaos (Fortrat et al., 1997). Ventilatory chaos therefore seems to be a feature of the brainstem central respiratory pattern generators. Whether this is an intrinsic property or the result of afferent feedback, vagal or otherwise, remains to be determined.
Acknowledgments
The authors are grateful to Brigitte Quenet, from the Ecole Supérieure de Physique et Chimie Industrielle, Paris, France, for her help.
This study was funded in part by a grant “Santé Environnement - Santé travail” of the French Agence Nationale pour la Recherche (ANR0003205, “Transport et transfert via le système pulmonaire humain”); it was also supported by the Association pour le Développement et l’Organisation de la Recherche en Pneumologie, Paris, France. Chi-Sang Poon was supported by U.S. National Institute of Health grants HL079503 and HL072849. Ziyad Samara was supported in part by a scholarship from the « Société de Pneumologie de Langue Française » and by a grant from the French “Ministère des Affaires Etrangères”. Mathieu Raux was a Lavoisier scholar of the French “Ministère des Affaires Etrangères”. Marie-Noëlle Fiamma was supported by a grant from the “Comité d’organisation de l’Assistance Respiratoire a Domicile d’Ile-de-France (C.A.R.D.I.F.)”, Fontenay-aux-Roses, France.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Ball T, Schreiber A, Feige B, Wagner M, Lucking CH, Kristeva-Feige R. The role of higher-order motor areas in voluntary movement as revealed by high-resolution EEG and fMRI. Neuroimage. 1999;10:682–694. doi: 10.1006/nimg.1999.0507. [DOI] [PubMed] [Google Scholar]
- Barahona M, Poon CS. Detection of nonlinear dynamics in short, noisy time series. Nature. 1996;381:215–217. [Google Scholar]
- Berkowitz RL, Coplan JD, Reddy DP, Gorman JM. The human dimension: how the prefrontal cortex modulates the subcortical fear response. Rev Neurosci. 2007;18:191–207. doi: 10.1515/revneuro.2007.18.3-4.191. [DOI] [PubMed] [Google Scholar]
- Brack T, Jubran A, Tobin MJ. Effect of resistive loading on variational activity of breathing. Am J Respir Crit Care Med. 1998;157:1756–1763. doi: 10.1164/ajrccm.157.6.9704114. [DOI] [PubMed] [Google Scholar]
- Briggs K. An improved method for estimating Lyapunov exponents of chaotic time series. Physics Letters. 1990;151:27–32. [Google Scholar]
- Burioka N, Cornelissen G, Halberg F, Kaplan DT. Relationship between correlation dimension and indices of linear analysis in both respiratory movement and electroencephalogram. Clin Neurophysiol. 2001;112:1147–1153. doi: 10.1016/s1388-2457(01)00566-1. [DOI] [PubMed] [Google Scholar]
- Burioka N, Cornelissen G, Halberg F, Kaplan DT, Suyama H, Sako T, Shimizu E. Approximate entropy of human respiratory movement during eye-closed waking and different sleep stages. Chest. 2003;123:80–86. doi: 10.1378/chest.123.1.80. [DOI] [PubMed] [Google Scholar]
- Burioka N, Suyama H, Sako T, Miyata M, Takeshima T, Endo M, Kurai J, Fukuoka Y, Takata M, Nomura T, Nakashima K, Shimizu E. Non-linear dynamics applied to human respiratory movement during sleep. Biomed Pharmacother. 2002;56(Suppl 2):370s–373s. doi: 10.1016/s0753-3322(02)00320-7. [DOI] [PubMed] [Google Scholar]
- Clague JE, Carter J, Pearson MG, Calverley PM. Effort sensation, chemoresponsiveness, and breathing pattern during inspiratory resistive loading. J Appl Physiol. 1992;73:440–445. doi: 10.1152/jappl.1992.73.2.440. [DOI] [PubMed] [Google Scholar]
- Colebatch JG, Adams L, Murphy K, Martin AJ, Lammertsma AA, Tochon-Danguy HJ, Clarck JC, Friston KJ, Guz A. Regional cerebral blood flow during volitional breathing in man. J Physiol. 1991;443:91–103. doi: 10.1113/jphysiol.1991.sp018824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daubenspeck JA. Influence of small mechanical loads of variability of breathing pattern. J Appl Physiol. 1981;50:299–306. doi: 10.1152/jappl.1981.50.2.299. [DOI] [PubMed] [Google Scholar]
- Del Negro CA, Wilson CG, Butera RJ, Rigatto H, Smith JC. Periodicity, mixed-mode oscillations, and quasiperiodicity in a rhythm-generating neural network. Biophys J. 2002;82:206–214. doi: 10.1016/S0006-3495(02)75387-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Douglas NJ, White DP, Weil JV, Pickett CK, Zwillich CW. Hypercapnic ventilatory response in sleeping adults. Am Rev Respir Dis. 1982;126:758–762. doi: 10.1164/arrd.1982.126.5.758. [DOI] [PubMed] [Google Scholar]
- Fiamma MN, Samara Z, Baconnier P, Similowski T, Straus C. Respiratory inductive plethysmography to assess respiratory variability and complexity in humans. Respir Physiol Neurobiol. 2007a;156:234–239. doi: 10.1016/j.resp.2006.12.001. [DOI] [PubMed] [Google Scholar]
- Fiamma MN, Straus C, Thibault S, Wysocki M, Baconnier P, Similowski T. Effects of hypercapnia and hypocapnia on ventilatory variability and the chaotic dynamics of ventilatory flow in humans. Am J Physiol Regul Integr Comp Physiol. 2007b;292:R1985–1993. doi: 10.1152/ajpregu.00792.2006. [DOI] [PubMed] [Google Scholar]
- Fortrat JO, Yamamoto Y, Hughson RL. Respiratory influences on non-linear dynamics of heart rate variability in humans. Biol Cybern. 1997;77:1–10. doi: 10.1007/s004220050361. [DOI] [PubMed] [Google Scholar]
- Iasemidis LD, Shiau DS, Pardalos PM, Chaovalitwongse W, Narayanan K, Prasad A, Tsakalis K, Carney PR, Sackellares JC. Long-term prospective on-line real-time seizure prediction. Clin Neurophysiol. 2005;116:532–544. doi: 10.1016/j.clinph.2004.10.013. [DOI] [PubMed] [Google Scholar]
- Klein DF. False suffocation alarms, spontaneous panics, and related conditions. An integrative hypothesis. Arch Gen Psychiatry. 1993;50:306–317. doi: 10.1001/archpsyc.1993.01820160076009. [DOI] [PubMed] [Google Scholar]
- Lei M, Meng The influence of noise on nonlinear time series detection based on Volterra-Wiener-Korenberg model. Chaos, Solitons and Fractals. 2008;36:512–516. [Google Scholar]
- Locher C, Raux M, Fiamma MN, Morelot-Panzini C, Zelter M, Derenne JP, Similowski T, Straus C. Inspiratory resistances facilitate the diaphragm response to transcranial stimulation in humans. BMC Physiol. 2006;6:7. doi: 10.1186/1472-6793-6-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lopata M, Onal E, Ginzburg AS. Respiratory muscle function during CO2 rebreathing with inspiratory flow-resistive loading. J Appl Physiol. 1983;54:475–482. doi: 10.1152/jappl.1983.54.2.475. [DOI] [PubMed] [Google Scholar]
- Mangin L, Fiamma MN, Straus C, Derenne JP, Zelter M, Clerici C, Similowski T. Source of human ventilatory chaos: Lessons from switching controlled mechanical ventilation to inspiratory pressure support in critically ill patients. Respir Physiol Neurobiol. 2008;161:189–196. doi: 10.1016/j.resp.2008.02.006. [DOI] [PubMed] [Google Scholar]
- Perez W, Tobin MJ. Separation of factors responsible for change in breathing pattern induced by instrumentation. J Appl Physiol. 1985;59:1515–1520. doi: 10.1152/jappl.1985.59.5.1515. [DOI] [PubMed] [Google Scholar]
- Poon CS, Barahona M. Titration of chaos with added noise. Proc Natl Acad Sci U S A. 2001;98:7107–7112. doi: 10.1073/pnas.131173198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poon CS, Merrill CK. Decrease of cardiac chaos in congestive heart failure. Nature. 1997;389:492–495. doi: 10.1038/39043. [DOI] [PubMed] [Google Scholar]
- Rachmuth G, Poon CS. Transistor analogs of emergent iono-neuronal dynamics. HSFP Journal. 2008;2:156–166. doi: 10.2976/1.2905393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rameckers H, Kohl J, Boutellier U. The influence of a mouthpiece and noseclip on breathing pattern at rest is reduced at high altitude. Respir Physiol Neurobiol. 2007;156:165–170. doi: 10.1016/j.resp.2006.09.001. [DOI] [PubMed] [Google Scholar]
- Ramonatxo M, Mercier J, Cohendy R, Prefaut C. Effect of resistive loads on pattern of respiratory muscle recruitment during exercise. J Appl Physiol. 1991;71:1941–1948. doi: 10.1152/jappl.1991.71.5.1941. [DOI] [PubMed] [Google Scholar]
- Raux M, Straus C, Redolfi S, Morelot-Panzini C, Couturier A, Hug F, Similowski T. Electroencephalographic evidence for pre-motor cortex activation during inspiratory loading in humans. J Physiol. 2007;578:569–578. doi: 10.1113/jphysiol.2006.120246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sako T, Burioka N, Suyama H, Nomura T, Takeshima T, Shimizu E. Nonlinear behavior of human respiratory movement during different sleep stages. Chronobiol Int. 2001;18:71–83. doi: 10.1081/cbi-100001172. [DOI] [PubMed] [Google Scholar]
- Sammon MP, Bruce EN. Vagal afferent activity increases dynamical dimension of respiration in rats. J Appl Physiol. 1991;70:1748–1762. doi: 10.1152/jappl.1991.70.4.1748. [DOI] [PubMed] [Google Scholar]
- Suyama H, Burioka N, Sako T, Miyata M, Shimizu E. Reduction of correlation dimension in human respiration by inhaling a mixture gas of 5% carbon dioxide and 95% oxygen. Biomed Pharmacother. 2003;57(Suppl 1):116s–121s. doi: 10.1016/j.biopha.2003.08.015. [DOI] [PubMed] [Google Scholar]
- Thibault S, Calabrese P, Benchetrit G, Baconnier P. Effects of resistive loading on breathing variability non linear analysis and modelling approaches. Adv Exp Med Biol. 2004;551:293–298. doi: 10.1007/0-387-27023-x_44. [DOI] [PubMed] [Google Scholar]
- Wysocki M, Fiamma MN, Straus C, Poon CS, Similowski T. Chaotic dynamics of resting ventilatory flow in humans assessed through noise titration. Respir Physiol Neurobiol. 2006;153:54–65. doi: 10.1016/j.resp.2005.09.008. [DOI] [PubMed] [Google Scholar]
- Yeragani VK, Radhakrishna RK, Tancer M, Uhde T. Nonlinear measures of respiration: respiratory irregularity and increased chaos of respiration in patients with panic disorder. Neuropsychobiology. 2002;46:111–120. doi: 10.1159/000066388. [DOI] [PubMed] [Google Scholar]
- Young DL, Eldridge FL, Poon CS. Integration-differentiation and gating of carotid afferent traffic that shapes the respiratory pattern. J Appl Physiol. 2003;94:1213–1229. doi: 10.1152/japplphysiol.00639.2002. [DOI] [PubMed] [Google Scholar]