Abstract
Meta-analysis is a vital tool in genetic epidemiology. However, meta-analyses to identify gene-disease associations are compromised when contributing studies have typed partially overlapping sets of markers. Currently, only marginal analyses are possible, and these are restricted to the subset of studies typing that marker. This does not allow full use of available data and leads to the confounding of marker effects by closely associated markers. We present a Bayesian approach that exploits prior information on underlying haplotypes to allow multi-marker analysis incorporating data from all relevant studies of a gene or region, irrespective of the markers typed. We present results from application of our approach to data on a possible association between PDE4D and ischemic stroke.
Introduction
The determination of the effect of genetic variation on susceptibility to common human disease, or the effect of genetic variation on the corresponding intermediate phenotypes, is one of the key problems of modern biomedicine. However, it is now clear that genetic effects due to common alleles are small and that detection requires both comprehensive SNP screens and large sample sizes1–3: many previous studies have been underpowered4,5, in terms of sample size and/or in terms of using sets of genetic markers that were not capable of representing unobserved genetic variants with sufficient accuracy. Recent genome-wide association studies on large case-control collections have partially overcome these difficulties and have been highly successful in identifying genetic associations in a number of diseases.6 However, synthesis of all available evidence and data pooling remains important and, in the case of several common diseases, has uncovered susceptibility loci that individual studies could not identify reliably.7
It is often desirable to incorporate into meta-analyses the results of prior gene-disease association studies from which only summary (rather than participant-level) data might be available. The current study is motivated by the desire to synthesize all available evidence regarding the putative association between the gene encoding phosphodiesterase 4D (PDE4D [MIM 600129]) and ischemic stroke (MIM #601367), first reported in 2003.8 PDE4D encodes proteins that degrade cAMP, a key signaling molecule that has a range of vascular effects,9 and the biological plausibility of PDE4D's influencing stroke risk provided added interest to this initial finding. However, a range of subsequent studies have largely failed to replicate the initial finding. A recent meta-analysis10 concluded that an effect of this gene on stroke was unlikely; however, this meta-analysis was restricted to single-SNP analyses of the six markers reported by five or more studies and therefore, as we see below, does not incorporate much of the relevant data.
A key difficulty with attempting a more exhaustive meta-analysis is that studies have typed partially overlapping SNP sets so that many SNPs are unobserved in each individual study; in fact, no SNP was present in all studies. Moreover, studies report only summary data, typically genotype or allele frequencies. The standard approach is to pool all available data on each directly typed SNP in turn. However, this is an inefficient approach if our interest is to detect an effect at a gene as a whole because data pooling is only possible from a subset of studies that typed the SNP in question. Univariate results are also difficult to interpret because they do not account for between-marker association due to linkage disequilibrium (LD). When individual patient data are available, imputating unobserved SNPs and using the observed SNP data makes it possible to incorporate data on all SNPs from all studies.11 However, current imputation methods cannot work with summary data and so are not applicable in this problem. We recently developed a Bayesian method for meta-analysis that accommodates summary SNP information from all studies of the same gene or region irrespective of the SNPs typed.12 The method is applicable to continuous traits but not to binary outcomes. Accordingly, we have now developed a Bayesian hierarchical model that regresses a binary outcome (e.g., disease: no disease) on summary data for multiple SNPs, allowing the SNPs available to vary by study. LD information on the set of markers is incorporated as prior information on haplotype frequencies, obtained from HapMap or other sources. For each SNP, the method provides effect estimates adjusted for the effect of all other SNPs and allows a global test of the gene-disease association. Although motivated by the association between PDE4D and stroke, the approach is generic and potentially widely applicable.
Material and Methods
Systematic Review of PDE4D and Stroke
For their systematic review, Bevan et al.10 searched two electronic databases (PubMed Medline and EMBASE) for literature published from 1996 to October 1, 2007 by using the keywords “stroke,” “SNP polymorphism,” “PDE4D,” and “phosphodiestrase 4D” in isolation and combination with one another. The literature search was limited to studies of humans. We obtained full texts of all the identified articles to examine the association between PDE4D and stroke in populations of European descent. We updated the literature search to August 12, 2008 but found no new relevant studies. This current analysis incorporated 14 data sets from populations of European descent, and a total of 12,929 subjects (5994 cases and 6935 controls) and 33 SNPs were genotyped in at least one study (Table S4 for study details). In the cases of Gretarsdottir8 and Kuhlenbaeumer,13 SNP data not included in the original publications were obtained from Brophy14 and Bevan10, respectively. Because our method relies on prior information on LD from HapMap, we restricted analysis to the 26 typed markers included in HapMap. No SNP was typed in every study, but there was partial overlap of SNP typing across several studies (see Table 1).
Table 1.
PDE4D SNP Sets Used by the Studies Analyzed
| Studies by Bibliographic Reference |
|||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SNPa | rs Number | 27 | 28 | 29 | 25 | 30 | 14 | 26 | 23 | 24 | 31 | 32 | 10 | 8 | 13 |
| 2 | rs152341 | • | |||||||||||||
| 3 | rs187481 | • | |||||||||||||
| 5 | rs27564 | • | |||||||||||||
| 9 | rs3117 | • | • | • | |||||||||||
| 13 | rs26949 | • | |||||||||||||
| 14 | rs26950 | • | |||||||||||||
| 15 | rs35382 | • | |||||||||||||
| 19 | rs4133470 | • | |||||||||||||
| 22 | rs26954 | • | |||||||||||||
| 26 | rs40512 | • | • | • | • | • | |||||||||
| 34 | rs27653 | • | • | • | • | ||||||||||
| 35 | rs26955 | • | |||||||||||||
| 37 | rs26956 | • | |||||||||||||
| 39 | rs3887175 | • | |||||||||||||
| 41 | rs152312 | • | • | • | • | • | • | • | |||||||
| 42 | rs153031 | • | • | • | • | ||||||||||
| 45 | rs12188950 | • | • | • | • | • | • | • | • | • | • | • | • | • | |
| 48 | rs37760 | • | |||||||||||||
| 83 | rs966221 | • | • | • | • | • | • | • | |||||||
| 87 | rs2910829 | • | • | • | • | • | • | ||||||||
| 89 | rs1396476 | • | • | • | • | • | |||||||||
| 175 | rs27171 | • | • | ||||||||||||
| 199 | rs27547 | • | • | ||||||||||||
| 219 | rs6450512 | • | |||||||||||||
| 220 | rs425384 | • | • | ||||||||||||
| 222 | rs27727 | • | • | • | |||||||||||
| Cases | 89 | 94 | 97 | 151 | 222 | 248 | 250 | 259 | 376 | 639 | 685 | 737 | 988 | 1159 | |
| Controls | 191 | 99 | 102 | 164 | 447 | 560 | 219 | 259 | 262 | 736 | 751 | 928 | 652 | 1564 | |
deCODE number.8
Bayesian Hierarchical Model
We model the single-locus counts of alleles in cases and controls reported by each study. Our model is written in terms of a set of underlying haplotype probabilities, and the case haplotype probabilities differ from control probabilities via parameters that can be interpreted as adjusted odds ratio (OR) values for each SNP. Below we describe the form of the likelihood and sketch a number of extensions, for instance allowing variation in the underlying haplotype probabilities across studies. The model is fitted in the Bayesian framework via Markov chain Monte Carlo; accordingly, we go on to describe the prior distributions and sampling scheme used.
Likelihood
Consider M markers with H underlying haplotypes and S studies reporting on some subset of the markers. Our data consist of the marginal minor-allele counts in cases and controls reported by each study at each marker. Take d = 1 to indicate cases and d = 0 to indicate controls, let denote the marginal minor-allele counts observed by study s; note that many of these will be unobserved. We can write these in terms of the (unobserved) H × 1 vector of counts of the underlying haplotypes, ', by summing over the haplotypes that contain the allele of interest; more formally, we define an M × H matrix D where Dij is 1 if haplotype j carries the minor allele at locus i and zero otherwise, so that
| (1) |
The haplotype counts are naturally assumed to have a multinomial distribution, , where are the appropriate haplotype probabilities and is the number of cases/controls in study s. Note that the pair of haplotypes within each person are assumed to be independent (i.e., Hardy-Weinberg equilibrium is assumed). Observing that , the sum of the haplotype counts, is fixed by design in cases and controls, we may reduce the number of free parameters needed to describe by one. Because , by conditioning on we may construct a mapping , where indicate the first H – 1 haplotype counts only:
| (2) |
where D[, H] denotes the Hth column of D, and the H × H – 1 matrix X is
We would like to use the above relationship between and , together with the fact that the haplotype counts have a multinomial distribution, to calculate the likelihood of the allele counts, , but this is not straightforward. Instead, we approximate the likelihood of the log-allele counts by a multivariate normal distribution distribution, with mean and variance written in terms of and and derived via the multivariate delta method, known to perform well for log-multinomial counts.15 Via details given in Appendix A, we obtain:
| (3) |
where is the multinomial covariance matrix of these first H – 1 haplotype probabilities. Note that where elements of are unobserved, for instance because a given marker is not typed in study s, the appropriate likelihood is easily obtained because the marginal distribution of any subset of the components of a multivariate normal distribution is also multivariate normal distribution, with a mean and variance easily obtained from the above. If we were interested solely in investigation of whether haplotype frequencies differ between cases and controls, we could work directly with the above model for . However, we also wish to investigate which SNPs might be associated with the disease. We therefore write the haplotype probabilities in cases, , in terms of the haplotype probabilities in controls, and M adjusted SNP log-ORs, which we denote . We assume SNP ORs combine log additively across loci so that the log-OR for a given haplotype is the sum of the log-ORs for the component SNP, i.e., the haplotypic log-ORs are given by , where D is the design matrix defined above. From16,
| (4) |
Equation (3) may be used directly to obtain the likelihood for controls. Substituting into (4) and the resulting expression for (parameterized by and β) into (3) gives the independent likelihood, , for cases. The full likelihood is then
So far we have worked with separate sets of haplotype frequencies in each study. We expect these to be similar, but possibly not identical, across studies and so model these hierarchically via a multinomial logit link to a set of Gaussian random effects:
| (5) |
where
| (6) |
Note that σHap gives a measure of the heterogeneity in haplotype frequencies across studies.
Model Fitting
We work within the Bayesian framework, so our objective is to calculate the posterior distribution for the parameters of interest, i.e., the probability distribution of those parameters given the observed data. We also want to allow inference on which SNPs affect the trait of interest, which we achieve by allowing some or all of the SNP OR β values to be exactly zero. We use m to indicate the model, that is, which SNPs are not zero, and so wish to calculate
We cannot calculate this analytically and so use Markov-chain Monte Carlo, specifically reversible jump Metropolis-Hastings (RJMH)17,18, to sample from the required posterior. The RJMH sampling scheme starts at an initial model and set of parameter values, m(0) and . To sample the next model and set of parameters, m(1) and θ(1), we propose moving from the current state to another model and/or set of parameter values, m∗ and θ∗, by using a proposal function q(m∗, θ∗|m, θ). We then accept these proposed values as the next sample with probability equal to the Metropolis-Hastings ratio:
If this new set of values is accepted, the proposed set is accepted as m(1) and θ(1); otherwise, the sample value remains equal to the current sample value, i.e., m(1) = m(0) and θ(1) = θ(0). It can be shown that this produces a sequence of samples that converge to the required posterior distribution.19 More details about the scheme used are in Appendix B.
Bayes Factors
Increasingly, Bayes factors (BFs) are being used in genetic epidemiology as an alternative to p values.6,20 A Bayes factor is defined as the posterior-to-prior odds of two competing models, that is, model mi in comparison to model mj
where D denotes the data. BF(mi, mj) is a measure of how much our prior beliefs about the relative merits of mi and mj change after observing the data.
Priors
Priors for β and σHap are βm ∼ N(0, 0.4) for m = 1, ..M and 1/σ2Hap ∼ Gamma[0.001, 0.001].
The prior for the log-ORs is realistically informative, suggesting that most of the density for the ORs lies between 0.5 and 2. Genetic ORs outside this range are rarely observed.3 If the causal variant is unobserved, one would expect adjusted ORs at SNPs in positive LD to be in the same direction (and in opposite directions if the LD is negative). This prior information could be reflected with a multivariate normal covariance matrix for the log-ORs, and we have implemented such a prior. However, this gave almost identical results to the independent priors above, so for simplicity, these are used here. A Gamma[0.001,0.001] prior for between-study precision is a standard reference prior;21 alternative priors give very similar results.
A vital part of our approach is the use of an informative prior distribution for the haplotype frequencies : this enables the model to share information between associated markers and obtain adjusted estimates of SNP ORs. In the current work this has been based on the 120 founding haplotypes from the HapMap trios of European ancestry (see Web Resources). We have accordingly assumed that , where denotes the H haplotype frequency estimates in HapMap.
We also need to specify a prior on the model space, which we do by specifying a prior on k SNPs in the model and then assuming that all models with k SNPs are equally likely. This could of course be modified where certain SNPs—perhaps because of prior evidence of functionality—are judged more likely to be causal than others.
We judged PDE4D to be a strong candidate gene for association with stroke and so allowed a prior probability of 10% that one or more SNP has a non-zero effect by using a truncated Poisson prior with appropriate mean (Figure S1 in the Supplemental Data). We also examined sensitivity to this prior.
Single-SNP Random-Effects Meta-Analysis
Where possible, we compared results from our multi-SNP model to those obtained from an orthodox single-SNP random-effects meta-analysis in both simulation studies and the PDE4D/stroke data set. In both cases additive ORs were calculated for each study via logistic regression. The study-specific estimates and their standard errors were pooled via random-effect models. The DerSimonian and Laird Q test, as well as the I222, were used for evaluating the degree of heterogeneity between studies.
Results
Simulation Studies
For these simulations we examined the effect of alterations in effect size (including no effect), the location and number of causal sites, allele frequency of causal marker, and whether the causal site was observed. Haplotypes for five biallelic markers on the PDE4D gene were simulated with a multinomial model, centered on HapMap-based frequencies. The LD pattern for the five loci is given in Figure 1. We partitioned multinomially drawn haplotypes into cases and controls by assigning disease status with a probability conditional on the presence of designated causal SNP(s) via a logistic regression model with desired causal SNP ORs. We then obtained marginal MAFs for each SNP by summing over the relevant haplotype frequencies. Data was simulated as though from 14 studies, with case and control numbers approximately equal to the 14 PDE4D/stroke studies obtained in our literature review.
Figure 1.
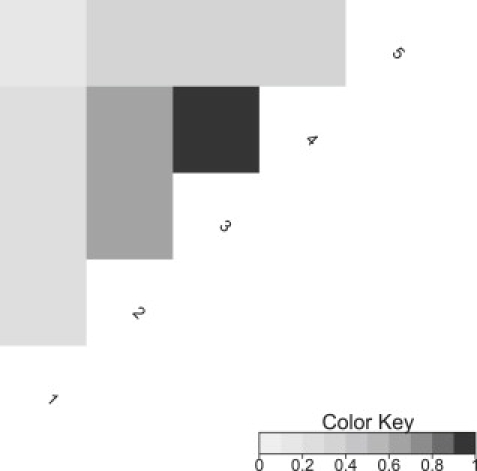
Pairwise LD between the Markers Used in the Simulation Studies
Based on the r2 pairwise LD measure.
To model potential heterogeneity in LD structure between different populations, we generated different haplotype probabilities, for s = 1,…14 and with which to stimulate each study and to use as prior information in our model, respectively. For each study a value was drawn for each haplotype from a normal distribution with a standard deviation of 0.1 centered on the corresponding log-haplotype probability from HapMap. Multinomial-logit transformations were then used for generating study-specific haplotype probabilities that sum to one. This means that the parameter σHap, which our model uses to capture study heterogeneity in haplotype frequencies, was set to 0.1 for the data simulation. For each replicate an additional set of haplotype probabilities was generated as above to act as prior information in place of the underlying HapMap probabilities; therefore, we also model possible heterogeneity between the HapMap population and the populations in the published studies.
Finally, to reflect the variation in SNP sets used by different studies, we introduced missingness (the level of missing data) in the same pattern as that observed in the real studies for SNPs 41–83 (see Tables 1 and 2). For each simulation scenario, 20 replicate data sets were generated in the same way. When a single causal site was simulated, single-SNP analysis produced significant results at multiple sites. Although the effect estimates were always largest and closest to the truth at the causal SNP, for ORs of 1.5 and above all other SNPs were significant at the 5% level in all replicated data sets. Therefore, univariate analysis of these data would most likely conclude that all five markers were possible causal sites. When the effect size was reduced to 1.25, all other SNPs were significant in between 65% and 100% of replicates (Table 3). When two causal sites were simulated, the univariate analysis substantially underestimated the effect at both sites. Because the two causal sites are in strong negative LD, the effect at each is confounded by the other, resulting in a bias toward the null hypothesis (Table 4). This highlights an important use of multiple-marker models: when there are multiple causal sites, adjustment of between-marker confounding may be essential for revealing an effect of the gene on disease.
Table 2.
Information on Missingness in Simulated Data Sets
| SNP 1 | SNP 2 | SNP 3 | SNP 4 | SNP 5 | |
|---|---|---|---|---|---|
| Mean allele Frequency | 0.37 | 0.43 | 0.44 | 0.44 | 0.46 |
| Number of studiesa | 7 | 4 | 13 | 1 | 7 |
| Average casesb | 6,058 | 3,178 | 11,488 | 1,976 | 6,214 |
| Average controlsb | 6,136 | 3,140 | 13,430 | 1,304 | 6,302 |
The same pattern of missingness was used in all scenarios for simulating each replicate data set. This is equivalent to the pattern of missingness for SNPs 42 to 83 in the real PDE4D data (see Table 1).
In each replicate, this is the number of studies to have measured the marker (there are 14 studies in total).
As a result of our simulation method, the number of cases and controls varies slightly in each replicate. However, these are the average numbers of cases and controls providing data on each marker.
Table 3.
Average Results from Single-SNP Meta-Analyses of Simulated Data Replicates
| SNP 1 |
SNP 2 |
SNP 3 |
SNP 4 |
SNP 5 |
|
|---|---|---|---|---|---|
| Number of studies |
7 |
4 |
13 |
1 |
7 |
| True OR | 1 | 1.5 | 1 | 1 | 1 |
| Proportion significanta | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| Mean OR (SE) | 0.82(0.01) | 1.51(0.02) | 1.38(0.01) | 1.39(0.02) | 0.78(0.01) |
| Mean CI length | 0.14 | 0.34 | 0.15 | 0.38 | 0.13 |
| True OR | 1 | 1.25 | 1 | 1 | 1 |
| Proportion significanta | 0.65 | 0.95 | 1.00 | 0.80 | 0.80 |
| Mean OR (SE) | 0.90(0.01) | 1.26(0.02) | 1.19(0.01) | 1.2(0.02) | 0.87(0.01) |
| Mean CI length | 0.15 | 0.30 | 0.13 | 0.34 | 0.15 |
| True OR | 1 | 2 | 1 | 1 | 1 |
| Proportion significanta | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| Mean OR (SE) | 0.70(0.01) | 2.03(0.02) | 1.74(0.01) | 1.76(0.03) | 0.66(0.01) |
| Mean CI length | 0.12 | 0.46 | 0.19 | 0.48 | 0.11 |
For each scenario results are means (SE) of the OR estimate over 20 analyses of replicate data sets simulated under identical conditions.
Proportion of replicates in which the SNP is significant at the 5% level.
Table 4.
Average Results from Single-SNP Meta-Analyses of Simulated Data Replicates
| SNP 1 |
SNP 2 |
SNP 3 |
SNP 4 |
SNP 5 |
|
|---|---|---|---|---|---|
| Number of studies |
7 |
4 |
13 |
1 |
7 |
| True OR | 1 | 1 | 1 | 1 | 1.5 |
| Proportion significanta | 1.00 | 0.95 | 1.00 | 0.95 | 1.00 |
| Mean OR (SE) | 1.17(0.01) | 0.79(0.01) | 0.79(<0.01) | 0.77(0.01) | 1.50(0.01) |
| Mean CI length | 0.19 | 0.18 | 0.09 | 0.21 | 0.25 |
| True OR | 1 | 1.5 | 1 | 1 | 1.5 |
| Proportion significanta | 0.15 | 0.75 | 0.90 | 0.15 | 0.95 |
| Mean OR (SE) | 0.96(0.01) | 1.18(0.01) | 1.09(<0.01) | 1.08(0.02) | 1.18(0.01) |
| Mean CI length | 0.16 | 0.25 | 0.11 | 0.29 | 0.18 |
For each scenario results are means (SE) of the OR estimate over 20 analyses of replicate data sets simulated under identical conditions.
Proportion of replicates in which the SNP is significant at the 5% level.
All Bayesian multi-SNP analyses use a truncated Poisson (0.1) prior on model space, as described in the Material and Methods, and were run for 20 million iterations. An analysis of one replicate for 20 million iterations takes around 2 hr to complete on a 2.5 GHz quad core desktop PC. Marginal posterior probabilities of selecting each SNP are presented. OR estimates are presented over all iterations and are conditional on inclusion in the model; note that when interpreting the latter, one must take care unless posterior probability is high. Our model consistently distinguished causal SNPs in all scenarios. When a single site was simulated as causal, for effect sizes of 1.5 and above the causal marker was selected with 100% posterior probability, whereas noncausal SNPs were given low posterior probabilties (the highest in these anlyses was 7%). When the effect size was reduced to 1.25, the causal site was still selected with high posterior probabiltity (81%), and the highest probability given to a noncausal marker was still only 14% (Table 5). Effect estimates were similar to the simulated values at causal SNPs, regardless of the choice of causal site. This remained true for multiple causal sites, showing that, in contrast to single-SNP analysis, our model successfully adjusts for most of the downward confounding the two sites exert on one another (Table 6). To investigate the performance of the model with SNPs of low allele frequencies, we derived a new set of haplotype probabilities for the multinomial generation model such that the allele frequency at SNP 2 was reduced from 0.43 to 0.14. On simulations based on these haplotype probabilities and a causal OR of 1.5 at SNP 2, the model performed equally well at adjusting for the between-marker confounding present in single-SNP analysis of the same data (Tables S1 and S2).
Table 5.
Average Results from Bayesian Multi-SNP Meta-Analyses of Simulated Data Replicates
| SNP 1 |
SNP 2 |
SNP 3 |
SNP 4 |
SNP 5 |
σHap |
|
|---|---|---|---|---|---|---|
| Number of studies |
7 |
4 |
13 |
1 |
7 |
– |
| True OR | 1 | 1.5 | 1 | 1 | 1 | – |
| Mean posterior probability (SE) | 0.02(0.05) | 0.99(0.05) | 0.07(0.19) | 0.05(0.09) | 0.04(0.06) | 1.00(0) |
| Mean OR (SE) | 1.00(<0.01) | 1.50(0.13) | 0.99(0.06) | 1.00(<0.01) | 1.00(<0.01) | 0.11(0.02)a |
| Mean BCI length | 0.02 | 0.39 | 0.05 | 0.07 | 0.04 | 0.10 |
| Mean OR present (SE)b | 1.02(0.05) | 1.50(0.13) | 0.94(0.08) | 0.97(0.13) | 1.02(0.08) | 0.11(0.02)a |
| Mean BCI length presentb | 0.12 | 0.38 | 0.27 | 0.29 | 0.22 | 0.10 |
| True OR | 1 | 1.25 | 1 | 1 | 1 | – |
| Mean posterior probability (SE) | 0.02(0.03) | 0.81(0.29) | 0.14(0.18) | 0.12(0.18) | 0.04(0.08) | 1.00(0) |
| Mean OR (SE) | 1.00(<0.01) | 1.22(0.12) | 1.01(0.04) | 1.01(0.04) | 1.00(<0.01) | 0.11(0.02)a |
| Mean BCI length | 0.02 | 0.31 | 0.14 | 0.12 | 0.03 | 0.10 |
| Mean OR present (SE)b | 1.00(0.07) | 1.26(0.08) | 1.01(0.16) | 1.00(0.14) | 1.00(0.08) | 0.11(0.02)a |
| Mean BCI length presentb | 0.13 | 0.26 | 0.31 | 0.34 | 0.19 | 0.10 |
| True OR | 1 | 2 | 1 | 1 | 1 | – |
| Mean posterior probability (SE) | < 0.01(0.01) | 1.00(<0.01) | 0.03(0.05) | 0.02(0.01) | 0.03(0.02) | 1.00(0) |
| Mean OR (SE) | 1.00(<0.01) | 1.98(0.05) | 1.00(<0.01) | 1.00(<0.01) | 1.00(<0.01) | 0.12(0.02)a |
| Mean BCI length | < 0.01 | 0.33 | 0.04 | 0.02 | 0.03 | 0.10 |
| Mean OR present (SE)b | 1.02(0.04) | 1.98(0.05) | 0.97(0.08) | 1.01(0.10) | 1.02(0.08) | 0.12(0.02)a |
| Mean BCI length presentb | 0.12 | 0.33 | 0.25 | 0.32 | 0.24 | 0.10 |
For each scenario, results are means (SE) of estimators over 20 analyses of replicate data sets simulated under identical conditions. In each analysis, OR estimates were taken as the median of the posterior sample.
These are point estimates of σHap and therefore are not ORs.
Calculated on the condition that the SNP was included in a model.
Table 6.
Average Results from Bayesian Multi-SNP Meta-Analyses of Simulated Data Replicates
| SNP 1 |
SNP 2 |
SNP 3 |
SNP 4 |
SNP 5 |
σHap |
|
|---|---|---|---|---|---|---|
| No. Studies |
7 |
4 |
13 |
1 |
– |
|
| True OR | 1 | 1 | 1 | 1 | 1.5 | – |
| Mean posterior probability (SE) | 0.03(0.04) | 0.03(0.05) | 0.01(<0.01) | < 0.01(0.01) | 1.00(<0.01) | 1.00(0) |
| Mean OR (SE) | 1.00(<0.01) | 1.00(<0.01) | 1.00(<0.01) | 1.00(<0.01) | 1.50(0.04) | 0.12(0.02)a |
| Mean BCI length | 0.02 | 0.03 | < 0.01 | < 0.01 | 0.18 | 0.10 |
| Mean OR present (SE)b | 1.00(0.05) | 1.04(0.07) | 1.03(0.03) | 1.03(0.05) | 1.50(0.04) | 0.12(0.02)a |
| Mean BCI length presentb | 0.14 | 0.22 | 0.18 | 0.14 | 0.18 | 0.10 |
| True OR | 1 | 1.5 | 1 | 1 | 1.5 | – |
| Mean posterior probability (SE) | 0.03(0.08) | 0.95(0.22) | 0.01(0.02) | 0.08(0.25) | 1.00(<0.01) | 1.00(0) |
| Mean OR (SE) | 1.00(<0.01) | 1.51(0.18) | 1.00(<0.01) | 1.01(0.09) | 1.52(0.1) | 0.11(0.02)a |
| Mean BCI length | 0.02 | 0.53 | 0.02 | 0.04 | 0.47 | 0.10 |
| Mean OR present (SE)b | 1.02(0.06) | 1.52(0.16) | 1.01(0.09) | 1.00(0.12) | 1.52(0.10) | 0.11(0.02)a |
| Mean BCI length presentb | 0.14 | 0.53 | 0.27 | 0.25 | 0.47 | 0.10 |
For each scenario, results are means (SE) of estimators over 20 analyses of replicate data sets simulated under identical conditions. In each analysis, OR estimates were taken as the median of the posterior sample.
These are point estimates of σHap and therefore are not ORs.
Calculated on the condition that the SNP was included in a model.
We simulated a scenario in which the causal marker has not been typed by deleting data on SNP 2 from the replicates in which this SNP was simulated as causal with an OR of 1.5. Prior haplotype probabilities in each replicate were collapsed accordingly, and data on the remaining four markers were analyzed by our model. This may be compared to results from the standard univariate analysis of the same data at noncausal sites (Table 3). In contrast to the univariate analysis, our model successfully corrected for confounding at SNPs 1 and 5. Furthermore, our model correctly inferred a single causal site, splitting the posterior probability between SNPs 3 and 4, which both have the strongest LD with the unobserved causal variant (Table 7). Encouragingly, when no causal site was simulated, average posterior probability over 200 replicates was ≤0.03 at all SNPs, indicating that the false-positive rates of our model are extremely low (Table S3).
Table 7.
Average Results from Bayesian Multi-SNP Meta-Analyses of Simulated Data Replicates
| SNP 1 |
SNP 2 |
SNP 3 |
SNP 4 |
SNP 5 |
σHap |
|
|---|---|---|---|---|---|---|
| Number of studies |
7 |
4 |
13 |
1 |
7 |
– |
| True OR | 1 | 1.5a | 1 | 1 | 1 | – |
| Mean posterior probability (SE) | 0.02(0.03) | – | 0.23(0.22) | 0.81(0.21) | 0.02(0.04) | 1.00(0) |
| Mean OR (SE) | 1.00(<0.01) | – | 1.04(0.12) | 1.34(0.12) | 1.00(<0.01) | 0.11(0.02)b |
| Mean BCI length | 0.02 | – | 0.34 | 0.42 | 0.02 | 0.10 |
| Mean OR present (SE)c | 0.98(0.06) | – | 1.19(0.25) | 1.39(0.03) | 0.96(0.05) | 0.11(0.02)b |
| Mean BCI length presentc | 0.18 | – | 0.56 | 0.29 | 0.16 | 0.10 |
Results are means (SE) of estimators over 20 analyses of replicate data sets simulated under identical conditions. In each analysis, OR estimates were taken as the median of the posterior sample.
Deleting data on the causal SNP 2 in these replicates simulated a scenario in which the causal SNP is unobserved.
These are point estimates of σHap and therefore are not ORs.
Calculated on the condition that the SNP was included in a model.
A Meta-Analysis of the Association between PDE4D and Stroke
To investigate heterogeneity in MAF estimates between the studies, and between the studies and HapMap, we plotted study-specific MAF estimates and 95% confidence intervals (CIs) for controls. This yielded concerns for SNPs 9 and 41 (Figure 2). The HapMap MAF for SNP 9 is substantially different from that reported by the three studies in which it was typed (p < 10−33 for a test of equality of proportions); because only Zee et al.23 report the rs number (as rs3117), it seems possible this SNP might have been misidentified. For SNP 41 the position is less clear, but the SNP shows substantial heterogeneity (p = 0.0041 for a test of equality of proportions). HapMap MAF estimates were not substantially different from those reported by studies for any other SNP, although the SNP 45 MAF reported by Meschia24 is noted as an outlier (Figures S2 and S3). In addition, SNPs 42 and 48 are identical in HapMap, meaning analysis of both SNPs simultaneously in our model is impossible because they would be identical in the underlying HapMap-defined haplotypes. Consequently, SNP 48, which was typed in only one study,8 was excluded from our analysis.
Figure 2.
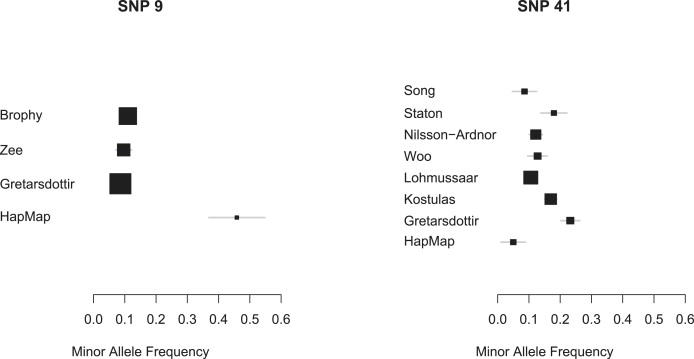
Study-Reported MAFs for Excluded SNPs 9 and 41
Both these SNPs were excluded from our analysis. The HapMap MAF for SNP 9 is very different from that reported by the three studies; because only Zee et al.23 report the rs number (as rs3117), this SNP might have been misidentified. The HapMap MAF for SNP 41 is substantially different from the average reported value, suggesting that HapMap provides a poor estimate. A binomial normal approximation was used for calculating 95% CIs. SNPs are indicated by their deCODE numbers.
Our analysis is thus based on 23 SNPs, which are divided among three LD blocks: block 1, SNPs 2–37; block 2, SNPs 39–89; and block 3, SNPs 175–222 (Figure 3). Because HapMap haplotype information is sparse over the complete set of 23 markers but reasonable within each LD block and indicates that there is very little LD between the blocks, we analyze each block independently.
Figure 3.
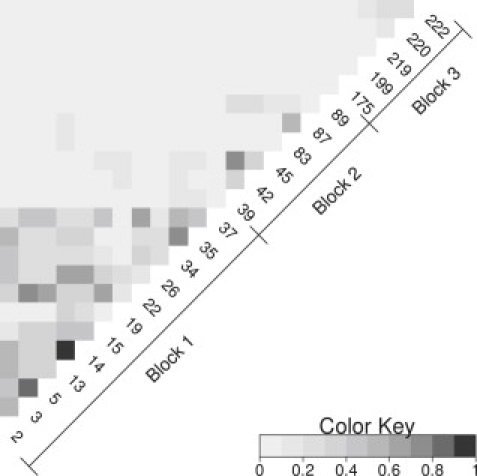
Pairwise LD between All 23 SNPs Analyzed
Estimates are based on HapMap data. SNPs are indicated by their deCODE numbers. Based on the r2 pairwise LD measure.
Tables 8, 9, and 10 present univariate meta-analysis of the SNPs in the three blocks. No SNP was significant at the 5% level; the strongest evidence of association is at SNPs 5, 175, 219, and 222, where 95% CIs just include 1 and moderately large effects are not excluded by the data. Significant p values from the DerSimonian and Laird test of heterogeneity in reported effect estimates was found at SNPs 42, 83, 87, and 89 (see Figure S4 for forest plots). This was mostly explained by Gretarsdottir8 (whose effect estimate is in the oppposite direction of that proposed by all other studies at SNP 42) and Staton25, who, unusually, found significant ORs for three of the six SNPs for which they reported results.
Table 8.
Single-SNP Analysis of PDE4D/Stroke Data on SNPs 2–37, or Block 1
| SNP 2 | SNP 3 | SNP 5 | SNP 13 | SNP 14 | SNP 15 | |
|---|---|---|---|---|---|---|
| Number of studies | 1 | 1 | 1 | 1 | 1 | 1 |
| ORa | 1.02 | 1.00 | 0.90 | 1.00 | 0.96 | 0.94 |
| 95% CI | (0.88,1.17) | (0.87,1.16) | (0.78,1.04) | (0.87,1.15) | (0.83,1.11) | (0.82,1.08) |
| SNP 19 | SNP 22 | SNP 26 | SNP 34 | SNP 35 | SNP 37 | |
| Number of studies | 1 | 1 | 5 | 4 | 1 | 1 |
| ORa | 1.12 | 0.94 | 1.02 | 0.99 | 0.98 | 0.91 |
| 95% CI | (0.95,1.31) | (0.81,1.09) | (0.93,1.12) | (0.91,1.08) | (0.86,1.13) | (0.78,1.06) |
Estimates obtained via the Mantel-Haenszel technique when the SNP was typed in just one study or from a random-effects meta-analysis when the SNP was typed in more than one study.
Table 9.
Single-SNP Analysis of PDE4D/Stroke Data on SNPs 39–89, or Block 2
| SNP 39 | SNP 42 | SNP 45 | SNP 83 | SNP 87 | SNP 89 | |
|---|---|---|---|---|---|---|
| Number of studies | 1 | 4 | 13 | 7 | 6 | 5 |
| ORa | 0.97 | 1.05 | 1.01 | 1.01 | 0.99 | 1.05 |
| 95% CI | (0.60,1.57) | (0.82,1.36) | (0.91,1.13) | (0.86,1.17) | (0.89,1.1) | (0.81,1.37) |
Estimates obtained via the Mantel-Haenszel technique when the SNP was typed in just one study or from a random-effects meta-analysis when the SNP was typed in more than one study.
Table 10.
Single-SNP Analysis of PDE4D/Stroke Data on SNPs 175–222, or Block 3
| SNP 175 | SNP 199 | SNP 219 | SNP 220 | SNP 222 | |
|---|---|---|---|---|---|
| Number of studies | 2 | 2 | 1 | 2 | 3 |
| ORa | 0.90 | 0.97 | 1.25 | 1.04 | 0.91 |
| 95% CI | (0.79,1.02) | (0.85,1.1) | (0.97,1.6) | (0.82,1.31) | (0.82,1.02) |
Estimates from random-effects meta-analyses.
Tables 11, 12, and 13 present results from our multi-SNP analysis of blocks 1, 2, and 3, respectively. There is no evidence for association: the posterior probability of non-zero effect is less than 7.34% at all SNPs. These null results for SNPs 5, 175, 219, and 222 reflect the extra information available to the Bayesian model through studies that have typed SNPs in high LD with 5, 175, 219, and 222, but not 5, 175, 219, and 222 themselves: absence of evidence for association in these studies makes association at 5, 175, 219, and 222 less likely.
Table 11.
Bayesian Multi-SNP Analysis of PDE4D/Stroke Data on SNPs 2–37, or Block 1
| SNP 2 | SNP 3 | SNP 5 | SNP 13 | SNP 14 | SNP 15 | ||
|---|---|---|---|---|---|---|---|
| Posterior probability | 0.01 | 0.03 | 0.03 | 0.01 | 0.01 | 0.01 | |
| OR | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| BCI | (1.00,1.00) | (1.00,1.00) | (0.98,1.00) | (1.00,1.00) | (1.00,1.00) | (1.00,1.00) | |
| OR presb | 0.99 | 1.46 | 0.80 | 1.02 | 1.01 | 0.97 | |
| BCI presb | (0.93,1.08) | (0.95,2.07) | (0.48,1.03) | (0.94,1.05) | (0.94,1.05) | (0.88,1.05) | |
| SNP 19 | SNP 22 | SNP 26 | SNP 34 | SNP 35 | SNP 37 | σHap | |
| Posterior probability | 0.01 | 0.02 | 0.01 | 0.01 | 0.01 | 0.01 | 1.00 |
| OR | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.07a |
| BCI | (1.00,1.00) | (1.00,1.00) | (1.00,1.00) | (1.00,1.00) | (1.00,1.00) | (1.00,1.00) | (0.03,0.2) |
| OR presb | 0.99 | 0.95 | 1.00 | 0.98 | 0.99 | 0.95 | 0.07a |
| BCI presb | (0.92,1.08) | (0.49,1.09) | (0.91,1.05) | (0.89,1.04) | (0.92,1.09) | (0.81,1.03) | (0.03,0.20) |
Point estimates of each parameter were taken as the median of the corresponding posterior sample.
These are point estimates of σHap and therefore are not ORs.
Calculated on the condition that the SNP was included in a model.
Table 12.
Bayesian Multi-SNP Analysis of PDE4D/Stroke Data on SNPs 39–89, or Block 2
| SNP 39 | SNP 42 | SNP 45 | SNP 83 | SNP 87 | SNP 89 | σHap | |
|---|---|---|---|---|---|---|---|
| Posterior probability | 0.02 | 0.04 | 0.01 | 0.01 | 0.01 | 0.01 | 1.00 |
| OR | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.38a |
| BCI | (1.00,1.00) | (1.00,1.05) | (1.00,1.00) | (1.00,1.00) | (1.00,1.00) | (1.00,1.00) | (0.28,0.52) |
| OR presb | 1.04 | 1.07 | 1.04 | 1.03 | 0.97 | 1.01 | 0.38a |
| BCI presb | (0.98,1.10) | (1.00,1.14) | (0.96,1.1) | (0.97,1.08) | (0.93,1.02) | (0.94,1.08) | (0.28,0.52) |
Point estimates of each parameter were taken as the median of the corresponding posterior sample.
These are point estimates of σHap and therefore are not ORs.
Calculated on the condition that the SNP was included in a model.
Table 13.
Bayesian Multi-SNP Analysis of PDE4D/Stroke Data on SNPs 175–222, or Block 3
| SNP 175 | SNP 199 | SNP 219 | SNP 220 | SNP 222 | σHap | |
|---|---|---|---|---|---|---|
| Posterior probability | 0.06 | 0.02 | 0.04 | 0.02 | 0.07 | 1.00 |
| OR | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.21a |
| BCI | (0.88,1.00) | (1.00,1.00) | (1.00,1.06) | (1.00,1.00) | (0.85,1.00) | (0.08,0.64) |
| OR presb | 0.89 | 0.99 | 1.15 | 1.05 | 0.88 | 0.21a |
| BCI presb | (0.80,1.00) | (0.88,1.11) | (0.92,1.69) | (0.87,1.28) | (0.66,1.00) | (0.08,0.64) |
Point estimates of each parameter were taken as the median of the corresponding posterior sample.
These are point estimates of σHap and therefore are not ORs.
Calculated on the condition that the SNP was included in a model.
The posterior probabilities of the null model in each block were 87.9%, 90.0%, and 81.6%, which, in comparison to a prior probability of 90.5% from the truncated Poisson prior described above, result in Bayes Factors against the null model of 1.3, 1.1, and 2.1, respectively. For all three blocks, we checked convergence by visually inspecting posterior plots and by running additional chains starting in the saturated model. Sensitivity to model-space prior was checked by changing the truncated Poisson mean to 0.05 and 0.2. Inference was similar in all these additional analyses (results not shown).
For block 2, sensitivity was further checked by excluding the Meschia,24 Staton25, and Gretarsdottir8 data, one study at a time. Meschia was excluded because of the outlying MAF reported for SNP 42 and Staton and Gretarsdottir because they explain most of the heterogeneity in reported ORs in this block. To explore small-study bias, we also ran an analysis with the five largest studies (those with > 500 cases) only. Again, inference was the same in all these additional analyses (Table S5). The consistently null result when the Gretarsdottir8 data were excluded is notable because exclusion of these data from univariate analysis results in a borderline significant OR at SNP 42 of 1.19. 95% CI: (1.02,1.39).
These further sensitivity analyses were not carried out for blocks 1 and 3 because there was no significant heterogeneity in reported effect estimates within these blocks, and too few studies contributed data to allow small-study bias to be explored (five and three studies for blocks 1 and 3, respectively).
Figures 4 and 5 provide two recommended diagnostics for our model. Figure 4 shows a forest plot of the estimated MAFs for SNP 45 (the SNP with most prior interest); these estimates were obtained from application of our model to block 2. Note that SNP 45 was not typed in Woo,26 so this estimate has been imputed on the basis of MAFs observed at other SNPs in close LD. Reassuringly, among studies that did type SNP 45, our model estimates are similar to reported estimates. Figure 5 shows a forest plot of study-specific effect estimates for SNP 45, again from application of our model to block 2. Model selection was turned off for this analysis, and the model was fixed with just SNP 45 present. A shrinkage prior, with 90.5% prior probabiltiy of no effect, enabled comparison with the above reversible jump analyses. Note that although restricting this analysis allowed an effect at SNP 45 alone, the analysis still combines evidence across all SNPs in block 2. Again, except for the imputed value for Woo, effect estimates are similar to those reported elsewhere. The global OR estimate was 1 95.5% of the time, confirming that although in isolation many study estimates are consistent with a sizeable effect, when information is combined across studies CIs become tighter around an OR of 1.
Figure 4.
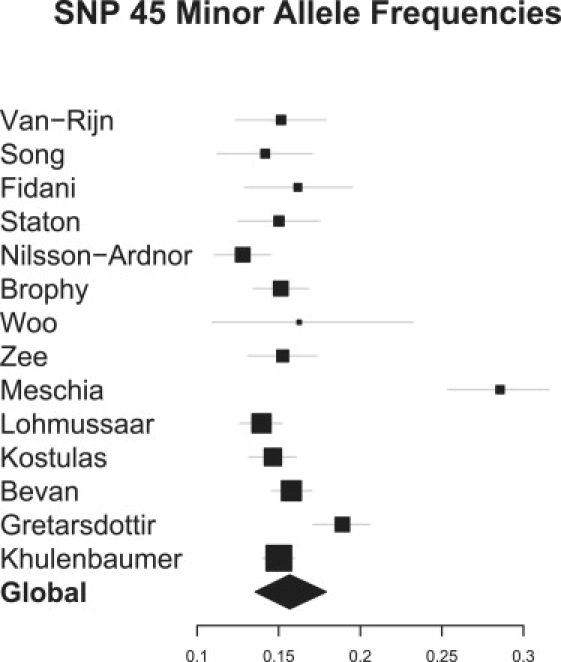
Bayesian Multilocus Analysis: Study-Specific MAF Estimates for SNP 45
These were estimated from application of our model to data on SNPs 39–89. Woo et al.26 did not type SNP 45,(26), so this estimate was imputed by our model. For each MAF, 95% credible intervals are given.
Figure 5.
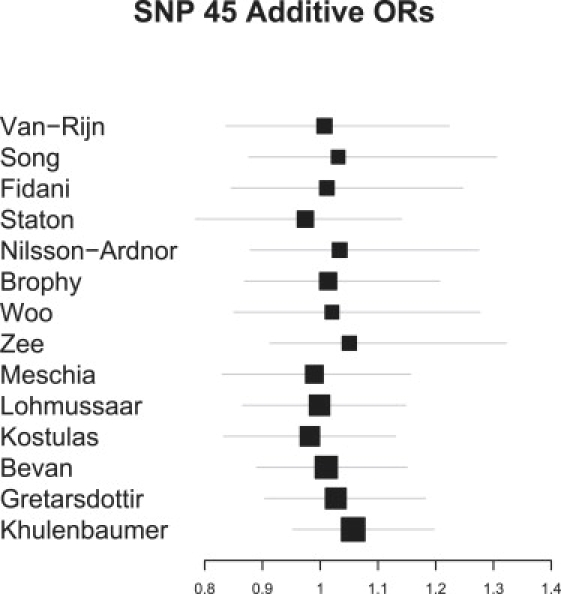
Bayesian Multilocus Analysis: Study-specific OR Estimates for SNP 45
These were estimated from application of our model to data on SNPs 39–89. The posterior probability for a global effect of SNP 45 on stroke was 5%, suggesting that although data from several studies are consistent with considerable effects, when data are pooled, any effect disappears. The global effect is omitted from the plot because the low posterior probability meant no reliable estimate was obtained. Woo et al. did not type SNP 4526, so this estimate was imputed by our model. For each OR, 95% credible intervals are given.
Discussion
Literature-based meta-analysis provides an important tool for the identification and characterization of genetic associations, but to date it has been restricted to single-SNP analyses. This is inefficient because only studies that have typed the particular SNP may be used, despite substantial variation in SNP sets between studies. Furthermore, single-SNP analysis is vulnerable to between-marker confounding, which hinders the identification of causal SNPs and can reduce power, as shown in our simulation results. We present a multimarker approach that allows simultaneous analysis of all SNPs and studies and thus maximizes the power to find gene-disease associations and for each SNP obtains effect estimates, adjusted for other SNPs. To form adjusted effect estimates, and allow sharing of information between correlated SNPs, we used HapMap data in the current analysis. Other sources of information on haplotype frequencies could be incorporated: in particular, when individual patient data (IPD) are available from one or more study, it could be incorporated to make likelihood contributions as haplotype frequency estimates. Inference is made in the Bayesian framework, via a reversible jump MCMC algorithm that allows calculation of the posterior probability that any SNP or set of SNPs is associated with disease, as well as estimation of effect size for any such set of SNPs. In particular, this allows a test of association at the gene level, which increases power and reduces the difficulty of interpreting multiple individual SNP results.
Our new method has enabled us to perform the most thorough meta-analysis to date of the association between PDE4D and stroke, and on the basis of these results, it seems likely that the association is null, or too small to be of clinical relevance. Our results overall were consistent with those from Bevan10: the power increase obtained through the use of our newly developed methods did not uncover any previously unidentified genetic associations. The evidence to date does not support PDE4D as a potential drug target for the prevention or treatment of stroke. However, we cannot exclude the possibility that causal variants not well tagged by the SNPs studied here exist. Under r2 thresholds of 0.7 and 0.8, the SNPs we analyze tag only 11% and 8% of the 1,542 SNPs typed in HapMap between the two most widely separated SNPs considered by Gretarsdottir.8 Our results—and indeed, all previous analyses of the association between PDE4D and stroke—therefore largely rely on Gretarsdottir et al.'s original identification of SNPs that accurately tag any causal variants in PDE4D. Despite the intense interest in this gene over the last 5 years, there might exist causal variants that are not well tagged, or that because of type II error are not associated with stroke in Gretarsdottir et al.. It is hoped that large whole-genome association studies currently in progress will resolve this issue in the near future.
Our model assumes that both LD structure and any gene-disease associations are similar across the individual studies. It is difficult to be certain that either of these assumptions is true, but diagnostics (see forest plots of control MAFs in Figures S2 and S3) provide no evidence that they are not. In particular MAFs in controls seem to be very consistent across the studies, and our estimate of the random-effects variance in control haplotype frequencies suggests little heterogeneity. Similarly, for most SNPs, we have found no evidence for study heterogeneity in effect. Where there was weak evidence of heterogeneity of study effects, notably for SNP 42, where one estimate of effect was in the opposite direction of estimates from the other three studies attempting to type it, our model proved more robust to this heterogeneity than single-locus analysis: exclusion of the outlying study resulted in a significant association in the frequentist (classical) analysis, but a null result in the Bayesian analysis, compatible with the analysis if all studies. This robustness is to be expected because our approach borrows information from SNPs in LD with SNP 42, and these data are inconsistent with an effect at SNP 42, regardless of the inclusion of the outlying study.
As we have shown in our simulation studies, our method is susceptible to confounding when the causal site is unobserved; however, in contrast to single-SNP analysis, our method was still able to correct for confounding at two of the four noncausal loci. Furthermore, in this scenario the ability of our method to provide inference about the number of causal sites is potentially valuable, although care must be taken if multiple causal sites are inferred because this may simply be an indication that a single causal site needs multiple markers to tag it. Finally, we note that our model is only intended for use with candidate genes, where the number of SNPs analyzed will be limited to the tens. Performance when our model is applied to more SNPs will depend on the sparseness of the data and the amount of prior information available on haplotype frequencies.
In summary, we have developed a novel Bayesian approach to the meta-analysis of genetic-association studies and applied this to provide the most conclusive evidence to date that there is no effect of PDE4D on stroke. We expect the method to be of wide applicability, given the increasing interest in meta-analysis of genetic-association studies. Our method is released as a cross-platform Java program under the GPL and is available for download from our website (see Web Resources).
Appendix A
For M markers with H underlying haplotypes, we define a multivariate normal approximation for observed log-allele counts, denoted by log(q) = (log(q1), ..log(qM))', parameterized by the first H – 1 unobserved haplotype probabilities, denoted by and the sample size n. Let p[−H] be the (unobserved) haplotype relative frequencies in the sample. In order to use the multivariate delta method to derive an approximate distribution of log(q), we need to define a mapping (and its derivative), . The Material and Methods section presents a mapping from the unobserved sample haplotype counts, h[−H], to the log allele counts; (2). By substituting h[−H] = 2np[−H], we obtain
| (A1) |
where design matrices D and X are defined in the methods section, and D[, H] denotes the Hth column of D. The derivative of g, required for the multivariate delta method below, is then
| (A2) |
where
| (A3) |
The multivariate delta method15 provides an approximate MVN distribution for a vector function, g, of p[−H] and n.
| (A4) |
where denotes the multinomial covariance matrix of these first H – 1 probabilities. Therefore, substituting Equation (A2) into Equation (A4), we obtain the following MVN for
| (A5) |
Appendix B
Moves Within the Model Space
As described in the Material and Methods, the model was fitted via a reversible jump MCMC algorithm, which enabled model selection. Whether it was necessary to include study-specific haplotype frequencies and all H haplotypes in the model was not part of the main study question, so it was decided that the study-specific haplotype frequencies and between-study variance parameter would always remain in the model. The question being investigated was whether each SNP has an association with disease, so the set of models between which the reversible jump algorithm was allowed to move was defined by all possible combinations of OR parameters being included or excluded for each marker. Therefore, if M markers are considered for analysis, there will be a set of possible models that reversible jump may move between.
Determining the probability of a model move was a two-stage process. First, the type of move was determined from four possibilities: adding a marker OR, removing a marker OR, swapping the OR of one marker for another, or making a “null” move where no change occurs. An addition can only occur when there are <M ORs present, a removal can only occur when there are >0 ORs present, and a swap can only occur when there are >1 ORs present. Swap, addition, and removal moves were each given a probability of happening, when such a move was available. The null move therefore had a chance of happening when all other move types were available, although this was increased by the probabilities assigned to other move types when they were unavailable.
Second, if an addition, removal, or swap move was selected, the markers to be involved in the move were picked from the markers available for the move (e.g., an addition can only involve markers with ORs currently excluded) with equal probability. Therefore, one determines the probability of a particular model move within the model space by multiplying the probability of the move type and, with the exception of a “null” move, the probability of selecting the particular marker(s) involved in the move.
Parameter Updates
We adopt a proposal mechanism that updates one parameter type at each iteration of the reversible jump algorithm. For each proposal made in the reversible jump algorithm, there are four types of parameters that may be updated:
-
•
Study-specific control haplotype probabilities
-
•
Grand mean control haplotype probabilities
-
•
Between-study haplotype standard error σHap
-
•
SNP log-ORs β.
The parameter type to update is chosen at random, with weighting equal to the number of occurrences of the parameter type in the model under consideration. Note that the variance parameters for all proposal distributions below are tuned to obtain an acceptance rate of approximately 0.4.
Updating Control Haplotype Probabilities and
For modeling the hierarchical relationship of the study-specific haplotype probabilities at each iteration for each study, parameters gs = (gs1, ..gsH) are stored. These define study-specific haplotype probabilities via the following multinomial-logit link;
| (B1) |
When a study-specific vector of haplotype probabilities, , is selected to be updated, an element of the corresponding gs is chosen at random, and a new value is drawn from a normal distribution centered on the current value, leading to gs∗. Applying Equation (B1) to gs∗ results in a new set of haplotype probabilities . Note that although gs and gs∗ only differ by one element, each element of and differs. The advantage of updating in this way is that the elements of are always between 0 and 1 and sum to 1. Grand mean haplotype probabilities are updated in the same way.
Updating Between-Study Haplotype Frequency Variance, σHap
Because this parameter must always be positive, it is updated on the log scale. This is also achieved via a normal distribution centered on the current (log) value.
Updating SNP Log-OR β Values
These are updated using a normal distribution centered on the current value.
Supplemental Data
Supplemental Data include four figures and five tables and can be found with this article online at http://www.ajhg.org/.
Supplemental Data
Web Resources
The URLs for data presented herein are as follows:
HapMap homepage, http://www.hapmap.org/
Java code, http://homepages.lshtm.ac.uk/∼encdpnew/
Online Mendelian Inheritance in Man (OMIM), http://www.ncbi.nlm.nih.gov/Omim
Acknowledgments
This work was supported by Medical Research Council research grant G0600580. L.S. was supported by a Wellcome Trust Senior Research Fellowship in Clinical Science. A.D.H. holds a British Heart Foundation Senior Research Fellowship (FS05/125).
References
- 1.Cardon L.R., Bell J.I. Association study designs for complex diseases. Nat. Rev. Genet. 2001;2:91–99. doi: 10.1038/35052543. [DOI] [PubMed] [Google Scholar]
- 2.Colhoun H.M., McKeigue P.M., Smith G.D. Problems of reporting genetic associations with complex outcomes. Lancet. 2003;361:865–872. doi: 10.1016/s0140-6736(03)12715-8. [DOI] [PubMed] [Google Scholar]
- 3.Ioannidis J.P.A., Trikalinos T.A., Khoury M.J. Implications of small effect sizes of individual genetic variants on the design and interpretation of genetic association studies of complex diseases. Am. J. Epidemiol. 2006;164:609–614. doi: 10.1093/aje/kwj259. [DOI] [PubMed] [Google Scholar]
- 4.Clayton D., McKeigue P.M. Epidemiological methods for studying genes and environmental factors in complex diseases. Lancet. 2001;358:1356–1360. doi: 10.1016/S0140-6736(01)06418-2. [DOI] [PubMed] [Google Scholar]
- 5.Zeggini E., Rayner W., Morris A.P., Hattersley A.T., Walker M., Hitman G.A., Deloukas P., Cardon L.R., McCarthy M.I. An evaluation of hapmap sample size and tagging snp performance in large-scale empirical and simulated data sets. Nat. Genet. 2005;37:1320–1322. doi: 10.1038/ng1670. [DOI] [PubMed] [Google Scholar]
- 6.Todd J.A., Walker N.M., Cooper J.D., Smyth D.J., Downes K., Plagnol V., Bailey R., Nejentsev S., Field S.F., Payne F. Robust associations of four new chromosome regions from genome-wide analyses of type 1 diabetes. Nat. Genet. 2007;39:857–864. doi: 10.1038/ng2068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Barrett J.C., Hansoul S., Nicolae D.L., Cho J.H., Duerr R.H., Rioux J.D., Brant S.R., Silverberg M.S., Taylor K.D., Barmada M.M. Genome-wide association defines more than 30 distinct susceptibility loci for Crohn's disease. Nat. Genet. 2008;40:955–962. doi: 10.1038/NG.175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Gretarsdottir S., Thorleifsson G., Reynisdottir S.T., Manolescu A., Jonsdottir S., Jonsdottir T., Gudmundsdottir T., Bjarnadottir S.M., Einarsson O.B., Gudjonsdottir H.M. The gene encoding phosphodiesterase 4d confers risk of ischemic stroke. Nat. Genet. 2003;35:131–138. doi: 10.1038/ng1245. [DOI] [PubMed] [Google Scholar]
- 9.Houslay M.D., Baillie G.S., Maurice D.H. camp-specific phosphodiesterase-4 enzymes in the cardiovascular system: a molecular toolbox for generating compartmentalized camp signaling. Circ. Res. 2007;100:950–966. doi: 10.1161/01.RES.0000261934.56938.38. [DOI] [PubMed] [Google Scholar]
- 10.Bevan S., Dichgans M., Gschwendtner A., Kuhlenbäumer G., Ringelstein E.B., Markus H.S. Variation in the pde4d gene and ischemic stroke risk: A systematic review and meta-analysis on 5200 cases and 6600 controls. Stroke. 2008;39:1966–1971. doi: 10.1161/STROKEAHA.107.509992. [DOI] [PubMed] [Google Scholar]
- 11.Marchini J., Howie B., Myers S., McVean G., Donnelly P. A new multipoint method for genome-wide association studies by imputation of genotypes. Nat. Genet. 2007;39:906–913. doi: 10.1038/ng2088. [DOI] [PubMed] [Google Scholar]
- 12.Verzilli C., Shah T., Casas J.P., Chapman J., Sandhu M., Debenham S.L., Boekholdt M.S., Khaw K.T., Wareham N.J., Judson R. Bayesian meta-analysis of genetic association studies with different sets of markers. Am. J. Hum. Genet. 2008;82:859–872. doi: 10.1016/j.ajhg.2008.01.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Kuhlenbaumer G., Berger K., Huge A., Lange E., Kessler C., John U., Funke H., Nabavi D.G., Stagbauer F.E.B.R., Stoll M. Evaluation of single nucleotide polymorphisms in the phosphodiesterase 4d gene (pde4d) and their association with ischaemic stroke in a large german cohort. J. Neurol. Neurosurg. Psychiatry. 2006;77:521–524. doi: 10.1136/jnnp.2005.073577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Brophy V.H., Ro S.K., Rhees B.K., Lui L.-Y., Lee J.M., Umblas N., Bentley L.G., Li J., Cheng S., Browner W.S. Association of phosphodiesterase 4d polymorphisms with ischemic stroke in a US population stratified by hypertension status. Stroke. 2006;37:1385–1390. doi: 10.1161/01.STR.0000221788.10723.66. [DOI] [PubMed] [Google Scholar]
- 15.Bishop Y., Fienberg S., Holland P. The MIT Press; Cambridge, MA: 1975. Discrete Multivariate Analysis. [Google Scholar]
- 16.Seaman S.R., Richardson S. Equivalence of prospective and retrospective models in the bayesian analysis of case-control tudies. Biometrika. 2004;91:15–25. [Google Scholar]
- 17.Green P. Reversible jump markov chain monte carlo computation and bayesian model determination. Biometrika. 1995;82:711–732. [Google Scholar]
- 18.Lunn D.J., Whittaker J.C., Best N. A Bayesian toolkit for genetic association studies. Genet. Epidemiol. 2006;30:231–247. doi: 10.1002/gepi.20140. [DOI] [PubMed] [Google Scholar]
- 19.Gilks W., Richardson S., Spiegelhalter D. Markov Chain Monte Carlo. In: Gilks W.R., Richardson S., Spiegelhalter D.J., editors. Practice. Second Edition. CRC Press; Boca Raton, FL: 1996. [Google Scholar]
- 20.Wakefield J. Bayes factors for genome-wide association studies: Comparison with p-values. Genet. Epidemiol. 2008;33:79–86. doi: 10.1002/gepi.20359. [DOI] [PubMed] [Google Scholar]
- 21.Spiegelhalter D., Abrams K., Myles J. Wiley; 2004. Bayesian Approaches to Clinical Trials and Health-Care Evaluation. [Google Scholar]
- 22.Higgins J.P.T., Thompson S.G., Deeks J.J., Altman D.G. Measuring inconsistency in meta-analyses. BMJ. 2003;327:557–560. doi: 10.1136/bmj.327.7414.557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Zee R.Y.L., Brophy V.H., Cheng S., Hegener H.H., Erlich H.A., Ridker P.M. Polymorphisms of the phosphodiesterase 4d, camp-specific (pde4d) gene and risk of ischemic stroke: A prospective, nested case-control evaluation. Stroke. 2006;37:2012–2017. doi: 10.1161/01.STR.0000230608.56048.38. [DOI] [PubMed] [Google Scholar]
- 24.Meschia J.F., Brott T.G., Brown R.D., Crook R., Worrall B.B., Kissela B., Brown W.M., Rich S.S., Case L.D., Evans E.W. Phosphodiesterase 4d and 5-lipoxygenase activating protein in ischemic stroke. Ann. Neurol. 2005;58:351–361. doi: 10.1002/ana.20585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Staton J.M., Sayer M.S., Hankey G.J., Attia J., Thakkinstian A., Yi Q., Cole V.J., Baker R., Eikelboom J.W. Association between phosphodiesterase 4d gene and ischaemic stroke. J. Neurol. Neurosurg. Psychiatry. 2006;77:1067–1069. doi: 10.1136/jnnp.2006.092106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Woo D., Kaushal R., Kissela B., Sekar P., Wolujewicz M., Pal P., Alwell K., Haverbusch M., Ewing I., Miller R. Association of phosphodiesterase 4d with ischemic stroke: A population-based case-control study. Stroke. 2006;37:371–376. doi: 10.1161/01.STR.0000198843.72824.0a. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


