Genome-wide Insights into the Patterns and Determinants of Fine-Scale Population Structure in Humans

Abstract

Studying genomic patterns of human population structure provides important insights into human evolutionary history and the relationship among populations, and it has significant practical implications for disease-gene mapping. Here we describe a principal component (PC)-based approach to studying intracontinental population structure in humans, identify the underlying markers mediating the observed patterns of fine-scale population structure, and infer the predominating evolutionary forces shaping local population structure. We applied this methodology to a data set of 650K SNPs genotyped in 944 unrelated individuals from 52 populations and demonstrate that, although typical PC analyses focus on the top axes of variation, substantial information about population structure is contained in lower-ranked PCs. We identified 18 significant PCs, some of which distinguish individual populations. In addition to visually representing sample clusters in PC biplots, we estimated the set of all SNPs significantly correlated with each of the most informative axes of variation. These polymorphisms, unlike ancestry-informative markers (AIMs), constitute a much larger set of loci that drive genomic signatures of population structure. The genome-wide distribution of these significantly correlated markers can largely be accounted for by the stochastic effects of genetic drift, although significant clustering does occur in genomic regions that have been previously implicated as targets of recent adaptive evolution.

Introduction

Identifying, quantifying, and understanding genome-wide patterns of population structure has been a major focus in studies of human population genetics.^1–4 The majority of analyses have focused on broad-scale patterns of structure among geographically diverse populations and have conclusively shown that 85%–95% of human genetic variation is attributable to differences among individuals and that 5%–15% is due to differences between populations.^5,6 Such analyses have provided considerable insight into human evolutionary history and the relationship among human populations and, more practically, are important for the design and analysis of disease mapping studies.^7–11

More recently, however, there has been increased interest in delineating levels of fine-scale population structure.^5,12,13 Many of these studies have used principal-component analysis (PCA) to probe population structure, and their aims can be broadly divided into two primary uses. First, PCA has been used for identifying and visualizing patterns of population structure, and typically these studies have focused on the top two or three principal components (PCs). The most well studied in this aspect has been European ancestry^14,15, where it has been demonstrated that the first PC approximates a northwest-southeast ancestry gradient.^16,17 A more recent example, consisting of a two-dimensional visual representation of PC1 and PC2 from 3,192 European individuals, shows a strong correlation with the actual geographical location of the samples.¹⁷ In addition, analysis of another global dataset consisting of 3,082 samples whose ancestry can be traced to different geographic locations reveals widespread signatures of structure that is visible in the top seven PCs.¹⁸

The second primary use of PCA has been to identify small panels of ancestry-informative markers (AIMs)^19,20, which are useful in correcting for stratification in genome-wide association studies (GWAS).^14,16,21 In these studies, only the top few hundred markers correlated with a PC are identified and retained. However, a more exhaustive collection of significantly correlated PC SNPs would facilitate a deeper understanding of the evolutionary forces governing intracontinental structure in humans.

Here, we apply PCA to a large global sample of individuals from the Human Genome Diversity Project–Centre d'Etude du Polymorphisme Humain (HGDP-CEPH) Panel. We analyze 643,884 SNPs genotyped in 944 unrelated individuals from 52 populations.²² The goals of our study are twofold. The first is to rigorously estimate the number of significant PCs in this dataset, as opposed to focusing on the top two or three PCs. In doing so, we find that substantial information exists about patterns of intracontinental structure in lower-ranked, yet significant, PCs. The second is to identify and analyze the set of markers significantly correlated with particular PCs to make population-genetic inferences about human evolutionary history. This expanded set of markers is considerably larger than previously described panels of AIMs and provides a roadmap to the genomic positions that drive signatures of fine-scale population structure in humans.

Material and Methods

Data

We downloaded SNP genotypes for more than 650,000 markers typed in 1043 individuals that compose the HGDP-CEPH panel.²² These individuals can be broadly classified into 52 populations and seven continental groups. We filtered the set of autosomal SNPs to retain only those that had less than 10% missing data and used an algorithm based on Hardy-Weinberg equilibrium to impute missing genotype data. We excluded known first- and second-degree relatives²³ as well as three additionally ambiguous samples (HGDP00980, HGDP00770, and HGDP00621). Our final dataset consisted of 643,884 autosomal SNPs and 944 unrelated individuals (Table S1 available online). The minor allele was recoded as 0 and the major allele as 1, and the diploid genotype for a polymorphism in each individual was recoded as 0, 1, or 2.

Principal-Component Analysis

To deal with the computational limitations in performing a singular-value decomposition (SVD) of large files (>2 GB) with standard numerical packages such as lapack, we computed an SVD of the 944 × 944 covariance matrix between individuals. Before computing the covariance matrix, we normalized each SNP genotype, X, by using the formula $\widehat{X}=(X-\overline{X})/\sqrt{p^{\ast }(1-p)}$, where $p=\overline{X}$/2 is the allele frequency.²⁴

Computing an SVD of the covariance matrix is equivalent to doing a PCA. We also calculated the proportion of variance explained by the ith PC as $v_i={\lambda }_i^2/\sum _{j=1}^{944}{\lambda }_j^2$, where λ_i is the eigenvalue associated with each PC. Instead of recovering the weights of the SNPs by using algebraic manipulations of the PC and the original genotypes, we used the proportion of variance explained by a linear model $y_i={\mu }_0+g_j$, where $yi$ is the ith PC, μ₀ is the intercept, and g_j is the j^th SNP genotype. For j = 1… 643,884, we computed the square of the sample correlation coefficient$R_{ij}^2$ and used this statistic to estimate the contribution of each SNP to the ith PC. We used the statistical software R for the computations.²⁵

Estimating the Significant Number of PCs

We computed the number of PCs significant at a threshold of p < 0.001 by using a parametric method based on the Tracy-Widom (TW) statistic.²⁴ To avoid the confounding effects of linkage disequilibrium (LD) and to meet specific distributional assumptions, we randomly selected a subset of 1,799 unlinked SNPs (spaced at least 1 Mb apart). A PCA of this subset was calculated as previously described, and the eigenvalue, λ_i, for each PC was calculated. A TW statistic for each λ_i was estimated, and empirical p values were used for assigning significance. In addition, we used two additional approaches to assess robustness in the inferred number of significant PCs. In the first method, we used an ANOVA framework to test each PC for a significant signature of structure.²⁰ The membership of each individual to one of the 52 populations was used as a covariate in the analysis. A p value was computed with null permutations of p, from the model $y_i={\mu }_0+p$, where p is the population label. Note that the p values are not monotonically increasing for this approach and that we therefore retained the smallest set of PCs that are all below the p value threshold of 0.001 as significant. In the second method, we estimated the test statistic, v_i, which is the proportion of variance explained for each PC. We permuted genotypes of each SNP across all individuals to compute a null covariance matrix and then estimated null statistics, $v_i^0$. We repeated this process ten times and pooled all null statistics to compute p values.

Testing PCs for Clinal Variation

To identify clinal patterns of variation within continents, we calculated the Spearman rank correlation, ρ, between the reported geographic coordinates of sampled individuals within each continent (on the basis of their population membership) and PC1. Correlations were calculated with respect to latitude, longitude, and the great-circle distance for each population from a common reference point of 0° latitude and 0° longitude. The haversine²⁶ formula was used for calculating the great-circle distance, D as $D=2^{\ast }{R}^{\ast }\text{arctan}(\sqrt{\alpha },\sqrt{1-\alpha )}$, where $\alpha ={\sin }^2(\varphi /2)+\cos {\left(\varphi \right)}^{\ast }{\sin }^2(\lambda /2)$,

R = 6371 km is the radius of the earth, and (ϕ,λ) is the location (latitude, longitude) in radians of an individual.

Identifying Significantly Correlated SNPs

We used the square of the sample correlation coefficient, R², to test the null hypothesis of no association between an SNP and a PC. For all 643,884 SNPs, we permuted the genotype ten times to obtain the null distribution of R², which we then pooled across all SNPs to get a p value for each hypothesis test. To account for multiple hypothesis tests, we controlled the false-discovery rate. The p value threshold was defined as p < 1/(number of polymorphic SNPs) in each continent, such that only one false positive was expected by chance. If all SNPs were polymorphic within a continent, this translates to an uncorrected p value of 1.5 × 10⁻⁶.

We analyzed the genome-wide distribution of significant SNPs by dividing the autosomal genome into nonoverlapping 500 kb bins. For the i^th bin, we estimated the probability p_i of observing x_i or more significantly correlated SNPs by using the hypergeometric distribution, which takes into account the number of significant SNPs in the bin, the number of SNPs in the bin, the total number of significant SNPs across all bins, and the number of nonsignificant SNPs across all bins. In addition, because the use of the hypergeometric distribution in the presence of LD is an approximation to the ideal case of independently sampled significant SNPs, we confirmed the robustness of the results by two independent analyses based on the Poisson distribution and Wallenius' noncentral hypergeometric distribution, which yielded similar estimates for the proportion of SNPs located in and out of clusters (data not shown).

Using Significantly Correlated SNPs to Confirm Stratification

In order to verify that the set of SNPs correlated with PC1 also shows the same pattern of variation across the samples as PC1 from the biplot, we used the program Structure (version 2.0).²⁷ For example, the 11,811 SNPs that were significantly correlated with PC1 in Africa were run through the model-based clustering algorithm implemented in Structure, and for different values of K (number of clusters), the results were plotted with the program distruct (version 1.1).²⁸

Coalescent Simulations

We used the coalescent simulation program ms to test the effects of SNP-ascertainment strategies, levels of population structure, and sample size on the estimated number of correlated markers.²⁹ We used previously described demographic parameters related to population splitting and bottlenecks.³⁰ Two continents representing Africa and Europe were simulated under different conditions, which involved varying the number of samples and/or the number of subpopulations within each continent. To obtain confidence intervals around the number of markers correlated to PC1 at a p value < 0.01 in each continent, we simulated 100 replicates.

We modeled ascertainment bias by using a double-hit ascertainment strategy, in which SNPs were discovered in four randomly sampled chromosomes from one of the European subpopulations, which is generally consistent with one of the discovery strategies of HapMap SNPs.³¹ The discovered SNPs were then “genotyped” in all individuals, and the ascertained and complete sets of markers were independently subjected to PCA as described above. In the second set of simulations, we increased the number of chromosomes in each continent from 200 to 1000 to evaluate the effect of sample size on the number of correlated markers.

A sample ms command line argument is included below, which generates 100,000 unlinked SNPs in two continents, each containing 1000 chromosomes split among four populations.

ms 2040 100000 -s 1 -I 8 250 250 250 250 250 250 250 290 -en 0.0005 1 0.24 -en 0.0005 2 0.24 –en 0.0005 3 0.24 -en 0.0005 4 0.24 -en 0.000975 5 0.077 -en 0.000975 6 0.077 -en 0.000975 7 0.077 -en 0.000975 8 0.077 -ej 0.0009875 8 7 -ej 0.0009875 7 6 -ej 0.0009875 6 5 -en 0.00475 5 0.00746 -en 0.004875 5 0.077 -en 0.0075 1 0.0625 -en 0.007625 1 0.24 -en 0.0075 2 0.0625 -en 0.007625 2 0.24 -en 0.0075 3 0.0625 -en 0.007625 3 0.24 -en 0.0075 4 0.0625 -en 0.007625 4 0.24 -ej 0.024 4 3 -ej 0.024 3 2 -ej 0.024 2 1 -ej 0.025 5 1 -en 0.0425 1 0.12

Integrating Results from Genome-wide Scans

Results from ten recent genome-wide scans were analyzed, and 722 regions that were identified as targets of selection in two or more scans were retained (for more details, see Akey et al.³²). Approximately 46,000 SNPs from these regions were present in the Illumina panel, which were used in the analysis.

Results

Estimating the Number of Significant PCs in the HGDP-CEPH Data

Researchers often use PCA to visualize population structure by constructing biplots of PCs that explain the most amount of variation in the data.^20,33 However, whereas previous work has primarily focused on the first two PCs, there is potentially much more information about population structure in additional PCs. Therefore, as a first step in analyzing the HGDP-CEPH data, we determined overall levels of structure in the entire dataset by estimating the number of PCs that explained more variation than expected by chance. There are a number of statistical approaches for determining the number of significant PCs. Here we used a test based on the TW distribution²⁴ and identified 18 significant PCs by using all 944 individuals. We also employed two additional methods to establish the robustness of the TW distribution and found similar results (Table S2). A detailed description of how these three methods were implemented is described in the Material and Methods. Thus, although the exact number of significant PCs varies depending on the specific test used, they all clearly show that lower-ranked PCs, which are not routinely studied, contain considerable information about population structure.

To visualize the potential information contained in the lower PCs, in Figure 1 we plotted PC1 versus PC2 and PC10 versus PC11. The plot of PC1 versus PC2 captures allele frequency variation on a global scale and follows a coarse approximation of the geographical arrangement of the populations that are present in the samples. This plot recapitulates results from previously reported empirical studies²², and the shape of the curve has been noted earlier both in empirical studies of genetic data and also from more theoretical explorations of various sampling schemes and population-genetic models.^34,35

Figure 1.

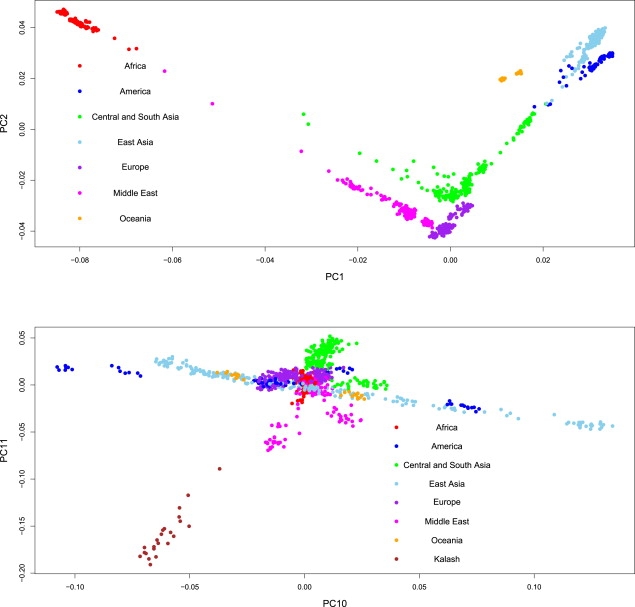
Change in Scale of Differentiation from Global to Local along PCs

The top panel shows a biplot of PC1 versus PC2, and the bottom panel is a biplot of PC10 versus PC11. Filled circles represent all 944 samples and are colored according to the continent of origin (indicated in the legend). In the bottom panel, brown filled circles are used for highlighting the Kalash population.

The biplot of PC10 versus PC11, however, represents a finer-scale change in allele frequency differences; it primarily separates the Kalash samples along PC10 and the American samples along PC11. This inference of local and regional structure is representative of the general pattern seen for lower-ranked significant PCs and is well supported by simulation and empirical results from recent studies.^18,31

Thus, the above results demonstrate that considerable information about fine-scale population structure is contained in lower-ranked PCs that explain more variation than expected by chance. In the following text, we apply this methodology to continental groups in the HGDP-CEPH data. Importantly, we also identify SNPs that are significantly correlated with these PCs, which allows more detailed inferences about the evolutionary forces shaping such fine-scale patterns of human population structure.

Significant Fine-Scale Population Structure Is Observed on All Continents

To explore intra-continental structure in more detail, we performed PCA separately on individuals grouped into seven continents: Africa (AF), America (AM), Central and South Asia (CSA), East Asia (EA), Europe (EU), Middle East (ME), and Oceania (OC). For each continent, the number of PCs that are significant according to the TW distribution is shown in Table 1. Note that there are not as many significant lower-ranked PCs within continents as were observed for the global sample. Intuitively, this makes sense because the low-ranked significant PCs in the global analysis correspond to the higher-ranked PCs identified in the continental analysis.

Table 1.

Number of Significant PCs in Each Continental Grouping

Continent	Populations	Number of Significanta PCs
All	52	18
Africa	7	4
America	5	4
Central and South Asia	9	5
East Asia	17	4
Europe	8	2
Middle East	4	5
Oceania	2	1

^ap < 0.001

Figure 2 provides a visual summary of consecutive biplots of the top five significant PCs from Africa. Similar PC plots are available for the remaining continents in Figures S1–S6. In the first plot, we confirm some of the salient features reported in results from previous studies.^22,36 The African hunter-gatherer (Biaka, Mbuti Pygmies, and San) and the pastoral (Youruba, Mandenka, and Bantu) samples cluster separately along PC1, whereas along PC2 the primary distinction is within the hunter-gatherer group, between the Biakas and the Mbutis. The third component separates the San, and the fourth and fifth components partition the pastoral populations, with the Bantu NE group in particular.

Figure 2.

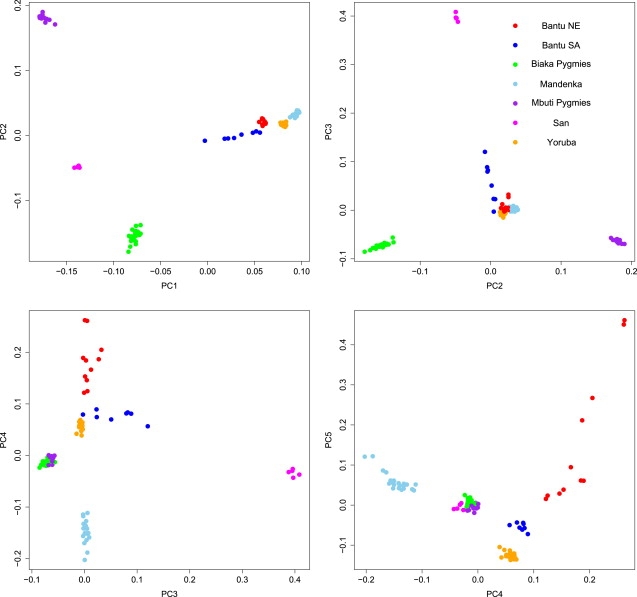
Intracontinental Population Stratification in Africa

The 102 African samples are represented as filled circles, and the color legend for the predefined population labels is indicated within each plot.

Clinal Variation Is a Common Feature of Intracontinental Structure

Many theoretical models of population structure, such as isolation-by-distance and stepping-stone models, predict clinal patterns of genetic variation.^37–40 To explore such patterns, we tested the correlation of PC1 with the geographical coordinates of sample locations for all continents by using Spearman's rank correlation coefficient (see Material and Methods). Table 2 summarizes the results of this test and demonstrates that significant evidence of clinal variation is observed for all continents (except a lack of correlation with latitude in the Middle East). Note that when one excludes “outlier” populations, such as the Kalash and Hazaras, which are thought to be more isolated and thus might deviate from simple isolation-by-distance or stepping-stone models more than the others,^5,41,42 the magnitude of the observed correlations increases (data not shown).

Table 2.

Summary of Clinal Patterns of Variation with PC1

Continent	Sample Size	Longitude		Latitude		Haversine Distance
		ρ	p Value	ρ	p Value	ρ	p Value
Africa	102	−0.76	2.2 × 10−16	0.74	2.2 × 10−16	−0.60	2.1 × 10−11
America	64	0.91	2.2 × 10−16	−0.91	2.2 × 10−16	−0.90	6.5 × 10−26
Central and South Asia	201	−0.39	1.0 × 10−8	−0.25	2 × 10−4	−0.39	1.0 × 10−8
East Asia	229	−0.51	2.7 × 10−16	−0.89	2.2 × 10−16	−0.15	1.9 × 10−2
Europe	158	−0.44	6.5 × 10−9	−0.86	2.2 × 10−16	−0.95	1.0 × 10−78
Middle East	162	−0.66	2.2 × 10−16	−0.03	7.1 × 10−1	−0.65	1.8 × 10−20
Oceania	28	0.85	1.3 × 10−8	−0.85	1.32 × 10−8	0.85	1.38 × 10−8

Identifying SNPs Significantly Correlated with PCs

Although PC biplots give a snapshot of the composite genome-wide patterns of variation, they do not provide information about the specific SNPs and genomic locations driving such signatures of population structure. To this end, we identified SNPs that are significantly correlated with individual PCs. The correlation of each SNP with a single PC can inform us about local changes in ancestry along the genome. One variant of this approach has been successfully applied to describing sets of AIMs that are used to control for confounding in association studies.^14,16,21 One selects these AIMs by retaining only the top few informative SNPs that can accurately reconstruct the global patterns of structure.

We extended this approach to look at the set of all SNPs that are significantly correlated to PCs. This enlarged set of SNPs, in addition to encompassing the set of AIMs, allows us to begin to make inferences about how evolutionary processes such as genetic drift and adaptation have impacted the more dynamic but locally restricted signatures of structure along the genome. The number of SNPs significantly correlated with the top two PCs in each continent is listed in Table 3.

Table 3.

Summary of Markers Correlated with PC1 and PC2

Continent	Number of Populations	Sample Size	Number PC1-Correlated Markers	Number PC2-Correlated Markers	Average FST
Africa	7	102	11811	1446	0.070
America	5	64	4217	3226	0.107
Central and South Asia	9	201	5239	2469	0.034
East Asia	17	229	6759	122	0.051
Europe	8	158	513	121	0.035
Middle East	4	162	2123	658	0.027
Oceania	2	28	2382	13	0.118

We were additionally interested in discovering whether information captured along the top PCs is recapitulated by the set of markers correlated to them. In the African samples, we analyzed the subset of most-informative SNPs correlated to PC1 and PC2 by using the program Structure.²⁷ As discussed above, our analysis of African samples demonstrates a separation of hunter-gatherers and pastoral groups along PC1. Figures S7 and S8 show the Structure-generated clustering profile of African individuals at K = 2 for PC1 and K = 3 for PC2. Both plots recreate the stratification profile in Figure 2, where the Bantu, Mandenka, and Yoruba samples cluster together separately from the Pygmy and San samples in the PC1 profile. In addition, the cluster coefficients for PC2 indicate that Mbuti Pygmies are distinct from the San and Biaka (see Figure S8).

Factors Affecting the Number of Correlated Markers

Table 3 shows that there is substantial variation in the number of correlated SNPs across continents. For example, Africa has the highest number SNPs significantly correlated with PC1. On the other hand, Europe has a paucity of PC1-correlated SNPs, which is curious because it is an order of magnitude lower than Central and South Asia despite similar levels of structure measured by average F_ST values (Table 3). Differences in the observed number of correlated markers among continents could result from a number of factors, such as differing magnitudes of intra-continental population structure, ascertainment bias, and sample size.

To investigate these issues, we performed coalescent simulations by using demographic parameters derived from a previously described calibrated model of human history in three populations with ancestry from the HapMap panel.³⁰ In our simulations, we modeled intracontinental structure in two continents, corresponding to Africa (high structure; mean F_ST = 0.048) and Europe (low structure; mean F_ST = 0.005) and sampled 1000 chromosomes from each continent. We then followed the same procedure that was used with the empirical data to perform within-continent PCA. Note that our primary purpose here is to investigate factors influencing the number of PC-correlated markers in the context of a demographic model broadly consistent with major features of human genomic variation, not with the exact demographic history per se.

The salient conclusions of these simulations can be summarized as follows. First, as expected, higher levels of population structure lead to more significantly correlated SNPs. Specifically, the proportion of PC1-correlated markers was approximately five times larger in Africa (mean = 0.0574; 95% CI = 0.0518-0.062) than in Europe (mean = 0.0103; 95% CI = 0.0098-0.0107). Additionally, the simulations demonstrate that ascertainment bias of SNP markers can have large consequences on the estimated proportion of significantly correlated PC SNPs. In particular, ascertainment bias tends to overestimate levels of population structure, particularly in the continents where SNPs were not initially discovered. The mean proportion of correlated markers in Africa was 0.105 (95% CI = 0.088-0.122), whereas in Europe it was 0.0201 (95% CI = 0.0193-0.021). This observation is due to the bias toward discovering common alleles^43–45, and the resulting overrepresentation of SNPs with a higher sampling variance of allele frequencies. Finally, sample sizes can also influence the number of correlated markers. Specifically, when the total number of chromosomes in Africa increases from 200 to 1000, the proportion of correlated markers also increases (data not shown).

In summary, we find that three factors, the amount of population structure, the SNP ascertainment strategy, and the sample size, play a role in determining the total number of PC-correlated markers and can explain the small number of PC-correlated markers in Europe, and they probably contribute to the variation in the number of PC-correlated markers among continents.

Genomic Distribution of Markers Significantly Correlated with PC1

Identifying sets of PC-correlated SNPs allows fine-scale mapping of genomic regions contributing to population structure. In addition to providing an informative set of markers that can be used in correcting for population stratification in genome-wide association studies, broad sets of PC-correlated SNPs will facilitate inferences on the evolutionary forces shaping patterns of intracontinental structure. The relative contribution of genome-wide stochastic effects mediated through genetic drift and locus-specific effects, such as selection, are difficult to separate; however, clustering of PC-correlated SNPs might be indicative of the locus-specific effects of positive selection⁴⁶ or recombination-rate heterogeneity.

To begin to explore these issues, we searched for clusters of significantly correlated PC1 SNPs by dividing the genome into nonoverlapping 500 kb bins and testing whether each bin contained significantly more PC-correlated markers than expected on the basis of the total number of SNPs in the bin (see Material and Methods). Figure 3 shows the genomic distribution of PC1-correlated SNPs for all continents. The number of significant (p < 1.8 × 10⁻⁶) SNP clusters ranged from approximately 30 to 120 across continents (Table 4), whereas we would expect less than one significant bin by chance at this threshold. Furthermore, the percent of PC1-correlated SNPs located in clusters ranged from 7% to 35% (Table 4), and on average almost 80% of all markers were present outside of clusters. Thus, although there is some evidence for clustering of significantly correlated PC1 SNPs, in general they are widely distributed throughout the genome, consistent with a predominant role of genetic drift in mediating patterns of fine-scale human structure.

Figure 3.

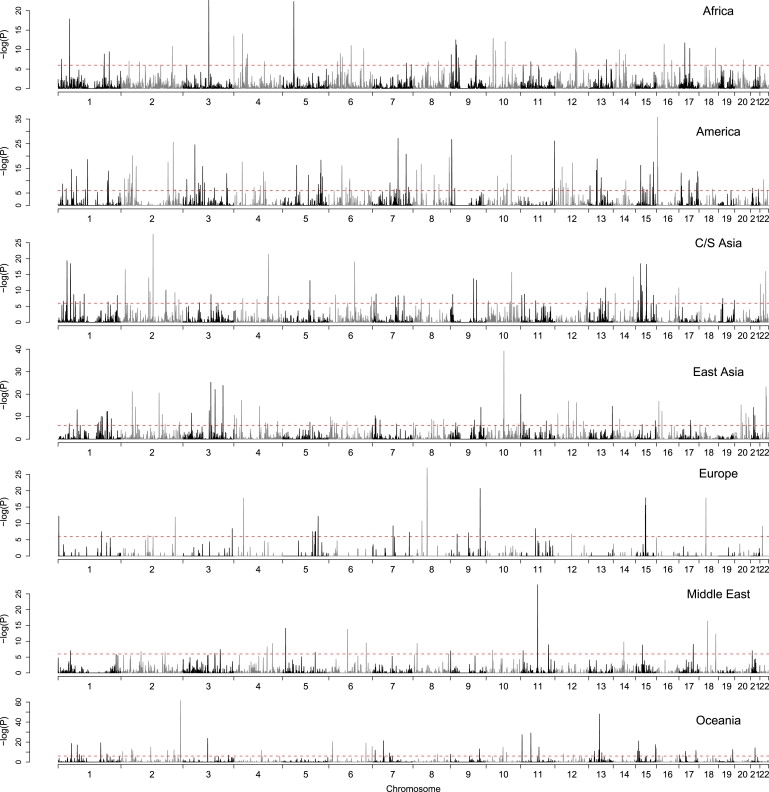
Genomic Distribution of PC1-Correlated SNPs

The genome was divided into nonoverlapping 500 kb bins (x axis), and each bin was tested for whether it contained more PC1-correlated SNPs than expected by chance (y axis). p values are plotted as −log₁₀ (p). Panels represent the seven continents, and the dashed red line corresponds to a p value of 1.8 × 10⁻⁶.

Table 4.

Distribution of PC1-Correlated SNPs Found in Clusters and in Selected Regions

Continent	Number of Clusters	Percent SNPs in Clustersa	Percent SNPs in Selected Regionsb	Percent Clustered SNPs in Selected Regionsc	Enrichment p Valued
Africa	61	7.0	8.9	18.0	2.2 × 10−16
America	120	35.2	6.9	8.2	8.8 × 10−3
C/S Asia	83	18.7	13.3	30.0	2.2 × 10−16
East Asia	95	19.1	8.7	14.0	3.0 × 10−13
Middle East	29	11.1	15.9	42.0	2.2 × 10−16
Oceania	57	28.8	6.8	8.9	1.1 × 10−2

^aDenotes the percentage of all PC1-correlated SNPs found in clusters.

^bDenotes the percentage of all PC1-correlated SNPs that are located in putatively selected regions of the genome (see text).

^cDenotes the percentage of all PC1-correlated SNPs that were found in clusters and also map to putatively selected regions.

^dP value resulting from a test of whether more PC1-correlated SNPs in clusters were also present in selected regions than expected by chance.

To better understand the potential causes of the identified clusters in more detail, we first compared the average recombination rate between bins with and without evidence of significant clustering. The average recombination rate in bins with clusters of PC1-correlated SNPs is significantly smaller than that in bins without clusters (1.32 and 1.56 cM/Mb, respectively; p = 1 × 10⁻⁶). Thus, as expected, the interaction of genetic drift and local recombination rates probably contributes to the observation of clusters of PC1-correlated SNPs.

Next, we tested whether more clustered PC1 SNPs were located in putatively selected genomic regions than would be expected by chance. We integrated the results from ten recent genome-wide scans for selection and identified 722 loci (see Material and Methods) that were supported in two or more studies.²⁹ Table 4 summarizes the salient details of PC1-correlated SNPs in clusters and selected regions, and for each continent we found that significantly more clustered PC1 SNPs were also present in selected regions than was expected by chance. Note that we have excluded Europe from this analysis because the number of PC1-correlated SNPs prevents robust inferences. Despite this enrichment, most PC1-correlated SNPs were located outside of clusters, and of those that were in clusters, the majority were not located in putatively selected regions. Thus, although the results of Table 4 suggest that selection might contribute to fine-scale population structure, it is likely to be of less importance than genetic drift.

Discussion

We have performed a detailed analysis of intra-continental structure in 944 individuals from seven continents. We find significant evidence for population structure within each continental group, and hence local, small-scale differentiation is a ubiquitous feature of even closely related human populations. Furthermore, the magnitude of intra-continental structure, as assessed either by mean F_ST or the number of significant PCs, varies among continents. Obviously, this might reflect genuine differences in the degree of fine-scale structure; however, additional variables such as the set of sampled populations, sample sizes, and ascertainment bias of markers preclude definitive interpretations from this data set. One particularly interesting observation was the strong signature of clinal variation in essentially every continental group (Table 2). Although correlations between patterns of human genetic variation and geography have previously been described in European samples, to our knowledge the general extension of such correlations to additional continents has not been appreciated.

In addition to characterizing patterns of intra-continental structure, we also identified the SNPs contributing to the predominant axes of variation. Contrary to previous work, which has primarily focused on small sets of AIMs that serve as proxies for population structure in genome-wide association studies, we have analyzed the entire set of SNPs correlated to the top two PCs. It is important to note that this set is not exhaustive because the main features of the PC biplot are recapitulated in all continents when the correlated markers are excluded from the analysis (data not shown). Rather, it is a conservative estimate of the number of markers that make the largest contribution to genetic variation between populations within continents.

We observed that within continents, the range of significantly PC1-correlated SNPs spanned an order of magnitude among continental groups. To explain the variation, we performed extensive coalescent simulations to test the effects of different characteristics of the data. Taken together, levels of population structure, the number of samples, and ascertainment bias influence the number of correlated markers. Although the effects of ascertainment bias can be mitigated through the use of data from complete sequencing projects such as the “1000 Genomes” project, more fundamental issues such as the optimal study design for sampling individuals and populations require further investigation.

We were particularly interested in the distribution of PC-correlated SNPs and whether they were clustered into discrete regions or evenly distributed throughout the genome. Interestingly, we did find that PC1-correlated SNPs in clusters were enriched for loci previously implicated as targets of positive selection (Table 4). Nevertheless, the majority of PC-correlated SNPs were broadly distributed throughout the genome. Thus, although positive selection might contribute to patterns of fine-scale population structure, the stochastic effects of genetic drift are most likely the predominant force governing intra-continental patterns of population structure in the HGDP samples.

In summary, now that we have increasingly dense catalogs of genetic variation, the details of fine-scale human population structure are becoming tractable.^{14–17,47–50} As microsatellite and SNP data give way to full resequencing data, the testing of increasingly refined hypotheses about fine-scale human population structure should yield new insights into the history and relationships among human genomes.

Supplemental Data

Supplemental Data include eight figures and two tables and can be found with this article online at http://www.ajhg.org/.