New information content in RNA base pairing deduced from quantitative analysis of high-resolution structures

Abstract

Non-canonical base pairs play important roles in organizing the complex three-dimensional folding of RNA. Here, we outline methodology developed both to analyze the spatial patterns of interacting base pairs in known RNA structures and to reconstruct models from the collective experimental information. We focus attention on the structural context and deformability of the seven pairing patterns found in greatest abundance in the helical segments in a set of well-resolved crystal structures, including (i–ii) the canonical A·U and G·C Watson-Crick base pairs, (iii) the G·U wobble pair, (iv) the sheared G·A pair, (v) the A·U Hoogsteen pair, (vi) the U·U wobble pair, and (vii) the G·A Watson-Crick-like pair. The non-canonical pairs stand out from the canonical associations in terms of apparent deformability, spanning a broader range of conformational states as measured by the six rigid-body parameters used to describe the spatial arrangements of the interacting bases, the root-mean-square deviations of the base-pair atoms, and the fluctuations in hydrogen-bonding geometry. The deformabilties, the modes of base-pair deformation, and the preferred sites of occurrence depend on sequence. We also characterize the positioning and overlap of the base pairs with respect to the base pairs that stack immediately above and below them in double-helical fragments. We incorporate the observed positions of the bases, base pairs, and intervening phosphorus atoms in models to predict the effects of the non-canonical interactions on overall helical structure.

Introduction

Recent discoveries linking tiny pieces of RNA, called microRNAs (miRNA), with the activity of thousands of genes are fueling excitement about the roles that these molecules play inside the cell [1–4]. Interestingly, the 20–25 nucleotides of mature miRNAs form ‘imperfect’ double-helical complexes with their RNA targets [5,6]. That is, the sequence of bases on the interacting strands is not perfectly complementary, with much, but not all, of the molecular complex held in place by canonical Watson-Crick pairs. The reasons for such imperfections and the potential functional role(s) that the non-canonical bases might play are open questions of biological relevance.

The double helices detected in the high-resolution structures of other types of RNA are also imperfect in that the bases on interacting fragments form non-canonical as well as Watson-Crick base pairs [7]. The likely importance of the non-canonical pairs in these and other RNA structures points to the need for methods that describe the observed interactions quantitatively. Computational schemes now in place to predict RNA tertiary structure [8,9] treat the non-canonical base pairs indirectly in the context of representative structural fragments or knowledge-based pairing potentials. Full understanding of RNA structure requires an approach that allows for precise generation of three-dimensional molecular models from mathematically rigorous, yet easily understandable descriptions of the spatial arrangements of the constituent nucleotide units. Such an approach has been key to advances in understanding how proteins guide the higher-order folding of DNA [10,11], and has recently been adapted by others to characterize the non-canonical interactions of RNA base pairs [12], albeit with a series of base-pair specific reference frames that obfuscate comparison of the various types of association.

The idea that non-canonical base pairs of RNA might play a significant biological role originated with the wobble hypothesis of Crick [13], which proposed the occurrence of a laterally ‘slipped’ configuration of purine and pyrimidine bases, allowing guanine to associate with uracil rather than cytidine and thereby providing a rationale for the roughly 60 codons on the 40 naturally occurring transfer RNA molecules. The G·U wobble pair and many of the other non-canonical base-base interactions anticipated by Saenger [14], from the hydrogen-bonding capabilities of the heterocyclic bases, occur in currently available high-resolution structures. Indeed, there are now enough structural examples of various non-canonical base pairs to extract both sequential trends and spatial rules of potential utility in genomic analysis and RNA modeling.

This article describes the computational approach that we have taken to identify the helical fragments and characterize the structural and sequential context and the spatial patterns of interacting base pairs in known RNA structures. We show how one can use the observed spatial patterns to rebuild the structures and to construct new models of RNA based on the collective experimental information. We focus on the dominant base pairs located in helical fragments, determining the rigid-body parameters that describe the three-dimensional arrangements of associated bases and the positioning of these base pairs with respect to the base pairs that stack immediately above and below them. The latter information helps to identify the helical fragments within the RNA structures. We also consider the positioning of the two phosphorus atoms within each base-pair step and the areas of overlap of the base rings at each step. We conclude with sample reconstructions of ‘imperfect’ RNA duplexes, illustrating the predicted effects of non-canonical base pairs on the equilibrium configurations of helical fragments. The modeled structures point to the key role of the non-canonical base pairs as sites of unique geometric recognition along the otherwise highly regular A-type helices constituted from Watson-Crick-paired ribonucleotides.

Methods

Base-pair identification

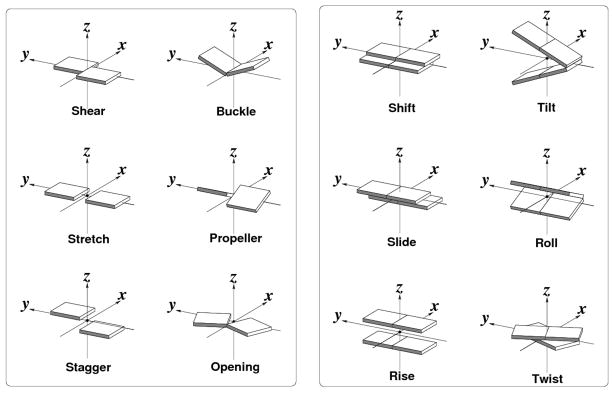
We use the 3DNA software package [15,16] to identify the base interactions and double-helical segments and to characterize the spatial arrangements of interacting bases and base pairs in RNA structures. Specifically, we use the following criteria to define a base pair: (i) the distance between the origins of the standard reference frames [17] embedded in each base must be 15 Å or less; (ii) the magnitude of the vertical offset of the base planes, the so-called Stagger [18] (see Figure 1 and the text below), must be 1.5 Å or less; (iii) the smaller of the two angles between the normals of the base planes, must be 30° or less; (iv) the distance between the glycosidic base atoms, i.e., the purine N9 and pyrimidine N1 atoms linked to the sugar-phosphate backbone, must be 4.5 Å or more; and (v) at least one pair of base nitrogen/oxygen atoms must be within a distance of 3.4 Å. A base pair is accepted if two or more pairs of hydrogen-bond donor and acceptor atoms lie within a distance of 3.4 Å in the selected configurations.

Figure 1.

Pictorial definitions of the rigid-body parameters used to describe the spatial arrangements of canonical and non-canonical RNA base pairs (left) and sequential base-pair steps (right). Block images of idealized Watson-Crick pairs, generated with 3DNA [15,16] and rendered with Xfig (http://www.xfig.org/), illustrate positive values of the designated parameters. Shading denotes the minor-groove/sugar edge of the bases and base pairs.

The geometric guidelines thus allow for unexpected base interactions, such as the hydrogen bonding of base and backbone atoms or the presence of rare tautomers. The latter features are not easily found in conventional hydrogen-bond analyses of nucleic acid interactions, which are based on the distances between pre-selected proton donor and acceptor atoms [19–21]. Modified bases can be treated by fitting the most closely related standard bases (adenine A, cytosine C, guanine G, uracil U) to the observed chemical species and then computing the relevant spatial parameters. The present investigation is limited, however, to the interactions of chemically unmodified bases in tautomerically preferred forms. The pairing of bases brought about by crystal packing is also ignored.

Helical segments

The spacing of base-pair centers is used to divide the chain into independent helical segments. A base-pair frame is first constructed by finding the ‘middle’ frame between associated bases [15,16,22]. Neighboring base pairs are then identified by finding all base pairs that lie within 7.5 Å of a given pair, where the distance is measured between the origins of the coordinate frames on neighboring base pairs. The nearby pairs are ordered by distance and divided into 3′- and 5′-neighbors on the basis of the directions of the chemical backbone. The pairs are sorted in spatial order and grouped into helical stretches of three or more base pairs, such that the terminal base pairs have neighbors on only one (3′ or 5′) side of the associated plane.

Because no limits are placed on residue number in the search for ‘neighboring’ base pairs, some of the helices are quasi-continuous in the sense that adjacent stacked nucleotide pairs are not necessarily linked by covalent bonds. Thus, the sequentially distant bases that occur at these ‘nicks’ in RNA helical structures are distinguished from those that are located at the 5′-and 3′-termini or within the chemically continuous, intact helical regions. Single bases inserted within or at the ends of an otherwise continuous helical stretch are also identified. Since there are also no restrictions on the angles between neighboring base-pair planes, both curved and straight double-helical stretches are identified.

Some of the bases contribute to higher-order interactions, such as U·A·U triplets with adenine concomitanty associated with two uracils. Thus, two or more paired components may fall at the same spatial ‘rung’ in a helical ladder. The different pairs typically fall into different spatial categories, e.g., intact vs. nicked pairs, unless the nucleotides forming the higher-order complex are all sequentially distant from the residues stacked above and below them in the helix. In such a case the paired components are all classified as inserts. Complete details of the higher-order base associations will be reported elsewhere.

Base-pair classification

Base pairs are described in terms of (i) the interacting edges, identities, and orientations of the constituent bases following the guidelines of Leontis and Westhof [23], (ii) the six rigid-body parameters — Shear, Stretch, Stagger, Buckle, Propeller, Opening [18] —that relate the coordinate frames on the two bases (Figure 1), and (iii) the locations of the pairs in helical regions, i.e., within or at the termini of chemically linked segments or at the ends of quasi-continuous base-paired stretches. The base edges are defined, following Leontis and Westhof [23], by chemical identity: W, corresponding to the locations of the base atoms involved in the two Watson-Crick hydrogen bonds common to A·U and G·C base pairs; H, corresponding to the atoms on purines (R) involved in Hoogsteen base pairing, e.g., R(N7), A(N6), and G(O6), and the corresponding atoms on the so-called ‘C–H’ edge of pyrimidines (Y), e.g., C(N4) and U(O4); and S, corresponding to the proton-acceptor atoms in closest proximity to the sugar ring, i.e., R(N3), G(N2), and Y(O2). The orientation of base pairs is established by the faces [24,25] of the interacting bases, which are distinguished by the directions of their embedded coordinate frames [15]. A minus symbol is reported if two bases form a pair with opposing faces, such as a Watson-Crick base pair, and a plus symbol if the bases share the same face, as a Hoogsteen interaction [26].

Dimeric structure

The spatial arrangements of interacting base pairs are described by (i) the six familiar base-pair step parameters — three angles called Tilt, Roll, and Twist and three quantities called Shift, Slide, and Rise with dimensions of distance [18] (Figure 1), (ii) the Cartesian coordinates (x_P, y_P, z_P) of the phosphorus atoms on each strand of the intervening sugar-phosphate backbones, expressed in the local dimeric coordinate frame (Figure 2) [27], and (iii) the shared overlap area of consecutive base pairs, obtained from the projections of the planar base rings on the dimeric reference frame [15]. The present analysis is restricted to chemically intact RNA dimers with normal 3′–5′ phosphodiester linkages on both strands

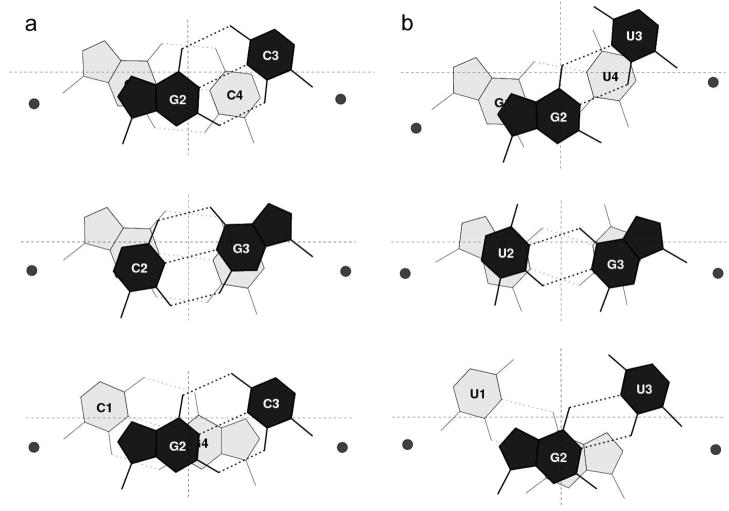
Figure 2.

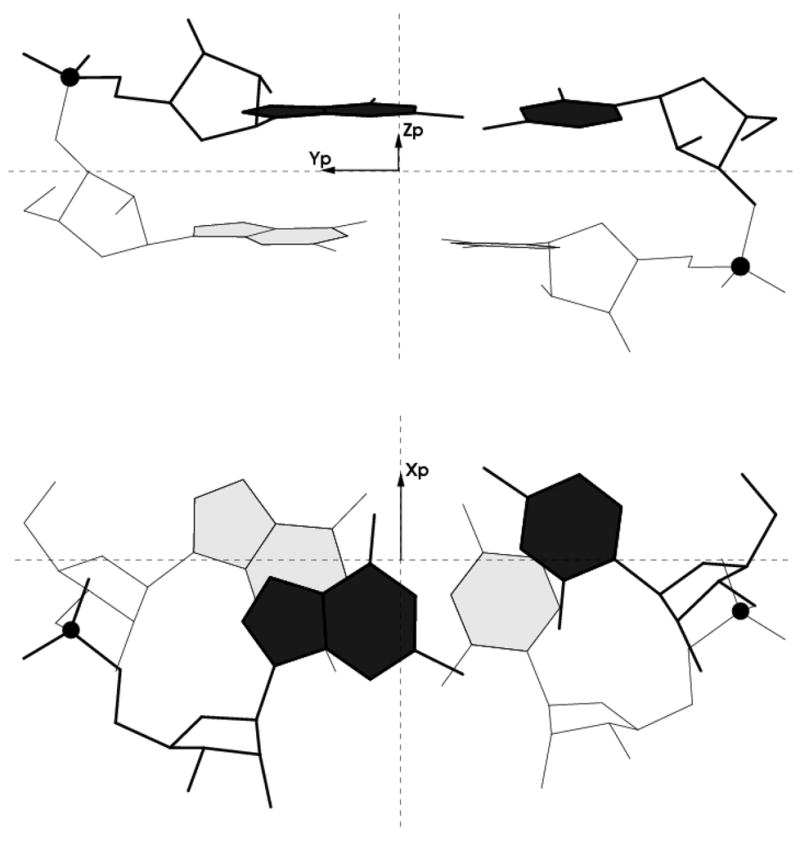
Illustration of the relative positions (x_P, y_P, z_P) of the phosphorus atoms (shown as black balls) with respect to the ‘middle’ frame of the GpG·CpC dinucleotide at step 10 in the 2.2 Å crystal complex of r(CGCGUCACACCGGUGAAGUCGC)₂ with lividomycin A (NDB_ID dr0022) [43]. Views looking toward the minor-groove/sugar edge (top) and perpendicular to the mean planes (bottom) of the tandem G·C pairs.

Dataset

RNA crystal structures were taken from the March, 2008 release of the Nucleic Acid Database [28]. The identities and geometric parameters of base pairs and helical fragments were collected in a relational database [29] and used in the present survey of base-base and base stacking interactions. The structures were divided according to biological function —transfer RNA (tRNA), ribozymes, protein-RNA complexes, drug-DNA complexes, ribosomal RNA (rRNA), and other RNA structures (including synthetic aptamers, pseudoknots, and ‘long’ duplexes) — and a ‘non-redundant’ subset of 469 structures of 3.5 Å or better resolution (listed in Table S1 in the Supplementary Materials) was then used for more detailed analyses of double-helical structure. The dataset is non-redundant in the sense that it contains only four of the currently solved ribosomal structures, namely the best resolved structures of the ribosomal subunits from Deinococcus radiodurans [30], Haloarcula marismortui [31], Escherichia coli [32], and Thermus thermophilus [33]. The multiple structures of other RNA molecules, which constitute a large fraction of the data (~70% of the paired and unpaired bases), are not filtered in the current survey.

Base-pair deformability

The average values of the six rigid-body parameters are suggestive of the rest state preferred by each base pair, and the pairwise covariance of variables, i.e., the differences between the mean squares and the squares of the means of all pairs of rigid-body parameters, is a measure of the intrinsic stiffness. The product of the eigenvalues of the 6×6 array of differences provides an estimate of the conformational entropy, or the volume of conformation space accessible to the base pair [34].

Model building

Sequence-dependent structural models of base-paired helices are generated with the rebuilding features of 3DNA [16]. The input to the rebuilding routines is the output of the structural analyses. That is, the reconstruction of base-base interactions uses the chemical identities and the six rigid-body parameters describing each base pair, and the build-up of successive base pairs employs the nucleotide sequence and the six base-pair step parameters relating consecutive base pairs. Phosphorus atoms are introduced at base-pair steps using the (x_P, y_P, z_P) values associated with the given dimers. The positions of the phosphorus atoms are then used to characterize the grooves of the rebuilt structures. The widths of the grooves correspond to the shortest interstrand distances between phosphorus atoms at each base-pair step, i.e., the distances of a given P atom from the two P atoms closest in either direction along the RNA helical axis, the shorter distance corresponding to the major-groove width and the longer to the minor-groove width.

Results

Nucleotide composition

The chemical makeup of the 17,328 base pairs found within the stacked, double-helical segments of the current set of RNA structures reflects the strong preferences for G·C and A·U Watson-Crick base pairing (Table 1). The proportion of G·C and A·U pairs within the helical domains (0.57 and 0.23, respectively) substantially exceeds the fraction expected from the nucleotide composition (0.32 G, 0.27 C, 0.23 A, 0.19 U) of the selected RNA structures. Whereas ~95% of the G·C pairs interact as intact or partially ‘melted’ Watson-Crick pairs like those found in double-helical DNA [35], only 81% of the A·U pairs associate in such a configuration. As noted below, a sizable proportion of the A·U pairs assemble as Hoogsteen complexes. The few examples of U·A·U triplets, constituted of Watson-Crick and Hoogsteen pairs, do not contribute to the relatively low incidence of A·U interactions in RNA helical domains. The third base in such associations almost always comes from a single-stranded region. The ‘melted’ Watson-Crick pairs are structurally perturbed compared to the canonical pairs. The bases tend to be more widely spaced in terms the so-called Stretch (Figure 1) or slipped past one another via Shear, with concomitant disruption of hydrogen bonding. About 20% of the helical base pairs associate via non-canonical forms.

Table 1.

Base-pair composition in RNA helical structures.

A	G	C	U	B/B′
384	980	313	3975†	A
	128	9913†	1282	G
		63	103	C
			187	U

^†Totals include canonical Watson-Crick base pairs: 9500 G·C; 3069 A·U. Counts exclude 386 pairs constituted from modified bases.

Dominant base pairs

Most (~90%) of the base pairs in the RNA helical domains associate in one of seven distinct hydrogen-bonding patterns: canonical Watson-Crick G·C and A·U pairs; wobble G·U pairs; sheared G·A pairs; Hoogsteen A·U pairs, wobble U·U pairs; and Watson-Crick-like G·A pairs (Figure 3 and Table 2). The relative populations of the canonical and the two wobble complexes are roughly comparable to those found previously from visual characterization of rRNA base pairs [36]. The constraints of double-helical structure and the consideration of other RNA structures contribute to the lower relative abundance of the other pairs.

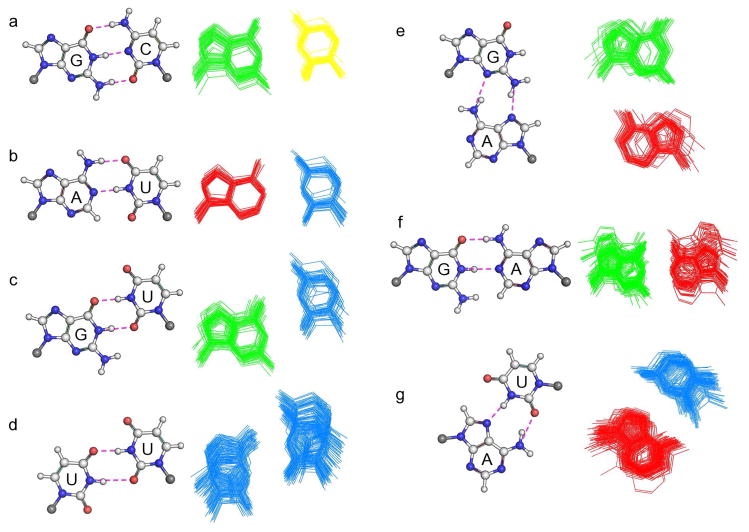
Figure 3.

Comparison of hydrogen-bonding interactions, chemical structures (including hydrogen atoms and double bonds), and relative displacement of the bases comprising the predominant base pairs in RNA helical structures. Images depict (a–b) the canonical G·C and A·U Watson-Crick pairs, (c) the wobble G·U pair, (d) the wobble U·U pair, (e) the sheared G·A pair, (e) the Watson-Crick-like G·A pair, and (f) the Hoogsteen A·U pair. Hydrogen bonds in ball-and-stick images on the left are designated by red dashed lines, with the nitrogen and oxygen atoms capable of donating and accepting protons highlighted respectively in blue and red. The double bonds appear as darkened sticks and the glycosyl carbons as gray balls. The superposed stick images on the right illustrate the range of base-pair deformations. Structures generated with 3DNA [15,16] using respectively the rigid-body parameters reported in Table 4 and the observed base-pair parameters of 50 representative examples. Composite images are obtained by superposition of the middle frames of each base pair and arrangement in a ‘top-down’ view perpendicular to the mean base-pair planes. Bases are color-coded by chemical sequence: A (red); U (light blue); G (green): C (yellow).

Table 2.

Predominant base-pairing interactions in RNA helical structures.^†

Base pair			Hydrogen bonds		Sign	Saenger	Leontis-Westhof		Number
Canonical
G·C	Watson-Crick		N2-H··· O2	2.79 (0.17)	−	XIX	cis	W/W	9500×0.90
			O6· · ·H-N4	2.92 (0.18)
			N1-H· · ·N3	2.89 (0.13)
A·U	Watson-Crick		N1· · ·H-N3	2.84 (0.14)	−	XX	cis	W/W	3069×0.93
			N6-H· · ·O4	2.97 (0.18)
Non-canonical
G·U		wobble	N1-H· · ·O2	2.79(0.16)	−	XXVIII	cis	W/W	1049×0.69
			O6· · ·H-N3	2.85(0.16)
G·A		sheared	N2-H· · ·N7	2.89(0.17)	+	XI	trans	H/S	509×0.59
			N3· · ·H-N6	3.03(0.18)
A·U		Hoogsteen	N6-H· · ·O2	2.91(0.21)	+	XXIII	trans	H/W	354×0.71
			N7· · ·H-N3	2.90(0.17)
U·U		wobble	O2· · ·H-N3	2.95(0.24)	−	XVI	cis	W/W	185×0.54
			N3-H· · ·O4	2.87(0.15)
G·A		Watson-Crick	N1-H· · ·N1	2.84(0.17)	−	VIII	cis	W/W	141×0.85
			O6· · ·H-N6	2.91(0.20)

^†Base pairs described in column 2 by the nomenclature introduced by Lee and Gutell [36] and grouped in columns 6–8 into the structural classes anticipated by Saenger [14] and employed by Leontis and Westhof [23] (see text for details). Hydrogen bonds described in column 4 by the mean values and standard deviations (subscripted values in parentheses) of the distances, in Ångstrom units, between the designated proton donor-acceptor pairs. The signs in column 5, i.e., − or +, respectively denote whether the interacting bases form a pair with opposing faces or share the same face [15]. The entries in the last column correspond to the number of base pairs of a given type and the fraction of those pairs (subscripted numbers expressed as multiplicative factors) with the hydrogen-bonding pattern specified in column 3.

Structural context

Each of the dominant base pairs has a unique spatial signature within the RNA helical domains (Table 3). That is, some base pairs occur with greater frequency within the interior than at a ‘nick’ or at either end of a stacked double-helical fragment. Other pairs resemble intercalating ligands in that they insert between covalently linked base pairs or stack at the end of a duplex. Like a nick in a regular DNA duplex, a ‘nick’ in the RNA helices corresponds to a break in the covalent link between stacked base pairs. The RNA backbone, however, is ‘broken’ in the sense that the stacked bases occur in sequentially distant nucleotides.

Table 3.

Distribution of paired bases in RNA helical structures.

Helical location†	Base-pair‡
	All	G·C_WC	A·U_WC	G·U_w	G·A_s	A·U_H	U·U_w	G·A_WC
Interior
intact	0.62	0.62	0.75	0.63	0.34	0.05	0.74	0.25
‘nick’	0.20	0.20	0.16	0.26	0.25	0.29	0.13	0.66
‘insert’	0.02	0.01	0.01	0.00	0.03	0.42	0.03	0.01
Terminus
intact	0.13	0.15	0.07	0.10	0.33	0.05	0.10	0.06
‘insert’	0.02	0.01	0.01	0.01	0.05	0.19	0	0.02

^†Fraction of the specified nucleotide association in different structural contexts within the arrays of stacked base pairs in high-resolution RNA structures: intact – sequential bases laterally attached to D-ribose sugars that are linked, in turn, via a normal 3′-5′ covalent phosphodiester linkage; ‘nick’ – bases or base pairs attached to sequentially distant sugars and thereby ‘broken’ by the folding of the nucleotide backbone; insert – single bases or base pairs that resemble intercalating ligands by stacking against or between chemically intact base-paired steps

^‡Base-pair subscripts correspond to the designations in Table 2: Watson-Crick (WC); w (wobble); H (Hoogsteen). ‘All’ refers to the 17,328 pairs of bases formed from all combinations of A, U, G, and C (Table 1).

Thus, the A·U Hoogsteen pair (A·U__H) stands out from other base pairs in terms of its intercalative properties and unlikely presence within intact, chemically continuous dinucleotide steps. By contrast, the G·A Watson-Crick-like pair (G·A__WC) has a higher propensity than other base pairs to flank ‘nicks’ within quasi-continuous helical domains, and the sheared G·A pair (G·A__s) to lie at the ends of stacked helical arrays. The canonical G·C Watson-Crick pair (G·C__WC) differs from its A·U counterpart (A·U__WC) in being more likely to terminate a helical fragment. The G·U wobble pair (G·U__w) is more apt than either of the canonical pairs to flank a ‘nick’ in an RNA helix, and the U·U wobble pair (U·U__w) has an apparent inability to stack at the ends of a duplex.

The overall distribution of base pairs within the RNA helical arrays resembles that of the dominant G·C Watson-Crick pairs. The ‘nicks’ and inserts that disrupt the organized structures occur, on average, every fourth base pair. The mean length of the quasi-continuous helical domains in the dataset, obtained from the quotient of the number of base pairs in the interior and the number at the termini of the stacked arrays, is 11.3 bp.

Base-pair deformability

The superposed images of hydrogen-bonding patterns in Figure 3 illustrate the overall deformability of the base-pair structures. Table 4 quantifies this information in terms of the mean values, standard deviations, and volumes of conformation space sampled by the rigid-body parameters that relate the dominant base pairs. The variability is also apparent in the dispersion of distances between hydrogen-bond donor and acceptor atoms (Table 2).

Table 4.

Average values and dispersion of base-pair parameters in RNA helical fragments.^†

	Rigid-body parameters
Base pair	Shear (Å)	Stretch (Å)	Stagger (Å)	Buckle (deg)	Propeller (deg)	Opening (deg)	V (deg3Å3)
G·C_WC	−0.20(0.41)	−0.15(0.17)	−0.04(0.40)	−3.4(8.4)	−8.7(8.5)	0.5(4.5)	6.5
A·U_WC	0.04(0.34)	−0.14(0.15)	0.04(0.39)	−0.3(8.4)	−9.0(8.7)	0.9(5.2)	6.4
G·U_w	−2.11(0.84)	−0.52(0.27)	−0.04(0.43)	−0.1(8.2)	−7.4(7.5)	−0.6(6.9)	25.1
G·A_s	6.78(0.23)	−4.40(0.55)	0.14(0.52)	1.5(11.0)	−3.2(9.1)	−5.4(8.4)	27.1
A·U_H	−4.06(0.80)	−1.92(0.84)	0.07(0.61)	−0.4(7.3)	1.0(10.8)	−95.1(17.4)	25.9
U·U_w	−2.34(0.59)	−1.63(0.31)	−0.09(0.47)	0.6(8.8)	−11.1(7.8)	−0.2(17.4)	49.8
G·A_WC	0.00(0.64)	1.52(0.40)	−0.29(0.41)	7.8(10.8)	−10.8(9.6)	−17.2(13.5)	86.2

^†Mean values and standard deviations (subscripted values in parentheses) for steps in all helical contexts. Subscripts correspond to designations in Tables 2,3. Parameters defined such that the first of the two bases in a given pair lies in the primary strand I. Values are identical for the reverse pair, defined with respect to the secondary strand II, except that Shear and Buckle are of the opposite sign.

The composite information reveals an intrinsic deformability in the non-canonical pairs beyond that in the Watson-Crick arrangements. The enhancement in deformation stems from greater variation in the three rigid-body parameters — Shear, Stretch, and Opening — that determine the hydrogen-bonding patterns (Table 4). By contrast, the ‘stiffer’ Watson-Crick pairs tend to distort via Stagger, Propeller, and Buckle — the three parameters that control the planarity of associated bases [15]. The hydrogen-bonding pattern is accordingly more variable in the non-canonical than in the canonical pairs. Evidence of this variability appears in the fraction of base pairs with the expected hydrogen-bond pattern (Table 2). Whereas ~90% of the Watson-Crick pairs associate through the expected donor-acceptor patterns, the proportion of non-canonical pairs with the expected patterns is lower, e.g., only 54% of U·U wobble pairs associate through O2···H-N3 and N3-H···O4 interactions. Some of the non-canonical pairs are ‘melted’ in the sense that they form fewer hydrogen bonds, but others make additional donor-acceptor contacts. The units of the rigid-body parameters, i.e., angles expressed in degrees and distance in Ångstrom units, complicate assessment of the relative deformabilities of different base pairs in terms of the accessible conformational volume V. A larger value of V does not necessarily indicate greater overall spatial movement. The root-mean-square deviations of the superimposed images yield the following deformability rankings: U·U__w (0.74 Å) > G·A__WC (0.54 Å) ≈ G·A__s (0.50 Å) > G·U__w (0.45 Å) ≈ A·U__H (0.43 Å) > G·C__WC (0.38 Å) A·U__WC (0.36 Å), a slightly different ordering from the computed values of V (Table 3). Surprisingly, some of the most deformable base pairs occur with greater likelihood in the duplex interior e.g., the U·U wobble pair, and some of the more rigid pairs occur at ‘nicks’ or resemble drug-like inserts, e.g., the A·U Hoogsteen pair. The relative stiffness of the latter arrangements comes at no surprise given the preferential crystallization of free A and U in Hoogsteen pairs [26].

Finally, the non-canonical base pairs have unique deformability profiles partially reflective of the pattern of interaction. For example, G and U tend to fluctuate via Shear along the short, hydrogen-bonded axis of the G·U wobble pair, but G and A tend to slide past one another via Stretch along the long axis of contact between sheared G·A pairs. The A·U Hoogsteen bases move along both axes and rotate in the base-pair plane via Opening. The major fluctuations of the U·U wobble and G·A Watson Crick pairs entail Shear and Opening.

Dimeric structure

The sequences of dimers found within the intact, double-helical stretches of high-resolution RNA structures reveal of the propensity of the non-canonical pairs to stack against canonical G·C and A·U pairs rather than other non-canonical pairs. Of the 91 unique base-pair steps that can be assembled from the seven dominant base-pairing patterns, only 48 occur in the present dataset, with structural examples for only 15 of the 45 possible combinations of consecutive, or tandem, non-canonical pairs (Table 5). The number of non-canonical pairs chemically linked to Watson-Crick pairs is over six times the number of dimers constituted from tandem non-canonical pairs. Some of the non-canonical base pairs, however, occur only in the latter context, e.g., the 5′-UpA-3′ ·5′-GpA-3′ (UA·GA) and 5′-ApG-3′ ·5′-ApU-3′ (AG·AU) dimers made up of an A·U Hoogsteen pair linked to a sheared G·A or A·G pair. Most of the dimers containing tandem non-canonical pairs, however, are constructs of wobble G·U and/or sheared G·A pairs. As expected from the large-number of canonical G·C pairs in the dataset, well over a third of the observed dimers are G·C constructs, and, surprisingly, more than half of these are GG·CC steps.

Table 5.

Populations and overlap of the unique dimers constituted from dominant base pairs within intact RNA helical domains.^†

C·G_WC	G·C_WC	U·A_WC	A·U_WC	U·G_w	G·U_w	A·G_s	G·A_s	U·A_H	A·U_H	U·U_w	A·G_WC	G·A_WC	bpi/bpi+1
6044.5	13354.1	7473.0	5742.9	775.0	1925.3	666.9	--	--	--	182.9	44.8	54.2	G·C_WC
	60811.3	5114.1	5729.9	1612.9	25213.5	3310.0	--	--	--	696.1	208.8	57.7	C·G_WC
		972.0	2493.3	202.8	456.1	77.7	--	--	--	23.6	--	34.3	A·U_WC
			1268.4	482.0	7911.8	69.5	--	--	--	208.2	16.4	145.3	U·A_WC
				315.3	424.1	328.3	15.7	--	--	52.9	--	--	G·U_w
					1114.4	--	--	--	--	--	48.8	79.3	U·G_w
						--	1310.6	--	--	611.1	--	--	G·A_s
							209.1	73.0	23.7	--	--	--	A·G_s
								--	--	--	--	--	A·U_H
									--	--	--	--	U·A_H
										31.7	--	--	U·U_w
											--	16.3	G·A_WC
												--	A·G_WC

^†Dimers limited to the 6755 intact, chemically linked base-pair steps in the interior of RNA helical fragments. Overlap measured by the area, in Ų, shared by the rings of stacked bases [15].

The areas of dimeric overlap, also included in Table 5, confirm the well-known stacking propensities of sequential Watson-Crick pairs [37]. That is, the purine-pyrimidine steps show the greatest stacking overlap and the pyrimidine-purine steps the least. The trend is similar but the stacking is more pronounced when a G·U wobble pair replaces one or both Watson-Crick pairs, with the greatest overlap occurring in self-complementary GU·GU steps. Tandem sheared G·A pairs and dimers constituted from U·U wobble and sheared G·A pairs also show appreciable overlap. The degree of base overlap, however, does not seem to govern the observed populations, e.g., wobble U·U pairs form preferentially next to canonical G·C pairs in relatively unstacked GU·UC (or UC·GU) dimers.

The sequence-dependent variation of base-pair overlap accompanies other subtle changes in dimeric structure. For example, the twist angle between tandem Watson-Crick G·C pairs increases and the bending, via Roll, becomes more negative with greater base-pair overlap, i.e., Twist_CG < Twist_GG < Twist_GC and Roll_CG > Roll_GG > Roll_GC, where CG, GG, and GC denote the sequence of bases on the leading strand of each dimer. Similar differences occur in DNA, albeit over a much wider range of conformational states [34,38]. The sequence-dependent patterns in RNA dimeric structure, illustrated in Figure 4 by atomic-level representations of tandem G·C pairs with the mean step parameters and phosphorus positions found in the current dataset, are less striking than the corresponding differences among the dimeric arrangements of tandem G·U pairs. The non-canonical pair introduces noticeable asymmetry in the sugar-phosphate backbone at the GG·UU step (Figure 4). The phosphorus atom on the G-containing strand is displaced by 1.5 Å and that on the U-containing strand by 1.0 Å relative to the corresponding positions in tandem G·C pairs. Although the phosphorus displacement is smaller and more symmetric, the twist angle differs appreciably in the G·U-containing purine-pyrimidine and pyrimidine dimers compared to their Watson-Crick counterparts, with the GU·GU step overtwisted by 15° and the UG·UG step undertwisted by −12° compared to the GC·GC and CG·CG steps, respectively. Some of these differences reflect the computation of base-pair parameters with respect to a common standard, rather than a series of reference frames, one specific for each non-canonical pair, that minimize the apparent ‘discrepancies’ [12,15,39].

Figure 4.

Images of hydrogen-bonded dimeric fragments illustrating the relative spatial arrangements of tandem G·C Watson-Crick and tandem G·U wobble base pairs and the backbone phosphorus atoms in double-helical RNA structures: (a) GG·CC, GC·GC, CG·CG steps; (b) GG·UU, GU·GU, UG·UG steps. Dimers constructed from the mean base-pair step parameters and (x_P, y_P, z_P) values associated with the given sequences (Table S2 in the Supplementary Materials). Spatial configurations of G·C and G·U pairs are specified by the mean values in Table 4. Bases are depicted by stick figures and phosphorus atoms by filled-in balls in a conventional ‘stacking’ diagram with the numbers denoting the directions of the primary (1→2) and secondary (3→4) strands and the shading the displacement of bases below (light gray) and above (black) the xy plane of each dimer. The x- and y-axes are denoted respectively by the finely dotted vertical and horizontal lines. Major-groove atoms lie on the upper edge and minor/sugar-groove atoms on the lower edge of each base.

Knowledge-based RNA double-helical structure

The images in Figure 5 show how the aforementioned changes in local dimeric geometry contribute to the double-helical structure of RNA. Compared to the local, sequence-dependent features of double-helical DNA, the variation of ribonucleotide sequence has a more subtle effect on chain configuration, e.g., the approximate uniformity of bending angles suppresses strong sequence-dependent curvature. The variation of base-pair step parameters, nevertheless, influences duplex structure. The ribbons of backbone phosphorus atoms associated with the idealized self-complementary G₁₁C₁₁·G₁₁C₁₁ and C₁₁G₁₁·C₁₁G₁₁ ‘block’ co-oligomers describe noticeably different pathways when models — generated from the mean base-pair, dimeric, and (x_P, y_P, z_P) parameters — are superimposed on the central base-pair steps. The small differences in intrinsic bending and twisting of the GC·GC, and CG·CG fragments at the central step, the only building block in each 22-mer with different intrinsic structure, displace corresponding phosphorus atoms at the chain ends by nearly 3 Å. The displacement of phosphorus atoms, in turn, perturbs the groove structure, with the configuration of the GC step widening and that of the CG step narrowing the deep major groove (Figure 6). The shallow, sugar-exposed minor groove shows much less sensitivity to sequence, with the variation in groove width an order-of-magnitude smaller than that of the major groove.

Figure 5.

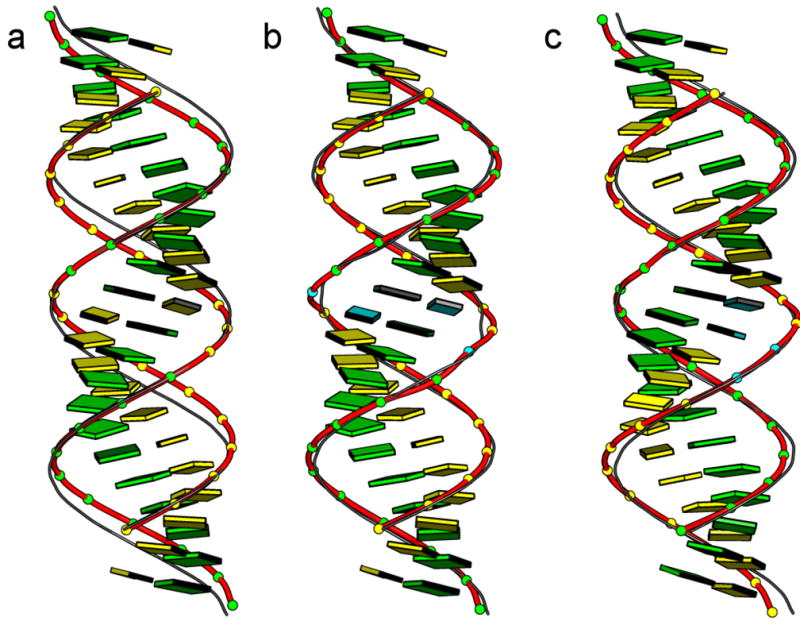
Superposed images illustrating the predicted structural response of double-helical RNA to the mean, sequence-dependent spatial arrangements of the constituent dimers. Changes in groove widths and base accessibilities in related structures are evident from the different styles used to represent the chain backbone: (a) the C₁₁G₁₁·C₁₁G₁₁ ‘block’ oligomer and (b) the C₁₀UG₁₁·C₁₀UG₁₁ pseudo ‘block’ oligomer with central pyrimidine-purine steps compared respectively to their, G₁₁C₁₁·G₁₁C₁₁ and G₁₁UC₁₀·G₁₁UC₁₀ counterparts with central purine-pyrimidine steps; and (c) the G22· C₁₀U₂C₁₀ pseudo homooligomer and the G₂₂·C₂₂ homooligomer with tandem G·U and G·C pairs, respecdtively, at the central purine-purine step. The backbones of the pyrimidine-purine and pseudo homooligomer models are depicted by thick ribbons and filled-in balls on phosphorus and those of the overlapping purine-pyrimidine and homooligomer models by thin ribbons. Images are aligned with respect to the central base-pair step of each structure and oriented such that the minor-groove edge of the central dimer faces the viewer. Bases are depicted for the pyrimidine-purine and pseudo homooligomer chains only. Color coding matches that in Figure 3.

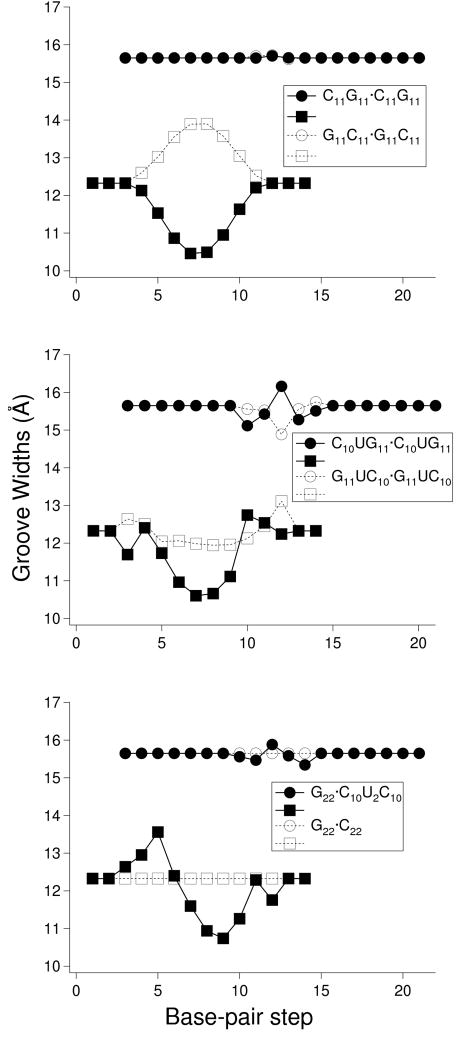
Figure 6.

Variation of RNA groove widths, measured by the shortest interstrand P···P distances, of the double-helical structures illustrated in Figure 5. Minor-groove widths, denoted by circles, correspond to the distances between P atoms at the designated base-pair steps on the leading strand 2 and those at steps once removed on the opposing strand 2, i.e., steps i on strand 1 and i–2 on strand 2. Major-groove widths, denoted by squares, correspond to the distances between P atoms at steps i on strand 1 and i+5 on strand 2.

The introduction of tandem G·U base pairs alters the effect of sequence on helical structure, with corresponding phosphorus atoms on superimposed G₁₁UC₁₀· G₁₁UC₁₀ and C₁₀UG₁₁· C₁₀UG₁₁ ‘block’ co-oligomers less widely separated and with lesser differences in major-groove width compared to the corresponding all-Watson-Crick paired oligomers with GC and CG steps (Figures 5,6). The lesser differences reflect not only the substitution of GU·GU by UG·UG at the central base-pair step but also the sequence-dependent features in the UC·GG or CU·GG dimers at the two flanking steps (Table S2 in Supplementary Materials). Tandem G·U base pairs at GG·UU steps both narrow and widen the major groove, creating a unique recognition motif within the ‘homopolymeric’ sequence G₂₂·C₁₀U₂C₁₀ (Figure 6).

Discussion

This article illustrates how one can gain new insights into RNA folding with computational techniques that analyze high-resolution structures in terms of rigorous, yet intuitively simple spatial parameters and allow for the exact construction of three-dimensional models from the observed values of those quantities. As shown here, the subtle repositioning of bases, base pairs, and phosphates that accompany the replacement of a canonical G·C Watson-Crick base pair by the closely related non-canonical G·U wobble pair perturbs overall double-helical structure, modifying the groove widths while concomitantly altering the chemical structure. The model systems explored to date to study the effects of G·U pairing on RNA helical structures, e.g., octamer duplexes [40,41], are too short to detect sequence-specific changes in groove dimensions. Changes in groove width modulate both the accessibility of the base pairs to external agents and the electrostatic potential associated with the base pair [42], thereby contributing to molecular recognition. Recognition of this sort may play a role in processing the imperfect duplexes formed by miRNA strands and their target RNAs. Base pairs that differ substantially from Watson-Crick arrangements will have pronounced effects on helical structure.

The collective conformational data also hint of sequence-dependent deformability within double-helical RNA. The non-canonical base pairs span a broader range of spatial forms with greater variation in both hydrogen-bonding and rigid-body parameters compared to canonical Watson-Crick pairs. Although some of this variation reflects the structural context in which the pairing occurs, i.e., non-canonical interactions located at the ends or adjacent to ‘nicks’ in the helical structure tend to span a wider range of conformational states, some of the deformability appears to reflect the poor fit of the interacting pairs within the confines of the RNA duplex. For example, the deformations of the U·U wobble pair resemble those of a undersized puzzle piece loosely moving about an oversized area, adopting a wide variety of hydrogen-bonded forms in different attempts to match the available site. The Watson-Crick-like G·A pair, by contrast, is much like an oversized puzzle piece, distorting significantly out of the plane via Stagger and Buckle to squeeze into the available space. Unlike DNA, which can both under- and overwind, double-helical RNA adopts an ‘extreme’ conformational state, the familiar A form, near the outer boundaries of steric accessibility. The non-canonical pairs thus provide the deformability and recognition signals that are difficult to transmit via the naturally ‘stiff’ Watson-Crick pairs.

Finally, the mean values and dispersion of observed conformational parameters provide useful benchmarks for the increasing number of atomic-level simulations of RNA structure. The future promise of these methods in deciphering the folding and dynamics of RNA rests on continuing improvements of the force fields that underlie the calculations. A number of critical properties of double-helical RNA described herein provide useful new checks of the computational predictions. The deformability profiles and patterns of spatial organization offer useful information for algorithms that aim to predict the secondary and tertiary folding of RNA from nucleotide sequence.