Optimizing Monoscopic kV Fluoro Acquisition for Prostate Intrafraction Motion Evaluation

Abstract

Monoscopic kV imaging during radiotherapy has been recently implemented for prostate intrafraction motion evaluation. However, the accuracy of 3D localization techniques from monoscopic imaging of prostate and the effect of acquisition parameters on the 3D accuracy have not been studied in detail, with imaging dose remaining a concern. In this paper we investigate methods to optimize the kV acquisition parameters and imaging protocol to achieve improved 3D localization and 2D image registration accuracy for minimal imaging dose. Prostate motion during radiotherapy was simulated using existing cine-MRI measurements, and was used to investigate the accuracy of various 3D localization techniques and the effect of kV acquisition protocol. We also investigated the relationship between mAs and the accuracy of the 2D image registration for localization of fiducial markers, and we measured imaging dose for a 30-cm diameter phantom to evaluate the necessary dose to achieve acceptable image registration accuracy. Simulations showed that the error in assuming the shortest path to localize the prostate in 3D using monoscopic imaging during a typical IMRT fraction will be less than ~1.5 mm for 95% of localizations, but will also depend on prostate motion distribution, treatment duration, and image acquisition and treatment protocol. Most uncertainty cannot be reduced from higher imaging frequency or acquiring during gantry rotation between beams. Measured maximum surface dose to the cylindrical phantom from monoscopic kV intrafraction acquisitions varied between 0.4–5.5 mGy, depending on acquisition protocol, and was lower than the required dose for CBCT (21.1 mGy). Imaging dose can be lowered by ~15–40% when mAs is optimized with acquisition angle. Images acquired during MV beam delivery require increased mAs to obtain the same level of registration accuracy, with mAs/registration increasing roughly linearly with field size and dose rate.

1. Introduction

Target tracking during radiotherapy has been the subject of much current research in attempt to compensate for target intrafraction motion. Target tracking can be used to limit the dosimetric effect of intrafraction motion by real-time adjustment of the treatment beam to conform to target motion, or by stopping treatment and re-adjusting the patient when the excursion exceeds an action limit. It is also useful for retrospective dosimetric evaluation. Target tracking methods for prostate radiotherapy include using implanted electromagnetic transponders (Kupelian et al., 2007) and using kV and MV projection imaging of implanted fiducial markers (Balter et al., 1995; Kitamura et al., 2002; Aubry et al., 2004; Adamson and Wu, 2008). Electromagnetic transponders and stereoscopic imaging allow for a full 3D localization of fiducial markers, however many clinics rely on monoscopic imaging for image guidance either from electronic portal imaging or from kV imaging using a single kV imager mounted on a linear accelerator gantry as is commercially available from several manufacturers.

Evaluation of prostate intrafraction motion has been recently implemented using fluoroscopy with a gantry mounted kV imager (Adamson and Wu, 2008). In this technique, kV images are acquired of implanted fiducial markers throughout treatment delivery and are registered to template images, providing a 2D localization of the prostate. A 3D localization is then achieved by combining information from kV acquisitions at various gantry angles (Adamson and Wu, 2008; Kotte et al., 2007; Aubry et al., 2004; Mao et al., 2008) or by using a 3D probability distribution (Poulsen et al., 2008). The intrafraction kV fluoro provides positional information throughout treatment delivery that can be supplemental to pre and post localizations using Cone Beam Computed Tomography (CBCT) or ultrasound imaging. Because the technique only requires monoscopic imaging capability, it is applicable in the large number of cancer centers with a gantry mounted kV imager, making use of the already widely available technology.

One of the greatest challenges for intrafraction motion evaluation using monoscopic kV fluoroscopy is achieving acceptable 3D localization accuracy. Each kV acquisition only provides 2D positional information; assumptions must be made to reconstruct a 3D trajectory of each fiducial marker. While the kV acquisitions provide verification of prostate position in 2D during treatment, a 3D localization is desirable for obvious reasons, including improved position verification during treatment and its usefulness for retrospective dosimetric analysis. Combined kV and MV orthogonal imaging for real-time tracking has been recently implemented to eliminate this problem (Wiersma et al., 2008) but requires larger implanted markers to be visible in MV images, causing major artifacts in kV CBCT images. Stereoscopic kV imaging may be used (Kitamura et al., 2002) but requires multiple imagers be installed in the treatment room, negating the benefit of applicability to clinics with single gantry mounted kV imager technology. Yet another alternative is the 2D–3D registration; however this requires more time to perform than a 2D-2D registration making real time tracking more difficult. Also magnification of fiducial markers in the prostate is largely insensitive to out of plane translations for on-board imager geometry.

Another solution is to estimate the 3D position using multiple acquisitions from unique gantry angles. Many methods have been developed to reconstruct a 3D trajectory from monoscopic imaging of prostate, including using the intersection with the preceding 2D localization (Aubry et al., 2004), using a time weighted average of the intersections with consecutive 2D localizations (Adamson and Wu, 2008), assuming the shortest 3D path that satisfies all 2D localizations from the fraction (Kotte et al., 2007), and using a 3D probability density to resolve the out of plane position (Poulsen et al., 2008). However, little is known about the error propagated from many of these methods and no direct comparison has been made between them.

Imaging dose can also be a concern when monoscopic kV fluoroscopy is utilized. Image quality increases with increasing dose, and a balance must be struck between minimizing dose and achieving sufficient image quality. One concern is that the imaging dose becomes excessive when performed on a regular basis (daily or weekly) and when kV intrafraction fluoroscopy is supplemental to CBCT acquisitions. Furthermore, higher dose levels are necessary when imaging is performed during MV beam delivery due to the increased scatter incident at the detector. Finally fluoroscopy dose can be concentrated at specific entrance angles so that the actual dose delivered to the patient is ambiguous and varies greatly by region.

The purpose of this study is to optimize the kV acquisition parameters and imaging protocol to achieve improved 3D localization and 2D image registration accuracy for minimal imaging dose from intrafraction imaging of prostate fiducial markers using a single gantry mounted kV imager. We compare the accuracy of several different 3D localization methods for monoscopic imaging and evaluate the effect of kV acquisition protocol, treatment protocol, and treatment duration. We also relate image registration accuracy to the delivered dose and estimate the dose for various kV acquisition protocols.

2. Methods & Materials

This study was divided into two parts. First, existing cine-MRI measurements of prostate intrafraction motion were used to simulate prostate motion and evaluate the accuracy of the intrafraction 3D localization with various acquisition parameters and 3D localization techniques for monoscopic imaging. Second, anthropomorphic phantom and patient kV acquisitions were used to evaluate the relationship between 2D registration error and mAs; the resulting imaging dose to achieve a given 2D registration accuracy criteria was estimated using central and surface dose measurements to a 30 cm diameter cylindrical phantom. The combination of the simulation study and the imaging dose study allow us to couple 2D registration accuracy and 3D localization accuracy with the estimated imaging dose for various intrafraction acquisition protocols.

2.1. Simulation Study

Monoscopic intrafraction motion evaluation was simulated using patient cine-MRI measurements as the prostate motion and with simulated kV acquisitions using a monoscopic gantry mounted imaging system during a radiotherapy treatment fraction. This study was performed to (1) quantify the 3D localization error to be expected when monoscopic imaging is used for prostate intrafraction motion evaluation, (2) compare accuracy of various 3D localization methods (including both retrospective and on-line methods), and (3) identify effective acquisition techniques to minimize the 3D localization error. By “3D localization methods” we refer to techniques of estimating the 3D position for monoscopic imaging rather than a direct measurement of the position in 3D.

Prostate intrafraction motion in the anterior-posterior (AP) and superior-inferior (SI) axes measured using sagittal cine-MRI was available to simulate the prostate motion (Ghilezan et al., 2005). The data set is summarized in Table 1. For each MRI image, positional measurements were made of 7 prostate points of interest. The total data set consisted of 490 point of interest tracks each approximately 8 minutes in length, for a total of 39183 point measurements. Right-left (RL) axis intrafraction motion was not measured using cine-MRI. Previous studies have shown that prostate motion in the RL-axis is small and is largely independent of the motion in other axes (Langen et al., 2008; Kupelian et al., 2007; Zelefsky et al., 1999). To evaluate the effect of the unmeasured RL motion on localization uncertainty, the simulation study was conducted with and without incorporating random RL motion from a normal distribution centered at zero with various standard deviations.

Table 1.

Summary of cine-MRI measurements of prostate intrafraction motion. The cine-MRI measurements were used to simulate prostate motion during treatment delivery.

cine-MRI data summary (Ghilezan et al., 2005)
number of patients	5
sessions per patient	2–3
acquisitions per session	5
acquisition length	~8 min
number of prostate points of interest	7
time between measurements	6 s
image orientation	sagittal*
total number of point of interest tracks	490
total number of measured points	39183

^*right-left axis motion was not measured

For each set of simulation parameters, all acquisitions in Table 1 were used to simulate prostate motion during the treatment fraction. Due to the random nature of prostate intrafraction motion and because for most cases the kV acquisitions were simulated only intermittently, multiple simulations of prostate motion throughout the treatment fraction could be achieved for each point of interest track by staggering the fraction starting time every 24 seconds and assuming a perfect target alignment before treatment. For fractions lasting ~7.5 minutes this resulted in 3 simulated trajectories per track, while shorter fraction durations resulted in a greater number of simulated prostate trajectories per acquisition. One simulation was performed with a treatment duration of 15.1 minutes, for which two prostate motion tracks from separate MRI sessions were spliced together to simulate prostate motion.

The simulated apparatus was a linear accelerator with a gantry mounted kV imager. The apparatus has been previously described in detail (Jaffray et al., 2002; Letourneau et al., 2005) and consists of a kV x-ray source and flat panel imager mounted opposite each other on the gantry orthogonal to the MV source. A standard IMRT plan consisting of 7 equispaced beams was used as the default treatment protocol, although other treatment protocols were simulated including a 5 equispaced beam arrangement and a Volumetric Modulated Arc Therapy (VMAT) fraction consisting of a slowly continuously rotating gantry. For the 7-beam arrangement a gantry speed of 0.5 revolutions / minute was assumed with treatment at each beam lasting 50 seconds for an overall treatment duration of ~7.5 minutes. The effect of treatment duration was also examined by decreasing the interval spent at each beam. For the intrafraction motion measurement, kV acquisitions were simulated at various times throughout the treatment process. The kV acquisition schedules included 1–5 acquisition(s) per treatment angle, both including and excluding acquisitions during gantry rotation, and acquiring at a set imaging frequency throughout the fraction using various frequencies.

3D localizations were reconstructed from the simulated kV acquisitions using a number of 3D localization methods. First, we examined using the intersection with the immediately preceding 2D localization that was acquired at a different gantry angle (Aubry et al., 2004). This method is perhaps the most intuitive: it assumes no motion between acquisitions at consecutive gantry angles. Ignoring SI-axis localization, for consecutive (and unique) gantry angles, monoscopic imaging will localize the prostate as two lines in the AP-RL plane. This method assumes the prostate position to be the intersection of these two lines. We refer to this method as “Intersection with Preceding Localization”. The second 3D localization method we examined uses a time weighted average of the intersections with consecutive (preceding and subsequent) 2D localizations from unique gantry angles. This is similar to the first method, but also takes into account the subsequent as well as previous gantry angle. It is described in more detail in a previous paper (Adamson and Wu, 2008), and we refer to it as “Average of Intersection with Consecutive Localizations”.

We also examined assuming the shortest path that satisfies all 2D localizations from the fraction. In an Appendix to their paper, Kotte et al. provide a set of linear equations that can be solved to find the shortest path solution (Kotte et al., 2007). We refer to this method as “Shortest Path”. The set of linear equations given by Kotte et al. can be modified to include full 3D localization information from volumetric imaging before and after the fraction. We evaluated the improvement in the 3D localization when assuming the shortest path and incorporating pre- and post-treatment 3D positions being known from volumetric imaging, and refer to this method as “Shortest Path + Pre & Post”.

Paulson et al. recently described in detail a method to use a 3D probability density to resolve the out of plane position for monoscopic imaging (Poulsen et al., 2008). This method uses a population probability distribution and utilizes the correlation between motion in the AP and SI axes for prostate. Each 2D localization represents a line in 3D space, and the point on the line with the highest population probability density is assumed to be the correct position. We implement their 3D localization method using the 3D Gaussian distribution calculated from the full cine-MRI data set from Table 1 with the corresponding input noise in the lateral axis, and we refer to this method as “3D Probability Density”.

It should be noted that the “Intersection with Preceding Localization” method and the “3D Probability Density” method can be performed real-time, while the “Average of Intersection with Consecutive Localizations” method is strictly retrospective because calculating the 3D position requires both the preceding and subsequent 2D localizations. The “Shortest Path” method is also retrospective because it calculates each 3D position using all 2D localizations from the fraction; however it may be adapted for real-time 3D localization when each 3D position is calculated using past and present 2D localizations only. We examine this case as well, and refer to it as “Shortest Path Real-Time”.

For each kV fluoroscopy acquisition the 3D localization error was quantified as the distance between the measured and actual (simulated from cine-MRI) fiducial position at the time of measurement. Only the position of the prostate at the time of the simulated kV fluoroscopy acquisitions was included in the error analysis.

2.2. Imaging Dose Evaluation

We estimated the necessary mAs and resulting imaging dose to achieve a desired level of accuracy in the 2D image registration of the prostate intrafraction motion evaluation. This study was performed to estimate (1) the required imaging dose for the intrafraction motion evaluation, (2) the dose reduction achievable when mAs is adjusted with acquisition angle, and (3) the additional imaging dose required for localization due to MV scatter when images are acquired during MV beam delivery.

For this study, kV images were automatically registered to template images derived from a CBCT where each template image is a digitally reconstructed radiograph (DRR) of the implanted markers. The image processing and automatic registration has been previously described in detail (Adamson and Wu, 2008), only a brief summary is given here. Image processing was performed on both the acquired kV images and the template images and included a gradient and smoothing. All implanted markers were registered collectively using a rigid 2D registration (including rotation) of a region of interest around the markers with cross correlation being the scoring function. All kV acquisitions were acquired using an Elekta Synergy and an Elekta Axxesse. Because clinically both CBCT and kV acquisitions for the intrafraction evaluation are acquired during the same fraction, no change in collimation or filtration was made; with the kV panel offset by 11.5 cm and the kV beam collimated to 20.7×41.0 cm² at the isocenter for all kV acquisitions. A setting of 120 kVp and a bowtie filter were used for all acquisitions. The flat panel imager used had 512×512 pixels with dimensions 0.518×0.518 mm² at the isocenter.

Analysis was first performed using an anthropomorphic phantom to investigate the relationship between mAs and 2D registration accuracy, and to evaluate the effect of MV scatter. KV projection images were acquired of the phantom with 3 radiopaque gold coils (Visicoil, Radiomed) placed in the prostate area to simulate patient geometry. The coils have a diameter of 0.35 mm and were used for both the phantom and patients. Images were acquired with varied mAs/frame both at an acquisition angle θ, of 0° (anterior-posterior projection) and 90° (lateral projection), representing the best and worst imaging geometry, respectively, where θ = G + 90° and G is the gantry angle. 150–200 frames were acquired at each setting of mAs/frame. KV images were acquired at θ = 90° both with and without the MV beam on, at various settings for MV beam delivery. Because the 2D registration was performed of each fluoroscopy image and a template image derived from the CBCT, and because no phantom motion occurred between the CBCT and fluoroscopy acquisitions, the expected offset for the registrations was 0.

Determining the necessary mAs/registration to achieve a desired registration accuracy is increasingly complex when kV images are acquired and the MV beam is delivered concurrently. Among other factors it will depend on MV beam dose rate, field size, and photon energy, as well as the gantry angle G, patient geometry, and distance from isocenter to the kV detector. The ability to acquire images during MV delivery is not as important when step-and-shoot or static IMRT is employed where kV images may be acquired during MLC movements between segments with no MV contamination. However when dynamic or sliding window IMRT is employed no such breaks in MV delivery occur. If for any case pre & post beam acquisitions are considered insufficient, kV images will need to be acquired during dynamic IMRT. Acquisition during MV delivery will also be important for VMAT delivery, where dose rate and gantry rotation are modulated throughout a treatment arc. We acquired kV images of the anthropomorphic phantom at θ = 90° to investigate the effect of MV beam dose rate, energy, and field size. For our apparatus, the distance from isocenter to kV imaging detector was fixed at 53.6 cm.

Clinically acquired kV projection images of patients were used to estimate the mAs/frame & imaging dose required clinically to achieve a desired level of 2D registration accuracy. The patient image data used is summarized in Table 2, and included CBCT projection images and kV fluoroscopy images. The fluoroscopy images were acquired during step-and-shoot IMRT, resulting in MV scatter being present in some images. The frames with MV scatter were detected using a mean pixel value thresholding technique (Adamson and Wu, 2008) and were excluded from analysis. Image acquisitions from 10 patients were included in this part of study.

Table 2.

Summary of clinically acquired kV images used to assess image registration accuracy vs. mAs/registration. Image acquisitions were included from 10 patients.

acquisition type	# frames averaged per registration	mAs / registration	# acquisitions used	total registrations
CBCT projection images at 1.6 mAs/frame (650 projections per CBCT)	1	1.6	2 per patient	12866
	2	3.2	4 per patient	12887
kV fluoroscopy images at 0.16 mAs/frame (150–200 frames per acquisition acquired at 5–7 distinct gantry angles)	1	0.16	2 per patient	12152
	3	0.48	9 per patient	12976
	6	0.96	max per patient (10–20)	8098

Some prostate motion will occur during CBCT acquisition and between the fluoroscopy acquisition and the CBCT acquisition, which makes the expected registration displacement ambiguous. For CBCT projection images, the CBCT acquisition time is relatively short (~2 minutes), and we disregard prostate motion and assume the expected registration displacement of CBCT projection images to the template images derived from the same CBCT to be zero. However, the fluoroscopy images are acquired at each beam angle so that a large time gap occurs between fluoroscopy acquisition and CBCT acquisition. For this case we minimize the effect of prostate motion by assuming the expected registration displacement in each axis to be the median displacement for all registrations from fluoroscopy images acquired at the same beam. Registration error was defined as the vector displacement from the expected.

We attempt to model the relationship between mAs/registration, m, and the probability, p, that a 2D registration will be within a threshold distance from the expected. The relationship between p and ln(m) resembles a sigmoid curve with p equal to 0 when ln(m) is −∞, with p increasing to 1 when ln(m) is ∞. The logit function can often be used to transform sigmoidal curves to be linear for use in least squares fitting. In this case p is transformed to ln(p / (1 − p)). We assume the relationship between ln(m) and ln(p / (1 − p)) is linear and model the relationship between m and p as:

$$\text{ln}\left(\raisebox{1ex}{$p$}\!\left/ \!\raisebox{-1ex}{$1-p$}\right.\right)=a(x,\theta )\times \text{ln}(m)+b(x,\theta )$$ (1)

where x is the error threshold and θ is the kV acquisition angle. The values of a(x, θ) and b(x, θ) are found using least squares fitting for each x and θ. According to the model, the probability of registration error being less than x for an image acquired at θ with m mAs is:

$$p(m,x,\theta )=\frac{1}{1+\text{exp}[-a(x,\theta )\times \text{ln}(m)-b(x,\theta )]}$$ (2)

It should be noted that a(x, θ) and b(x, θ) will also depend upon the scatter incident at the detector when MV radiation is also present. We may also express equation 1 as:

$$m(p,x,\theta )=\text{exp}\left[\frac{1}{a(x,\theta )}\left(\text{ln}\left(\raisebox{1ex}{$p$}\!\left/ \!\raisebox{-1ex}{$1-p$}\right.\right)-b(x,\theta )\right)\right]$$ (3)

Here m(p, x, θ) is the mAs to achieve a proportion p of registrations within x mm of the expected for acquisitions at angle θ.

The anthropomorphic phantom data was used to test the linearity of ln(p / (1 − p)) vs. ln(m) and evaluate the goodness of fit for the model in equations 1–3. The clinically acquired patient images were then used to calculate population values of a(x, θ) and b(x, θ), and estimate the necessary mAs to achieve 95% of registrations within 1 and 2 mm, at various values of θ with no MV scatter.

To couple mAs with imaging dose, a method was developed to calculate the center and surface dose to a cylindrical 30-cm diameter acrylic phantom due to kV acquisitions with any combination of mAs and θ. The dose/mAs due to 1 kV acquisition was measured at the phantom center and along the phantom surface at 5° increments. For the measurement, the couch was not in the beam and due to symmetry the measurements could be used to calculate the dose from any combination of kV acquisitions given θ and mAs. A farmer chamber was used with a calibration coefficient for the kV range from an Accredited Dosimetry Calibration Laboratory (ADCL). The surface dose calculation method was verified by comparing surface dose calculations with point measurements for a CBCT acquisition, which were in agreement to within 0.5%.

3. Results

3.1. Simulation Study

Table 3 is a summary of the results for the simulation study, showing the parameters of each simulation and the resulting 3D localization measurement error. Error in the SI-axis was negligible for all cases and hence was not included in the table. Simulation 1 in the table serves as a reference for comparison with the other simulated intrafraction motion evaluations.

Table 3.

Summary of simulation study using cine-MRI measurements as prostate intrafraction motion. T is the time between kV acquisitions. SI-axis root mean square error was negligible for all cases and hence was not included in the table.

simulation #	treatment protocol	kV acquisition schedule	treatment duration	right-left input noise	3D localization method	root mean square error (mm)			percentile of vector error (mm)
			(min)	σ (mm)		RL	AP	Vect.	90%	95%	99%
1	7 beam IMRT	1 per beam	7.5	0.50	shortest path	0.53	0.55	0.76	1.16	1.48	2.40
2	7 beam IMRT	1 per beam	7.5	0.00	shortest path	0.35	0.46	0.58	0.85	1.19	2.15
3	7 beam IMRT	1 per beam	7.5	0.25	shortest path	0.40	0.49	0.63	0.94	1.24	2.14
4	7 beam IMRT	1 per beam	7.5	0.75	shortest path	0.68	0.63	0.93	1.50	1.87	2.63
5	7 beam IMRT	1 per beam	7.5	0.50	shortest path + pre & post	0.49	0.54	0.73	1.13	1.40	2.27
6	7 beam IMRT	1 per beam	7.5	0.50	shortest path real-time	0.61	0.74	0.96	1.39	1.89	3.18
7	7 beam IMRT	1 per beam	7.5	0.50	av. of intersection with consecutive loc.	0.65	0.56	0.86	1.33	1.68	2.72
8	7 beam IMRT	1 per beam	7.5	0.50	intersection with preceding localization	0.71	0.78	1.06	1.57	2.04	3.64
9	7 beam IMRT	1 per beam	7.5	0.50	3D probability density	0.45	0.81	0.93	1.42	1.90	3.11
10	7 beam IMRT	1 per beam	1.9	0.50	shortest path	0.43	0.39	0.59	0.94	1.16	1.68
11	7 beam IMRT	1 per beam	3.8	0.50	shortest path	0.47	0.47	0.66	1.04	1.29	1.97
12	7 beam IMRT	1 per beam	15.1	0.50	shortest path	0.63	0.70	0.94	1.43	1.84	3.16
13	7 beam IMRT	2 per beam (pre and post MV delivery)	7.5	0.50	shortest path	0.53	0.53	0.75	1.17	1.46	2.25
14	7 beam IMRT	5 per beam (acq. between segments)	7.5	0.50	shortest path	0.55	0.55	0.78	1.21	1.50	2.37
15	7 beam IMRT	5 per beam + gantry rotation (T = 6s)	7.5	0.50	shortest path	0.53	0.53	0.74	1.18	1.45	2.13
16	7 beam IMRT	continuous (T = 6 s)	7.5	0.50	shortest path	0.51	0.51	0.72	1.13	1.39	2.03
17	7 beam IMRT	continuous (T = 30s)	7.5	0.50	shortest path	0.58	0.53	0.78	1.20	1.52	2.39
18	7 beam IMRT	continuous (T = 60s)	7.5	0.50	shortest path	0.55	0.55	0.79	1.23	1.56	2.45
19	5 beam IMRT	1 per beam	6.0	0.50	shortest path	0.51	0.54	0.74	1.16	1.46	2.26
20	VMAT	continuous (T = 6s)	4.0	0.50	shortest path	0.44	0.41	0.60	0.93	1.17	1.82

Simulations 1–4 in Table 3 show the effect of adding random motion in the RL axis. Because motion in the RL axis was not measured using cine-MRI, motion was simulated using a normal distribution with various standard deviations, σ. The added random noise increased the 3D localization error in both the RL and AP axes. Because some motion will occur in the RL axis clinically, an input σ of 0.50 mm was used for the reference simulation. This value is on the same order as those reported by Kotte (σ_intra = 0.4 mm) and Litzenberg (σ_intra = 0.18 mm), however our simulated RL motion is time independent which is almost certainly not the case (Langen et al., 2008; Kotte et al., 2007). Because of this, our use of 0.50 mm for the input σ will likely exaggerate the 3D localization error.

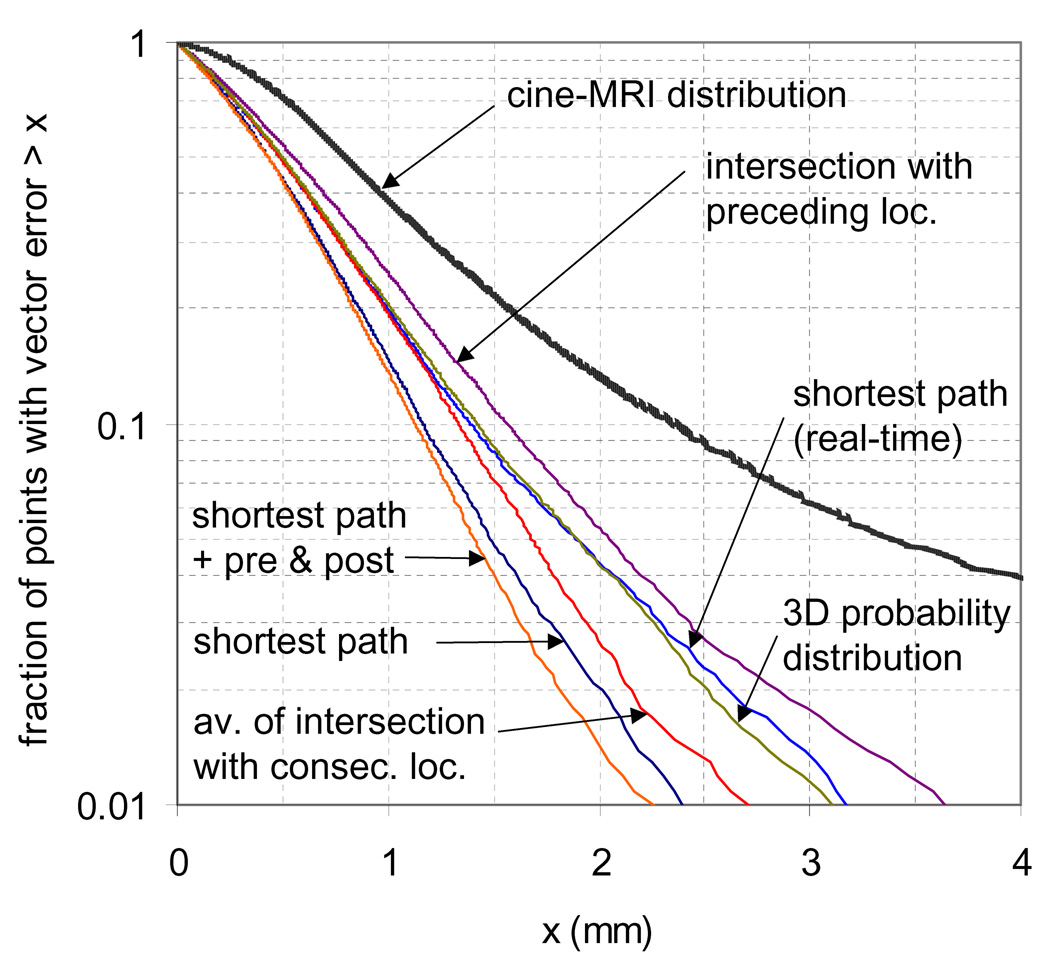
Simulations 1 and 5–9 in Table 3 compare the measurement error of each 3D localization method. The fraction of measurements with vector error less than a threshold x is plotted for these same simulations in Figure 1. Also plotted in the figure is the distribution of the cine-MRI simulated motion for a 7.5 minutes treatment, with an input σ_RL of 0.5 mm, and correcting to zero at treatment initiation. The cine-MRI distribution shown is the vector displacement in the AP and RL axes (SI displacement excluded). Of all the 3D localization methods, assuming the shortest path satisfying all 2D localizations yielded the most accurate results (95% within 1.5 mm), and was slightly improved when the pre and post 3D position could also be incorporated (95% within 1.4 mm). Of the 3D localization methods that can be used for real-time analysis, assuming the shortest path and using a 3D probability distribution both performed similarly (95% within 1.9 mm).

Figure 1.

Localization error from cine-MRI motion simulation & cine-MRI motion distribution using various 3D localization techniques. The cine-MRI distribution shown is the vector displacement from the expected in the AP and RL axes, with σ_RL = 0.5 mm

Simulations 1, and 10–12 of Table 3 compare the 3D localization error for various treatment durations, and show an error increase with increasing treatment duration. For the same simulations Table 4 shows the standard deviation of the distribution of simulated and measured points, and shows larger simulated motion distributions for increased treatment duration. Hence the 3D localization uncertainty for monoscopic imaging is dependant upon the underlying prostate motion distribution, and any decrease in treatment duration will lead to a smaller distribution of prostate intrafraction motion and a more accurate 3D localization. When utilizing the 3D localization uncertainties reported here, any knowledge about the expected prostate motion distribution should be taken into consideration and compared to the distributions of the simulated motion in Table 4. Also given in Table 4 for comparison is the distribution of prostate intrafraction motion for the 8 minute tracks of 11 patients measured with implanted electronic transponders (Litzenberg et al., 2006).

Table 4.

Standard deviation in each axis of the simulated and measured prostate position for simulations 1, and 10–12 from Table 3. Also given is the distribution of prostate intrafraction motion measured using electromagnetic transponders (Litzenberg et al., 2006).

	simulation 1		simulation 10		simulation 11		simulation 12		σIntra from
	t = 7.5 min		t = 1.9 min		t = 3.8 min		t = 15.1 min		Litzenberg
	sim.	meas.	sim.	meas.	sim.	meas.	sim.	meas.	t = 8 min
σRL (mm)	0.5	0.5	0.5	0.4	0.5	0.5	0.5	0.6	0.2
σAP (mm)	1.7	1.5	0.9	0.9	1.2	1.1	2.6	2.4	0.8
σSI (mm)	1.4	1.4	0.8	0.8	1.0	1.0	1.9	1.9	1.2

Table 4 also shows that a small bias exists for AP-axis data measured using monoscopic imaging and assuming the shortest path. Intrafraction motion measurements made by EPID or kV imaging using the shortest path assumption may result in estimates of the intrafraction motion that are slightly smaller than actual. No bias is seen in the SI-axis, since errors from 3D localization in this axis are negligible.

Simulations 1 and 13–15 in Table 3 compare the 3D localization accuracy of various kV acquisition schedules. This compared the effect of excluding (simulation 14) and including (simulation 15) kV acquisitions during gantry rotation. Differences due to the number of kV acquisitions per beam and acquiring during gantry rotation between beams had a negligible effect on the 3D localization accuracy.

The effect of acquisition rate on the 3D localization accuracy is summarized by simulations 16–18 of Table 3. For these simulations, a constant acquisition rate was used throughout the treatment fraction. Here we show the results for a period between acquisitions, T, of 6, 30, and 60 seconds. There was little improvement in 3D localization accuracy with decreasing T, which may be because much of the 3D localization error is inherent and cannot be recovered by an increased acquisition rate. It should be noted that the cine-MRI measurements from which the simulated motion was derived had an imaging period of 6s, and hence motion of higher frequencies was disregarded.

The effect of treatment protocol on the 3D localization was also evaluated; its effect is summarized by simulations 1, 19, and 20 in Table 3. We compared the 7 beam IMRT treatment protocol to a 5 beam IMRT treatment protocol. While the 5 beam protocol required less delivery time it also included fewer acquisitions at unique θ. The result was a negligible difference in 3D localization accuracy. Simulation 20 consisted of a slowly rotating gantry with acquisitions every 6 seconds, representing a VMAT treatment technique. The short treatment duration, relatively high acquisition rate, and a constantly rotating gantry lead to an improvement in 3D localization accuracy.

3.2. Imaging Dose Evaluation

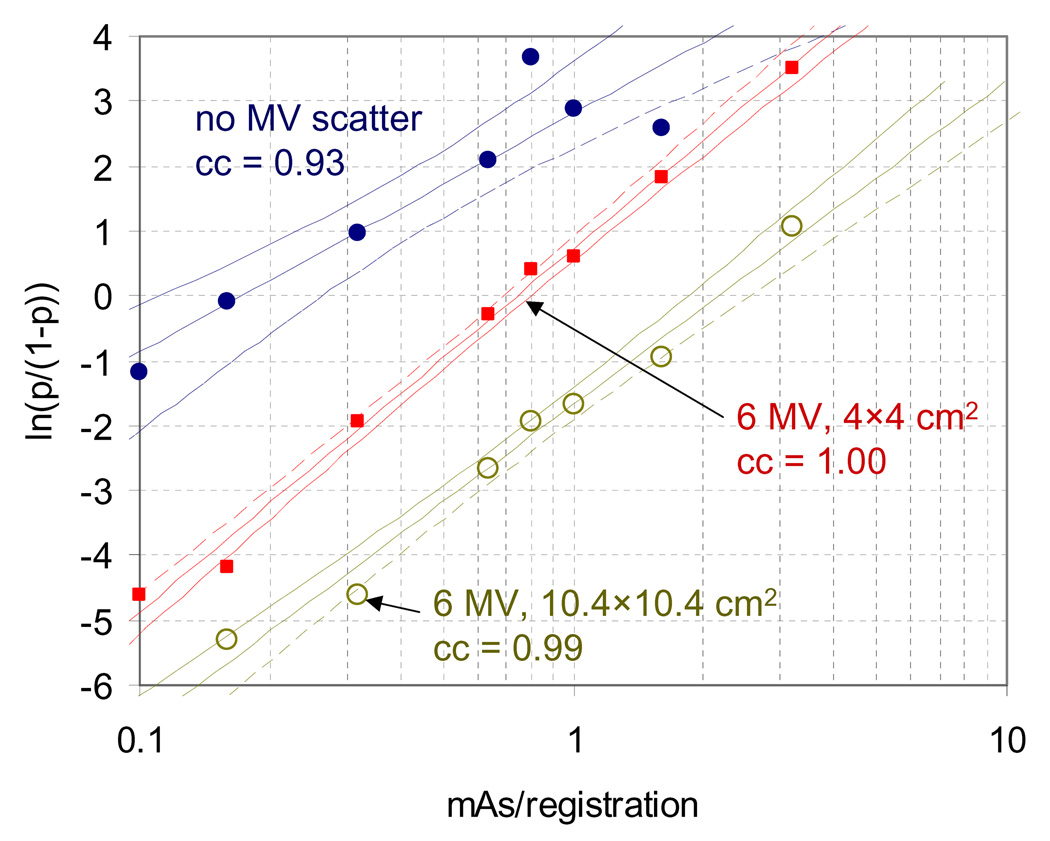
Analysis of the kV acquisitions of the anthropomorphic phantom demonstrated that the relationship between ln(p/(1−p)) and ln(m) was highly linear, as shown in Figure 2 for x = 1 mm with various acquisition settings. Also shown are the 95% confidence interval and the correlation coefficient (cc) for each curve.

Figure 2.

Plot of ln(p/(1−p)) vs. mAs/registration using kV acquisitions of an anthropomorphic phantom with implanted fiducial markers. Measured values and least squares fits from equation 1 are shown for kV acquisitions with no MV scatter, scatter from 6 MV photons delivered at 445 mu/min collimated to 4×4 cm², and scatter from 6 MV photons delivered at 445 mu/min collimated to 10.4×10.4 cm². 95% confidence intervals and correlation coefficients (cc) are also shown for each fit.

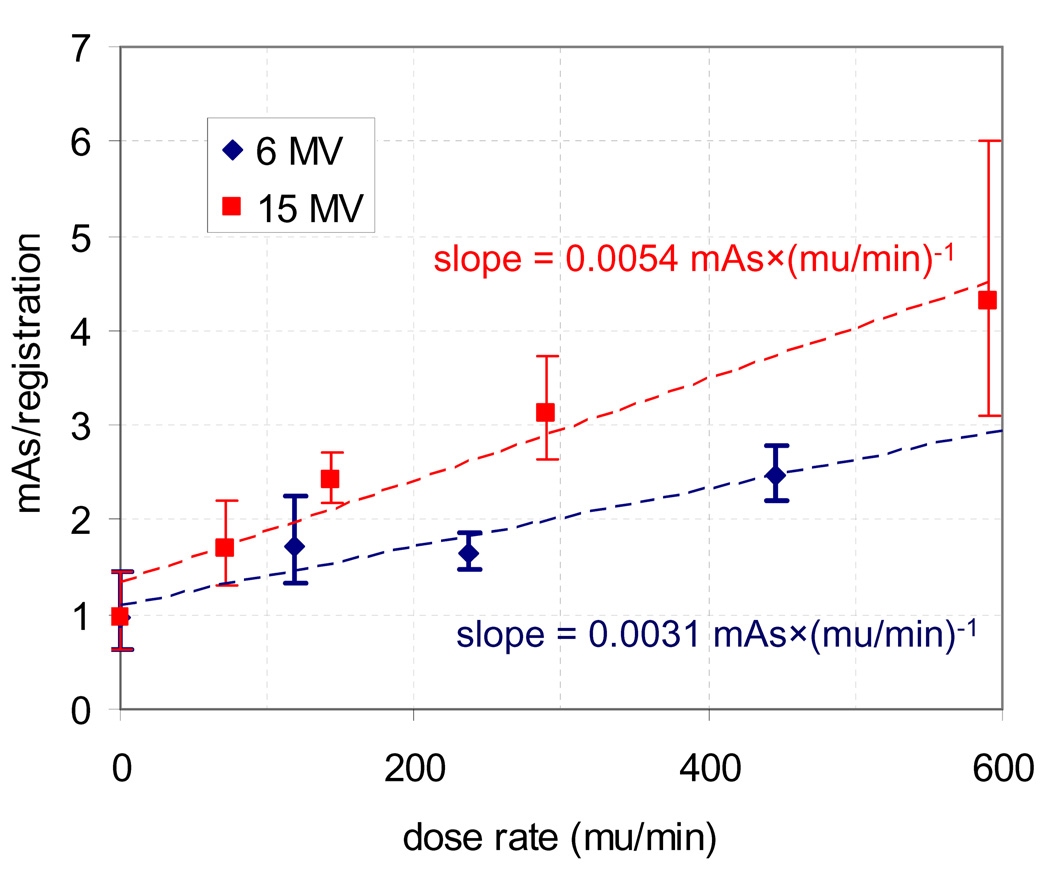
Figure 3 shows the necessary mAs to achieve 95% of registrations with error less than 1 mm as a function of dose rate for 6 and 15 MV. A field size of 4×4 cm² was used with θ = 90° for all acquisitions, and each point was calculated from the phantom data using equation 3 with distinct values of a and b for each dose rate. Also shown is the 95% confidence interval for each point and a linear fit for each energy. Although the relationship between required mAs/registration and dose rate did have a non-linear component for 15 MV, it can be roughly estimated as being linear as shown in the figure. As seen here, for lateral kV acquisitions of the anthropomorphic phantom the required mAs/registration to achieve 95% of registrations within 1 mm increased from 1.0 to 2.5 when MV scatter was introduced from a 6 MV beam at a dose rate of 445 mu/min and a field size of 4×4 cm². The estimated slopes were 0.0054 mAs×(mu/min)⁻¹ for 15 MV and 0.0031 mAs×(mu/min)⁻¹ for 6 MV, however the relationship may likely vary as patient geometry and θ are varied.

Figure 3.

Effect of dose rate on the necessary mAs/registration to achieve 95% of registrations with error less than 1 mm. For each energy a field size of 4×4 cm² was used with θ= 90°.

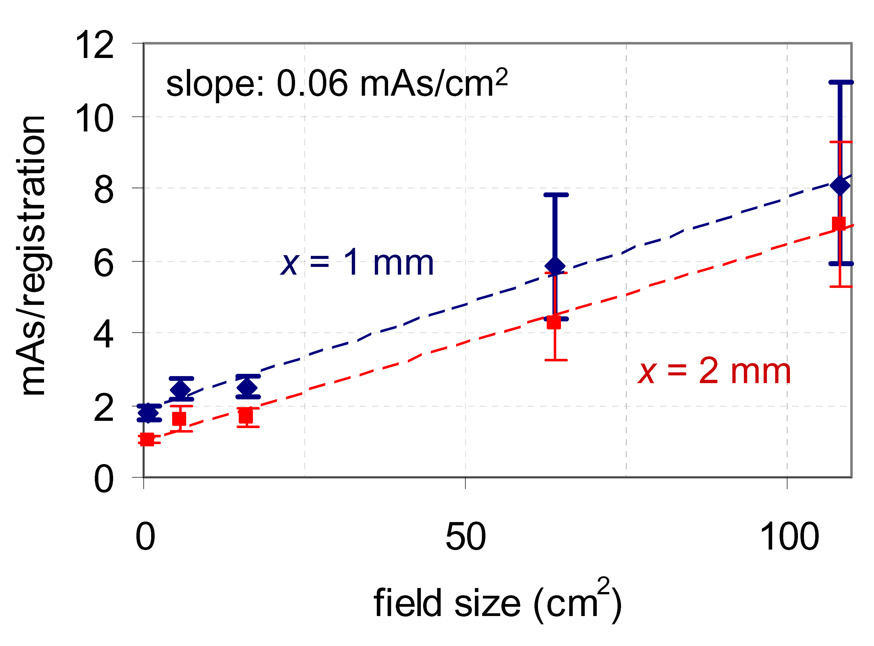
The effect of field size is shown in Figure 4 for scatter from 6 MV photons delivered at 445 monitor units (mu) per minute. Here a dose rate of 445 mu/min was used with θ = 90° for all acquisitions, and each point was calculated from the phantom data using equation 3 with distinct values of a and b for each field size. The plot shows an approximately linear relationship exists between field size and necessary mAs/registration. The slope for this case was measured to be ~0.06 mAs/cm² for accuracy criteria of 95% within 1 and 2 mm, however the effect may likely vary on a case by case basis for other energies, patient geometries, and acquisition angles.

Figure 4.

Effect of field size on the necessary mAs/registration to achieve 95% of registrations with error less than x for 6 MV photons delivered to the phantom at 445 mu/min with θ = 90°.

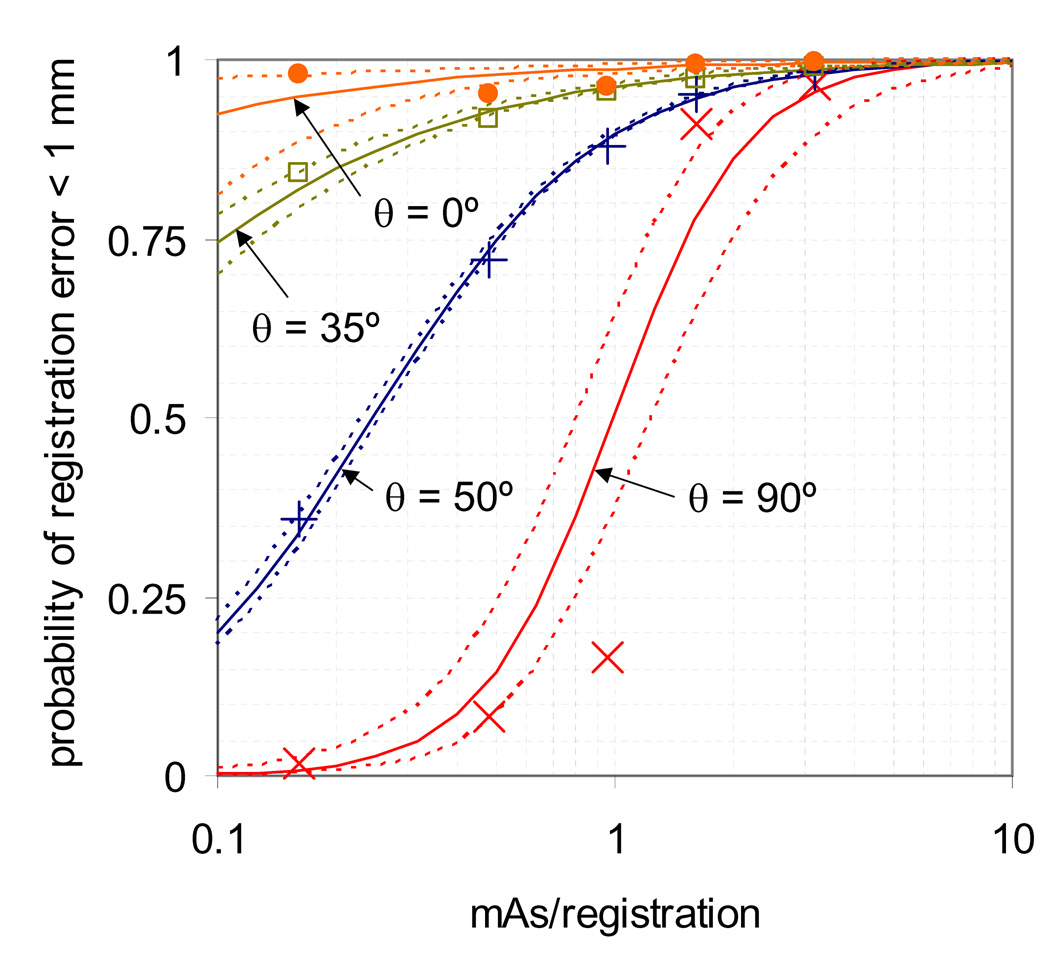
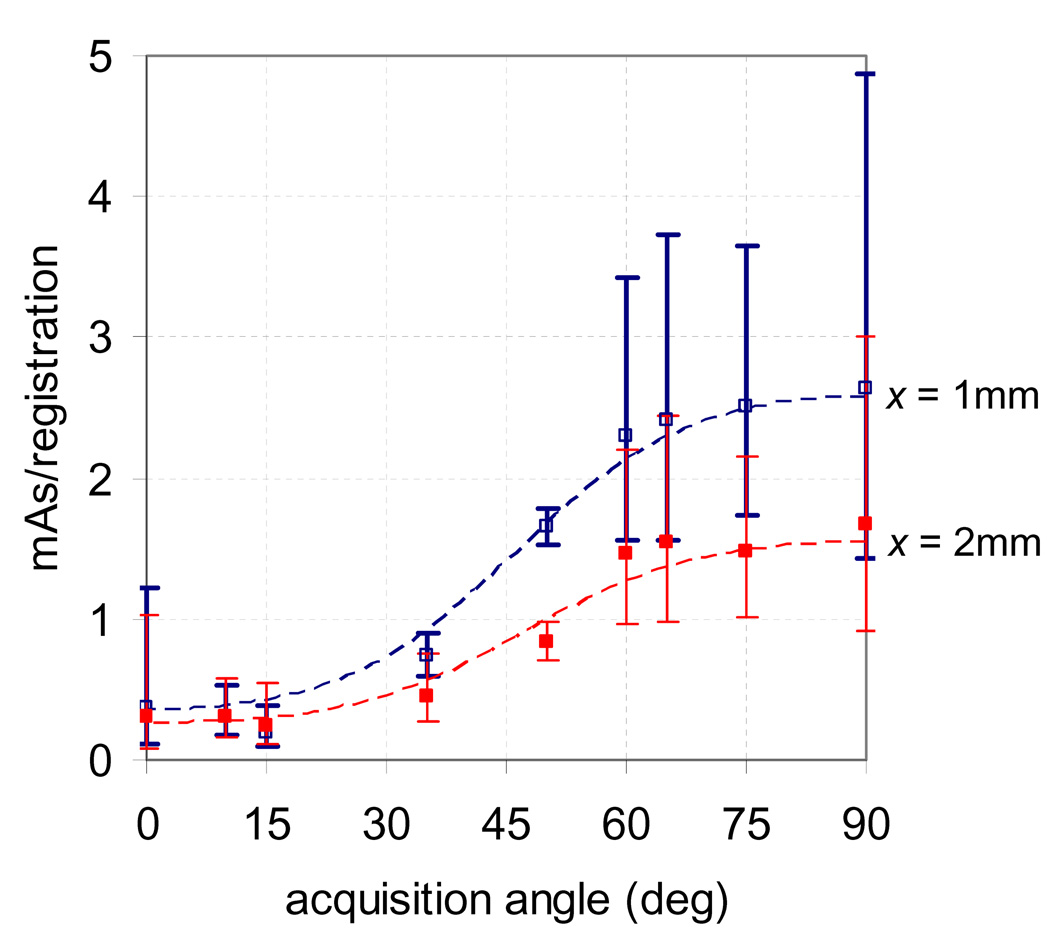
Plotted in Figure 5 is the probability of registration error less than 1 mm vs. mAs/registration with the corresponding model from equation 2 for the patient data at various values of θ. The 95% confidence intervals for the model are also shown. The patient data fit the model from equations 1–3 well, with correlation coefficients (cc) between 0.94 and 1.00, with the exception of at θ= 0°, where cc = 0.72 and all measurements of p were ≥ 0.95. The model was then used to estimate the necessary mAs to achieve 95% of registrations within 1 and 2 mm for various θ, and is shown in Figure 6 with corresponding 95% confidence intervals. The required mAs was largest for lateral projections (θ= 90°) and smallest for anterior and posterior projections (θ= 0°) and ranged between 0.2 and 2.6 for x = 1 mm and between 0.2 and 1.7 for x = 2 mm.

Figure 5.

Proportion of registrations within 1 mm of expected as a function of mAs/image, with the corresponding model from equation 2. Data is shown for patient acquisitions with the MV beam off at various values of acquisition angle θ. Also given is the 95% confidence interval of each fit.

Figure 6.

Estimated necessary mAs to achieve 95% of registrations with error less than 1 and 2 mm, as predicted using patient data. A kV acquisition angle of 0° corresponds to anterior-posterior acquisitions while 90° corresponds to lateral acquisitions.

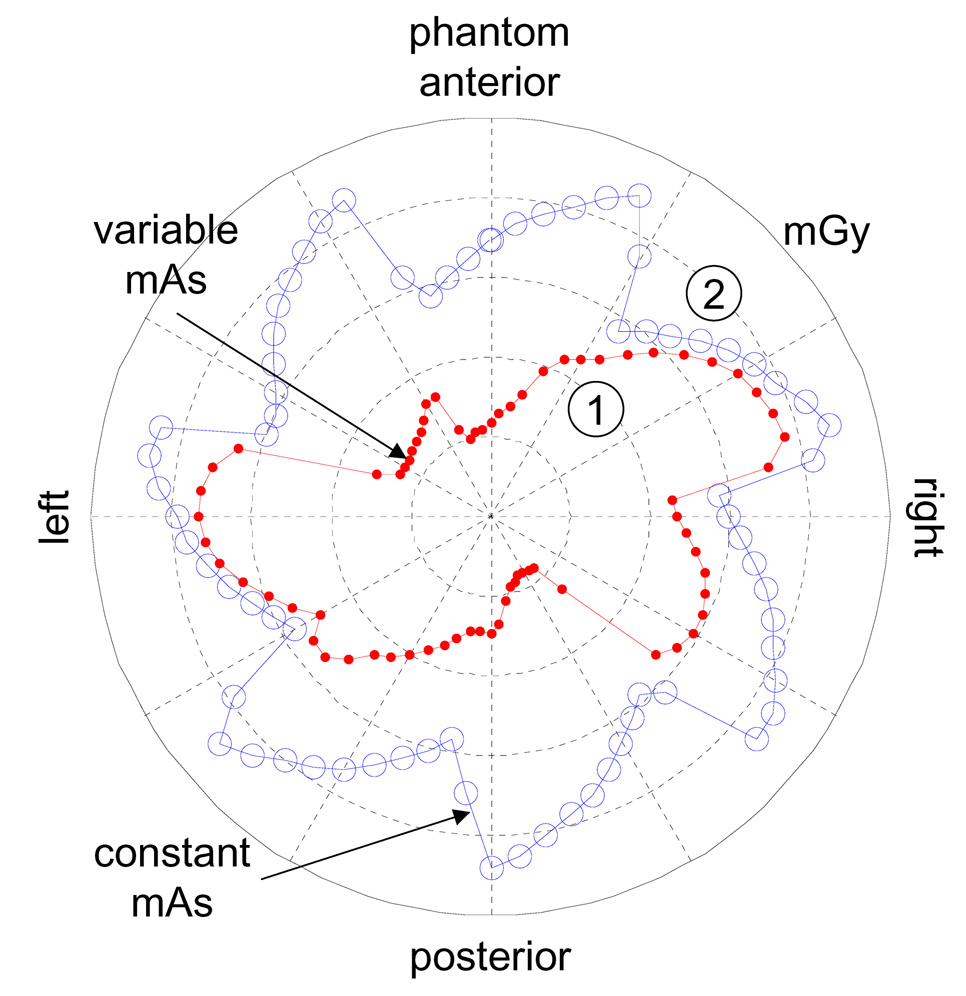
Mean surface, max surface, and center dose to the cylindrical phantom are compared in Table 5 for various kV acquisition protocols using the mAs necessary to achieve 95% of 2D registrations within 1 mm of expected with no MV beam scatter. For protocols with a constant mAs, the maximum value from Figure 6 was used. Acquisition protocols in the table include 5 kV acquisitions per beam using a fixed mAs over all θ, as well as 1, 2, and 5 acquisitions per beam using a variable mAs vs. θ (see Figure 6), and 5 acquisitions per beam with added acquisitions during gantry rotation every 6 seconds using variable mAs vs. θ. Also shown in the table for comparison is the dose for a clinical CBCT acquisition of the prostate area. For all acquisition protocols (except CBCT) a 7 equispaced beam arrangement was assumed. The surface dose for acquisition protocols 1 and 4 from Table 5 are found in Figure 7. The largest dose reduction when mAs was varied with θ was at the anterior and posterior surfaces.

Table 5.

Max surface, mean surface, and center dose to a 30-cm diameter acrylic phantom due to kV fluoroscopy and CBCT acquisitions. Seven equispaced treatment angles were used for fluoroscopy acquisitions. For variable mAs/frame, the values given in Figure 6 were with x = 1.0 mm.

acquisition type:	# frames per treatment angle	acq. during gantry rotation	mAs/frame:	cylindrical phantom dose (mGy)
				max surface	mean surface	center
1. between segments	5	no	2.6	2.2	1.8	1.2
2. before beam on	1	no	variable	0.4	0.2	0.14
3. before & after beam on	2	no	variable	0.8	0.4	0.3
4. between segments	5	no	variable	1.9	1.1	0.7
5. between segments + gantry rotation (T = 6s)	5	yes	variable	2.6	1.4	0.9
6. current technique (Adamson and Wu, 2008)	~200	no	0.16	5.5	4.5	2.9
7. CBCT (5.5 Hz)	650 total	yes	1.6	21.1	21.1	12.7

Figure 7.

Imaging dose to phantom surface in mGy due to 5 kV acquisitions per treatment angle using 7 equispaced treatment angles. Dose is shown when variable mAs values are used to achieve 95% of registrations with vector error less than 1 mm (see Figure 6), and using a constant value of 2.6 mAs for all θ.

The data in Table 5 shows that prostate intrafraction motion can be measured using low dose in comparison to CBCT, even when a constant mAs/acquisition vs. θ is used. Comparing doses from acquisitions 1 and 4 from Table 5, shows that dose can be reduced by ~15–40% when the mAs/acquisition is varied with θ. Acquiring images during gantry rotation increases dose, the amount of which will depend upon the imaging frequency and number of frames acquired. The imaging dose increased by ~30% when acquisitions were made during gantry rotation every 6 seconds using a variable mAs/acquisition (see acquisitions 4 and 5 from Table 5).

4. Discussion

To date, few studies have been performed investigating the achievable accuracy of monoscopic imaging for prostate. The most extensive study was recently made by Poulsen, who developed a method of resolving the out of plane position using a population 3D probability (Gaussian) density and compared it to assuming the motion component along the imager axis to be zero (Poulsen et al., 2008). For our simulation study, the 3D Gaussian distribution for Poulsen’s method was estimated using the same population of cine-MRI data from which the simulated prostate motion was drawn and hence represents a best case scenario as no bias is expected between the population data and measured data. Also here we have applied Poulsen’s method for a gantry mounted kV imager, where the acquisition angle is defined by the treatment protocol.

The most important factors affecting 3D localization accuracy were the 3D localization method used and the treatment duration. Retrospective 3D localization methods were more accurate than methods that could be used real-time, which is intuitive because they utilize more information. Because of this, when real-time 3D localization is necessary a retrospective method can be used post treatment to improve the 3D localization. The effect of treatment duration can be explained in that shorter treatment duration will translate into less time between acquisitions at unique gantry angles, which will in turn translate into less prostate motion between acquisitions and less error.

While we evaluated 3D localization accuracy in the simulation study, we did not account for 2D registration error. It should be noted that the 2D registration error is not uniform across both axes. Due mostly to the orientation of the implanted coils, for our case the 2D registration error is larger in the SI axis than in the rotating axis (Adamson and Wu, 2008). On the other hand, uncertainty from the 3D localization is propagated mostly into the rotating axis (AP and RL axes). Hence the uncertainty from 2D registration error and 3D localization error will mostly affect separate axes, meaning that in general the localization error in the SI axis can be controlled by adjusting the mAs/registration, while the localization error in the AP and RL axes can be controlled to some extent by adjusting the acquisition protocol.

In Figure 6 we presented the necessary mAs to achieve 95% of registrations within 1 and 2 mm of the expected when no MV scatter is present. It may be possible to adjust these values for MV scatter using Figure 3 and Figure 4; however some precautions should be taken. While they may be useful for approximations, Figure 3 and Figure 4 were calculated using anthropomorphic phantom rather than patient acquisitions, and included only acquisitions at θ = 90°. A more detailed investigation of the effect of MV scatter on the kV registration accuracy could be made involving Monte Carlo simulations of the scatter, but is outside the scope of this study.

We considered dose to a 30-cm diameter cylindrical acrylic phantom. Although the actual patient dose will be highest for bone and may vary considerably from these measurements due to geometrical and compositional differences (Islam et al., 2006; Ding et al., 2007), the dose numbers are useful for comparison purposes. More specifically, the phantom surface and center doses from the intrafraction fluoroscopy acquisitions were much lower than the dose measured for a typical CBCT. This may be attributed to a number of reasons: first, the intrafraction fluoroscopy acquisitions can utilize a much lower mAs/acquisition because they are used to image high contrast radiopaque markers as opposed to CBCT, where soft tissue visibility is also important. The dose required will be further reduced if larger fiducial markers are used. Second, the number of projection images acquired is typically much larger for CBCT compared to intrafraction fluoroscopy in the cases presented here. Third, as shown in Figure 7, although the surface dose from the kV acquisitions does have “hot spots”, it is still spread out over 7 equispaced angles as opposed to concentrated in one area. It should be noted that the large variation in required mAs vs. θ is due to the geometry of the pelvis, and that these results are specific to prostate radiotherapy. Furthermore, acquisitions were not included for patients with hip prosthesis, which will also affect the relationship between θ and the necessary mAs and imaging dose.

5. Conclusions

Fiducial markers in the prostate can be localized in 3D with reasonable accuracy by combining monoscopic imager acquisitions from multiple angles throughout treatment delivery (95% within ~1.5mm). The 3D localization accuracy is dependant upon the inherent prostate motion distribution, treatment time, kV acquisition protocol, treatment protocol, and 3D localization method. Assuming the shortest path satisfying all 2D localizations as described by Kotte (Kotte et al., 2007) provided the most accurate retrospective 3D localization and can be slightly improved when full 3D localizations can be incorporated from pre and post treatment volumetric imaging. A real-time 3D localization can be performed at the cost of increased localization error (95% within 1.5 mm increased to 95% within 1.9 mm) and was most accurate using the shortest path algorithm calculated using only past and present 2D localizations, or using a 3D probability density to resolve the out of plane position (Poulsen et al., 2008). Most of the 3D localization uncertainty is inherent to the lack of full 3D information from monoscopic imaging, and cannot be reduced by increased imaging frequency. Use of a VMAT treatment protocol improved 3D localization accuracy most likely due to the decrease in treatment duration. Optimal 3D localization accuracy may be achieved by assuming the shortest path satisfying all 2D localizations, incorporating pre and post 3D localization information, and employing treatment protocols that minimize treatment duration.

Prostate intrafraction motion evaluation using kV monoscopic imaging can be achieved with very low doses, (0.4–5.5 mGy max phantom surface dose for kV intrafraction acquisitions, vs. 21.1 mGy max phantom surface dose for CBCT). Optimizing the mAs vs. acquisition angle can decrease dose by ~15–40%. Acquiring during MV delivery will require additional mAs to achieve the same level of registration accuracy, and will depend on MV beam dose rate, field size, energy, as well as acquisition angle, patient geometry, distance from kV detector to isocenter, etc. For lateral kV acquisitions of an anthropomorphic phantom, the required mAs/registration to achieve 95% of registrations within 1 mm increased from 1.0 to 2.5 when MV scatter was introduced from a 6 MV beam at a dose rate of 445 mu/min and a field size of 4×4 cm². The necessary mAs/registration increased roughly linearly with field size and with dose rate.