Abstract
The relatively new technique of vapor pressure osmometry was utilized to determine the preferential interaction of five common solution additives (arginine HCl, guanidine HCl, glycerol, glucose, and urea) using three different model proteins (BSA, lysozyme, and α-chymotrypsinogen). Results for guanidine, glycerol, glucose, and urea are comparable to literature values, which utilized the dialysis/densimetry technique. However, values for arginine differ greatly from literature values, making it unclear what is the nature of arginine-protein interactions. A repeat of the dialysis/densimetry measurements reported in the literature supports the vapor pressure osmometry measurements and reveals a never before seen trend in the interaction of arginine with proteins as a function of concentration. This trend is dependent on the protein size and shows arginine to be unique among solution additives. For concentrations below 0.5 M, arginine has a preferential interaction coefficient near zero (slightly greater than zero for small proteins but decreases as the size of the protein increases) which indicates that arginine is neither strongly bound nor excluded from the protein surface. This trend differs greatly from cosolutes which influence the protein folding equilibrium. However, as the concentration of arginine increases beyond 0.5 M, arginine becomes increasingly excluded. Such behavior might be indicative of the protein surface becoming saturated with arginine, thus causing any additional arginine added to the solution to be excluded from interacting with the surface. All of this behavior is most likely the result of a balance between the affinity arginine has for the peptide backbone and certain amino acids and the repulsion generated by surface tension increment and volume exclusion effects. In addition, such behavior may explain why arginine has little effect on protein folding equilibrium but is an effective aggregation suppressor.
Keywords: Arginine, Preferential Interaction Coefficient, Vapor Pressure Osmometry, Aggregation
Introduction
Due to the advancement of recombinant DNA technology and cell biology, the past two decades have seen an explosive growth in biopharmaceuticals.1 However, rapid commercialization of these protein drug candidates is hindered by physical and chemical instabilities of proteins. Of these degradation pathways, protein aggregation (the assembly of non-native protein conformations into multimeric states) is arguably the most common and troubling manifestation of protein instability, occurring in almost all phases of development.2 Protein aggregates are usually nonnative in structure, may exhibit reduced biological activity, and can remain soluble and/or precipitate from solution. In addition to reducing efficacy, if administered to a patient, aggregates can cause adverse reactions, such as an immune response, sensitization, or even anaphylactic shock.3 Therefore, if even a small amount of aggregates form during formulation or storage, a product can be rendered unacceptable.
The most prevalent method for combating protein aggregation, in addition to tuning buffer conditions, is to add to the solution a low molecular weight additive (also commonly referred to as a cosolute or excipient), such as salts, sugars, polyols, etc., which have the propensity to deter aggregation.4,5 Unfortunately, due to the diversity in protein chemistry and structure, additives that work well for a particular protein may not work universally. In addition, the interaction between common solution additives and proteins is typically weak, thus requiring a high concentration of additives to be effective.6 Therefore, there is great interest in developing new solution additives that are very effective at deterring aggregation and are also potent at low concentrations. However, the current understanding of the mechanisms by which commonly used additives deter aggregation is limited.7
In a few cases, qualitative mechanistic models have been developed to describe how a particular additive deters aggregation. For example, during aggregation, it is generally believed that a protein molecule that is initially in the native state (N) reversibly passes through a partially unfolded state (U), which is aggregation prone, before proceeding to form an aggregate (An):8
| (1) |
In this model, there are two types of additives which will deter aggregation, folding stabilizers and aggregation suppressors. A folding stabilizer is classified as any additive which shifts the folding equilibrium from the partially unfolded state toward the native state. It has been demonstrated that such additives (e.g. sucrose, glucose, polyols, etc.) are preferentially excluded from the protein-solvent interface and thus exhibit an unfavorable interaction with the protein. This unfavorable interaction is greater for the partially unfolded species due to a larger solvent exposed surface area and is minimized when the protein adapts a state with minimal surface area, such as its native state.9 Thus, it is generally believed that such additives deter aggregation by decreasing the number of aggregate prone species. As a consequence, folding stabilizers are typically added to refolding buffers to enhance proper folding and are used during storage to stabilize the native state. However, the aggregated state also exhibits a smaller solvent exposed surface area, thus high concentrations of such additives could actually promote aggregation.1,10 Moreover, during refolding, aggregation is a competing pathway under kinetic control, and to avoid the irreversible loss of protein from aggregation, refolding is typically done at substantially high dilutions due to the fact that aggregation is a intermolecular reaction while protein folding is a unimolecular process. To refold proteins at a reasonable concentration, an aggregation suppressing additive, which specifically inhibits association, must be added to the solution.11
One such additive is the amino acid arginine.12 It has been well documented that arginine has very little effect on the folding equilibrium, yet it deters aggregation during refolding and storage.13-15 Therefore, it is assumed that arginine is an aggregation suppressant, and not a conformational stabilizer, such as sucrose. Based on the limited data available, researchers have proposed different hypotheses to explain the phenomenon.6,11,13,16 In addition, researchers have attempted to discover or develop other additives that are similar to arginine, but more effective in hindering aggregation.17-21 Yet, the mechanism by which arginine functions is still not well understood.
One way to investigate this mechanism is via preferential interaction measurements, which can give information about how additives interact with proteins.12 In order to elucidate the mechanism of action by which arginine suppresses aggregation and to aid in the development of new solution additives, we set out to determine the cosolute-protein preferential interaction coefficient, Γμ3, for the interaction of arginine with three common proteins. We utilized the relatively new technique of vapor pressure osmometry (VPO) to measure the parameter, in addition to densimetry.22-24 This parameter, defined below, describes the interaction between a cosolute and a protein, thus gives valuable insight into the mechanism by which a particular additive suppresses aggregation. Our results indicate that arginine HCl is neither strongly bound nor excluded from the protein surface in the concentration range of 0-0.5 M. Such an interaction and the ability to specifically slow association is consistent with a “neutral crowder” mechanism, first developed by our lab.7,11
Cosolute-Protein Preferential Interaction Coefficient Γμ3
The preferential interaction coefficient of interest, Γμ3, is defined by the partial derivative describing the change in cosolute molality (m3) with respect to protein molality (m2) at constant temperature (T), pressure (P), and cosolute chemical potential (μ3) 22:
| (2) |
The subscripts used indicate solution components in Scatchard notation: water (subscript 1), the protein (subscript 2), and the cosolute (subscript 3).25 Alternatively, a thermodynamically equivalent definition can be expressed by the partial derivative which relates the chemical potential of the protein to that of the cosolute, at constant T, P, and protein molal concentration (m2):
| (3) |
These partial derivatives indicate that Γμ3 is both a measure of how the chemical potential of the protein is perturbed by the presence of the cosolute and a measure of how the cosolute concentration must change to maintain a constant chemical potential when protein is added to the solution. The later description has been interpreted using a two-domain model as the difference in the cosolute concentration between the local domain surrounding the protein and the bulk solution.26,27 Under such interpretations, additives with a positive Γμ3 are typically described as being preferentially bound to the protein surface due to an increase in the concentration of the cosolute in the local domain and this favorable interaction, as indicated by eq 3, lowers the chemical potential of the protein. The opposite is true for additives with a negative Γμ3, which are typically described as being preferentially excluded from the surface of the protein.
Other Preferential Interaction Coefficients
Though the preferential interaction coefficient, Γμ3, is essential in understanding how cosolute molecules interact with a protein, the parameter, however, cannot be measured directly. Therefore, an approximation must be obtained. This can be accomplished by defining other preferential interaction coefficients. The first is the isoosmolal preferential interaction coefficient Γμ1, which is defined by the partial derivative describing the change in cosolute molality (m3) with respect to protein molality (m2) at constant T, P, and water chemical potential (μ1):
| (4) |
The constraint of constant μ1 can be achieved via vapor pressure equilibrium and thus the parameter defined by eq 4 can be determined directly by VPO techniques, as described later.22
The second preferential interaction coefficient is the dialysis equilibrium preferential interaction coefficient Γμ1,μ3, which is assumed to be approximately equal to Γμ3 and is defined by the partial derivative describing the change in cosolute molality (m3) with respect to protein molality (m2) at constant T, μ1, μ3:
| (5) |
The constraints of constant μ1 and μ3, while allowing pressure to vary, can be achieved via dialysis equilibrium, given that the protein cannot diffuse across the membrane, thus the parameter defined by eq 5 can be determined by dialysis/densimetry techniques.28-31
Dialysis/Densimetry Technique for Determining Γμ1,μ3
For several decades, the only established method for approximating the preferential interaction coefficient Γμ3 has been through measuring Γμ1,μ3 via dialysis/densimetry techniques. As described elsewhere, the change in mass and volume resulting from allowing a protein solution to reach dialysis equilibrium with the solvent (here solvent refers to the cosolute-water solution) can be attributed to a change in the mass and partial specific volume of the protein.32,33 By doing so, Γμ1,μ3 can be related to the partial specific volume at infinite dilution of the protein before (ϕ2o) and after dialysis (ϕ2’o), along with the partial specific volume of the cosolute (), the density of the solvent (ρso), and the molecular weights of the protein (M2) and cosolute (M3):
| (6) |
The partial specific volume of the protein is taken at infinite dilution since this value represents the partial specific volume with no protein-protein interactions and can be determined by extrapolating apparent specific volume data (ϕ), as determined through density measurements of the protein solution (ρ), to zero protein mass concentration (C2):
| (7) |
The partial specific volume of the cosolute at a given concentration is assumed to be the same as that for a solution with no protein, thus it can be determined from changes in solvent density with respect to cosolute mass fraction (z3):
| (8) |
Thermodynamic Relationship between Osmolality and the Preferential Interaction Coefficient Γμ3
Recently, a new methodology utilizing vapor pressure osmometry has been introduced as a means for approximating the preferential interaction coefficient Γμ3.22,34 The advantage of this technique over dialysis/densimetry is that only a relatively small volume of sample is needed for the measurements and numerous Γμ3 data points covering a wide range of cosolute concentrations can be gathered in a single day. A vapor pressure osmometer is essentially a highly accurate dew point hygrometer. It uses the dew point temperature of a small volume of air in equilibrium with an aqueous solution to report the osmolality (Osm) of the solution (via the Clausius-Clapeyron equation), which is related to the activity of the water (a1) in the solution:
| (9) |
To use such measurements to determine the preferential interaction coefficient, a relationship must be expressed relating the parameter to the activity of water. This is done by substituting in the relationship between chemical potential and activity into eq 3 and substituting in the Gibbs-Duhem relationship for one of the solutes. This produces two alternative equations relating Γμ3 to the activity of water:
| (10) |
| (11) |
However, the change in the activity of the cosolute (eq 10) or the protein (eq 11) cannot be measured independently, thus their values must be approximated. One such method is to assume that the change in the activity of either solute in the three component solution is approximately the same as in a two component solution containing only that solute and water. By doing so, the change in the activity of the protein and the cosolute can be approximated from osmolality measurements via the Gibbs-Duhem relationship:
| (12) |
| (13) |
where the superscript o(i) represents a two component solution lacking component i. By applying the chain rule and Euler’s reciprocity to eqs 10 and 11, along with substituting in these approximations, the definition of osmolality (eq 9), and a symbol to simplify the expression,
| (14) |
two alternative and equally valid approximations can be expressed relating Γμ3 to solution osmolality:
| (15) |
| (16) |
Moreover, the second approximation can be further simplified by realizing that
| (17) |
which simplifies eq 16 to
| (18) |
It should be noted that an alternate approach has been developed in which the osmolality increment (i.e. the difference between the osmolality of the three component mixture and the osmolality of the two component solutions at the same respective solute concentration) is used to estimate the preferential interaction coefficient.35 However, it can be shown from thermodynamic reasoning that such an approach is nothing more than an approximation of eq 18. In the analysis presented here, both eqs 15 and 18 were utilized to compute the preferential interaction coefficient. Though both equations typically give similar results, it should be noted that all results reported in this document are an average of the two results.
An Exact Relationship Linking Γμ1,μ3 and Γμ3
It is clear that the two techniques for approximating the preferential interaction coefficient measure different parameters. Therefore, it is desirable to know the relationship between the two parameters so that a comparison of the results from the two techniques can be made. As derived elsewhere, an exact thermodynamic relationship between Γμ1,μ3 and Γμ3 can be expressed utilizing the preferential interaction coefficients Γμ1 and Γμ3, along with the partial molar volume of water () and the cosolute ():24
| (19) |
Experimental Methods
Proteins and Reagents
Bovine serum albumin (BSA) (A3059), hen egg white lysozyme (L6876), and bovine α-chymotrypsinogen A type II (aCgn) (C4879), were attained from Sigma-Aldrich (St. Louis, MO). L-Arginine hydrochloride (argHCl), urea, guanidine hydrochloride (gdnHCl), glucose, glycerol, sodium phosphate monobasic, citric acid, and sodium hydroxide were also attained from Sigma-Aldrich in the highest available grade. Double distilled water was obtained from an in-house distilled water supply that was further purified by a Milli-Q® Academic water purification system.
The concentration of BSA, lysozyme, and aCgn, were determined by absorbance using extinction coefficients of 0.658 mL*mg-1cm-1 at 278 nm, 2.74 mL*mg-1cm-1 at 281 nm, 1.97 mL*mg-1cm-1 at 282 nm, respectively.28 No corrections were made for cosolute concentrations since the concentrations were typically low due to the protein solutions being diluted with pure water for the purpose of producing a sample with an optical density of about 1.0.
Preparation of Solutions for VPO Measurements
Osmolality measurements were carried out according to the previously described procedure.22 For improved accuracy, all samples were prepared gravimetrically using a Mettler Toledo balance with a precision of 0.1 mg. Partial molar volume values of the solutes (evaluated using eq 8) and density values of the solutions were used to determine concentration. Though a three component system was utilized for the derivation of eqs 15 and 18, it was found that a pH buffering salt was necessary for the measurements, mainly to stabilize the protein solution and to control the pH of the guanidineHCl and arginineHCl solutions. Since the concentration of the buffering salt is constant for every sample, not to mention low, it has no contribution to the computed slopes used in eqs 15 and 18. Therefore, the molal concentration of the buffer can be lumped together with that of the water, thus system can still be treated as a three component system (i.e. solvent, protein, and additive).
Stock solutions of both BSA and lysozyme and stock solutions of the cosolutes were each prepared in a 40 mM sodium phosphate buffer, pH 6.0 (aCgn measurements were conducted in 20 mM sodium citrate buffer, pH 3.5). Stock solutions of the cosolutes were used so that a series of samples could be easily produced with varying solute concentrations by dilution with the buffer. The protein stock solutions were further purified by placing the solutions under dialysis for 48 hours at room temperature against two changes of buffer (1 L each). To obtain the best possible results from the VPO measurements, the protein solutions were concentrated to within 100-200 mg/mL (depending on the solubility of the protein) using Millipore® ultrafiltration tubes. To determine the concentration, samples of each stock solution were diluted gravimetrically with water to a final optical density of about 1.0 and the concentration determined spectrophotometrically with a PerkinElmer Lambda 35 UV/Vis spectrometer. It should be noted that the protein stock solutions were stored at 4°C and used with in one week of their preparation.
Eqs 15 and 18 require that osmolality measurements for the three component solution at various cosolute concentrations be taken at a constant protein molal concentration. However, it is difficult to prepare such solutions and therefore, samples with a constant molar volume were prepared instead. To correct for this, a relationship between constant protein molal concentration (m2) and constant protein molar concentration ([2]), derived elsewhere, is used to obtain values for the desired parameter:22
| (20) |
A Wescor Vapro® vapor pressure osmometer (model 5520) was used for all osmometry measurements. The instrument was calibrated using 0.1, 0.29, and 1 mol/kg osmolality standards provided by Wescor. Due to slight drifts in the calibration points, the instrument was recalibrated after every four measurements and the thermocouple was cleaned daily using concentrated ammonium hydroxide. Even though the instrument is designed to measure osmolality readings as high as 3.2 mol/kg, the accuracy of measurements above the last calibration point of 1 mol/kg is significantly impaired from extrapolating the calibration curve and increased system noise at high solute concentrations. It was discovered during the course of such measurements that this error significantly influenced the accuracy of the results. Therefore, cosolute concentration was limited so that all measurements were below 1.2 mol/kg. The data sets for each cosolute included at least 20 individually made solutions (both for the sets with and without the protein). Each sample contained approximately 200 μL of solution (100 μL of diluted cosolute stock solution and 100 μL of the protein stock solution). A minimum of three measurements on each solution were made. If the standard deviation for a particular solution was greater than 2 mmol/kg, more measurements were taken or another sample was prepared. For a given solute, data representing the dependence of osmolality on solute molality were fitted by a quadratic equation, with all fitting parameters floated. Data were weighted by the standard deviation of the individual osmolality measurements for the same solution using the nonlinear fitting program Igor Pro. Using a cubic function or other fitting curves did not improve the fitting for any of the data.
Determination of the Isoosmolal Preferential Interaction Coefficient (Γμ1)
Though the isoosmolal preferential interaction coefficient Γμ1 can be determined directly from osmolality (via eq 17) it is difficult to obtain an accurate measure of the relationship between osmolality and protein concentration for every cosolute concentration. This is mainly due to the fact that osmolality does not change significantly over the available range of protein concentration. However, it can be approximated by comparing the molal concentration of the cosolute in the protein solution (m3) to that in a two component solution at the same osmolality (i.e. the same water chemical potential) (m3Δ):
| (21) |
By using such a procedure, the preferential interaction coefficient Γμ3 can be determined using both approximation methods from just three series of samples, a series containing all three components at various cosolute concentrations, a series of just protein and water at various protein concentrations, and a series of just the cosolute and water at various cosolute concentrations. (See Table 1 for experimentally determined partial molar volumes and osmolality dependence on solute molality for two-component solutions.)
Table 1. Summary of Solute Partial Molar Volume and Dependence of Solution Osmolality on Solute Molality for Two-Component Solutions.
| cosolute (comp. 3) | partial molar volume (L/mol) × 102 | Ω3o(2) (pH 6.0)a | Ω3o(2) (pH 3.5)b | range (m) mol/kg |
|---|---|---|---|---|
| argHCl | (14.21 ± 0.01) + (0.22 ± 0.01)m3 | (1.716 ± 0.001) - (0.674 ± 0.004)m3 | (1.678 ± 0.001) - (0.542 ± 0.002)m3 | m3<0.70 |
| gdnHCl | (6.94 ± 0.01) + (0.048 ± 0.003)m3 | (1.795 ± 0.01) - (0.598 ± 0.002)m3 | (1.747± 0.001) - (0.4906 ± 0.002)m3 | m3<0.76 |
| glucose | (11.192 ± 0.003) + (0.044 ± 0.003)m3 | 1.016 ± 0.001 | 1.013 ± 0.001 | m3<1.20 |
| glycerol | (7.118 ± 0.003) - (0.030 ± 0.001)m3 | 0.9956 ± 0.0005 | 0.974 ± 0.001 | m3<1.14 |
| urea | (4.452 ± 0.002) - (0.117 ± 0.003)m3 | (0.9744 ± 0.0005) - (0.0918 ± 0.001)m3 | (0.916 ± 0.001) - (0.008 ± 0.001)m3 | m3<1.22 |
| protein (comp. 2) | partial molar volume (L/mol) | Ω2o(3) (pH 6.0)a | Ω2o(3) (pH 3.5)b | range (m)mol/kg |
|---|---|---|---|---|
| BSA | 47.731 ± 0.001 | 3.6 ± 0.9 | N/A | 1.9 ≤ m2 ≤ 2.1 |
| lysozyme | 10.005 ± 0.001 | 3.2 ± 0.9 | N/A | 3.5 ≤ m2 ≤ 3.8 |
| aCgn | 17.910 ± 0.001 | N/A | 4.4 ± 0.8 | 1.65 ≤m2 ≤1.75 |
The base buffer was 40 mM Na-Phosphate
The base buffer was 20 mM Na-Citrate.
Dialysis/Densimetry Determination of the Preferential Interaction Coefficient
Density measurements were carried out according to the previously described procedure.29 Lyophilized protein was dried in a desiccator at room temperature for 2 days under high vacuum to remove trace amounts of water. Five samples of the dried protein were dissolved at a concentration ranging from 5 to 25 mg/mL in 4 mL of buffer solutions containing the cosolute at the desired concentration and pH. For the constant molality measurements, 2 mL of each sample were set aside, tightly sealed, and left at room temperature overnight prior to the densimetry measurements. In the constant chemical potential experiments, the other 2 mL of each protein sample were transferred to a dialysis bag and dialyzed at room temperature for 48 hours against two changes of solvent (400-500 mL each) prior to densimetry measurements. The density of each solution was measured using an Anton Paar DMA 4500 density meter, accurate to within 0.00001 g/mL. After the density measurements, samples of each protein solution were diluted gravimetrically with water to a final optical density of about 1.0 and the concentrations were determined spectrophotometrically with a PerkinElmer Lambda 35 UV/Vis spectrometer.
Results
Comparison between Γμ3, Γμ1,μ3, and Literature Values
To evaluate the reliability of the results determined from VPO measurements, which is a relatively new technique, a comparison was made with data found in the literature (most of which was determined by dialysis/densimetry measurements, a well established technique). Tables 2-4 summarize the preferential interaction coefficients over the concentration range detailed in the last column of Table 1, for BSA, lysozyme, and aCgn, respectively, in combination with five common cosolutes (arginine, guanidine, glucose, glycerol, and urea). Theoretically, the preferential interaction coefficients Γμ3 and Γμ1,μ3 are independent of protein concentration, which has been demonstrated elsewhere, thus there was no need to repeat the measurements at other protein concentrations.22,36 To make the comparison with literature values, Γμ1,μ3 was computed using eq 19. All of the results shown in Tables 2-4 support the assumption that Γμ1,μ3 is approximately equal to Γμ3 because there is no significant difference between Γμ3 and Γμ1,μ3 values for any cosolute-protein system tested. Therefore, a direct comparison can be made between Γμ3 values measured by VPO and Γμ1,μ3 values measured by dialysis/densimetry.
Table 2. Summary of Preferential Interaction Coefficients for BSA as Measured by VPOa and Comparison to Literature Values.
| cosolute | Ω3 | Γμ1 | Γμ3b | Γμ1,μ3 | Γμ1,μ3Lit |
|---|---|---|---|---|---|
| argHCl | (1.713 ± 0.003) - (0.611 ± 0.006)m3 | (-1.64 ± 0.6) + (1.7 ± 3.9)m3 - (13.3 ± 5.4)m32 | (1.72 ± 0.96)[3] - (23.2 ± 4.0) [3]2 | (1.43 ± 0.96)[3] - (22.8 ± 4.0) [3]2 | (12.6 ± 4.5)[3] - (22.0 ± 5.3)[3]2 c |
| gdnHCl | (1.755 ± 0.001) - (0.576 ± 0.005)m3 | (-1.8 ± 0.4) + (11.2 ± 1)m3 | (12.4 ± 1)[3] | (12.3 ± 1)[3] | (13.0 ± 1.2)[3]d |
| glucose | (1.055 ± 0.001) - (0.004 ± 0.002)m3 | (-1.4 ± 0.6) - (17.8 ± 0.8)m3 | (-20.6 ± 0.4)[3] | (-20.8 ± 0.4)[3] | (-19.8 ± 0.9)[3]e |
| glycerol | (1.014 ± 0.001) - (0.0012 ± 0.001)m3 | (-4.1 ± 0.8) - (12.3 ± 1.2)m3 | (-14.0 ± 0.4)[3] | (-14.3 ± 0.4)[3] | (-12 ± 4)[3]f |
| urea | (0.963 ± 0.002) - (0.092 ± 0.002)m3 | (-5.0 ± 0.4) + (6.2 ± 0.6)m3 | (6.4 ± 0.4)[3] | ( 6.2 ± 0.4)[3] | (6 ± 2)[3]g |
It should be noted that [3] represents the molar concentration of the cosolute.
The base buffer was 40 mM Na-Phosphate, pH 6.0 and BSA concentration held constant at 1.8 mM.
Calculated from data in Reference 37.
Calculated from data in Reference 30.
Calculated from data in Reference 29.
Calculated from data in Reference 41.
Calculated from data in Reference 36.
Table 4. Summary of Preferential Interaction Coefficients for α-Chymotrypsinogen A as Measured by VPOa.
| cosolute | Ω3 | Γμ1 | Γμ3b | Γμ1 μ3 |
|---|---|---|---|---|
| argHCl | (1.676 ± 0.001) - (0.514 ± 0.004)m3 | (-2.8 ± 0.8) + (0.2 ± 5.8)m3 - (6.6 ± 8.1)m32 | (0.9 ± 0.7)[3] - (10.5 ± 2.5)[3]2 | (0.5 ± 0.7)[3] - (10.4 ± 2.5)[3]2 |
| gdnHCl | (1.736 ± 0.001) - (0.488 ± 0.002)m3 | (-0.8 ± 0.6) + (4.1 ± 1.1)m3 | (4.0 ± 1)[3] | (3.9 ± 1)[3] |
| glucose | (1.022 ± 0.001) - (0.001 ± 0.002)m3 | (-4.5 ± 1.2) - (5.1 ± 0.8)m3 | (-5.2 ± 0.5)[3] | (-5.8 ± 0.5)[3] |
| glycerol | (0.999 ± 0.001) - (0.002 ± 0.002)m3 | (-3.7 ± 0.8) - (13.6 ± 1.2)m3 | (-15.0 ± 0.7)[3] | (-15.3 ± 0.7)[3] |
| urea | (0.902 ± 0.001) - (0.015 ± 0.001)m3 | (-6.6 ± 0.8) + (8.8 ± 1.0)m3 | (9.4 ± 1)[3] | (9.1 ± 1)[3] |
BSA is the most common model protein used in literature for preferential interaction coefficients, thus there is more data available for the cosolutes and pH used for the VPO measurements, making it the ideal protein to evaluate the reliability of the VPO measurements. For guanidine HCl, glucose, glycerol, and urea, the trends between Γμ3 values and cosolute concentration for BSA computed from VPO measurements are nearly identical to those reported in the literature. This gives confidence that VPO is a reliable methodology for determining the preferential interaction coefficient. However, for BSA, the results for arginine HCl differ significantly from the literature values, as well as for lysozyme, thus making it unclear which values were most representative of the preferential interaction coefficient. Thus a repeat of the dialysis/densimetry measurements was conducted to resolve this dilemma.
Comparison of VPO Results to Dialysis/Densimetry Measurements
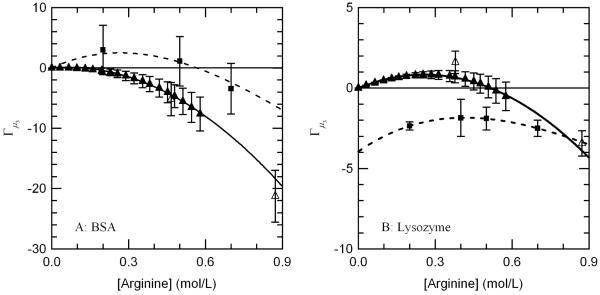
The preferential interaction coefficient Γμ1,μ3 for arginine was determined by dialysis/densimetry measurement techniques at two different arginine concentrations for both BSA and lysozyme (see Table 5). For comparison, these results were plotted against the trends computed from VPO measurements in addition to the literature values, as depicted in Figure 1. It is clear that the results determined by dialysis/densimetry measurements conducted in our lab confirm the VPO results and bring into question the reliability of the literature values. For BSA (Figure 1.a), both of the values measured by dialysis/densimetry follow the VPO trend, in particular, the preferential interaction coefficient for arginine is close to zero at low concentrations and gradually becomes increasingly negative. This differs from the literature values, which depict the preferential interaction coefficient for arginine as being significantly greater than zero at low to moderate concentrations, and then decreasing and becoming increasingly negative at high concentrations.
Table 5. Preferential Interaction Coefficients for Proteins in Arginine HCl Solutionsa as Determined by Dialysis/Densimetry Measurements.
| [arginine] (M) | ϕ2 o (mL/g) | ϕ2’o (mL/g) | Γμ 1μ3 |
|---|---|---|---|
| BSA, pH 6.0 | |||
| 0.47 | 0.708 ± 0.002 | 0.713 ± 0.001 | (-5.2 ± 2.8) |
| 0.87 | 0.717 ± 0.002 | 0.734 ± 0.002 | (-21.3 ± 4.3) |
| lysozyme, pH 6.0 | |||
| 0.38 | 0.713 ± 0.002 | 0.706 ± 0.002 | (1.6 ± 0.7) |
| 0.87 | 0.697 ± 0.002 | 0.710 ± 0.002 | (-3.4 ± 0.8) |
The base buffer was 40 mM sodium phosphate, pH 6.0.
Figure 1.
Comparison of Arginine Γμ3 values from VPO measurements (▲), dialysis/densimetry measurements (△), and literature values obtained from Reference 37 (■) for (A) BSA and (B) lysozyme.
For lysozyme (Figure 1.b), the values determined by dialysis/densimetry confirm that the preferential interaction coefficient for arginine is slightly positive at low concentrations and decreases and becomes increasingly negative at high concentrations. This differs significantly from the literature values, which depict the preferential interaction coefficient for arginine being negative and somewhat constant over the entire concentration range tested. In addition the literature values seem to indicate the value for the preferential interaction coefficient is nonzero at zero arginine concentration, which is an unrealistic result.
Though the new results for BSA do not differ significantly from the literature, they do differ greatly for lysozyme. The significance of these new results is that they indicate a common trend in the interaction between arginine and protein molecules, as opposed to conflicting trends previously reported.37 That is arginine seems to be neither strongly bound nor attracted to the surface of the protein and becomes excluded only at high concentrations. This has never been observed before and is a result that characterizes arginine as unique among solutions additives studied.
Discussion
Interpretation of Preferential Interaction Coefficient Values
The new results for the preferential interaction of arginine, as measured by VPO and dialysis/densimetry, differ significantly from literature values.37 This alters the interpretation of how arginine interacts with protein molecules. Before, based on the literature values for BSA, many assumed that arginine was a bound additive (except in the case of lysozyme, where it was thought that the positively charged protein repelled the positively charged arginine molecule). The VPO results seem to indicate something different, and in the case for lysozyme, the opposite trend is observed. For BSA, in the concentration range of 0-0.3 M, Γμ3 is approximately zero and gradually becomes negative as the concentration increases. As for lysozyme, Γμ3 values seem to indicate that arginine is slightly bound for concentrations less than 0.5 M and then gradually becomes excluded as the concentration increases. However, for both proteins, Γμ3 values seem to indicate that arginine is neither strongly bound nor excluded from the surface of the protein for arginine concentrations less than 0.5 M but becomes excluded at higher concentrations.
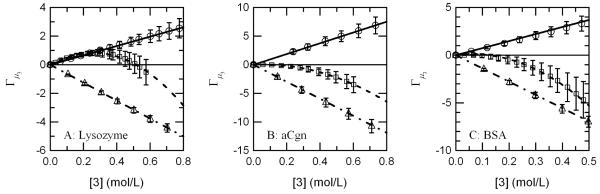
This trend is further exemplified when the preferential interaction of arginine is compared to denaturing and stabilizing cosolutes. In Figure 2, a comparison has been made with urea and glycerol for all three proteins tested, and it shows that preferential interaction values for arginine typically fall in between values for urea and glycerol. This differs from the trend obtained from the literature which seem to indicate arginine being strongly bound to BSA and strongly excluded from lysozyme.37
Figure 2.
Comparison of arginine preferential interaction coefficient values (□) to that for urea (○) (a preferentially bound and denaturing cosolute) and glycerol (△) (a preferentially excluded and stabilizing cosolute) for all three proteins tested, (A) lysozyme, (B) aCgn, and (C) BSA.
These new results seem to explain why arginine has little to no effect on protein folding equilibrium. The preferential interaction coefficient, Γμ3, is a measure of how the cosolute perturbs the free energy of the protein and according to the Wyman linkage relation,
| (22) |
(where ΔGou is the Gibbs free energy change of unfolding and Ku is the equilibrium constant for unfolding) additives which have a greater affinity for the unfolded state over the native state, will shift the folding equilibrium toward the unfolded state (the opposite being true for additives which are repelled by the unfolded state).38 Our preferential interaction measurements seem to indicate that arginine has little interaction with proteins. However, these measurements indicate only how a cosolute interacts with a protein in its native state, but assuming that the trend holds for the unfolded state, arginine should have no effect on the unfolding equilibrium because it does not significantly perturb the free energy of either state. However, some results seem to indicate that arginine has a very slight destabilizing effect at high concentrations for some proteins (including lysozyme).39 This effect, though, is very minor when compared to guanidine HCl (1 M arginine HCl decreases the melting temperature by about 1 °C for lysozyme versus a decrease of about 13-17 °C for guanidine HCl at a similar concentration). Those results seem to indicate that arginine has a very slight affinity for the unfolded or partially unfolded state but not enough to have a significant effect on the folding equilibrium.
Relationship of Arginine Preferential Interaction to Concentration and Protein Size
An interesting trend can be observed when the arginine preferential interaction coefficients for all three proteins tested are plotted together. Figure 3 reveals that not only is there a unique trend in the preferential interaction coefficient for arginine with concentration but there is also a trend with protein size as well. Γμ3 values for α-Chymotrypsinogen (a 25.7 kDa protein) fall in between the values for lysozyme (a 14.3 kDa protein) and BSA (a 66.4 kDa protein). Since there is no clear trend with the charge of the protein (i.e. the positively charged arginine seems to be most attracted to the positively charged proteins), these results seem to indicate that as the protein size increases, arginine becomes increasingly excluded from the protein surface.
Figure 3.
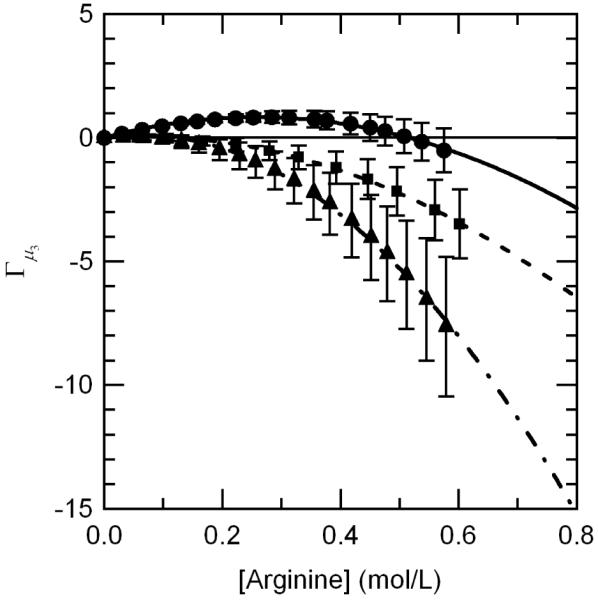
Comparison of arginine preferential interaction coefficient values for all three proteins tested demonstrating the relationship with arginine concentration and protein size; lysozyme, 14.3 kDa (●), aCgn, 25.7 kDa (■), and BSA, 66.4 kDa (▲).
The reason for this behavior is not quite clear. It has been shown that arginine interacts with amino acid residues in almost the same fashion and to almost the same extent as guanidine, with both compounds showing a strong affinity for most residues, especially aromatic residues.6 This behavior may explain why arginine shows a slight affinity for proteins and a slightly stronger affinity for unfolded proteins, since aromatic residues are typically buried in a folded protein. However, surface tension also increases with increasing arginine concentration, much more so than with guanidine.6 Such behavior tends to repel additives from the protein surface and enhance the binding of water, since the protein surface constitutes a solvent interface at which there must be interfacial tension. This, in addition to the fact that arginine is a much larger molecule than guanidine (i.e. the solvation layer surrounding a protein molecule that is inaccessible to the additive but accessible to water increases as the size of the additive increases) further increases the relative repulsion of arginine with respect to protein size. Thus, the attraction the guanidino residue of arginine has for the protein surface plus the repulsion generated by the greater surface tension increment and the greater size may account for why arginine is neither strongly attracted nor strongly excluded from the protein at low to moderate concentrations. In other words, arginine experiences a balance of attraction and repulsion from the protein surface. Also, the fact that arginine becomes increasingly excluded as the size of the protein increases and is not strongly attracted to the unfolded state, indicates that the repulsion effects are more dominant than the attractive effects since guanidine tends to be more attracted to proteins as the size increases (i.e. there is more surface area to bind to as the size of the protein increases).
However, the attraction that guanidino residues have for a protein and the repulsion generated by surface tension increments and volume exclusion tend to be linear with cosolute concentration at low concentrations. Therefore, if the affinity and repulsion experienced by arginine is additive, then the preferential interaction coefficient should display a linear trend with respect to arginine concentration. However, this is clearly not the trend shown in Figure 3. If arginine has a similar affinity for the protein as guanidine but if such interactions are hindered by surface tension increment (which tends to enhance the binding of water) and steric exclusion effects (which limits the number of additive molecules bound), then it might be possible for the protein surface to become saturated with arginine at a low concentration if the protein does not unfold to allow for more binding. If this happened, any additional arginine added to the solution upon saturation would be merely excluded from the surface.
One means of evaluating such a hypothesis would be to describe the preferential interaction coefficient in terms of the amount of cosolute and water molecules bound to the protein surface:
| (23) |
where gi represents grams of component i per gram of water, and Ai depicts grams of component i bound per gram of protein.6,27 Eq 23 shows that the preferential interaction coefficient is merely a balance between the binding of the cosolute and the binding of water (A3 is always greater than or equal to zero with values being less than the bulk concentration for excluded cosolutes and vice versa for bound cosolutes). However, in order to determine the amount of cosolute molecules bound, A3, the amount of water bound, A1, must be known, not to mention its relationship with cosolute concentration. Other studies have shown that about 0.2-0.3 grams of water typically binds to a gram of protein in the absence of cosolute molecules.6 This number is supported by preferential interaction coefficient values for highly excluded cosolutes (A3 is very small for such cosolutes, thus ξμ3 is approximately equal to -0.3*g3 at low concentrations).
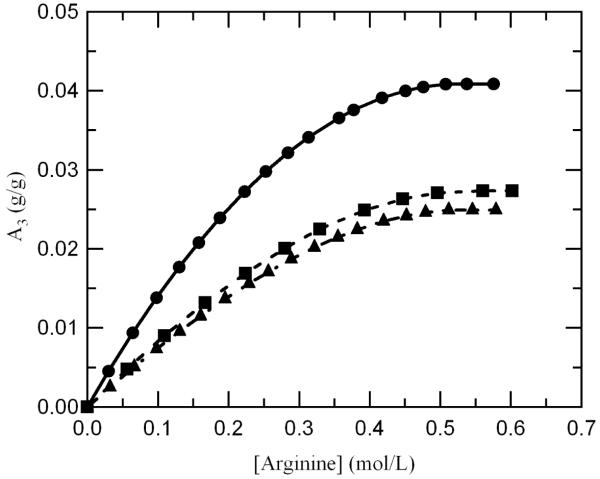
However, it is not clear how high concentrations of different cosolutes influence A1, especially for cosolute molecules which seem to influence the binding of water. For example, preferential interaction data for glycerol indicate that A1 must be at least 0.44 g/g or otherwise A3 would be negative (which would be an unrealistic result). An A1 value of 0.44 g/g indicates that glycerol enhances the binding of water, which is a well known phenomenon due to the solvophobic effects of glycerol and other polyols.40 Typically, it is assumed that A1 remains constant over the entire concentration range since there is a solvation layer accessible to water but not to the cosolute if the cosolute is larger than water. Assuming A1 is 0.3 g/g, arginine A3 values for all three proteins tested were computed from preferential interaction coefficient data. The results indicate that A3 reaches a peak between 0.4-0.5 M and remains constant thereafter, which supports the hypothesis. (See Figure 4) Moreover, this trend holds for A1 values ranging from 0.20-0.45 g/g (assumed to be a typical range for A1 in the presence of a cosolute), which further indicates that the protein surface becomes saturated at about 0.5 M. However, this is a very crude method for determining the amount of arginine bound, since there are no experimental tools for determining A1, and preferential interaction coefficient measurements for arginine are limited to concentrations of less than 0.7 M. The best possible method for exploring this phenomenon is molecular dynamics simulations of arginine interacting with proteins. This would help to elucidate where on the protein surface arginine is interacting and how concentration affects these interactions.
Figure 4.
Comparison of arginine binding (assuming A1=0.3 g/g) for all three proteins tested demonstrating that arginine possibly saturates the surface of the protein at high concentrations leading to preferential exclusion; lysozyme, 14.3 kDa (●), aCgn, 25.7 kDa (■), and BSA, 66.4 kDa (▲).
Conclusions
The results presented here depict how arginine interacts with proteins in the native state and differs from previous reports in that our results indicate that arginine is neutral with respect to binding to the surface of the protein, while previous reports seem to indicate that arginine is strongly bound to some proteins and strongly excluded from others. Our results also reveal why arginine has little effect on the folding equilibrium, because it is neither attracted nor repelled by proteins, which is a hypothesis first proposed by our lab.11
In addition to the results presented here, other researchers have noted that arginine reduces attractive protein-protein interactions as indicated by a shift from a negative to a positive osmotic second virial coefficient.12 Previous work in our lab has shown that arginine significantly decreases the rate of association of globular proteins (as measured by surface plasmon resonance) but only slightly increases the rate of dissociation.11 This differs from guanidine, which only slightly decreases the rate of association but greatly increases the rate of dissociation. Thus, guanidine, in some cases, deters aggregation and promotes refolding by stabilizing the partially unfolded state, whereas, arginine deters aggregation and promotes refolding by slowing association. Such behavior may be explained by a gap effect mechanism, first proposed by our lab.7 The theory states that an additive which is large relative to water but has a negligible effect on the free energy of isolated protein molecules should selectively raise the activation energy for the association reaction and thus deter aggregation. This is because the additive, which solvates isolated protein molecules, cannot solvate the gap that forms between two protein molecules during association, which is entropically unfavorable and thus raises the free energy for the association transition state. The key aspect of this theory is that the additive cannot be strongly bound nor excluded from the protein surface. Excluded additives prefer not to solvate protein molecules; thus, such additives would not deter association due to a gap effect. Strongly bound additives typically promote the unfolding of protein molecules; thus, any gap effect is counteracted by a large increase in aggregation prone species. The preferential interaction coefficient values for arginine reported here seem to support such a theory, because arginine is much larger than water and it is neither strongly bound nor excluded from the protein surface.
Table 3. Summary of Preferential Interaction Coefficients for Lysozyme as Measured by VPOa and Comparison to Literature Values.
| cosolute | Ω3 | Γμ1 | Γμ3b | Γμ1,μ3 | Γμ1,μ3Lit |
|---|---|---|---|---|---|
| argHCl | (1.670 ± 0.001) - (0.560 ± 0.004)m3 | (-1.9 ± 0.3) + (5.2 ± 2.2)m3 - (6.5 ± 3.3)m32 | (5.8 ± 0.4)[3] - (10.8 ± 1.4)[3]2 | (5.5 ± 0.4)[3] - (10.6 ± 1.4)[3]2 | (-3.6 ± 1.6) + (8.0 ± 9)[3] - (9.2 ± 11.3)[3]2 c |
| gdnHCl | (1.770 ± 0.001) - (0.584 ± 0.002)m3 | (-2.0 ± 0.3) + (2.9 ± 0.6)m3 | (3.7 ± 1)[3] | (3.6 ± 1)[3] | N/A |
| glucose | (1.026 ± 0.001) - (0.001 ± 0.002)m3 | (-2.8 ± 0.3) - (2.4 ± 0.5)m3 | (-2.74 ± 0.3)[3] | (-3.07 ± 0.3)[3] | N/A |
| glycerol | (1.018 ± 0.001) - (0.002 ± 0.002)m3 | (-2.2 ± 0.3) - (5.7 ± 0.5)m3 | (-6.3 ± 0.3)[3] | (-6.5 ± 0.3)[3] | N/A |
| urea | (0.962 ± 0.001) - (0.090 ± 0.002)m3 | (-4.3 ± 0.3) + (2.7 ± 0.3)m3 | (3.4 ± 1)[3] | (3.2 ± 1)[3] | (6 ± 1)[3] d |
Footnotes
The authors acknowledge funding support from the National Institutes of Health and the Singapore-MIT Alliance through SMA-1.
References
- (1).Frokjaer S, Otzen DE. Nat. Rev. Drug Discovery. 2005;4:298. doi: 10.1038/nrd1695. [DOI] [PubMed] [Google Scholar]
- (2).Wang W. International Journal of Pharmaceutics. 2005;289:1. doi: 10.1016/j.ijpharm.2004.11.014. [DOI] [PubMed] [Google Scholar]
- (3).Carpenter JF, Kendrick BS, Chang BS, Manning MC, Randolph TW. Methods in Enzymology. 1999;309:236. doi: 10.1016/s0076-6879(99)09018-7. [DOI] [PubMed] [Google Scholar]
- (4).Wang W. International Journal of Pharmaceutics. 1999;185:129. doi: 10.1016/s0378-5173(99)00152-0. [DOI] [PubMed] [Google Scholar]
- (5).Cleland JL, Powell MF, Shire SJ. Critical Reviews in Therapeutic Drug Carrier Systems. 1993;10:307. [PubMed] [Google Scholar]
- (6).Arakawa T, Ejima D, Tsumoto K, Obeyama N, Tanaka Y, Kita Y, Timasheff SN. Biophysical Chemistry. 2007;127:1. doi: 10.1016/j.bpc.2006.12.007. [DOI] [PubMed] [Google Scholar]
- (7).Baynes BM, Trout BL. Biophysical Journal. 2004;87:1631. doi: 10.1529/biophysj.104.042473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (8).Lumry R, Eyring H. Journal of Physical Chemistry. 1954;58:110. [Google Scholar]
- (9).Timasheff SN. Advances in Protein Chemistry. 1998;51:355. doi: 10.1016/s0065-3233(08)60656-7. [DOI] [PubMed] [Google Scholar]
- (10).Minton AP. Current Opinion in Biotechnology. 1997;8:65. doi: 10.1016/s0958-1669(97)80159-0. [DOI] [PubMed] [Google Scholar]
- (11).Baynes BM, Wang DIC, Trout BL. Biochemistry. 2005;44:4919. doi: 10.1021/bi047528r. [DOI] [PubMed] [Google Scholar]
- (12).Tsumoto K, Umetsu M, Kumagai I, Ejima D, Philo JS, Arakawa T. Biotechnology Progress. 2004;20:1301. doi: 10.1021/bp0498793. [DOI] [PubMed] [Google Scholar]
- (13).K RCR, Lilie H, Rudolph R, Lange C. Protein Science. 2005;14:929. doi: 10.1110/ps.041085005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (14).Arakawa T, Tsumoto K. Biochemical and Biophysical Research Communications. 2003;304:148. doi: 10.1016/s0006-291x(03)00578-3. [DOI] [PubMed] [Google Scholar]
- (15).Shiraki K, Kudou M, Fujiwara S, Imanaka T, Takagi M. Journal of Biochemistry. 2002;132:591. doi: 10.1093/oxfordjournals.jbchem.a003261. [DOI] [PubMed] [Google Scholar]
- (16).Liu Y.-d., Li J.-j., Wang F.-w., Chen J, Li P, Su Z.-g. Protein Expression and Purification. 2007;51:235. doi: 10.1016/j.pep.2006.07.001. [DOI] [PubMed] [Google Scholar]
- (17).Kudou M, Shiraki K, Fujiwara S, Imanaka T, Takagi M. European Journal of Biochemistry. 2003;270:4547. doi: 10.1046/j.1432-1033.2003.03850.x. [DOI] [PubMed] [Google Scholar]
- (18).Shiraki K, Kudou M, Nishikori S, Kitagawa H, Imanaka T, Takagi M. European Journal of Biochemistry. 2004;271:3242. doi: 10.1111/j.1432-1033.2004.04257.x. [DOI] [PubMed] [Google Scholar]
- (19).Shiraki K, Kudou M, Sakamoto R, Yanagihara I, Takagi M. Biotechnology Progress. 2005;21:640. doi: 10.1021/bp049769w. [DOI] [PubMed] [Google Scholar]
- (20).Okanojo M, Shiraki K, Kudou M, Nishikori S, Takagi M. Journal of Bioscience and Bioengineering. 2005;100:556. doi: 10.1263/jbb.100.556. [DOI] [PubMed] [Google Scholar]
- (21).Hamada H, Shiraki K. Journal of Biotechnology. 2007;130:153. doi: 10.1016/j.jbiotec.2007.03.003. [DOI] [PubMed] [Google Scholar]
- (22).Courtenay ES, Capp MW, Anderson CF., Jr. M. T. R. Biochemistry. 2000;39:4455. doi: 10.1021/bi992887l. [DOI] [PubMed] [Google Scholar]
- (23).Anderson CF, Courtenay ES, M. T. Record J. Journal of Physical Chemistry B. 2002;106:418. [Google Scholar]
- (24).Anderson CF, Felitsky DJ, Hong J, Record MT. Biophysical Chemistry. 2002;101-102:497. doi: 10.1016/s0301-4622(02)00159-x. [DOI] [PubMed] [Google Scholar]
- (25).Scatchard G. Journal of American Chemical Society. 1946;68:2315. doi: 10.1021/ja01215a054. [DOI] [PubMed] [Google Scholar]
- (26).Baynes BM, Trout BL. Journal of Physical Chemistry B. 2003;107:14058. [Google Scholar]
- (27).Record MT, Anderson CF. Biophysical Journal. 1995;68:786. doi: 10.1016/S0006-3495(95)80254-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (28).Gekko K, Timasheff SN. Biochemistry. 1981;20:4667. doi: 10.1021/bi00519a023. [DOI] [PubMed] [Google Scholar]
- (29).Arakawa T, Timasheff SN. Biochemistry. 1982;21:6536. doi: 10.1021/bi00268a033. [DOI] [PubMed] [Google Scholar]
- (30).Arakawa T, Timasheff SN. Biochemistry. 1984;23:5924. doi: 10.1021/bi00320a005. [DOI] [PubMed] [Google Scholar]
- (31).Timasheff SN, Xie G. Biophysical Chemistry. 2003;105:421. doi: 10.1016/s0301-4622(03)00106-6. [DOI] [PubMed] [Google Scholar]
- (32).Casassa EF, Eisenberg H. Journal of Physical Chemistry. 1961;65:427. [Google Scholar]
- (33).Casassa EF, Eisenberg H. Thermodynamic analysis of multicomponent solutions. Vol. 19. Academic Press; New York: 1964. [DOI] [PubMed] [Google Scholar]
- (34).Zhang W, Capp MW, Bond JP, Anderson CF, M. Thomas Record J. Biochemistry. 1996;35:10506. doi: 10.1021/bi960795f. [DOI] [PubMed] [Google Scholar]
- (35).Hong J, Capp MW, Anderson CF, Record MT. Biophysical Chemistry. 2003;105:517. doi: 10.1016/s0301-4622(03)00112-1. [DOI] [PubMed] [Google Scholar]
- (36).Courtenay ES, Capp MW, M. Thomas Record J. Protein Science. 2001;10:2485. doi: 10.1110/ps.ps.20801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (37).Kita Y, Arakawa T, Lin T-Y, Timasheff SN. Biochemistry. 1994;33:15178. doi: 10.1021/bi00254a029. [DOI] [PubMed] [Google Scholar]
- (38).Wyman J., Jr. Linked functions and reciprocal effects in hemoglobin: a second look. Vol. 19. Academic Press; New York: 1964. [DOI] [PubMed] [Google Scholar]
- (39).Ishibashi M, Tsumoto K, Tokunaga M, Ejima D, Kita Y, Arakawa T. Protein Expression and Purification. 2005;42:1. doi: 10.1016/j.pep.2005.03.028. [DOI] [PubMed] [Google Scholar]
- (40).Timasheff SN. Annual Review of Biophysics and Biomolecular Structure. 1993;22:67. doi: 10.1146/annurev.bb.22.060193.000435. [DOI] [PubMed] [Google Scholar]
- (41).Gekko K, Morikawa T. The Journal of Biochemistry. 1981;90:39. doi: 10.1093/oxfordjournals.jbchem.a133468. [DOI] [PubMed] [Google Scholar]