Abstract
We report a new deconvolution method for fluorescence lifetime imaging microscopy (FLIM) based on the Laguerre expansion technique. The performance of this method was tested on synthetic and real FLIM images. The following interesting properties of this technique were demonstrated. 1) The fluorescence intensity decay can be estimated simultaneously for all pixels, without a priori assumption of the decay functional form. 2) The computation speed is extremely fast, performing at least two orders of magnitude faster than current algorithms. 3) The estimated maps of Laguerre expansion coefficients provide a new domain for representing FLIM information. 4) The number of images required for the analysis is relatively small, allowing reduction of the acquisition time. These findings indicate that the developed Laguerre expansion technique for FLIM analysis represents a robust and extremely fast deconvolution method that enables practical applications of FLIM in medicine, biology, biochemistry, and chemistry.
Index Terms: Discrete Laguerre basis expansion, fluorescence decay deconvolution method, fluorescence lifetime imaging microscopy (FLIM), global analysis
I. INTRODUCTION
Fluorescence lifetime imaging microscopy (FLIM) is based on the measurement of the time that a fluorescence system spends in the excited state before returning to the ground state after light excitation. Thus, lifetime measurement provides information about the localization of a specific fluorophore and its surrounding environment [1]–[4]. This functionality of FLIM has been exploited to study cell metabolism, including measurements of pH [5]–[7], Ca+ concentration [8]–[10], NADH [11], [12], oxygen concentration [13], [14], and fluorescence resonant energy transfer (FRET) [15], [16]. Moreover, since fluorescence lifetime is derived from relative intensity values, it provides useful information about biological tissue composition despite the heterogeneity and strong optical scattering. Thus, FLIM also represents a powerful functional imaging modality for clinical applications [17]–[20].
FLIM can be performed either in the frequency domain or in the time domain [21], [22]. Although frequency-domain FLIM requires simpler experimental setups, it has limited temporal dynamic range and does not allow the analysis of complex decays. Time-domain FLIM, on the other hand, requires more complex instrumentation, but is often more suitable for studying such decays. Time-domain FLIM data is usually obtained by acquiring a series of time-gated fluorescence intensity maps at increasing delays after excitation by ultrashort light pulses. The temporal series of relative fluorescence intensity values for each pixel in the field of view conforms the measured fluorescence decay curve. Mathematically, the measured fluorescence intensity decay is given by the convolution of the intrinsic fluorescence decay or impulse response function (IRF) with the excitation light pulse. To estimate the fluorescence IRF at a given pixel, the excitation light pulse must be deconvolved from the measured fluorescence intensity decay.
The most commonly used deconvolution technique is the nonlinear least-square iterative reconvolution method [23], [24]. This method applies a least-squares minimization algorithm to compute the parameters of a multiexponential model of the fluorescence decay. The reconvolution method, however, involves the successive calculation of a large number of convolutions and is very time consuming. This issue represents a limiting factor, particularly in the context of FLIM, where the analysis of a single image requires deconvolution at every pixel of the image [21]. Furthermore, iterative methods require the acquisition of a considerable number of data samples, which would also increase the acquisition time.
An alternative noniterative rapid lifetime determination technique (RLD) for mono- and biexponential decays [25] has been extensively used in many FLIM applications. RLD, however, requires the assumption of a negligibly short excitation pulse and is restricted to a reduced number of data points, leading to imprecise results [26]. More recently, several other alternative methods for FLIM analysis have been reported. Lee and French et al. [27] proposed the use of a stretch exponential function to fit the fluorescence decays from tissue FLIM images. Although the stretch exponential method provides a good fit of the measured fluorescence decays, this technique does not perform actual deconvolution of the excitation light pulse.
Global analysis algorithms have also been proposed for the analysis of FLIM images [28]–[31]. This approach considers prior information (i.e., spatial invariance of the lifetime of each fluorescent species in the image) to significantly reduce the degrees of freedom in the fitting algorithm, resulting in better estimation of the relevant parameters (i.e., global time constants and maps of relative amplitudes). Verveer et al. showed, for frequency domain FLIM images [28]–[30], that a global fitting was able to accurately estimate the parameters from a system of two exponential decays, whereas pixel-by-pixel analysis could only extract a single average lifetime. Pelet et al. [31] reported a fast global fitting algorithm using iterative convolution to extract two lifetimes of a biexponential system. This method used morphological information derived from the images to make educated initial guesses for the global fitting parameters. Although all these methods have shown significant improvement in fitting quality and computation speed, they still have to assume a single or biexponential model for the decay function and are too computationally expensive for practical application.
In complex biological systems, fluorescence emission typically originates from several fluorophores and is affected by light absorption and scattering. From such a complex medium, however, it is not entirely adequate to analyze the time-resolved fluorescence decay transient in terms of multiexponential functions [27], [32]. Moreover, different multiexponential expressions can reproduce experimental fluorescence decay data equally well, suggesting an advantage in avoiding any a priori assumption about the functional form of the IRF decay physics. Recently, we reported a novel model-free deconvolution method for time-resolved fluorescence point spectroscopy data [33], in which the IRF is expanded on the discrete time Laguerre basis [34]. We demonstrated that this method is able to expand any fluorescence intensity decay of arbitrary form, converging to a correct solution significantly faster than conventional multiexponential approximation methods [33]. Extending on the early work, the goal of the present study was to develop a new method for fluorescence lifetime imaging microscopy analysis, based on the Laguerre expansion technique [33], [34]. The proposed method, which can also be viewed as a global analysis approach, has been tested on synthetic and experimental FLIM images, and its performance was compared against other methods for FLIM analysis.
II. Methods
A. Laguerre FLIM Deconvolution Method
The Laguerre deconvolution technique expands the fluorescence impulse response functions (IRF) on the discrete time Laguerre basis [33]. The Laguerre functions (LF) have been suggested as an appropriate orthonormal basis for expanding asymptotically exponential relaxation dynamics, due to their built-in exponential term [34]. Because the Laguerre basis is complete and orthonormal, a unique characteristic of this approach is that it can reconstruct a fluorescence response of arbitrary form.
In the context of time-domain FLIM, the series of measured time-gated fluorescence intensity maps H(r, t) are given by the convolution of IRF h(r, t) with the excitation light pulse x(t)
| (1) |
where r denotes pixel location, t denotes time gate, K determines the extent of the system memory, T is the sampling interval, h(r, t) is the intrinsic IRF at the pixel r, and N is the number of time-gated images.
The Laguerre deconvolution technique uses the orthonormal set of LF to expand the IRF
| (2) |
where cj (r) are the unknown Laguerre expansion coefficients (LEC) at the pixel r, which are to be estimated from the input-output data; denotes the jth order LF; and L is the number of LFs used to model the IRF.
The LF basis is defined as
| (3) |
The order j of each LF is equal to its number of zero-crossing (roots). The Laguerre parameter (0 < α < 1) determines the rate of exponential decline of the LF and defines the time scale for which the Laguerre expansion of the system impulse response is most efficient in terms of convergence [34]. Thus, fluorescence IRF with longer lifetime may require a larger α for efficient representation. Commonly, the parameter α is selected based on the kernel memory length K and the number of Laguerre functions L, so that all the LFs decline sufficiently close to zero by the end of the impulse response [33], [34].
By inserting (2) into (1), the convolution equation (1) becomes
| (4) |
where is the discrete convolution of the excitation input with the LF of order j, commonly denoted as the “key variable” [34]. The unknown expansion coefficients cj (r) are then estimated by generalized linear least-square fitting, using the data H(r, t) and .
The proposed FLIM deconvolution method takes advantage of the orthogonality of the Laguerre functions [34], which implies that the expansion coefficients are independent from each other and can be estimated separately. This condition allows us to reformulate the computation of the Laguerre expansion coefficients given in (4) as follows. Let us first resample the key variables at the times tk, k = 1, 2,…, N, at which the images H(r, t) were acquired. By considering the case when j = 0 in (4), the first expansion coefficient can be estimated using the images H(r, tk) and the first resampled key variable by solving the following system of linear equations:
| (5) |
The analytical solution of c0(r) as defined in (5) using a least-square approach is given by
| (6) |
Where is a vector containing the N values of the key variable, and is defined as
| (7) |
Finally, (6) can be rewritten in a term-by-term form as
| (8) |
The previous expression indicates that the complete map of coefficients c0(r) is given simply by the sum of the delayed images H(r, tk) weighted by the values at the corresponding gated times tk, k = 1, 2,…, N, and normalized by the sum of squares of the key variable values over all the gated times. Since this operation involves only the sum of N weighted images, its computation can be performed very fast.
Once the map of the first expansion coefficient c0(r) is computed, the maps of the higher expansion coefficient cj (r)(j = 1,…, L −1) can be estimated using a similar approach described as follows. Let us generalize the method for the estimation of the jth expansion coefficient map cj (r). First, the N “residual images” resulting after the estimation of the previous map cj−1(r) are computed as follows:
| (9) |
with initial condition H0(r, tk) = H (r, tk).
Finally, cj (r) is solved by updating (8) as follows:
| (10) |
Again, the estimation of the complete maps of the L expansion coefficients involves only sums and subtractions of matrixes, making the process very fast. Once the maps of expansion coefficients are estimated, the map of lifetimes can be determined by first constructing the IRF at every pixel using (2). The lifetime map is then computed by interpolating the time point at which the IRF becomes 1/e of its maximum value. This last process involves matrix subtractions and arrays division, thus demanding longer computation time than the estimation of cj (r).
B. Global Analysis: The Laguerre Expansion and Biexponential Methods
In the context of FLIM, it can often be assumed that the fluorescence signal is coming from a given number of molecular species with different lifetimes, whose relative contribution vary spatially, but the lifetime values themselves remain invariant. Under this condition, instead of analyzing each pixel separately, it may be more accurate to analyze all pixels simultaneously. This approach is adopted in global analysis. Recently, global analysis has been applied to FLIM data, in which the pixel decays are assumed biexponential, with fixed global time constants and a spatially variable intensity ratio of the two lifetime components [28]–[31]. Similarly, our proposed Laguerre FLIM deconvolution method uses a common Laguerre basis to expand the decays at every pixel of the complete images, and estimate the maps of expansion coefficients. Thus, the Laguerre method can be considered as a global analysis approach. In this section, we demonstrate how the Laguerre expansion technique is analytically related to the global biexponential fitting approach.
Let us assume that the deconvolved image h(r, t) given in (2) can also be expressed as a biexponential expansion as follows:
| (11) |
Here, the global time constants (τ1, τ2) and the intensity ratio of the two lifetime components A1(r) at every pixel r have to be estimated from the data by global analysis. The parameter s represents a scaling factor, which for simplicity, is not carried on in the rest of the analysis.
Let us also assumed that each exponential component in (11) is expanded using the same Laguerre basis as in (2), yielding the following relations:
| (12) |
Inserting (12) in (11), the expression of the deconvolved image becomes
| (13) |
Finally, from (2) and (13), we can relate the expansion coefficients cj (r) of the deconvolved image h(r, t) to the intensity ratio of the two lifetime components A1(r) as follows:
| (14) |
Equation (14) clearly shows that each Laguerre expansion coefficient cj (r) is linearly related to the intensity ratio of the two lifetime components A1(r). In practice, we may not need to estimate the global time constants (τ1, τ2) and compute their expansion coefficients {a1,j, a2,j} and the actual values of A1(r). The relation given by (14) demonstrated that the relative contribution of the two exponential components can be indirectly monitored extremely quickly by means of the expansion coefficients cj (r).
C. Synthetic FLIM Image Generation
The synthetic FLIM images of 64 × 64 pixels were generated by means of a biexponential model, with fixed decay constants (2 and 12 ns) and increasing relative contributions of the shortest lifetime. White noise of zero mean and two different variance levels was added to the data, yielding two different sets of images, at approximately 40- and 26-dB signal-to-noise ratios (SNRs). A laser pulse (see Section II-E) was used as the excitation signal for our simulation. All the data sets were convolved with the laser signal and arranged accordingly to form the synthetic FLIM image series for our simulation.
D. Validation of the Laguerre Method Against Standard and Global Algorithms
The Laguerre deconvolution technique was applied to the synthetic FLIM images, using model orders ranging from 3–6 LFs. Three other deconvolution algorithms were also applied to validate our technique. The first was based upon the standard “biexponential” fitting, where all three parameters (two time constants and relative amplitude) are estimated independently at every pixel. The second was a “time invariant” fit method [28], where the two time constants are extracted from a decay curve calculated from the sum of all pixels, and kept fixed for the computation of the relative amplitudes at every pixel. The third was a recently developed “global” analysis approach that uses iterative convolutions to extract the two global lifetime components corresponding to the whole image, and the map of relative amplitudes. The code for the global analysis was provided by Dr. Serge Pelet, from the Department of Mechanical Engineering and Division of Biological Engineering, at the Massachusetts Institute of Technology [31].
E. Experimental FLIM Images Acquisition
Four sets of measured FLIM images were used for algorithm validation. Data was collected from: 1) a solution of Rose Bengal (R3877, Sigma-Aldrich, St. Louis, MO) in ethanol; 2) a solution of Rhodamine B (25 242, Sigma-Aldrich) in ethanol; 3) rat glioma C6 cells (ATCC CCL-107) stained with JC-1 (J-aggregate formation of the lipophilic cation, Molecular Probes); and 4) rat glioma C6 cells (ATCC CCL-107) stained with Rhodamine 123 (Molecular Probes). An inverted microscope (Axiovert 200, Carl Zeiss, Germany) operating in epi-illumination mode was utilized for the FLIM image acquisition. A subnanosecond nitrogen laser (MNL200, Lasertechnik Berlin, Berlin, Germany) was used to provide excitation at 337.1 nm with a full-width at half-maximum (FWHM) pulse duration of ~700 ps (maximum pulse energy 100 μJ, repetition rate 0–50 Hz). A picosecond gated ICCD imaging system (PicoStar HR12, LaVision, Gottingen, Germany) was used for gated time-domain image acquisition.
III. Results
A. Laguerre Method Accuracy Tested on Synthetic FLIM Images
Fig. 1 depicts the map of the model-derived lifetimes of the synthetic FLIM images at 40 dB SNR and the corresponding maps of estimated lifetimes, normalized mean square error (NMSE), and first three Laguerre expansion coefficients (LEC-0 to LEC-2). The map of estimated lifetime values closely resembled the map of the synthetic lifetime values. The normalized mean square errors (NMSE) estimated from the reconstructed decays computed at every pixel of the image showed values below 2%. The maps of LEC-0 and LEC-2 resembled the variation in the lifetime values, while LEC-3 showed the opposite trend. These findings suggested that the Laguerre expansion coefficients are correlated with the lifetime values. A synthetic and estimated decay at a sample pixel and the corresponding normalized error (Nerr) and residual autocorrelation function (ACorr) are shown in Fig. 1 (bottom panels). The Nerr was below 5% and the ACorr was mostly contained within the 95% confidence interval (dotted lines). These observations indicate an excellent fit between the synthetic and estimated fluorescence decays, showing that the fluorescence IRF was properly estimated by the Laguerre deconvolution.
Fig. 1.
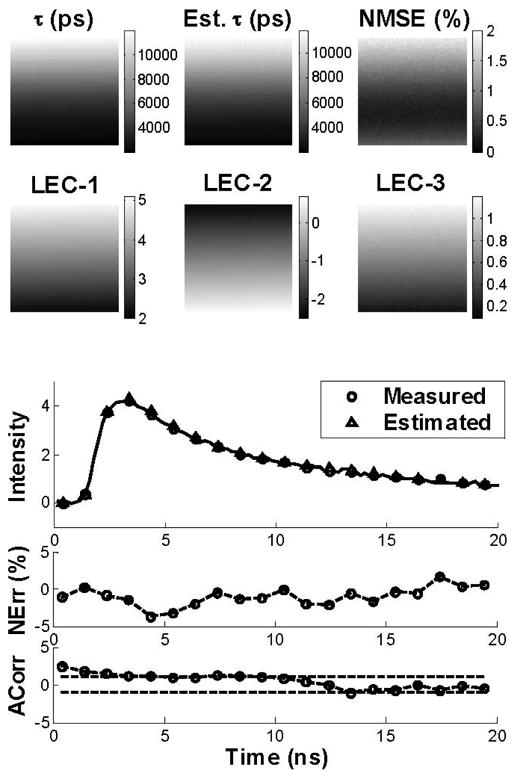
Synthetic images. Top panels: Analysis of the FLIM images at 40-dB SNR, showing the maps of the model-derived lifetimes, the estimated lifetimes, the normalized mean square error (NMSE), and the first three Laguerre expansion coefficients (LEC-0 to LEC-2). The bar-scales (left side of the maps) show the range of values on the maps. Bottom panels: Synthetic and estimated decays from a sample pixel of the image are shown with the corresponding normalized estimation error (NErr) and its autocorrelation function (Acorr).
Similar results were obtained from the analysis of the synthetic FLIM images at 26-dB SNR (Fig. 2). In this case, however, the map of estimated lifetimes appeared noisy and biased comparing to the synthetic lifetime map, although still resembling the lifetime variation. The NMSE values were higher (about 10%) than in the 40-dB case. The maps of LECs were noisier when compared to the ones obtained at 40-dB SNR but still resembled the variation in the lifetime values. The NErr was below 10% and the ACorr was mostly contained within the 95% confidence interval (dotted lines). These observations also indicate a good fit between the synthetic and estimated fluorescence decays in spite of the considerable noise level, suggesting robustness of the Laguerre technique.
Fig. 2.
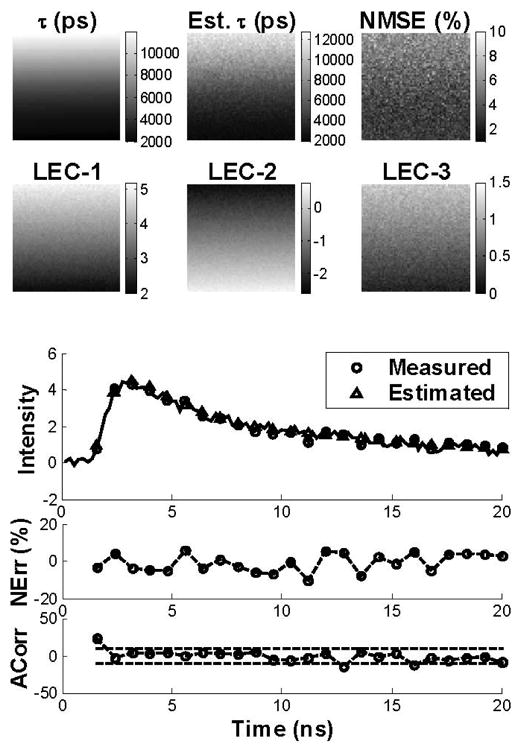
Synthetic images. Top panels: Analysis of the FLIM images at 26-dB SNR, showing the maps of the model-derived lifetimes, the estimated lifetimes, the normalized mean square error (NMSE), and the first three Laguerre expansion coefficients (LEC-0 to LEC-2). The bar-scales (left side of the maps) show the range of values on the maps. Bottom panels: Synthetic and estimated decays from a sample pixel of the image are shown with the corresponding NErr and Acorr.
B. Global Analysis: The Laguerre Expansion and Biexponential Methods
To quantify the accuracy of the Laguerre technique for estimating the lifetime values of the image pixel decays, we applied a correlation analysis between the synthetic and the estimated lifetimes. The results (Fig. 3) showed a perfect (r = 1) and near perfect (r = 0.99) correlation between estimated and synthetic lifetimes at 40-dB and 26-dB SNR, respectively.
Fig. 3.
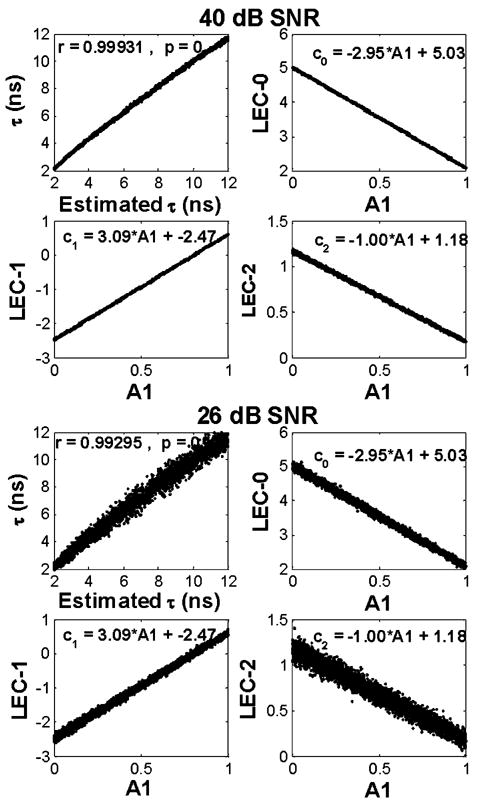
Synthetic images. Correlation between synthetic and estimated lifetimes; and the linear relations between the LECs and the intensity ratio A1 of the two underlying lifetime components. Top panels: 40-dB images. Bottom panels: 26-dB images. The equations correspond to the least-square solution of a linear fitting to the LEC versus A1 data.
As shown in (14), each LEC cj (r) is linearly related to the intensity ratio of the two underlying lifetime components A1(r) from the biexponential model. By means of analysis of the synthetic biexponential FLIM images, it was possible to confirm experimentally the linear relation between cj (r) and A1(r). As observed in Fig. 3 at both 40-dB and 26-dB SNR, the first three LECs were linearly related to the relative intensity A1(r) of the two underlying lifetime components. More interestingly, these linear relations were unaffected by the noise level (40 dB left, 26 dB right), as shown by the linear equations derived from least-square fitting of the LECs versus A1(r) data. Furthermore, these linear relations derived from data fitting were compared against the ones obtained analytically using (14). The results (Table I) indicate that the analytical derivation of the cj (r) equations under both noise levels resembled very closely the actual cj (r) versus A1(r) relations obtained by data fitting.
TABLE I.
Linear Relations Between LECS (cj ) and A1 Derived Analytically and From Data Fitting
C. Validation of the Laguerre Methods Against Current Algorithms
The results obtained from the analysis of the synthetic FLIM images by the Laguerre deconvolution technique were compared against the performance by standard and global methods. The results of this intermethodology comparison are summarized in Fig. 4 and Table II. The true intensity ratios A1(r) and their estimated values using the standard biexponential, time invariant, global analysis, and Laguerre methods, at 40- and 26-dB SNR are shown in Fig. 4. All tested algorithms provided a good estimation of the A1(r). The Laguerre and the time invariant algorithms were almost insensitive to the noise level and provided good estimation of A1(r) at both 40- and 26-dB SNR. The global analysis and the standard biexponential algorithms performed well at 40-dB SNR, but were sensitive to the noise level providing less accurate estimation at 26-dB SNR. The standard biexponential algorithm provided the less accurate estimation overall. The histograms of the deviations of the estimated A1(r) from their true values by all the algorithms tested are also given in Fig. 4. The Laguerre and the time invariant methods presented small deviations from the true A1(r) values (less than 0.03 ns and 0.1 ns at 40- and 26-dB SNR, respectively), although the time invariant method performed slightly better. The global fitting and the standard biexponential methods presented larger deviation from the true A1(r) values (less than 0.05 ns and 0.2 ns at 40- and 26-dB SNR, respectively).
Fig. 4.
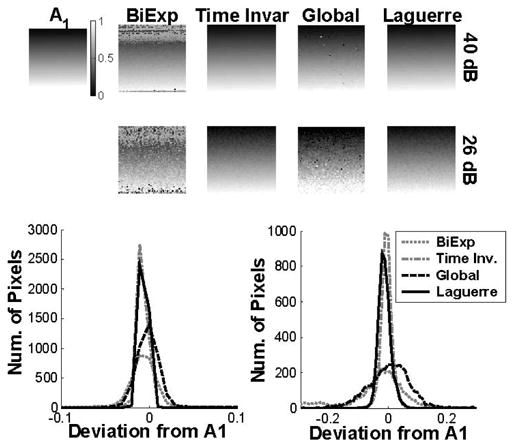
Comparison of the deconvolution methods. Top panels: True intensity ratio A1 (ranging from 0 to 1) of the two lifetime components, and the corresponding estimated values using the standard biexpoential, time invariant, global, and Laguerre methods, at 40-dB and 26-dB SNR. Bottom panels: Histogram of the deviations of the estimated A1 from their true values by each of the algorithms tested.
TABLE II.
Computation Time by The Four Methods
| Computation Time (s) | |||||
|---|---|---|---|---|---|
| BiExp | Time Invar. | Global | Laguerre* | ||
| SNR | 40 dB | 5007.2 | 508.3 | 380.8 | (0.4) 1.1 |
| 26 dB | 3954.5 | 534.1 | 683.9 | (0.4) 1.1 | |
The value within paranthesis is the time spent for computing the maps of LEC, while the second value is the total time spent for computing the maps of LEC and lifetime.
In addition, the computation time spent by each algorithm to analyze the synthetic FLIM images were assessed and compared (Table II). By far, the Laguerre deconvolution approach was the fastest of all methods tested (0.4 s to compute the LECs, and 1.1 s to compute the lifetime values). The computational time was also insensitive to the noise level. The global fitting and the time invariant algorithms showed similar computation time (~380–700 s), and the standard biexponential method presented by far the slowest performance (> 3000 s). These results indicate that the Laguerre method was at least two orders of magnitude faster than the global analysis and the time invariant algorithms, and at least three orders of magnitude faster than the standard biexponential method.
D. Analysis of the Measured FLIM Images
1) Fluorescence Lifetime Standards
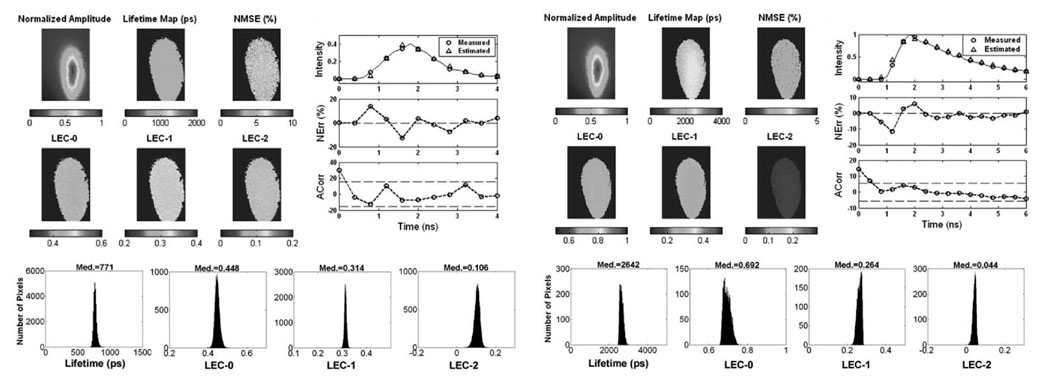
Results of the analysis of FLIM images from the solution of Rose Bengal in ethanol are presented in Fig. 5. The intensity map showed higher values at the center of the image, while the lifetime map was uniform with values at about 750 ps. The maps of Laguerre expansion coefficients were also uniform. The map of NMSE showed values below 10%, indicating a very good fitting for every pixel of the image. The Nerr were below 20% and randomly distributed around zero. The autocorrelation function of the residuals was mostly contained within the 95% confidence interval (dotted lines). These observations also indicate a good fit between the measured and estimated fluorescence decays. The map histograms indicate the range of lifetime and LECs values present in the image. All the parameters showed a narrow distribution. The lifetime was centered at 771 ps, the LEC-0 at 0.448, the LEC-1 at 0.314, and the LEC-2 at 0.106. The average lifetime value was very close to the lifetime of 769 ps obtained from spectroscopy measurements of equivalent solution with a time-resolved fluorescence spectroscopy system, as previously reported [33].
Fig. 5.
Results of the analysis of FLIM images from Rose Bengal in ethanol (Upper panels). Color panels: maps of normalized intensity values, lifetimes, NMSE, and normalized LECs. The bar-scales on the bottom of the maps show the range of values on the maps. Upper right panels: measured and estimated decays corresponding to a sample pixel of the image and the corresponding NErr and Acorr. Bottom panels: map histograms indicating the distribution of lifetime and LECs values in the image. Results of the analysis of FLIM images from Rhodamin B in ethanol are also shown below.
Results of the analysis of FLIM images from the solution of Rhodamin B in ethanol are also presented in Fig. 6. For this case, the lifetime map was uniform with values ~2500 ps. The maps of Laguerre expansion coefficients were also uniform. The map of NMSE showed values below 5%. The Nerr and ACorr also indicate good fit. The parameter histograms also showed a narrow distribution, with the lifetime centered at 2642 ps, the LEC-0 at 0.692, the LEC-1 at 0.264, and the LEC-2 at 0.044. The average lifetime value was very close to the lifetime of 2872 ps obtained spectroscopically [33].
Fig. 6.
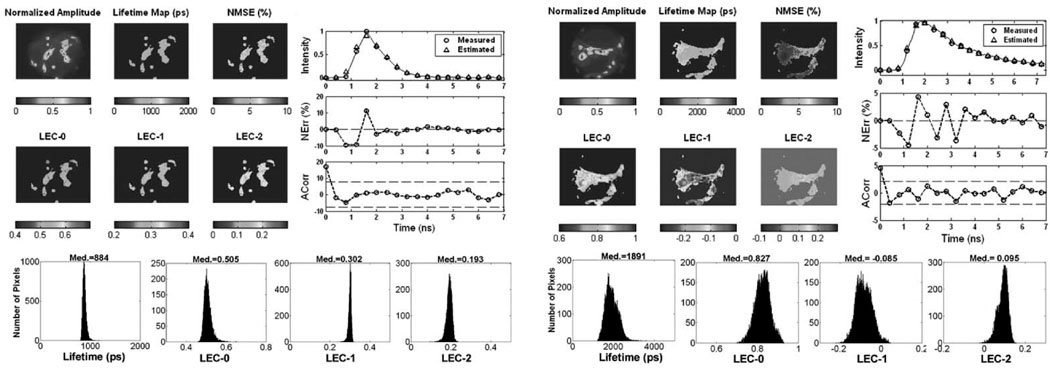
Results of the analysis of FLIM images from glioma cells in JC-1 (upper panels). Color panels: maps of normalized intensity values, lifetimes, NMSE and normalized LECs. The bar-scales on the bottom of the maps show the range of values on the maps. Upper right panels: measured and estimated decays corresponding to a sample pixel of the image and the corresponding NErr and Acorr. Bottom panels: map histograms indicating the distribution of lifetime and LEC values in the image. Results of the analysis of FLIM images from gliomacells in R123 are also shown below.
2) Live Cell Imaging
The FLIM images from the glioma cells stained with JC-1 are presented in Fig. 6. The intensity image presented a large variability across the cell, while the maps of lifetime and Laguerre expansion coefficients were also uniform. The map of NMSE, and the Nerr and ACorr showed good fit between measured and estimated decays. All the parameter histograms showed a narrow distribution. The lifetime was centered at 884 ps, the LEC-0 at 0.505, the LEC-1 at 0.302, and the LEC-2 at 0.193.
The FLIM images from the glioma cells stained with R-123 dye are also given in Fig. 6. The intensity image presented different levels with higher values on the cell membrane. The lifetime map was uniform in the areas corresponding to the glioma cells, presenting values around 1800–2000 ps. Longer lifetimes, in the order of 2000–2500 ps, were also present in the vicinity of the cells, but were less representative. The map of LEC-0 showed values in the order of 0.85–0.9 within the cell areas, and lower values (<0.85) in the vicinity of the cells. The map of LEC-1 presented similar distribution as LEC-0, although showing negative values in the range of −0.2– 0, where the cell areas corresponded to the less negative values. The map of LEC-2 showed values between 0 and 0.1. The map of NMSE showed values below 5%, and the Nerr was below 5% and randomly distributed around zero. The autocorrelation function of the residuals was contained within the 95% confidence interval (dotted lines). The lifetime histogram was centered at 1891 ps and was broad covering a range of 1500–2500 ps. The histogram of LEC-0 and LEC-1 were also broad (covering values between 0.7–0.9 and −0.2–0, respectively) and centered at 0.827 and −0.085, respectively. The histogram of LEC-2 presented a short tail towards the lower values and was centered at 0.095.
IV. Discussion
Validation in synthetic FLIM images
The Laguerre deconvolution technique was successfully tested in a set of synthetic FLIM images covering a broad range of lifetime values (2–12 ns) derived from a biexponential model. This lifetime range was chosen intentionally, since a number of biologically relevant fluorophores emit in this time scale. The choice of a biexponential model was also adequate, since current FLIM analytical methods (including the ones compared in this study) are not usually applied for more than two exponential components. The proposed Laguerre deconvolution method was found versatile and robust as demonstrated by its ability to accurately retrieve the underlying IRFs at every pixel of the synthetic FLIM images covering a broad dynamic range under moderate noise condition (40- and 26-dB SNR).
Our results demonstrated that each Laguerre expansion coefficient is highly correlated with the intrinsic lifetime value. For the case of the multiexponential deconvolution, the estimated average lifetime usually correlates with the intrinsic radiative lifetime. However, the individual multiexponential parameters (decay constants and pre-exponential coefficients) may not necessarily correlate to the intrinsic lifetimes. This was shown in Fig. 4, where the standard biexponential method was not able to accurately estimate the intensity ratio of the two underlying lifetime components A1(r). The lack of correlation between individual multiexponential parameters and the radiative lifetime is a result of the intrinsic nature of the multiexponential model. This model does not represent an orthogonal expansion of the fluorescence IRF. Therefore, the estimated fitting parameters are not independent from each other (the value of one parameter would be determined by both the data to be fitted and the value of the other fitting parameters) [32]. In contrast, the Laguerre basis provides an orthogonal expansion of the IRF. Consequently, the value of each LEC depends exclusively on the data to be fitted, making them highly correlated to the actual decay lifetime values [33].
Global analysis
Another interesting observation is that the Laguerre deconvolution technique represents a way of performing global analysis on the FLIM images. In the context of classical global analysis for FLIM, the spatial invariance of the lifetimes of each exponential component (fluorescence specie) is often assumed [28], [31]. That is, a global analysis algorithm will estimate a unique set of time constants for the entire image, and maps of relative intensities of the underlying exponential components. Similarly, the Laguerre technique uses a unique Laguerre basis (defined by the Laguerre parameter α) to expand the complete set of IRFs at every pixel of the images. Thus, only a single parameter α and the maps of LECs are to be estimated from the data. Thus, the estimation of the spacial invariant time constants can be related to the estimation of the Laguerre parameter α, and the computation of the maps of relative exponential intensities to the computation of the maps of LECS. One advantage of the Laguerre method, however, is that for any value of the Laguerre parameter α, the corresponding basis of LF is complete and orthonormal. Thus, it is certain that the maps of expansion coefficients can always be found and are unique for the defined Laguerre basis. In contrast, deconvolution with the multiexponential approach may yield more than one solution, even when the number of exponential or the values of the time constants are prefixed.
We also demonstrated, both mathematically (14) and experimentally (from the analysis of the synthetic data, Table I), that for the specific case of two fluorescence species in a single image, each LEC is linearly related to the relative intensity A1(r) of the two lifetime components. Thus, the maps of LECs are correlated to the map of A1(r) and indirectly reflect the spatial variation of the biexponential relative intensities. These two findings indicates that the maps of Laguerre expansion coefficients constitute an extremely fast and original way of representing spatial distribution of time-resolved characteristics of fluorescence species in a field of view, and has the potential for quantitative interpretation of FLIM data.
It is important to note that, for the case of the synthetic data, the two exponential components were known a priori, so it was possible to compute their Laguerre expansion coefficients {a1,j, a2,j} and the relative intensity values A1(r). In practice, however, we may not need to estimate the global time constants of the fluorescence species to compute the map of relative amplitudes. The relation given by (14) demonstrated that the map of relative intensities can be indirectly but extremely fast monitored by means of the maps of Laguerre expansion coefficients. And even when the actual values of A1(r) be required, a globally biexponential fit can always be performed on the estimated IRFs obtained by the Laguerre technique. The values of A1(r) can then be estimated using {a1,j, a2,j} from the derived global time constants on (14). This approach will represent a much faster way of performing global analysis on the complete FLIM image, since only curve fittings instead of deconvolution operations are required.
Validation against other methods
This study also demonstrates the advantages of the proposed Laguerre deconvolution technique with respect to conventional and other recently proposed deconvolution methods [28], [31]. Our results indicated that the Laguerre and the time invariant methods provide the best performance in terms of estimating the A1(r) values of the synthetic images. One explanation for the good performance of the time invariant method is that the synthetic FLIM images were, in fact, generated by two exponential components with fixed time constants. This is exactly the assumption made by the time invariant method. However, when the data diverges from this strict assumption, as is often the case in practical application, the time invariant method would probably perform less accurately, as it has been demonstrated in other studies [26], [28], and [31]. In contrast, the Laguerre method does not make any assumption about the functional form (decay function) of the data. Moreover, and due to the orthogonality of the Laguerre basis, our method has the capability of always expanding any IRF of arbitrary form. Thus, the Laguerre deconvolution technique is a suitable approach for the analysis of time-domain fluorescence data from complex systems. It is also relevant to notice that the global analysis methods provided a good estimation of the relative intensities from the synthetic data, in spite of not reaching the accuracy of the Laguerre method (especially under noisy conditions). This particular result together with the poor performance showed by the standard biexponential method indicate that global approaches outperform pixel-by-pixel methods for the analysis of FLIM data, as it has already been supported by other studies [28], [31].
Computation speed
One of the most important finding of this study was the clear advantage in terms of computation speed of the Laguerre deconvolution technique over the other methods considered. The proposed Laguerre method takes advantages of the orthogonality of the Laguerre functions. This implies that the expansion coefficients are independent from each other, and therefore, each of them can be estimated separately. Unlike standard FLIM global methods, which involve the iterative computation of convolutions, the estimation of the complete maps of the LECs involves only sums and subtractions of the complete delayed images, making this process extremely fast. Furthermore, since the set of expansion coefficients summarize the temporal properties of the IRF [33], a complete characterization of the fluorescence decay at every pixel of the image can be achieved in a few seconds. Due to its ultrafast performance, the Laguerre method has the potential to be applied for the study of dynamics events, allowing for monitoring temporal and spatial variation of time-resolved characteristics of fluorescence specimens. Thus, we consider that the proposed Laguerre deconvolution technique for FLIM analysis could have a great impact in a broad range of applications in medicine, biology, biochemistry, and chemistry.
Validation in experimental FLIM images
The Laguerre deconvolution method was also successfully tested on measured FLIM images from both fluorescence lifetime standards and glioma cells stained with fluorescence probes. The fact that the fluorescence standard lifetime values obtained by the Lagurre method were very close to their literature reported values [33], confirms the accuracy of our technique. Also important was our finding that short lifetimes (rose Bengal in ethanol) could be accurately retrieved by the Laguerre technique, suggesting the convenience of performing actual deconvolution for the analysis of fast fluorescence decays. For the case of the FLIM images from glioma cells stained with Rhodamine 123, the lifetimes obtained (~2000 ps) were slightly shorter than the ones (2500–2800 ps) reported in a previous study [35]. One possible explanation for this difference may be related to the analytical methods used. The referred above study applied plain curve fitting to analyze the FLIM data, while our method performed actual deconvolution of the excitation pulse from the complete images. Since the width of the excitation pulse cannot always be infinitesimally short, the convolved IRF (which corresponds to the measured decay curved fitted by standard methods) is always broader than the actual IRF (estimated by our method). Thus, a shorter but more realistic lifetime value by our technique is expected.
The observations that the maps of the LEC resemble the distribution of lifetimes in the cell images also support the idea of using the LEC as a new domain of representing spatial distribution of time-resolve information for FLIM applications. These results could be translated to other more interesting application, such as fluorescence energy resonance transfer (FRET) experiments [15], [16]. In FRET experiments, one expects to measure two different lifetimes produced by interacting and noninteracting proteins. The noninteracting labeled proteins exhibit a natural lifetime of the dye, whereas the interacting proteins will exhibit a shorter lifetime due to the quenching of the emission by energy transfer. The spatial configuration of the donor and acceptor is fixed upon binding, which determines the decrease in the donor lifetime. When FRET is imaged with FLIM, the decay model is assumed to be biexponential with spatially invariant lifetimes. Therefore, an ultrafast global analysis approach, such as the Laguerre deconvolution method, could represent a powerful tool for evaluating the populations and properties of bound and unbound proteins states in cells. Although the results of the present study are encouraging, we realize that the proposed Laguerre method still need to be thoroughly validated on a broad variety of FLIM applications.
Another observation is that the Laguerre method needs only half or less of the acquired delayed images available for the analysis of the measured FLIM data. This indicates that accurate estimation of the IRF at every pixel can be achieved with considerably few data points with the proposed technique, in contrast to standard FLIM deconvolution methods that require the acquisition of tens of delayed images [21]. Therefore, since less delayed images would be needed, our method would not only allow for a significant reduction of the computation time but also of the acquisition time. This would be highly desirable in the context of functional fluorescence lifetime imaging, where real-time acquisition is required.
Finally, most algorithms used on current FLIM systems require the assumption that the excitation light pulses are negligibly short, so that the fluorescence emission can be approximated to the intrinsic IRF [21]. To accommodate this requirement, these systems need to use ultrafast (i.e., femtosecond) light sources, which are in general too expensive and sophisticated to be used in practical applications. Since our proposed Laguerre technique deconvolves the excitation light pulse from the measured images within seconds, the requirement of an ultrashort excitation pulse can be relaxed. Thus, our technique has the potential for promoting the development of less expensive and less complex FLIM systems that could be used in a variety of practical applications.
V. Conclusion
We have developed and tested a new method for analysis of fluorescence lifetime imaging microscopy data based on the Laguerre expansion technique [33], [34]. The results of this study demonstrated a number of interesting properties. 1) The intrinsic fluorescence intensity decays of any form can be estimated at every pixel of the image as an expansion on a Laguerre basis, without a priori assumption of its functional form, thus providing a robust and versatile method for FLIM analysis. 2) Since the fluorescence IRF at every pixel is expanded in parallel using a common Laguerre basis, the computation speed is extremely high, performing at least two orders of magnitude faster than standard deconvolution algorithms. 3) The estimated maps of Laguerre expansion coefficients offer a new domain for representing the spatial distribution of the time-resolved characteristics of the fluorescence specimens imaged by FLIM. 4) The Laguerre deconvolution technique represents a way of performing global analysis in the FLIM images very fast and accurate. 5) The number of images required to expand the fluorescence IRF is relatively low, thus allowing the reduction of the acquisition time. In addition, since actual deconvolution of the excitation pulse is performed, ultrafast light sources are not longer required, allowing to promote the development of less expensive FLIM systems.
Although our method still have to be validated on a broad variety of FLIM applications, the results of this study indicate that the Laguerre deconvolution technique represents a more robust and extremely fast analytical method. The developed technique will likely enable the use of FLIM in practical real-time applications in medicine, biology, biochemistry, and chemistry.
Acknowledgments
The authors would like to thank Prof. M. Gundersen from the Department of Electrical Engineering/Electro-Physics, University of Southern California, Los Angeles, for his support on the experimental aspects of this study. The authors are also grateful to Dr. S. Pelet from the Department of Mechanical Engineering and Division of Biological Engineering, Massachusetts Institute of Technology, for providing the codes for the global analysis algorithm used in this study.
Biographies
Javier A. Jo (M’98) received the Diploma in electrical engineering from the Pontifical Catholic University of Peru, Lima, Peru, in 1997, and the M.S. degree in electrical engineering and the Ph.D. degree in biomedical engineering from the University of Southern California, Los Angeles, in 2000 and 2002, respectively.
He is currently a Research Scientist in the Department of Surgery of Cedars-Sinai Medical Center, Los Angeles. His research interests include developing advanced analytical methods for time-resolved fluorescence spectroscopy and imaging with application in cardiovascular and cancer diagnosis.

Qiyin Fang (M’02) received the B.S. degree in physics from Nankai University in 1995, and the M.S. degree in 1998 in applied physics and the Ph.D. degree in 2002 in biomedical physics, both from East Carolina University.
He is currently an Assistant Professor in the Department of Engineering Physics, McMaster University, Hamilton, ON, Canada. Prior to his current position, he was a Research Scientist in the Biophotonics Research and Technology Development Laboratory at Cedars-Sinai Medical Center, Los Angeles, CA. His research interests include optical spectroscopy and imaging for biomedical and clinical applications and ultrafast laser pulse interaction with biological systems.

Laura Marcu received the Diploma in mechanical engineering (precision mechanics and optical instruments) from the Polytechnic Institute of Bucharest, Bucharest, Romania, in 1984, and the M.S. and Ph.D. degrees in biomedical engineering from the University of Southern California, Los Angeles, in 1995 and 1998, respectively.
Presently, she is Director of the Biophotonics Research and Technology Development Lab in the Department of Surgery at the Cedars-Sinai Medical Center, Los Angeles, where she has established a research program in biophotonics. She is also a Research Associate Professor in the Departments of Electrical Engineering-Electrophysics and Biomedical Engineering at the University of Southern California, Los Angeles. Her current research involves application of optical spectroscopy and imaging to medicine and biology.

Footnotes
This work was supported by the National Institute of Health under Grant R01 HL 67377 and by The Whitaker Foundation.
Contributor Information
Javier A. Jo, J. A. Jo is with the Biophotonics Research and Technology Development, Department of Surgery, Cedars-Sinai Medical Center, Los Angeles, CA 90048 USA (e-mail: joj@cshs.org)..
Qiyin Fang, Q. Fang is with the Department of Engineering Physics, McMaster University, Hamilton, ON L8S4L8, Canada (e-mail: gfang@mcmaster.ca)..
Laura Marcu, L. Marcu is with Biophotonics Research and Technology Development, Department of Surgery, Cedars-Sinai Medical Center, Los Angeles, CA 90048 USA and the Departments of Electrical and Biomedical Engineering, University of Southern California, Los Angeles, CA 90048 USA (e-mail: lmarcu@bmsrs.usc.edu)..
References
- 1.Dowling K, Dayel MJ, Hyde SCW, French PMW, Lever MJ, Hares JD, Dymoke-Bradshaw AKL. High resolution time-domain fluorescence lifetime imaging for biomedical applications. J Modern Opt. 1999;46:199–209. [Google Scholar]
- 2.Tadrous PJ. Methods for imaging the structure and function of living tissues and cells: 2. Fluorescence lifetime imaging. J Pathology. 2000;191:229–234. doi: 10.1002/1096-9896(200007)191:3<229::AID-PATH623>3.0.CO;2-B. [DOI] [PubMed] [Google Scholar]
- 3.Sauer M, Tinnefeld P. Spectrally-resolved fluorescence lifetime imaging of single molecules on surfaces and in living cells. Biophys J. 2001;80:789. [Google Scholar]
- 4.Elson D, Requejo-Isidro J, Munro I, Reavell F, Siegel J, Suhling K, Tadrous P, Benninger R, Lanigan P, McGinty J, Talbot C, Treanor B, Webb S, Sandison A, Wallace A, Davis D, Lever J, Neil M, Phillips D, Stamp G, French P. Time-domain fluorescence lifetime imaging applied to biological tissue. Photochem Photobiol Sci. 2004;3:795–801. doi: 10.1039/b316456j. [DOI] [PubMed] [Google Scholar]
- 5.Sanders R, Draaijer A, Gerritsen HC, Houpt PM, Levine YK. Quantitative pH imaging in cells using confocal fluorescence lifetime imaging microscopy. Anal Biochem. 1995;227:302–308. doi: 10.1006/abio.1995.1285. [DOI] [PubMed] [Google Scholar]
- 6.Carlsson K, Liljeborg A, Andersson RM, Brismar H. Confocal pH imaging of microscopic specimens using fluorescence lifetimes and phase fluorometry: Influence of parameter choice on system performance. J Microscopy-Oxford. 2000;199:106–114. doi: 10.1046/j.1365-2818.2000.00722.x. [DOI] [PubMed] [Google Scholar]
- 7.Lin HJ, Herman P, Lakowicz JR. Fluorescence lifetime-resolved pH imaging of living cells. Cytometry A. 2003;52A:77–89. doi: 10.1002/cyto.a.10028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Lakowicz JR, Szmacinski H, Nowaczyk K, Johnson ML. Fluorescence lifetime imaging of calcium using quin-2. Cell Calcium. 1992;13:131–147. doi: 10.1016/0143-4160(92)90041-p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Szmacinski H, Lakowicz JR, Lederer WJ, Nowaczyk K, Johnson ML. Fluorescence lifetime imaging microscopy (FLIM)—Calcium imaging in living cells using quin-2. Biophys J. 1994;66:A275. [Google Scholar]
- 10.Christensen KA, Christensen KA. Measurement of calcium in macrophage vacuolar compartments using ratiometric and fluorescence lifetime imaging microscopy. Mol Biol Cell. 2000;11:730. [Google Scholar]
- 11.Lakowicz JR, Szmacinski H, Nowaczyk K, Johnson ML. Fluorescence lifetime imaging of free and protein-bound nadh. Proc Nat Acad Sci USA. 1992;89:1271–1275. doi: 10.1073/pnas.89.4.1271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Urayama P, Zhong W, Beamish JA, Minn FK, Sloboda RD, Dragnev KH, Dmitrovsky E, Mycek MA. A UV-visible-NIR fluorescence lifetime imaging microscope for laser-based biological sensing with picosecond resolution. Appl Phys B. 2003;76:483–496. [Google Scholar]
- 13.Gerritsen HC, Sanders R, Draaijer A, Levine YK. Fluorescence lifetime imaging of oxygen in cells. J Fluoresc. 1997;7:11–16. doi: 10.1007/BF01881442. [DOI] [PubMed] [Google Scholar]
- 14.Hartmann P, Ziegler W, Holst G, Lubbers DW. Oxygen flux fluorescence lifetime imaging. Sens Actuators B, Chem. 1997;38:110–115. [Google Scholar]
- 15.Elangovan M, Day RN, Periasamy A. Nanosecond fluorescence resonance energy transfer-fluorescence lifetime imaging microscopy to localize the protein interactions in a single living cell. J Microscopy-Oxford. 2002;205:3–14. doi: 10.1046/j.0022-2720.2001.00984.x. [DOI] [PubMed] [Google Scholar]
- 16.Murata S, Herman P, Lin HJ, Lakowicz JR. Fluorescence lifetime imaging of nuclear DNA: Effect of fluorescence resonance energy transfer. Cytometry. 2000;41:178–185. doi: 10.1002/1097-0320(20001101)41:3<178::aid-cyto4>3.0.co;2-n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Mizeret J, Stepinac T, Hansroul M, Studzinski A, van den Bergh H, Wagnieres G. Instrumentation for real-time fluorescence lifetime imaging in endoscopy. Rev Sci Instrum. 1999;70:4689–4701. [Google Scholar]
- 18.Cubeddu R, Pifferi A, Taroni P, Torricelli A, Valentini G, Rinaldi F, Sorbellini E. Fluorescence lifetime imaging: An application to the detection of skin tumors. IEEE J Sel Topics Quantum Electron. 1999 Jul/Aug;5(4):923–929. [Google Scholar]
- 19.Siegel J, Elson DS, Webb SED, Lee KCB, Vlanclas A, Gambaruto GL, Leveque-Fort S, Lever MJ, Tadrous PJ, Stamp GWH, Wallace AL, Sandison A, Watson TF, Alvarez F, French PMW. Studying biological tissue with fluorescence lifetime imaging: Microscopy, endoscopy, and complex decay profiles. Appl Opt. 2003;42:2995–3004. doi: 10.1364/ao.42.002995. [DOI] [PubMed] [Google Scholar]
- 20.Tadrous PJ, Siegel J, French PMW, Shousha S, Lalani EN, Stamp GWH. Fluorescence lifetime imaging of unstained tissues: Early results in human breast cancer. J Pathology. 2003;199:309–317. doi: 10.1002/path.1286. [DOI] [PubMed] [Google Scholar]
- 21.Cubeddu R, Comelli D, D’Andrea C, Taroni P, Valentini G. Time-resolved fluorescence imaging in biology and medicine. J Phys D, Appl Phys. 2002;35:R61–R76. [Google Scholar]
- 22.Gratton E, Breusegem S, Sutin J, Ruan Q, Barry N. Fluorescence lifetime imaging for the two-photon microscope: Time-domain and frequency-domain methods. J Biomed Opt. 2003;8:381–390. doi: 10.1117/1.1586704. [DOI] [PubMed] [Google Scholar]
- 23.Ware WR, Doemeny LJ, Nemzek TL. Deconvolution of fluorescence and phosphorescence decay curves. A least square method. J Phys Chem. 1973;77:2038–2048. [Google Scholar]
- 24.Johnson ML, Frasier SG. Non-linear least-square analysis. Methods Enzymol. 1985;117:301–342. [Google Scholar]
- 25.Periasamy A, Sharman KK, Demas JN. Fluorescence lifetime imaging microscopy using rapid lifetime determination method: Theory and applications. Biophys J. 1999;76:A10. [Google Scholar]
- 26.Niesner R, Peker B, Schlusche P, Gericke KH. Noniterative biexponential fluorescence lifetime imaging in the investigation of cellular metabolism by means of NAD(P)H autofluorescence. Chemphyschem. 2004;5:1141–1149. doi: 10.1002/cphc.200400066. [DOI] [PubMed] [Google Scholar]
- 27.Lee KCB, Siegel J, Webb SED, Leveque-Fort S, Cole MJ, Jones R, Dowling K, Lever MJ, French PMW. Application of the stretched exponential function to fluorescence lifetime imaging. Biophys J. 2001;81:1265–1274. doi: 10.1016/S0006-3495(01)75784-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Verveer PJ, Squire A, Bastiaens PIH. Global analysis of fluorescence lifetime imaging microscopy data. Biophys J. 2000;78:2127–2137. doi: 10.1016/S0006-3495(00)76759-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Verveer PJ, Squire A, Bastiaens PIH. Improved spatial discrimination of protein reaction states in cells by global analysis and deconvolution of fluorescence lifetime imaging microscopy data. J Microscopy-Oxford. 2001;202:451–456. doi: 10.1046/j.1365-2818.2001.00917.x. [DOI] [PubMed] [Google Scholar]
- 30.Verveer PJ, Bastiaens PIH. Evaluation of global analysis algorithms for single frequency fluorescence lifetime imaging microscopy data. J Microscopy-Oxford. 2003;209:1–7. doi: 10.1046/j.1365-2818.2003.01093.x. [DOI] [PubMed] [Google Scholar]
- 31.Pelet S, Previte MJR, Laiho LH, So PTC. A fast global fitting algorithm for fluorescence lifetime imaging microscopy based on image segmentation. Biophys J. 2000;87:2807–2817. doi: 10.1529/biophysj.104.045492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Lakowicz JR. Principles of Fluorescence Spectroscopy. 2. Norwell, MA: Kluwer/Plenum; 1999. [Google Scholar]
- 33.Jo JA, Fang Q, Papaioannou T, Marcu L. Fast nonparametric deconvolution of fluorescence decay for analysis of biological systems. J Biomed Opt. 2004;9(4):743–752. doi: 10.1117/1.1752919. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Marmarelis VZ. Identification of nonlinear biological systems using Laguerre expansion of kernels. Ann Biomed Eng. 1993;21:573–589. doi: 10.1007/BF02368639. [DOI] [PubMed] [Google Scholar]
- 35.Schneckenburger H, Stock K, Lyttek M, Strauss WS, Sailer R. Fluorescence lifetime imaging (FLIM) of rhodamine 123 in living cells. Photochem Photobiol Sci. 2004;3:127–131. doi: 10.1039/b306129a. [DOI] [PubMed] [Google Scholar]