The mechanics of explosive seed dispersal in orange jewelweed (Impatiens capensis)

Abstract

Explosive dehiscence ballistically disperses seeds in a number of plant species. During dehiscence, mechanical energy stored in specialized tissues is transferred to the seeds to increase their kinetic and potential energies. The resulting seed dispersal patterns have been investigated in some ballistic dispersers, but the mechanical performance of a launch mechanism of this type has not been measured. The properties of the energy storage tissue and the energy transfer efficiency of the launch mechanism were quantified in Impatiens capensis. In this species the valves forming the seed pod wall store mechanical energy. Their mass specific energy storage capacity (124 J kg⁻¹) was comparable with that of elastin and spring steel. The energy storage capacity of the pod tissues was determined by their level of hydration, suggesting a role for turgor pressure in the energy storage mechanism. During dehiscence the valves coiled inwards, collapsing the pod and ejecting the seeds. Dehiscence took 4.2±0.4 ms (mean ±SEM, n=13). The estimated efficiency with which energy was transferred to the seeds was low (0.51±0.26%, mean ±SEM, n=13). The mean seed launch angle (17.4±5.2, mean ±SEM, n=45) fell within the range predicted by a ballistic model to maximize dispersal distance. Low ballistic dispersal efficiency or effectiveness may be characteristic of species that also utilize secondary seed dispersal mechanisms.

Introduction

Seed dispersal affects many aspects of plant biology. Rates of species invasion, the capacity to respond to climatic change, and population and community structures are all influenced by dispersal patterns (Harper, 1977; Primack and Miao, 1992; Schupp and Fuentes, 1995; Cain et al., 2000; Bass et al., 2006). Wind, water, animals, and/or ballistic mechanisms may be employed to move seeds away from the parent plant (Howe and Smallwood, 1982; Willson and Traveset, 2000; Levin et al., 2003), either singly or in combination (Beattie and Lyons, 1975; Stamp and Lucas, 1983; Cain et al., 2000).

Many ballistic seed dispersers use explosive dehiscence to eject seeds from the fruit (Howe and Smallwood, 1982; Levin et al., 2003), either as a primary dispersal mechanism (Swaine et al., 1979) or as a precursor to other secondary methods (Stamp and Lucas, 1983). Stored mechanical energy from fruit tissues is transferred to the seeds as they are launched (Niklas, 1992; Edwards et al., 2005). Seed velocities (Hinds and Hawksworth, 1965; Swaine et al., 1979; Garrison et al., 2000), dispersal distances (Schmitt et al., 1985; Malo, 2004; Narbona et al., 2005), and launch angles (Stamp and Lucas, 1983; Trapp, 1988; Garrison et al., 2000) have been quantified during ballistic dispersal, but the mechanical properties of the energy-storing tissues that power seed ejection have not been characterized.

By directly measuring the mechanical properties of these tissues, performance in a ballistic dispersal system can be assessed in new ways. Measurements of this type were undertaken in orange jewelweed (Impatiens capensis, Meerb.), a herbaceous annual with a ballistic seed dispersal mechanism. The capacity of the tissue for storing and releasing energy, the effectiveness of the dispersal mechanism in transferring this energy to the seeds during dehiscence, and the role of tissue hydration in elastic energy storage were quantified.

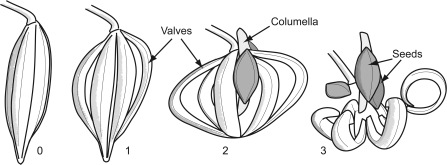
The jewelweed seedpod consists of five outer valves that coil rapidly during dehiscence, ejecting the seeds (Fig. 1; Schmitt et al., 1985; Caris et al., 2006). Preliminary observations indicated that loss of turgor in the pod valves prevented dehiscence, leading to the hypothesis that mechanical energy storage in the valves would be determined by their level of hydration. A portion of the stored energy is transferred to the seeds during dehiscence. The distance this transferred energy carries the seeds is determined by a number of factors: seed mass; interactions between the seeds and the air; and their launch trajectories. Air resistance during flight creates a velocity-dependent drag force on the seed (Swaine et al., 1979; Garrison et al., 2000; Vogel, 2005). For a given drag–velocity relationship, launch velocity, and seed mass, there is an optimum launch angle for maximizing flight distance (Price and Romano, 1998). If maximizing seed dispersal distance increases parental fitness (Howe and Smallwood, 1982; Augspurger, 1984; Willson and Traveset, 2000), then the launch angle may be tuned by natural selection to ensure this. It was therefore hypothesized that the measured launch angle of the seeds would match that predicted by a computer model to maximize projection distance.

Fig. 1.

Sequential video tracings of an I. capensis seed pod before and during dehiscence. The numbers show the time in milliseconds from the start of dehiscence.

The hypotheses were tested using a combination of high-speed video analyses of dehiscence, computer modelling of seed flight trajectories, and measurements of the mechanical properties of the valve tissue. Video sequences of seed ejection were used to calculate the transfer of kinetic and potential energy to the seeds. The launch angle was measured from the video sequences, and a computer model (Vogel, 1988) was used to determine whether this launch angle maximized seed dispersal distance. Valve coils from the pods were connected to an ergometer, and their capacity for storing mechanical work was determined. This has enabled the quantification, for the first time, of the properties of the power source in an explosive dehiscence mechanism, the effectiveness of the mechanism in transferring energy to the ejected seeds, and whether the seeds are launched along a trajectory that maximizes dispersal distance.

Materials and methods

Seed pods of orange jewelweed (Impatiens capensis, Meerb.) were collected from plants in Wellesley, MA, USA during September 2008. Impatiens capensis produces both chasmogamous and cleistogamous flowers (Waller, 1979, 1984). Both flower types produce explosively dehiscent seed pods (Schmitt et al., 1985). The distally located chasmogamous pods were used for the present study. The cut stems of collected pods were immediately placed in a container of water to minimize dehydration during transfer to the lab.

High-speed video recording of dehiscence

The stems of individual pods were placed in a clamp in the field of view of a horizontally aligned video camera with the long axis of the pod hanging vertically downwards, the typical in situ alignment. Pod length was measured with digital calipers. A mirror placed above the pod at a 45º angle to the vertical allowed a simultaneous top view. Three 500 W floodlights were used to illuminate the seed pods. Dehiscence was triggered by gently touching the distal end of the pod with fine forceps. Video sequences were captured to a PC laptop using an AOS Technologies X-PRI high-speed camera (AOS Technologies, Baden Daettwil, Switzerland) with a Micro-Nikkor 105 mm 1:2.8 lens (Nikon Inc., Melville, NY, USA). The frame resolution was 600×400 pixels, and the frame rate was 2000 Hz. After dehiscence the seeds and pod fragments were collected and weighed with a precision balance.

Video analyses

The main aim of the video analyses was to determine the total amount of mechanical work done on the seeds during pod dehiscence. This is the sum of the changes in seed translational and rotational kinetic energies and gravitational potential energy during seed launch. Analyses were carried out using Image J (Version 1.04g, Abramoff et al., 2004). The estimated position of the centre of mass of each seed was tracked in both the vertical and horizontal planes. Each seed was tracked from the time it became visible until the moment it left contact with the propelling coil or coils that were transferring energy to the seed. Data were collected from the 45 seeds released by 13 pods. Seed position was plotted with respect to time. A smoothing interpolation in Igor Pro was used to remove random noise from the position data, which were differentiated with respect to time to determine the seed centre of mass velocity. The magnitude of the resultant velocity vector in the vertical plane (v_v, m s⁻¹) was calculated as:

where v_v,x and v_v,y were the x and y components of the velocity within that plane (m s⁻¹).

The magnitude of the resultant velocity vector in the horizontal plane (v_h, m s⁻¹) was calculated as:

where v_h,x and v_h,y were the x and y components of the velocity within that plane (m s⁻¹). The magnitude of the resultant velocity vector (v_res, m s⁻¹) was calculated as:

The launch angle of a seed relative to the horizontal (ϕ, radians) was calculated as:

Seed mechanical energy calculations

The translational kinetic energy of a seed (E_K,trans in J) was calculated as:

where m was seed mass (kg) and v_res,l (m s⁻¹) was the resultant launch velocity as the seed lost contact with the collapsing pod.

The rotational kinetic energy of a seed (E_K,trans in J) was calculated as:

where I was the moment of inertia of the seed about the centre of rotation, and ω was its angular velocity (rad s⁻¹) as the seed lost contact with the propelling coil. In mechanical situations involving axial rotation, I serves as the rotational analogue of mass. ω=π/T rad s⁻¹, where T was the time taken for a half-rotation of the seed. The mid point of the half-rotation period coincided with loss of contact from the collapsing pod.

The seeds approximated a laterally compressed, prolate spheroid (Fig. 1). A representative sample of 13 seeds spanning the mass range encountered in the video analyses was selected for moment of inertia measurements. The moments of inertia during rotation in the longitudinal and equatorial planes were calculated from the periods of oscillation of the seeds about a pivot point. The pivot was created by inserting an insect pin into the seeds at the end of either the longitudinal or equatorial axes, with the pin perpendicular to the longitudinal or equatorial planes, respectively. The seed and pin were balanced on top of a glass measuring cylinder, and the seed was allowed to swing back and forth through an arc about the pivot point formed by the long axis of the pin. The alternate arrangements allowed pendulum rotation of the seed in either its longitudinal or equatorial planes.

High-speed video was obtained at 500 Hz of each seed rotating about the pivot in both orientations, determining the period of the oscillation (t) in seconds. This period was used to calculate the moment of inertia (I) about the pivot point in kg m² using the following equation derived from the basic mechanics of a pendulum:

where c is the distance between the centre of mass and the pivot (m), and g is the acceleration due to gravity (m s⁻²). The seeds were approximately symmetrical in shape, so the centre of mass was assumed to fall at the mid point of the longitudinal and equatorial axes. The moment of inertia about the centre of mass was calculated using the parallel axis theorem as:

As the diameter of the pin was small (0.3 mm), the moment of inertia about its long axis as a component of the total measured moment of inertia was assumed to be negligible.

The linear relationships between seed moment of inertia and seed mass in both orientations was determined. Seed moment of inertia (kg m⁻²) during rotation in the longitudinal plane = 8.24×10⁻¹⁵±2.57×10⁻¹⁵m–8.52×10⁻¹⁵±2.55×10⁻¹⁴ (R²=0.84, n=13). Seed moment of inertia during rotation in the equatorial plane = 1.97×10⁻¹⁵±5.63×10⁻¹⁶m–2.97×10⁻¹⁵±5.58×10⁻¹⁵ (R²=0.82, n=13). These relationships were used to predict the moments of inertia of the filmed seeds from their measured mass.

The change in gravitational potential energy (J) during launch was calculated as:

where Δh was the change in vertical position (m) during the time period from the seed becoming visible as the pod started to burst until the seed left contact with the pod tissue. Only positive changes in seed E_p during launch were included in the sum of total added energy.

The total energy added to a seed during launch (J) was calculated as:

For a given pod, the sum of the energy added to all of the seeds was calculated.

Measurement of valve coil mechanical properties

The mechanical properties of valve coils collected from the 13 pods recorded in the high-speed video experiments were measured. These experiments had two main aims: to measure the amount of work that could be stored by the coils; and to determine the extent to which work storage was dependent on coil hydration. The coils remained in a tight spiral after being released from the pod. These could be partially unrolled by careful manipulation while viewed under a dissecting microscope. The head of a size 1 insect pin was attached to each end of the coil with cyanoacrylate glue (Krazy Glue, Elmer's Products, Inc., Columbus, OH, USA). The pins were used to anchor the coil to an ergometer (300B-LR; Aurora Scientific, Ontario, Canada). This controlled coil length and measured force. The time elapsed from pod burst to attachment to the ergometer was typically <1 min.

The amount of work stored in a valve coil was determined by applying a ramp stretch at a rate of 0.25 mm s⁻¹. Maximum length during the ramp stretch was set to coincide with the in situ maximum length of the coil in the pod as measured before pod burst. Coil length during ramp stretches was controlled using Dynamic Muscle Control software (version 4.0; Solwood Enterprises Inc., Blacksburg, VA, USA). The force and position data were captured on a PC via a 604A analogue-to-digital interface (Aurora Scientific) and a PCI analogue-to-digital card (PCI-6503; National Instruments, Austin, TX, USA). Preliminary experiments determined that the measured amount of stored work was not affected by the rate of stretching. The amount of work done during stretching was calculated by integrating the force–length curve using Igor Pro (Version 5.0.4.8, WaveMetrics, USA). Data obtained from any coil that failed at the attachment point to the pins were discarded. The total amount of work stored in a given pod was calculated by assuming that the total mass of valve coils had the same mass specific energy storage capacity as for the measured coil.

A separate set of experiments were carried out to determine the effects of valve coil hydration on work storage. Coils were collected by triggering pod dehiscence and immediately weighed. A coil was attached to the ergometer as previously described, and a ramp stretch was applied at a rate of 0.25 mm s⁻¹. Subsequently, one end of the coil was unclamped so it could hang from the lever arm of the ergometer, and the coil was allowed to dehydrate. The ergometer reading was monitored until the coil mass, accounting for the added mass of the pin attachments, reached 90% of its initial value. At this point the coil was re-clamped and a further 0.25 mm s⁻¹ ramp stretch applied. This procedure was repeated at 80, 70, 60, and 50% of the original coil mass following further dehydration and reattachment. The coil was then immersed in a container of water and allowed to rehydrate. Mass was monitored until it returned to the initial value. A final ramp stretch was then applied as a control. The work stored by the coil was calculated as previously described. Work and mass were expressed as a percentage of their values during the initial ramp stretch.

Predicting seed dispersal distance and optimum launch angle

A computer program (Vogel, 1988) was used to estimate dispersal distance for the observed seed launch velocities, and to investigate how launch angle affected dispersal distance for the observed range of launch speeds. Starting with an initial launch angle and speed, the program used an iterative approach, taking into account the effects of drag, to calculate new values of speed and direction at 1 ms intervals. Jewelweed seeds are laterally compressed, prolate spheroids that tumble during flight. The seed was assumed to incur drag equal to that acting on a sphere, with a frontal area equal to the mean of the maximum and minimum possible frontal areas of the seed. The dimensions of the seeds used for moment of inertia analyses were as follows: length of longitudinal axis (L_long), 5.26±0.09 mm; length of the major equatorial axis (L_eq,maj), 2.30±0.06 mm; and length of the minor equatorial axis (L_eq,min), 1.31±0.04 mm (mean±SEM, n=13). The frontal area of the approximately elliptical maximum (A_max) and minimum (A_min) frontal areas were calculated as:

The mean frontal area of the sample of seeds was 5.93 mm². A sphere with an equivalent frontal area would have a diameter of 2.75 mm. A sphere provides a reasonable basis for the drag estimate as the drag coefficient of a sphere (0.47) falls within the range measured for seeds (0.3–0.8, Killiçkan and Güner, 2006; Afonso Júnior et al., 2007; Zewdu, 2007).

The trajectory calculations used a launch height of 1.1 m, corresponding to mean pod height in the field. Dispersal distance was calculated in this way as the proximity of the camera, lights, and their stands to the seed pods meant that collisions prevented accurate direct measurements from being obtained. To determine the optimal launch angle, the median and maximum launch speeds were used as initial inputs, and the launch angle was systematically changed until the angle for maximum dispersal distance at each speed was found.

Data analysis

All statistical analyses were carried out using SPSS (Version 14.0, SPSS Inc., USA). A general linear model (GLM) with valve coil mass as the independent variable and the amount of work stored as the dependent variable was used to test for the effects of changing coil hydration on work storage capacity. A post hoc Scheffé test was used to make pair-wise comparisons between mean work storage values for each mass category. A one-sample t-test was used to determine whether the observed mean launch angle was significantly different from the 0° mean of a random angle distribution within the possible –90° to 90° range, and whether the mean launch angle was significantly different from the optima predicted by the ballistic model.

Results

Seed trajectories and energies

Dehiscence, from initial splitting of the pod wall, to complete coiling of the valves, took 4.2±0.4 ms (mean ±SEM, n=13; Fig. 1). Mean seed properties, launch trajectories, and energies are shown in Table 1. The mean launch velocity (1.24 m s⁻¹) was lower than previously reported in other herbaceous ballistic dispersers (2.1–2.6 m s⁻¹, Arceuthobium spp., Hinds and Hawksworth, 1965; 4.6 m s⁻¹, Vicia sativa, 4.7 m s⁻¹, Croton capitatus, Garrison et al., 2002). The distribution of predicted seed dispersal distances had a heavy positive skew (Fig. 2), qualitatively similar to seed distributions previously measured in this species (Stamp and Lucas, 1983; Schmitt et al., 1985).

Table 1.

Mass, trajectory, and estimated energy of launched I. capensis seeds

	Mean± SEM (n)	Range
Mean number of seeds per pod	3.46±0.16 (13)	2–5
Mean seed mass (mg)	10.7±0.4 (45)	7.7–19.7
Mean seed launch velocity (m s−1)	1.24±0.14 (45)	0.20–4.08
Mean seed launch angle relative to the horizontal (°)	17.4±5.2 (45)	–57.5 to 82.7
Mean seed translational kinetic energy (μJ)	13.0±3.1 (45)	0.16–88.9
Mean seed rotational kinetic energy (μJ)	0.043±0.011 (45)	0.001–0.46
Added gravitational potential energy (μJ)	0.049±0.020 (45)	0–0.27
Total transferred energy per seed (μJ)	13.1±6.0 (45)	0.16–89.2
Mean transferred energy per pod (μJ)	45.3±22.0 (13)	1.7–289.7

Fig. 2.

Frequency distribution of predicted I. capensis seed dispersal distances. Dispersal distances were calculated from measured launch trajectories using a ballistics model (Vogel, 1988) (n=45).

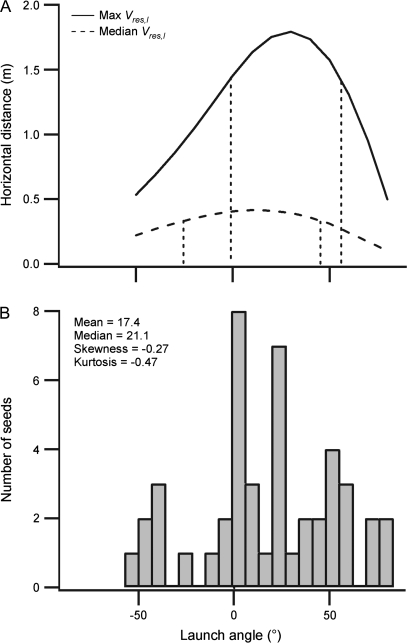
The computer model used to estimate seed trajectories predicted optimum launch angles for maximizing distance of 12.7° and 29.7° at launch speeds of 1.02 m s⁻¹ (median measured launch speed) and 4.08 m s⁻¹ (maximum measured launch speed), respectively (Fig. 3A). At a launch speed of 1.02 m s⁻¹ ≥80% of the maximum potential distance could be achieved within a launch angle range from –25.2° to 45.4°. With a launch speed of 4.08 m s⁻¹ the corresponding angle range was –1.0° to 55.2° (Fig. 3A). The mean measured launch angle of the seeds (17.4°, Table 1) was significantly different from 0° (one-sample t-test, t=.3, P=0.002, df=44). This suggests that the launch angles were not randomly distributed within the potential range of –90° to 90°, but were skewed towards the positive end of this range (Fig. 3B). The measured launch angle was not significantly different from the predicted optimum at 1.02 m s⁻¹ (one-sample t-test, t=0.90, P=0.374, df=44), and significantly lower than the predicted optimum at 4.08 m s⁻¹ (one-sample t-test, t=–2.35, P=0.02, df=44).

Fig. 3.

Optimal and measured seed launch angles. (A) Relationships between predicted seed dispersal distance and launch angle at the maximum (4.08 m s⁻¹) and median (1.02 m s⁻¹) measured launch speeds. Vertical dotted lines indicate the launch angles giving 80% of maximum dispersal distance for each curve. (B) Frequency distribution of measured seed launch angles (n=45).

The majority of the energy transferred to the seeds during launch was in the form of translational kinetic energy (Table 1). In comparison, added amounts of rotational kinetic and gravitational potential energy accounted for <0.1% of the total.

Mechanical properties of the valve coils

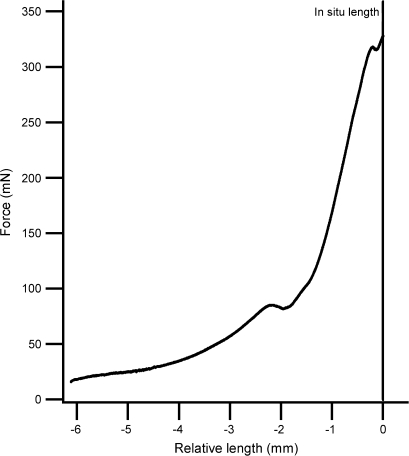
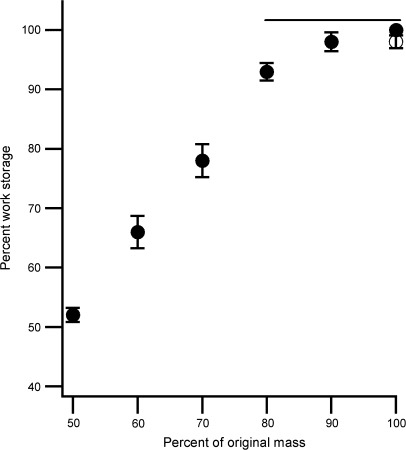
The physical and mechanical properties of the pod valves are shown in Table 2. In addition to the valves and seeds, the pods contained a central, axial columella to which the seeds were loosely attached (Fig. 1). This had mean wet and dry masses of 10.1±2.5 mg and 1.2±0.2 mg, respectively (mean ±SEM, n=13). Immediately after pod burst the coils were ∼85% water by mass (Table 2). A representative valve coil force–extension curve is shown in Fig. 4. The work stored by the valve coils changed significantly with their level of hydration (Fig. 5; GLM, F_6,35=131, P <0.001). The final measured work storage on rehydrating the coils to 100% of their original mass was not significantly different from the initial value (Scheffé, P=0.99). On average, 0.5% of the energy stored in the valve coils was transferred to the launched seeds (Table 2).

Table 2.

Physical and mechanical properties of I. capensis pod valves

	Mean ± SEM (n)	Range
Mean valve coil fresh mass (mg)	14.0±2.7 (13)	11–32
Mean valve coil dry mass (mg)	2.04±0.04 (13)	1.07–2.44
Mean valve coil energy density (J kg−1)	124±29 (13)	38–411
Mean estimated stored elastic energy per pod (μJ)	8870±1360 (13)	3000–16 400
Percentage of stored energy transferred to seeds	0.51±0.26 (13)	0.04–2.60

Fig. 4.

Representative force–extension curve for an I. capensis valve coil. Length is shown relative to the in situ coil length (14.0 mm).

Fig. 5.

Relationship between stored energy and I. capensis valve coil mass. Filled symbols, work storage measured during a progressive decrease in mass due to dehydration. Open symbol, work stored after rehydration to initial mass. The horizontal line shows a homogenous subset as established by Scheffé’s post hoc test (P > 0.05). Data are shown as mean ±SEM (n=6).

Discussion

Effectiveness of energy storage and transfer

The valve coils are highly effective energy storage structures (Table 2, Fig. 4). Their mass specific energy storage capacity (124 J kg⁻¹) exceeded that of both elastin (95 J kg⁻¹, Gosline et al., 2002) and spring steel (115 J kg⁻¹, Gosline et al., 2002). Overall, the efficiency of energy transfer to the seeds was low. Only 0.51% of the valve coil energy was transferred as increased kinetic energy and gravitational potential energy in the seeds (Table 2). Energy transfer was also highly variable, with a wide range of estimates for energy transfer to a given seed (0.2–89 μJ). The upper end of the transferred energy range can project a seed ∼2 m, although this rarely occurred, resulting in a distribution of predicted dispersal distances that was leptokurtic and positively skewed (Fig. 2). This indicates an inherent unreliability in the launch mechanism. During dehiscence, rapid coiling of the pod valves shortened the pod longitudinally, collapsing the columella and ejecting the seeds (Fig. 1). In the mature pod there are no direct connections between the seeds and the pod tissue. Consequently, many seeds fell from the pod with little if any contact from the collapsing structure, resulting in limited energy transfer and dispersal from the parent plant.

It was hypothesized that tissue hydration would be necessary for energy storage in the valve coil tissue. This proved to be the case. A decline in the wet mass of the coils was associated with a decline in their capacity to store mechanical energy (Fig. 5). This stored energy was released as the pod valves rapidly curled inwards (Fig. 1). Qualitatively similar curvature has been observed in other plant tissues. For example, longitudinal quadrants of plant stems typically reflex outwards when excised from the intact stem (Hofmeister, 1859, 1860). This curvature is generated by turgor pressure and differences in cell structure between the outer and inner layers of the stem (Niklas and Paolillo, 1997, 1998). Thick-walled epidermal cells with longitudinally arranged cellulose microfibrils act as a tension-bearing envelope which holds a hydrostically inflated inner core of thin-walled tissue in compression (Niklas and Paolillo, 1997, 1998). Release of tension in the envelope creates outward curvature as the tension-bearing layer shortens and the formerly compressed layer expands. The pod valves of jewelweed may also be two-ply structures, although to generate inward curvature the arrangement of the tension-bearing and compressed tissues would have to be reversed relative to that in a stem. Further examination of pod valve anatomy is required to establish whether this structural arrangement is the basis for energy storage and release in this system.

Comparative performance of ballistic dispersal mechanisms

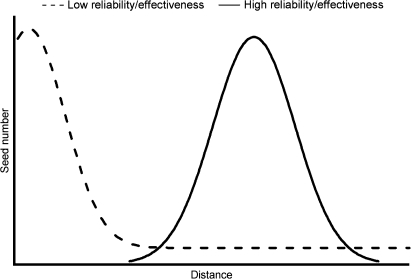
Are plant ballistic dispersal mechanisms typically inefficient and/or unreliable? No directly comparable data concerning the efficiency of energy transfer during seed launch are available. The relative effectiveness of ballistic mechanisms in different species can, however, be inferred from the seed dispersal patterns they produce (Fig. 6). Positively skewed seed dispersal distributions similar to those of I. capensis have been observed in a number of species (Ohkawara and Higashi, 1994; Malo, 2004; Narbona et al., 2005). From a purely mechanical standpoint, primary ballistic dispersal is frequently ineffective in these species (Fig. 6). In contrast, some plant species have seed distributions with greater mean dispersal distances, no positive skew, and few, if any, seeds landing adjacent to the parent plant (Fig. 6). This indicates effective and reliable transfer of stored energy to the seeds. Several factors may underlie these differences in dispersal performance: selection pressures arising from the effects of distance from the parent plant on seedling survival; the relative importance of secondary dispersal mechanisms; and the mechanical design of the launch mechanism.

Fig. 6.

Representative seed dispersal distributions for plants with ballistic dispersal mechanisms of different efficiencies and/or reliabilities.

Populations of I. capensis show local clustering of particular genotypes and limited gene flow (Schoen and Latta, 1989; Argyres and Schmitt, 1990; Paoletti and Holsinger, 1999), and an increase in inbreeding depression with distance from the parent plant (Schmitt and Gamble, 1990). This suggests that within heterogeneous environments I. capensis populations adapt to local conditions (Schmitt and Gamble, 1990) and that frequent and consistent long-distance ballistic dispersal would be unlikely to increase parental fitness. Long-distance seed movements in jewelweed are achieved using secondary dispersal via water (Trewick and Wade, 1986; Perrins et al., 1993; Tabak and von Wettberg, 2008). The high lipid content of the seeds (52% of dry mass, Nozzolillo and Thie, 1984) lowers their density, increasing buoyancy. Unfortunately low-density seeds make poor projectiles in comparison with the small, dense seeds typical of primarily ballistic dispersers (Garrison et al., 2000). For a given mass of seed, decreasing its density increases its volume and surface area (assuming shape does not change). This increases drag, reducing dispersal distance for a given amount of transferred energy. Investment in a secondary dispersal strategy by I. capensis may therefore impair primary ballistic dispersal performance irrespective of the effectiveness of the launch mechanism.

In contrast to I. capensis, Geranium maculatum has a ballistic distribution characteristic of a reliable launch mechanism (Stamp and Lucas, 1983). Secondary dispersal is of limited importance in this species (Culver and Beattie, 1978) and the effects of inbreeding depression are severe (Ågren and Willson, 1991; Chang, 2006). This may create a selection pressure favouring the development of effective ballistic mechanisms that reliably move seeds as far as possible from close relatives. Ultimately, reliable launching may require greater material investment in the launch structures. Unlike I. capensis, G. maculatum seeds are cupped by fruit tissue (Yeo, 1984), probably increasing the reliability of stored energy transfer to the seeds and explaining the absence of launch failures in this species.

Is launch angle optimized?

Modelling of the effects of launch angle on seed dispersal distance predicted optimum launch angles at the median (1.02 m s⁻¹) and maximum (4.08 m s⁻¹) launch speeds of 12.1° and 28.4°, respectively (Fig. 3). The mean measured launch angle (17.4°) fell within this range. Given the potential range of –90° to 90°, a random distribution of launch angles would have a mean value of 0°. A single-sample t-test showed that the mean launch angle was significantly different from zero, but not significantly different from the predicted optimum launch angle for the median launch speed. This suggests that launch angles were constrained to some extent (Fig. 3). Similar non-random launch angle distributions have been observed for seeds in other species (Vicia sativa and Croton capitatus; Garrison et al., 2000). The coincidence between the measured mean launch angle and the predicted angle range for maximizing dispersal distance seems to be at odds with the inefficiency and inconsistency of energy transfer from the valve coils to the seeds (Table 1, Fig. 2). Considering the angle distribution as a whole, fine-tuning to match the predicted range of optima was actually quite limited. The measured range of angles (–57.5° to 82.7°) spanned most of the potential range and had a greater variability than in other species that show tuning of launch angles (standard deviation of 35 compared with 24 and 25 for V. sativa and C. capitatus, respectively; Garrison et al., 2000). Ultimately, failure to constrain the launch angle tightly may have a limited effect on dispersal performance. Although for any given launch speed there is an optimum angle for maximizing dispersal distance, the range of launch angles that allow for 80% or better of the maximum predicted dispersal distance is quite broad (Fig. 3A). An I. capensis seed at median launch speed could achieve 80% or better of the maximum predicted dispersal distance for this speed with a launch angle range from –25.2° to 45.4°.

Conclusions

The seed pod valves of I. capensis were effective mechanical energy-storing structures, with a mass specific energy storage capacity of 1.24 J kg⁻¹. Energy storage capacity was dictated by the level of hydration of the valve tissue, suggesting a role for turgor pressure in the energy storage and release mechanism. The transfer of stored energy to the seeds during dehiscence was 0.51% efficient. Energy transfer was inconsistent, producing a positively skewed seed dispersal distribution. The seed launch angles were variable, but non-randomly distributed. Mean launch angle fell within the range predicted by a ballistic model to maximize dispersal distance. The relative reliability and effectiveness of a ballistic dispersal mechanism can be inferred from the seed distribution it produces. Low ballistic dispersal efficiency or effectiveness may be characteristic of species that also rely on secondary seed dispersal mechanisms, and reflect greater relative allocation of reproductive biomass to the secondary mechanism.