Abstract
The factors that control the reactivities of aryl radicals toward hydrogen-atom donors were studied by using a dual-cell Fourier-transform ion cyclotron resonance mass spectrometer (FT – ICR). Hydrogen-atom abstraction reaction efficiencies for two substrates, cyclohexane and isopropanol, were measured for twenty-three structurally different, positively-charged aryl radicals, which included dehydrobenzenes, dehydronaphthalenes, dehydropyridines, and dehydro(iso)quinolines. A logarithmic correlation was found between the hydrogen-atom abstraction reaction efficiencies and the (calculated) vertical electron affinities (EA) of the aryl radicals. Transition state energies calculated for three of the aryl radicals with isopropanol were found to correlate linearly with their (calculated) EAs. No correlation was found between the hydrogen-atom abstraction reaction efficiencies and the (calculated) enthalpy changes for the reactions. Measurement of the reaction efficiencies for the reactions of several different hydrogen-atom donors with a few selected aryl radicals revealed a logarithmic correlation between the hydrogen-atom abstraction reaction efficiencies and the vertical ionization energies (IE) of the hydrogen-atom donors, but not the lowest homolytic X – H (X = heavy atom) bond dissociation energies of the hydrogen-atom donors. Examination of the hydrogen-atom abstraction reactions of twenty-nine different aryl radicals and eighteen different hydrogen-atom donors showed that the reaction efficiency increases (logarithmically) as the difference between the IE of the hydrogen-atom donor and the EA of the aryl radical decreases. This dependence is likely to result from the increasing polarization, and concomitant stabilization, of the transition state as the energy difference between the neutral and ionic reactants decreases. Thus, the hydrogen-atom abstraction reaction efficiency for an aryl radical can be “tuned” by structural changes that influence either the vertical EA of the aryl radical or the vertical IE of the hydrogen atom donor.
Introduction
The mechanisms of hydrogen-atom abstraction by radicals have been of interest for decades.1 However, the ability to predict the rates of such seemingly “simple” reactions has proven to be a challenge due to a poor understanding of the nature of the transition states for these reactions. As a result, the factors that control the efficiency of hydrogen-atom abstraction for different types of radicals are still not well understood. However, such knowledge could be extremely valuable, for example, for a better understanding of radical-induced DNA degeneration and the design of less cytotoxic pharmaceuticals.2,3,4,5,6,7,8 Aromatic carbon-centered σ-radicals9,10 (e.g., phenyl radicals and derivatives) and related biradicals2,11,12,13 have been identified as the biologically active intermediates of certain drugs and antitumor antibiotics. Such species can abstract hydrogen atoms from the sugar moiety in DNA, which can lead to DNA cleavage and eventually cell death.2,3,4,5,6,9,11,12,13,14,15,16,17 Hence, a better understanding of the factors that control their reactivities is of great interest.
Previous studies have shown that substituents can influence the reactivities of aryl radicals in solution.18,19,20 For example, a solution study of hydrogen-atom abstraction by several different aryl radicals from nineteen different hydrogen-atom donors, including various hydrocarbons, acetone, methyl acetate, thiophenol, cyclohexane, and toluene, showed the reactivity ordering: p-tolyl radical < phenyl radical < p-bromophenyl radical < p-nitrophenyl radical.18 A similar trend (i.e., phenyl radical < p-chlorophenyl radical < p-nitrophenyl radical) has also been observed for hydrogen-atom abstraction from cyclohexane19,20 and toluene20 in solution. These trends in reactivity are thought to result from polar effects; increasing the electronegativity of a substituent in an aryl radical increases the polarity of the transition state for hydrogen-atom abstraction from a given substrate, which in turn stabilizes the transition state and leads to a greater reaction rate. However, only a few different aryl radicals have been studied thus far. In order to more fully understand the factors that control the reactivities of aryl radicals in hydrogen-atom abstraction reactions, a systematic study of a large number of structurally different aryl radicals is needed.
To address this need, we have examined the reactivities of a variety of aryl radicals by using the “distonic ion approach”.15,21,22,23,24,25,26 This approach involves the generation of aryl radicals in the gas phase that carry a chemically-inert, positively-charged functionality that permits manipulation in a Fourier-transform ion cyclotron resonance mass spectrometer (FT – ICR). Previous studies from our laboratory have shown that: (1) such positively-charged aryl radicals possess chemical properties similar to those of related neutral aryl radicals in solution;21,22,23,24 (2) fluorine substitution of the aryl radicals increases their hydrogen-atom abstraction reaction efficiency for the substrates thiophenol, 1,4-cyclohexadiene, and tetrahydrofuran;21 (3) the efficiency of hydrogen-atom abstraction from tributyltin hydride, benzeneselenol, thiophenol and tetrahydrofuran is similarly increased by electron-withdrawing substituents either meta (e.g., H < Br ~ Cl < CN) or ortho (e.g., H < CF3 ~ Cl ~ F) to the radical site (substituents in the para-position were not examined);22 (4) the trends in reactivity for positively-charged dehydro(iso)quinolines, dehydrobenzenes, and dehydronaphthalenes in hydrogen-atom abstraction reactions from tetrahydrofuran and 2-methyltetrahydrofuran are not a result of differences in reaction enthalpy, the size of the radical, or the position of the radical site in the aromatic ring system; instead, the reactivity trends for these aryl radicals reflect differences in the (calculated) vertical electron affinities (EA) of the radical sites;22,23 and (5) the reaction efficiency for hydrogen-atom abstraction from sugars also increases as the (calculated) vertical EA of the radical site in the aryl radical increases.15
Although only a small number of aryl radicals having a relatively narrow range of EAs have been examined, these studies suggest that there is an important relationship between the EA of the aryl radical and the efficiency with which the aryl radical undergoes hydrogen-atom abstraction reactions. We report here a systematic gas-phase study on the efficiency of hydrogen-atom abstraction from eighteen hydrogen-atom donors by twenty-three aryl radicals (a – w; Chart 1). We also include experimental data for six additional aryl radicals (aa – ff; Chart1) that have been reported previously.23,27,28 The twenty-nine aryl radicals studied here were chosen in order to span a relatively broad range of EA values.
Chart 1.
Aryl Radicals Studied
Experimental Methods
All experiments were carried out by using a Finnigan FTMS 2001 Fourier-transform ion cyclotron resonance mass spectrometer (FT – ICR) with an Odyssey data station. This instrument contains a dual cell consisting of two identical 2 in. cells collinearly aligned with the magnetic field produced by a 3 T superconducting magnet. The two cells are separated by a common wall called the “conductance limit” that contains a 2 mm hole in the center for transfer of ions between the two cells. This plate and the other trapping plates were maintained at +2 V unless specified otherwise. The two cells are differentially pumped by two Edward diffusion pumps (800 L/s), and each is backed by an Alcatel 2012 mechanical pump. A nominal base pressure of less than 1 × 10−9 torr was indicated by an ionization gauge on each side of the dual cell.
Cyclohexane (99%) and isopropanol (99.5%) were obtained from Sigma-Aldrich (purities were confirmed by mass spectrometry before use). Bromobenzene (Fisher), 3-iodopyridine (KARL Industries), 4-iodopyridine (Lancaster), pyridine (Mallinckrodt), 1,3-diiodobenzene, 1,4-diiodobenzene, 1-bromo-3-fluoro-4-iodobenzene, 1,3-dichloro-5- iodobenzene, 4,4′-diiodobiphenyl, 3-fluoropyridine, 1,2,4,5-tetrafluoro-3,6- diiodobenzene, 1-iodo-3,5-dinitrobenzene, 2-chloro-5-nitropyridine, 2-chloro-3- nitropyridine, quinoline, 5-nitroquinoline, 6-nitroquinoline, 5-nitroisoquinoline and 1,5- dinitronaphthalene (Sigma-Aldrich) were used as received. 1-Bromo-4- iodonaphthalene23 and 4-nitroquinoline,29 were synthesized30,31,32 according to published procedures and characterized by using 1H NMR and mass spectrometry.
The reagents necessary for producing each aryl radical were introduced into one cell of the instrument via a heated solids probe, a Varian leak valve or a batch inlet equipped with an Andonian leak valve, depending on their volatilities. The aryl radicals were formed by using a multistep procedure developed in our laboratories.21,22,23,24 Precursor ions for the positively-charged dehydrobenzenes (a, b, c, f, g, i, k, l, n, t; Chart 1) and dehydronaphthalenes (d, e) were generated by reaction of pyridine, 3-fluoropyridine or quinoline with the corresponding halo- or nitro-substituted benzene or naphthalene radical cation formed by electron ionization (EI: typically 11 – 30 eV electron energy, 5 – 6 μA filament current, and 30 – 100 ms ionization time). Precursor ions for the positively-charged dehydroquinolines (h, m, p), dehydroisoquinolines (j) and dehydropyridines (r, s, u, v, w) were generated by protonation of the corresponding iodo- or nitro-substituted quinoline, isoquinoline or pyridine via chemical ionization (CI). Finally, precursor ions for the positively-charged N-phenyldehydropyridines (o, q) were generated via the reaction of either 3- or 4-iodopyridine with bromobenzene radical cation formed by EI.
The other cell was “cleaned” by ejecting any ions formed upon EI via the application of a potential of −2 V to the remote trapping plate of that cell for 12 ms. The precursor ions were transferred through the 2 mm hole in the common trapping plate into the other cell by grounding the conductance limit plate for 120 – 210 μs, and cooled for 1.0 – 1.5 s (i.e., by emission of light and collisions with the neutral molecules present in the cell). The cooled ions were then subjected to a homolytic carbon-iodine or carbon-nitrogen bond cleavage to form the desired positively-charged aryl radicals (a – w; Chart 1) by using sustained off-resonance irradiated collision-activated dissociation33 (SORI – CAD). This was accomplished by collisional activation with an argon target (pulsed into the cell at a nominal peak pressure of ca. 1 × 10−5 torr) for 0.3 – 0.6 s while irradiating the ions at a frequency 1 kHz higher than their cyclotron frequency. The product ions were then allowed to cool for ca. 0.3 – 1.0 s. The desired ions were isolated by ejecting all other ions from the cell via the application of a stored-waveform inverse Fourier transform34 (SWIFT) excitation pulse to the excitation plates of the cell. The isolated positively-charged aryl radicals were allowed to react with each hydrogen-atom donor (introduced into the other cell via a batch inlet equipped with an Andonian leak valve) for a variable period of time (typically 2 – 1000 s) until at least 90% of the radical population had reacted (except for radical a, which reacts too slowly to follow that long).
Detection was carried out by using “chirp” excitation at a bandwidth of 2.6 MHz, an amplitude of 124 Vp-p and a sweep rate of 3.2 kHz/μs. All spectra were recorded as 64 k data points and subjected to one zero fill prior to Fourier transformation. The elemental compositions of the primary products of the reactions were identified based on their exact mass-to-charge ratios (m/z). Since the concentration of the neutral hydrogen-atom donor is much higher than that of any ion, the reactions between the positively-charged aryl radicals and the hydrogen-atom donors follow pseudo-first order kinetics. The pseudo-first order reaction rate constant (k′) was determined from the slope of a semi logarithmic plot of the relative abundance of the reactant ion versus reaction time (square of the linear correlation coefficient ≥ 0.99). The second order reaction rate constant (kexp) was obtained by dividing k′ by the concentration of the neutral hydrogen-atom donor. The difference between the absolute pressure and the pressure measured by the ion gauges was estimated each day by measuring rates of reactions that can be assumed to occur at the collision rate (i.e., highly exothermic, barrier less reactions). For example, electron transfer to carbon disulfide radical cation was used to obtain a correction factor for cyclohexane, and proton transfer from protonated methanol was used to obtain a correction factor for isopropanol. The collision rate constants (kcoll) were calculated by a parameterized trajectory theory.35 The reaction efficiencies (Eff.) are given as kexp/kcoll.
Statistical data analysis
An empirical approach was used to evaluate the relationship between the hydrogen-atom abstraction reaction efficiency (dependent variable, Y, in the model) and either the (calculated) vertical EA of the aryl radical, the vertical IE of the hydrogen-atom donor, or the difference between EA and IE (EA, IE or IE – EA: independent variable, X, in the model). Box-Cox transformations of Y were used to make the data behave according to a linear regression model.36,37 The principal idea of this approach is to restrict attention to transformations indexed by an unknown parameter, λ, and then to estimate λ and the regression coefficients of the model by maximum likelihood, as described below. An automated procedure in the SAS/STAT software package38 was employed to identify “trial” transformations. If the new (transformed) Y is denoted as Y′, the Box-Cox procedure examines a family of transformations described by
| (1a) |
| (1b) |
where the family of transformations includes the natural logarithm (λ = 0), inverse (λ = −1), square root (λ = 0.5), quadratic (λ = 2), cubic (λ = 3), and other transformations. The regression model is described by
| (2a) |
| (2b) |
where β0 and β1 are regression coefficients and εi is an error term. The likelihood function for the regression model is
| (3a) |
| (3b) |
where the parameters λ, β0, β1 and σ2 are estimated by maximizing the likelihood function. The detailed maximization method has been described by Box and Cox,36 and Draper and Smith.37 The estimated λ was used to choose the final transformation. For example, the correlation between the hydrogen-atom abstraction reaction efficiency (Eff.) and the (calculated) vertical EA for the aryl radical was examined for both cyclohexane and isopropanol by using equations 3a and 3b. In this case, the likelihood function is maximized when the value of λ is zero; therefore, the optimal transformation for Eff. is ln(Eff.). Similar linear correlations were found between ln(Eff.) and the vertical IE of the hydrogen-atom donor, and ln(Eff.) and the difference in energy between IE and EA (i.e., IE – EA).
Computational Methods
Molecular geometries for all species were optimized at the density functional (DFT) level of theory by using the 6-31+G(d) basis set.39 The DFT calculations used the three-parameter exchange functional of Becke,40 which was combined with the gradient-corrected correlation functional of Lee, Yang and Parr41 (B3LYP). All DFT geometries were verified to be local minima by computation of analytic vibrational frequencies, and these scaled42 (scale factor: 0.9804) frequencies were used to compute zero-point vibrational energies (ZPVE) for all species. DFT calculations for the doublet states of the radicals employed an unrestricted formalism.
In order to compute vertical EAs for the aryl radicals, single-point calculations using the optimized geometry for each aryl radical were also carried out for the states that are produced when a single electron is added to the nonbonding σ orbital of each molecule.43 For the aryl radicals studied here, these calculations involve (zwitterionic) singlet states.44 The EAs of the aryl radicals were computed as [E0(monoradical; doublet state)] − [E0(monoradical + electron; singlet state)]. Note that because these are vertical EAs, zero-point vibrational energies (ZPVEs) and 298 K thermal contributions to the enthalpy are not included.
In order to calculate the enthalpy changes (ΔHrxn) associated with hydrogen-atom abstraction by the various aryl radicals from the hydrogen atom donors (cyclohexane and isopropyl alcohol), the total energy of the reactants (i.e., aryl radical plus either cyclohexane or isopropyl alcohol) was subtracted from the total energy of the products (i.e., arene plus either cyclohexyl radical or 2-hydroxy-2-propyl radical). These energies were corrected for differences in the zero point vibrational energies, but thermal corrections (i.e., to 298 K) were not employed.
Molecular geometries for aryl radicals g, l, n and isopropanol, as well as the hydrogen-atom abstraction transition states for each of these aryl radicals with isopropanol, were also optimized at the MPW1K level of theory45 by using the 6-31+G(d,p) basis set.39 The MPW1K functional is a modification of the Perdew-Wang gradient-corrected exchange functional, with one parameter optimized to give the best fit to kinetic data for forty radical reactions.45 The MPW1K/6-31+G(d,p) method was chosen for the transition state calculations because it has been shown45,46 to provide better estimates of barrier heights for hydrogen-atom abstraction reactions than the B3LYP functional. All MPW1K geometries were verified to be local minima (or transition states) by computation of analytic vibrational frequencies, and these (unscaled) frequencies were used to compute zero-point vibrational energies (ZPVE) and 298 K thermal contributions (H298 – E0) for all species. “Activation enthalpies” for aryl radicals g, l and n were computed as the difference in enthalpy between the transition state and the separated reactants (i.e., aryl radical and isopropanol). All MPW1K calculations employed an unrestricted formalism.
All DFT calculations were carried out with the Gaussian 9847 electronic structure program suite.
Results and Discussion
A. Hydrogen-Atom Abstraction Reaction Efficiencies for Several Different Aryl Radicals and Two Hydrogen-Atom Donors (Cyclohexane and Isopropanol)
The influence of polar effects and reaction enthalpies on the hydrogen-atom abstraction reactions for a large set of aromatic carbon-centered σ-radicals (Table 1) was studied by measuring the efficiencies of their reactions (i.e., second-order reaction rate constant/collision rate constant) with two hydrogen-atom donors, cyclohexane and isopropanol. The aryl radicals studied included the following types: (1) dehydrobenzenes with a positively-charged substituent in the para position (b, c, f, k, t), (2) dehydrobenzenes with a positively-charged substituent in the meta position (g, i, l, n), (3) dehydrobiphenyl with a positively-charged substituent in the para position (a), (4) dehydropyridinium cations where the radical site is either ortho (w), meta (q, s, u, v) or para (o, r) to the nitrogen atom, (5) 1-dehydronaphthalenes with a positively-charged substituent in either the 4- (d) or 5-position (e), and (6) 4-, 5-, and 6-dehydroquinolinium cations (h, m, p) and 5-dehydroisoquinolinium cation (j). For those aryl radicals that contain an electron-withdrawing substituent other than a pyridinium ring, the relationship between the substituent and the radical site varies from ortho (k, v), to meta (l, n), to para (u) to a different aromatic ring (d, e, f, i). One aryl radical (t) contains four electron-withdrawing substituents. In addition, the relative sizes of the aryl radicals vary from those containing one aromatic ring (r, s, u, v, w) to those containing two (c, f, g, h, i, j, k, l, m, n, o, p, q, t) and three (a, b, d, e) aromatic rings.
Table 1.
Hydrogen-Atom Abstraction Reaction Efficiencies (Eff.) and Calculated Vertical Electron Affinities (EA) for Aryl Radicals
| radical | Eff. (%)a cyclohexane | Eff. (%)a isopropanol | Eff. ratio (cyclohexane/isopropanol) | EAb (eV) |
|---|---|---|---|---|
| a | 0.0034 ± 0.0008 | 0.0029 ± 0.0002 | 1.2 | 3.31 |
| b | 0.059 ± 0.011 | 0.029 ± 0.001 | 2.0 | 4.05 |
| c | 0.068 ± 0.019 | 0.046 ± 0.001 | 1.5 | 4.38 |
| d | 0.051 ± 0.004 | 0.060 ± 0.020 | 0.85 | 4.60 |
| e | 0.074 ± 0.007 | 0.060 ± 0.013 | 1.2 | 4.66 |
| f | 0.10 ± 0.03 | 0.065 ± 0.001 | 1.5 | 4.68 |
| g | 0.13 ± 0.04 | 0.15 ± 0.03 | 1.0 | 4.87 |
| h | 0.90 ± 0.01 | 0.45 ± 0.01 | 2.0 | 4.89 |
| i | 0.26 ± 0.04 | 0.29 ± 0.08 | 0.90 | 5.05 |
| j | 1.3 ± 0.3 | 2.0 ± 0.1 | 0.65 | 5.06 |
| k | 2.2 ± 0.5 | 0.96 ± 0.07 | 2.4 | 5.08 |
| l | 0.28 ± 0.01 | 0.36 ± 0.05 | 0.78 | 5.11 |
| m | 1.7 ± 0.1 | 2.8 ± 0.4 | 0.61 | 5.21 |
| n | 1.2 ± 0.3 | 1.4 ± 0.2 | 1.0 | 5.40 |
| o | 6.6 ± 1.8 | 5.3 ± 0.3 | 1.2 | 5.59 |
| p | 7.0 ± 0.4 | 4.7 ± 0.2 | 1.5 | 5.69 |
| q | 12 ± 2 | 11 ± 1 | 1.3 | 5.78 |
| r | 11 ± 3 | 9.9 ± 0.1 | 1.1 | 5.89 |
| s | 16 ± 3 | 20 ± 2 | 0.84 | 6.11 |
| t | 24 ± 1 | 13 ± 2 | 2.0 | 6.18 |
| u | 20 ± 1 | 28 ± 2 | 0.71 | 6.28 |
| v | 27 ± 4 | 24 ± 2 | 1.1 | 6.46 |
| w | 33 ± 2 | 61 ± 1 | 0.54 | 6.69 |
Hydrogen-atom abstraction reaction efficiency = second-order hydrogen-atom abstraction rate constant/collision rate constant (kexp/kcoll). Uncertainties are the standard deviations of the experimental data.
Calculated at the (U)B3LYP/6- 31+G(d)//(U)B3LYP/6-31+G(d) level of theory.
Despite the differences in their structures, all of the aryl radicals display similar reactivity toward cyclohexane and isopropanol, i.e., hydrogen-atom abstraction was the only reaction observed. However, the measured hydrogen-atom abstraction reaction efficiencies for a – w are quite different, and span about four orders of magnitude (Table 1).
Calculated electron affinities
Electron affinity is defined here as the energy difference between the positively-charged aryl radical (doublet ground state) and the zwitterion (singlet state) that is formed by addition of an electron to the radical site (thus generating a negatively-charged phenide moiety at the radical site while keeping the positively-charged moiety intact) at the ground-state geometry (i.e., this is a “vertical” electron affinity).43 It has been shown previously22,48 that calculated adiabatic and vertical electron affinities for a number of positively-charged aryl radicals differ by a relatively constant amount. Hence, either value can be used to examine trends in the abilities of such aryl radicals to accept an electron. Vertical electron affinities (vEA), rather than adiabatic electron affinities, were chosen for this study because they are more relevant to the model used to rationalize the observed reactivity correlations (vide infra). The (U)B3LYP/6-31+G(d)//(U)B3LYP/6-31+G(d) level of theory was used for all of the vEA calculations because this method has been shown to provide quite good agreement with experimentally determined electron affinities for a series of small molecules (for the molecules in the test set, the average absolute error is ca. 0.2 eV).49 Throughout the remainder of the discussion we will refer to the calculated vertical electron affinities as simply “EAs”.
The calculated EAs for aryl radicals a – w are listed in Table 1. The calculated EAs for aa – ff are 5.84 eV, 5.78 eV, 4.98 eV, 4.94 eV, 5.37 eV, and 5.12 eV, respectively. The calculated EAs of the radicals range from 3.31 eV (a) to 6.69 eV (w). As has been noted previously, the magnitude of the EA associated with the radical site of an aryl radical is affected by not only the distance between the formally positively-charged nitrogen atom and the radical site22,23,48 but also the presence of substituents.22,23 For the aryl radicals where the distances between the formally positively-charged nitrogen atom and the radical site are approximately the same, several trends are apparent. First, σ-electron withdrawing substituents increase the EA of the aryl radical, as illustrated by the following EA orderings: (1) c (4.38 eV) < f (4.68 eV); (2) c (4.38 eV) < k (5.08 eV); (3) c (4.38 eV) < cc (4.98 eV); (4) c (4.38 eV) < dd (4.94 eV); (5) g (4.87 eV) < i (5.05 eV); (6) g (4.87 eV) < n (5.40 eV); (7) g (4.87 eV) < l (5.11 eV); (8) g (4.87 eV) < ee (5.37 eV); and (9) g (4.87 eV) < ff (5.12 eV). Second, the EA orderings, s (6.11 eV) < u (6.28 eV) < v (6.46 eV), and c (4.38 eV) < f (4.68 eV) < k (5.08 eV), indicate that a substituent adjacent to the radical site increases the EA more than a remote substituent does. Third, the EA ordering of meta-substituted aryl radicals, g (4.87 eV) < l (5.11 eV) ~ ff (5.12 eV) < ee (5.37 eV) < n (5.40 eV), reveals that the ability of a substituent to increase the EA follows the order: Cl ~ Br < CN < NO2, which is consistent with their electron withdrawing abilities (as reflected by their Hammett constants, σm: Cl (0.37 ± 0.03) ~ Br (0.37 ± 0.04) < CN (0.62 ± 0.05) < NO2 (0.71 ± 0.04)).50 Fourth, a substituent in the same aromatic ring as the radical site has a greater influence on the EA than one in a different aromatic ring (e.g., f (4.68 eV) < k (5.08 eV)). Finally, the EA of the aryl radical decreases when the proton attached to the formally positively-charged nitrogen atom is replaced with a phenyl group, (e.g., o (5.59 eV) < r (5.89 eV), and q (5.78 eV) < s (6.11 eV)).
In most cases, decreasing the distance between the formally positively-charged nitrogen atom and the radical site increases the EA for the aryl radical, as illustrated by the following EA orderings: (1) a (3.31eV) < c (4.38 eV) < g (4.87 eV) < o (5.59 eV) < q (5.78 eV); (2) h (4.89 eV) < m (5.21 eV) < p (5.69 eV) < aa (5.84 eV); (3) j (5.06 eV) < bb (5.78 eV); and (4) r (5.89 eV) < s (6.11 eV) < w (6.69 eV).
Relationship between hydrogen-atom abstraction reaction efficiency and EA
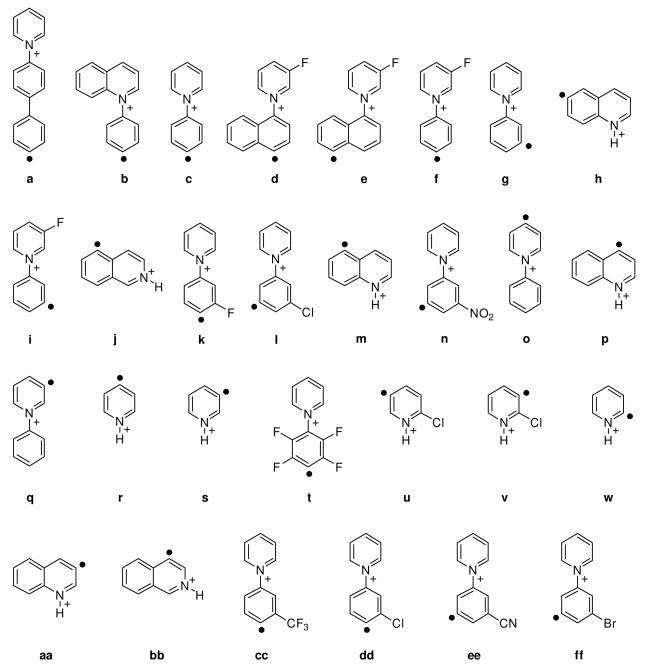
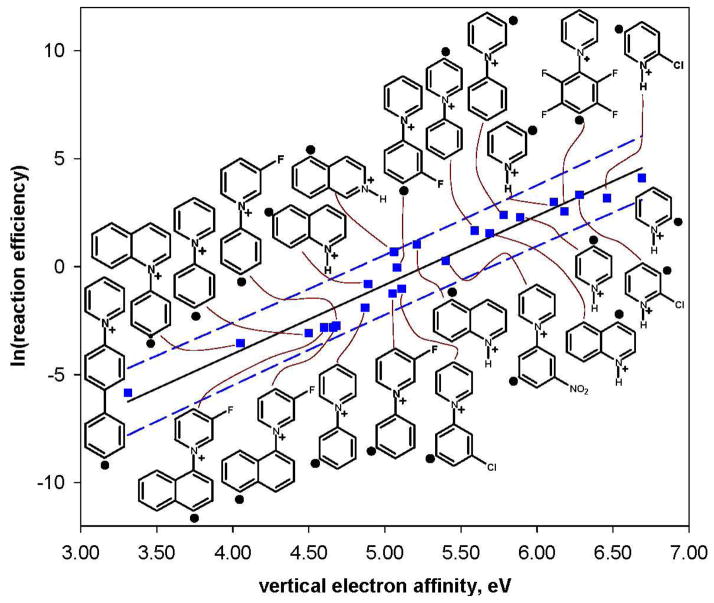
A plot of the reaction efficiency for hydrogen-atom abstraction from cyclohexane versus EA for twenty-three aryl radicals, a – w, is shown in Figure 1. Statistical analysis of these data by using the Box-Cox procedure indicated that the best linear correlation is obtained by using the natural logarithm of the reaction efficiency. A plot of the natural logarithm of the reaction efficiency for hydrogen-atom abstraction from cyclohexane versus EA for the twenty-three aryl radicals is shown in Figure 2. The 95% prediction interval51 is also shown in Figure 2. It is rather remarkable that the reactivity (i.e., reaction efficiency) of the twenty-three aryl radicals appears to depend only on their EAs even though these aryl radicals vary greatly in size, and many of them contain substituents.
Figure 1.
Reaction efficiencies (%) for hydrogen-atom abstraction from cyclohexane versus calculated vertical electron affinities (eV) for twenty-three aryl radicals. The data are fit to an exponential trend line (R2 = 0.94).
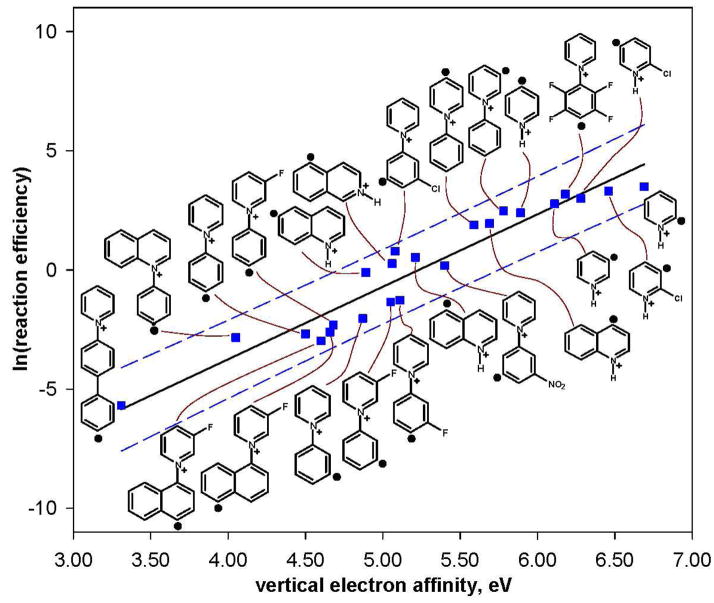
Figure 2.
Natural logarithm of the reaction efficiencies for hydrogen-atom abstraction from cyclohexane versus calculated vertical electron affinities (eV) for twenty-three aryl radicals. The data are fit to a linear trend line (R2 = 0.92); the dashed lines represent the 95% prediction interval.51
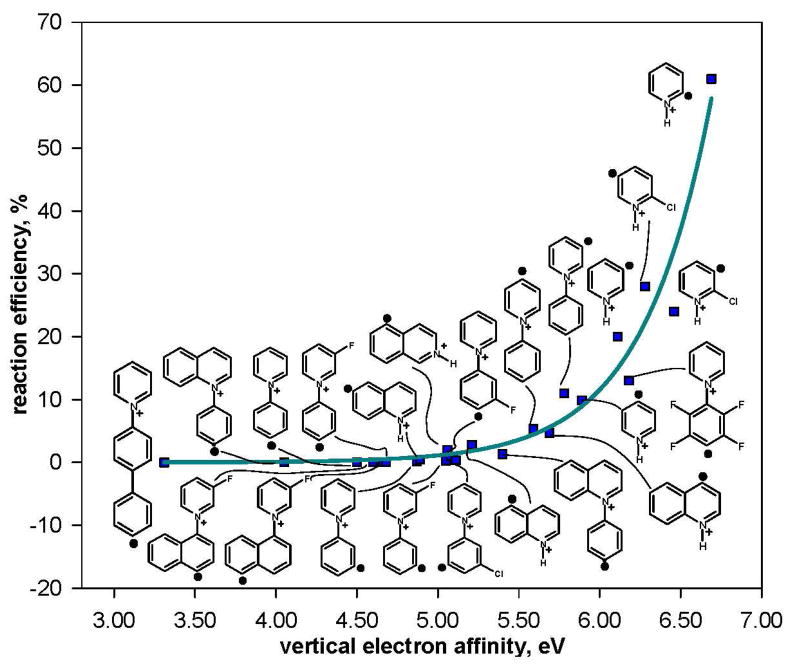
A similar relationship between the reaction efficiency and EA also exists for the other hydrogen-atom donor studied: isopropanol (note that for this hydrogen-atom donor, the dominant hydrogen-atom abstraction site is the α-carbon atom52). A plot of the reaction efficiency for hydrogen-atom abstraction from isopropanol versus EA for the twenty-three aryl radicals, a – w, is shown in Figure 3. Statistical analysis of these data by using the Box-Cox procedure also indicated that the best linear correlation is obtained by using the natural logarithm of the reaction efficiency (Figure 4).
Figure 3.
Reaction efficiencies (%) for hydrogen-atom abstraction from isopropanol versus calculated vertical electron affinities (eV) for twenty-three aryl radicals. The data are fit to an exponential trend line (R2 = 0.95).
Figure 4.
Natural logarithm of the reaction efficiencies for hydrogen-atom abstraction from isopropanol versus calculated vertical electron affinities (eV) for twenty-three aryl radicals. The data are fit to a linear trend line (R2 = 0.94); the dashed lines represent the 95% prediction interval.51
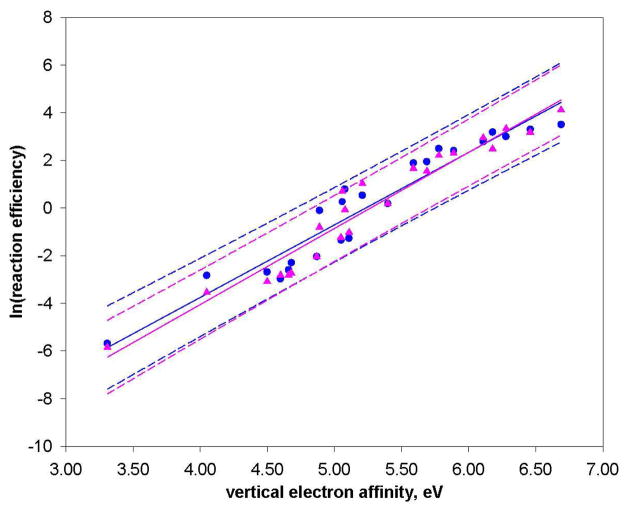
Comparison of reaction efficiencies and EA for cyclohexane and isopropanol
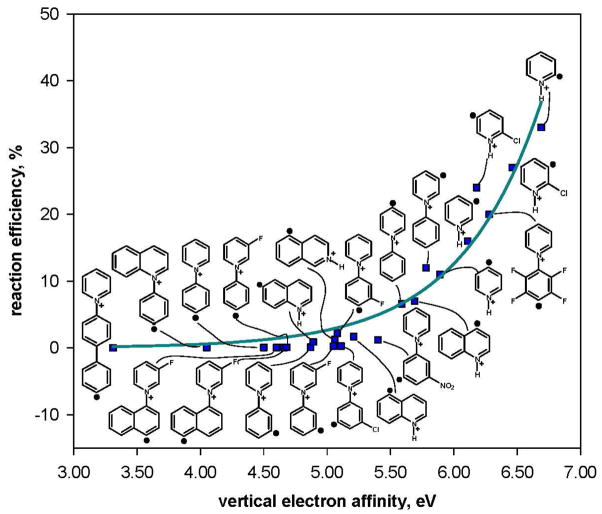
In order to determine whether the type of hydrogen-atom donor (i.e., cyclohexane or isopropanol) influences the reaction efficiencies for the twenty-three aryl radicals, a statistical analysis using the Box-Cox procedure was performed where data (i.e., reaction efficiencies and EAs) for both cyclohexane and isopropanol were combined. Again, the best linear correlation is obtained by using the natural logarithm of the reaction efficiency (Figure 5). The correlation between the natural logarithm of the reaction efficiency and EA is excellent, which is rather surprising considering the fact that the structures, polarities and homolytic C–H bond dissociation energies53 (H–cyclohexyl: 95.5 ± 1.0 kcal/mol; H–C(CH3)2(OH): 91 ± 1 kcal/mol) for the two hydrogen-atom donors are quite different. The similarity of the reactivity of these two hydrogen-atom donors is also reflected in the reaction efficiency ratio (i.e., Eff. (cyclohexane)/Eff. (isopropanol)) listed in Table 1; for most of the aryl radicals, the reaction efficiency ratio is close to one.
Figure 5.
Natural logarithm of the reaction efficiencies for hydrogen-atom abstraction from cyclohexane (blue) and isopropanol (pink) versus calculated vertical electron affinities (eV) for twenty-three aryl radicals. Data for each hydrogen-atom donor are fit to a linear trend line; the dashed lines represent the 95% prediction interval.51
Polar effects
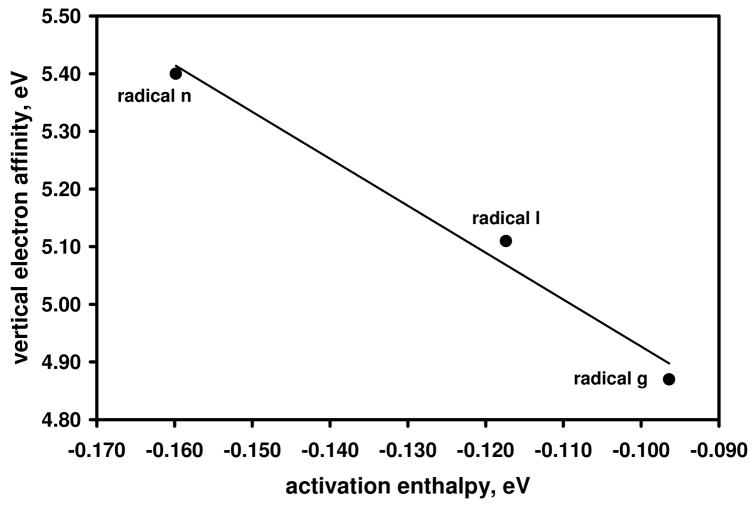
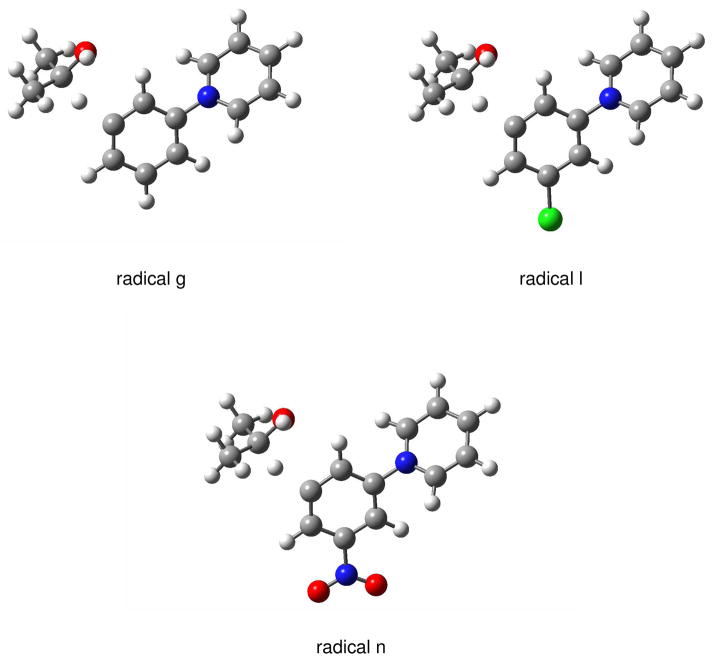
The dependence of the reaction efficiency on the EA for the aryl radicals can be qualitatively explained by polar effects; that is, lowering the energy of the transition state by increasing its polar character (i.e., the degree of charge transfer in the transition state). Support for this hypothesis is obtained from the linear correlation that exists between the calculated ((U)B3LYP/6-31+G(d)) EAs and calculated (UMPW1K/6-31+G(d,p)) activation enthalpies (i.e., the enthalpy difference between the separated reactants and the transition state) for aryl radicals g, l and n (Figure 6). The calculated (UMPW1K/6-31+G(d,p)) transition-state structures for hydrogen-atom abstraction from isopropanol by aryl radicals g, l and n are shown in Figure 7. In the transition states, the distances between the hydrogen atom being transferred and the α-carbon in isopropanol (1.185 Å, 1.178 Å, and 1.170 Å for aryl radicals g, l, and n, respectively) are much shorter than the distances between the hydrogen atom being transferred and the radical site (1.610 Å, 1.632 Å, and 1.661 Å for aryl radicals g, l, and n, respectively). Hence, the structures of the transition states are closer to those for the reactants than those for the products; that is, they are “early” transition states. For these three aryl radicals, the most highly reactive radical n has the earliest transition state while the least reactive radical g has the latest. Further, because all of the (calculated) reaction enthalpies (ΔHrxn) associated with hydrogen-atom abstraction from either cyclohexane or isopropanol by aryl radicals a – w are highly exothermic (described in the next section), it is likely that “early” transition states exist for all of these reactions.
Figure 6.
Calculated ((U)B3LYP/6-31+G(d)) vertical electron affinities (eV) versus calculated (UMPW1K/6-31+G(d,p)) activation enthalpies (eV) for aryl radicals g, l and n. The activation enthalpies are the differences in enthalpies between the separated reactants and the transition state. The data are fit to a linear trend line (R2 = 0.98).
Figure 7.
Calculated (UMPW1K/6-31+G(d,p)) transition-state structures for hydrogen-atom abstraction from isopropanol by aryl radicals g, l and n. The distances between the hydrogen atom being transferred and the α-carbon atom in isopropanol are 1.185 Å, 1.178 Å and 1.170 Å, respectively. The distances between the hydrogen atom being transferred and the radical site are 1.610 Å, 1.632 Å and 1.661 Å, respectively.
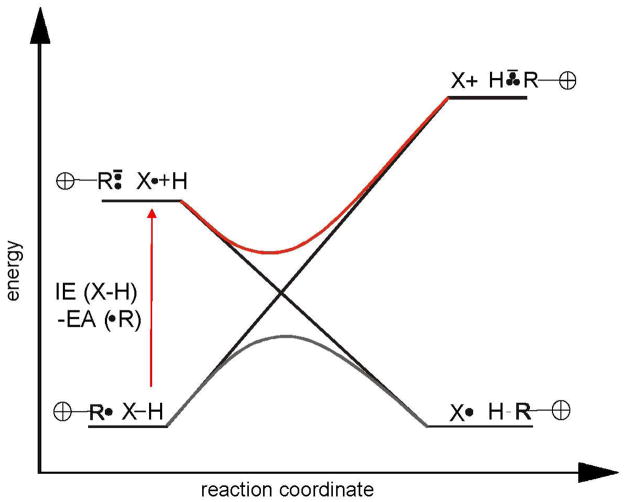
Figure 8 shows an avoided ionic curve crossing diagram that can be used to consider relative energies of hydrogen-atom abstraction transition states.54,55,56,57 The diagram is based on an avoided crossing of the ground state and a hypothetical ionic excited state of the reactants ([R•][X–H] and [R••−][X•H+], respectively), having the same geometry (hence, vertical EA and IE are relevant), and products ([X•][H–R] and [X+][H•••R−], respectively), again with the same geometry. For an “early” transition state (e.g., like those associated with hydrogen-atom abstraction by the positively-charged aryl radicals studied here; vide supra), the energy gap between the ground state ([R•][X–H]) and hypothetical ionic excited state ([R••−][X•H+]) of the reactants (here, approximated by the molecular IE of the hydrogen-atom donor58 minus the EA of the aryl radical at the radical site) is the most important factor controlling the energy of the transition state.22,23,54,55,56,57 Here, the vertical IEs of the hydrogen-atom donors, isopropanol (IE = 10.44 eV59) and cyclohexane (IE = 10.32 eV60), are similar; however, the EAs of the aryl radicals vary widely. Thus, a larger EA for an aryl radical (e.g., 3.31 eV (a) versus 6.69 eV (w)) leads to a smaller energy gap (e.g., 7.0 eV (a) versus 3.6 eV (w) for the hydrogen-atom donor, cyclohexane) between the hypothetical ionic excited state and the ground state of the reactants, which in turn lowers the energy of the transition state. The reaction efficiency for hydrogen-atom abstraction from either cyclohexane or isopropanol should therefore increase as the EA of the aryl radical increases.
Figure 8.
A hypothetical ionic avoided curve crossing diagram for the abstraction of a hydrogen atom from X–H by a positively-charged radical, R•
Reaction enthalpies
The (calculated) enthalpy changes (ΔHrxn) associated with all of the hydrogen-atom abstraction reactions studied here are shown in Table 2. All of the reactions are exothermic, and the exothermicity varies over a relatively narrow range (i.e., from −22.9 kcal/mol to −16.2 kcal/mol for cyclohexane, and from −27.4 kcal/mol to −21.6 kcal/mol for isopropanol; Table 2).
Table 2.
Calculated Enthalpy Changes (ΔHrxn) and Reaction Efficiencies (Eff.) for Hydrogen-Atom Abstraction from Cyclohexane and Isopropanol
| radical | cyclohexane | isopropanol | ||
|---|---|---|---|---|
| ΔHrxn (kcal/mol)a | Eff. (%)b | ΔHrxn (kcal/mol)a | Eff. (%)b | |
| a | −16.2 | 0.0034 ± 0.0008 | −21.6 | 0.0029 ± 0.0002 |
| b | −17.0 | 0.059 ± 0.011 | −22.4 | 0.029 ± 0.001 |
| c | −17.3 | 0.068 ± 0.019 | −22.8 | 0.046 ± 0.001 |
| d | −16.8 | 0.051 ± 0.004 | −22.3 | 0.060 ± 0.020 |
| e | −16.7 | 0.074 ± 0.007 | −22.1 | 0.060 ± 0.013 |
| f | −17.4 | 0.10 ± 0.03 | −22.9 | 0.065 ± 0.001 |
| g | −17.2 | 0.13 ± 0.04 | −22.6 | 0.15 ± 0.03 |
| h | −18.0 | 0.90 ± 0.01 | −23.4 | 0.45 ± 0.01 |
| i | −17.3 | 0.26 ± 0.04 | −22.7 | 0.29 ± 0.08 |
| j | −18.0 | 1.3 ± 0.3 | −23.4 | 2.0 ± 0.1 |
| k | −20.0 | 2.2 ± 0.5 | −25.4 | 0.96 ± 0.07 |
| l | −17.3 | 0.28 ± 0.01 | −22.7 | 0.36 ± 0.05 |
| m | −18.1 | 1.7 ± 0.1 | −23.6 | 2.8 ± 0.4 |
| n | −18.0 | 1.2 ± 0.3 | −23.4 | 1.4 ± 0.2 |
| o | −18.8 | 6.6 ± 1.8 | −24.2 | 5.3 ± 0.3 |
| p | −17.9 | 7.0 ± 0.4 | −23.3 | 4.7 ± 0.2 |
| q | −20.3 | 12 ± 2 | −25.7 | 11 ± 1 |
| r | −19.0 | 11 ± 3 | −24.4 | 9.9 ± 0.1 |
| s | −21.2 | 16 ± 3 | −26.7 | 20 ± 2 |
| t | −22.9 | 24 ± 1 | −28.3 | 13 ± 2 |
| u | −21.8 | 20 ± 1 | −27.3 | 28 ± 2 |
| v | −21.8 | 27 ± 4 | −27.2 | 24 ± 2 |
| w | −22.0 | 33 ± 2 | −27.4 | 61 ± 1 |
Calculated at the (U)B3LYP/6-31+G(d)//(U)B3LYP/6-31+G(d) level of theory.
Hydrogen-atom abstraction reaction efficiency = second-order hydrogen-atom abstraction rate constant/collision rate constant (kexp/kcoll). Uncertainties are the standard deviations of the experimental data.
While the hydrogen-atom abstraction reaction efficiencies do (loosely) parallel the reaction enthalpies (Table 2), several inconsistencies exist: (1) the calculated ΔHrxn for aryl radical b with cyclohexane (−17.0 kcal/mol) is only 0.8 kcal/mol greater than that for aryl radical a (−16.2 kcal/mol), but the hydrogen-atom abstraction reaction efficiency from cyclohexane is about seventeen times greater for b (0.059%) than for a (0.0034%); (2) for aryl radicals c and i, the calculated ΔHrxn for hydrogen-atom abstraction from cyclohexane is identical (−17.3 kcal/mol), but the reaction efficiencies are drastically different (c: 0.068%; i: 0.26%); (3) the calculated ΔHrxn for aryl radical a with isopropanol (−21.6 kcal/mol) is only slightly less than that for radical b (−22.4 kcal/mol), but the hydrogen-atom abstraction reaction efficiencies for these two radicals differ by one order of magnitude (a: 0.0029%; b: 0.029%); and (4) for aryl radicals h and p, the calculated ΔHrxn for hydrogen-atom abstraction from isopropanol (−23.4 and −23.3 kcal/mol, respectively) is nearly identical, but the reaction efficiencies are very different (h: 0.45%; p: 4.7%).
Summary of Reactivity
For the aryl radicals studied here, the reactivity towards the hydrogen-atom donors, cyclohexane and isopropanol, appears to depend only on the EA of the aryl radical. There is no obvious dependence on either the size of the aryl radical or the reaction enthalpy associated with the hydrogen-atom abstraction. Because the EA of an aryl radical can be altered either by changing the electron density at the radical site (e.g., by adding electron-withdrawing or electron-donating substituents), or by changing the distance between the formally positively-charged nitrogen atom and the radical site, it should be possible to “tune” the reactivities of aryl radicals in hydrogen-atom abstraction reactions via such structural modifications.
B. Hydrogen-Atom Abstraction Reaction Efficiencies for Two Selected Aryl Radicals and Several Different Hydrogen-Atom Donors
The previous section focused on the factors that influence the hydrogen-atom abstraction reaction efficiencies for a variety of different aryl radicals and two hydrogen-atom donors (i.e., cyclohexane and isopropanol). In this section, the dependence of the reaction efficiencies of two selected aryl radicals (g and l) on the identity of the hydrogen-atom donor is examined. The reaction efficiency for hydrogen-atom abstraction by aryl radical g has been measured previously for twelve different hydrogen-atom donors: ethanol,61 tert-butanol,61 glycine,62 tetrahydrofuran,22 1,4-dioxane,63 valine,62 ribose,15 2-deoxy-D-ribose,15 1-O-methyl- 2-deoxy-D-ribose,15 proline,62 benzeneselenol22 and tributyltin hydride.22 Reaction efficiencies for hydrogen-atom abstraction by aryl radical l have also been measured previously for eleven different hydrogen-atom donors: ethanol,61 tert-butanol,61 glycine,62 tetrahydrofuran,22 valine,62 ribose,15 2-deoxy-D-ribose,15 1-O-methyl-2-deoxy-D-ribose,15 proline,62 benzeneselenol22 and tributyltin hydride.22 Reaction efficiencies for hydrogen-atom abstraction by aryl radicals g and l for L-alanine were measured here. These data, along with the data for cyclohexane and isopropanol, were used to evaluate possible correlations between the hydrogen-atom abstraction reaction efficiencies and either the IEs, or the relevant homolytic bond dissociation energies, of the hydrogen-atom donors.
Relationship between hydrogen-atom abstraction reaction efficiency and IE of the hydrogen-atom donor
Vertical ionization energies for several different hydrogen-atom donors are listed in Table 3 (note that some of these values are experimentally determined,59,60,64,65,66,67,68,69,70 and some are calculated). Vertical ionization energies, rather than adiabatic ionization energies, were chosen for this study because they are more relevant to the ionic avoided curve crossing model described above.58 Throughout the remainder of the discussion we will refer to a vertical ionization energy as simply “IE”.
Table 3.
Vertical Ionization Energies (IE) for Several Hydrogen-Atom Donors
| hydrogen-atom donor | IE, calc. (eV) | IE, exp. (eV) |
|---|---|---|
| ethanol | 10.64a | |
| tert-butanol | 10.26b | |
| isopropanol | 10.24c | 10.44d |
| cyclohexane | 10.20c | 10.32e |
| glycine | 10.0f | |
| L-alanine | 9.8g | |
| tetrahydrofuran | 9.74e | |
| 1,4-dioxane | 9.4h | |
| valine | 9.29c | |
| ribose | 9.1i | |
| 2-deoxy-D-ribose | 9.0i | |
| 1-O-methyl-2-deoxy-D-ribose | 9.0i | |
| proline | 9.0f | |
| benzeneselenol | 8.9j | |
| tributyltin hydride | 8.8k |
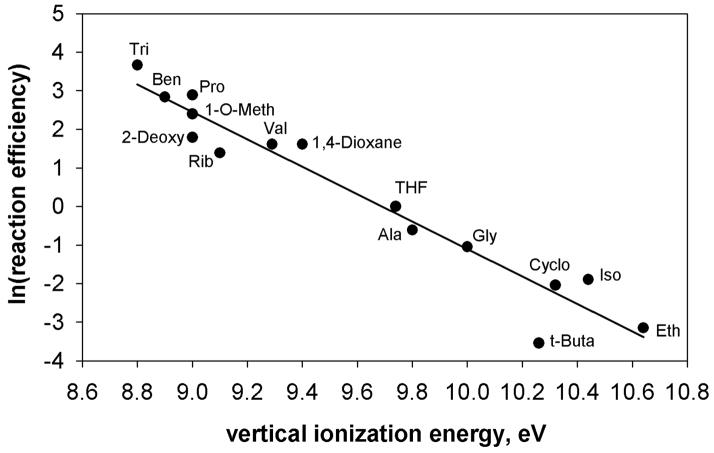
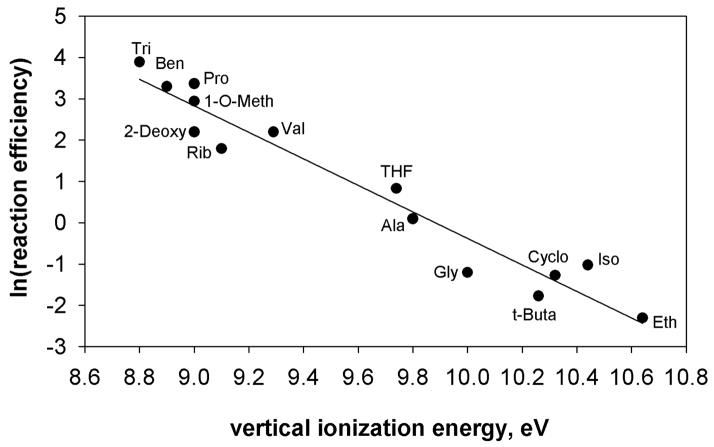
Statistical analysis of the hydrogen-atom abstraction reaction efficiencies for aryl radical g and the IEs of the (fifteen) hydrogen-atom donors using the Box-Cox procedure indicated that the best linear correlation is obtained by using the natural logarithm of the reaction efficiency. A plot of the natural logarithm of the hydrogen-atom abstraction reaction efficiency for aryl radical g versus IE for the fifteen different hydrogen-atom donors is shown in Figure 9. A similar analysis (i.e., Box-Cox) of the hydrogen-atom abstraction reaction efficiencies for aryl radical l and the IEs of the (fourteen) hydrogenatom donors also indicates that the best linear correlation is obtained by using the natural logarithm of the reaction efficiency. A plot of the natural logarithm of the hydrogen-atom abstraction reaction efficiency for aryl radical l versus IE for the fourteen hydrogen-atom donors is shown in Figure 10.
Figure 9.
Natural logarithm of the reaction efficiencies for hydrogen-atom abstraction from fifteen different hydrogen-atom donors by N-(3-dehydrophenyl)pyridinium cation (g) versus the vertical ionization energies (eV) of the hydrogen-atom donors. The data are fit to a linear trend line (R2 = 0.94). The hydrogen-atom donors are: tributyltin hydride (Tri), benzeneselenol (Ben), proline (Pro), 2-deoxy-D-ribose (2-Deoxy), 1-Omethyl-2-deoxy-D-ribose (1-O-Meth), ribose (Rib), valine (Val), 1,4-dioxane, tetrahydrofuran (THF), L-alanine (Ala), glycine (gly), cyclohexane (cyclo), isopropanol (Iso) and ethanol (Eth).
Figure 10.
Natural logarithm of the reaction efficiencies for hydrogen-atom abstraction from fourteen different hydrogen-atom donors by N-(3-chloro-5-dehydrophenyl)pyridinium cation (l) versus the vertical ionization energies (eV) of the hydrogen-atom donors. The data are fit to a linear trend line (R2 = 0.95). The hydrogen-atom donors are: tributyltin hydride (Tri), benzeneselenol (Ben), proline (Pro), 2-deoxy-D-ribose (2-Deoxy), 1-O-methyl-2-deoxy-D-ribose (1-O-Meth), ribose (Rib), valine (Val), tetrahydrofuran (THF), L-alanine (Ala), glycine (gly), cyclohexane (cyclo), isopropanol (Iso) and ethanol (Eth).
For each set of data, the EA of the aryl radical (i.e., either g or l) is constant, but the IEs of the hydrogen-atom donors vary widely. Based on the ionic avoided curve crossing model described above, for any given aryl radical, the energy of the transition state for hydrogen-atom abstraction is predicted to increase as the vertical IE of the hydrogen-atom donor increases.58 Figures 9 and 10 show that the data are entirely consistent with this prediction.
Comparison of hydrogen-atom abstraction reaction efficiency and homolytic bond dissociation energy of the hydrogen-atom donor
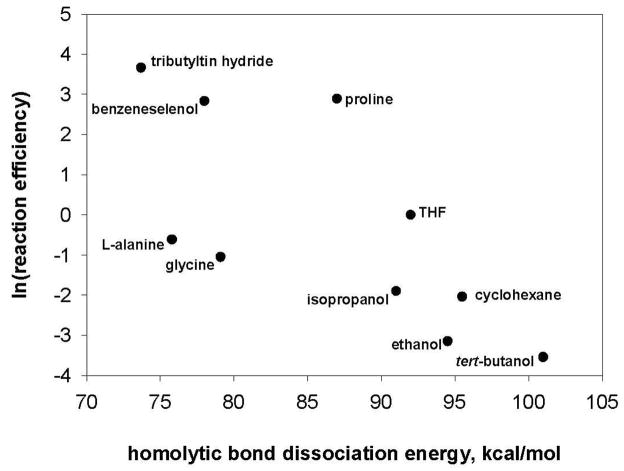
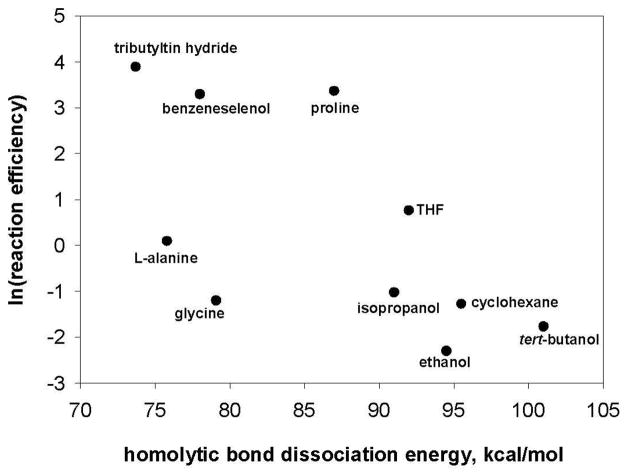
In contrast to the good correlation that is found to exist between the hydrogen-atom abstraction reaction efficiencies for the aryl radicals and the IEs of the hydrogen-atom donors (vide supra), no such correlation is found between the hydrogen-atom abstraction reaction efficiencies and the lowest (relevant) homolytic bond dissociation energies (BDEs)22,53,61,62,71,72,73,74,75 of the hydrogen-atom donors (Table 4). Plots of the hydrogen-atom abstraction reaction efficiencies for aryl radicals g and l versus the lowest homolytic BDEs (i.e., those involving a hydrogen atom) for the ten hydrogen-atom donors studied are shown in Figures 11 and 12.
Table 4.
Homolytic Bond Dissociation Energies (BDE) and Hydrogen-Atom Abstraction Reaction Efficiencies (Eff.) for Aryl Radicals g and l
| hydrogen-atom donor | BDEa (kcal/mol) | Eff. (%)b (g) | Eff. (%)b (l) |
|---|---|---|---|
| ethanol | 94.5c | 0.043d | 0.1d |
| tert-butanol | 101d | 0.029d | 0.17d |
| cyclohexane | 95.5e | 0.13 | 0.28 |
| glycine | 79.1f | 0.35g | 0.3g |
| isopropanol | 91e | 0.15 | 0.36 |
| L-alanine | 75.8f | 0.54 | 1.1 |
| tetrahydrofuran | 92e | 1h | 2.3h |
| benzeneselenol | 78i | 17h | 27h |
| proline | 87j | 18g | 29g |
| tributyltin hydride | 73.7k | 39i | 49i |
BDEs are given for the α C–H bond in ethanol, glycine, isopropanol, L-alanine, proline and tetrahydrofuran; for the C–H bond in cyclohexane and tert-butanol; for the Se–H bond in benzeneselenol; and for the Sn–H bond in tributyltin hydride. Experimentally-determined values are shown in bold; calculated values are shown in italics.
Hydrogen-atom abstraction reaction efficiency = second-order hydrogen-atom abstraction rate constant/collision rate constant (kexp/kcoll).
Reference 71.
Reference 61.
Reference 53.
Reference 72.
Reference 62.
Reference 22.
Reference 74.
Average of the BDE values for cis- and trans-proline; reference 75.
Reference 73.
Figure 11.
Natural logarithm of the reaction efficiencies for hydrogen-atom abstraction by aryl radical g versus the lowest homolytic bond dissociation energies (kcal/mol) for several different hydrogen-atom donors.
Figure 12.
Natural logarithm of the reaction efficiencies for hydrogen-atom abstraction by aryl radical l versus the lowest homolytic bond dissociation energies (kcal/mol) for several different hydrogen-atom donors.
C. Hydrogen-Atom Abstraction Reaction Efficiencies and (IE – EA) for the Reacting System
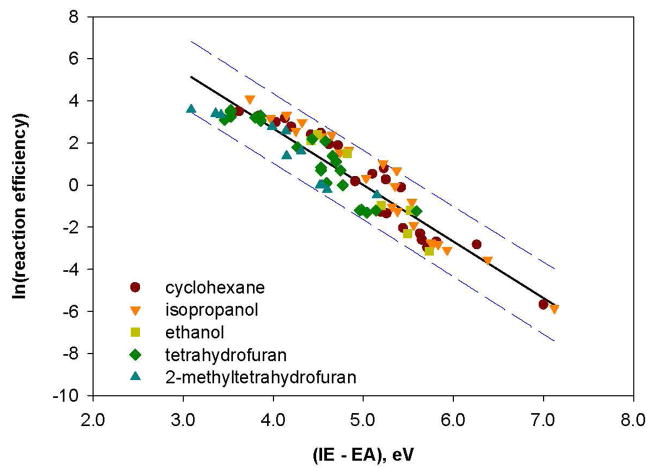
To summarize, the hydrogen-atom abstraction reaction efficiencies for the aryl radicals studied here have been shown to be affected by not only the EA of the aryl radical but also the IE of the hydrogen-atom donor. Because the ionic avoided curve crossing model (described above) predicts that the reaction efficiencies should also depend on the difference between the IE of the hydrogen-atom donor and the EA of the aryl radical (i.e., (IE – EA)), it was of interest to examine this relationship by using several different aryl radicals and hydrogen-atom donors. Thus, reaction efficiencies (measured here for cyclohexane and isopropanol, or measured previously) for hydrogenatom abstraction from ethanol by seven different aryl radicals (g, k, l, n, q, s, t),61,76 from tetrahydrofuran by twenty different aryl radicals (b, c, d, e, f, g, h, i, j, l, m, q, s, t, aa, bb, cc, dd, ee, ff),22,23,27,28,63 and from 2-methyltetrahydrofuran by eleven different aryl radicals (b, d, e, f, h, i, j, m, s, aa, bb),23 were studied. The calculated (IE – EA) values and the reaction efficiencies for hydrogen-atom abstraction are listed in Table 5. Statistical analysis (Box-Cox) of these data indicated that the best linear correlation is obtained by using the natural logarithm of the hydrogen-atom abstraction reaction efficiency (Figure 13). This correlation is consistent with the ionic avoided curve crossing model, which predicts that the energy of the transition state for hydrogen-atom abstraction decreases as (IE – EA) increases.54,55,56,57
Table 5.
Calculated Values for (IE – EA) and Hydrogen-Atom Abstraction Reaction Efficiencies (Eff.) for Several Aryl Radicals and Hydrogen-Atom Donors
| radical | hydrogen-atom donor | (IE – EA), eV | Eff. (%)a |
|---|---|---|---|
| a | cyclohexane | 7.01 | 0.0034 ± 0.0008 |
| b | cyclohexane | 6.27 | 0.059 ± 0.011 |
| c | cyclohexane | 5.94 | 0.068 ± 0.019 |
| d | cyclohexane | 5.72 | 0.051 ± 0.004 |
| e | cyclohexane | 5.66 | 0.074 ± 0.007 |
| f | cyclohexane | 5.64 | 0.10 ± 0.03 |
| g | cyclohexane | 5.45 | 0.13 ± 0.04 |
| h | cyclohexane | 5.43 | 0.90 ± 0.01 |
| I | cyclohexane | 5.27 | 0.26 ± 0.04 |
| j | cyclohexane | 5.26 | 1.3 ± 0.3 |
| k | cyclohexane | 5.24 | 2.2 ± 0.5 |
| l | cyclohexane | 5.21 | 0.28± 0.01 |
| m | cyclohexane | 5.11 | 1.7 ± 0.1 |
| n | cyclohexane | 4.92 | 1.2 ± 0.3 |
| o | cyclohexane | 4.73 | 6.6 ± 1.8 |
| p | cyclohexane | 4.63 | 7.0 ± 0.4 |
| q | cyclohexane | 4.54 | 12 ± 2 |
| r | cyclohexane | 4.43 | 11 ± 3 |
| s | cyclohexane | 4.21 | 16 ± 3 |
| t | cyclohexane | 4.14 | 24 ± 1 |
| u | cyclohexane | 4.04 | 20 ± 1 |
| v | cyclohexane | 3.86 | 27 ± 4 |
| w | cyclohexane | 3.63 | 33 ± 2 |
| a | isopropanol | 7.13 | 0.0029 ± 0.0002 |
| b | isopropanol | 6.39 | 0.029 ± 0.001 |
| c | isopropanol | 6.06 | 0.046 ± 0.001 |
| d | isopropanol | 5.84 | 0.060 ± 0.020 |
| e | isopropanol | 5.78 | 0.060 ± 0.013 |
| f | isopropanol | 5.76 | 0.065 ± 0.001 |
| g | isopropanol | 5.57 | 0.15 ± 0.03 |
| h | isopropanol | 5.55 | 0.45 ± 0.01 |
| i | isopropanol | 5.39 | 0.29 ± 0.08 |
| j | isopropanol | 5.38 | 2.0 ± 0.1 |
| k | isopropanol | 5.36 | 0.96 ± 0.07 |
| l | isopropanol | 5.33 | 0.36 ± 0.05 |
| m | isopropanol | 5.23 | 2.8 ± 0.4 |
| n | isopropanol | 5.04 | 1.4 ± 0.2 |
| o | isopropanol | 4.85 | 5.3 ± 0.3 |
| p | isopropanol | 4.75 | 4.7 ± 0.2 |
| q | isopropanol | 4.66 | 11 ± 1 |
| r | isopropanol | 4.55 | 9.9 ± 0.1 |
| s | isopropanol | 4.33 | 20 ± 2 |
| t | isopropanol | 4.26 | 13 ± 2 |
| u | isopropanol | 4.16 | 28 ± 2 |
| v | isopropanol | 3.98 | 24 ± 2 |
| w | isopropanol | 3.75 | 61 ± 1 |
| g | ethanol | 5.77 | 0.043 |
| k | ethanol | 5.56 | 0.30 ± 0.03 |
| l | ethanol | 5.53 | 0.1 |
| n | ethanol | 5.24 | 0.38 ± 0.06 |
| q | ethanol | 4.86 | 4.5 ± 0.7 |
| s | ethanol | 4.53 | 11 ± 1 |
| t | ethanol | 4.46 | 8.2 ± 1.8 |
| b | tetrahydrofuran | 5.69 | 0.29 |
| c | tetrahydrofuran | 5.36 | 0.3 |
| d | tetrahydrofuran | 5.14 | 0.27 |
| e | tetrahydrofuran | 5.08 | 0.31 |
| f | tetrahydrofuran | 5.06 | 0.30 |
| g | tetrahydrofuran | 4.87 | 1 |
| h | tetrahydrofuran | 4.85 | 2 |
| dd | tetrahydrofuran | 4.80 | 3 |
| cc | tetrahydrofuran | 4.76 | 4 |
| i | tetrahydrofuran | 4.69 | 1.1 |
| j | tetrahydrofuran | 4.68 | 8 |
| l | tetrahydrofuran | 4.63 | 2.3 |
| ff | tetrahydrofuran | 4.62 | 2 |
| m | tetrahydrofuran | 4.53 | 9 |
| ee | tetrahydrofuran | 4.37 | 6 |
| bb | tetrahydrofuran | 3.96 | 22 |
| q | tetrahydrofuran | 3.96 | 21 |
| aa | tetrahydrofuran | 3.90 | 25 |
| s | tetrahydrofuran | 3.63 | 26 |
| t | tetrahydrofuran | 3.56 | 22 |
| b | 2-methyltetrahydrofuran | 5.15 | 0.62 |
| d | 2-methyltetrahydrofuran | 4.60 | 0.80 |
| e | 2-methyltetrahydrofuran | 4.54 | 1.0 |
| f | 2-methyltetrahydrofuran | 4.52 | 1.0 |
| h | 2-methyltetrahydrofuran | 4.31 | 5 |
| i | 2-methyltetrahydrofuran | 4.15 | 4.0 |
| j | 2-methyltetrahydrofuran | 4.14 | 13 |
| m | 2-methyltetrahydrofuran | 3.99 | 16 |
| bb | 2-methyltetrahydrofuran | 3.42 | 28 |
| aa | 2-methyltetrahydrofuran | 3.36 | 30 |
| s | 2-methyltetrahydrofuran | 3.09 | 38 |
| m | diethyl ether | 4.43 | 8.1 |
| m | butyl methyl ether | 4.43 | 14 |
| g | tert-butanol | 5.39 | 0.029 |
| l | tert-butanol | 5.15 | 0.17 |
| q | tert-butanol | 4.48 | 10 |
| s | tert-butanol | 4.15 | 23 |
| g | tributyltin hydride | 3.9 | 39 |
| l | tributyltin hydride | 3.7 | 49 |
| ee | tributyltin hydride | 3.4 | 71 |
| q | tributyltin hydride | 3.0 | 74 |
| s | tributyltin hydride | 2.7 | 89 |
| g | benzeneselenol | 4.0 | 17 |
| l | benzeneselenol | 3.8 | 27 |
| ff | benzeneselenol | 3.8 | 27 |
| ee | benzeneselenol | 3.5 | 38 |
| b | L-alanine | 5.8 | 0.063 ± 0.001 |
| c | L-alanine | 5.4 | 0.084 ± 0.009 |
| f | L-alanine | 5.1 | 0.12 ± 0.005 |
| g | L-alanine | 4.9 | 0.54 ± 0.01 |
| i | L-alanine | 4.8 | 0.96 ± 0.01 |
| l | L-alanine | 4.7 | 1.1 ± 0.01 |
| g | proline | 4.1 | 18 |
| l | proline | 3.9 | 29 |
| s | proline | 3.2 | 43 |
| t | proline | 2.8 | 33 |
| g | glycine | 5.1 | 0.35 |
| l | glycine | 4.9 | 0.3 |
| g | valine | 4.42 | 5 |
| l | valine | 4.18 | 9 |
| g | 1,4-dioxane | 4.5 | 5 |
| g | ribose | 4.2 | 4 |
| l | ribose | 4.0 | 6 |
| ff | ribose | 4.0 | 7 |
| q | ribose | 3.3 | 32 |
| s | ribose | 3.0 | 53 |
| g | 2-deoxy-D-ribose | 4.1 | 6 |
| l | 2-deoxy-D-ribose | 3.9 | 9 |
| ff | 2-deoxy-D-ribose | 3.9 | 8 |
| q | 2-deoxy-D-ribose | 3.2 | 32 |
| s | 2-deoxy-D-ribose | 2.9 | 54 |
| g | 1-O-methyl-2-deoxy-D-ribose | 4.1 | 11 |
| l | 1-O-methyl-2-deoxy-D-ribose | 3.9 | 19 |
| ff | 1-O-methyl-2-deoxy-D-ribose | 3.9 | 20 |
| q | 1-O-methyl-2-deoxy-D-ribose | 3.2 | 47 |
| s | 1-O-methyl-2-deoxy-D-ribose | 2.9 | 61 |
Hydrogen-atom abstraction reaction efficiency = second-order hydrogen-atom abstraction rate constant/collision rate constant (kexp/kcoll). Uncertainties (where listed) are the standard deviations of the experimental data.
Figure 13.
Natural logarithm of the reaction efficiencies for hydrogen-atom abstraction from five different hydrogen-atom donors by twenty-two different aryl radicals versus (IE – EA) (eV). The data are fit to a linear trend line (R2 = 0.88); the dashed lines represent the 95% prediction interval.51
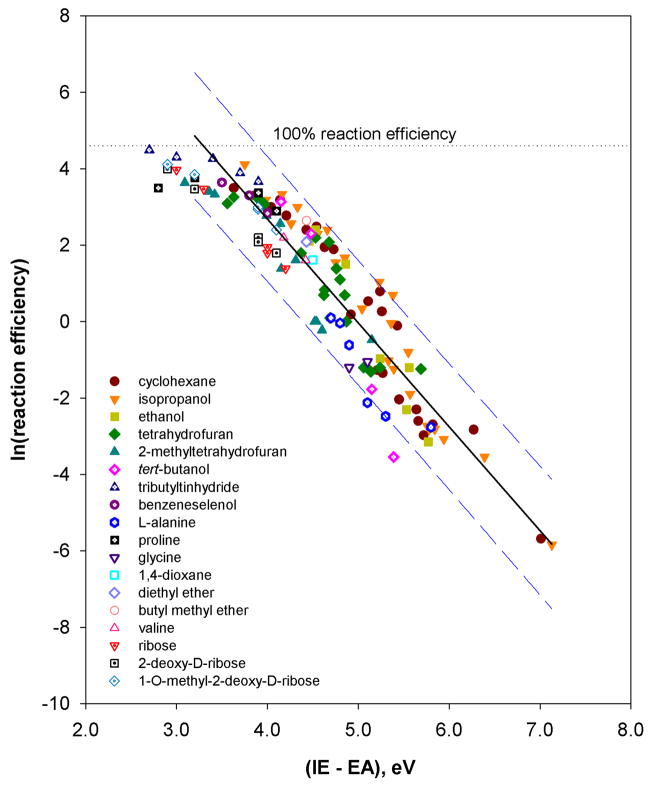
Finally, the data set was expanded (Table 5) by including experimental data obtained previously for twelve additional hydrogen-atom donors: tert-butanol (g, l, q, s),61 tributyltin hydride (g, l, q, s, ee),22 benzeneselenol (g, l, ee, ff),22 proline (g, l, q, t),62 valine and glycine (g, l),62 three sugars, ribose, 2-deoxy-D-ribose, 1-O-methyl-2-deoxy-D-ribose (g, l, q, s, ff),15 diethyl ether and butyl methyl ether (m)63 and 1,4-dioxane (g).63 The experimental data for L-alanine (obtained here for b, c, f, g, i and l) was also included in the data set. A plot of the natural logarithm of the hydrogen-atom abstraction reaction efficiencies versus (IE – EA) is shown in Figure 14. Except for those data points where (IE – EA) is less than about 3.10 eV (very fast reactions), and the reaction of aryl radical g with tert-butanol (this reaction is slower than expected, which is likely due to steric hindrance), a very good correlation is obtained.
Figure 14.
Natural logarithm of the reaction efficiencies for hydrogen-atom abstraction from eighteen different hydrogen-atom donors by twenty-nine different aryl radicals versus (IE – EA) (eV). The data are fit to a linear trend line (R2 = 0.87); the dashed lines represent the 95% prediction interval.51 The horizontal dotted line represents 100% reaction efficiency.
Conclusions
The reactivity of aryl radicals in hydrogen-atom abstraction reactions is influenced by not only the vertical electron affinity (EA) of the aryl radical but also the vertical ionization energy (IE) of the hydrogen-atom donor. The reaction efficiency for hydrogen-atom abstraction increases logarithmically as the EA of the aryl radical increases, or as the IE of the hydrogen-atom donor decreases. The reactivity does not appear to be influenced by either the reaction enthalpy or the bond dissociation energy of the hydrogen-atom donor.
The observed reactivity is consistent with the ionic avoided curve crossing model, which predicts that the reaction efficiency for hydrogen-atom abstraction increases as the difference between the IE of the hydrogen-atom donor and the EA of the aryl radical (i.e., IE – EA) decreases. This dependence results from the increasing polarization, and concomitant stabilization, of the transition state as (IE – EA) decreases. Thus, the reaction efficiency for hydrogen-atom abstraction can be “tuned” by structural changes that alter either the EA of the aryl radical or the IE of the hydrogen-atom donor.
Supplementary Material
Acknowledgments
We thank Professor Tim Zwier (Purdue University), Professor Terry McMahon (University of Waterloo) and Dr. Jean Futrell (Pacific Northwest National Laboratory) for helpful discussions. Financial support by the National Institutes of Health is also gratefully acknowledged.
Footnotes
Supporting Information Available: Tables of Cartesian coordinates, electronic energies, zero-point vibrational energies, and 298 K thermal contributions for the ground states of aryl radicals a – w, the “parent” (closed-shell) cations of a – w, the transition states for aryl radicals g, l and n, cyclohexane, cyclohexyl radical, isopropanol, 2-hydroxy-2-propyl radical and valine. Complete ref. 47. This material is available free of charge via the Internet at http://pubs.acs.org.
References and Notes
- 1.See for example: Donahue NM. Chem Rev. 2003;103:4593. doi: 10.1021/cr020650g.Pardo L, Banfelder JR, Osman R. J Am Chem Soc. 1992;114:2382.Tiu GC, Tao FM. Chem Phys Lett. 2006;428:42.Roberts BP. Chem Soc Rev. 1999;28:25.Chen Y, Tschuikow-Roux E. J Phys Chem. 1993;97:3742.Galano A, Alvarez-Idaboy JR, Bravo-Pérez G, Ruiz-Santoyo ME. Phys Chem Chem Phys. 2002;4:4648.Blowers P, Masel R. AIChE Journal. 2000;46:2041.Strong HL, Brownawell ML, San Filippo J., Jr J Am Chem Soc. 1983;105:6526.Mebel AM, Lin MC, Yu T, Morokuma K. J Phys Chem A. 1997;101:3189.
- 2.Kraka E, Cremer D. J Am Chem Soc. 2000;122:8245. [Google Scholar]
- 3.Griffiths J, Murphy JA. J Chem Soc Chem Commun. 1991:1422. [Google Scholar]
- 4.Wender PA, Jeon R. Org Lett. 1999;1:2117. doi: 10.1021/ol9903279. [DOI] [PubMed] [Google Scholar]
- 5.Wender PA, Jeon R. Bioorg Med Chem Lett. 2003;13:1763. doi: 10.1016/s0960-894x(03)00212-9. [DOI] [PubMed] [Google Scholar]
- 6.Griffiths J, Murphy JA. J Chem Soc Chem Commun. 1992:24. [Google Scholar]
- 7.Hoffner J, Schottelius MJ, Feichtinger D, Chen P. J Am Chem Soc. 1998;120:376. [Google Scholar]
- 8.Chen P. Angew Chem Int Ed Engl. 1996;35:1478. [Google Scholar]
- 9.Greenley TL, Davies MJ. Biochimica et Biophysica Acta. 1993;1157:23. doi: 10.1016/0304-4165(93)90074-i. [DOI] [PubMed] [Google Scholar]
- 10.Hazlewood C, Davies MJ. Archives Biochem Biophys. 1996;332:79. doi: 10.1006/abbi.1996.0319. [DOI] [PubMed] [Google Scholar]
- 11.Meunier B, Pratviel G, Bernadou J Bull Soc Chim Fr. 1994;131:933. [Google Scholar]
- 12.Nicolaou KC, Dai WM. Angew Chem Int Ed. 1991;30:1387. [Google Scholar]
- 13.Pratviel G, Bernadou J, Meunier B. Angew Chem Int Ed Engl. 1995;34:746. [Google Scholar]
- 14.Hazlewood C, Davies MJ, Gilbert BC, Packer JE. J Chem Soc Perkin Trans 2. 1995:2167. [Google Scholar]
- 15.Ramírez-Arizmendi LE, Heidbrink JL, Guler LP, Kenttämaa HI. J Am Chem Soc. 2003;125:2272. doi: 10.1021/ja020632g. [DOI] [PubMed] [Google Scholar]
- 16.Murphy JA, Griffiths J Nat Prod Rep. 1993;10:551. doi: 10.1039/np9931000551. [DOI] [PubMed] [Google Scholar]
- 17.Pogozelski WK, Tullius TD. Chem Rev. 1998;98:1089. doi: 10.1021/cr960437i. [DOI] [PubMed] [Google Scholar]
- 18.Pryor WA, Echols JT, Smith K. J Am Chem Soc. 1966;88:1189. [Google Scholar]
- 19.Takayama K, Masanori K, Migita T. Chem Lett. 1973:193. [Google Scholar]
- 20.Migita T, Takayama K, Abe Y, Kosugi M. J Chem Soc Perkin Trans 2. 1979:1137. [Google Scholar]
- 21.Li RM, Smith RL, Kenttämaa HI. J Am Chem Soc. 1996;118:5056. [Google Scholar]
- 22.Heid0brink JL, Ramirez-Arizmendi LE, Thoen KK, Guler L, Kenttämaa HI. J Phys Chem A. 2001;105:7875. [Google Scholar]
- 23.Petucci C, Nyman M, Guler L, Kenttämaa H. J Am Chem Soc. 2002;124:4108. doi: 10.1021/ja012243c. [DOI] [PubMed] [Google Scholar]
- 24.Thoen KK, Smith RL, Nousiainen JJ, Nelson ED, Kenttämaa HI. J Am Chem Soc. 1996;118:8669. [Google Scholar]
- 25.Yates BF, Bouma WJ, Radom L. J Am Chem Soc. 1984;106:5805. [Google Scholar]
- 26.Yates BF, Bouma WJ, Radom L. Tetrahedron. 1986;42:6225. [Google Scholar]
- 27.Heidbrink JL., PhD . Thesis. Purdue University; 2001. [Google Scholar]
- 28.Ramirez-Arizmendi LE., PhD . Thesis. Purdue University; 2001. [Google Scholar]
- 29.Petucci CJ., PhD . Thesis. Purdue University; 2001. [Google Scholar]
- 30.Lucas HJ, Kennedy ER. In: Organic Synthesis. Blatt AH, editor. John Wiley and Sons; New York: 1943. p. 351. [Google Scholar]
- 31.Stang PJ, Hanack M, Subramanian LR. Synthesis. 1982;2:85. [Google Scholar]
- 32.Woodgate PD, Herbert JM, Denny WA. Heterocycles. 1987;26:1029. [Google Scholar]
- 33.Gauthier JW, Trautman TR, Jacobson DB. Anal Chim Acta. 1991;246:211. [Google Scholar]
- 34.Chen L, Wang TCL, Ricca TL, Marshall AG. Anal Chem. 1987;59:449. doi: 10.1021/ac00130a016. [DOI] [PubMed] [Google Scholar]
- 35.Su T, Chesnavich WJ. J Chem Phys. 1982;76:5183. [Google Scholar]
- 36.Box GEP, Cox DR. J Roy Statist Soc B. 1964;26:211. [Google Scholar]
- 37.Draper NR, Smith H. Applied Regression Analysis. 2. John Wiley and Sons, Inc; New York: 1981. pp. 225–226. [Google Scholar]
- 38.SAS/STAT, Version 8, SAS Institute, Inc., 1999.
- 39.Hehre WJ, Ditchfield R, Pople JA. J Chem Phys. 1972;56:2257.Hariharan PC, Pople JA. Theoret Chimica Acta. 1973;28:213.Francl MM, Petro WJ, Hehre WJ, Binkley JS, Gordon MS, DeFrees DJ, Pople JA. J Chem Phys. 1982;77:3654.Clark T, Chandrasekhar J, Schleyer PVR. J Comp Chem. 1983;4:294.Frisch MJ, Pople JA, Binkley JS. J Chem Phys. 1984;80:3265.
- 40.Becke AD. J Chem Phys. 1996;104:1040. [Google Scholar]
- 41.Lee C, Yang W, Parr RG. Phys Rev B. 1988;37:785. doi: 10.1103/physrevb.37.785. [DOI] [PubMed] [Google Scholar]
- 42.Foresman JB, Frisch Æ. Exploring Chemistry with Electronic Structure Methods. 2. Gaussian, Inc.; Pittsburgh, PA: 1996. [Google Scholar]
- 43.Note that, for these calculations, we are computing the vertical electron affinity of the radical site, not the vertical electron affinity of the molecule.
- 44.Because the aryl radicals studied here contain a formal positive charge on the nitrogen atom, the state that is produced when an electron is added to the nonbonding orbital is formally zwitterionic, i.e., it contains localized positive (π) and negative (σ) charges.
- 45.Lynch BJ, Fast PL, Harris M, Truhlar DG. J Phys Chem A. 2000;104:4811. [Google Scholar]
- 46.See also: Lingwood M, Hammond JR, Hrovat DA, Mayer JM, Borden WT. J Chem Theory Comput. 2006;2:740. doi: 10.1021/ct050282z.
- 47.Frisch MJ, et al. Gaussian 98, Revision A. 7, Inc.; Pittsburgh PA: 1998. [Google Scholar]
- 48.Nash JJ, Kenttämaa HI, Cramer CJ. J Phys Chem A. 2006;110:10309. doi: 10.1021/jp062857+. [DOI] [PubMed] [Google Scholar]
- 49.For a recent review, see: Rienstra-Kiracofe JC, Tschumper GS, Schaefer HF, III, Nandi S, Ellison GB. Chem Rev. 2002;102:231. doi: 10.1021/cr990044u.
- 50.Sjöström M, Wold S. Chem Scripta. 1976;9:200. [Google Scholar]
- 51.Note that a prediction interval bears the same relationship to a future observation that a confidence interval bears to an unobservable population parameter. Prediction intervals predict the distribution of individual points, whereas confidence intervals estimate the true population mean or other quantity of interest that cannot be observed. Here, the 95% prediction interval is the Y range for a given X where there is a 95% probability that the next measurement made will lie within this interval.
- 52.Jing L, Guler LP, Pates G, Kenttämaa HI. J Phys Chem A. doi: 10.1021/jp802257m. in press. [DOI] [PubMed] [Google Scholar]
- 53.McMillen DF, Golden DM. Ann Rev Phys Chem. 1982;33:493. [Google Scholar]
- 54.Donahue NM, Clarke JS, Anderson JG. J Phys Chem A. 1998;102:3923. [Google Scholar]
- 55.Donahue NM. J Phys Chem A. 2001;105:1489. doi: 10.1021/jp002121r. [DOI] [PubMed] [Google Scholar]
- 56.Clarke JS, Kroll JH, Donahue NM, Anderson JG. J Phys Chem A. 1998;102:9847. doi: 10.1021/jp002121r. [DOI] [PubMed] [Google Scholar]
- 57.Clarke JS, Rypkema HA, Kroll JH, Donahue NM, Anderson JG. J Phys Chem A. 2000;104:4458. [Google Scholar]
- 58.In the ionic avoided curve crossing model, it is the vertical IE of the X-H bond of the hydrogen-atom donor that is associated with the hypothetical ionic excited state of the reactants (i.e., [R••−][X•H+]). Since it is extremely difficult, if not impossible, to determine the IE for a specific chemical bond in a polyatomic molecule (e.g., a hydrogen-atom donor), we use the IE of the molecule as an approximation for the energy of the hypothetical ionic excited state.
- 59.Benoit FM, Harrison AG. J Am Chem Soc. 1977;99:3980. [Google Scholar]
- 60.Kimura K, KatsumataSAchiba Y, Yamazaki T, Iwata S. Handbook of HeI Photoelectron Spectra of Fundamental Organic Compounds. Japan Scientific Society Press; Tokyo: 1981. [Google Scholar]
- 61.Guler LP, Jing L, Nash JJ, Kenttämaa HI. unpublished work. [Google Scholar]
- 62.Huang YQ, Guler L, Heidbrink J, Kenttämaa H. J Am Chem Soc. 2005;127:3973. doi: 10.1021/ja044676w. [DOI] [PubMed] [Google Scholar]
- 63.Petzold CJ, Nelson ED, Lardin HA, Kenttämaa HI. J Phys Chem A. 2002;106:9767. [Google Scholar]
- 64.Ohno K, Imai K, Harada Y. J Am Chem Soc. 1985;107:8078. [Google Scholar]
- 65.Benoit FM, Harrison AG. J Am Chem Soc. 1977;99:3980. [Google Scholar]
- 66.Cannington PH, Ham NS. J Electron Spectrosc Relat Phenom. 1983;32:139. [Google Scholar]
- 67.Bieri G, Asbrink L, Von Niessen W. J Electron Spectrosc Relat Phenom. 1982;27:129. [Google Scholar]
- 68.Baker AD, Armen GH, Guang-di Y. J Org Chem. 1981;46:4127. [Google Scholar]
- 69.Beltram G, Fehlner TP, Mochida K, Kochi JK. J Electron Spectrrosc Relat Phenom. 1980;18:153. [Google Scholar]
- 70.Debies TP, Rabalais JW. J Electron Spectrosc Relat Phenom. 1974;3:315. [Google Scholar]
- 71.Dyke JM, Groves AP, Lee EPF, Niavaran MHZ. J Phys Chem A. 1997;101:373. [Google Scholar]
- 72.Rauk A, Yu D, Armstrong DA. J Am Chem Soc. 1997;119:208. [Google Scholar]
- 73.Burkey TJ, Majewski M, Griller D. J Am Chem Soc. 1986;108:2218. doi: 10.1021/ja00269a017. [DOI] [PubMed] [Google Scholar]
- 74.Leeck DT, Li RM, Chyall LJ, Kenttämaa HI. J Phys Chem. 1996;100:6608. [Google Scholar]
- 75.Block DA, Yu D, Armstrong DA, Rauk A. Can J Chem. 1998;76:1042. [Google Scholar]
- 76.Jing LH, Guler LP, Nash JJ, Kenttämaa HI. J Am Soc Mass Spectrom. 2004;15:913. doi: 10.1016/j.jasms.2004.02.009. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.