Experimental Free Energy Surface Reconstruction From Single-Molecule Force Spectroscopy Using Jarzynski’s Equality

Abstract

We used the atomic force microscope to manipulate and unfold individual molecules of the titin I27 domain and reconstructed its free energy surface using Jarzynski’s equality. The free energy surface for both stretching and unfolding was reconstructed using an exact formula that relates the nonequilibrium work fluctuations to the molecular free energy. In addition, the unfolding free energy barrier, i.e., the activation energy, was directly obtained from experimental data for the first time. This Letter demonstrates that Jarzynski’s equality can be used to analyze nonequilibrium single-molecule experiments, and to obtain the free energy surfaces for molecular systems, including interactions for which only nonequilibrium work can be measured.

One way to probe molecular properties is to drive a system out of equilibrium and to observe the response. Interpretation of data from dynamic measurements allows one to reconstruct both the equilibrium properties of molecules and responses to external perturbations [?]. Equilibrium parameters are usually deduced from kinetic measurements, and it remains challenging to relate nonequilibrium distribution data to equilibrium properties [1]. Advances in single-molecule manipulation and measurement techniques have made it possible to directly probe the dynamics of molecular interactions [2, 3]. The nonequilibrium work theorem, i.e., Jarzynski’s equality [4], relates nonequilibrium measurements of nanoscale systems to equilibrium properties [5–7]. It promises to extract thermodynamic parameters such as free energies from single-molecule measurements.

Forced unfolding of single molecules, now achievable using the atomic force microscope (AFM) and laser optical tweezers, has been used to probe the molecular interactions and mechanical properties of individual molecules [2, 8]. In these experiments, single molecules are held at both ends and stretched while the cantilever spring restoring force (F_s) is measured. Applying an external force drives the system out of equilibrium, and transitions between states are directly observed as the system settles to a new equilibrium state. However, interpretation of these results and deduction of equilibrium properties from these nonequilibrium measurements remains controversial [9–12].

It has been widely anticipated that equilibrium free energy differences can be derived from nonequilibrium measurements using Jarzynski’s equality [4]. The difference in equilibrium free energy ΔG is related to the fluctuations of work performed during a nonequilibrium process W_λ by [4, 7]

$${\langle e^{-\beta W_{\lambda }}\rangle }_N\equiv \int d{W}_{\lambda }\rho (W_{\lambda })e^{-\beta W_{\lambda }}=e^{-\beta \mathrm{\Delta }G},$$ (1)

where β= (1/k_BT), k_B is the Boltzmann constant, and T is the temperature of the thermal bath. The 〈…〉_N represents an average over N realizations of the process, and the equality is exact in the limit N → ∞. The nonequilibrium work distribution ρ(W_λ) depends on the schedule for varying the work parameter λ, which is the external perturbation. The equality is simple; however, its application to interpreting single-molecule results is not straightforward. The equation involves the thermodynamic work done on the system and the controlled work parameter with W_λ = ∫Fdλ. In AFM experiments, the system includes the cantilever spring and the molecule plus water, and λ refers to the change in cantilever anchor to stage distance (see Fig. 1), not the tip-to-sample distance, which measures the molecule end-to-end distance z, i.e., the order parameter, or reaction coordinate.

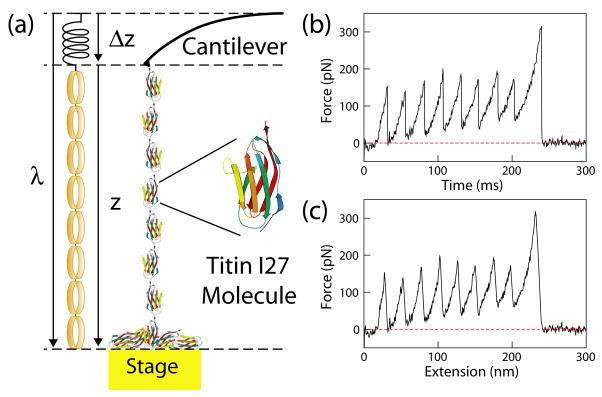
FIG. 1.

(color). Single-molecule pulling experiments using AFM. (a) One end of the molecule is attached to the cantilever tip and the other end to a gold substrate, whose position is controlled by a piezoelectric actuator. An analogue of the single-molecule force measurements is illustrated. The cantilever spring obeys Hooke’s law, whereas the protein molecular spring follows the worm-like chain model (illustrated using rubber bands). (b) A representative force versus time trace, taken at 1.00 μm/s using a cantilever with a spring constant of 0.04 N/m. Each force peak represents unfolding of an individual titin I27 domain, with the final peak resulting from the detachment of the molecule from the AFM tip. (c) Corresponding force-extension curve. The tip force baseline was determined using the part of the force curve where the molecule is completely detached from the tip, when the cantilever spring is at its equilibrium position.

We briefly review the experimental setup to which Eq. (1) applies. Consider at time t = 0, the system is at an equilibrium state λ (0) = λ_A. We perform external work on the system by controlling the work parameter following a predetermined schedule, λ (t), from an initial state λ_A to a final state λ_B. The system is then allowed to relax to equilibrium while λ is held constant at λ_B. Since we do not perform external work on the system during relaxation, we can omit this last step and the equality still holds. Hence Jarzynski’s equality allows us to determine the G(λ) from an equilibrated state A to an arbitrary state B.

A proof-of-principle experiment and molecular dynamics simulations testing the Jarzynski estimator have been performed [13, 14]. The experimental test involved stretching individual RNA molecules reversibly and irreversibly using optical tweezers, and the free energy of unfolding, i.e., the stability of the molecules, was determined. However, the usefulness of Jarzynski’s equality lies with its ability to obtain directly the entire free energy landscape, which could only be estimated using kinetic approaches to date [?]. We will show that Jarzynski’s equality can be used to determine directly the free energy profile of molecular stretching and unfolding, including the free energy barrier of unfolding.

Our system of interest is the mechanical unfolding of the I27 domain of human cardiac titin [15]. The mechanical properties of the immunoglobulin (Ig)-like domains are directly correlated with the protein’s biological function in the muscles [2]. The kinetic barrier of these mechanical proteins is important in determining the dynamic behavior of the proteins during the stretch-release process. Therefore, the titin free energy surface, including the unfolding barrier height, is useful for quantification of titin’s function in the heart muscle.

We used AFM to stretch individual molecules of eight serially linked repeats of the titin I27 domain, as illustrated in Fig. 1. The protein was stretched when the substrate stage was moved by λ, which was set at a constant velocity v, i.e., λ = vt. The cantilever displacement from its equilibrium position Δz was recorded, and the molecular end-to-end distance as a function of time was calculated using z = λ − Δz. The force curves are aligned using the best worm-like chain (WLC) fit of the force below the unfolding force. This method has been shown to minimize the effect of instrument drift that affects the measured values [16]. To correctly calculate ΔG as a function of the molecular end-to-end distance, we used an exact expression that connects the nonequilibrium fluctuations of work to the Gibbs free energy G(z) [6]

$$e^{-\beta G(z)}={\langle \delta (z-z_t)e^{-\beta [W_z(t)-U_0(z_0,{\lambda }_A)]}\rangle }_N$$ (2)

where z₀ and z_t are the end-to-end distances of the molecule at times 0 and t during one realization of the process, F_m is the force on the molecule, W_z(t) is the mechanical work done on the molecule up to time t, δ(z−z_t) is the Dirac δ function, and U₀ is the potential energy stored in the cantilever spring at time 0.

To calculate G(z) using Eq. (2), we divided each of the N trajectories of duration τ into discrete time steps δt so T = τ/δt, where T is the total number of time steps in a given trajectory,

$$\begin{array}{l}exp[-\beta G(z^{(m)})]\approx \frac{1}{NT}\sum _{n=1}^N\sum _{s=1}^T{\delta }_{\epsilon }(z^{(m)}-z_{n,s})\\ \times exp(-\beta [W_{n,s}-U(z_{n,0},{\lambda }_A)])\end{array}$$ (3)

where z_n,s is z at the sth time step for the nth trajectory, z_n,0 is the initial value of z for the nth trajectory, and W_n,s is the work performed up to time t_s = sδt for the nth trajectory. We divided the z-axis into bins of width ∈ and let z^(m) represent the mid-point of the mth bin. The δ function is 1/∈ when z_n,t falls inside the mth bin and 0 otherwise. Integration starts from the beginning of the curve, where the cantilever is close to its resting position, z = 0, at t = 0. This initial condition is required for using Jarzynski estimator, which states that the process needs to start from an equilibrated state. It is also advantageous when using Eq. (3) that the initial energy stored in the cantilever spring, U₀(z₀, λ_A), is close to 0. We compare this result to the approximate free energy surface derived from

$$e^{-\beta G_z}\approx {\langle e^{-\beta \int F_{m}dz-U_0(z_0,{\lambda }_A)}\rangle }_N$$ (4)

The unfolding free energy surface of titin I27 determined from Eq. (4) and Eq. (3) are very similar, perhaps due to the relatively stiff cantilever used in AFM. However, it is physically and theoretically more meaningful to use Eq. (3), since determination of the entire free energy surface relies on converting the coordinate from t to z. Figure 2 displays the free energy surface measured at three different velocities, determined using Eq. (3).

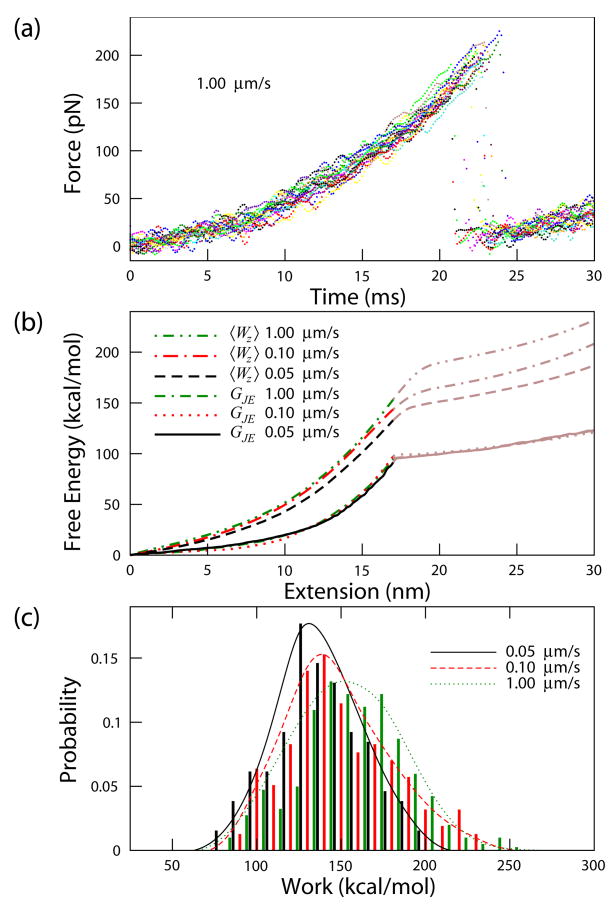
FIG. 2.

(color). Free energy reconstruction of titin I27 for pulling velocities of 0.05, 0.10, and 1.00 μm/s obtained using 64, 132, and 226 curves, respectively. (a) Typical unfolding force versus time curves for titin I27 domain taken at 1.00 μm/s. Shown are 20 curves smoothed using a smoothing spline for display purposes. (b) Free energy G(z) calculated using the Jarzynski estimator G_JE applied to the raw data. The averaged work, $\langle W_z\rangle ={\sum }_i^N{W}_z/N$, where W_z = ∫F dz, is displayed for comparison. 〈W_z〉 is larger than the equilibrium free energy G_JE by about a factor of 2 and is velocity dependent, whereas G_JE is velocity independent. The curves are accurate up to the transition state (solid line). (c) Distributions of work for z as a function of pulling velocity. The calculated work includes stretching and unfolding one domain. The curve fit to each distribution is a smoothing spline fit to the data as a guide to the eye.

The unfolding free energy barrier $\mathrm{\Delta }{G}_u^{‡}$ can be calculated from the reconstructed free energy curve. Using 0.6 nm as the distance between the native and the transition state (x_u) [10, 17], we calculated the unfolding free energy barrier $\mathrm{\Delta }{G}_u^{‡}$ for pulling velocities of 0.05, 0.10, and 1.00 μm/s, to be 11.0, 11.7, and 11.4 kcal/mol, from Eq. (3) and 11.5, 11.5, and 10.7 kcal/mol from Eq. (4), respectively. The uncertainty in the averaged $\mathrm{\Delta }{G}_u^{‡}=11.4$ and 11.2 kcal/mol, calculated using the bootstrap method, is 0.4 and 0.3 kcal/mol for Eqs. (3) and (4), respectively. This result compares favorably to an estimated value of 10–16 kcal/mol [11, 18, 19]. A major source of error for $\mathrm{\Delta }{G}_u^{‡}$ from Jarzynski estimator comes from the uncertainty in x_u. Using the largest estimated error of 0.07 nm uncertainty in x_u [10], the estimated uncertainty of $\mathrm{\Delta }{G}_u^{‡}$ is 1.2 kcal/mol.

The free energy surface is accurately reconstructed from z = 0 to 17 nm, the transition state. The free energy of unfolding is insensitive to the distance of reconstruction. As an example, if we use 15 nm or 19 nm, $\mathrm{\Delta }{G}_u^{‡}$ changes by 2.5 and 0.4%, respectively, for the pulling velocity of 0.05 μm/s. The vast majority of the proteins in the ensemble are in the folded state (99.9997 % using the free energy ΔG_u from Ref. [20]) so the contribution from the initially unfolded proteins is negligible. To minimize the contribution from other unfolded domains to the measured free energy, we analyzed only the first domain stretching event. Using all domain unfolding events in the analysis changes $\mathrm{\Delta }{G}_u^{‡}$ by less than 2%.

Note that it is not possible to compare our results directly to published values, since $\mathrm{\Delta }{G}_u^{‡}$ has not been determined, and only kinetic information is available. Chemical denaturant studies gave an estimated unfolding rate constant $k_u^0$ of 6×10⁻⁴s⁻¹ [19], while forced-unfolding studies gave an estimated $k_u^0$ of 10⁻³–10⁻⁶s⁻¹ [2, 9–11], and the $\mathrm{\Delta }{G}_u^{‡}$ was then calculated using $k_u^0=k_0{e}^{-\beta \mathrm{\Delta }{G}_u^{‡}}$. Since the prefactor k₀ of protein unfolding is unknown, the free energy barrier can only be estimated by this procedure [21, 22]. However, combining our free energy determination with the kinetic information, we can determine the prefactor 1/k₀ to be 6 μs, which lies within the expected range [21, 23].

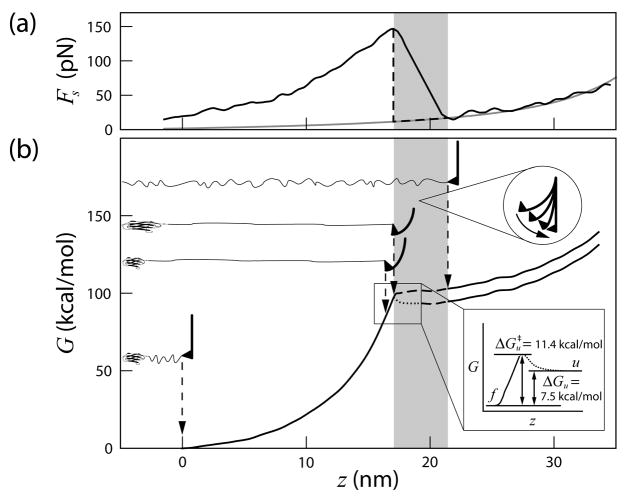
The free energy surface immediately past the transition state cannot be reconstructed with high accuracy from constant velocity unfolding experimental data. This is because the force exerted on the molecule is discontinuous when the domain ruptures and expands against the cantilever. In the region where the domain ruptures and the cantilever snaps back to its equilibrium position, the assumption that the force on the molecule (F_m) is balanced by the cantilever spring restoring force (F_s) no longer holds. Therefore, using the measured F_s gave rise to an overestimate of the free energy. Note that even though the snapping process is almost instantaneous (small change in t, hence λ), the change in z is significant because Δz = F_s/k_s, where k_s is the cantilever spring constant (see Fig. 3). A lower pulling velocity and larger spring constant will reduce the size of the snapping region. However, we can estimate the folding free energy barrier $\mathrm{\Delta }{G}_f^{‡}$ from the equilibrium unfolding free energy determined from chemical denaturant studies [20]. Using ΔG_u = 7.5 kcal/mol, we obtained $\mathrm{\Delta }{G}_f^{‡}=3.9\text{kcal}/\text{mol}$, in the expected range for titin I27. Figure 3 summarizes the reconstructed free energy surface and its relation to pulling experiments.

FIG. 3.

Free energy surface of titin I27. (a) A typical force versus extension curve. The gray curve is the WLC fit to the following domain. The shaded region indicates that, when the domain ruptures and the cantilever snaps, the force on the molecule is not registered and, therefore, the free energy surface may not be recovered with high accuracy. The dashed line indicates an approximation of the force exerted on the molecule. (b) The free energy surface of unfolding titin I27. The cantilever position and the molecular extension at each stage are illustrated. The curve is composed of the reconstructed free energy surface up to the transition state (solid) and estimated free energy change [20] and distance [24] beyond the transition state (dotted).

One requirement for using Jarzynski’s equality is that the schedule for varying the work parameter λ must be predetermined [4], which means that constant force ramp is not an appropriate schedule. A constant dF_s/dt requires force feedback and, since the measured force F_s fluctuates from one pull to another, the result is a different schedule of λ for each realization. On the other hand, the dynamic force spectroscopy method commonly used in AFM pulling of proteins is particularly suitable for such analysis because the schedule for pulling is predetermined and remains the same for all experiments performed at the same velocity.

Using nonequilibrium single-molecule measurements and Jarzynski’s equality, we have reconstructed the free energy surface of both mechanical stretching and unfolding of the I27 domain of human cardiac titin. Since the profile is an equilibrium property, the reverse of the free energy surface of stretching is equivalent to that of protein folding from an extended state. The unfolding free energy barrier and the prefactor were determined directly from experimental measurements without having to assume either a two- or a three- state model, which are major sources of error in the event of populated intermediate states. In fact, with adequate resolution and accuracy, an intermediate state should be directly resolvable in the free energy curve. The topography and the roughness of the folding free energy landscape can also be determined. Reconstruction of free energy surfaces directly from experimental data is valuable to obtain fundamental thermodynamic properties such as the free energy barrier of unfolding, to understand the mechanical properties of the molecule, and to compare with theory and simulation results [25]. With a complete characterization of the free energy surface of molecular processes, questions such as whether thermal, chemical, and mechanical unfolding probe the same process may be resolved. Moreover, since the free energy surface is determined in a particular environment, how the free energy surface changes with environmental parameters such as temperature, solution ionic concentration, and acidity may now be evaluated. Quantification of the molecular response to external parameters should lead to a better understanding of molecular behavior in the complex cellular environment.