Quantitative force mapping of an optical vortex trap

Abstract

This paper describes the quantitative force mapping of micron-sized particles held in an optical vortex trap. We present a simple and efficient model, which accounts for the diffraction of the strongly localized optical field of the tightly focused laser beam, the spherical aberration introduced by the dielectric glass-to-water interface, employs the multidipole approximation for force calculations, and is able to reproduce, with quantitative agreement, the experimentally measured force map.

The optical trapping and manipulation of micron-sized objects is now an established technique with proven applications in biology, chemistry, and physics. The accurate modeling of an optical trap is a sophisticated problem and a number of different solutions have been proposed. The dipole approximation¹ and the geometric ray optics approach² are two traditional methods for studying the trapping of small (radius R⪡0.1λ) and large (R⪢λ) particles, respectively. The intermediate region (R∼λ), however, is less well established and, unfortunately, it is in this size regime that most particles of interest are to be found. Recent reviews of some of the most frequently cited models that explore this region have been provided by Nieminen et al.³ and Viana et al.⁴

This paper presents a theoretically simple and efficient approach for accurately mapping the absolute optical forces that act on micron-sized objects trapped in an optical vortex beam. Optical vortex traps have been shown to exhibit special properties that can be extremely beneficial in the context of optical manipulation. For particles with a refractive index higher than the surrounding medium, vortex traps have been shown to offer increased trapping efficiency.^{5, 6} This implies that lower power can be used, reducing the potential for photodamage and photobleaching when trapping fragile particles (such as biological cells and organelles).⁶ The hollow core of a vortex trap can also be used to trap low-refractive-index particles⁷ and more recently has been used to manipulate aqueous droplets dispersed in oil.^{8, 9}

Although a number of experiments have now been carried out using optical vortices for trapping applications,^{5, 6, 7, 8, 9, 10} only a handful of papers have provided theoretical insights into their trapping properties and compared them with experimental measurements.^{11, 12, 13} Given the potential impact vortex traps may have on optical manipulation, it is important to fully understand the trapping behavior of optical vortices by comparing predictions with experimental measurements.

In this work, we employed a linearly polarized optical vortex beam, which contains two high-intensity side lobes near the laser focus.^{6, 14} We simulated the three-dimensional distribution of the strongly focused optical field through the glass-water interface by applying Maxwell’s boundary conditions and the vectorial Debye integral. To create the optical force map, we employed a multidipole approach. The simulated results are quantitatively compared with experimental measurements of the optical forces exerted on different micron-sized spherical polystyrene beads trapped at different distances from the glass-water interface in the optical vortex trap. Our results show that the aberrations introduced by the tight focusing through the glass-water interface slightly change the shape of the force map as well as the maximum trapping force when the vertical distance between the trap and the glass-water interface is varied. We believe our model is simple and easy to implement, and is not restricted by the properties of the strongly focused trapping beam or the shape of the trapped objects.

The vectorial Debye integral, which was originally presented by Richards and Wolf in 1959,¹⁵ is generally used to calculate the electromagnetic field associated with strongly focused systems and has been demonstrated to agree with experiments.^{14, 16, 17} Here, we follow Richards and Wolf and apply Maxwell’s boundary conditions to calculate the electric field passing through the glass-water interface as the beam is focused into the water. The strongly focused electric fields of the x-polarized Lagueree-Gaussian (${\mathrm{LG}}_0^1$) vortex beam can be expressed as^{18, 19, 20} (see Ref. 21, supplemental material, for a derivation)

$$\mathbf{E}(\rho ,\varphi ,z)=\left[\begin{array}{c}{E}_x\\ E_y\\ E_z\end{array}\right]=\frac{-i{k}_{1}f}{2\pi }\underset{0}{\overset{{\theta }_{\max }}{\int }}\underset{0}{\overset{2\pi }{\int }}\left(\frac{\sqrt{2}f\sin \theta }{w}\right)\times \exp (-\frac{f^2{\sin }^2\theta }{w^2})\exp \left(i\phi \right)\sin \theta \sqrt{\cos \theta }\times \exp \left[i{k}_1\rho \sin \theta \cos (\phi -\varphi )\right]\times \exp [i{k}_1{z}_0\cos \theta +i{k}_2\cos {\theta }^{\prime }(z-z_0)]\times t\left[\begin{array}{c}{\cos }^2\phi \cos {\theta }^{\prime }+{\sin }^2\phi \\ \cos \phi \sin \phi (\cos {\theta }^{\prime }-1)\\ -\cos \phi \sin {\theta }^{\prime }\end{array}\right]d\phi d\theta ,$$ (1)

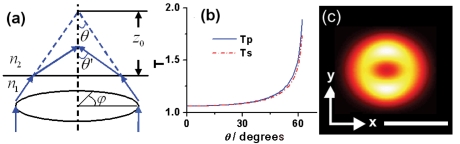
where φ is the azimuthal coordinate in the incident plane, θ (θ′) is the incident (reflection) angle of light measured from the optical axis, as shown in Fig. 1(a), k_i=2πn_i∕λ₀ (i=1 and 2) is the wave number, n_i are the refractive indices of the glass coverslip (n₁=1.5) and water (n₂=1.33) (because the refractive index of the oil and glass coverslip are matched, here we consider the two as a single entity), n₁ sin θ_max=NA (where NA is the numerical aperture of the objective lens), $\sqrt{\cos \left(\theta \right)}$ is the apodization factor for an aplanatic lens, z₀ is the distance of the geometric focus from the glass-water interface [as shown in Fig. 1a], f is the focal length of the objective, and w is the beam waist before the objective lens. t is the complex amplitude transmission coefficients of the beam, where we have assumed, for both s and p polarization components, t_s≈t_p=t, as shown in Fig. 1b. The simulated focal intensity when light is focused at the top of the coverslip (z₀=0) is shown in Fig. 1c. The exact position of the focal plane will vary with z₀, due to the optical aberration through the glass-water interface. Despite this, changes in the lateral dimensions of the ${\mathrm{LG}}_0^1$ beam in the focal plane are negligible.

Figure 1.

(a) Schematic illustrating the geometry and coordinate system we used in our studies. (b) The complex amplitude transmission coefficients of s and p polarized beam as a function of different incident angles from glass to water. (c) Simulated intensity profile when light is focused on the top of coverslip. The white scale bar represents 1 μm.

Here, we consider the particle as being composed of many small dipoles and use a traditional electric dipole approximation²² to calculate the optical potential in which the particle resides. The contribution to the total force is calculated from gradient of the associated dipole potential energy W_i,

$$F={\partial }_r\sum W_i={\partial }_r\sum [\pi {\epsilon }_0{n}_2^2\Delta R^3\frac{{(n_3∕n_2)}^2-1}{{(n_3∕n_2)}^2+2}{\mid E_i\mid }^2\cdot \frac{{\left(2\Delta R\right)}^3}{4\pi {\left(\Delta R\right)}^3∕3}],$$ (2)

where n₃=1.6 is the refractive index of a typical polystyrene particle. We treat every small dipole as a cube and assume that the dipole potentials of a traditional sphere of radius ΔR and a cube of side length 2ΔR can be linearly related through the ratio of their volumes, (2ΔR)³∕[4π(ΔR)³∕3].

To verify our model, we conducted experiments where we used a conventional hydrodynamic drag-force approach to establish the strength of the optical trap. In our experiments, polystyrene microspheres (Duke Scientific) were suspended in water and stably trapped in three dimensions in the center of the strongly focused ${\mathrm{LG}}_0^1$ beam.⁶ Fluid flow was simulated by laterally translating the microscope stage at a known velocity relative to the optical trap approximately in the y direction. The applied fluid flow caused a tiny displacement of the bead from the trapping center, which we analyzed to determine the strength of the transversal optical force.

We calculated the drag force F_d using Stokes’s law, employing the Faxen correction, to fifth order,²³ to account for the influence of the nearby coverslip on the hydrodynamic drag force

$$F_d=6\pi \eta R\nu {[1-\frac{9}{16}\frac{R}{D}+\frac{1}{8}{\left(\frac{R}{D}\right)}^3-\frac{45}{256}{\left(\frac{R}{D}\right)}^4-\frac{1}{16}{\left(\frac{R}{D}\right)}^5]}^{-1},$$ (3)

where η is the viscosity of the solution, D is the distance of the center of trapped bead from the coverslip, and ν is the instantaneous velocity of the particle relative to the sample chamber. The particle displacement was measured from the captured video with subpixel accuracy using a custom-made program. For our measurements, each uncompressed video sequence was low-pass two-dimensional frequency filtered to suppress the impact of noise. A Canny edge detection routine was then applied to estimate the particle location in each frame. Finally, the program fitted spline curves to the particles’s pixellated radial intensity profiles, enabling the measurement of lateral displacements in the optical trap with subpixel resolution.

In this paper, we explore the effect on trap strength by varying the longitudinal position of the trap in the sample z₀ with respect to the glass-water interface. Prior to trapping, the geometric focal plane was set with the beam focused on the top surface of the coverslip to avoid the aberration from the dielectric interface. The geometric focal plane was then raised and fixed at a known distance z₀. To reduce errors incurred while varying z₀ the longitudinal shift was checked after each experiment by moving the geometric focal plane back to the coverslip and was found to exhibit a variation of less than 1 μm. Prior to each experiment, the flatness of the coverslip was checked and confirmed to vary by less than 1 μm across the moving region. Three different diameters of polystyrene beads (3, 5, and 10 μm in diameter) were used in our experiments. These were all tested using two values for z₀:10 and 20 μm above the coverslip. To make sure our experiments were reliable, the experiments were repeated at least three times for each combination of parameters (z₀, R, and ν).

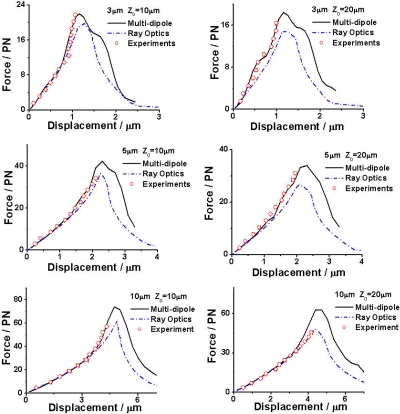
Figure 2 presents our experimental measurements of the trapping force, superimposed on the curves predicted by both our multidipole model and a conventional ray optics model.² The transverse forces are calculated at the equilibrium position z for stably trapped microbeads where ∂F_z(z)=0. In all cases, the experimental values quantitatively agree with our multidipole theoretical predictions. Our experimental results verify that the distance of the geometric focal plane from the coverslip influences the trapping force due to a spherical aberration, in agreement with our computational model.

Figure 2.

Quantitative force mapping of vortex trapped polystyrene beads that were 3, 5, and 10 μm in diameter. The geometric focal planes are located at 10 μm distance (left column) and 20 μm distance (right column) from the glass-water interface (i.e., the distance above the surface of the coverslip). Black solid lines: simulation using our model, blue dash dot: simulation using the ray optics model, and red circles (the error bars are comparable to or smaller than the circles that depict the data): experimental measurement. The incident powers before the objective are 32 mW (3 μm), 44 mW (5 μm), and 61 mW (10 μm).

It is necessary to point out that our approach primarily considers the potential energy associated with the optical field. As such, we only consider the gradient force of the potential energy of the particle and do not discuss any surface (scattering) effects. Since most proposed methods are described in terms of Mie scattering and do not consider the reactive energy inside the particle, it is perhaps surprising that our experimental data fits our model so well, particularly for the 10 μm diameter case, which is in the established Mie regime.

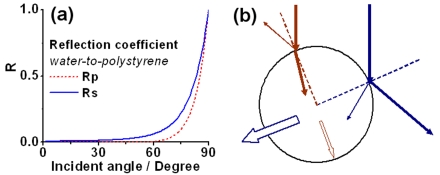
As shown in Fig. 2, when the trapping position was located close to the edge of the particles, they were seen to escape before the drag force reached the maximum potential optical trapping force. We believe this phenomenon is caused by a significant increase in the force due to the surface reflection of the optical beam when the focus is close to the edge of the particle. Figure 3a illustrates this effect: when light illuminates the particle at a small angle of incidence the reflection is negligible, but this reflection significantly increases when the incident angle is larger than 60°. When the beam focus is close to the center of the particle, most of the trapping light illuminates it at a low angle, strengthening the validity of the dipole approximation. When the beam focus is close to the edge of the particle, however, the light illuminates the surface of the particle at large incidence angles [see Fig. 3b]. In this case, the effect of momentum transfer due to surface reflection is significantly increased. Because our multidipole model does not explicitly include terms to describe the effect of reflection at the surface, under such circumstances it becomes invalid. Therefore, we attribute the effect of the varying surface reflection coefficient as the chief cause of the mismatch of the dipole approximation with the experimental data for large particle displacements. However, for small particle displacements (less than the radius of the particle), which is the regime of interest for most applications, our model works extremely well, even for comparatively large particles.

Figure 3.

(a) Simulated intensity reflection coefficients (from water to polystyrene particle) vs incident angles of the light beam. (b) Schematic illustrating the escape force exerted on the trapped bead caused by the reflection of the optical beam when the trapping position is close to the center (red) and the edge (blue) of the particle. The thickness of the arrows shows the magnitude of light (solid arrows) and force (hollow arrows).

In summary, our model explicitly accounts for the diffraction of the strongly localized optical field and the spherical aberration introduced by the dielectric interface, employing the multidipole approximation for force calculations. Our model is simple and the numerical calculations are efficient; it is surprising how well this simple model agrees with our experimental measurements, provided the displacement of the particle in the trap remains smaller than the radius of the particle. This ability to quantitatively predict the optical forces exerted on the trapped particle, together with the simplicity of our model, should offer a better understanding and mean towards the optical control of micron-sized particles.