Closing the lid on DNA end-to-end stacking interactions

Abstract

Recent experiments suggest that short DNA strands associate by end-to-end stacking. Here, we report interactions between DNAs with modified ends. DNA duplexes, 20 bp long, were capped with short T₄ loops at 2, 1 or 0 ends, and were placed in solutions containing 20 mM Mg²⁺. Association was observed only in constructs with one or more uncapped ends. DNA-DNA interactions were characterized by measuring variations in small angle x-ray scattering (SAXS) curves at the lowest scattering angles. Second virial coefficients were computed from the SAXS data. Our results confirm that end-to-end stacking plays an important role in short strand DNA-DNA interactions.

Biological helices, such as nucleic acid duplexes or α-helical segments of proteins, self assemble into precisely designed structures that regulate life. Since the phosphate backbones of DNA and RNA are highly negatively charged, charge compensation must be provided by counterions, ranging from small cations such as K⁺ or Mg²⁺, to basic polyamines or proteins. Counterions play a critical role in modulating interhelical interactions, providing electrostatic screening for these highly charged polymers, and even facilitating the attraction of like charged strands under certain ionic conditions.^{1, 2} A recent review³ traces the evolution of theories of counterion localization around charged cylinders, beginning with the pioneering mean field theory of Derjaguin, Landau, Verwey, and Overbeek and leading to sophisticated computational models (Ref. ³ and references within). Most of these models take into account the breakdown of mean field theories in the presence of the large charge density (∼2 e∕3.4 Å) or high surface electrostatic potential of DNA molecules. Different origins for attractive forces are predicted, ranging from hydration through ionic correlations.

In an effort to provide experimental data for comparison to the numerous and often conflicting theories, we have undertaken studies of interactions between short DNA strands as a function of valence and concentration of ions in solution.^{4, 5} The use of short, rigid (far less than a persistence length) helices enables comparisons with models that account for the atomically detailed structure of DNA. In the past, such studies have provided new information about the distribution of mono-, di- or trivalent ions around DNA strands. Additional experimental studies of the small angle scattering of solutions containing short duplexes, revealed an unexpected interhelical attraction in solutions containing more than a threshold level of divalent counterions.⁴ The consideration of end effects^{6, 7, 8, 9} and previous study of B-DNA crystal formation¹⁰ led us to conjecture that short DNA helices were able to “stack up” in an end-to-end configuration, though the exact mechanism was not revealed. The notion of favorable end-to-end stacking of short DNA strands, facilitated by base stacking of hydrophobic ends, was also highlighted in a recent publication,¹¹ suggesting an intriguing biological origin for these forces. The computation of the magnitude of the base stacking energies validated the proposal of end-to-end stacking. Here, we describe experimental evidence of end-to-end stacking of short DNA strands, obtained by measurement on DNA helices that are “capped” at one or both ends to partially or completely block end-to-end association.

The strength of forces between DNA strands was assessed from small angle x-ray scattering (SAXS) profiles of solutions containing DNA. All measurements were carried out at the C1 station of the Cornell High Energy Synchrotron Source (CHESS) using a previously described experimental setup.¹² The measured scattering intensity I(Q) (in which Q=4π sin θ∕λ, 2θ is the scattering angle and λ is the x-ray wavelength) is the product of a form factor P(Q), reflecting the electron density distribution within each scattering element (each DNA strand) and an intermolecule structure factor S(Q), which reports on interactions between DNAs.¹³ The form factor for each construct was extracted from measurements carried out in very dilute solutions where the intermolecular interactions are negligible, as explained in Ref. 5. The analysis of DNA-DNA interactions using SAXS was extensively discussed in Ref. 4.

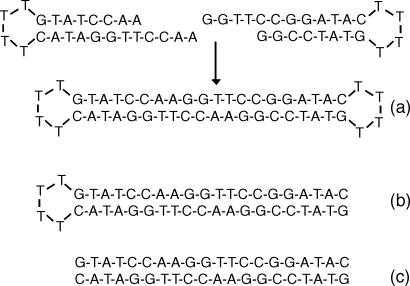
The presence of end-to-end stacking of short DNAs was tested by studying DNA-DNA interactions in solutions containing 20 base-pair long DNAs (∼76 Å), terminated with T₄ loops at 2, 1, or 0 ends, DNA “dumbbells,” DNA “semidumbbells” or short double-strand DNA (dsDNA) with unmodified ends (Fig. 1). All single-strand DNA oligomers for this experiment were purchased from Integrated DNA Technologies (IDT), Coralville, IA. The dumbbell DNA with 20 bp stem capped at both ends was constructed^{14, 15, 16} by base-pairing two DNA hairpins at equal molar amounts with T₄ loop at one end of the stem and a 4 nt complementary overhang at the other end. Double-strand 20 bp DNA and 20 bp duplex DNA with T₄ loop at only one end were used as control. Standard annealing procedures provided by IDT were applied. Each DNA sample was hydrated and dialyzed against 20 mM MgCl₂ solution buffered at 1 mM Sodium 3-(N-Morpholino)-propanesulfonic acid (NaMOPS) pH 7.

Figure 1.

(a) Dumbbell DNA, consisting of a 20 bp duplex capped by T₄ loop at both ends, was constructed by intermolecular base pairing of two hairpins. (b) Semidumbbell DNA, consisting of a 20 bp duplex capped by a T₄ loop at one end, was constructed by intramolecular base pairing of a 44 nt long single-strand of DNA. (c) 20 bp double-stranded DNA was constructed by annealing together two complementary strands.

Shape differences at the lowest angles of the scattering profiles are easily assessed by matching the curve amplitudes in the high Q regime,⁵ where scattering is nearly identical for all constructs. The presence of the terminal loops leads to small differences between scattering profiles for the constructs. However, direct comparison of the scattering profiles acquired at the lowest DNA concentration of 0.1 mM shown in Fig. 2, which correspond to molecular form factors, indicates, that the differences are nearly negligible. As the DNA concentration increases, a clear difference between scattering from dumbbells, semidumbbells, and dsDNA is measured in the low Q regime, characteristic of S(Q) measurements (Fig. 2). The strength of intermolecular interactions can be quantified by extracting the second virial coefficient (A₂) of each DNA system. Based on the following:¹⁷

$$\frac{P(Q=0)}{I(c,Q=0)}=\frac{1}{S(c,Q=0)}=1+2M{A}_{2}c,$$

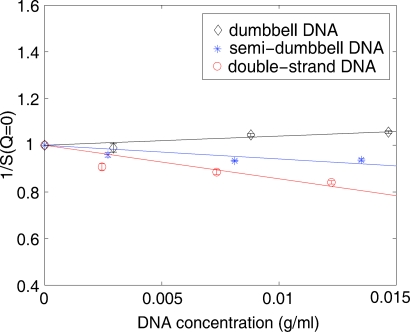
where c represents the concentration of DNA in units of g∕ml and M is the molecular weight of DNA respectively, A₂ can be obtained by linear fit once the structure factor profile S(Q) is extracted from the experimental data. As described above, the scattering profiles collected at the lowest DNA concentration, 0.1 mM, were used as form factors P(Q). S(c,Q=0) was calculated by extrapolation of the low Q region of S(Q). The linear fit of 1∕S(c,Q=0) versus c (Fig. 3) yields the A₂ values for dumbbell, semidumbbell, and dsDNA solutions: 1.4×10⁻⁴, −2.2×10⁻⁴, −5.9×10⁻⁴(mol ml g⁻²), respectively. The latter two, negative values of A₂ suggest that the semidumbbell and ds exhibit weak attraction at 20 mM Mg²⁺, consistent with the previous observation that the low Q upturn occurs when [Mg²⁺]>10 mM.⁴ The smaller negative (but larger absolute) value of A₂ of dsDNA solution reflects the fact that the attraction between dsDNA molecules is stronger than that between semidumbbell DNA molecules under the same ionic conditions. Interestingly, the slightly positive A₂, indicating marginal repulsion, is observed in solutions of dumbbell DNAs, in which the end-to-end stacking effect is expected to be suppressed by the T₄ loops capping both ends of DNA. To summarize our experimental data, both the magnitude and the sign of the attraction vary for the different constructs. The long range correlations in three types of DNA model systems are distinct presumably due to molecular structural differences.

Figure 2.

Scattering profiles I(Q) were measured for each sample at four different DNA concentrations: 0.1, 0.2, 0.6, and 1.0 mM. For each concentration, curves were normalized in the high Q regime to highlight differences in curve shape in the low Q region (see text).

Figure 3.

The inverse of the structure factor S(Q=0) is plotted as a function of DNA concentration (g/ml). A linear fit was performed to derive the second virial coefficient from these data. Dumbbell DNA shows marginal repulsion (A₂>0) while weak attraction (A₂<0) is observed in semi-dumbbell and ds DNA.

It is more accurate to interpret the result of A₂ analysis by exploring the definition and physical meaning of the second virial coefficient. A₂ is defined¹⁷ as

$$A_2\equiv \frac{N_a}{2M^2}{\int }_V\{1-\exp [-\frac{u\left(\stackrel{⃑}{r}\right)}{k_{B}T}]\}{d}^3\stackrel{⃑}{r},$$

where N_a is Avogadro’s number, M is the molecular weight, V represents the three-dimensional space in which the integral is carried out, and $u\left(\vec{r}\right)$ is the intermolecular potential, which depends on the relative position of two molecules. It is evident from the above expression that, at a fixed temperature T, the only factor affecting the sign of A₂ is the intermolecular potential. If $u\left(\vec{r}\right)$ is, on balance, more positive than negative over all space, the factor $1-\exp (-u\left(\stackrel{\rightharpoonup }{r}\right)∕k_{B}T)$ also exhibits more positive values and A₂ tends to be positive. A more positive $u\left(\vec{r}\right)$ means two molecules will experience stronger repulsion as the interparticle distance decreases below the equilibrium distance which minimizes the intermolecular potential. A similar argument can be made for the opposite case of attraction. The interpretation of both the sign and magnitude of A₂ is a simple way to quantify and compare intermolecular potentials. Our results suggest that, even in the presence of 20 mM Mg²⁺, the interactions between dumbbell DNAs are slightly repulsive, while interactions between dsDNAs at the same concentration are attractive. Modeling of the potential using adaptive Poisson-Boltzmann solver (APBS) (Ref. ¹⁸) does not indicate a buildup of charge around the T₄ loop. We therefore propose that the observed attraction results from the favorable free energy provided by the interaction between hydrophobic ends. These base pairs are exposed only in uncapped constructs; the T₄ loop blocks this type of contact between adjacent strands. This result is consistent with measurements on semidumbbell DNA, which indicate weaker attraction (smaller A₂) than dsDNA, due to the presence of one cap. It is important to point out that, at (fixed) room temperature, it is the potential profile that influences the sign and magnitude of A₂. The molecular weight also plays a role in determining the magnitude of A₂ but it is much less significant in our case.

In conclusion, we have investigated the behavior of dumbbell, semidumbbell, and ds 20 bp DNA molecules mediated by divalent counterions through SAXS experiments. Measurements of the second virial coefficient show distinct interaction modes among these three DNA model systems. Both the structure of the DNA molecule and the electrostatic screening of Mg²⁺ result in modification of the intermolecular potential, which along with temperature, sets the value of A₂. Our study also highlights the importance of end-to-end base stacking in short strand DNA-DNA interaction. While lateral (side by side) attraction is not ruled out, it may in fact depend on achieving a critical strand length.¹¹