Abstract
The purpose of this investigation was to determine the contribution of muscle O2 consumption (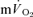 ) to pulmonary O2 uptake (
) to pulmonary O2 uptake (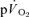 ) during both low-intensity (LI) and high-intensity (HI) knee-extension exercise, and during subsequent recovery, in humans. Seven healthy male subjects (age 20–25 years) completed a series of LI and HI square-wave exercise tests in which
) during both low-intensity (LI) and high-intensity (HI) knee-extension exercise, and during subsequent recovery, in humans. Seven healthy male subjects (age 20–25 years) completed a series of LI and HI square-wave exercise tests in which 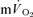 (direct Fick technique) and
(direct Fick technique) and 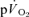 (indirect calorimetry) were measured simultaneously. The mean blood transit time from the muscle capillaries to the lung (MTTc-l) was also estimated (based on measured blood transit times from femoral artery to vein and vein to artery). The kinetics of
(indirect calorimetry) were measured simultaneously. The mean blood transit time from the muscle capillaries to the lung (MTTc-l) was also estimated (based on measured blood transit times from femoral artery to vein and vein to artery). The kinetics of 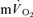 and
and 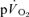 were modelled using non-linear regression. The time constant (τ) describing the phase II
were modelled using non-linear regression. The time constant (τ) describing the phase II 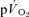 kinetics following the onset of exercise was not significantly different from the mean response time (initial time delay +τ) for
kinetics following the onset of exercise was not significantly different from the mean response time (initial time delay +τ) for 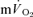 kinetics for LI (30 ± 3 vs 30 ± 3 s) but was slightly higher (P < 0.05) for HI (32 ± 3 vs 29 ± 4 s); the responses were closely correlated (r= 0.95 and r= 0.95; P < 0.01) for both intensities. In recovery, agreement between the responses was more limited both for LI (36 ± 4 vs 18 ± 4 s, P < 0.05; r=−0.01) and HI (33 ± 3 vs 27 ± 3 s, P > 0.05; r=−0.40). MTTc-l was ∼17 s just before exercise and decreased to 12 and 10 s after 5 s of exercise for LI and HI, respectively. These data indicate that the phase II
kinetics for LI (30 ± 3 vs 30 ± 3 s) but was slightly higher (P < 0.05) for HI (32 ± 3 vs 29 ± 4 s); the responses were closely correlated (r= 0.95 and r= 0.95; P < 0.01) for both intensities. In recovery, agreement between the responses was more limited both for LI (36 ± 4 vs 18 ± 4 s, P < 0.05; r=−0.01) and HI (33 ± 3 vs 27 ± 3 s, P > 0.05; r=−0.40). MTTc-l was ∼17 s just before exercise and decreased to 12 and 10 s after 5 s of exercise for LI and HI, respectively. These data indicate that the phase II 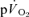 kinetics reflect
kinetics reflect 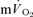 kinetics during exercise but not during recovery where caution in data interpretation is advised. Increased
kinetics during exercise but not during recovery where caution in data interpretation is advised. Increased 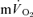 probably makes a small contribution to
probably makes a small contribution to 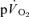 during the first 15–20 s of exercise.
during the first 15–20 s of exercise.
The kinetics of the pulmonary oxygen uptake ( ) response to exercise is frequently used to provide a non-invasive estimate of the contribution of skeletal muscle oxidative metabolism to energy turnover (e.g. Barstow et al. 1996; Gerbino et al. 1996; Grassi et al. 1997; Brittain et al. 2001; Burnley et al. 2002; Pringle et al. 2003; Koppo et al. 2004; Jones et al. 2004; Gurd et al. 2006; Chin et al. 2007). In these studies, the time constant (τ) describing the rate at which
) response to exercise is frequently used to provide a non-invasive estimate of the contribution of skeletal muscle oxidative metabolism to energy turnover (e.g. Barstow et al. 1996; Gerbino et al. 1996; Grassi et al. 1997; Brittain et al. 2001; Burnley et al. 2002; Pringle et al. 2003; Koppo et al. 2004; Jones et al. 2004; Gurd et al. 2006; Chin et al. 2007). In these studies, the time constant (τ) describing the rate at which 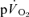 rises in the fundamental exponential phase of the response (phase II) is assumed to approximate the kinetics with which muscle oxygen consumption (
rises in the fundamental exponential phase of the response (phase II) is assumed to approximate the kinetics with which muscle oxygen consumption (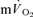 ) rises following the onset of exercise (Barstow et al. 1990; Grassi et al. 1996; Koga et al. 2005; Whipp & Rossiter, 2005). Moreover, the amplitude of the
) rises following the onset of exercise (Barstow et al. 1990; Grassi et al. 1996; Koga et al. 2005; Whipp & Rossiter, 2005). Moreover, the amplitude of the 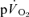 response above the pre-exercise baseline is considered to closely reflect the increase in
response above the pre-exercise baseline is considered to closely reflect the increase in 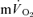 (Poole et al. 1991, 1992). However, few studies have simultaneously measured
(Poole et al. 1991, 1992). However, few studies have simultaneously measured 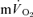 and
and 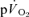 following the onset of exercise in humans. Indeed, the assumption of close agreement between the kinetics of
following the onset of exercise in humans. Indeed, the assumption of close agreement between the kinetics of 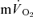 and
and 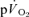 is based upon a computer simulation study (Barstow et al. 1990) and one study which reported that the τ for
is based upon a computer simulation study (Barstow et al. 1990) and one study which reported that the τ for 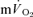 (∼36 s) and the τ for
(∼36 s) and the τ for 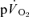 (∼32 s) were similar during moderate-intensity (i.e. below gas exchange threshold, GET) cycle exercise (Grassi et al. 1996). Koga et al. (2005) also reported that the τ for
(∼32 s) were similar during moderate-intensity (i.e. below gas exchange threshold, GET) cycle exercise (Grassi et al. 1996). Koga et al. (2005) also reported that the τ for 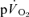 (∼30 s) was similar to the τ for
(∼30 s) was similar to the τ for 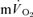 (∼26 s), as estimated from Doppler measures of femoral artery blood flow and blood samples drawn from the femoral vein, during heavy-intensity (>GET) knee-extension exercise. However, in these studies the
(∼26 s), as estimated from Doppler measures of femoral artery blood flow and blood samples drawn from the femoral vein, during heavy-intensity (>GET) knee-extension exercise. However, in these studies the 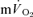 kinetics could not be determined accurately since the transit time of blood from the femoral artery and vein was not measured. Similarly, the assumption that the magnitude of the
kinetics could not be determined accurately since the transit time of blood from the femoral artery and vein was not measured. Similarly, the assumption that the magnitude of the 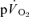 response chiefly represents the increase in
response chiefly represents the increase in 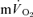 during exercise is based upon a limited number of studies which indicate that the
during exercise is based upon a limited number of studies which indicate that the 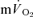 response contributes ∼85–95% to the
response contributes ∼85–95% to the 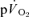 response in both the fundamental phase and the slow component phase (evident only in >GET exercise) of the response (Poole et al. 1991, 1992; Koga et al. 2005). These issues clearly require further exposition, ideally with simultaneous and high-fidelity measurements of
response in both the fundamental phase and the slow component phase (evident only in >GET exercise) of the response (Poole et al. 1991, 1992; Koga et al. 2005). These issues clearly require further exposition, ideally with simultaneous and high-fidelity measurements of 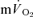 and
and 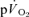 during both low-intensity and high-intensity exercise. Moreover, the kinetics of
during both low-intensity and high-intensity exercise. Moreover, the kinetics of 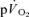 is often assumed to reflect the kinetics of
is often assumed to reflect the kinetics of 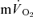 during recovery from exercise (Gerbino et al. 1996; Barstow et al. 2000; Cunningham et al. 2000) but, to our knowledge, there are presently no published data on the relationship between the
during recovery from exercise (Gerbino et al. 1996; Barstow et al. 2000; Cunningham et al. 2000) but, to our knowledge, there are presently no published data on the relationship between the 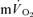 and
and 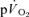 responses after exercise.
responses after exercise.
The 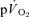 response to exercise has been shown to exhibit several phases (Whipp et al. 1982): the initial ‘cardio-dynamic phase’ (or phase I), which is believed to reflect the immediate increase in cardiac output and thus pulmonary blood flow; the ‘fundamental’ (phase II) exponential-like response towards the steady state, believed to have a similar time course to, and be predominantly reflective of, changes in
response to exercise has been shown to exhibit several phases (Whipp et al. 1982): the initial ‘cardio-dynamic phase’ (or phase I), which is believed to reflect the immediate increase in cardiac output and thus pulmonary blood flow; the ‘fundamental’ (phase II) exponential-like response towards the steady state, believed to have a similar time course to, and be predominantly reflective of, changes in 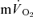 (see above); and phase III, the steady-state (for low-intensity GET (<GET) exercise) or the slow component (for >GET exercise). The phase I–phase II interface, normally observed after ∼15–20 s of exercise, is heralded by a fall in end-tidal O2 partial pressure and an increase in end-tidal CO2 partial pressure, reflecting the arrival at the lung of blood that has been deoxygenated by the contracting muscles (Whipp et al. 1982). Various approaches have been used to ‘isolate’ the phase II
(see above); and phase III, the steady-state (for low-intensity GET (<GET) exercise) or the slow component (for >GET exercise). The phase I–phase II interface, normally observed after ∼15–20 s of exercise, is heralded by a fall in end-tidal O2 partial pressure and an increase in end-tidal CO2 partial pressure, reflecting the arrival at the lung of blood that has been deoxygenated by the contracting muscles (Whipp et al. 1982). Various approaches have been used to ‘isolate’ the phase II 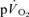 response when the objective is to determine the τ value, including exponential modelling of the phase I response (e.g. Barstow et al. 1996; Pringle et al. 2003; Koga et al. 2005), and elimination of the first 15–25 s of exercise data to ensure that the phase II curve fit is not ‘contaminated’ by phase I (e.g. Gerbino et al. 1996; Brittain et al. 2001; Koppo et al. 2004; Jones et al. 2004; Gurd et al. 2006). However, to our knowledge, the transit time for blood flow from the contracting muscles to reach the lungs following the onset of exercise has not been determined and it is therefore possible that ‘phase I’ of the
response when the objective is to determine the τ value, including exponential modelling of the phase I response (e.g. Barstow et al. 1996; Pringle et al. 2003; Koga et al. 2005), and elimination of the first 15–25 s of exercise data to ensure that the phase II curve fit is not ‘contaminated’ by phase I (e.g. Gerbino et al. 1996; Brittain et al. 2001; Koppo et al. 2004; Jones et al. 2004; Gurd et al. 2006). However, to our knowledge, the transit time for blood flow from the contracting muscles to reach the lungs following the onset of exercise has not been determined and it is therefore possible that ‘phase I’ of the 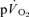 response contains a contribution from the exercising limbs; if so, this could potentially complicate, or even nullify, estimations of
response contains a contribution from the exercising limbs; if so, this could potentially complicate, or even nullify, estimations of  kinetics from
kinetics from 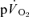 kinetics.
kinetics.
The purpose of the present study was therefore to examine the contribution made by the contracting muscles to pulmonary oxygen uptake through simultaneous measurement of 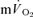 and
and 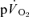 following the onset of low-intensity (<GET) and high-intensity (>GET), sub-maximal, knee-extension exercise and during subsequent recovery. With the assumption that removal of a period of time containing the
following the onset of low-intensity (<GET) and high-intensity (>GET), sub-maximal, knee-extension exercise and during subsequent recovery. With the assumption that removal of a period of time containing the 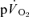 phase I from analysis effectively ‘time-aligns’ the
phase I from analysis effectively ‘time-aligns’ the 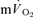 and
and 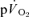 responses, we hypothesised that there would be no significant difference between the τ for the phase II
responses, we hypothesised that there would be no significant difference between the τ for the phase II 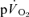 kinetics and the τ for the fundamental
kinetics and the τ for the fundamental 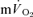 kinetics during either low-intensity or high-intensity exercise or recovery. Moreover, assuming that the increased contractile activity is essentially confined to the quadriceps muscle group during knee-extension exercise, we hypothesised that the contracting muscles would make an appreciable (>85%) contribution to the increase in
kinetics during either low-intensity or high-intensity exercise or recovery. Moreover, assuming that the increased contractile activity is essentially confined to the quadriceps muscle group during knee-extension exercise, we hypothesised that the contracting muscles would make an appreciable (>85%) contribution to the increase in 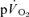 both in the fundamental and slow component phases of the response. A secondary purpose of the study was to determine the blood transit time from femoral artery to femoral vein and from femoral vein to femoral artery at the two exercise intensities in order to estimate the blood transit time from the sites of gas exchange within the contracting muscles to the lungs. Given the anticipated greater demand for muscle blood flow at higher work rates, we hypothesised that the blood mean transit time from muscle to lung would be shorter during high-intensity exercise than during low-intensity exercise.
both in the fundamental and slow component phases of the response. A secondary purpose of the study was to determine the blood transit time from femoral artery to femoral vein and from femoral vein to femoral artery at the two exercise intensities in order to estimate the blood transit time from the sites of gas exchange within the contracting muscles to the lungs. Given the anticipated greater demand for muscle blood flow at higher work rates, we hypothesised that the blood mean transit time from muscle to lung would be shorter during high-intensity exercise than during low-intensity exercise.
Methods
Subjects
Seven healthy male subjects, aged 20–25 years, with mean height of 1.82 m (range: 1.77–1.85 m), mean body mass of 78.4 kg (68.0–87.3 kg), and body fat percentage of 18.2% (10.4–24.2%), participated in the experiment. The subjects were untrained or recreationally active, having a maximal oxygen uptake (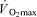 ) measured on the cycle ergometer of 49.1 ml min−1 kg−1 (45.7–54.7 ml min−1 kg−1). The quadriceps muscle mass of the experimental leg was 2.34 ± 0.11 kg (2.01–2.69 kg) (Krustrup, 2004). None of the subjects trained for competition. The subjects were fully informed of the risks and discomforts associated with the experimental procedures, and all provided written consent. The study was carried out in accordance with the guidelines contained in the Declaration of Helsinki and was approved by the Ethics Committee of Copenhagen and Frederiksberg communities.
) measured on the cycle ergometer of 49.1 ml min−1 kg−1 (45.7–54.7 ml min−1 kg−1). The quadriceps muscle mass of the experimental leg was 2.34 ± 0.11 kg (2.01–2.69 kg) (Krustrup, 2004). None of the subjects trained for competition. The subjects were fully informed of the risks and discomforts associated with the experimental procedures, and all provided written consent. The study was carried out in accordance with the guidelines contained in the Declaration of Helsinki and was approved by the Ethics Committee of Copenhagen and Frederiksberg communities.
Exercise model and pre-experimental procedures
Subjects performed dynamic one-legged knee-extensor exercise in a supine position on an ergometer that permitted the exercise to be confined to the quadriceps muscle (Andersen et al. 1985; Bangsbo et al. 1990). The subjects had several visits to the laboratory in order to become familiarised with the exercise model. After at least three familiarisation sessions, the subjects performed an incremental exercise test in order to determine the maximal power output of the knee extensors, which was 66 W (54–82 W). Pulmonary gas exchange and ventilation was measured (CPX/D MedGraphics, Saint Paul, MN, US) throughout the incremental test. The 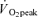 was defined as the highest 30 s mean value recorded before the subject's volitional termination of the test. The gas exchange threshold (GET) was determined from a cluster of measures including: (1) the first disproportionate increase in carbon dioxide output (
was defined as the highest 30 s mean value recorded before the subject's volitional termination of the test. The gas exchange threshold (GET) was determined from a cluster of measures including: (1) the first disproportionate increase in carbon dioxide output (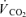 ) from visual inspection of individual plots of
) from visual inspection of individual plots of 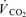 versus
versus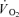 ; (2) an increase in
; (2) an increase in 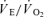 (
(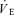 , expiratory ventilation) with no increase in
, expiratory ventilation) with no increase in 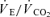 ; (3) an increase in end-tidal O2 tension with no fall in end-tidal CO2 tension. The power outputs that would require 60% of the GET (i.e. low-intensity exercise, LI: 18 W (14–22 W)) and 50% of the difference (Δ) between the GET and
; (3) an increase in end-tidal O2 tension with no fall in end-tidal CO2 tension. The power outputs that would require 60% of the GET (i.e. low-intensity exercise, LI: 18 W (14–22 W)) and 50% of the difference (Δ) between the GET and 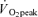 (i.e. high-intensity exercise, HI: 47 W (38–58 W)) were calculated and used in the main experiment. This method of normalising exercise intensity is standard practice in studies of
(i.e. high-intensity exercise, HI: 47 W (38–58 W)) were calculated and used in the main experiment. This method of normalising exercise intensity is standard practice in studies of 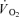 kinetics (e.g. Roston et al. 1987; Gerbino et al. 1996).
kinetics (e.g. Roston et al. 1987; Gerbino et al. 1996).
Main experiment
Subject preparation
The subjects arrived at the laboratory at 8 am after consuming a standard breakfast including fruit juice and cereal. While subjects lay in the supine position, one arterial and two venous catheters were placed under local anaesthesia. The arterial catheter, used for collection of blood samples and for green dye measurement, was inserted ‘antegrade’ into the femoral artery of the right leg (experimental leg) with the tip positioned ∼2 cm proximal to the inguinal ligament. The second catheter, used for collection of venous blood samples and for green dye measurements, was placed ‘retrograde’ in the femoral vein of the right leg with the tip positioned 6 cm distal to the inguinal ligament. The third catheter, used for measurements of thigh blood flow, was placed ‘antegrade’ into the femoral vein of the right leg with the tip positioned 2 cm distal to the inguinal ligament. A thermistor (Edslab, T.D. Probe, 94-030-2.5F, Baxter A/S, Allerod, Denmark) for measurement of blood temperature was advanced ∼8 cm beyond the tip of the venous catheter.
Experimental protocol
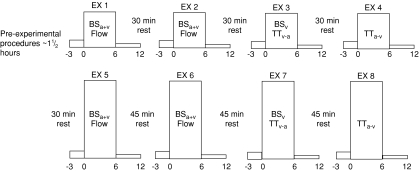
The exercise protocol consisted of four 6 min LI bouts (EX1–4) followed by four 6 min HI bouts (EX5–8; Fig. 1). The LI bouts and HI bouts were interspersed with 30 min and 45 min rest periods, respectively (see Fig. 1). These recovery durations were selected to ensure that muscle blood flow, blood gases and metabolites, and 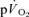 had returned to baseline before the commencement of the next exercise bout (Krustrup et al. 2004a; Burnley et al. 2006). Pulmonary gas exchange was measured throughout all exercise tests. Before EX1–2 and EX5–6, blood flow was measured and femoral arterial and venous blood samples were obtained. For 30 s immediately prior to the onset of exercise the leg was passively moved in order to accelerate the ergometer flywheel and ensure a constant power output from the onset of exercise. Blood was drawn from the femoral artery and vein during passive exercise and frequently during the initial phase of exercise, i.e. arterial samples were obtained after −5, 0 and 5 and 10 s and venous samples were taken after 6, 9, 12, 15 and 18 s. For the rapid initial sampling of venous blood a rack of stop-cocks was used (Bangsbo et al. 2000; Krustrup, 2004). Further arterial and venous samples were collected at ∼0.5, 1, 1.5, 2, 3 and 6 min of exercise, as well as after 5, 15, 30, 45, 60 s, and 2, 3, 4.5 and 6 min of recovery. In order to account for the transit time of blood from the artery through the muscle capillary bed and to the collection point at the vein (mean transit time (MTT); Bangsbo et al. 2000), from 0.5 to 1.5 min the arterial sample was taken approximately 6 s before the venous sample and for the remainder of the exercise 5 s before. Blood flow was measured at rest, during passive exercise, from 20–30, 45–55, 95–105, 125–135, 185–195 and 330–345 s of exercise as well as after 20–30, 45–55, 95–105, 125–135, 185–195 and 370–385 s of recovery (see Fig. 1). During EX3 and EX6, venous blood samples were obtained at rest, during passive exercise and frequently during exercise. Additionally, femoral vein-to-femoral artery time to appearance and mean transit time was measured at rest, during passive exercise and at 6, 35, 60, 90, 120, 180 and 270 s of exercise and 6, 35, 60, 90, 120, 180 and 270 s into the recovery period (Fig. 1). During EX4 and EX8 artery-to-vein time to appearance and mean transit time was measured at rest, during passive exercise and at 6, 35, 60, 90, 120, 180 and 270 s of exercise and 6, 35, 60, 90, 120, 180 and 270 s into the recovery period (Fig. 1). An occlusion cuff placed below the knee was inflated (240 mmHg) 30 s prior to exercise and remained inflated throughout exercise in order to avoid contribution of blood from the lower leg.
had returned to baseline before the commencement of the next exercise bout (Krustrup et al. 2004a; Burnley et al. 2006). Pulmonary gas exchange was measured throughout all exercise tests. Before EX1–2 and EX5–6, blood flow was measured and femoral arterial and venous blood samples were obtained. For 30 s immediately prior to the onset of exercise the leg was passively moved in order to accelerate the ergometer flywheel and ensure a constant power output from the onset of exercise. Blood was drawn from the femoral artery and vein during passive exercise and frequently during the initial phase of exercise, i.e. arterial samples were obtained after −5, 0 and 5 and 10 s and venous samples were taken after 6, 9, 12, 15 and 18 s. For the rapid initial sampling of venous blood a rack of stop-cocks was used (Bangsbo et al. 2000; Krustrup, 2004). Further arterial and venous samples were collected at ∼0.5, 1, 1.5, 2, 3 and 6 min of exercise, as well as after 5, 15, 30, 45, 60 s, and 2, 3, 4.5 and 6 min of recovery. In order to account for the transit time of blood from the artery through the muscle capillary bed and to the collection point at the vein (mean transit time (MTT); Bangsbo et al. 2000), from 0.5 to 1.5 min the arterial sample was taken approximately 6 s before the venous sample and for the remainder of the exercise 5 s before. Blood flow was measured at rest, during passive exercise, from 20–30, 45–55, 95–105, 125–135, 185–195 and 330–345 s of exercise as well as after 20–30, 45–55, 95–105, 125–135, 185–195 and 370–385 s of recovery (see Fig. 1). During EX3 and EX6, venous blood samples were obtained at rest, during passive exercise and frequently during exercise. Additionally, femoral vein-to-femoral artery time to appearance and mean transit time was measured at rest, during passive exercise and at 6, 35, 60, 90, 120, 180 and 270 s of exercise and 6, 35, 60, 90, 120, 180 and 270 s into the recovery period (Fig. 1). During EX4 and EX8 artery-to-vein time to appearance and mean transit time was measured at rest, during passive exercise and at 6, 35, 60, 90, 120, 180 and 270 s of exercise and 6, 35, 60, 90, 120, 180 and 270 s into the recovery period (Fig. 1). An occlusion cuff placed below the knee was inflated (240 mmHg) 30 s prior to exercise and remained inflated throughout exercise in order to avoid contribution of blood from the lower leg.
Figure 1. Schematic representation of the experimental protocol.
The subjects performed four 6 min moderate-intensity knee-extensor exercise bouts (EX1–4) interspersed with 30 min rest periods, followed by four 6 min high-intensity knee-extensor exercise bouts (EX5–8) interspersed with 45 min rest periods. During EX1–2 and EX5–6, femoral arterial blood samples (BSa) and venous blood samples (BSv) were collected and thigh blood flow was measured. During EX3 and EX7, the vein-to-artery transit time (TTv-a) was determined and venous blood samples were collected. During EX4 and EX8, the artery-to-vein transit time (TTa-v) was determined.
In addition to the protocol outlined above, in which four repeats of each of the LI and HI bouts were completed, the subjects returned to the laboratory on a number of other occasions to complete further ‘non-invasive’ trials, identical to those described above, during which pulmonary gas exchange only was measured. This was done to increase the signal-to-noise ratio for the 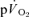 response and hence improve confidence in the outcomes of the mathematical modelling procedures employed to describe the kinetics (Lamarra et al. 1987; see later). In total, the subjects completed 7–10 transitions to LI exercise and 5–7 transitions to HI exercise for the determination of
response and hence improve confidence in the outcomes of the mathematical modelling procedures employed to describe the kinetics (Lamarra et al. 1987; see later). In total, the subjects completed 7–10 transitions to LI exercise and 5–7 transitions to HI exercise for the determination of 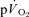 kinetics.
kinetics.
Measurements and analyses
Thigh blood flow measurements
Femoral venous blood flow (i.e. thigh blood flow) was measured by the constant infusion thermodilution technique (Andersen & Saltin, 1985) as modified by González-Alonso et al. (2000). Briefly, venous and infusate temperatures were measured continuously before and during ice-cold saline infusion (10–15 s) at a rate of 120 ml min−1 to achieve a drop in venous blood temperature of ∼0.6–2°C. Resting blood flow measurements were made using an infusion rate of 30 ml min−1 maintained for 30–45 s.
Blood analyses
Arterial and venous blood samples were immediately analysed for 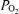 , O2 saturation and haemoglobin (ABL510, Radiometer, Copenhagen, Denmark) from which O2 content was calculated.
, O2 saturation and haemoglobin (ABL510, Radiometer, Copenhagen, Denmark) from which O2 content was calculated.
Artery-to-vein and vein-to-artery transit times
To determine the femoral artery-to-vein time to appearance (TAPa-v) and mean transit time (MTTa-v), 3 mg of indocyanine green (ICG, Becton Dickenson) at a concentration of 5 mg ml−1 was rapidly injected into the femoral artery, immediately followed by a flush of 5 ml isotonic saline. Blood was withdrawn from the femoral vein at a rate of 30 ml min−1 for measurements of ICG concentration with a linear densitometer. The densitometer output was sampled at a frequency of 100 Hz with a computer. The time from injection to the time of appearance and the time when the curve peaked was calculated as described by Bangsbo et al. 2000 and corrected by the transit time of the catheter (i.e. the dead space of the catheter divided by the pump flow). Accordingly, femoral vein-to-artery time to appearance (TAPv-a) and mean transit time (MTTv-a) was determined by injections of ICG (6 mg, 5 mg ml−1) into the femoral vein and with blood withdrawal from femoral artery at a rate of 30 ml min−1. When calculating the capillary-to-lung transit time (MTTc-l) the following equation was used:
| (1) |
since it has been observed that the transit time from the muscle capillary bed to the femoral vein is two-thirds of the transit time from the femoral artery to the femoral vein (Bangsbo et al. 2000) and that the transit time from the femoral vein to the lung is two-thirds of the transit time from the femoral vein to the femoral artery, based on calculations of the venous and arterial volume.
Pulmonary gas exchange
Pulmonary gas exchange and ventilation were determined breath by breath throughout all of the exercise tests with a fast-response gas analyser and pneumotachograph system (CPX/D MedGraphics, Saint Paul, MN, US). The response time of the gas analysers was < 80 ms for O2 and < 150 ms for CO2. Subjects wore a nose clip and breathed through a low-dead-space, low-resistance mouthpiece that was securely attached to the volume transducer. The inspired and expired gas volume and gas concentration signals were continuously sampled via a capillary line connected to the mouthpiece. Prior to each test, the gas analyser was calibrated using gases of known concentration and the pneumotachograph was calibrated using a precision 3 l calibration syringe over a range of flows. The time delay between the volume and gas concentration signals was measured and used to phase-align the signals. Pulmonary gas exchange variables were calculated according to standard algorithms (Beaver et al. 1981) and displayed breath by breath.
Mathematical modelling of the 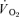 response
response
The breath-by-breath pulmonary 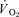 data from each test were initially examined to exclude aberrant breaths caused by coughing, swallowing, sighing, etc. and those values lying more than 4 standard deviations from the local mean were removed. These breath-by-breath data sets were subsequently linearly interpolated to provide values every second. For each subject, the identical repetitions of each exercise condition were then time-aligned to the start of exercise and ensemble-averaged to reduce the breath-to-breath noise and enhance the underlying physiological response characteristics (Lamarra et al. 1987). For muscle
data from each test were initially examined to exclude aberrant breaths caused by coughing, swallowing, sighing, etc. and those values lying more than 4 standard deviations from the local mean were removed. These breath-by-breath data sets were subsequently linearly interpolated to provide values every second. For each subject, the identical repetitions of each exercise condition were then time-aligned to the start of exercise and ensemble-averaged to reduce the breath-to-breath noise and enhance the underlying physiological response characteristics (Lamarra et al. 1987). For muscle 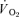 , the mean value for each of the sampling periods throughout exercise and recovery was calculated and used in subsequent curve fitting.
, the mean value for each of the sampling periods throughout exercise and recovery was calculated and used in subsequent curve fitting.
In the case of the on-transient, the first 20 s of pulmonary 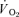 data after the onset of exercise (i.e. the Phase I response) was deleted and a non-linear least-square algorithm was used to fit the data as described in the following mono-exponential (LI; eqn (2)) or bi-exponential equation (HI; eqn (3)) (Özyener et al. 2001; Whipp & Rossiter, 2005). The muscle
data after the onset of exercise (i.e. the Phase I response) was deleted and a non-linear least-square algorithm was used to fit the data as described in the following mono-exponential (LI; eqn (2)) or bi-exponential equation (HI; eqn (3)) (Özyener et al. 2001; Whipp & Rossiter, 2005). The muscle 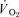 data were modelled, unfiltered, from the onset of exercise using eqn (2) for LI and eqn (3) for HI. However, in three subjects, no
data were modelled, unfiltered, from the onset of exercise using eqn (2) for LI and eqn (3) for HI. However, in three subjects, no 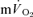 slow component could be reliably discerned during HI and these data were therefore fitted using eqn (2).
slow component could be reliably discerned during HI and these data were therefore fitted using eqn (2).
| (2) |
| (3) |
where: 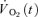 represents the absolute
represents the absolute 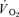 at a given time t;
at a given time t; 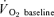 represents the mean
represents the mean 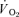 in the final 30 s of the baseline period; Ap, Tdp and τp represent the amplitude, time delay and time constant, respectively, describing the fundamental increase in
in the final 30 s of the baseline period; Ap, Tdp and τp represent the amplitude, time delay and time constant, respectively, describing the fundamental increase in 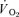 above baseline; and As, Tds and τs represent the amplitude, time delay before the onset of, and time constant describing the development of, the
above baseline; and As, Tds and τs represent the amplitude, time delay before the onset of, and time constant describing the development of, the 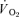 slow component, respectively. An iterative process was used to minimise the sum of the squared errors between the fitted function and the observed values. It should be noted that the Tdp is included to enhance the goodness-of-fit of the exponential to the phase II response and is not necessarily the same as the duration of phase I.
slow component, respectively. An iterative process was used to minimise the sum of the squared errors between the fitted function and the observed values. It should be noted that the Tdp is included to enhance the goodness-of-fit of the exponential to the phase II response and is not necessarily the same as the duration of phase I.
For the off-transient, the 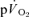 and
and 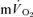 responses were fitted either with eqn (4) (LI – pulmonary and muscle; HI – muscle) or eqn (5) (HI – pulmonary), (Özyener et al. 2001; Whipp & Rossiter, 2005). In eqn (5), a separate time delay term for the slow phase was not included as it is reasonable to assume that both the
responses were fitted either with eqn (4) (LI – pulmonary and muscle; HI – muscle) or eqn (5) (HI – pulmonary), (Özyener et al. 2001; Whipp & Rossiter, 2005). In eqn (5), a separate time delay term for the slow phase was not included as it is reasonable to assume that both the 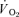 fundamental and slow components were present at the start of the recovery period (Cunningham et al. 2000).
fundamental and slow components were present at the start of the recovery period (Cunningham et al. 2000).
| (4) |
| (5) |
For muscle 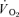 , the mean response time (MRTp) for the fundamental phase of the response in both LI and HI was calculated by summing the Tdp and τp since this parameter best describes the overall
, the mean response time (MRTp) for the fundamental phase of the response in both LI and HI was calculated by summing the Tdp and τp since this parameter best describes the overall 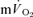 kinetics following the onset of contractions (Koga et al. 2005; Whipp & Rossiter, 2005). In addition, the mean response time for the entire
kinetics following the onset of contractions (Koga et al. 2005; Whipp & Rossiter, 2005). In addition, the mean response time for the entire 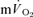 and
and 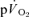 responses in exercise and recovery (MRTt) were calculated by fitting a single exponential curve through the data from the onset (or offset) of exercise. For the on-and off-transient, for both LI and HI, the functional ‘gain’ (Gp) of the fundamental component of
responses in exercise and recovery (MRTt) were calculated by fitting a single exponential curve through the data from the onset (or offset) of exercise. For the on-and off-transient, for both LI and HI, the functional ‘gain’ (Gp) of the fundamental component of 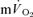 and
and 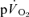 was computed by dividing the asymptotic amplitude of the fundamental
was computed by dividing the asymptotic amplitude of the fundamental 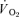 response (Ap) by the change in work rate. The magnitude of the
response (Ap) by the change in work rate. The magnitude of the 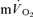 and
and 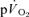 slow components was also estimated for both the onset and offset of HI exercise by calculating the difference between the
slow components was also estimated for both the onset and offset of HI exercise by calculating the difference between the 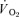 values at 2 and 6 min of exercise or recovery.
values at 2 and 6 min of exercise or recovery.
Calculations
Thigh O2 uptake was calculated by multiplying blood flow with arterial–venous O2 difference. A continuous blood flow curve was constructed for each subject by linear interpolation of the measured blood flow data points to obtain time-matched values of blood flow with the blood variables. Total thigh O2 uptake was calculated as the area under the uptake curves.
Statistics
Data were analysed using a two-factor (condition × time) repeated measure analysis of variance (ANOVA), with significance set at P < 0.05. Significant interactions and main effects were subsequently analysed using a Newman–Keuls post hoc test. Differences in 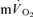 and
and 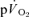 kinetics were tested using the Student paired t test and relationships between
kinetics were tested using the Student paired t test and relationships between 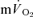 and
and 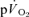 kinetics were explored using Pearson product moment correlation coefficients. Data are presented as means ± standard error of the mean (s.e.m.), unless otherwise stated.
kinetics were explored using Pearson product moment correlation coefficients. Data are presented as means ± standard error of the mean (s.e.m.), unless otherwise stated.
Results
Femoral artery-to-vein and vein-to-artery mean transit time
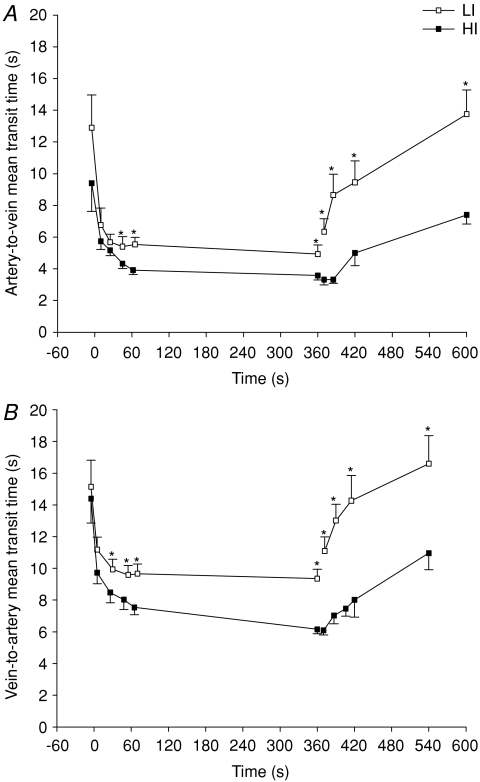
Mean transit time from the femoral artery to vein (MTTa-v) and vein to artery (MTTv-a) are presented in Fig. 2. Briefly, MTTa-v was ∼7 and 5 s after 9 and 355 s of LI, with corresponding values of ∼6 and 4 s in HI (Fig. 2A). After 25 s and 6 min of recovery from LI, MTTa-v increased (P < 0.05) to ∼9 and 14 s, with corresponding values of ∼3 and 7 s for HI exercise (Fig. 2B). MTTa-v was lower (P < 0.05) in HI than in LI from 45 to 355 s of exercise and throughout recovery (Fig. 2A).
Figure 2. Mean artery-to-vein (A) and vein-to-artery (B) transit times during 6 min of low-intensity and high-intensity sub-maximal knee-extensor exercise followed by a 6 min recovery period.
Values are mean ±s.e.m. *LI significantly different from HI.
MTTv-a was ∼11 and 9 s after 5 and 355 s of LI, with corresponding values of ∼10 and 6 s during HI (Fig. 2B). After 30 s and 6 min of recovery from LI, MTTv-a increased (P < 0.05) to ∼13 and 17 s, with corresponding values of ∼7 and 11 s for HI exercise (Fig. 2B). MTTv-a was lower (P < 0.05) in HI than in LI from 25 to 355 s of exercise and throughout recovery (Fig. 2B).
Femoral artery-to-vein and vein-to artery time to appearance
TAPa-v was 3.0 ± 0.5 and 2.7 ± 0.4 s after 9 and 355 s of LI, with corresponding values of 2.6 ± 0.4 and 2.1 ± 0.3 s in HI. After 25 s and 6 min of recovery, TAPa-v was 5.0 ± 0.9 and 8.3 ± 1.3 s in LI, respectively, and 1.9 ± 0.2 s and 3.9 ± 0.5 s in HI, respectively. TAPa-v was lower (P < 0.05) in HI than in LI from 45 to 355 s of exercise and throughout recovery.
TAPv-a was 7.6 ± 0.6 and 6.5 ± 0.5 s after 5 and 355 s of LI, respectively, with corresponding values of 6.9 ± 0.7 and 4.0 ± 0.3 s in HI. After 30 s and 6 min of recovery, TAPv-a was 9.5 ± 0.9 and 12.5 ± 1.4 s in LI, respectively, and 5.1 ± 0.5 and 7.6 ± 1.0 s in HI. TAPv-a was lower (P < 0.05) in HI than in LI from 25 s to 355 s of exercise and throughout recovery.
Capillary-to-lung mean transit time
Estimated capillary-to-lung time to appearance (TAPc-l) was 12 s during passive exercise and decreased to 7 and 6 s after 5 s of exercise and at the end of LI, with the corresponding values for HI being 6 and 4 s, respectively. Estimated TAPc-l increased to 10 s after 25 s of recovery in LI but was unaltered during the first 23 s of recovery in HI (∼5 s). After 5 min of recovery in LI and HI, the estimated capillary-to-lung time to appearance values were 14 and 8 s, respectively.
Estimated capillary-to-lung mean transit time (MTTc-l) was 17 s during passive exercise and decreased to 12 and 9 s after 5 s of exercise and at the end of LI, respectively, with the corresponding values for HI being 10 and 6 s, respectively. Estimated MTTc-l increased to 12 and 14 s after 10 and 25 s of recovery in LI but was unaltered during the first 23 s of recovery in HI. After 5 min of recovery in LI and HI, the estimated MTTc-l values were 20 and 12 s, respectively.
Muscle and pulmonary oxygen uptake and ventilation
For LI, mono-exponential modelling provided an adequate characterization of the on-transients for both 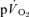 and
and 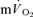 for all subjects. For HI, bi-exponential modelling provided superior characterization of the on-transient
for all subjects. For HI, bi-exponential modelling provided superior characterization of the on-transient 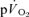 kinetics for all subjects. However, for
kinetics for all subjects. However, for 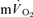 on-kinetics, the data for four subjects were best described by a bi-exponential model, whereas the fit was not improved by bi-exponential modelling in the remaining three subjects. Mono-exponential modelling provided an adequate characterization of the off-transient for LI for both
on-kinetics, the data for four subjects were best described by a bi-exponential model, whereas the fit was not improved by bi-exponential modelling in the remaining three subjects. Mono-exponential modelling provided an adequate characterization of the off-transient for LI for both 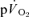 and
and 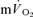 . The off transient for HI was better fitted with a bi-exponential model for
. The off transient for HI was better fitted with a bi-exponential model for 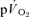 , and a mono-exponential model for
, and a mono-exponential model for 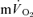 . Pulmonary ventilation at the end of LI and HI was 18 ± 2 and 35 ± 5 l min−1, respectively.
. Pulmonary ventilation at the end of LI and HI was 18 ± 2 and 35 ± 5 l min−1, respectively.
On-transient responses: comparison of  and
and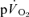 kinetics
kinetics
The group mean parameters of the 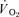 response for the on-transients of both
response for the on-transients of both 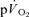 and
and 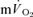 for each of the intensities are reported in Table 1 and illustrated in Fig. 3 (LI) and Fig. 4 (HI). As would be expected, the baseline and end-exercise
for each of the intensities are reported in Table 1 and illustrated in Fig. 3 (LI) and Fig. 4 (HI). As would be expected, the baseline and end-exercise 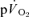 values were significantly higher than the corresponding values for
values were significantly higher than the corresponding values for 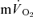 both for LI and HI (Table 1). The τp was significantly longer for
both for LI and HI (Table 1). The τp was significantly longer for 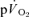 compared to
compared to 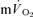 for both LI (30 ± 3 vs 26 ± 3 s; P < 0.05) and HI (32 ± 3 vs 25 ± 4 s; P < 0.01). However, the 95% confidence intervals (95% CI) surrounding the estimates of τp, which were ± 4–5 s for
for both LI (30 ± 3 vs 26 ± 3 s; P < 0.05) and HI (32 ± 3 vs 25 ± 4 s; P < 0.01). However, the 95% confidence intervals (95% CI) surrounding the estimates of τp, which were ± 4–5 s for 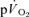 and ± 7 s for
and ± 7 s for 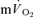 (Table 1), overlapped such that the values were functionally similar. The correlation between τp for
(Table 1), overlapped such that the values were functionally similar. The correlation between τp for 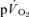 and
and 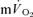 was significant both for LI (r= 0.94; P < 0.01) and HI (r= 0.94; P < 0.01). When the τp for
was significant both for LI (r= 0.94; P < 0.01) and HI (r= 0.94; P < 0.01). When the τp for 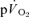 was compared with the MRTp for
was compared with the MRTp for 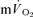 (i.e. Tdp+τp, which is equivalent to the overall response of
(i.e. Tdp+τp, which is equivalent to the overall response of 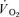 following the start of contractions; Koga et al. 2005; Whipp & Rossiter, 2005), there was no significant difference for LI (30 ± 3 vs 30 ± 4 s) but a small significant difference remained for HI (32 ± 3 vs 29 ± 3 s, P < 0.05). There was a significant correlation between the τp for
following the start of contractions; Koga et al. 2005; Whipp & Rossiter, 2005), there was no significant difference for LI (30 ± 3 vs 30 ± 4 s) but a small significant difference remained for HI (32 ± 3 vs 29 ± 3 s, P < 0.05). There was a significant correlation between the τp for 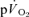 and the MRTp for
and the MRTp for 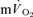 both for LI (r= 0.95; P < 0.01) and HI (r= 0.95; P < 0.01; Fig. 5). The overall kinetics (as reflected in MRTt) were significantly slower for
both for LI (r= 0.95; P < 0.01) and HI (r= 0.95; P < 0.01; Fig. 5). The overall kinetics (as reflected in MRTt) were significantly slower for 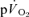 compared to
compared to 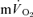 .
.
Table 1.
Muscle and pulmonary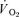 kinetics during low-intensity (LI) and high-intensity (HI) knee-extension exercise
kinetics during low-intensity (LI) and high-intensity (HI) knee-extension exercise
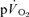 |
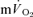 |
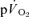 |
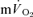 |
|
|---|---|---|---|---|
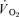 (l min−1) (l min−1) |
0.25 ± 0.08* | 0.05 ± 0.01 | 0.25 ± 0.09* | 0.05 ± 0.01 |
| Tdp (s) | 22 ± 2* | 4 ± 1 | 24 ± 3* | 4 ± 3 |
| τp (s) | 30 ± 3* | 26 ± 3 | 32 ± 3* | 25 ± 4 |
| 95% CI (s) | 4 ± 2 | 7 ± 3 | 5 ± 2 | 6 ± 2 |
| Ap (l min−1) | 0.30 ± 0.02 | 0.33 ± 0.03 | 0.70 ± 0.06 | 0.69 ± 0.05 |
| Gp (ml min−1 W−1) | 8.1 ± 0.6 | 8.9 ± 0.6 | 9.5 ± 0.9 | 9.7 ± 0.8 |
| Tds (s) | — | — | 169 ± 26 | 152 ± 14 |
| As′ (l min−1) | — | — | 0.15 ± 0.03 | 0.12 ± 0.02 |
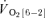 (l min−1) (l min−1) |
— | — | 0.17 ± 0.04 | 0.13 ± 0.02 |
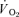 (l min−1) (l min−1) |
0.55 ± 0.03* | 0.38 ± 0.04 | 1.07 ± 0.06* | 0.79 ± 0.06 |
| MRTt (s) | 64 ± 7* | 34 ± 4 | 85 ± 8 | 37 ± 5xs |
Significantly different (P < 0.05) from corresponding value for 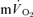 . Tdp, τp and Ap represent the time delay, time constant and amplitude terms, respectively, for the fundamental component, and Tds and As′ represent the time delay and amplitude terms, respectively, for the slow component of muscle and pulmonary O2 uptake (see eqns (2) and (3) and associated text). Note that the Tdp is a model parameter that does not necessarily reflect the duration of ‘phase I’. 95% CI is the 95% confidence interval surrounding the estimation of the corresponding time constant; Gp is the response gain of the fundamental component (
. Tdp, τp and Ap represent the time delay, time constant and amplitude terms, respectively, for the fundamental component, and Tds and As′ represent the time delay and amplitude terms, respectively, for the slow component of muscle and pulmonary O2 uptake (see eqns (2) and (3) and associated text). Note that the Tdp is a model parameter that does not necessarily reflect the duration of ‘phase I’. 95% CI is the 95% confidence interval surrounding the estimation of the corresponding time constant; Gp is the response gain of the fundamental component (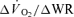 );
); 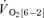 is the increase in O2 uptake between the second and sixth minutes of exercise; and MRTt is the mean response time for the entire response; see text for further details.
is the increase in O2 uptake between the second and sixth minutes of exercise; and MRTt is the mean response time for the entire response; see text for further details.
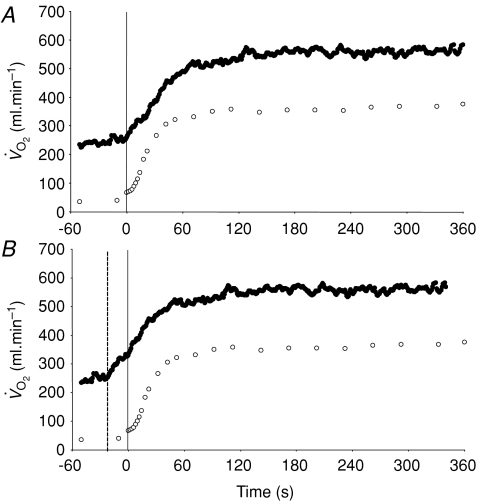
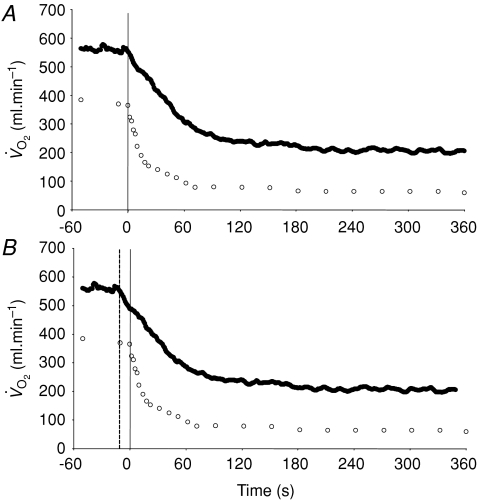
Figure 3. Group mean muscle oxygen uptake (○) and pulmonary oxygen uptake (•) across the transition to 6 min of low-intensity exercise The continuous vertical line represents the onset of exercise.
A illustrates the ‘raw’ data whereas in B the pulmonary data have been ‘time-aligned’ to the muscle data by moving the data back by a time equal to the time delay preceding the phase II increase in pulmonary oxygen uptake (dashed vertical line).
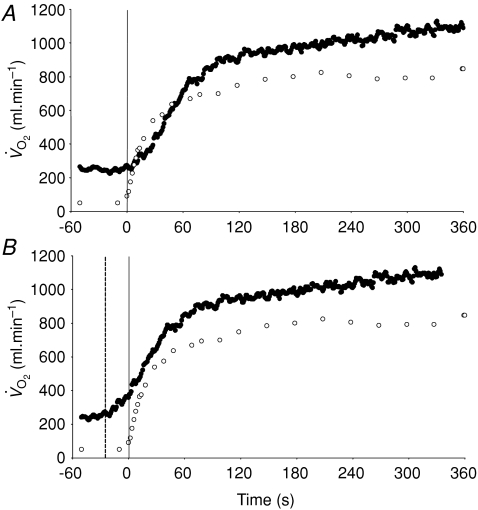
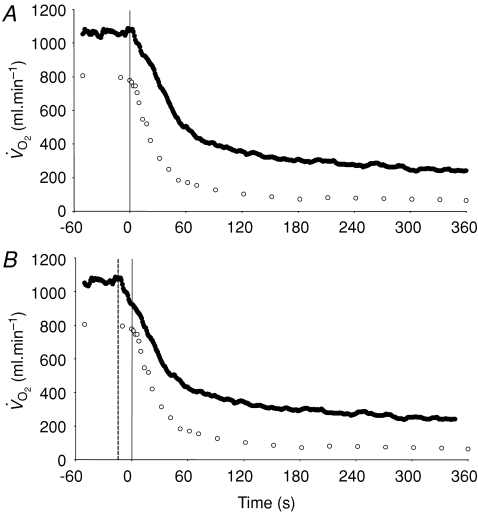
Figure 4. Group mean muscle oxygen uptake (○) and pulmonary oxygen uptake (•) across the transition to 6 min of high-intensity exercise.
The continuous vertical line represents the onset of exercise. A illustrates the ‘raw’ data whereas in B the pulmonary data have been ‘time-aligned’ to the muscle data by moving the data back by a time equal to the time delay preceding the phase II increase in pulmonary oxygen uptake (dashed vertical line).
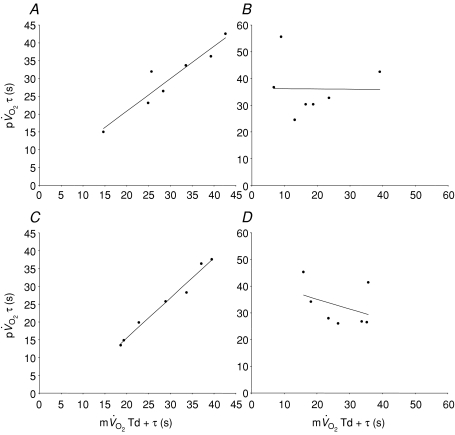
Figure 5. Pearson product moment correlation coefficients between the time constant for the phase II3 of pulmonary oxygen uptake and the mean response time for the fundamental increase in muscle oxygen uptake for low-intensity exercise (A; r= 0.95) and recovery (B; r=−0.01) and high-intensity exercise (C; r= 0.95) and recovery (D; r=−0.40).
Note the close agreement for the on-transient and the poor agreement for the off-transient.
Ap was not significantly different between the muscle and lung (Table 1) and essentially all of the increase in 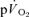 could be attributed to the increase in
could be attributed to the increase in 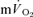 both for LI (0.30 ± 0.02 vs 0.33 ± 0.03 l min−1) and HI (0.70 ± 0.06 vs 0.69 ± 0.05 l min−1). The Ap for
both for LI (0.30 ± 0.02 vs 0.33 ± 0.03 l min−1) and HI (0.70 ± 0.06 vs 0.69 ± 0.05 l min−1). The Ap for 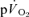 and
and 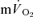 were significantly correlated both for LI exercise (r= 0.77, P < 0.05) and HI exercise (r= 0.76, P < 0.05). For HI, neither the Tds (169 ± 26 vs 152 ± 14 s) nor the As (0.15 ± 0.03 vs 0.12 ± 0.02 l min−1) were significantly different between
were significantly correlated both for LI exercise (r= 0.77, P < 0.05) and HI exercise (r= 0.76, P < 0.05). For HI, neither the Tds (169 ± 26 vs 152 ± 14 s) nor the As (0.15 ± 0.03 vs 0.12 ± 0.02 l min−1) were significantly different between 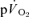 and
and 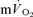 . A slow component in
. A slow component in 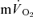 could not be confidently discerned in three subjects, but, in the remaining four subjects, 83% of the
could not be confidently discerned in three subjects, but, in the remaining four subjects, 83% of the 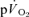 slow component could be accounted for by the
slow component could be accounted for by the 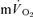 slow component. Moreover, there was no significant difference between the
slow component. Moreover, there was no significant difference between the 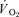 [6-2] for
[6-2] for 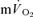 and
and 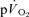 (0.13 ± 0.02 and 0.17 ± 0.04 l min−1).
(0.13 ± 0.02 and 0.17 ± 0.04 l min−1).
Off-transient responses: comparison of 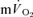 and
and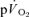 kinetics
kinetics
The group mean parameters of the 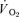 response for the off-transients of both
response for the off-transients of both 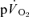 and
and 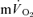 for each of the intensities are reported in Table 2 and illustrated in Figs 6 and 7. As would be expected, the baseline and end-recovery
for each of the intensities are reported in Table 2 and illustrated in Figs 6 and 7. As would be expected, the baseline and end-recovery 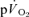 values were significantly higher than the corresponding values for
values were significantly higher than the corresponding values for 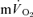 both for LI and HI (Table 2). τp was significantly longer for
both for LI and HI (Table 2). τp was significantly longer for 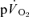 compared to
compared to 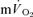 in recovery from both LI (36 ± 4 vs 18 ± 4 s; P < 0.05) and HI (33 ± 3 vs 24 ± 2 s; P < 0.01). The 95% confidence intervals (95% CI) surrounding the estimates of τp (± 3–5 s for
in recovery from both LI (36 ± 4 vs 18 ± 4 s; P < 0.05) and HI (33 ± 3 vs 24 ± 2 s; P < 0.01). The 95% confidence intervals (95% CI) surrounding the estimates of τp (± 3–5 s for 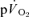 and ± 7 s for
and ± 7 s for 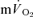 ; Table 2), did not overlap for recovery after LI but did overlap for HI. The correlations between the τp for
; Table 2), did not overlap for recovery after LI but did overlap for HI. The correlations between the τp for 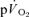 and
and 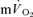 were not significant either after LI (r=−0.01) or after HI (r= 0.64). The τp for
were not significant either after LI (r=−0.01) or after HI (r= 0.64). The τp for 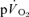 was significantly greater than the MRTp for
was significantly greater than the MRTp for 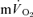 after LI (36 ± 4 vs 18 ± 4 s; P < 0.05) whereas there was no significant difference after HI (33 ± 3 vs 27 ± 3 s). The correlations between τp for
after LI (36 ± 4 vs 18 ± 4 s; P < 0.05) whereas there was no significant difference after HI (33 ± 3 vs 27 ± 3 s). The correlations between τp for 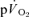 and the MRTp for
and the MRTp for 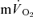 were not significant either after LI (r=−0.01) or HI (r=−0.40; Fig. 5). The overall kinetics (as reflected in MRTt) were significantly slower for
were not significant either after LI (r=−0.01) or HI (r=−0.40; Fig. 5). The overall kinetics (as reflected in MRTt) were significantly slower for 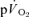 compared to
compared to 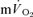 . The Ap was not significantly different between pulmonary and muscle either after LI (0.36 ± 0.02 vs 0.31 ± 0.03 l min−1) or after HI (0.75 ± 0.05 vs 0.72 ± 0.06 l min−1).
. The Ap was not significantly different between pulmonary and muscle either after LI (0.36 ± 0.02 vs 0.31 ± 0.03 l min−1) or after HI (0.75 ± 0.05 vs 0.72 ± 0.06 l min−1).
Table 2.
Muscle and pulmonary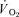 kinetics in the recovery from low-intensity and high-intensity knee-extensor exercise
kinetics in the recovery from low-intensity and high-intensity knee-extensor exercise
 |
 |
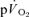 |
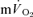 |
|
|---|---|---|---|---|
 (l min−1) (l min−1) |
0.55 ± 0.02* | 0.38 ± 0.03* | 1.07 ± 0.05* | 0.79 ± 0.07 |
| Tdp (s) | 11 ± 3* | 0 ± 2 | 14 ± 3* | 3 ± 3 |
| τp (s) | 36 ± 4* | 18 ± 4 | 33 ± 3* | 24 ± 2 |
| 95% CI (s) | 3 ± 0 | 7 ± 3 | 5 ± 3 | 7 ± 2 |
| Ap (l min−1) | 0.36 ± 0.02 | 0.31 ± 0.03 | 0.75 ± 0.05 | 0.72 ± 0.06 |
| Gp (ml min−1 W−1) | 9.6 ± 0.7* | 8.3 ± 0.8 | 10.6 ± 0.7 | 10.2 ± 0.9 |
| Tds (s) | — | — | 151 ± 19 | — |
| As′ (l min−1) | — | — | 0.05 ± 0.01 | — |
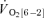 (l min−1) (l min−1) |
— | — | 0.11 ± 0.02* | 0.06 ± 0.02 |
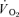 (l min−1) (l min−1) |
0.20 ± 0.01* | 0.08 ± 0.02 | 0.27 ± 0.07* | 0.08 ± 0.01 |
| MRTt (s) | 54 ± 4* | 13 ± 2 | 56 ± 3* | 35 ± 8 |
Significantly different (P < 0.05) from corresponding value for 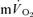 . Tdp, τp and Ap represent the time delay, time constant and amplitude terms, respectively, for the fundamental component, and Tds and As′ represent the time delay and amplitude terms, respectively, for the slow component of muscle and pulmonary O2 uptake (see eqns (4) and (5) and associated text). Note that the Tdp is a model parameter that does not necessarily reflect the duration of ‘phase I’. 95% CI is the 95% confidence interval surrounding the estimation of the corresponding time constant; Gp is the response gain of the fundamental component (
. Tdp, τp and Ap represent the time delay, time constant and amplitude terms, respectively, for the fundamental component, and Tds and As′ represent the time delay and amplitude terms, respectively, for the slow component of muscle and pulmonary O2 uptake (see eqns (4) and (5) and associated text). Note that the Tdp is a model parameter that does not necessarily reflect the duration of ‘phase I’. 95% CI is the 95% confidence interval surrounding the estimation of the corresponding time constant; Gp is the response gain of the fundamental component (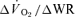 );
); 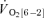 is the increase in O2 uptake between the second and sixth minutes of exercise; and MRTt is the mean response time for the entire response; see text for further details.
is the increase in O2 uptake between the second and sixth minutes of exercise; and MRTt is the mean response time for the entire response; see text for further details.
Figure 6. Group mean muscle oxygen uptake (○) and pulmonary oxygen uptake (•) in the recovery from low-intensity exercise.
The continuous vertical line represents the end of exercise. A illustrates the ‘raw’ data whereas in B the pulmonary data have been ‘time-aligned’ to the muscle data by moving the data back by a time equal to the time delay preceding the phase II decrease in pulmonary oxygen uptake (dashed vertical line).
Figure 7. Group mean muscle oxygen uptake (○) and pulmonary oxygen uptake (•) in the recovery from high-intensity exercise.
The continuous vertical line represents the end of exercise. A illustrates the ‘raw’ data whereas in B the pulmonary data have been ‘time-aligned’ to the muscle data by moving the data back by a time equal to the time delay preceding the phase II decrease in pulmonary oxygen uptake (dashed vertical line).
The τp was not significantly different between LI exercise and HI exercise for either 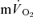 (LI: 26 ± 3 vs HI: 25 ± 4 s) or
(LI: 26 ± 3 vs HI: 25 ± 4 s) or 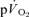 (LI: 30 ± 3 vs HI: 32 ± 3 s), (Tables 1 and 2). For the off-transients, the τp was not significantly different between LI exercise and HI exercise for either
(LI: 30 ± 3 vs HI: 32 ± 3 s), (Tables 1 and 2). For the off-transients, the τp was not significantly different between LI exercise and HI exercise for either 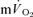 (LI: 18 ± 4 vs HI: 24 ± 2 s) or
(LI: 18 ± 4 vs HI: 24 ± 2 s) or 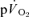 (LI: 36 ± 4 vs HI: 33 ± 3 s) (Tables 1 and 2). There was no significant difference between the τp in the on-transient compared to the off-transient for
(LI: 36 ± 4 vs HI: 33 ± 3 s) (Tables 1 and 2). There was no significant difference between the τp in the on-transient compared to the off-transient for 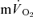 or
or 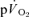 at either exercise intensity (Tables 1 and 2). The
at either exercise intensity (Tables 1 and 2). The 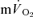 and
and 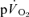 responses of a representative subject are shown for LI and HI in Figs 8 and 9, respectively.
responses of a representative subject are shown for LI and HI in Figs 8 and 9, respectively.
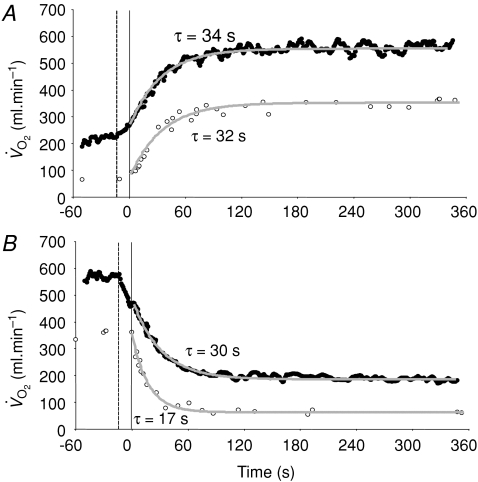
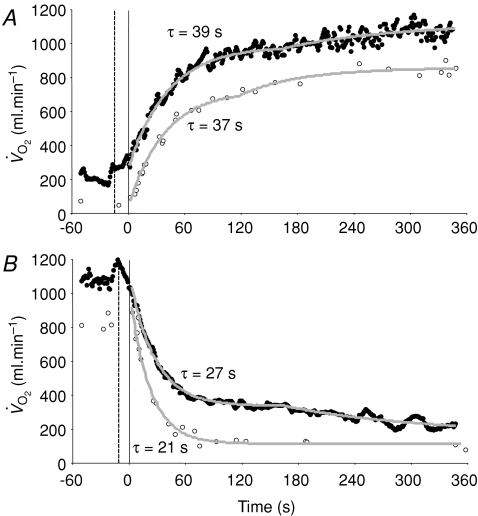
Figure 8. Muscle (○) and pulmonary (•) oxygen uptake responses to LI exercise (A) and subsequent recovery (B), with corresponding model fits and time constant values shown.
The pulmonary data have been ‘time-aligned’ to the muscle data by moving the data back by a time equal to the time delay preceding the phase II decrease in pulmonary oxygen uptake (dashed vertical line).
Figure 9. Muscle (○) and pulmonary (•) oxygen uptake responses to HI exercise (A) and subsequent recovery (B), with corresponding model fits and time constant values shown.
The pulmonary data have been ‘time-aligned’ to the muscle data by moving the data back by a time equal to the time delay preceding the phase II decrease in pulmonary oxygen uptake (dashed vertical line).
Discussion
The major finding of the present investigation was that the τ for 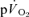 in phase II reflected
in phase II reflected 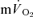 kinetics following the onset of both LI and HI knee-extensor exercise. In contrast, in recovery, no relationships between
kinetics following the onset of both LI and HI knee-extensor exercise. In contrast, in recovery, no relationships between 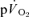 and
and 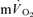 kinetics were observed. The amplitude terms for
kinetics were observed. The amplitude terms for 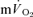 and
and 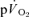 were not significantly different at either intensity, indicating that other tissues are contributing little to
were not significantly different at either intensity, indicating that other tissues are contributing little to 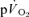 during knee-extensor exercise. The capillary-to-lung time to appearance was estimated to be 12 s during passive exercise and 7 and 6 s after 5 s of exercise in LI and HI, respectively. Even with the inclusion of a ∼4 s delay in
during knee-extensor exercise. The capillary-to-lung time to appearance was estimated to be 12 s during passive exercise and 7 and 6 s after 5 s of exercise in LI and HI, respectively. Even with the inclusion of a ∼4 s delay in 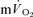 , the findings suggest that the contracting muscles are beginning to contribute to the
, the findings suggest that the contracting muscles are beginning to contribute to the 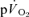 response within the first 20 s of exercise. The estimated mean time from the muscle capillaries to the lung was 17 s just before exercise and 10–12 s after 5 s of exercise, giving an average muscle-to-lung time delay in the initial phase of exercise of ∼15 s. This value is rather similar to the 15–20 s which is attributed to the phase I increase in
response within the first 20 s of exercise. The estimated mean time from the muscle capillaries to the lung was 17 s just before exercise and 10–12 s after 5 s of exercise, giving an average muscle-to-lung time delay in the initial phase of exercise of ∼15 s. This value is rather similar to the 15–20 s which is attributed to the phase I increase in 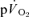 and frequently excluded from analysis when the goal is to estimate
and frequently excluded from analysis when the goal is to estimate 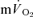 kinetics (e.g. Gerbino et al. 1996; Brittain et al. 2001; Koppo et al. 2004; Jones et al. 2004; Gurd et al. 2006). Overall, the data indicate that, with appropriate consideration of the phase I response,
kinetics (e.g. Gerbino et al. 1996; Brittain et al. 2001; Koppo et al. 2004; Jones et al. 2004; Gurd et al. 2006). Overall, the data indicate that, with appropriate consideration of the phase I response, 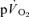 kinetics closely reflect
kinetics closely reflect 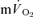 kinetics during LI and HI exercise, but not during subsequent recovery.
kinetics during LI and HI exercise, but not during subsequent recovery.
Although 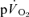 kinetics is frequently used to provide a non-invasive window on muscle oxidative metabolism during exercise, relatively few studies have simultaneously measured
kinetics is frequently used to provide a non-invasive window on muscle oxidative metabolism during exercise, relatively few studies have simultaneously measured 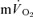 and
and  kinetics during exercise and none have done so during subsequent recovery. In the present study, we measured
kinetics during exercise and none have done so during subsequent recovery. In the present study, we measured 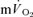 and
and 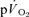 simultaneously in an isolated muscle model during both GETli and GEThi exercise and subsequent recovery, and we employed multiple rest–exercise–rest transitions (4 for
simultaneously in an isolated muscle model during both GETli and GEThi exercise and subsequent recovery, and we employed multiple rest–exercise–rest transitions (4 for 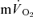 and 5–10 for
and 5–10 for 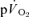 ) to reduce the 95% CI surrounding the estimation of τ (to ∼± 3–7 s) and enhance confidence in our descriptions of the kinetics of
) to reduce the 95% CI surrounding the estimation of τ (to ∼± 3–7 s) and enhance confidence in our descriptions of the kinetics of 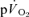 and
and 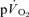 . The data show that the
. The data show that the 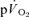 τp provides an acceptably close estimate (i.e. to within approximately 10%) of the kinetics of
τp provides an acceptably close estimate (i.e. to within approximately 10%) of the kinetics of 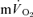 following the onset of exercise. For LI exercise, although the
following the onset of exercise. For LI exercise, although the 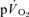 τp was significantly greater than the
τp was significantly greater than the 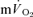 τp (30 vs 26 s), when the time delay preceding the increase in
τp (30 vs 26 s), when the time delay preceding the increase in 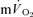 was taken into account through calculation of the
was taken into account through calculation of the 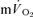 MRTp, the values were identical. In addition, the
MRTp, the values were identical. In addition, the 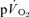 τp was significantly correlated with both the
τp was significantly correlated with both the 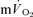 τp (r= 0.94) and the
τp (r= 0.94) and the 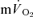 MRTp (r= 0.95). For HI, the
MRTp (r= 0.95). For HI, the 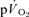 τp was significantly greater than the
τp was significantly greater than the 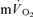 τp but the difference was reduced when the
τp but the difference was reduced when the 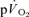 τp was compared to the
τp was compared to the 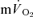 MRTp (32 vs 29 s; P < 0.05). Again, the
MRTp (32 vs 29 s; P < 0.05). Again, the 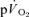 τp was significantly correlated with both the
τp was significantly correlated with both the 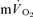 τp (r= 0.94) and the
τp (r= 0.94) and the 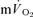 MRTp (r= 0.95).
MRTp (r= 0.95).
The conclusion that the 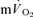 and
and 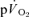 τp values were functionally identical is reinforced by the finding that the 95% CI values (∼± 4 s for
τp values were functionally identical is reinforced by the finding that the 95% CI values (∼± 4 s for 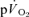 and ∼± 6 s for
and ∼± 6 s for 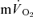 ) overlapped for both LI and HI. In agreement, Koga et al. (2005) reported that the τp for
) overlapped for both LI and HI. In agreement, Koga et al. (2005) reported that the τp for 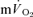 kinetics (estimated from Doppler measures of leg blood flow and measurements of the O2 content of the femoral vein) was not significantly different from the τp for
kinetics (estimated from Doppler measures of leg blood flow and measurements of the O2 content of the femoral vein) was not significantly different from the τp for 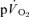 kinetics during GEThi knee-extension exercise (group mean τp, 26 and 30 s, respectively). However, these authors did not attempt to account for transit delays between the femoral artery and the muscle capillaries or between the capillaries and the venous blood collection site but simply compared the τp values for the exponential increases in
kinetics during GEThi knee-extension exercise (group mean τp, 26 and 30 s, respectively). However, these authors did not attempt to account for transit delays between the femoral artery and the muscle capillaries or between the capillaries and the venous blood collection site but simply compared the τp values for the exponential increases in 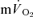 and
and 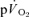 . Similarly, Grassi et al. (1996) reported that the τp for
. Similarly, Grassi et al. (1996) reported that the τp for 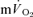 and
and 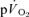 kinetics was not significantly different (group mean τp, 36 and 32 s, respectively) during GETli cycle exercise in trained subjects. In this study, the authors reported a long time delay (∼10–15 s) before
kinetics was not significantly different (group mean τp, 36 and 32 s, respectively) during GETli cycle exercise in trained subjects. In this study, the authors reported a long time delay (∼10–15 s) before 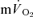 began to increase but transit delays were not appropriately corrected (Bangsbo et al. 2000).
began to increase but transit delays were not appropriately corrected (Bangsbo et al. 2000).
To our knowledge, the present investigation is the first to simultaneously measure 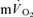 and
and 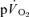 during recovery from exercise. The
during recovery from exercise. The 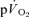 kinetics in recovery are often used to provide insight into changes in muscle oxidative metabolism following the termination of exercise (Gerbino et al. 1996; Barstow et al. 2000; Cunningham et al. 2000; Brittain et al. 2001). However, the present study demonstrates that no relationship exists between
kinetics in recovery are often used to provide insight into changes in muscle oxidative metabolism following the termination of exercise (Gerbino et al. 1996; Barstow et al. 2000; Cunningham et al. 2000; Brittain et al. 2001). However, the present study demonstrates that no relationship exists between 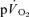 and
and 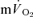 kinetics during recovery from exercise. For LI, the
kinetics during recovery from exercise. For LI, the 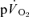 τp was significantly greater than both the
τp was significantly greater than both the 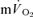 τp and the
τp and the 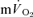 MRTp, whereas for HI, the
MRTp, whereas for HI, the 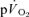 τp was significantly greater than the
τp was significantly greater than the 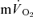 τp but not the
τp but not the 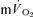 MRTp (mean difference of 6 s). The 95% CI's did not overlap for the recovery from LI (in which the
MRTp (mean difference of 6 s). The 95% CI's did not overlap for the recovery from LI (in which the 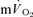 kinetics were surprisingly fast), but did overlap for the recovery from HI exercise. The correlations between the
kinetics were surprisingly fast), but did overlap for the recovery from HI exercise. The correlations between the 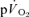 τp and the
τp and the 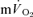 τp and MRT τp were non-significant both for LI exercise and HI exercise. Collectively, these data question the practice of using
τp and MRT τp were non-significant both for LI exercise and HI exercise. Collectively, these data question the practice of using 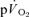 kinetics to reflect
kinetics to reflect 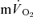 kinetics in the recovery from exercise. An explanation for the disparity between
kinetics in the recovery from exercise. An explanation for the disparity between 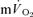 and
and 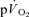 kinetics during recovery may be that the energy turnover in the muscle decreases rapidly following the cessation of exercise whereas energy turnover in the rest of the body remains higher for longer due to the effects on metabolism of elevated core temperature, lactate clearance and/or muscle or hepatic gluconeogenesis, pulmonary ventilation and cardiac work (Gaesser & Brooks, 1984). Our data might be considered to be inconsistent with those of Rossiter et al. (2002) who reported close agreement between the muscle [PCr] (used as a proxy for
kinetics during recovery may be that the energy turnover in the muscle decreases rapidly following the cessation of exercise whereas energy turnover in the rest of the body remains higher for longer due to the effects on metabolism of elevated core temperature, lactate clearance and/or muscle or hepatic gluconeogenesis, pulmonary ventilation and cardiac work (Gaesser & Brooks, 1984). Our data might be considered to be inconsistent with those of Rossiter et al. (2002) who reported close agreement between the muscle [PCr] (used as a proxy for 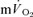 ) and
) and 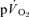 kinetics during both exercise and recovery. It is difficult to provide an explanation for the discrepancy in the results of these two studies, although it cannot be ruled out that the normally close relationship between muscle [PCr] and
kinetics during both exercise and recovery. It is difficult to provide an explanation for the discrepancy in the results of these two studies, although it cannot be ruled out that the normally close relationship between muscle [PCr] and 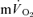 kinetics is dissociated in the recovery from exercise. In this regard, it is interesting to note that longer [PCr] kinetics in the recovery from exercise are predicted by the model of muscle energy balance proposed by Kushmerick (1998) in which slower recovery kinetics are considered to be a consequence of alterations in forward and backward creatine kinase flux rates.
kinetics is dissociated in the recovery from exercise. In this regard, it is interesting to note that longer [PCr] kinetics in the recovery from exercise are predicted by the model of muscle energy balance proposed by Kushmerick (1998) in which slower recovery kinetics are considered to be a consequence of alterations in forward and backward creatine kinase flux rates.
An important purpose of the present investigation was to estimate the mean transit time from the muscle capillaries to the lung during exercise and recovery. It should be noted that while the transit time from the capillaries to the femoral vein has been well studied to account for approximately 2/3 of the transit time from the femoral artery to femoral vein, the blood transit time from the femoral vein to the lungs assumed to be 2/3 of the transit time from the femoral vein to the femoral artery is more uncertain, since it is based on calculations of the volume of the venous and arterial side. The estimated time from the muscle capillaries to the lung was 17 s just before exercise and 10–12 s after 5 s of exercise. If an ∼4 s delay in 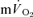 is included, the muscle-to-lung time delay is therefore rather similar to the 15–20 s which is often attributed to the phase I increase in
is included, the muscle-to-lung time delay is therefore rather similar to the 15–20 s which is often attributed to the phase I increase in 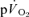 . However, based on estimated capillary-to-lung time to appearance it is likely that deoxygenated blood from the exercising limbs begins to arrive at the lung after 10–12 s of exercise. When the goal is to use the
. However, based on estimated capillary-to-lung time to appearance it is likely that deoxygenated blood from the exercising limbs begins to arrive at the lung after 10–12 s of exercise. When the goal is to use the 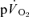 response in phase II to estimate
response in phase II to estimate 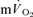 kinetics, it is important that the curve-fitting procedure is not distorted by the inclusion of any phase I data (Whipp & Rossiter, 2005). Because both the
kinetics, it is important that the curve-fitting procedure is not distorted by the inclusion of any phase I data (Whipp & Rossiter, 2005). Because both the 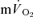 and phase II
and phase II 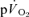 responses are well described by a mono-exponential function, the omission from the model fit of several seconds of
responses are well described by a mono-exponential function, the omission from the model fit of several seconds of 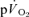 data which might potentially include a contribution from
data which might potentially include a contribution from 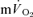 is preferable to including data that are not exclusively in the phase II region since this will distort the curve fit and result in erroneous τp values. It should be cautioned, however, that the muscle-to-lung transit delay is likely to be appreciably shorter during more intense exercise (Bangsbo et al. 2000) with corresponding effects on the duration of phase I and implications for the approach taken to modelling the phase II
is preferable to including data that are not exclusively in the phase II region since this will distort the curve fit and result in erroneous τp values. It should be cautioned, however, that the muscle-to-lung transit delay is likely to be appreciably shorter during more intense exercise (Bangsbo et al. 2000) with corresponding effects on the duration of phase I and implications for the approach taken to modelling the phase II 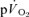 kinetics (Barstow et al. 1990; Wilkerson et al. 2006). In the immediate period following the cessation of exercise, the muscle-to-lung transit delay is shorter than is the case at the onset of exercise and the duration of phase I in the
kinetics (Barstow et al. 1990; Wilkerson et al. 2006). In the immediate period following the cessation of exercise, the muscle-to-lung transit delay is shorter than is the case at the onset of exercise and the duration of phase I in the 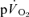 response during recovery (which will still represent a conflation of immediate changes in pulmonary blood flow and the blunted arrival of deoxygenated blood at the lung) should also be expected to be shorter.
response during recovery (which will still represent a conflation of immediate changes in pulmonary blood flow and the blunted arrival of deoxygenated blood at the lung) should also be expected to be shorter.
The fundamental component amplitudes of the 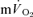 and
and 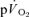 responses in the transition from rest to exercise and from exercise to subsequent recovery were not significantly different for either LI or HI exercise, indicating that the changes in
responses in the transition from rest to exercise and from exercise to subsequent recovery were not significantly different for either LI or HI exercise, indicating that the changes in 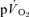 from the relevant baseline are almost entirely due to changes in
from the relevant baseline are almost entirely due to changes in 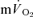 during the single-leg knee-extension exercise employed in the present study. Consistent with this, the relatively low rates of pulmonary ventilation elicited by the exercise (∼18 and 35 l min−1 during LI and HI, respectively) would not be expected to contribute significantly to whole-body
during the single-leg knee-extension exercise employed in the present study. Consistent with this, the relatively low rates of pulmonary ventilation elicited by the exercise (∼18 and 35 l min−1 during LI and HI, respectively) would not be expected to contribute significantly to whole-body 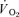 (Aaron et al. 1992). Koga et al. (2005) also reported no significant difference between the fundamental component amplitudes of the estimated
(Aaron et al. 1992). Koga et al. (2005) also reported no significant difference between the fundamental component amplitudes of the estimated 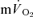 and
and 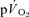 responses during high-intensity two-legged knee-extension exercise, with the increase in
responses during high-intensity two-legged knee-extension exercise, with the increase in 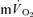 making a ∼95% contribution to the increased
making a ∼95% contribution to the increased 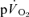 . Over a wide range of sub-maximal work rates during upright cycle ergometer exercise,
. Over a wide range of sub-maximal work rates during upright cycle ergometer exercise, 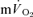 makes ∼85–90% contribution to the measured
makes ∼85–90% contribution to the measured 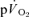 due to the greater proportional contribution on the extra-muscular ‘support’ process such as the increased O2 cost of ventilatory and cardiac work in this mode of exercise (Poole et al. 1992).
due to the greater proportional contribution on the extra-muscular ‘support’ process such as the increased O2 cost of ventilatory and cardiac work in this mode of exercise (Poole et al. 1992).
During exercise performed above the GET, a delayed-onset ‘slow component’ of the 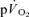 kinetics has been identified which elevates
kinetics has been identified which elevates 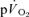 to values that are higher than would be predicted for the work rate (Whipp & Wasserman, 1972; Barstow & Molé, 1991; Barstow et al. 1996). While the mechanistic bases for this phenomenon have not been entirely resolved (Krustrup et al. 2004b; Jones & Poole, 2005; Zoladz et al. 2008), there is evidence that the
to values that are higher than would be predicted for the work rate (Whipp & Wasserman, 1972; Barstow & Molé, 1991; Barstow et al. 1996). While the mechanistic bases for this phenomenon have not been entirely resolved (Krustrup et al. 2004b; Jones & Poole, 2005; Zoladz et al. 2008), there is evidence that the 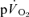 slow component is chiefly determined by processes intrinsic to the contracting muscles which result in a progressive loss of muscle efficiency (Poole et al. 1991; Rossiter et al. 2002; Krustrup et al. 2004b,c, 2008). Consistent with this view, ∼80% of the
slow component is chiefly determined by processes intrinsic to the contracting muscles which result in a progressive loss of muscle efficiency (Poole et al. 1991; Rossiter et al. 2002; Krustrup et al. 2004b,c, 2008). Consistent with this view, ∼80% of the 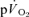 slow component could be attributed to a similar slow component in
slow component could be attributed to a similar slow component in 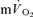 in the present study. This finding is in keeping with previous studies which have suggested that the
in the present study. This finding is in keeping with previous studies which have suggested that the 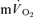 slow component contributes ∼85% to the
slow component contributes ∼85% to the 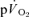 slow component during two-legged knee-extension exercise (Koga et al. 2005) and cycle ergometer exercise (Poole et al. 1991). In addition, neither the time delay prior to the
slow component during two-legged knee-extension exercise (Koga et al. 2005) and cycle ergometer exercise (Poole et al. 1991). In addition, neither the time delay prior to the 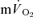 and
and 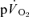 slow components becoming manifest, nor the change in
slow components becoming manifest, nor the change in 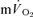 and
and 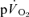 between 2 and 6 min, were significantly different in our study. The data therefore indicate that the
between 2 and 6 min, were significantly different in our study. The data therefore indicate that the 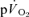 slow component closely corresponds to metabolic changes occurring within the contracting skeletal muscle fibres (Poole et al. 1991; Krustrup et al. 2004b,c; Rossiter et al. 2002). It is of note, however, that in our study, the
slow component closely corresponds to metabolic changes occurring within the contracting skeletal muscle fibres (Poole et al. 1991; Krustrup et al. 2004b,c; Rossiter et al. 2002). It is of note, however, that in our study, the 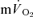 slow component could only be confidently determined using the exponential model fits in 4 of the 7 subjects. One explanation for this is the relatively low intensity of exercise employed. A slow component in
slow component could only be confidently determined using the exponential model fits in 4 of the 7 subjects. One explanation for this is the relatively low intensity of exercise employed. A slow component in 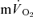 has been clearly demonstrated at higher exercise intensities (Bangsbo et al. 2000; Krustrup et al. 2004b). Another explanation is the relatively small number of blood samples that were drawn over the latter minutes of HI exercise which might have made it more difficult to fit an exponential function to the data. The good agreement between the change in
has been clearly demonstrated at higher exercise intensities (Bangsbo et al. 2000; Krustrup et al. 2004b). Another explanation is the relatively small number of blood samples that were drawn over the latter minutes of HI exercise which might have made it more difficult to fit an exponential function to the data. The good agreement between the change in 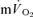 and
and 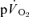 between 2 and 6 min of HI exercise indicates, however, that the slow component in
between 2 and 6 min of HI exercise indicates, however, that the slow component in 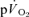 originated in the contracting muscles.
originated in the contracting muscles.
In conclusion, the kinetics of 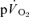 (including the amplitude and time constant of the fundamental, phase II, response) provide a faithful reflection of the corresponding kinetics of
(including the amplitude and time constant of the fundamental, phase II, response) provide a faithful reflection of the corresponding kinetics of 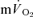 following the onset of both low-intensity and high-intensity knee-extension exercise. The mean response time from the muscle capillaries to the lung was ∼17 s just before exercise and ∼12 s and ∼10 s for low-intensity and high-intensity exercise, respectively, after 5 s of exercise. Apparently, the arrival of deoxygenated blood from the contracting muscles makes a contribution to
following the onset of both low-intensity and high-intensity knee-extension exercise. The mean response time from the muscle capillaries to the lung was ∼17 s just before exercise and ∼12 s and ∼10 s for low-intensity and high-intensity exercise, respectively, after 5 s of exercise. Apparently, the arrival of deoxygenated blood from the contracting muscles makes a contribution to 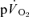 within the first 15–20 s of exercise at these intensities, but the contribution is quantitatively small such that removal of this phase from consideration does not distort the fidelity of the relationship between
within the first 15–20 s of exercise at these intensities, but the contribution is quantitatively small such that removal of this phase from consideration does not distort the fidelity of the relationship between 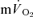 kinetics and phase II
kinetics and phase II 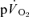 kinetics. In recovery, however, no relationship between
kinetics. In recovery, however, no relationship between 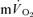 and
and 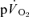 kinetics was observed. Thus, caution should be applied when
kinetics was observed. Thus, caution should be applied when 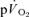 kinetics are used to estimate
kinetics are used to estimate 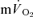 kinetics following the cessation of exercise.
kinetics following the cessation of exercise.
Acknowledgments
We thank the subjects for their committed participation. The excellent technical assistance of Winnie Taagerup, Ingelise Kring and Jens Jung Nielsen is greatly appreciated. The study was supported by the Danish Ministry of Culture (Kulturministeriets Udvalg for Idrætsforskning).
Glossary
Abbreviations
- A
amplitude
- CI
confidence interval
- G
gain
- MRT
mean response time
- MTTa-v
mean artery-to-vein transit time
- MTTv-a
mean vein-to-artery transit time
- MTTc-l
mean capillary-to-lung transit time
- TAPa-v
femoral artery-to-vein time to appearance
- TAPv-a
femoral vein-to-artery time to appearance
- TAPc-l
capillary-to-lung time to appearance
- Td
time delay
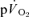
pulmonary oxygen uptake
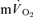
muscular oxygen uptake
Author contributions
The experiment was performed at the Department of Exercise and Sport Sciences, University of Copenhagen, Copenhagen, Denmark. P. Krustrup, A.M. Jones, J.A.L. Calbet and J. Bangsbo designed the study. All authors conducted the main experiments. J.A.L. Calbet catheterised the subjects. P. Krustrup and J. Bangsbo analysed the muscle data and collected multiple-transition pulmonary data. D.P. Wilkerson and A.M. Jones analysed the pulmonary data and carried out the mathematical modelling. P. Krustrup and A.M. Jones wrote the first draft of the manuscript. All authors developed the manuscript and approved the final version of the manuscript.
References
- Aaron EA, Johnson BD, Seow CK, Dempsey JA. Oxygen cost of exercise hyperpnea: measurement. J Appl Physiol. 1992;72:1810–1817. doi: 10.1152/jappl.1992.72.5.1810. [DOI] [PubMed] [Google Scholar]
- Andersen P, Adams RP, Sjøgaard G, Thorboe A, Saltin B. Dynamic knee extension as a model for the study of an isolated exercising muscle in man. J Appl Physiol. 1985;59:1647–1653. doi: 10.1152/jappl.1985.59.5.1647. [DOI] [PubMed] [Google Scholar]
- Andersen P, Saltin B. Maximal perfusion of skeletal muscle in man. J Physiol. 1985;366:233–249. doi: 10.1113/jphysiol.1985.sp015794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bangsbo J, Gollnick PD, Graham TE, Juel C, Kiens B, Mizuno M, Saltin B. Anaerobic energy production and O2 deficit-debt relationship during exhaustive exercise in humans. J Physiol. 1990;422:539–559. doi: 10.1113/jphysiol.1990.sp018000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bangsbo J, Krustrup P, González-Alonso J, Boushel R, Saltin B. Muscle oxygen uptake kinetics at onset of intense dynamic exercise. Am J Physiol Regul Integr Comp Physiol. 2000;279:R899–R906. doi: 10.1152/ajpregu.2000.279.3.R899. [DOI] [PubMed] [Google Scholar]
- Barstow TJ, Jones AM, Nguyen PH, Casabury R. Influence of muscle fiber type and pedal frequency on oxygen uptake kinetics of heavy exercise. J Appl Physiol. 1996;81:1624–1650. doi: 10.1152/jappl.1996.81.4.1642. [DOI] [PubMed] [Google Scholar]
- Barstow TJ, Lamarra N, Whipp BJ. Modulation of muscle and pulmonary O2 uptakes by circulatory dynamics during exercise. J Appl Physiol. 1990;68:979–989. doi: 10.1152/jappl.1990.68.3.979. [DOI] [PubMed] [Google Scholar]
- Barstow TJ, Molé PA. Linear and nonlinear characteristics of oxygen uptake kinetics during heavy exercise. J Appl Physiol. 1991;71:2099–2106. doi: 10.1152/jappl.1991.71.6.2099. [DOI] [PubMed] [Google Scholar]
- Barstow TJ, Scremin AM, Mutton DL, Kunkel CF, Cagle TG, Whipp BJ. Peak and kinetic cardiorespiratory responses during arm and leg exercise in patients with spinal cord injury. Spinal Cord. 2000;38:340–345. doi: 10.1038/sj.sc.3101014. [DOI] [PubMed] [Google Scholar]
- Beaver WL, Lamarra N, Wasserman K. Breath-by-breath measurement of true alveolar gas exchange. J Appl Physiol. 1981;51:1662–1675. doi: 10.1152/jappl.1981.51.6.1662. [DOI] [PubMed] [Google Scholar]
- Brittain CJ, Rossiter HB, Kowalchuk JM, Whipp BJ. Effect of prior metabolic rate on the kinetics of oxygen uptake during moderate-intensity exercise. Eur J Appl Physiol. 2001;86:125–134. doi: 10.1007/s004210100514. [DOI] [PubMed] [Google Scholar]
- Burnley M, Doust JH, Jones AM. Effects of prior heavy exercise, prior sprint exercise and passive warming on oxygen uptake kinetics during heavy exercise in humans. Eur J Appl Physiol. 2002;87:424–432. doi: 10.1007/s00421-002-0647-8. [DOI] [PubMed] [Google Scholar]
-
Burnley M, Doust JH, Jones AM. Time required for the restoration of normal heavy exercise
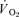 kinetics following prior heavy exercise. J Appl Physiol. 2006;101:1320–1327. doi: 10.1152/japplphysiol.00475.2006. [DOI] [PubMed] [Google Scholar]
kinetics following prior heavy exercise. J Appl Physiol. 2006;101:1320–1327. doi: 10.1152/japplphysiol.00475.2006. [DOI] [PubMed] [Google Scholar] - Chin LM, Leigh RJ, Heigenhauser GJ, Rossiter HB, Paterson DH, Kowalchuk JM. Hyperventilation-induced hypocapnic alkalosis slows the adaptation of pulmonary O2 uptake during the transition to moderate-intensity exercise. J Physiol. 2007;583:351–364. doi: 10.1113/jphysiol.2007.132837. [DOI] [PMC free article] [PubMed] [Google Scholar]
-
Cunningham DA, Croix CM, Paterson DH, Özyener F, Whipp BJ. The off-transient pulmonary oxygen uptake (
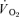 ) kinetics following attainment of a particular
) kinetics following attainment of a particular 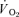 during heavy-intensity exercise in humans. Exp Physiol. 2000;85:339–347. [PubMed] [Google Scholar]
during heavy-intensity exercise in humans. Exp Physiol. 2000;85:339–347. [PubMed] [Google Scholar] - Gaesser GA, Brooks GA. Metabolic bases of excess post-exercise oxygen consumption: a review. Med Sci Sports Exerc. 1984;16:29–43. [PubMed] [Google Scholar]
- Gerbino A, Ward SA, Whipp BJ. Effects of prior exercise on pulmonary gas-exchange kinetics during high-intensity exercise in humans. J Appl Physiol. 1996;80:99–107. doi: 10.1152/jappl.1996.80.1.99. [DOI] [PubMed] [Google Scholar]
- González-Alonso J, Quistorff B, Krustrup P, Bangsbo J, Saltin B. Heat production in human skeletal muscle at the onset of intense dynamic exercise. J Physiol. 2000;524:603–615. doi: 10.1111/j.1469-7793.2000.00603.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grassi B, Marconi C, Meyer M, Rieu M, Cerretelli P. Gas exchange and cardiovascular kinetics with different exercise protocols in heart transplant recipients. J Appl Physiol. 1997;82:1952–1962. doi: 10.1152/jappl.1997.82.6.1952. [DOI] [PubMed] [Google Scholar]
- Grassi B, Poole DC, Richardson RS, Knight DR, Erickson BK, Wagner PD. Muscle O2 uptake kinetics in humans: implications for metabolic control. J Appl Physiol. 1996;80:988–998. doi: 10.1152/jappl.1996.80.3.988. [DOI] [PubMed] [Google Scholar]
- Gurd BJ, Peters SJ, Heigenhauser GJ, Leblanc PJ, Doherty TJ, Paterson DH, Kowalchuk JM. Prior heavy exercise elevates pyruvate dehydrogenase activity and speeds O2 uptake kinetics during subsequent moderate-intensity exercise in healthy young adults. J Physiol. 2006;577:985–996. doi: 10.1113/jphysiol.2006.112706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones AM, Poole DC. Oxygen uptake dynamics: from muscle to mouth – an introduction to the symposium. Med Sci Sports Exerc. 2005;37:1542–1550. doi: 10.1249/01.mss.0000177466.01232.7e. [DOI] [PubMed] [Google Scholar]
- Jones AM, Wilkerson DP, Wilmshurst S, Campbell IT. Influence of L-NAME on pulmonary O2 uptake kinetics during heavy-intensity cycle exercise. J Appl Physiol. 2004;96:1033–1038. doi: 10.1152/japplphysiol.00381.2003. [DOI] [PubMed] [Google Scholar]
- Koga S, Poole DC, Shiojiri T, Kondo N, Fukuba Y, Miura A, Barstow TJ. Comparison of oxygen uptake kinetics during knee extension and cycle exercise. Am J Physiol Regul Integr Comp Physiol. 2005;288:R212–R220. doi: 10.1152/ajpregu.00147.2004. [DOI] [PubMed] [Google Scholar]
-
Koppo K, Bouckaert J, Jones AM. Effects of training status and exercise intensity on phase II
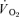 kinetics. Med Sci Sports Exerc. 2004;36:225–232. doi: 10.1249/01.MSS.0000113473.48220.20. [DOI] [PubMed] [Google Scholar]
kinetics. Med Sci Sports Exerc. 2004;36:225–232. doi: 10.1249/01.MSS.0000113473.48220.20. [DOI] [PubMed] [Google Scholar] - Krustrup P. Denmark: University of Copenhagen; Muscle oxygen uptake and energy turnover during dynamic exercise in humans PhD thesis. ISBN: 87-89361-87-3. [Google Scholar]
- Krustrup P, Hellsten Y, Bangsbo J. Intense interval training enhances human skeletal muscle oxygen uptake in the intial phase of exercise at high but not at low intensities. J Physiol. 2004a;559:335–345. doi: 10.1113/jphysiol.2004.062232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krustrup P, Secher NH, Relu MU, Hellsten Y, Söderlund K, Bangsbo J. Neuromuscular blockade of slow twitch muscle fibres elevates muscle oxygen uptake and energy turnover during submaximal exercise in humans. J Physiol. 2008;526:6037–6048. doi: 10.1113/jphysiol.2008.158162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krustrup P, Söderlund K, Mohr M, Bangsbo J. The slow component of oxygen uptake during intense submaximal exercise in man is associated with additional fibre recruitment. Pflügers Arch. 2004b;447:855–866. doi: 10.1007/s00424-003-1203-z. [DOI] [PubMed] [Google Scholar]
- Krustrup P, Söderlund K, Mohr M, Bangsbo J. Slow-twitch fiber glycogen depletion elevates moderate-exercise fast-twitch fiber activity and O2 uptake. Med Sci Sports Exerc. 2004c;36:973–982. doi: 10.1249/01.mss.0000128246.20242.8b. [DOI] [PubMed] [Google Scholar]
- Kushmerick MJ. Energy balance in muscle activity: simulations of ATPase coupled to oxidative phosphorylation and to creatine kinase. Comp Biochem Physiol B Biochem Mol Biol. 1998;120:109–123. doi: 10.1016/s0305-0491(98)00026-1. [DOI] [PubMed] [Google Scholar]
- Lamarra N, Whipp BJ, Ward SA, Wasserman K. Effect of interbreath fluctuations on characterizing exercise gas exchange kinetics. J Appl Physiol. 1987;62:2003–2012. doi: 10.1152/jappl.1987.62.5.2003. [DOI] [PubMed] [Google Scholar]
- Özyener F, Rossiter HB, Ward SA, Whipp BJ. Influence of exercise intensity on the on-and off-transient kinetics of pulmonary oxygen uptake in humans. J Physiol. 2001;533:891–902. doi: 10.1111/j.1469-7793.2001.t01-1-00891.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
-
Poole DC, Gaesser GA, Hogan MC, Knight DR, Wagner PD. Pulmonary and leg
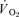 during submaximal exercise: implications for muscular efficiency. J Appl Physiol. 1992;72:805–810. doi: 10.1152/jappl.1992.72.2.805. [DOI] [PubMed] [Google Scholar]
during submaximal exercise: implications for muscular efficiency. J Appl Physiol. 1992;72:805–810. doi: 10.1152/jappl.1992.72.2.805. [DOI] [PubMed] [Google Scholar] - Poole DC, Schaffartzik W, Knight DR, Derion T, Kennedy B, Guy HJ, Prediletto R, Wagner PD. Contribution of exercising legs to the slow component of oxygen uptake kinetics in humans. J Appl Physiol. 1991;71:1245–1260. doi: 10.1152/jappl.1991.71.4.1245. [DOI] [PubMed] [Google Scholar]
- Pringle JS, Doust JH, Carter H, Tolfrey K, Campbell IT, Sakkas GK, Jones AM. Oxygen uptake kinetics during moderate, heavy and severe intensity “submaximal” exercise in humans: the influence of muscle fibre type and capillarisation. Eur J Appl Physiol. 2003;89:289–300. doi: 10.1007/s00421-003-0799-1. [DOI] [PubMed] [Google Scholar]
- Rossiter HB, Ward SA, Kowalchuk JM, Howe FA, Griffiths JR, Whipp BJ. Dynamic asymmetry of phosphocreatine concentration and O2 uptake between the on-and off-transients of moderate-and high-intensity exercise in humans. J Physiol. 2002;541:991–1002. doi: 10.1113/jphysiol.2001.012910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roston WL, Whipp BJ, Davis JA, Cunningham DA, Effros RM, Wasserman K. Oxygen uptake kinetics and lactate concentration during exercise in humans. Am Rev Respir Dis. 1987;135:1080–1084. doi: 10.1164/arrd.1987.135.5.1080. [DOI] [PubMed] [Google Scholar]
- Whipp BJ, Rossiter H. The kinetics of oxygen uptake: physiological inferences from the parameters. In: Jones AM, Poole DC, editors. Oxygen Uptake Kinetics in Sport, Exercise and Medicine. London and New York: Routledge; 2005. pp. 62–94. [Google Scholar]
- Whipp BJ, Ward SA, Lamarra N, Davis JA, Wasserman K. Parameters of ventilatory and gas exchange dynamics during exercise. J Appl Physiol. 1982;52:1506–1513. doi: 10.1152/jappl.1982.52.6.1506. [DOI] [PubMed] [Google Scholar]
- Whipp BJ, Wasserman K. Oxygen uptake kinetics for various intensities of constant-load work. J Appl Physiol. 1972;33:351–356. doi: 10.1152/jappl.1972.33.3.351. [DOI] [PubMed] [Google Scholar]
- Wilkerson DP, Berger NJ, Jones AM. Influence of hyperoxia on pulmonary O2 uptake kinetics following the onset of exercise in humans. Respir Physiol Neurobiol. 2006;153:92–106. doi: 10.1016/j.resp.2005.09.006. [DOI] [PubMed] [Google Scholar]
-
Zoladz JA, Gladden LB, Hogan MC, Nieckarz Z, Grassi B. Progressive recruitment of muscle fibers is not necessary for the slow component of
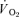 kinetics. J Appl Physiol. 2008;105:575–580. doi: 10.1152/japplphysiol.01129.2007. [DOI] [PubMed] [Google Scholar]
kinetics. J Appl Physiol. 2008;105:575–580. doi: 10.1152/japplphysiol.01129.2007. [DOI] [PubMed] [Google Scholar]