Abstract
Arterial pressure is regulated over long periods of time by neural, hormonal and local control mechanisms, which ultimately determine the total blood volume and how it is distributed between the various vascular compartments of the circulation. A full understanding of the complex interplay of these mechanisms can be greatly facilitated by the use of mathematical models. In 1967, Guyton and Coleman published a model for long-term control of arterial pressure that focused on renal control of body sodium and water and thus total blood volume. The central point of their model is that the long-term level of arterial pressure is determined exclusively by the ‘renal function curve’, which relates arterial pressure to urinary excretion of salt and water. The contribution of the sympathetic nervous system to setting the long-term level of arterial pressure in the model is limited. In light of the overwhelming evidence for a major role of the sympathetic nervous system in long-term control of arterial pressure and the pathogenesis of hypertension, new mathematical models for long-term control of arterial pressure may be necessary. Despite the prominence and general acceptance of the Guyton–Coleman model in the field of hypertension research, we argue here that it overestimates the importance of renal control of body fluids and total blood volume in blood pressure regulation. Furthermore, we suggest that it is possible to construct an alternative model in which sympathetic nervous system activity plays an important role in long-term control of arterial pressure independent of its effects on total blood volume.
The central argument
Mean systemic arterial pressure is the product of the rate at which blood is ejected from the left ventricle (cardiac output) into the arterial compartment and arteriolar resistance, which determines the rate at which blood moves from the arterial to the venous compartment. Regulation of arterial pressure involves a complex interaction of renal control mechanisms, which determine total blood volume, and mechanisms regulating the heart and vasculature to distribute that volume between the arterial and venous compartments (since the heart and lungs have relatively little blood storage capacity).
On the surface, it seems logical to link the regulation of blood pressure to regulation of blood volume. However, since arterial pressure is also expressed as the quotient of stressed arterial blood volume and arterial compliance, it is more accurate to link the regulation of arterial pressure to arterial blood volume. In that context, it is clear that total blood volume is not the major determinant of arterial pressure but rather of how that volume is distributed between the arterial and venous compartments.
The central argument of this article is that renal control of total blood volume is not the only factor that affects the long-term level of arterial pressure and that a previous mathematical model built on this foundation is therefore incomplete (Guyton & Coleman, 1967). As an alternative theoretical construct, we propose that the autonomic nervous system dynamically monitors the complex status of the cardiovascular system and exerts exquisite control over the distribution of blood volume in a variety of physiological conditions. We hypothesize that, in combination with powerful hormonal controllers of sodium and water balance (Bie, 2009), the autonomic nervous system is uniquely positioned as an important long-term controller of arterial pressure and that new mathematical models incorporating these mechanisms need to be developed.
The Guyton–Coleman model centres on renal control of blood volume and minimizes the role of the nervous system in long-term control of arterial pressure
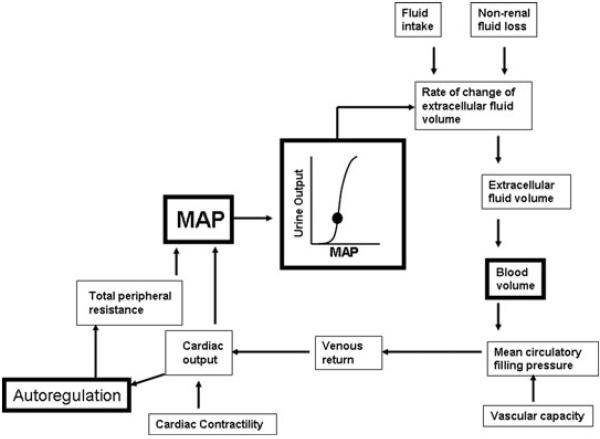
Although many mathematical models for short-term regulation of arterial pressure exist (Kappel & Peer, 1993; Ursino et al. 1994; Ursino & Magosso, 2003; Arts et al. 2005; Broskey & Sharp, 2007), there are relatively few for long-term control. The most well-known and accepted long-term model was first published by Guyton & Coleman (1967). The core concept around which the ‘G–C model’ is structured is shown in Fig. 1. Boxes with bold lines highlight key components of the model that will be discussed.
Figure 1. Schematic diagram of the core concept of the Guyton-Coleman model for long-term control of arterial pressure.
Adapted from figure 6–4 of Guyton (1980). See text for details.
The foundation of the G–C model is the ‘renal function curve’ or ‘pressure–natriuresis curve’, which ultimately ties mean arterial pressure to total blood volume, mandating only one possible steady-state combination of the two variables. Simply stated, the steady-state relationship between the perfusion pressure of the kidney, which is essentially mean arterial pressure (MAP), and the excretion of sodium and water, establish the ‘equilibrium point’ around which MAP is regulated. The balance between input of sodium and water and renal excretion of sodium and water determines extracellular fluid volume and therefore blood volume. Non-renal fluid losses are considered to be minor and fairly constant.
The fundamental idea is that whenever arterial pressure increases above the ‘equilibrium point’, the kidneys will excrete more sodium and water,which will then decrease blood volume and cardiac output and restore arterial pressure to its normal level. The opposite occurs when arterial pressure falls. The renal function curve is said to have ‘infinite gain’ in that, even for minute changes in arterial pressure, the kidneys will always regulate pressure back to normal. Indeed, the G–C model predicts that this mechanism dominates all other pressure-controlling systems over time; ‘The infinite gain principle dictates that the long-term level to which arterial pressure is regulated can never change except by altering one of the above two factors, changing either the level of net fluid intake or changing the renal function curve’ (Guyton et al. 1988).
A limitation of the G–C model is that control of arterial pressure is almost entirely dependent on regulating one variable, namely blood volume. As we have previously discussed, from a teleological perspective, it seems unlikely that regulation of arterial pressure, which is vital to perfusion of the brain and heart, would be dependent on control of a single variable such as blood volume (Osborn, 2005). Moreover, the experimental support for a direct relationship between blood volume and the long-term level of arterial pressure in humans is extremely poor (Conway, 1984).
It is important to note in Fig. 1 that the G–C model did indicate that the relationship between blood volume and venous return to the heart is also dependent on ‘vascular capacity’ which, to a large extent, is a function of venous capacitance, since veins are many times more compliant that arteries (Guyton et al. 1973; Levy, 1979; Rothe, 1983). This means that, technically, the model did not assume that blood volume alone was the driving force for venous return and cardiac output. However, since the primary controller of vascular capacity is thought to be the sympathetic nervous system and the G–C model minimized the role of the sympathetic nervous system as an important long-term controller of arterial pressure regulation of ‘vascular capacitance’ was not extensively considered (Guyton et al. 1988). As a result, the G–C model focused on regulation of blood volume as the sole long-term determinant of arterial pressure.
Although the G–C model acknowledges that the nervous system controls arteriolar resistance and venous capacitance, it also dictates that the only way the nervous system can increase arterial pressure in the long term is by an increase in sympathetic nerve activity to the renal vascular bed and a rightward shift of the renal function curve. In other words, sympathetic activity to non-renal vascular beds (e.g. splanchnic and skeletal muscle) is insignificant in long-term control of arterial pressure, since it does not affect the renal function curve and thus total blood volume.
Another reason why the role of the sympathetic nervous system is underappreciated in the G–C model is that the primary controller of sympathetic activity is represented as a simple arterial baroreceptor reflex arc. The issue of whether or not the arterial baroreceptor reflex is important in long-term control of arterial pressure is still debated 40 years after the G–C model was first published (Barrett & Malpas, 2005; Brooks & Sved, 2005; Lohmeier et al. 2005; Osborn et al. 2005; Thrasher, 2005). Guyton presented two empirical arguments for dismissing the arterial baroreceptor reflex as a long-term controller of arterial pressure (Guyton, 1980). First, arterial baroreceptors adapt and therefore cannot provide an accurate long-term negative feedback signal to the brain regarding arterial pressure. Second, surgical removal of the afferent projections of arterial baroreceptors (sinoaortic denervation; SAD), which removes tonic inhibitory input to the sympathetic premotor neurons in the brainstem, results in a transient increase in arterial pressure but does not lead to chronic hypertension (Cowley et al. 1973). This latter point was used to support the argument that the pressure–natriuresis relationship dominated over sympathetic control of arterial pressure over long periods of time in SAD animals (Cowley et al. 1980; Guyton, 1988). However, it is now clear that the return of arterial pressure to normal levels after SAD is not due to the pressure–natriuresis relationship but rather to a normalization of sympathetic nerve activity (Osborn & England, 1990; Osborn et al. 2005; Malpas et al. 2006). The mechanisms responsible for regulating sympathetic activity in SAD animals are unknown. One possibility is that that cardiopulmonary receptors compensate for the loss of arterial baroreceptor input, but the observation that arterial pressure is normal in rats with lesions of the nucleus tractus solitarius (Schreihofer & Sved, 1992), the site of synaptic input for both arterial and cardiopulmonary afferents, argues against this idea. Overall, these studies are consistent with the idea that the nervous system is important in long-term control of arterial pressure but that ‘non-arterial baroreflex’ mechanisms dominate over the arterial baroreceptor reflex in long-term control of sympathetic activity and arterial pressure (Osborn et al. 2005). However, these concepts have not been incorporated into any current mathematical model for long-term control of arterial pressure. This subject is discussed in more detail below.
The G–C model predicts that a single haemodynamic profile in all forms of hypertension is triggered and maintained by blood volume expansion alone
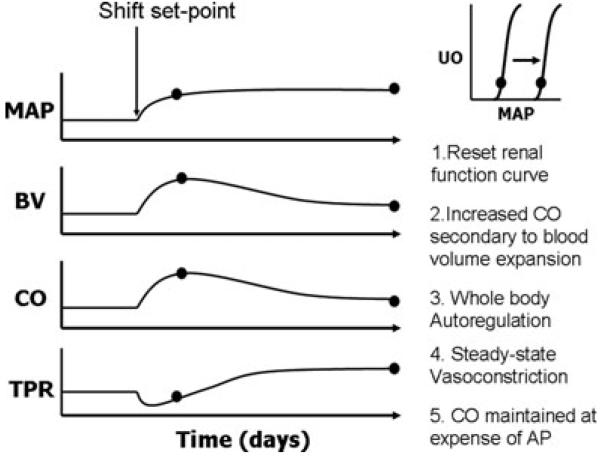
The G–C model predicts that all forms of experimental and human essential hypertension are due to primary renal dysfunction, represented by a primary shift of the renal function curve to a higher operating pressure. This results in blood volume expansion, which sets into motion the ‘whole body autoregulation haemodynamic profile’, which is characterized by an initial increase in cardiac output and a subsequent increase in total peripheral resistance and a return of cardiac output to near normal levels (Guyton, 1991). As shown in Figs 1 and 2, increased blood volume and cardiac output result in hyperperfusion of tissues, which triggers an autoregulatory vasoconstrictor response of systemic arterioles. The model predicts that this ‘whole body autoregulation’ response is what mediates the increase in peripheral resistance in the later phases of hypertension. It is important to note that the sustained increase in resistance is dependent on sustained blood volume expansion, albeit at levels within 5% of control (Guyton, 1992). In other words, increased blood volume alone is the driving factor for initiation and maintenance of hypertension according to this theory. The model dictates that a shift of the renal curve alone determines the steady-state value of the arterial pressure, whereas ‘whole body autoregulation’ establishes the balance between cardiac output and peripheral resistance (Guyton, 1991).
Figure 2. Schematic representation of the combined effects of shifting the ‘renal function curve’ and ‘whole body autoregulation’ as proposed by Guyton (1989).
Numbers 1-5 indicate the temporal sequence of events whereby a shift of the renal function curve (1) results in expansion of BV and increased CO (2). This is followed by whole body autoregulation (3) resulting in vasoconstriction (4) which results in increased TRR and normalization of CO (5). Abbreviations: MAP; mean arterial pressure; BV, blood volume; CO, cardiac output; TPR, total peripheral resistance; and UO, urine output.
The G–C model is restrained by its dependence on the renal function curve control of blood volume and a single haemodynamic profile to explain all forms of hypertension. A recent study conducted in conscious, freely moving dogs has shown that pressure natriuresis only occurs when arterial pressure falls by 20% or increases by 10% from control levels (Seeliger et al. 2005). These investigators concluded that pressure natriuresis can be an important regulator of sodium and water balance, but only under pathophysiological conditions. More to the point, studies in normal rats (Greene et al. 1990; Krieger et al. 1990), dogs (Krieger et al. 1990) and humans (Sullivan & Ratts, 1983) have reported chronic salt-induced increases in blood volume and cardiac output but no change in arterial pressure, since peripheral vascular resistance was decreased. These studies are inconsistent with the concepts of a ‘chronic renal function curve’ or blood volume as the exclusive long-term determinant of arterial pressure. Finally, although blood volume expansion and whole body autoregulation may explain some forms of hypertension, there are numerous examples where hypertension occurs independent of volume expansion and, in most cases, is associated with decreased blood volume (Conway, 1984). A mathematical model capable of simulating the several haemodynamic profiles that are known to occur in hypertension (Conway, 1984), which are not necessarily triggered and/or maintained by changes in total blood volume, is clearly needed.
The autonomic nervous system is uniquely positioned as an important long-term controller of arterial pressure
In the 40 years since the G–C model was introduced, there has been an avalanche of new knowledge related to autonomic regulation of the circulation. We now know that the sympathetic nervous system is much more complex than a simple ‘all-or-none’ system that is activated under conditions of stress. Acutely, the sympathetic nervous system is capable of generating very precise response patterns to a variety of stimuli such that sympathetic nerve activity (SNA) to the heart, kidneys, gastrointestinal tract and skeletal muscle distribute blood flow to where it is most needed in those conditions. This topic has been extensively discussed in the excellent text by Korner (2007) and recent review by Guyenet (2006). It has been proposed that similar distinct response patterns occur over long periods of time and contribute to neurogenic cardiovascular diseases such as hypertension (Folkow, 1982; Conway, 1984; Korner, 2007), but this remains to be conclusively proven.
In addition to precise response patterns of efferent sympathetic pathways, it is also clear that the brain receives a constellation of afferent inputs that are integrated and ultimately processed to generate these differential efferent SNA response patterns. The role of arterial and cardiopulmonary afferents in control of sympathetic activity has been intensively studied, and the neural pathways are well worked out (Guyenet, 1990). These neural inputs to the brainstem relay information regarding the pressure/volume status of arterial, cardiopulmonary and venous compartments. However, it is now known that baroreceptor afferents provide only a fraction of the signals to the brain regarding cardiovascular homeostasis, and their importance in long-term control of sympathetic activity is eclipsed by a multitude of other sensory inputs to the central nervous system.
For example, an area of investigation that began at the time the G–C model was introduced is the role of circumventricular organs (CVOs) in long-term regulation of autonomic function (Johnson & Loewy, 1990). These structures, which are found in the brainstem and hypothalamus, have a poor blood brain–barrier, which provides a communication portal between the cardiovascular system and the brain. In mammals, the key CVOs are the area postrema (AP), subfornical organ (SFO) and the organum vasculosum of the lamina terminalis (OVLT). The CVOs contain receptors for numerous hormones, including angiotensin II, vasopressin, aldosterone, oestrogen, leptin and insulin, to name a few. In addition, the OVLT is believed to be the location of central osmoreceptors, which mediate the sympathetic responses to changes in plasma sodium concentration. As such, the circumventricular organs ‘sense’ not only plasma sodium concentration but also hormones that signal changes in body fluid homeostasis and energy balance. The neural projections from these sites ultimately input to the paraventricular nucleus of the hypothalamus, the ‘central command centre’ for maintenance of homeostasis. The role of CVOs in regulation of autonomic function has been discussed in several excellent reviews (Johnson & Loewy, 1990; McKinley et al. 2004; Guyenet, 2006).
Although it is abundantly clear that the brain receives numerous neural and blood-borne signals related to the cardiovascular, body fluid and energy status of the body, the mechanisms whereby these signals are integrated and ultimately result in the generation of state-specific sympathetic patterns are largely unknown. A complete understanding of the extreme complexity of these neural interactions requires experimental studies in animals and humans in combination with mathematical modelling, similar to the approach that Guyton and Coleman used to study the role of the kidney in the regulation of arterial pressure.
The Guyton–Coleman model cannot serve as the starting point for a computational model incorporating recent advances in autonomic neuroscience
If a new model is to be generated, then where do we start? One suggestion would be to modify the G–C model, since it is already firmly established. We feel this would be unsuccessful for several reasons. First and foremost, the core concept of the model is that renal control of blood volume is the sole determinant of the long-term level of arterial pressure and, as we have argued in this article, we believe this approach is incorrect. Indeed, the model dictates that the only way the sympathetic nervous system can regulate pressure is by changes in renal nerve activity that alter the renal function curve. This is not true, since some models of neurogenic hypertension, such as the angiotensin II–salt model, are not dependent on renal nerves (King et al. 2007; Burke et al. 2008). Second, the code for the model is not easily accessible. Third, although not discussed in detail in this article, the original model is based on a single systemic vascular bed, which restrains the haemodynamic performance of the model.
Establishment of a new mathematical model for long-term control of arterial pressure
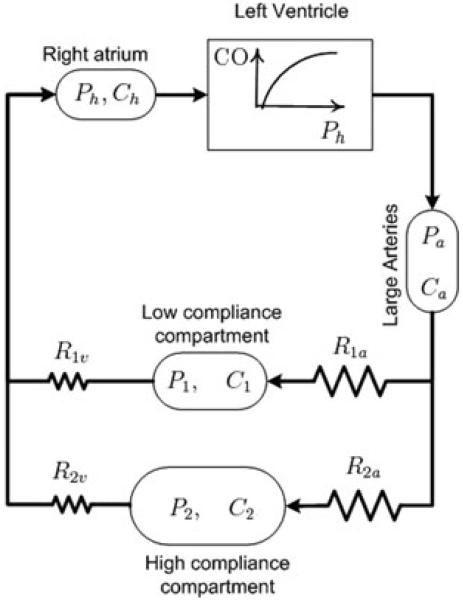
In the preceding pages, we have summarized what we feel are deficiencies in the most widely accepted model for long-term control of arterial pressure. However, in order to make significant progress in the field it is important to move beyond criticizing existing models and propose a new one. Inspired by the vision of Dr Guyton, we have taken the first steps to develop a new model with the long-term goal of incorporating recent advances in autonomic neurosciences. The foundation of the model, in terms of the circulatory components, has been presented in preliminary form (V.A. Averina, G.D. Fink & J.W. Osborn, unpublished observation) and is illustrated in Fig. 3. The development of the model is structured on the following core concepts. First, although we recognize that total blood volume can impact long-term control of arterial pressure, our model is designed to understand how blood volume is distributed between the arterial and venous compartments as well as individual vascular beds. Therefore, although our model will include a pressure–natriuresis relationship (renal function curve), it will not have ‘infinite gain’ (Seeliger et al. 2005); it will operate primarily as a ‘back-up’ to hormonal controllers of sodium and water balance (Bie, 2009) and reset to long-term changes in arterial pressure (Reinhardt et al. 1994). Second, the new model includes a ‘high-compliance’ and ‘low-compliance’ vascular bed arranged in parallel. Third, the model will allow for the sympathetic nervous system to differentially regulate nerve activity to these parallel vascular beds, as well as arteries and veins, affecting their compliances, unstressed volumes and resistances. This feature permits the simulation of several haemodynamic profiles of hypertension in conditions of an increase, decrease or no change in total blood volume, which is consistent with the literature (Conway, 1984). Fourth, future iterations of the model will incorporate ‘non-baroreflex’ mechanisms for long-term regulation of sympathetic activity. Finally, the details of the model (underlying assumptions, mathematical description, code for numerical simulations, parameter estimation, etc) will be in the public domain to enhance collaboration among all interested investigators. We feel this is the best mechanism to foster our collective understanding of long-term control of arterial pressure as well as the pathogenesis of hypertension.
Figure 3. Schematic representation of the parallel vascular bed model upon which a new mathematical model will be developed.
The model assumes that the Frank–Starling mechanism of the left ventricle is the primary determinant of systemic blood flow. Cardiac output (CO) is determined by the filling pressure (Ph) and compliance (Ch) of the heart. Arterial pressure (Pa) is a function of arterial blood volume and compliance of the arterial compartment (Ca). Pressure in vascular bed 1 (P1) is determined by its compliance (C1) and volume, which is established by arteriolar (R1a) and venous resistance (R1v) to flow across it. Similarly, pressure in vascular bed 2 (P2) is determined by its compliance (C2) and volume, which is established by arteriolar (R2a) and venous resistance (R2v) to flow across it. Although not illustrated, the sympathetic nervous system will differentially regulate the contribution of resistance and compliance of each vascular bed, and total blood volume will primarily be regulated by hormonal controllers of sodium and water excretion.
Perspectives
Dr Guyton's pioneering studies, combining mathematical modelling with animal experimentation, have made an indelible contribution to our understanding of the role of the kidney in long-term control of arterial pressure. He was a man far ahead of his time and laid the groundwork for decades of intensive research on the mechanisms of arterial pressure regulation and hypertension. The original model was published over 40 years ago and, although some modifications have been made over the years, the foundation upon which the model was constructed has not changed. Although the longevity of the model is a testimonial to the vision of Drs Guyton and Coleman, it should also not be surprising that after 40 years the model is lagging behind new discoveries in cardiovascular and neuroscience research. The time is upon us to either update the G–C model or to generate an entirely new one.
We approached this problem by asking ourselves the following question. Is it possible to retain the essential features of the G–C model and simply update it with recent advances in autonomic neuroscience? Upon close examination, we felt this was not the correct approach for reasons we have discussed above. That led us to start at the beginning to create a new model. Although still in its infancy, we are committed to bringing the ‘Guytonian’ passion and spirit for integrative physiology to generate a new mathematical model that will merge the fields of systems cardiovascular and neuroscience research together with the long-term goal of advancing our understanding of the neurogenic mechanisms of cardiovascular diseases. We approach this tremendous endeavour recognizing the importance of the inclusion of our colleagues in open and objective dialogue. Hopefully, this paper is the beginning of that dialogue.
References
- Arts T, Delhaas T, Bovendeerd P, Verbeek X, Prinzen F. Adaptation to mechanical load determines shape and properties of heart and circulation: the CircAdapt model. Am J Physiol Heart Circ Physiol. 2005;288:H1943–H1954. doi: 10.1152/ajpheart.00444.2004. [DOI] [PubMed] [Google Scholar]
- Averina V, Othmer H, Fink G, Osborn J. The CNS-MAP-Controller hypothesis: a new mathematical model for long-term control of mean arterial pressure (MAP) Exp Biol. 2008 [Google Scholar]
- Barrett C, Malpas S. Problems, possibilities, and pitfalls in studying the arterial baroreflexes' influence over long-term control of blood pressure. Am J Physiol Regul Integr Comp Physiol. 2005;288:R837–R845. doi: 10.1152/ajpregu.00456.2004. [DOI] [PubMed] [Google Scholar]
- Bie P. Blood volume, blood pressure and total body sodium: internal signalling and output control. Acta Physiol. 2009;195:187–196. doi: 10.1111/j.1748-1716.2008.01932.x. [DOI] [PubMed] [Google Scholar]
- Brooks V, Sved A. Pressure to change? Re-evaluating the role of baroreceptors in the long-term control of arterial pressure. Am J Physiol Regul Integr Comp Physiol. 2005;288:R815–R818. doi: 10.1152/ajpregu.00012.2005. [DOI] [PubMed] [Google Scholar]
- Broskey J, Sharp MK. Evaluation of mechanisms of postflight orthostatic intolerance with a simple cardiovascular system model. Ann Biomed Eng. 2007;35:1800–1811. doi: 10.1007/s10439-007-9341-7. [DOI] [PubMed] [Google Scholar]
- Burke SL, Evans RG, Moretti JL, Head GA. Levels of renal and extrarenal sympathetic drive in angiotensin II-induced hypertension. Hypertension. 2008;51:878–883. doi: 10.1161/HYPERTENSIONAHA.107.100800. [DOI] [PubMed] [Google Scholar]
- Conway J. Hemodynamic aspects of essential hypertension in humans. Physiol Rev. 1984;64:617–660. doi: 10.1152/physrev.1984.64.2.617. [DOI] [PubMed] [Google Scholar]
- Cowley AW, Jr, Liard JF, Guyton AC. Role of the baroreceptor reflex in daily control of arterial blood pressure and other variables in dogs. Circ Res. 1973;32:564–576. doi: 10.1161/01.res.32.5.564. [DOI] [PubMed] [Google Scholar]
- Cowley JAW, Quillen EW, Barber BJ. Further evidence for lack of baroreceptor control of long-term level of arterial pressure. In: Sleight P, editor. Arterial Baroreceptors and Hypertension. Oxford University Press; New York, Toronto: 1980. pp. 391–399. [Google Scholar]
- Folkow B. Physiological aspects of primary hypertension. Physiol Rev. 1982;62:347–504. doi: 10.1152/physrev.1982.62.2.347. [DOI] [PubMed] [Google Scholar]
- Greene AS, Yu ZY, Roman RJ, Cowley AW., Jr Role of blood volume expansion in Dahl rat model of hypertension. Am J Physiol Heart Circ Physiol. 1990;258:H508–H514. doi: 10.1152/ajpheart.1990.258.2.H508. [DOI] [PubMed] [Google Scholar]
- Guyenet PG. Role of the ventral medulla oblongata in blood pressure regulation. In: Loewy AD, Spyer KM, editors. Central Regulation of Autonomic Functions. Oxford University Press; New York, Oxford: 1990. pp. 145–167. [Google Scholar]
- Guyenet PG. The sympathetic control of blood pressure. Nat Rev Neurosci. 2006;7:335–346. doi: 10.1038/nrn1902. [DOI] [PubMed] [Google Scholar]
- Guyton AC. Circulatory Physiology III: Arterial Pressure and Hypertension. W. B. Saunders Co.; Philadephia: 1980. [Google Scholar]
- Guyton AC. Hypertenson: a neural disease? Arch Neurol. 1988;45:178–179. doi: 10.1001/archneur.1988.00520260064021. [DOI] [PubMed] [Google Scholar]
- Guyton AC. Dominant role of the kidneys and accessory role of whole-body autoregulation in the pathogenesis of hypertension. Am J Hypertens. 1989;2:575–585. doi: 10.1093/ajh/2.7.575. [DOI] [PubMed] [Google Scholar]
- Guyton AC. Abnormal renal function and autoregulation in essential hypertension. Hypertension. 1991;18(5 Suppl):III49–III53. doi: 10.1161/01.hyp.18.5_suppl.iii49. [DOI] [PubMed] [Google Scholar]
- Guyton AC. Kidneys and fluids in pressure regulation. Small volume but large pressure changes. Hypertension. 1992;19(1 Suppl):I2–I8. doi: 10.1161/01.hyp.19.1_suppl.i2. [DOI] [PubMed] [Google Scholar]
- Guyton AC, Coleman TG. Long-term Regulation of the Circulation: Interrelationships with Body Fluid Volumes. W. B. Saunders Co.; Philadelphia: 1967. [Google Scholar]
- Guyton AC, Jones CE, Coleman TG. Circulatory Physiology: Cardiac Ouput and its Regulation. W. B. Saunders Co.; Philadelphia: 1973. [Google Scholar]
- Guyton AC, Montani J-P, Hall JE, Manning RD. Computer models for desiging hypertension experiments and studying concepts. Am J Med Sci. 1988;294:320–326. doi: 10.1097/00000441-198804000-00018. [DOI] [PubMed] [Google Scholar]
- Johnson AK, Loewy AD. Circumventricular organs and their role in visceral functions. In: Loewy AD, Spyer KM, editors. Central Regulation of Autonomic Functions. Oxford University Press; New York, Oxford: 1990. pp. 247–267. [Google Scholar]
- Kappel F, Peer RO. A mathematical model for fundamental regulation processes in the cardiovascular system. J Math Biol. 1993;31:611–631. doi: 10.1007/BF00161201. [DOI] [PubMed] [Google Scholar]
- King AJ, Osborn JW, Fink GD. Splanchnic circulation is a critical neural target in angiotensin II salt hypertension in rats. Hypertension. 2007;50:547–556. doi: 10.1161/HYPERTENSIONAHA.107.090696. [DOI] [PubMed] [Google Scholar]
- Korner P. Essential Hypertension and its Causes. Oxford University Press; New York: 2007. [Google Scholar]
- Krieger JE, Liard J-F, Cowley AW., Jr Hemodynamics, fluid volume, and hormonal responses to chronic high-salt intake in dogs. Am J Physiol Heart Circ Physiol. 1990;259:H1629–H1636. doi: 10.1152/ajpheart.1990.259.6.H1629. [DOI] [PubMed] [Google Scholar]
- Levy MN. The cardiac and vascular factors that determine systemic blood flow. Circ Res. 1979;44:739–747. doi: 10.1161/01.res.44.6.739. [DOI] [PubMed] [Google Scholar]
- Lohmeier T, Hildebrandt D, Warren S, May P, Cunningham J. Recent insights into the interactions between the baroreflex and the kidneys in hypertension. Am J Physiol Regul Integr Comp Physiol. 2005;288:R828–R836. doi: 10.1152/ajpregu.00591.2004. [DOI] [PubMed] [Google Scholar]
- McKinley MJ, Clarke IJ, Oldfield BJ. The Human Nervous System. Elsevier; Amsterdam: 2004. Circumventricular organs; pp. 562–591. [Google Scholar]
- Malpas S, Ramchandra R, Guild S, Budgett D, Barrett C. Baroreflex mechanisms regulating mean level of SNA differ from those regulating the timing and entrainment of the sympathetic discharges in rabbits. Am J Physiol Regul Integr Comp Physiol. 2006;291:R400–R409. doi: 10.1152/ajpregu.00204.2005. [DOI] [PubMed] [Google Scholar]
- Osborn J, Jacob F, Guzman P. A neural set point for the long-term control of arterial pressure: beyond the arterial baroreceptor reflex. Am J Physiol Regul Integr Comp Physiol. 2005;288:R846–R855. doi: 10.1152/ajpregu.00474.2004. [DOI] [PubMed] [Google Scholar]
- Osborn JW. Hypothesis: set-points and long-term control of arterial pressure. A theoretical argument for a long-term arterial pressure control system in the brain rather than the kidney. Clin Exp Pharmacol Physiol. 2005;32:384–393. doi: 10.1111/j.1440-1681.2005.04200.x. [DOI] [PubMed] [Google Scholar]
- Osborn JW, England SK. Normalization of arterial pressure after barodenervation: role of pressure natriuresis. Am J Physiol Regul Integr Comp Physiol. 1990;259:R1172–R1180. doi: 10.1152/ajpregu.1990.259.6.R1172. [DOI] [PubMed] [Google Scholar]
- Reinhardt HW, Corea M, Boemke W, Pettker R, Rothermund L, Scholz A, Schwietzer G, Persson PB. Resetting of 24-h sodium and water balance during 4 days of servo-controlled reduction of renal perfusion pressure. Am J Physiol Heart Circ Physiol. 1994;266:H650–H657. doi: 10.1152/ajpheart.1994.266.2.H650. [DOI] [PubMed] [Google Scholar]
- Rothe CF. Reflex control of veins and vascular capacitance. Physiol Rev. 1983;63:1281–1342. doi: 10.1152/physrev.1983.63.4.1281. [DOI] [PubMed] [Google Scholar]
- Schreihofer AM, Sved AF. Nucleus tractus solitarius and control of blood pressure in chronic sinoaortic denervated rats. Am J Physiol Regul Integr Comp Physiol. 1992;263:R258–R266. doi: 10.1152/ajpregu.1992.263.2.R258. [DOI] [PubMed] [Google Scholar]
- Seeliger E, Wronski T, Ladwig M, Rebeschke T, Persson PB, Reinhardt HW. The ‘body fluid pressure control system’ relies on the renin–angiotensin–aldosterone system: balance studies in freely moving dogs. Clin Exp Pharmacol Phys. 2005;32:394–399. doi: 10.1111/j.1440-1681.2005.04201.x. [DOI] [PubMed] [Google Scholar]
- Sullivan JM, Ratts TE. Hemodynamic mechanisms of adaptation to chronic high sodium intake in humans. Hypertension. 1983;5:814–820. doi: 10.1161/01.hyp.5.6.814. [DOI] [PubMed] [Google Scholar]
- Thrasher T. Baroreceptors, baroreceptor unloading, and the long-term control of blood pressure. Am J Physiol Regul Integr Comp Physiol. 2005;288:R819–R827. doi: 10.1152/ajpregu.00813.2004. [DOI] [PubMed] [Google Scholar]
- Ursino M, Antonucci M, Belardinelli E. Role of active changes in venous capacity by the carotid baroreflex: analysis with a mathematical model. Am J Physiol Heart Circ Physiol. 1994;267:H2531–H2546. doi: 10.1152/ajpheart.1994.267.6.H2531. [DOI] [PubMed] [Google Scholar]
- Ursino M, Magosso E. Short-term autonomic control of cardiovascular function: a mini-review with the help of mathematical models. J Integr Neurosci. 2003;2:219–247. doi: 10.1142/s0219635203000275. [DOI] [PubMed] [Google Scholar]