The GC Skew Index: A Measure of Genomic Compositional Asymmetry and the Degree of Replicational Selection

Abstract

Circular bacterial chromosomes have highly polarized nucleotide composition in the two replichores, and this genomic strand asymmetry can be visualized using GC skew graphs. Here we propose and discuss the GC skew index (GCSI) for the quantification of genomic compositional skew, which combines a normalized measure of fast Fourier transform to capture the shape of the skew graph and Euclidean distance between the two vertices in a cumulative skew graph to represent the degree of skew. We calculated GCSI for all available bacterial genomes, and GCSI correlated well with the visibility of GC skew. This novel index is useful for estimating confidence levels for the prediction of replication origin and terminus by methods based on GC skew and for measuring the strength of replicational selection in a genome.

Introduction

In circular bacterial chromosomes, the replication process starts from a finite replication origin (ori) and continues bidirectionally along the two arms (i.e. the replichores) until the replication complex reaches the replication terminus (ter), located directly opposite of ori (Rocha, 2004a; Rocha, 2004b). Replication is obviously the most fundamental and essential process in the cell cycle of bacteria, and replication also exerts genome-wide mutational and selection pressure, shaping genomic polarity with asymmetrically biased nucleotide composition in leading and lagging strands (Lobry and Louarn, 2003; Lobry and Sueoka, 2002). This compositional skew can be easily observed by plotting the normalized excess of guanine (G) over cytosine (C) content in a subgenomic region with sliding windows along the complete genome sequence (Lobry, 1996). Such a GC skew graph segregates the genome into two regions: one with an excess of G over C corresponding to the leading strand, and the other with an excess of C over G corresponding to the lagging strand. Moreover, the shift points of the GC skew graphs are reportedly correlated with the loci of ori and ter (Frank and Lobry, 1999). GC skew is observed in many bacterial species with circular chromosomes, although with varying clarity of the shift points, and GC skew is usually not detectable in symbionts and bacteria with linear chromosomes (Worning et al. 2006) or in archaeal genomes, which employ different machinery for the replication process (Grabowski and Kelman, 2003; Lopez et al. 1999; Myllykallio et al. 2000). GC skew is also observed in local genomic regions primarily introduced by RNA synthesis (Fujimori et al. 2005), but the overall genomic polarity due to replication is present regardless of these local effects, and the GC skew is thus observed in intergenic regions as well as in the third nucleotide positions in codons. Although the underlying causes for GC skew is not completely understood, hydrolytic deamination of cytosine in the leading strand in single-stranded state during replication, is suggested as the major contributing factor (Rocha, 2004b).

Because only a few ori and ter positions had been identified by experimental means, analysis of GC skew was first utilized for the computational prediction of ori and ter positions by examining available genome sequences (Frank and Lobry, 2000). Similar method using nucleotide gradients of T/C and A/G is utilized for the detection of unidirectional replication in mitochondria (Krishnan et al. 2004; Seligmann et al. 2006). To improve the accuracy of prediction, cumulative diagrams are commonly employed to balance out the noise in sequence composition and to eliminate the requirement for window slides (Grigoriev, 1998), coupled with purine and keto excesses and GC skew (Freeman et al. 1998). However, predictions based on these methods are less accurate in genomes where GC skew cannot be strongly observed (Zawilak et al. 2001). To observe the control of replicational selection on the various genomic properties, genomic compositional skews are also used in conjunction with other genomic features such as the gene orientation (McLean et al. 1998), the distribution of RAG oligomers recognized by the FtsK translocase (Hendrickson and Lawrence, 2006), and the codon bias of genes along the genome (Daubin and Perriere, 2003). To our knowledge, however, no method to quantify the strength of GC skew has been proposed; therefore, it is difficult to compare the effects of replicational selection across bacterial genomes.

In this work, we present the GC skew index (GCSI), which quantifies the strength of GC skew of a given genome by combining Fourier power spectral analysis with the Euclidean distance between the maximum and minimum of the cumulative skew vector. Spectral analysis using fast Fourier transform (FFT) is able to identify the frequency components contributing to a given signal, and it has been applied successfully to the field of bioinformatics (Dodin et al. 2000; Katoh et al. 2002; Yin and Yau, 2005). Because GC skew emerges from the mutational selection in the two replichores, the greatest contributing frequency component of GC skew should be at 1 Hz, with two clear shift points. This observation of a 1-Hz signal combined with the degree of skew calculated by the distance measure between the two vertices of a cumulative skew diagram effectively quantifies the skew of genomic compositional asymmetry.

Materials and Methods

Sequences and software

Complete circular chromosomal sequences of 303 bacteria and complete genome sequences of 29 archaeal genomes in GenBank format were selected and obtained from the NCBI RefSeq FTP repository (ftp://ftp.ncbi.nih.gov/genomes/Bacteria/). All analyses were conducted using the G-language Genome Analysis Environment version 1.6.11 (Arakawa et al. 2003; Arakawa and Tomita, 2006). The positional coordinate system for the genomic sequence used in this work was set to originate at 0, unlike that of GenBank, which uses 1 for the position of the first base.

Calculation of GC skew

GC skew was defined as the normalized excess of C over G in a given sequence, (C − G)/(C + G), which is calculated with sliding windows along the genome. GC skew is defined to be 0 when the amount of C equals that of G. To eliminate the use of window slides, cumulative skew can be calculated as the cumulative sum of the walker graph score at each nucleotide position along the genome, with scores A = 0, T = 0, G = 1, and C = −1. In this work, however, the cumulative GC skew was calculated by taking the cumulative sum of the GC skew in each of the windows, to normalize the cumulative skew strength without it being affected by the length of the genome.

Fast fourier transform

FFT is the computationally optimized derivation of discrete Fourier transform (DFT) for the number of sampling units in the power of two. FFT transforms a given signal in the time domain to reveal the frequency components comprising the input signal. GC skew can be thought of as a signal along the continuous axis of genomic position, which was used in place of the time domain in this work. DFT F(k) of a signal of length N, f (n), where n = 0, 1, …, N − 1, at frequency k was calculated as follows:

$$F(k)\hspace{0.17em}=\hspace{0.17em}\sum _{n=0}^{N\hspace{0.17em}-\hspace{0.17em}1}f(n)e^{-i2\pi kn/N}$$ (1)

where i = √ 1̅. The power spectrum PS(k) of F(k) was further defined as

$$\mathrm{PS}(k)\hspace{0.17em}=\hspace{0.17em}|F(k){|}^2,\hspace{0.17em}k\hspace{0.17em}=\hspace{0.17em}0,\hspace{0.17em}1,\hspace{0.17em}2,\hspace{0.17em}\dots ,\hspace{0.17em}N\hspace{0.17em}-\hspace{0.17em}1$$ (2)

at each frequency k. In this power spectrum, GC skew shows the greatest contributing component at 1-Hz frequency, corresponding to the two replichores shifting between two regions of opposite polarity as in a sine curve (Arakawa et al. 2007). The Math:FFT module of Perl (http://search.cpan.org/~rkobes/Math-FFT-1.28/FFT.pm) was used for FFT calculation. To level the effects of genome size when comparing the diverse bacterial species, all genome sequences were divided into 4096 windows, and then the GC skew used as the initial signal, the cumulative GC skew, and the power spectra were calculated in these windows. Number of windows must be the power of two for effective FFT calculation, and here 2¹² = 4096 windows were used to take account of the effects of gene positioning, since this window size roughly corresponds the size of genes (about 1kbp) in bacterial genomes. This window size also eliminates other local mutational factors including those within genes, generated by functional requirements in RNA synthesis and translation.

GC skew index

Because cumulative skew should remain around zero under conditions of no strand bias and inversely increase its value in both positive and negative directions where bias is strong, Euclidean distance between the maximal and minimal vertices can be used as a measure of skew. The limitation of this approach and the central challenge for the quantification of genomic compositional skews, however, reside in the mathematical assessment of the skew structure to have exactly two regions physically balanced in length but with opposite polarity of nucleotide content. FFT is a good method for such a purpose, because it is able to reveal the contributing frequency components. Therefore, we used FFT to assess the fitness of the skew to the replicational selection model and combined this with the Euclidean distance between the two vertices of cumulative skew to calculate the GCSI. The GCSI is defined as the normalized average of the Euclidean distance between the two vertices of cumulative skew (dist) and the ratio of spectral strength at 1 Hz and the average strength of spectra in frequency regions 2 Hz or above (SR). Because the replicational selection is the single most dominant factor for GC strand bias, the ratio of spectral strength at 1-Hz frequency and that of all other spectra or their average must be greater than 1. SR was normalized by division with the rounded maximal SR of all bacterial genomes, which we defined here as 6000. Likewise, dist was normalized by 600.

Statistical assessment of the significance of GCSI

Significance of the GCSI values is tested using the distribution of GCSI calculated using two sets of randomized data: GCSI calculated using shuffled GC skew, where the window order is randomized using the GC skew values calculated with the original genome sequence, and GCSI calculated using shuffled genome, where the entire nucleotide sequence of the genome is shuffled while conserving the original nucleotide content. Due to calculation costs, statistical test was conducted using 1000 shuffled GC skew and 100 shuffled genome data sets. Distribution of the resulting GCSI values for the randomized data set was firstly tested for its normality using Kolmogorov-Smirnov Lilliefors test, and the significance of the original GCSI value is calculated using the z-score in the distribution of the randomized data set.

Results

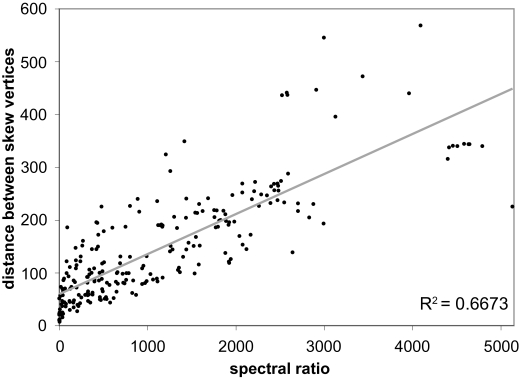
To test the applicability of GCSI for the quantification of GC skew strength, we first assessed the correlation between the Euclidean distance of the two vertices of cumulative GC skew, dist, and the Fourier power spectrum ratio, SR, using all genomes (Fig. 1). The two measures correlated with an R² value of 0.6673, showing that the predominance of the 1-Hz frequency component leads to a stronger degree of skew.

Figure 1.

Scatter plot of spectral ratio RS against the Euclidean distance between the two vertices in cumulative graph dist. RS measures the goodness-of-fit of the “shape” of the overall GC skew to be partitioned into two segments corresponding the two replichores, by calculating the relative predominance of the spectral strength of the 1-Hz frequency component over other frequencies upon applying Fast Fourier Transform. dist measures the degree of bias in the leading and lagging strands, by calculating the Euclidean distance between the average GC skew in the two replichores. RS is generally correlated with dist, therefore combination of these two measures as GCSI should correctly represent both the shape of the graph and the degree of skew.

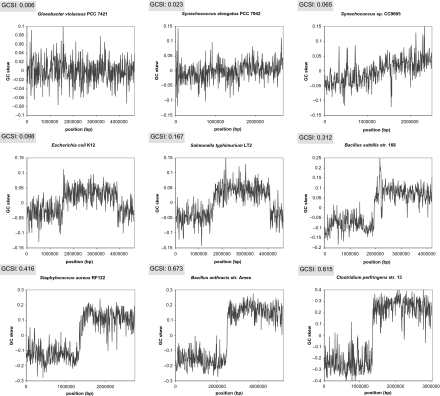
Using the measures dist and SR, GCSI was calculated for 304 bacterial genomes; 50 selected species are shown in Table 1 (see supplementary information for comprehensive listings). From the comprehensive list, nine genomes were further selected to illustrate the GC skew graphs plotted with 500 windows at various GCSI values (Fig. 2). As a control, GCSI was also calculated for 29 archaeal genomes, most of which showed no GC skew (Table 2). Because GCSI was normalized by the rounded maximum values of SR and dist, it ranged from 0 to 1. GCSI in bacterial genomes ranged from 0.006 for Gloeobacter violaceus to 0.815 for Clostridium perfringens (mean, 0.207; median, 0.145; SD, 0.173). The majority of archaeal genomes had GCSI <0.05, and the highest GCSI among archaeal genomes (0.122 of Halobacterium sp.) was low compared to those of bacterial genomes. GC skew was not clearly observable in species with GCSI <0.05, but it showed clear shift points when GCSI >0.10. Due to the limited number of iterations, normality test for the statistical assessment using shuffled genome sequence did not score well, but that using shuffled GC skew passed the test in all genome analyzed. The z-score was generally low and therefore not significant when GCSI <0.05 (especially <0.02), where the GCSI values may not be accurate. On the other hand, GCSI >0.05 scored extremely high z-scores, and therefore these values accurately depict the polarity of the genomes.

Table 1.

GCSI, spectral ratio RS, and the Euclidean distance between the two vertices in cumulative graph dist for randomly selected 50 bacterial chromosomes. Significance was calculated using 1) 1000 samples by shuffling GC skew windows, and 2) 100 samples by shuffling the entire nucleotide sequence of the genome while conserving the nucleotide composition, and the p-value from the normality test and the significance of the original GCSI value using the distribution of randomized samples was given as the z-score.

							shuffled GC skew				shuffled genome
species	accession	GCSI	SR	dist	mean	SD	z-Score	p-value (Lillefors)	mean	SD	z-Score	p-value (Lillefors)
Gloeobacter violaceus PCC 7421	NC_005125	0.006	2.006	7.103	0.006002	7.88E–05	1	8.08E–62	0.002587	0.000671	5	0.014
Synechocystis sp. PCC 6803	NC_000911	0.009	0.296	10.443	0.008784	8.10E–05	0	1.12E–68	0.005882	0.000706	4	0.000
Mycoplasma hyopneumoniae 232	NC_006360	0.019	0.149	22.387	0.018741	9.19E–05	0	3.39E–86	0.008964	0.002092	4	0.015
Synechococcus elongatus PCC 7942	NC_007604	0.024	35.953	24.632	0.020612	8.28E–05	35	8.91E–63	0.005043	0.000938	19	0.022
Shigella boydii Sb227	NC_007613	0.035	120.160	29.756	0.024878	7.99E–05	124	7.41E–67	0.009254	0.000518	49	0.000
Frankia alni ACN14a	NC_008278	0.040	125.894	35.514	0.029676	7.46E–05	139	1.95E–54	0.005153	0.000263	132	0.006
Thiobacillus denitrificans ATCC 25259	NC_007404	0.042	161.970	34.606	0.028922	8.35E–05	160	2.43E–69	0.003939	0.000703	54	0.923
Tropheryma whipplei str. Twist	NC_004572	0.048	9.110	56.698	0.047333	8.84E–05	7	1.78E–79	0.02598	0.000883	24	0.063
Geobacter sulfurreducens PCA	NC_002939	0.054	167.963	47.796	0.039911	8.49E–05	163	1.80E–80	0.007165	0.000401	116	0.024
Rhodopseudomonas palustris BisB5	NC_007958	0.064	365.258	40.691	0.033991	8.07E–05	376	1.32E–66	0.011625	0.000239	220	0.000
Polaromonas sp. JS666	NC_007948	0.071	424.069	43.091	0.035995	8.13E–05	433	7.59E–58	0.00298	0.000621	109	0.003
Shigella flexneri 2a str. 2457T	NC_004741	0.077	320.650	60.344	0.050368	8.16E–05	326	4.89E–71	0.008386	0.000448	153	0.000
Haemophilus influenzae 86–028NP	NC_007146	0.084	177.860	82.588	0.068907	8.17E–05	180	2.15E–63	0.00523	0.001235	63	0.143
Mycoplasma genitalium G37	NC_000908	0.086	103.679	93.248	0.077794	9.01E–05	94	3.10E–78	0.018262	0.002466	27	0.007
Buchnera aphidicola str. APS (Acyrthosiphon pisum)	NC_002528	0.090	84.815	99.584	0.083067	8.06E–05	86	1.40E–71	0.022281	0.002142	31	0.114
Helicobacter pylori HPAG1	NC_008086	0.097	182.961	97.720	0.081517	8.68E–05	174	1.75E–77	0.00802	0.001226	72	0.043
Escherichia coli K12	NC_000913	0.098	486.480	69.038	0.057613	8.13E–05	497	1.84E–69	0.004953	0.00069	134	0.000
Corynebacterium glutamicum ATCC 13032	NC_006958	0.104	321.871	92.134	0.076862	8.03E–05	333	1.69E–61	0.012113	0.000354	258	0.044
Helicobacter pylori J99	NC_000921	0.106	187.288	108.770	0.090726	8.31E–05	186	2.02E–66	0.018694	0.000701	124	0.008
Rhodospirillum rubrum ATCC 11170	NC_007643	0.113	763.008	59.247	0.049457	8.74E–05	726	4.72E–77	0.003081	0.000736	149	0.017
Helicobacter acinonychis str. Sheeba	NC_008229	0.119	239.480	118.460	0.098801	8.17E–05	243	1.12E–62	0.007669	0.001377	80	0.477
Escherichia coli O157:H7 str. Sakai	NC_002695	0.121	662.307	79.123	0.06602	8.36E–05	658	3.89E–68	0.008232	0.000316	356	0.068
Dehalococcoides sp. CBDB1	NC_007356	0.127	490.612	102.952	0.085878	8.61E–05	473	1.69E–72	0.010229	0.0009	129	0.144
Neisseria meningitidis Z2491	NC_003116	0.138	484.060	117.689	0.098156	8.08E–05	498	7.08E–66	0.004362	0.000929	144	0.129
Neisseria gonorrhoeae FA 1090	NC_002946	0.142	508.853	119.737	0.099867	8.29E–05	510	2.72E–60	0.006794	0.001039	130	0.122
Yersinia pestis KIM	NC_004088	0.148	785.937	99.533	0.083032	8.47E–05	772	4.61E–63	0.017378	0.00027	485	0.002
Rickettsia typhi str. Wilmington	NC_006142	0.161	437.431	149.404	0.124586	8.32E–05	437	9.13E–71	0.048368	0.000704	159	0.533
Salmonella typhimurium LT2	NC_003197	0.167	1107.149	89.390	0.074569	7.57E–05	1217	4.49E–65	0.002732	0.000705	232	0.001
Yersinia pseudotuberculosis IP 32953	NC_006155	0.174	951.989	113.617	0.094763	8.49E–05	933	8.63E–77	0.017276	0.000232	676	0.054
Dechloromonas aromatica RCB	NC_007298	0.199	1366.887	101.487	0.084655	8.43E–05	1350	3.78E–73	0.002758	0.000606	322	0.260
Chromohalobacter salexigens DSM 3043	NC_007963	0.220	1568.376	106.845	0.089121	8.36E–05	1561	1.67E–69	0.02062	0.000186	1070	0.000
Shewanella denitrificans OS217	NC_007954	0.231	1611.284	116.055	0.096797	8.05E–05	1666	3.01E–60	0.009546	0.000429	515	0.005
Bacteroides fragilis YCH46	NC_006347	0.253	1464.908	157.144	0.13104	8.95E–05	1362	3.16E–75	0.003523	0.000726	343	0.046
Chlamydophila pneumoniae AR39	NC_002179	0.256	1169.869	189.710	0.158179	8.84E–05	1101	3.49E–72	0.007879	0.00137	180	0.311
Methylobacillus flagellatus KT	NC_007947	0.267	1921.680	127.706	0.106502	7.90E–05	2026	5.99E–66	0.005942	0.000789	330	0.057
Bacillus licheniformis ATCC 14580	NC_006270	0.271	1879.614	137.460	0.114632	8.87E–05	1764	3.54E–88	0.003241	0.000753	355	0.299
Desulfotalea psychrophila LSv54	NC_006138	0.298	2118.652	145.143	0.12104	8.74E–05	2018	1.04E–70	0.034761	0.000188	1393	0.002
Bacillus subtilis subsp. subtilis str. 168	NC_000964	0.312	2041.257	169.785	0.141571	8.43E–05	2017	1.59E–71	0.008504	0.000492	615	0.067
Streptococcus thermophilus LMG 18311	NC_006448	0.319	1827.666	200.247	0.166958	8.66E–05	1758	6.60E–73	0.015441	0.000843	360	0.245
Lactococcus lactis subsp. lactis Il1403	NC_002662	0.329	1753.562	218.954	0.182543	8.30E–05	1759	1.10E–73	0.022	0.000455	673	0.000
Streptococcus pyogenes SSI-1	NC_004606	0.332	1881.246	210.648	0.175623	8.53E–05	1836	5.66E–74	0.040869	0.000363	802	0.269
Streptococcus mutans UA159	NC_004350	0.378	2260.651	226.932	0.189192	8.33E–05	2259	6.68E–72	0.023889	0.000534	662	0.000
Bacillus halodurans C-125	NC_002570	0.406	2702.537	216.866	0.180803	7.92E–05	2841	1.12E–62	0.028966	0.000211	1788	0.643
Buchnera aphidicola str. Bp (Baizongia pistaciae)	NC_004545	0.409	1415.720	348.910	0.290845	8.67E–05	1359	3.03E–70	0.011699	0.002443	162	0.005
Staphylococcus aureus subsp. aureus COL	NC_002951	0.420	2398.078	263.652	0.219797	8.72E–05	2290	2.05E–70	0.02288	0.000463	857	0.124
Lactobacillus johnsonii NCC 533	NC_005362	0.438	2512.013	274.215	0.228599	8.63E–05	2425	8.56E–71	0.038523	0.000349	1142	0.001
Ehrlichia ruminantium str. Welgevonden	NC_005295	0.579	2583.741	436.829	0.364108	7.99E–05	2694	6.11E–61	0.047406	0.000605	879	0.837
Lactobacillus plantarum WCFS1	NC_004567	0.615	5130.119	225.397	0.187914	8.59E–05	4977	4.07E–76	0.008182	0.000715	848	0.001
Bacillus anthracis str. Sterne	NC_005945	0.669	4584.878	344.506	0.287173	8.28E–05	4611	1.26E–62	0.020516	0.000228	2840	0.271
Clostridium perfringens str. 13	NC_003366	0.815	4092.849	568.720	0.474015	7.93E–05	4301	1.73E–62	0.108625	0.000249	2832	0.153

Figure 2.

GC skew graphs plotted with 500 windows for nine bacteria at different levels of GCSI. GC skew is not observable for the first two species at GCSI <0.05, and becomes evident at GCSI >0.08. At GCSI >0.1, graphs increase their skewness and the shift points and two replichores can be clearly discerned from the graph. Note that the range of Y-axis extends as GCSI values increase. Overall, GCSI correlates with and correctly captures the degree of skew.

Table 2.

GCSI, spectral ratio RS, and the Euclidean distance between the two vertices in cumulative graph dist for 29 archaeal chromosomes. See Table 1 legend for the details of the test of significance.

							shuffled GC skew				shuffled genome
species	accession	GCSI	SR	dist	mean	SD	z-Score	p-value (Lillefors)	mean	SD	z-Score	p-value (Lillefors)
Thermotoga maritima MSB8	NC_000853	0.079	55.630	89.074	0.07431	8.28E–05	55	7.84E–73	0.053342	0.000293	87	0.6718442
Aeropyrum pernix K1	NC_000854	0.040	3.985	47.125	0.039355	8.41E–05	2	9.80E–70	0.024235	0.000362	42	0.0041011
Pyrococcus abyssi GE5	NC_000868	0.045	26.443	51.771	0.043226	8.29E–05	25	4.59E–69	0.012958	0.000897	36	0.172579
Methanocaldococcus jannaschii DSM 2661	NC_000909	0.087	14.536	102.413	0.085427	8.30E–05	13	4.54E–70	0.039171	0.000559	84	0.5234979
Methanothermobacter thermautotrophicus str. Delta H	NC_000916	0.045	67.648	47.539	0.039698	7.85E–05	70	8.45E–61	0.007545	0.001076	35	0.0004862
Archaeoglobus fulgidus DSM 4304	NC_000917	0.020	3.695	23.137	0.019366	8.57E–05	2	1.63E–72	0.012813	0.000474	14	0.0639122
Pyrococcus horikoshii OT3	NC_000961	0.105	75.244	117.845	0.098287	8.08E–05	76	1.23E–64	0.043455	0.000316	193	0.5840531
Thermoplasma acidophilum DSM 1728	NC_002578	0.046	43.474	50.894	0.042499	8.71E–05	40	2.08E–69	0.014096	0.000693	46	0.0003436
Halobacterium sp. NRC-1	NC_002607	0.122	617.687	84.760	0.070717	8.43E–05	609	1.26E–70	0.006544	0.000784	147	0.3059486
Thermoplasma volcanium GSS1	NC_002689	0.044	39.413	49.277	0.041153	9.40E–05	33	2.58E–83	0.010706	0.001065	31	0.0006178
Sulfolobus solfataricus P2	NC_002754	0.042	17.321	48.204	0.040254	8.11E–05	16	5.41E–62	0.009386	0.000742	43	0.0113624
Sulfolobus tokodaii str. 7	NC_003106	0.033	1.862	39.909	0.033345	8.61E–05	0	2.92E–68	0.023109	0.000452	22	0.0383977
Pyrobaculum aerophilum str. IM2	NC_003364	0.038	6.535	44.690	0.037329	8.94E–05	5	3.60E–75	0.035224	0.000278	9	0.1593346
Pyrococcus furiosus DSM 3638	NC_003413	0.025	0.167	29.587	0.024742	8.62E–05	0	1.43E–69	0.005934	0.00129	14	0.3798953
Methanopyrus kandleri AV19	NC_003551	0.023	9.398	26.361	0.022049	8.20E–05	8	1.48E–70	0.01687	0.000478	12	0.0002658
Methanosarcina acetivorans C2A	NC_003552	0.012	2.813	13.871	0.011641	7.88E–05	1	7.19E–61	0.003945	0.000539	14	0.1568932
Methanosarcina mazei Go1	NC_003901	0.015	2.817	17.149	0.014374	8.09E–05	1	4.87E–64	0.004366	0.000714	14	0.0536714
Nanoarchaeum equitans Kin4-M	NC_005213	0.034	3.562	40.488	0.033818	7.74E–05	2	1.39E–66	0.012129	0.002861	7	0.0388642
Methanococcus maripaludis S2	NC_005791	0.041	21.214	46.718	0.039014	7.67E–05	21	4.53E–55	0.01073	0.001159	25	0.0074146
Picrophilus torridus DSM 9790	NC_005877	0.032	2.862	37.785	0.031568	7.96E–05	1	6.30E–68	0.027789	0.000466	8	0.1271154
Haloarcula marismortui ATCC 43049	NC_006396	0.007	5.473	8.170	0.006896	8.40E–05	4	4.38E–62	0.003083	0.000636	6	0.0262528
Haloarcula marismortui ATCC 43049	NC_006397	0.027	8.093	31.154	0.026042	7.79E–05	7	7.89E–64	0.017283	0.002185	4	5.38E–05
Thermococcus kodakarensis KOD1	NC_006624	0.023	12.060	26.681	0.022315	7.73E–05	11	1.29E–58	0.007225	0.000882	18	0.0146136
Sulfolobus acidocaldarius DSM 639	NC_007181	0.036	11.514	41.648	0.034791	8.63E–05	10	9.33E–75	0.006642	0.001216	23	0.2043022
Methanosarcina barkeri str. fusaro	NC_007355	0.014	11.210	15.497	0.012995	7.86E–05	10	6.92E–63	0.013765	0.000319	0	8.15E–05
Natronomonas pharaonis DSM 2160	NC_007426	0.027	96.855	22.716	0.019012	8.05E–05	99	3.44E–67	0.004615	0.000762	29	1.68E–05
Methanosphaera stadtmanae DSM 3091	NC_007681	0.087	85.030	96.236	0.08028	8.38E–05	83	6.57E–71	0.023236	0.000748	85	0.2877452
Methanospirillum hungatei JF-1	NC_007796	0.027	17.105	30.715	0.025674	7.94E–05	16	3.41E–72	0.014578	0.000342	36	0.0096521
Methanococcoides burtonii DSM 6242	NC_007955	0.044	44.608	48.355	0.040381	8.44E–05	43	1.67E–66	0.029311	0.000319	46	0.0895566

As can be seen from the GC skew graphs in Figure 2, the degree of skew correlates with GCSI. No skew was observable for G. violaceus and Synechococcus elongatus PCC 7942, with GCSI values of 0.006 and 0.023, respectively, but a gradual rise from negative values to positive values was observed for Synechococcus sp. CC9605, with a GCSI of 0.065, although the skew was not well defined. GC skew became visible at a GCSI of 0.098 in Escherichia coli K12, and the clarity was increased in correlation with the GCSI values for scores greater than 1, as represented by the increasing range of the y-axis from ±0.15 at GCSI values around 1 to ±0.4 at a GCSI of 0.815.

Discussion

The nucleotide sequence of a genome is structured and controlled by a myriad of selection pressures, especially in subgenomic regions, as typified by the fact that coding regions are shaped by the essential order and usage of codons. In addition to such requirements in the subgenomic regions, circular bacterial chromosomes experience genome-wide selection through the replication process. The chiral nucleotide composition in the two replication arms is significant; however, with regard to the evolutionary aspects of replicational selection on bacterial chromosomes, no useful method to quantify the degree of genomic compositional asymmetry has been proposed, unlike the wealth of codon bias measures (Suzuki et al. 2005). This lack of indices for genomic compositional skews was likely due to the difficulty of mathematical formulation and detection of the skewing shape of GC skew graphs. To distinguish the degree of skew, we utilized FFT to observe the predominance of the 1-Hz frequency component, which corresponds to the replicational selection on the two replichores, over other frequency components. Combined with the Euclidean distance between the two vertices in cumulative skew graphs, the formulated GCSI captured the strength of GC skew in bacterial chromosomes, as shown by the above results. GCSI scores are diverse even within bacterial genomes with circular chromosomes, ranging from a number of genomes with extremely low values therefore implying the lack of observable GC skew in the genome, to groups of genomes with clear skews as can be seen in Bacilli.

The majority of the archaeal genomes had GCSI <0.05, at which point no noticeable skew is observed even in bacterial genomes. This is also confirmed by the z-score in the statistical test using randomized data, with low z-scores (therefore implying less significance) when GCSI is less than 0.05. Thus, 0.05 can be employed as a threshold value to determine whether GC skew is present in a genome and therefore whether replicational selection is acting on the organism. Because the GCSI values do not show a Gaussian distribution, however, it should be noted that the indices are not necessarily proportionate with each other. Therefore, GCSI values should not be compared in terms of ratios but in terms of their rank orders. For the direct comparison of quantitative degrees of skew calculated as the ratio of two values, the use of Euclidean distance may be more suitable. However, significant Euclidean distance between the two vertices of cumulative skew may not always result from the polarity exhibited by the GC skew graph; it could also result from local regions of highly biased nucleotide content. Therefore, to ascertain that the skews are controlled by replicational selection, genomes used for such analyses should be selected beforehand using GCSI or SR at sufficiently high thresholds (e.g. 0.07 for GCSI and 200 for SR, also noting the z-scores).

GCSI would be a useful index for the estimation of confidence levels for bioinformatics analyses using genomic compositional skews. Predictions of replication origin and terminus by the observation of shift points (i.e. vertices) of cumulative skew diagrams become erroneous when the GC skew is not well defined. However, the confidence level can be easily estimated by taking into account of the magnitude of the GCSI. In this work we have only described the index for GC skew, although the same method is applicable to purine and keto excesses or any other genomic compositional skews, given that the selection is on the two replichores. Similarly, for comparative studies of genomic features related to evolutionary pressures and replication machinery, GCSI can also be used as a measure of replicational selection.