A decision aid for intensity-modulated radiation-therapy plan selection in prostate cancer based on a prognostic Bayesian network and a Markov model

Abstract

Objective

The prognosis of cancer patients treated with intensity modulated radiation therapy (IMRT) is inherently uncertain, depends on many decision variables, and requires that a physician balance competing objectives: maximum tumor control with minimal treatment complications.

Methods

In order to better deal with the complex and multiple objective nature of the problem we have combined a prognostic probabilistic model with multi-attribute decision theory which incorporates patient preferences for outcomes.

Results

The response to IMRT for prostate cancer was modeled. A Bayesian network was used for prognosis for each treatment plan. Prognoses included predicting local tumor control, regional spread, distant metastases, and normal tissue complications resulting from treatment. A Markov model was constructed and used to calculate a quality-adjusted life-expectancy which aids in the multi-attribute decision process.

Conclusions

Our method makes explicit the tradeoffs patients face between quality and quantity of life. This approach has advantages over current approaches because with our approach risks of health outcomes and patient preferences determine treatment decisions.

1 Introduction

Radiation therapy (RT) for the treatment of cancer has undergone a major change in the past decade. Intensity modulated radiation therapy (IMRT), predicated on technical and physical advances, provides the capability of significantly improved dose localization. This capability allows the physician to prescribe a higher tumor dose with a reduced risk of complications. The competing goals of maximizing tumor control while minimizing normal tissue complications is a complicated decision which is typically made using radiation beam intensity optimization algorithms as de facto decision making algorithms, guided by physician experience, but without explicit representation of physician knowledge.

Optimization algorithms select values of the large number of beam intensities that comprise an IMRT treatment. These algorithms minimize the value of an objective function that attempts to embody the goals of the treatment. Multiple objectives are used for a particular tissue, such as limits on the maximum dose, the minimum dose and the degree of dose uniformity. The total number of objectives used in a particular case depends on the type and location of the tumor but typically ranges from 5 to 20. An important limitation with the current approach is that the multiple objective problem of IMRT is transformed to a single objective function by adding many functions together, each weighted by a scalar importance factor. The values of the importance factors are not known a priori, so a trial-and-error process is required. This process takes extra time, and reduces the solution space that can be explored.

Our approach to improving this process is to couple the results of a multiobjective optimization to a decision aid consisting of a Bayesian network used for prognosis and a Markov model. The multiobjective optimization yields a set of treatment plans (specifically, a Pareto optimal set [1]) that span the range of possible dose distributions. This range includes plans that provide good coverage of the tumor with significantly high doses to normal tissues to plans that better spare the normal tissues at the expense of lower doses to the tumor.

The Bayesian network – also known as a belief network – provides probabilities for outcomes related to treatment of the tumor and for each of the outcomes related to normal tissue. The network is designed to model the clinical decision making process involved in choosing among different treatment plans, and it predicts the probability that a given plan will result in control of the disease, and treatment complications. Conditional probability tables are derived from prospective clinical trials, results from the research literature, and the beliefs of practicing clinicians. The Bayesian network produces probabilities over some fixed period of time corresponding to the length of the study from which they are derived. We transform these prognostic probabilities to constant annual probabilities for the state transitions in the Markov model. We use utilities from the literature and evaluate the Markov model with a cohort simulation to compute a quality adjusted life expectancy (QALE) for each IMRT treatment plan. This work builds on our original introduction of the Bayesian network to predict disease control using IMRT for prostate cancer [2,3]. In this paper, we describe a more mature version of the network, and extend it with a Markov model.

2 Materials and methods

We provide a brief review of prostate cancer and its management with RT as it is incorporated into the qualitative structure of both the Bayesian network and the Markov model. There are a number excellent reviews on the topic, for example Ref. [4]. In this work we focus on the prostate (tumor), and treatment complications in the rectum, and the bladder.

Prostate cancer is typically staged and risk stratified by three attributes: 1) TNM stage, the local extent of the disease and its degree of spread to lymph nodes or distant sites in the body, 2) Gleason score, a measure of the histologic tumor-cell differentiation, and 3) PSA, the amount of the protein PSA that is released into the bloodstream. Taken as a group, these three tests are predictive of the likelihood of clinical progression and the response to therapy.

The clinical model for prostate cancer progression is that tumor cells spread to the lymph nodes and then metastasize to distant sites, typically the skeleton, liver, or lungs. In the setting of localized prostate cancer the goal of RT is to kill the tumor cells within the prostate gland. In patients at high risk of regional lymph node spread the pelvic lymph nodes are often electively treated.

The primary instrument used to monitor a patient's progress after RT is the level of circulating PSA. Although PSA levels are not a perfect measure for the disease, or disease recurrence, the test is quick to perform, is inexpensive, and is in widespread use. The PSA level is the clinical marker for both regrowth of the primary tumor and metastasis. PSA levels typically fall in the months after RT due to the radiation absorbed by PSA-producing cells in the prostate. If PSA levels remain at or near the post-RT nadir, patients are said to have biochemical no-evidence of disease (BNED) [5]. If PSA levels rise after reaching a nadir – termed PSA failure – it can be difficult to determine whether the failure is due to local disease alone or distant metastasis. Early PSA failure, however, often suggests progression of occult metastatic disease.

An IMRT treatment plan is based on a patient's internal geometry as determined by a CT scan taken before treatment begins. The plan is defined by many variables that describe the physical orientation and intensity of hundreds of x-ray beamlets. Each of these variables is set by the optimization algorithm. This algorithm calculates the dose to each tissue of interest. A number of dose metrics can be defined for each candidate treatment plan, and these are used in treatment plan selection.

The current paradigm for IMRT optimization is to generate a treatment plan and then to examine 2- and 3-dimensional displays of the dose distributions overlaid upon the patient's CT images. The goals of the plan are set by the physician and include dosimetric objectives. For prostate therapy these objectives might include a requirement to deliver at least 72 Gy to 95% of the tumor, while treating no more than 50% of the rectum to 50 Gy, and no more than 15% of the rectum to 70 Gy. There may be 5−20 such objectives for each plan, and each is assigned a different weighting factor for the optimization algorithm. The objectives themselves, and their associated weighting factors are then varied by a “guess-and-check” process until the optimizer (typically a physicist or dosimetrist) and physician are satisfied that a plan is as optimal – meets most of the objectives – as this process can achieve.

The information available to choose between competing IMRT treatment plans include clinical trials designed to provide outcome probabilities for a selected set of variables, retrospective studies which seek to determine variables predictive of treatment outcome, and information from experts in the field. The experts include physicians, physicists, and dosimetrists. The physicists and dosimetrists are responsible for running the optimization routines. Physicians have a comprehensive view of the entire disease process, including some appreciation of the likelihood of different outcomes for a patient.

We have chosen a Bayesian network to model the process of prognosis. The process for creating a Bayesian network involves writing down all of the variables which affect the outcome of the treatment, and drawing links between all of those variables which influence one another. The next step is to remove nodes for which there is insufficient evidence for experts to form beliefs. We do not include, for example, any of the underlying cellular mechanisms of prostate cancer because the connection to health outcomes is incompletely understood and current clinical practice does not consider them. Next, a literature search unveils which of the nodes can be populated by probabilities from clinical studies. Nodes for which clinical studies do not exist must be modeled as belief nodes, with their conditional probabilities taken from expert opinions, or the research literature. The list is paired down to a set of nodes which can be reasonably assessed from experts. Finally, modeling techniques are employed in order to make the modeling process tractable. These techniques include divorcing and the noisy-or. Divorcing introduces an intermediate variable between parent nodes and the child node in order to reduce the complexity of the problem. The noisy-or is a method of modeling variables which independently influence an event, and may include a background probability for the event. There are also Bayesian networks termed “learning” which attempt to model the network structure from data; we do not address these approaches here.

Even with probabilities for tumor control and for radiation-induced complications it is not clear how much tumor control one should sacrifice in order to keep the complication probabilities low. We utilize a Markov model to calculate a quality adjusted life expectancy in order to rank treatment plans. A Markov model evaluated with a cohort simulation models probabilistic events by following a simulated cohort of patients through discrete states with defined transition probabilities between states. Utilities for complication and disease states come from the literature. Transition probabilities related to RT treatment are calculated from the Bayesian network, and life expectancies come from the literature.

Next we describe the Bayesian network and the Markov model and the connections between the two. In order to avoid confusion, we denote nodes of the Bayesian network with BN:SMALL CAPITALS and nodes of the Markov model with MM:SMALL CAPITALS.

3 The Bayesian network

Bayesian networks have been described extensively elsewhere [6,7]. We describe only the most basic properties, and introduce notation. The nodes of a Bayesian network represent uncertain events, and the arrows between nodes represent probabilistic dependencies between these events. If nodes A and B influence node X, A and B are said to be the parents of X, and X is said to be the child of A and B. Conditional probability tables provide the quantitative connections between parents and children. The probability that X will take on the value x_i given that the parent states are a_j and b_k is P (X = x_i|A = a_j, B = b_k). The Bayesian network is implemented with Hugin software (www.Hugin.com).

3.1 Tumor control

Our Bayesian network for prostate cancer prognosis following RT is an unconnected network, consisting of three separate networks for tumor control, rectal complications, and bladder complications. The part of the network for tumor control is depicted in Fig. 1. The network calculates the probability that a patient will develop distant metastasis after treatment with RT. There are two paths to distant metastasis: (a) initial lymph node involvement and/or (b) recurrence of the primary. The second path also includes a background rate of distant metastasis, usually attributed to occult metastasis already present at the time of RT.

Fig. 1.

The Bayesian Network to predict the incidence of distant metastasis given a patient's clinical characteristics and an IMRT treatment plan. Shading indicates evidence nodes particular to a patient (white); evidence nodes particular to a given IMRT plan (black); and chance nodes (gray).

Patients with lymph node involvement that is detectable before treatment have a different set of treatment options, and our network does not consider these patients. Our patient cohort may have occult lymph node involvement. The probability of lymph node involvement conditioned on T-stage, Gleason score, and PSA have been determined by examination of nodes after lymphadectomy [8]. BN:Lymph Node Control is the probability that lymph nodes are controlled, conditioned on whether they are involved, and whether they are treated. If the lymph nodes are not controlled the probability to develop distant metastasis is 90%. Treating the lymph nodes affects the probability of normal tissue complication as discussed below.

The conditional probabilities for BN:BNED come from a clinical trial [9]. This study used recursive partitioning techniques to find a joint probability for BNED given three clinical measurements of disease – pretreatment-PSA, Gleason score, and T-stage – and the minimum dose delivered to 95% of the treatment volume (D₉₅). Recursive partitioning generates a decision tree based on many clinical variables and their tree is represented in our node BN:BNED. The study grouped patients into one of four groups with different 5-year BNED probabilities (16%, 41%, 67%, 84%).

Small changes in pretreatment tests or D₉₅ can cause a plan to make a large discrete step between BNED groups. As an example, a patient with a Gleason score of 7, T-stage of T2a, PSA of 15 ng/ml receiving 76.0 Gy of radiation has a predicted cure rate of 41%, but if the dose is increased to just 76.5 Gy the cure rate increases to 84%. We model the a priori probability distribution for BN:D95 as a linear function of D₉₅. In this way we can maintain the discrete dose levels in the original study, and still incorporate the belief of physicians that larger doses are more likely to control the tumor.

Much of the expert-experience driven decision making occurs in the BN:PSA Control node of the network. We consider two IMRT plan parameters related to the size of a radiation “cold spot” in the patient treatment volume (PTV), and the equivalent uniform dose (EUD) [10] which is defined as the actual uniform dose which would result in the same amount of cell killing in the PTV as the non-uniform dose-distribution contained in the treatment plan. We calculate the EUD for prostate tumors using the linear quadratic model following the example of [11]. The conditional probability table for BN:PSA Control reflects the belief that larger values of the equivalent uniform dose and smaller “cold spots” within the PTV increase the probability of tumor control.

We chose to divorce the nodes BN:EUD and BN:PTV Cold Spot from the node BN:BNED by introducing the qualitatively similar node BN:PSA Control for several reasons. Most importantly it reduces one node with 144 conditional probabilities to two nodes with smaller probability tables. This choice of nodes also results in one node, BN:BNED, with a probability table populated by a prospective clinical trial. The conditional probability table for BN:PSA Control is used to incorporate personalized decisions.

The nodes BN:BNED and BN:PSA Control yield the probability that a patient's PSA will be controlled after RT. The prognosis for patients with PSA failure, however, is not well defined. An additional indicator is the post-RT PSA doubling time (PSA-DT) [12]. Patients with a PSA-DT of < 3 months had a 7.0-fold increase in the chance of developing distant metastasis than patients with a a PSA-DT of > 12 months. Our network is for pretreatment plan selection and PSA-DT is not yet known. In order to predict the PSA-DT the patient is placed into a high, medium, or low risk group conditioned on T-stage, Gleason score, and PSA. The conditional probabilities for BN:PSA-DT from BN:RISK GROUP are not explicitly given in [12] and we performed a manual fit to the data. An intermediate-risk patient, for example, has a 12.5%, 12.5%, 25%, 50% probability to have a PSA-DT of < 3, 3−6, 6−12, > 12 months, respectively.

Development of distant metastasis is modeled through two independent causes, one predicted by PSA level, modeled in the node BN:DM1, and one predicted by occult pretreatment lymph node involvement, modeled in the node BN:DM2. Either path leads to distant metastasis, and BN:Distant Metastasis is an “or” node which is positive if either BN:DM1 or BN:DM2 is positive.

P(DM1= yes|PSA Control= no) comes directly from [12]. There are also patients who develop distant metastasis without PSA failure, that is, some patients with a steady PSA level are found to have evidence of clinical failure using, for example, a CT scan, chest X-ray, or tissue biopsy. The sensitivity and specificity for the ASTRO definition of biochemical failure are 73% and 76%, respectively [13], which has been incorporated into the conditional probabilities for P(DM1= yes|PSA Control= yes). The complete conditional probability table for the node BN:DM1 is presented in Table I.

Table 1.

Conditional probability table for BN:DM_1.

PSA Control	yes				no
PSA DT	< 3	3 − 6	6 − 12	>12	< 3	3−6	6 − 12	>12
P(DM_1) = yes	0.12	0.10	0.05	0.02	0.49	0.41	0.20	0.07
P(DM_1) = no	0.88	0.90	0.95	0.98	0.51	0.59	0.80	0.93

3.2 Normal tissue complications

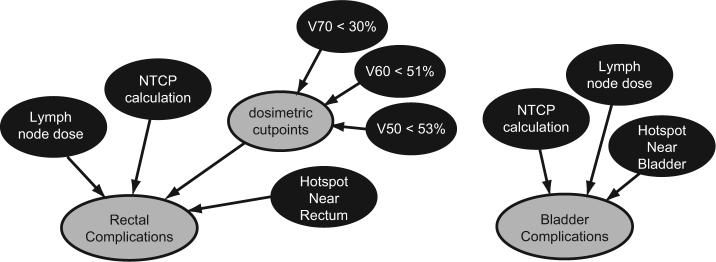
The part of the Bayesian network dedicated to predicting complications is depicted in Fig. 2. In prostate cancer, the rectum and the bladder are the two primary organs at risk for complication. The complication probability is a combination of a normal tissue complication probability (NTCP) computation, a consideration of hotspots in regions near the organ at risk (OAR) at the time of imaging, and three dosimetric objectives. The dosimetric cutpoints are binary – either contained or exceeded by the treatment plan – and come from a retrospective analysis of patient data [14].

Fig. 2.

The Bayesian network to predict the incidence of rectal complications from an NTCP calculation, dosimetric cutpoints, elective lymph node radiation, and the properties of a nearby hotspot. Shading indicates evidence nodes particular to a given IMRT plan (black), and chance nodes (gray)

We calculate the NTCP with the Lyman-Kutcher method [15-17], which relies on clinical data for the uniform radiation dose which results in a 50% complication rate for an organ (T D₅₀) along with parameters describing volume dependence n and slope m of the NTCP vs. dose. There are many studies with clinical data fit to the Lyman-Kutcher model for rectal complications, and the parameters used in our calculation [T D₅₀ = 80.4 Gy, n = 0.148, m = 0.146] are averages from three of these studies [18-20] which use the clinical endpoint of grade 2 rectal bleeding. This endpoint is very similar to the description presented to patients for utility determination (see Sect. 4).

The NTCP model includes dose-volume information using an organ volume as visualized by a CT scan. This choice is based on an anatomically static model and during the course of RT the position of the organ is not fixed and can move into regions which are not considered by the IMRT optimization algorithm. Therefore, a treatment plan which contains a hotspot – defined as a dose higher than T D₅₀ – near an OAR is less desirable than a plan which does not contain a nearby hotspot. Our model considers doses within 1.0 cm of the OAR.

Bladder complications are a less likely side effect of RT, and only one study was found fitting bladder complications to the Lyman-Kutcher model [21]. This study uses an endpoint similar to the bladder complication health state for which we have utility.

4 The Markov model

The Bayesian network predicts the probability over a fixed period of time that a patient will develop distant metastasis and complications due to treatment.

Higher doses to the tumor result in an increased probability of cure, but also result in increased doses to nearby tissue and hence increase the probability of a complication. The choice of a plan is determined by balancing these factors. We use a Markov cohort simulation with a half-cycle correction [22,23] to compute a predicted quality adjusted life expectancy for each plan using probabilities from the Bayesian network, and utilities from the literature for prostate cancer health states.

The Markov model depicted in Fig. 3 has states MM:Post-RT, MM:Distant Metastasis, the absorbing state MM:Death, three tunnel states for the first three years of biochemical failure, and a state for those with biochemical failure who do not develop distant metastasis within the first 3 years. Each state is denoted by a circular node and has associated transition probabilities (denoted by lines with arrows) to move to other states in the model, or to stay in the same state. When the probability for a transition is zero, no line is drawn. The probability for death from natural causes comes from life tables, all other transition probabilities are derived from the Bayesian network as described below.

Fig. 3.

The Markov model used to calculate the quality-adjusted life expectancy of a patient using transition probabilities from the Bayesian network.

We evaluate the Markov model with a cohort simulation with a half-cycle correction [22,23]. The cohort simulation takes into account an annual rate of discounting at 3% [24], and the cycle-length is 1 year. The probability for death from natural causes comes from Social Security Administration (SSA) life tables [25] and is age and gender dependent. The model runs from the time of RT until the patient would be 119 years old, which is the oldest age for which the SSA has life expectancy data. The utilities for health states used in the QALE calculation are previously published [26] and are reproduced in Table II. We use two sets of values, the average values of the utilities reported, and utilities which are 2 standard deviations below the average, representing a complication averse individual. The survival probability for patients who develop distant metastasis is 50% at 5 years. The cohort simulation is calculated with Gnumeric Spreadsheet software.

Table 2.

Utilities for complication states.

Health state	average	complication-averse
Urinary difficulty	0.88	0.62
Bowel problems	0.71	0.19
Urinary and bowel (both)	0.70	0.19
Metastatic cancer	0.25	0.03

Qualitatively the Markov model follows patients through two pathways to distant metastasis, one via biochemical failure after RT, and one directly to distant metastasis without biochemical failure. Both transition probabilities are from the node BN:Distant Metastasis, with different evidence entered into the network. The transition directly to MM:Distant Metastasis is calculated from BN:Distant Metastasis when evidence for BN:PSA Control is entered as YES. When evidence for BN:PSA Control is entered as NO the transitions from the MM:BIOCHEMICAL FAILURE states to MM:Distant Metastasis are calculated from BN:Distant Metastasis. The transition probability into MM:BIOCHEMICAL FAILURE, YEAR 1 is derived from P (BN:PSA Control) when only the initial treatment evidence is entered into the network.

The prognostic probabilities from the Bayesian network are cumulative probabilities for certain events at certain time points, defined by clinical studies. The probability calculated in BN:BNED, for example, is the probability to have biological no evidence of disease at t = 5 years after the beginning of RT. These prognostic, cumulative probabilities are transformed into annual transition probabilities for the Markov model. Each annual transition probability is calculated by assuming a constant annual rate, r_a, related to the cumulative probability of an event from the Bayesian network as p_c = 1 − e^−rat where p_c is a cumulative probability from the Bayesian network, and the subscript a denotes annual. The annual transition probability p_a for the Markov model is then simply p_a = 1 − e^−ra.

The Markov model, however, needs transition probabilities beyond the endpoints of the studies. There are three approaches which could be used in this situation: let the transition probability persist unchanged throughout the lifetime of the cohort simulation, set the transition probability to zero at the time period set by the length of the trial, or reduce the transition probability to a “trickle effect” at the end of the trial. The last option assumes that the trial is long enough to capture most, but not all, of the clinical events. We use the latter two options in our cohort simulation, depending on an extrapolation of published data, and the opinions of experts. Tunnel states are another method which we use to subject patients to a risk for a fixed period of time.

After 5 years the transition probability into MM:BIOCHEMICAL FAILURE, YEAR 1 and the transition probability to develop distant metastasis without biochemical failure is set to zero. The probability for the development of distant metastasis is higher in the first few years after a patient develops a rising PSA level [12]. The model accommodates this with tunnel states for the first three years after biochemical failure. The rate in the later stage is set to one third that of the initial rate. Once the model reaches 15 years post-RT the probability to transition into MM:Distant Metastasis from MM:BIOCHEMICAL FAILURE, YEAR 4 is turned off.

We consider long term complications only, and approximate each complication as occurring at the end of the 2nd year of the simulation and persisting throughout the lifetime of the patient. Complications are assumed to affect each state of the Markov model with an equal probability, and they do not affect transition probabilities into other Markov states. The effects of complications are neglected for patients with metastatic cancer. Complications are computed within the cycle summation of the cohort simulation.

5 Treatment selection

In Fig. 4 we present a sensitivity study for the responses of the QALE and probability to develop distant metastasis from increasing the tumor dose as represented by D₉₅. The probability of complications is tied to increasing dose, and we simultaneously increase the probability of rectal complications linearly from 2% to 7% as dose increases from 70 to 80 Gy. The probability of bladder complications is fixed at half the rate of rectal complications. Risk group classifications are according to the National Comprehensive Cancer Network practice guidelines recurrence risk groups (www.nccn.org).

Fig. 4.

Life expectancy (dashed line), QALE (dot-dased line), and probability of developing distant metastasis for an intermediate risk (left) and a high risk (right) 60 year old patient as a function of D₉₅. The vertical scale on the far left refers to years for the LE plot, and quality-adjusted life-years for the QALE plots, while the vertical scale on the far right refers to the probability of developing distant metastasis.

The intermediate risk patient has a pretreatment PSA level of 15 ng/ml, Gleason score of 7, and TNM stage T2a. The high risk patient has a pretreatment PSA level of 22 ng/ml, Gleason score of 8, and TNM stage T2c. For both patients the lymph node dose was set to yes, the EUD was 20% above D₉₅, and the plan contained a cold spot of 5%. Clinical trials have shown little evidence of improved outcomes by raising the dose of the intermediate risk patient above 74 Gy or for treating a high risk patient with less than 75 Gy [9]. Therefore we examine doses in different ranges for two sample patients. Utilities for health states were the average values listed in Table II. For comparison, a healthy 60 year old man has a life expectancy of 20.0 years [25], and with a 3% discount rate has a QALE of 14.4 years.

In both cases the LE and QALE rise as D₉₅ increases, indicating that for both sample patients, dose escalation is worth the additional complication. For the high risk patient all of the benefit of dose escalation is reaped at 78 Gy, and predicts an increase in life expectancy of 7.2 months, and an increase in QALE of 6.0 months (quality adjusted). A dose escalation from 71 to 74 Gy for the intermediate risk patient predicts an increase in life expectancy of 10.8 months, and an increase in QALE of 8.4 months. The greater increase in QALE as compared to LE for the intermediate risk patient is due to the lower value of D₉₅. With lower doses, a dose escalation does not incur as many additional complications.

This result is robust against variations in the parameters in the model. Specifically, varying the sizes of the effects of BN:EUD and BN:PTV Cold Spot within ranges specified by experts does not change the preferred does for intermediate or high risk patients. Similarly, varying cure rate of a lymph node dose does not change the plan ranking because it affects all plans equally. Whether or not to treat lymph nodes, however, is an option we address in Table III.

Table 3.

QALE for treatments with and without elective whole pelvic radiation therapy.

age	risk group	personality	PORTa	WPRT65%b	WPRT20%c
60	intermediate	no comps	11.8	11.3	10.9
		avg-utils	12.3	12.5	12.1
		LE-max	12.5	13.1	12.7
	high	no comps	8.6	9.4	8.3
		avg-utils	9.5	10.7	9.6
		LE-max	9.6	11.3	10.1
75	intermediate	no comps	6.9	6.6	6.4
		avg-utils	7.2	7.3	7.1
		LE-max	7.3	7.7	7.4
	high	no comps	5.4	5.7	5.1
		avg-utils	5.9	6.5	6.0
		LE-max	6.0	6.8	6.2

^aPORT = prostate only RT.

^bWPRT = whole pelvic RT assuming 65% LN cure rate.

^cWPRT = whole pelvic RT assuming 20% LN cure rate.

Elective lymph node irradiation is generally associated with a higher rate of side effects and is often called whole-pelvic radiation therapy (WPRT) because the entire pelvic region receives radiation [27,28]. Table III presents the QALE for elective lymph node irradiation for 3 sample patients with different attitudes towards life quality with complications. Bold face type indicates when either prostate-only RT or WPRT yield a longer QALE, regardless of the assumed cure rate of whole-pelvic RT. The patient labeled “avg-utils” values each complication state according to the average utilities listed in Table II. The patient “LE-max” makes all decisions in order to maximize life expectancy, regardless of the severity of the complication outcome, and all complication utilities are set to 1.0. A recent study of prostate cancer complication state utilities found that 17% of those surveyed were in this category [29]. For the complication averse patient we used the utilities from Table II which were 2 standard deviation below the average. Intermediate risk patients were modeled to receive 74 Gy, and high risk patients received 78 Gy. For this study we modeled WPRT as increasing the likelihood complications by 8% in each OAR [28]. The prostate-only and whole-pelvic model treatment plans in this study are identical except for the additional cure rate and additional complications from the pelvic dose. In our model the Bayesian network calculates a 26% chance of lymph node involvement (BN:LNI) for the high risk sample patients, and a 10% chance for the intermediate risk patients. The cure rate for elective lymph node irradiation is not known, and we examine two values, a 65% cure rate, and a 20% cure rate, which are varied in the conditional probability table for the node BN:Lymph Node Control.

As expected, the LE maximizing patients receive the most benefit from elective lymph node RT, which has the highest cure rate. For all patients who are stongly complication-averse prostate-only therapy provides the highest QALE. For the high risk sample patients with average utilities the increased likelihood of death from nodal disease spread for prostate-only RT outweighs the increased complication rate incurred from whole-pelvic RT. The choice is more complicated for the sample patients with average attitudes towards risk and for the high-risk complication-averse patients because the choice of treatment plan depends on the treating physician's belief in the curative ability of lymph node irradiation. The QALE values are closer together for older patients because lifetime-persisting complications that occurred at an older age will impact the QALE calculation for a shorter period of time. These sample patients, however, need not be used as treatment guidelines, and are only meant to illustrate the use of the decision aid in treatment selection.

We compare predictions for overall survival and development of distant metastasis from our network with treatment outcomes from a recent clinical study of intermediate and high-risk prostate cancer patients treated with RT [30]. This study followed patients for up to 10 years after treatment, and is one of the only studies to consider both distant metastasis and overall survival as study endpoints. Many clinical studies in prostate RT end with biochemical failure. This patient population received androgen deprivation therapy (ADT) concurrent with RT, beginning two months prior to RT. ADT typically consists of a drug regimine which prevents the release of, or interferes with the actions of male sex hormones with the intended effect of preventing prostate cell growth.

Modeling a clinical study from data presented in the literature has a limitation in that patient data is presented in summary form only in a clinical report. Data sets with age, clinical scoring, treatment information, and outcome are rarely reported. Specifically, the triplet of clinical scoring (Gleason sum, PSA level, and Tstage) taken together have far greater predictive power than each does individually [4]. Furthermore, our model includes patient-specific dosimetry which is not reported by clinical studies. Modeling limitations aside, however, it is instructive to see if a simulated cohort which approximates the averages of clinical information performs similarly to a reported patient cohort. Our simulated cohort includes a patient population with all combination of clinical variables reported by the study, and the contribution of each collection of clinical variables is weighted by the product of the frequencies of each individual variable. All patients are assumed to be the average age in the study, which is 70 years old.

Kaplan-Meier curves for overall survival are presented in Fig. 5. The clinical results include a 95% confidence interval (CI) only for the data point at year 10 of ±3 years, we apply the same CI as an approximation for the entire time course. We have applied a conservative 5% uncertainty to the model prediction to account for the previously mentioned modeling limitations. The model predictions for overall survival in Fig. 5a all fall within the 3 year CI. The model predicts a 5% greater incidence of distant metastasis at year 10 as shown in 5b. The difference between the prediction and clinical results are partly due to the increase in cure rate for some patients with ADT, a complex effect which is not taken into account in the model. This difference is less apparent in the overall survival curve because a small increase in the number of patients who develop distant metastasis will not greatly affect the average overall survival of the group as a whole.

Fig. 5.

a) Overall survival and b) metastasis-free survival from a recent clinical analysis [30] (solid circles) compared with predictions from the model (x marks).

6 Discussion

Previous IMRT plan ranking systems have relied on a subset of the parameters we have included, such as cold spots within the PTV, NTCP, EUD or modified versions of these metrics [31,32]. Only one ranking system seeks to include the beliefs of practicing physicians [33]. None of these works include both clinical results and physician experience, and patient preferences are not considered. These previous publications rank IMRT plans by means of a newly introduced metric, the interpretation of which tends to be opaque to the clinician. The method reported here is the first decision aid in IMRT to combine the major dosimetric parameters of a treatment plan with clinical results, physician experience, and patient preferences.

Previous decision models in prostate cancer have utilized a Markov model and have focused on comparisons of RT vs. radical prostatectomy [34,35,29] or on the cost effectiveness of X-ray radiation therapy [36] or proton radiation therapy [37]. The transition probabilities for these models were taken from the literature and represented average outcomes based only on a patient's pre-treatment characteristics. Prognosis in these models was meant to assist with the decision between treatment modalities. We consider patients who have already elected to receive RT, and our decision model intends to determine which of several RT treatment plans is preferable for a particular patient.

A Bayesian network is well suited to assist with prognosis in IMRT plan selection because physicians draw upon many sources of information to predict an outcome. Clinical trials report on the predictive power of a set of variables chosen before the study begins. Retrospective studies mine past results for predictive variables, many of which are different than those covered in clinical trials. Physicians must combine these sources and they supplement that information with their subjective degree of belief in outcomes.

The Bayesian network described is a model of the radiation therapy process from the perspective of a clinician prescribing radiation therapy. It does not attempt to model the basic causal biological and radiobiological processes of cancer, although there are some such elements. For example, the PSA value and Gleason score are measures of abnormal antigen production and numbers of mitotically abnormal cells which do provide a connection between therapy and the basic processes. Most of the nodes in the model, however, reflect empirical observations that may or may not have direct biological corollaries. It is anticipated that as understanding of the biological basis of prostate cancer grows, our model will develop in parallel.

Prognosis is of central importance in health care, although there have been few previous efforts at developing prognostic Bayesian networks in cancer [38-40]. The uncertainty present in predicting the future, however, makes the Bayesian network formalism well suited to this task, and the usefulness of Bayesian networks for medical prognostication is clearly recognized [41,42]. Part of the problem may lie in the fact that there are often competing outcomes to a cancer treatment, including side effects and complications that can be severe and cannot be neglected when designing a therapy regime for a patient. There are no simple, established methods to use a Bayesian network to rank results with multiple outcomes. Influence diagrams are one attempt to combine utilities and probabilities of outcomes, but as others have noted influence diagrams do not easily lend themselves to the time-dependent task of cost accounting with disease states and utilities [43].

The limitations of the Bayesian network and Markov model are complemented by the strengths of the other in our decision aid. The Bayesian network calculates the probabilities of the set of possible outcomes. The Markov model uses transition probabilities calculated from those probabilities to predict life expectancies. The use of QALE allows us to combine the disparate outcomes in a simple, clinically useful metric.

Our model shows that for prostate cancer treatment decisions the benefits reaped from dose escalation could be worth the additional cost of incurring a higher probability of treatment complications, at least up to the highest doses for which our model has conditional probabilities. This reflects the way in which physicians act in the field of prostate cancer plan selection, and serves as a valuable proof of principle for our decision aid. Future work will include applying our Bayesian network and Markov model-based QALE ranking to cases of IMRT for head-and-neck cancer, which generally have lower survival probabilities, more severe possible complications, and a considerably more complex decision structure.

7 Conclusions

We have developed a prognostic Bayesian network for prostate cancer IMRT plan selection and extended it to calculate a quality adjusted life expectancy using an established, well understood method, a Markov model evaluated with a cohort simulation. By developing a Bayesian network and a Markov model which work in concert we are able to combine clinical reports with physician experience to make detailed predictions as the efficacy of individual plans, and we are able to rank each plan with a QALE calculation. In the context of multiobjective optimization this model provides a more sophisticated method of ranking treatment plans than is available through current standard approaches. The method is the first of its kind in IMRT to simultaneously consider empirical probabilities, physician degree of belief, and patient preferences.