Abstract
Paradigms requiring either a GO or a NO-GO response are often used to study the neural mechanisms of response inhibition. Here this issue is examined from the perspective of event-related beta (14-30 Hz) oscillatory activity. Two macaque monkeys performed a task that began with a self-initiated lever depression and maintenance (sustained motor output) and required a visual pattern discrimination followed by either a lever release (GO) or continued lever-holding (NO-GO) response. Analyzing simultaneous local field potentials (LFPs) from primary somatosensory, frontal motor, and posterior parietal cortices, we report two results. First, beta oscillation desynchronized shortly after stimulus presentation, the onset of which was approximately the same for both the GO and NO-GO conditions (∼110 ms). Since it is well known that beta desynchronization is a reliable indicator of movement preparation, this result suggests that early motor preparation took place in both conditions. Second, following the GO/NO-GO decision (∼190 ms), beta activity rebounded significantly (∼300 ms) only in the NO-GO condition. Coherence and Granger causality measures revealed that the dynamical organization of the rebounded beta network was similar to that existing during the sustained motor output prior to stimulus onset. This finding suggests that response inhibition led to the restoration of the sensorimotor network to its prestimulus state.
Keywords: neural oscillations, movement maintenance, motor preparation, response inhibition, movement execution
The inhibition of inappropriate responses following sensory information analysis and decision making is an important part of goal-oriented behavior. The GO/NO-GO task has been widely used to study the underlying neural mechanisms of response inhibition. In both humans (Kiefer et al., 1998; Falkenstein et al., 1999; Bokura et al., 2001) and nonhuman primates (Sasaki and Gemba, 1986; Sasaki et al., 1989), past research has implicated the prefrontal cortex as the brain region responsible for generating the NO-GO signal that inhibits inappropriate responses. A tacit assumption behind this research is that the motor system initiates active movement preparation upon the reception of stimulus input. After stimulus discrimination and GO/NO-GO decision, movement execution proceeds unimpeded in the GO condition, whereas the motor system is restored back to its prestimulus state by the prefrontal NO-GO signal in the NO-GO condition. Thus far, however, empirical data directly supporting this scenario has been lacking. Single unit evidence of motor preparation in behaving monkeys performing GO/NO-GO paradigms came from the delay period following an instruction cue (Kalaska and Crammond, 1995). ERP studies of movement preparation in humans relied on the P3 component (Jackson et al., 1999) which is known to contain the contribution of many other cognitive factors (Polich and Herbst, 2000; Herrmann and Knight, 2001).
Oscillatory neural activity in the frequency range of 14-30 Hz occurring at both pre- and post-central cortical sites (Murthy and Fetz, 1992; Sanes and Donoghue, 1993; MacKay and Mendonca, 1995; Baker et al., 1997; Baker et al., 1999) is known as the beta rhythm. While its functional role remains only partly explained (Salenius and Hari, 2003; Brovelli et al., 2004; Jensen et al., 2005), the decrease of beta power (desynchronization) relative to a baseline level is considered a reliable indicator of the onset of movement preparation, movement execution and even motor imagery (Pfurtscheller et al., 1997; Pfurtscheller et al., 1997a; Pfurtscheller and Lopes da Silva, 1999; Kuhn et al., 2004). For movement in response to an acute stimulus input, however, the event-related change of beta activity is poorly understood. The first goal of the present study was to evaluate the temporal evolution of beta oscillations in an experimental paradigm where a differential GO or NO-GO response was required based on stimulus discrimination. By comparing the onset latencies of beta desynchronization in both GO and NO-GO conditions, we sought to test the hypothesis that stimulus input triggers motor preparation, irrespective of subsequent response selection.
Brovelli et al. (2004) have characterized the prestimulus state of the sensorimotor system by applying coherence and Granger causality analysis to the aforementioned GO/NO-GO experiment. It is shown that pre- and post-central beta activity is synchronized as part of a coherent network, with the post-central sites exerting causal influence on the pre-central sites. The second goal of the present study was to measure the beta rebound latency and characterize the rebounded beta network with the same coherence and Granger causality analysis employed by Brovelli et al. (2004). The hypothesis to be tested is that beta activity rebounds following the GO/NO-GO decision for the NO-GO condition and the rebounded beta oscillatory network has the same dynamical organization as that of the prestimulus state.
The goals above were accomplished by sampling local field potential data simultaneously from multiple sites in the sensorimotor cortex of two macaque monkeys performing a visuomotor GO/NO-GO task. The adaptive multivariate autoregressive (AMVAR) modeling technique was applied to sliding windows of 100 ms in duration to extract temporal functions of spectral power, coherence and Granger causality (Ding et al., 2000; Kaminski et al., 2001). The data from each window was treated as coming from an approximately piecewise stationary stochastic process. The AMVAR method enabled unbiased estimates of spectral quantities over short analysis windows, and the use of such short windows allowed the relatively accurate determination of the onset latency of both event-related beta desynchronization and rebound.
Experimental Procedures
Paradigm and data acquisition
Two macaque monkeys (GE and LU) were trained to discriminate visual stimuli at the Laboratory of Neuropsychology, National Institute of Mental Health (Bressler et al., 1993; Ledberg et al., 2007). Each stimulus consisted of four solid squares arranged as (1) right-slanted line, (2) left-slanted line, (3) right-slanted diamond, or (4) left-slanted diamond; see Fig. 1(a). The monkey initiated each trial by depressing and holding steady a mechanical lever with the preferred hand. After a variable time delay, one of the four stimuli was shown on a display screen for 100 ms. The monkey released the lever (the GO condition) for one visual pattern type (line or diamond regardless of orientation), and maintained lever depression (the NO-GO condition) for the other. Response time (RT) was defined as the time between stimulus onset and lever release. The experiment was conducted in sessions. GO and NO-GO trials occurred randomly with equal probability within each session. The stimulus-response contingency (line-GO versus diamond-GO) was switched from session to session.
Figure 1.
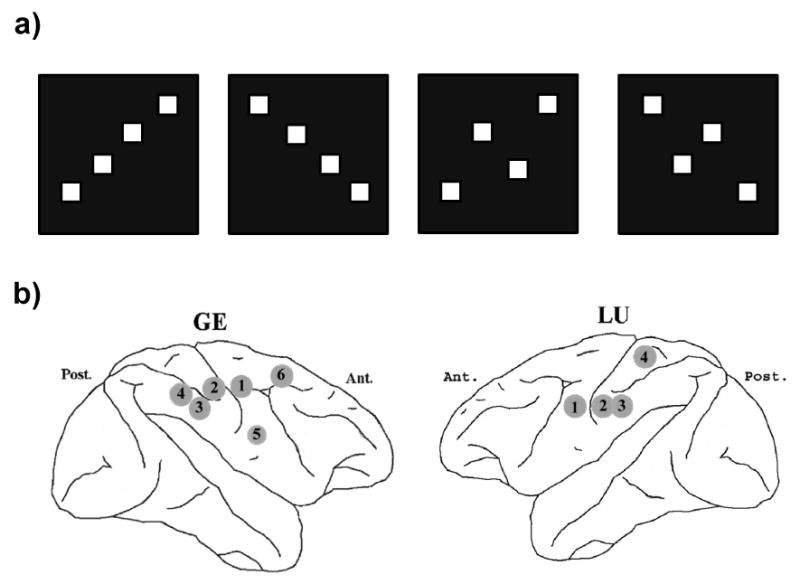
(a) Four types of stimuli. From left to right: right-slanted line, left-slanted line, right-slanted diamond, and right-slanted diamond. (b) A schematic of electrode placement in monkey GE (left) and LU (right). Electrode locations are designated by arbitrary numbers (Brovelli et al., 2004). GE: site 1 = primary motor cortex (M1), site 2 = primary somatosensory cortex (S1), site 3 = posterior parietal cortex (7b), site 4 = posterior parietal cortex (7a), site 5 = ventral premotor cortex, and site 6 = dorsal premotor cortex. LU: site 1 = primary motor cortex (M1), site 2 = primary somatosensory cortex (S1), site 3 = posterior parietal cortex (7b), and site 4 = superior parietal cortex.
Animal care was in accordance with institutional guidelines at the time. Surgical procedures were as previously described (Bressler et al., 1993; Ledberg et al., 2007). Recording sites, marked visually during surgery and verified postmortem, were distributed on a number of gyral regions in the hemisphere contralateral to the performing hand. The sites selected for this study were from pre- and post-central cortical areas of each monkey (6 in GE, right hemisphere and 4 in LU, left hemisphere). A schematic of electrode placement is shown in Fig. 1(b) where the numerical designation is the same as that of a previous report (Brovelli et al., 2004). At each site surface-to-depth LFPs were simultaneously recorded from multiple chronically implanted bipolar teflon-coated platinum electrodes with the less-advanced electrode tip extending ∼0.5 mm into the dura and the more-advanced tip extending ∼2.5 mm into the cortex. The LFP data were analog filtered (-6 dB at 1 and 100 Hz, 6 dB per octave falloff) and digitized at 200 samples/s (Hz). Data acquisition began about 90 ms prior to stimulus onset (0 ms) and continued until 505 ms post stimulus. Trials having artifacts and incorrect behavioral responses (false positive and false negatives) were excluded from further analysis. For each monkey, data from three experimental sessions having similar RT histograms were combined to yield approximately 954 GO trials for GE and 778 GO trials for LU. For the NO-GO condition, matching numbers of trials were chosen from the same sessions.
Data analysis
Sliding window approach
The Adaptive MultiVariate AutoRegressive (AMVAR) modeling method (Ding et al., 2000; Ding et al., 2006) was applied to sliding analysis windows. See Appendix for the mathematical formulation. Each window was 100 ms (20 points) in length and stepped forward in 5 ms increment. A total of 101 windows resulted for the entire recorded time period [-90 ms, 505 ms]. The time designation of each window corresponded to the middle of the covered interval. For each recording site the ensemble mean was removed from each trial. This allowed the residuals to be treated as coming from a zero-mean stochastic process which is required for AMVAR data modeling (Ding et al., 2000). A model order of 10 was determined by the Akaike Information Criterion (Akaike, 1974).
Spectral quantities and their time-frequency plots
For each analysis window, three spectral quantities were estimated: power, coherence, and Granger causality (Ding et al., 2006). See Appendix for their definitions. Power at a given frequency measures the degree of synchronization in a local neural ensemble. Coherence and Granger causality are interdependence measures. Coherence gauges the degree of synchrony between two distant neural ensembles. Granger causality further evaluates whether one neural ensemble exerts a causal influence on another via synaptic transmission (Brovelli et al., 2004; Ding et al., 2006). When combined with the sliding window approach, these spectral quantities appear as time-frequency plots, which give a thorough characterization of the temporal dynamics of an oscillatory neural network. For display, the time-frequency plots were averaged across recording sites for power and pairs of sites for coherence and Granger causality.
Latency of beta desynchronization and rebound
Prominent beta peaks in spectral power were seen in both monkeys in the prestimulus time interval [-90 ms, 0 ms]. For each monkey, the beta frequency range was chosen to be 15-25 Hz for GE and LU, corresponding to peak frequency ± 5 Hz. Power in the beta frequency range averaged over all recording sites was plotted as a function of time with sliding analysis windows. To detect the onset latency of event-related beta desynchronization, beta power in the prestimulus time interval [-90 ms, 0 ms] was used as the baseline for each condition in each monkey. Following stimulus onset, the time at which the averaged beta band power declined 10% compared to the baseline was defined as the onset of beta desynchronization. To detect the onset latency of beta rebound in the NO-GO condition, the minimum value of the post-stimulus beta power function was identified. The time at which this beta power increased by at least 10% above this minimum was defined as the latency of beta rebound. Beta band coherence and Granger causality were also plotted for comparison.
Network analysis
To investigate the dynamical organization of the beta network after its rebound in the NO-GO condition, a post-rebound window of analysis was selected and referred to as the recurrence window. Based on visual inspection of the time-frequency plots of power, coherence and Granger causality, the re-establishment of strong oscillatory activity following the beta rebound in each monkey was ascertained, and the recurrence window was defined to be [395 ms, 505 ms] for GE and [300 ms, 505 ms] for LU. Coherence and Granger causality analysis was performed on the data from the recurrence window and compared with the known results obtained from the experiment during the prestimulus time period (Brovelli et al., 2004).
Significance testing
(1) For coherence and Granger causality during the prestimulus time period, Brovelli et al. (2004) have adopted a random permutation approach (Nichols and Holmes, 2002) to create a baseline null-hypothesis situation for testing the significance of their values in the beta frequency range. Consider the data from two recording sites (A and B). Randomly pairing data for site A with data for site B from a different trial leads to the formation of a synthetic ensemble of trials for which there is no interdependence. Performing such random pairing with many different permutations will result in the null-hypothesis distribution for the interdependence quantity of interest from which a threshold can be derived that corresponds to a given p value. The value from the actual data is compared with the threshold for the assessment of statistical significance. For the recurrence window the same threshold values obtained by Brovelli et al. (2004) for the prestimulus time window were used in order to facilitate the comparison of the network dynamics between the two time periods. (2) Between the GO and the NO-GO conditions there are two temporal functions of averaged beta band power. The statistical significance of their difference was evaluated by calculating the standard deviation of the difference in a prestimulus time interval [-90 ms, 0 ms]. Following stimulus onset, the difference between the two functions at each time point was considered significant if it was more than twice the prestimulus standard deviation. The regions of significant difference were also illustrated on the beta coherence and Granger causality plots for comparison.
Results
Time-frequency analysis
Power spectra were computed and averaged across recording sites in each monkey for each of the sliding analysis windows over the entire trial time period. Coherence and Granger causality spectra were computed for all pairwise combinations of sites and then averaged in each monkey for each window. Fig. 2 shows the result for GE (a) and LU (b) (left column: power; center column: coherence; and right column: Granger causality) where the top row is the GO condition, the middle row is the NO-GO condition, and the bottom row are the beta band power, coherence and Granger causality plotted as functions of time for both conditions.
Figure 2.
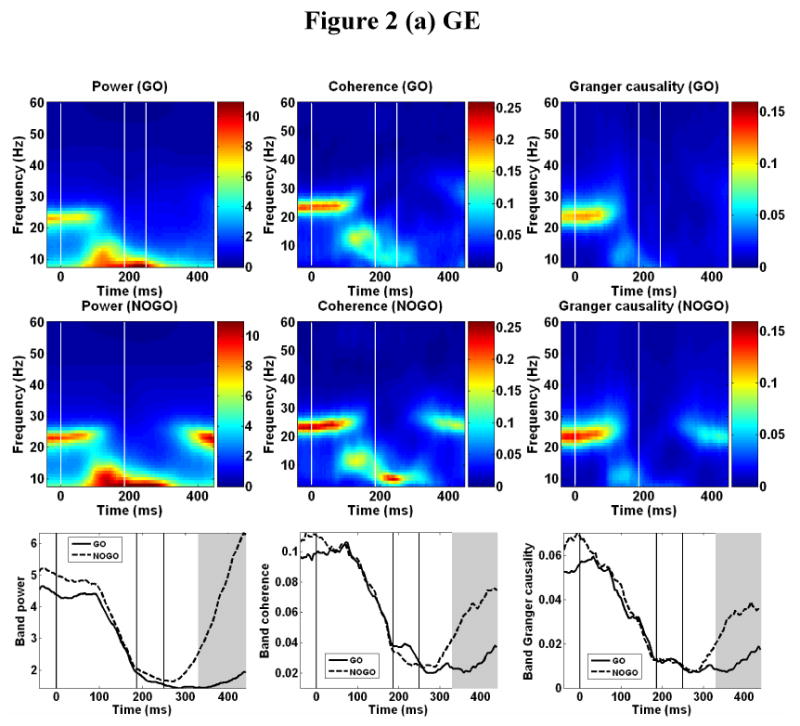
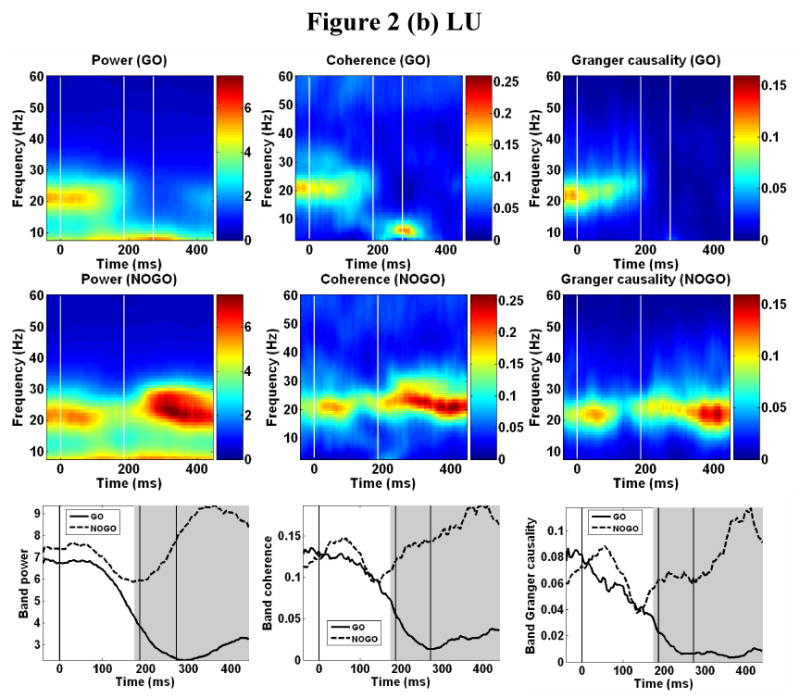
Time-frequency plots. Averaged power spectra (left column) computed over all sites, and averaged coherence spectra (middle column) and Granger causality spectra (right column) computed over all site pairs in GE (a) and LU (b). Top row: GO condition, middle row: NOGO condition, and bottom row: power, coherence, and Granger causality averaged in beta band as functions of time for both GO and NOGO conditions. Here power is in arbitrary units. Gray shading in bottom row indicates regions of significant statistical difference based on beta power. The vertical lines in the plots denote stimulus onset (0 ms), GO/NO-GO decision time, and average response time (GO conditions only), respectively.
Post-stimulus beta desynchronization was seen as a decline in averaged power in the beta frequency range in both the GO and NO-GO conditions. In the GO condition, beta power decreased markedly shortly after stimulus onset. The latency of onset of event-related beta desynchronization was determined to be 108 ms for LU and 118 ms for GE, with an average of 113 ± 7 ms (Mean ± SD). The state of beta depression continued until the end of the recorded period. In the NO-GO condition, beta desynchronization was also observed following stimulus onset, where the onset latency was determined to be 118 ms for LU and 114 ms for GE, with an average of 116 ± 3 ms. However, in contrast to the GO condition, beta activity in the NO-GO condition rebounded significantly at approximately 260 ms for LU and approximately 300 ms for GE. The rebounded beta activity was sustained until the end of the trial. Note that the rebounded beta oscillation in LU was stronger than that existing prior to stimulus onset. Together with beta power, coherence and Granger causality in the beta frequency range decreased rapidly after around 110 ms in both GO and NO-GO conditions, indicating the dissolution or substantial weakening of the beta oscillatory network. For the NO-GO condition, beta coherence and power rebounded with beta power, suggesting that the beta rebound is part of the re-establishment of the oscillatory network that existed prior to the stimulus.
The temporal events (beta desynchronization and rebound) at individual recording sites were largely consistent with that seen in Fig. 2 (not shown). In both monkeys, the post-central sites 2 and 3 desynchronized earlier than the pre-central site 1, and rebounded earlier as well. Sites 5 and 6 in monkey GE had weak beta activity and the events in their time-frequency plots were not as well resolved. A quantitative determination of event onset times is hard to achieve as the data from site to site are highly variable, making the use of a uniform statistical criterion (e.g., 10% change in value against some reference level) difficult to apply. Thus the timing information obtained from the averaged beta power (Fig. 2) was used in the sequel.
Network analysis
Data from the post-rebound recurrence window was subjected to power, coherence and Granger causality analysis. Three recording sites common to both monkeys were selected: site 1 = primary motor (M1), site 2 = primary somatosensory (S1), and site 3 = posterior parietal area 7b. The threshold for significant coherence at p < 0.005 was 0.016 for LU and 0.020 for GE, and for significant Granger causality was 0.011 for LU and 0.012 for GE (Brovelli et al., 2004).
Averaged power, coherence and Granger causality spectra are shown in Fig. 3 for both monkeys. For all three spectral quantities, peaks in the beta frequency range (14 to 30 Hz) are readily identified for both monkeys, demonstrating a high degree of consistency. For each pairwise combination of recording sites (S1-M1, S1-7b and 7b-M1), coherence in the beta frequency range was greater than the threshold and thus deemed to be significant (not shown). The interdependent activity between a pair of sites can be further decomposed into its directional components. As shown in Fig. 4(a) for one pair of sites (S1 and M1 in GE), the significant coherence came from one area exerting unidirectional causal influence on the other (S1→M1 but not vice versa). To further understand the dynamical organization of the beta oscillatory network, such decomposition was carried out for all site pairs. In Figs. 4(b) and 4(c), significant Granger causal influences are indicated by lines with arrowheads whose thickness signifies the magnitude of causal influence in the beta band. In GE, M1 received Granger causal influences from both S1 and 7b. S1 also exerted a relatively strong Granger causal influence on 7b, and received a relatively weak return influence. In LU, a relatively strong Granger causal influence was directed from S1 and 7b to M1, while M1 returned a smaller Granger causal influence to S1 and 7b. As in GE, S1 exerted a relatively strong Granger causal influence on 7b, and received a relatively weak return influence. To further evaluate the contribution of each recording site to the overall network organization we computed the ratio between total Granger causal output and total Granger causal input in the beta range for all the sites. In GE, this ratio was: S1 = 7.40, 7b = 5.20, and M1 = 0 (meaning not significant). In LU, the ratio was: S1 = 4.50, 7b = 1.50, and M1 = 0.28.
Figure 3.
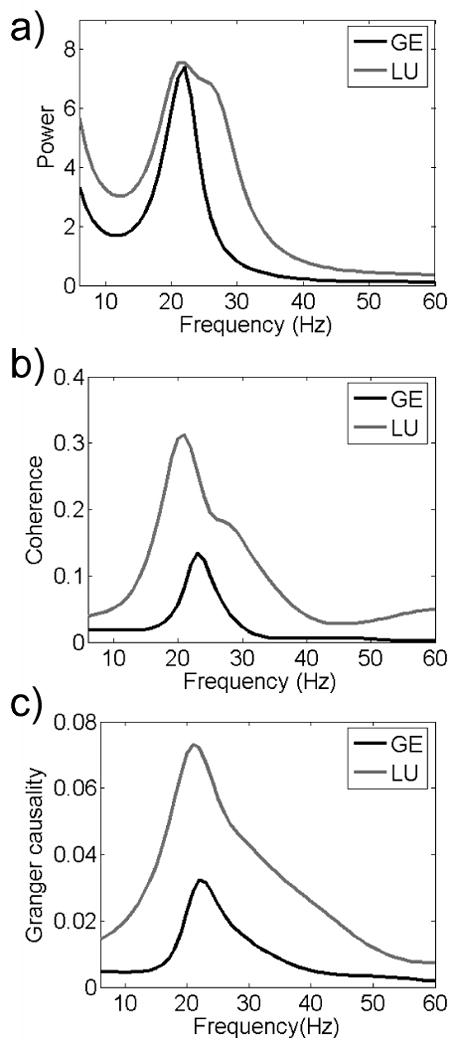
Averaged power spectra over three sites (S1, M1, and 7b) (a), and averaged coherence spectra (b) and averaged Granger causality spectra (c) computed over all pairwise combinations in the recurrence windows for GE (black curves) [395 ms, 505 ms] and LU (gray curves) [300 ms, 505 ms], respectively. Power is in arbitrary units.
Figure 4.
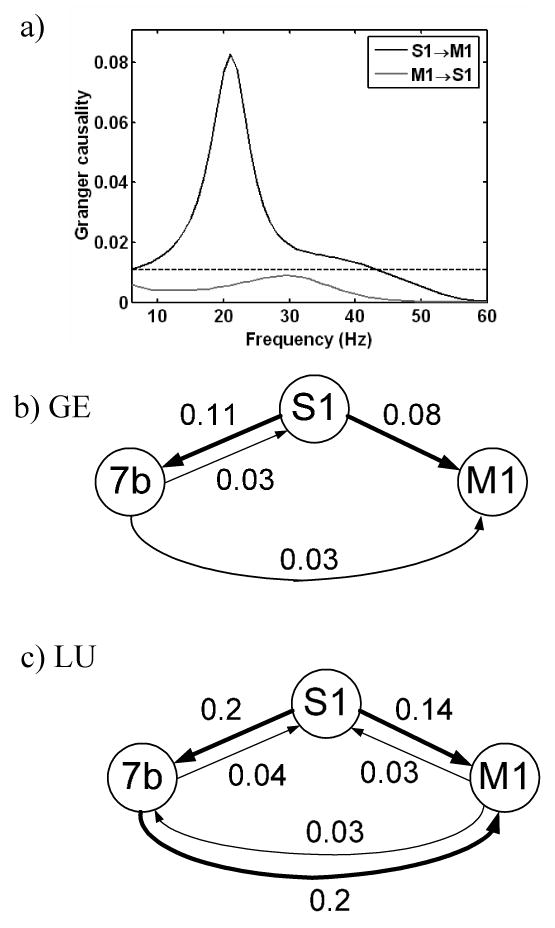
Results of Granger causality analysis. Granger causality spectra for S1→M1 and M1→S1 in GE (a). The horizontal dashed line indicates significance threshold. Schematic diagrams of Granger causal influences during the recurrence window in GE (b) and LU (c). The thickness of the lines between recording sites and the numbers near the lines indicate the Granger causality values in the beta band. The arrowheads indicate the direction of Granger causal influence. S1: primary somatosensory cortex, 7b: posterior parietal cortex, and M1: primary motor cortex.
Discussion
Time-frequency analysis was carried out on local field potentials from the sensorimotor cortex of two macaque monkeys performing a visuomotor GO/NO-GO task. Beta desynchronization was observed for both GO and NO-GO conditions shortly after stimulus onset. Following the GO/NO-GO decision, significant beta rebound occurred in the NO-GO condition, but not in the GO condition within the time interval of recording [-90 ms, 505 ms]. These events can be better understood by examining their latency of occurrence in relation to the timing of stimulus-evoked activation onsets and the response decision obtained from event-related potential (ERP) analysis of the same experiment (Ledberg et al., 2007). In that study, the onset time of stimulus-evoked activation was determined as the time at which the average ERP first began to depart significantly from the baseline, and the time of response decision was determined as the time at which average ERPs from the GO and NO-GO conditions first began to significantly diverge.
Table 1 lists the onset times of: (a) stimulus-evoked activation; (b) beta desynchronization; (c) GO/NO-GO response decision; (d) mean RT for the GO condition, and (e) beta rebound for the NO-GO condition. The stimulus-evoked activation onset time and the GO/NO-GO response decision time for each monkey are taken from Ledberg et al. (2007). The entries in the table are averages of the individual times from all the sites involved in the sensorimotor beta network. The entries for beta desynchronization and rebound are from beta power averaged across recording sites (Fig. 2). From the table, it can be seen that the stimulus-evoked activation preceded the beta desynchronization by 20-30 ms. The latencies of beta desynchronization onset, averaged over the two monkeys, were approximately the same for the GO (113 ± 7 ms) and NO-GO (116 ± 3 ms) conditions. The GO/NO-GO response decision occurred at approximately 190 ms after stimulus onset for both GE and LU. In the GO condition, the mean RT is 250 ms for GE and 272 ms for LU. In the NO-GO condition, beta activity began to rebound around 300 ms for GE and 260 ms for LU. As indicated earlier, the quantitative timing data from individual sites were difficult to ascertain. However, on average, the order of events stays qualitatively the same. In particular, the beta desynchronization time is not significantly different between the GO and the NO-GO conditions.
Table 1.
Event times for monkeys GE and LU.
| Monkey | GE | LU | ||
|---|---|---|---|---|
| Event (ms) | GO | NO-GO | GO | NO-GO |
| Stimulus-evoked activation | 84 | 84 | 88 | 88 |
| Beta desynchronization | 118 | 114 | 108 | 118 |
| GO/NO-GO response decision | 188 | 188 | 186 | 186 |
| Mean response time | 250 | * | 272 | * |
| Beta rebound | * | 300 | * | 260 |
Note: The symbol ‘*’ means the values were not available.
It should be noted that the timing information based on ERPs (Ledberg et al., 2007) has a temporal precision of 5 ms (i.e., the sampling interval), but the timing information for oscillatory activity from the sliding window approach used in the present study is necessarily more smeared. Considering that the time designation for each window is the middle point of the covered time interval (100 ms), event onset from time-frequency analysis tends to get an earlier time label, because the window also senses activity 50 ms beyond its designated time label. Since most of the events in Table 1 are separated by more than 50 ms, their order of occurrence is not affected by the smearing. For the comparison between stimulus-evoked activation (ERP determined event) and beta desynchronization (time-frequency analysis determined event), even though their timing separation is less than 50 ms, as the above reasoning suggests, their order of occurrence is likely to be correct. Thus, while the specific numerical values in Table 1 are good for illustrative purposes, the qualitative order of event onset inferred from these values reflects physiological reality. However, there are situations where the difference in timing resolution between the two approaches can lead to interpretational difficulties. For example, in the bottom row of Fig. 2(b), the divergence between the GO and NO-GO conditions occurred before the GO/NO-GO decision. A likely reason is that, for the point in the divergence zone before the GO/NO-GO decision time, part of the corresponding analysis window sensed activity beyond the GO/NO-GO decision time.
If beta desynchronization is taken as an indication of movement preparation, the above onset latency data support the hypothesis that, when the stimuli for the GO response and the stimuli for the NO-GO response are equally likely, stimulus input triggers preparatory activity in the sensorimotor system. These data further accentuate the importance of the prefrontal cortex and other high order association areas in the inhibition of inappropriate responses in the NO-GO condition for accurate task performance (Pfefferbaum et al., 1985; Sasaki and Gemba, 1986; Sasaki et al., 1989; Jodo and Kayama, 1992; Eimer, 1993; Kiefer et al., 1998; Konishi et al., 1998; Falkenstein et al., 1999; Konishi et al., 1999; Bokura et al., 2001; Liddle et al., 2001; Watanabe et al., 2002; Roche et al., 2004). Specifically, in the absence of this top-down inhibition, movement preparation initiated by stimulus input would likely lead to overt behavioral responses for both the GO and NO-GO conditions. For the latter condition this would constitute a false-positive error.
Response inhibition is thought to be achieved by a “NO-GO signal” propagating from the frontal association cortices to the sensorimotor system (Sasaki and Gemba, 1986; Sasaki et al., 1989; Sasaki et al., 1993; Kiefer et al., 1998; Falkenstein et al., 1999; Bokura et al., 2001). Clearly, such a signal must occur following the GO/NO-GO decision. This is consistent with the observation in Table 1 that beta depression (desynchronization), considered as evidence of continued preparation for possible movement, lasted well beyond the GO/NO-GO decision time for both monkeys. However, it is worth noting that Sasaki et al. (Sasaki and Gemba, 1986; Sasaki et al., 1989; Sasaki et al., 1993) reported that in macaque monkeys the NO-GO bias signal was generated in the prefrontal cortex with a time delay between 110-150 ms. This time is earlier than the GO/NO-GO decision time (∼190 ms) in our data. The use of different experimental paradigms or differences in recording sites may underlie this timing discrepancy.
For the NO-GO condition, beta activity rebounded following the GO/NO-GO decision time in both monkeys. While the neuronal mechanisms of response inhibition are not clear, it may be assumed that beta recurrence signified the termination of movement preparation. For voluntary movement, the post-movement beta rebound is thought to reflect an idling state of the brain (Pfurtscheller et al., 1997b) or active immobilization (Salmelin et al., 1995), and is thought to be independent of sensory input (Salmelin et al., 1995; Pfurtscheller et al., 1996). In the present experiment, the beta rebound took place in the NO-GO condition when there was no overt movement, but it may nonetheless reflect a type of active immobilization.
Our previous work analyzing data from the same experiment for the time period before stimulus onset found that beta activity mediated causal influences from primary somatosensory cortex (S1) to posterior parietal area 7b, and from both S1 and 7b to primary motor cortex M1 (Brovelli et al., 2004; Chen et al., 2006; Ding et al., 2006). Based on these results it was hypothesized that the functional role of the beta network is to facilitate the processing of sensory feedback information for the maintenance of the depressed hand lever. For the NO-GO condition, as the lever pressure was maintained until the end of the recorded time period, it is thus reasonable to suggest that beta rebound signaled the resumption of the same network in support of sensorimotor integration. We tested this idea in the present study by analyzing the Granger causality patterns among S1, M1 and 7b for both monkeys in the beta recurrence window following the GO/NO-GO decision time. Essentially, the same pattern of connectivity as that during the prestimulus time period was found after beta rebound. In particular, the ratio between total causal output and total causal input was highest at the primary somatosensory site in both monkeys, indicating a sensory processing bias in the network's function. This result can also be seen as lending support to the notion that sensory feedback is important in the organization of coherent beta oscillatory activity (Conway et al., 1995; Baker et al., 1997; Baker et al., 1999; Kilner et al., 2000; Cassim et al., 2001; Kilner et al., 2003; Brovelli et al., 2004). Baker et al. (1997, 1999) showed that, during a precision grip task, sensorimotor beta oscillations were coherent with contralateral hand EMG. Cassim et al. (2001) reported that beta synchronization disappeared after subjects were sensory-deafferented.
In sum, power, coherence and Granger causality in the beta frequency range as functions of time were shown to yield information that complements the traditional event-related potential studies. While these functions may not directly shed light on the neural mechanisms of response preparation and inhibition, they could nevertheless reliably indicate, via beta desynchronization and rebound, the onset and the completion of these two events, respectively. When contrasted between GO and NO-GO conditions, these timing data supported the conclusions that (1) response preparation is initiated upon reception of stimulus input regardless of future response selection and (2) for the NO-GO condition the sensorimotor cortex is restored to the prestimulus state upon the completion of response inhibition.
Acknowledgments
This work was supported by National Institute of Mental Health Grants MH064204, MH071620, and MH070498. We thank the referees for insightful comments.
List of abbreviations
- RT
response time
- ERP
event-related potential
- LFP
local field potential
- AMVAR
adaptive multivariate autoregressive
- SD
standard deviation
- S1
primary somatosensory cortex
- M1
primary motor cortex
- 7b
posterior parietal area 7b
Appendix
The essential steps of the AMVAR spectral analysis can be summarized as follows. Consider a specific analysis window. Let p channels of LFP recordings at time t be denoted by Xt =(x1t,x2t,…,xpt)T where T stands for matrix transposition. Assume that the data are described by a MultiVariate AutoRegressive (MVAR) model:
| (1) |
where Et is a temporally uncorrelated residual error series with covariance matrix Σ, and Ak are p×p coefficient matrices to be estimated from data (Ding et al., 2000; Ding et al., 2006). The MVAR model order m was determined by the Akaike Information Criterion (AIC) (Akaike, 1974). For the data analyzed in this study m = 10 (50 ms) was chosen as a tradeoff between sufficient spectral resolution and over-parameterization. Once the model coefficients Ak and Σ are estimated, the spectral matrix can be evaluated as
| (2) |
where the asterisk denotes matrix transposition and complex conjugation and is the transfer function. The power spectrum of channel l is given by Sll(f) which is the l-th diagonal element of the spectral matrix S(f). The coherence spectrum between channel l and channel k is:
| (3) |
The value of coherence ranges from one to zero, with one indicating maximum interdependence between channel l and channel k at frequency f and zero indicating no interdependence. For p=2 in Eq. (1) the Granger causality spectrum from x2t to x1t is defined as (Geweke, 1982; Brovelli et al., 2004)
| (4) |
which can be interpreted as the proportion of x2t 's causal contribution to the power of the x1t series at frequency f. The logarithm is taken to preserve certain favorable statistical properties. Similarly, the causality spectrum from x1t and x2t can be obtained by switching the indices 1 and 2 in Eq. (4). The MVAR model is fit adaptively to each sliding window, resulting in the time-frequency plots of power, coherence and Granger causality.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Akaike H. New Look at Statistical-Model Identification. IEEE Trans Automat Contr Ac. 1974;19:716–723. [Google Scholar]
- Baker SN, Kilner JM, Pinches EM, Lemon RN. The role of synchrony and oscillations in the motor output. Exp Brain Res. 1999;128:109–117. doi: 10.1007/s002210050825. [DOI] [PubMed] [Google Scholar]
- Baker SN, Olivier E, Lemon RN. Coherent oscillations in monkey motor cortex and hand muscle EMG show task-dependent modulation. J Physiol. 1997;501(Pt 1):225–241. doi: 10.1111/j.1469-7793.1997.225bo.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bokura H, Yamaguchi S, Kobayashi S. Electrophysiological correlates for response inhibition in a Go/NoGo task. Clin Neurophysiol. 2001;112:2224–2232. doi: 10.1016/s1388-2457(01)00691-5. [DOI] [PubMed] [Google Scholar]
- Bressler SL, Coppola R, Nakamura R. Episodic multiregional cortical coherence at multiple frequencies during visual task performance. Nature. 1993;366:153–156. doi: 10.1038/366153a0. [DOI] [PubMed] [Google Scholar]
- Brovelli A, Ding M, Ledberg A, Chen Y, Nakamura R, Bressler SL. Beta oscillations in a large-scale sensorimotor cortical network: directional influences revealed by Granger causality. Proc Natl Acad Sci U S A. 2004;101:9849–9854. doi: 10.1073/pnas.0308538101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cassim F, Monaca C, Szurhaj W, Bourriez JL, Defebvre L, Derambure P, Guieu JD. Does post-movement beta synchronization reflect an idling motor cortex? Neuroreport. 2001;12:3859–3863. doi: 10.1097/00001756-200112040-00051. [DOI] [PubMed] [Google Scholar]
- Chen Y, Bressler SL, Ding M. Frequency decomposition of conditional Granger causality and application to multivariate neural field potential data. J Neurosci Methods. 2006;150:228–237. doi: 10.1016/j.jneumeth.2005.06.011. [DOI] [PubMed] [Google Scholar]
- Conway BA, Halliday DM, Farmer SF, Shahani U, Maas P, Weir AI, Rosenberg JR. Synchronization between motor cortex and spinal motoneuronal pool during the performance of a maintained motor task in man. J of Physiol (Lond) 1995;489:917–924. doi: 10.1113/jphysiol.1995.sp021104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ding M, Chen Y, Bressler SL. Granger Causality: Basic Theory and Application to Neuroscience. In: Schelter B, W M, Timmer J, editors. Handbook of Time Series Analysis. Weinheim: Wiley-VCH Verlag; 2006. pp. 437–460. [Google Scholar]
- Ding MZ, Bressler SL, Yang WM, Liang HL. Short-window spectral analysis of cortical event-related potentials by adaptive multivariate autoregressive modeling: data preprocessing, model validation, and variability assessment. Biol Cybern. 2000;83:35–45. doi: 10.1007/s004229900137. [DOI] [PubMed] [Google Scholar]
- Eimer M. Effects of Attention and Stimulus Probability on Erps in a Go/Nogo Task. Biol Psychol. 1993;35:123–138. doi: 10.1016/0301-0511(93)90009-w. [DOI] [PubMed] [Google Scholar]
- Falkenstein M, Hoormann J, Hohnsbein J. ERP components in Go/Nogo tasks and their relation to inhibition. Acta Psychol (Amst) 1999;101:267–291. doi: 10.1016/s0001-6918(99)00008-6. [DOI] [PubMed] [Google Scholar]
- Herrmann CS, Knight RT. Mechanisms of human attention: event-related potentials and oscillations. Neurosci Biobehav Rev. 2001;25:465–476. doi: 10.1016/s0149-7634(01)00027-6. [DOI] [PubMed] [Google Scholar]
- Jackson SR, Jackson GM, Roberts M. The selection and suppression of action: ERP correlates of executive control in humans. Neuroreport. 1999;10:861–865. doi: 10.1097/00001756-199903170-00035. [DOI] [PubMed] [Google Scholar]
- Jensen O, Goel P, Kopell N, Pohja M, Hari R, Ermentrout B. On the human sensorimotor-cortex beta rhythm: sources and modeling. Neuroimage. 2005;26:347–355. doi: 10.1016/j.neuroimage.2005.02.008. [DOI] [PubMed] [Google Scholar]
- Jodo E, Kayama Y. Relation of a Negative ERP Component to Response-Inhibition in a Go/No-Go Task. Electroencephalogr Clin Neurophysiol. 1992;82:477–482. doi: 10.1016/0013-4694(92)90054-l. [DOI] [PubMed] [Google Scholar]
- Kalaska JF, Crammond DJ. Deciding Not to Go - Neuronal Correlates of Response Selection in a Go/Nogo Task in Primate Premotor and Parietal Cortex. Cereb Cortex. 1995;5:410–428. doi: 10.1093/cercor/5.5.410. [DOI] [PubMed] [Google Scholar]
- Kaminski M, Ding MZ, Truccolo WA, Bressler SL. Evaluating causal relations in neural systems: Granger causality, directed transfer function and statistical assessment of significance. Biol Cybern. 2001;85:145–157. doi: 10.1007/s004220000235. [DOI] [PubMed] [Google Scholar]
- Kiefer M, Marzinzik F, Weisbrod M, Scherg M, Spitzer M. The time course of brain activations during response inhibition: evidence from event-related potentials in a go no go task. Neuroreport. 1998;9:765–770. doi: 10.1097/00001756-199803090-00037. [DOI] [PubMed] [Google Scholar]
- Kilner JM, Baker SN, Salenius S, Hari R, Lemon RN. Human cortical muscle coherence is directly related to specific motor parameters. J Neurosci. 2000;20:8838–8845. doi: 10.1523/JNEUROSCI.20-23-08838.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kilner JM, Salenius S, Baker SN, Jackson A, Hari R, Lemon RN. Task-dependent modulations of cortical oscillatory activity in human subjects during a bimanual precision grip task. Neuroimage. 2003;18:67–73. doi: 10.1006/nimg.2002.1322. [DOI] [PubMed] [Google Scholar]
- Konishi S, Nakajima K, Uchida I, Kikyo H, Kameyama M, Miyashita Y. Common inhibitory mechanism in human inferior prefrontal cortex revealed by event-related functional MRI. Brain. 1999;122:981–991. doi: 10.1093/brain/122.5.981. [DOI] [PubMed] [Google Scholar]
- Konishi S, Nakajima K, Uchida I, Sekihara K, Miyashita Y. No-go dominant brain activity in human inferior prefrontal cortex revealed by functional magnetic resonance imaging. Eur J Neurosci. 1998;10:1209–1213. doi: 10.1046/j.1460-9568.1998.00167.x. [DOI] [PubMed] [Google Scholar]
- Kuhn AA, Williams D, Kupsch A, Limousin P, Hariz M, Schneider GH, Yarrow K, Brown P. Event-related beta desynchronization in human subthalamic nucleus correlates with motor performance. Brain. 2004;127:735–746. doi: 10.1093/brain/awh106. [DOI] [PubMed] [Google Scholar]
- Ledberg A, Bressler SL, Ding MZ, Coppola R, Nakamura R. Large-scale visuomotor integration in the cerebral cortex. Cereb Cortex. 2007;17:44–62. doi: 10.1093/cercor/bhj123. [DOI] [PubMed] [Google Scholar]
- Liddle PF, Kiehl KA, Smith AM. Event-related fMRI study of response inhibition. Hum Brain Mapp. 2001;12:100–109. doi: 10.1002/1097-0193(200102)12:2<100::AID-HBM1007>3.0.CO;2-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKay WA, Mendonca AJ. Field potential oscillatory bursts in parietal cortex before and during reach. Brain Res. 1995;704:167–174. doi: 10.1016/0006-8993(95)01109-9. [DOI] [PubMed] [Google Scholar]
- Murthy VN, Fetz EE. Coherent 25- to 35-Hz oscillations in the sensorimotor cortex of awake behaving monkeys. Proc Natl Acad Sci U S A. 1992;89:5670–5674. doi: 10.1073/pnas.89.12.5670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nichols TE, Holmes AP. Nonparametric permutation tests for functional neuroimaging: A primer with examples. Hum Brain Mapp. 2002;15:1–25. doi: 10.1002/hbm.1058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pfefferbaum A, Ford JM, Weller BJ, Kopell BS. ERPs to Response Production and Inhibition. Electroencephalogr Clin Neurophysiol. 1985;60:423–434. doi: 10.1016/0013-4694(85)91017-x. [DOI] [PubMed] [Google Scholar]
- Pfurtscheller G, Lopes da Silva FH. Event-related EEG/MEG synchronization and desynchronization: basic principles. Clin Neurophysiol. 1999;110:1842–1857. doi: 10.1016/s1388-2457(99)00141-8. [DOI] [PubMed] [Google Scholar]
- Pfurtscheller G, Neuper C. Motor imagery activates primary sensorimotor area in humans. Neurosci Lett. 1997;239:65–68. doi: 10.1016/s0304-3940(97)00889-6. [DOI] [PubMed] [Google Scholar]
- Pfurtscheller G, Neuper C, Andrew C, Edlinger G. Foot and hand area mu rhythms. Int J Psychophysiol. 1997a;26:121–135. doi: 10.1016/s0167-8760(97)00760-5. [DOI] [PubMed] [Google Scholar]
- Pfurtscheller G, Stancak A, Jr, Edlinger G. On the existence of different types of central beta rhythms below 30 Hz. Electroencephalogr Clin Neurophysiol. 1997b;102:316–325. doi: 10.1016/s0013-4694(96)96612-2. [DOI] [PubMed] [Google Scholar]
- Pfurtscheller G, Stancak A, Jr, Neuper C. Post-movement beta synchronization. A correlate of an idling motor area? Electroencephalogr Clin Neurophysiol. 1996;98:281–293. doi: 10.1016/0013-4694(95)00258-8. [DOI] [PubMed] [Google Scholar]
- Polich J, Herbst KL. P300 as a clinical assay: rationale, evaluation, and findings. International J Psychophysiol. 2000;38:3–19. doi: 10.1016/s0167-8760(00)00127-6. [DOI] [PubMed] [Google Scholar]
- Roche RAP, Dockree PM, Garavan H, Foxe JJ, Robertson IH, O'Mara SM. EEG alpha power changes reflect response inhibition deficits after traumatic brain injury (TBI) in humans. Neurosci Lett. 2004;362:1–5. doi: 10.1016/j.neulet.2003.11.064. [DOI] [PubMed] [Google Scholar]
- Salenius S, Hari R. Synchronous cortical oscillatory activity during motor action. Curr Opin Neurobiol. 2003;13:678–684. doi: 10.1016/j.conb.2003.10.008. [DOI] [PubMed] [Google Scholar]
- Salmelin R, Hamalainen M, Kajola M, Hari R. Functional segregation of movement-related rhythmic activity in the human brain. Neuroimage. 1995;2:237–243. doi: 10.1006/nimg.1995.1031. [DOI] [PubMed] [Google Scholar]
- Sanes JN, Donoghue JP. Oscillations in local field potentials of the primate motor cortex during voluntary movement. Proc Natl Acad Sci U S A. 1993;90:4470–4474. doi: 10.1073/pnas.90.10.4470. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sasaki K, Gemba H. Electrical activity in the prefrontal cortex specific to no-go reaction of conditioned hand movement with colour discrimination in the monkey. Exp Brain Res. 1986;64:603–606. doi: 10.1007/BF00340499. [DOI] [PubMed] [Google Scholar]
- Sasaki K, Gemba H, Nambu A, Matsuzaki R. No-go activity in the frontal association cortex of human subjects. Neurosci Res. 1993;18:249–252. doi: 10.1016/0168-0102(93)90062-u. [DOI] [PubMed] [Google Scholar]
- Sasaki K, Gemba H, Tsujimoto T. Suppression of visually initiated hand movement by stimulation of the prefrontal cortex in the monkey. Brain Res. 1989;495:100–107. doi: 10.1016/0006-8993(89)91222-5. [DOI] [PubMed] [Google Scholar]
- Watanabe J, Sugiura M, Sato K, Sato Y, Maeda Y, Matsue Y, Fukuda H, Kawashima R. The human prefrontal and parietal association cortices are involved in NO-GO performances: An event-related fMRI study. Neuroimage. 2002;17:1207–1216. doi: 10.1006/nimg.2002.1198. [DOI] [PubMed] [Google Scholar]


