Proper Analysis of Secondary Phenotype Data in Case-Control Association Studies

Abstract

Case-control association studies often collect extensive information on secondary phenotypes, which are quantitative or qualitative traits other than the case-control status. Exploring secondary phenotypes can yield valuable insights into biological pathways and identify genetic variants influencing phenotypes of direct interest. All publications on secondary phenotypes have used standard statistical methods, such as least-squares regression for quantitative traits. Because of unequal selection probabilities between cases and controls, the case-control sample is not a random sample from the general population. As a result, standard statistical analysis of secondary phenotype data can be extremely misleading. Although one may avoid the sampling bias by analyzing cases and controls separately or by including the case-control status as a covariate in the model, the associations between a secondary phenotype and a genetic variant in the case and control groups can be quite different from the association in the general population. In this article, we present novel statistical methods that properly reflect the case-control sampling in the analysis of secondary phenotype data. The new methods provide unbiased estimation of genetic effects and accurate control of false-positive rates while maximizing statistical power. We demonstrate the pitfalls of the standard methods and the advantages of the new methods both analytically and numerically. The relevant software is available at our website.

INTRODUCTION

There is a proliferation of genomewide association (GWA) studies worldwide. These studies usually employ the case-control design, which consists of a sample of cases (i.e. diseased individuals) and a sample of controls (i.e., disease-free individuals). Most GWA studies measure a variety of quantitative or qualitative traits other than the disease trait that defines the case-control status. Exploring these secondary phenotypes can discover genetic variants influencing previously unstudied phenotypes and provide important clues about causal pathways. Although the main interest of case-control association studies lies in the comparison of cases and controls, analysis of secondary phenotype data may supplement the case-control comparison in the initial reports or become the primary focus of subsequent publications.

Indeed, recent months have seen an explosion of publications on genetic variants influencing human quantitative traits, such as height [Weedon et al., 2007; Sanna et al., 2008; Weedon et al., 2008; Lettre et al., 2008; Gudbjartsson et al., 2008], body mass index (BMI) [Frayling et al., 2007; Loos et al., 2008], and lipid levels [Saxena et al., 2007; Willer et al., 2008; Kathiresan et al., 2008]. The data for those publications came mostly from case-control association studies of complex diseases (e.g., diabetes, cancer and hypertension). The most recent publications were based on meta-analysis of multiple GWA studies involving thousands or tens of thousands of individuals.

All publications on quantitative traits have relied on standard linear regression analysis (i.e., classical least-squares estimation under the linear model). Five types of analysis have been conducted to assess the effects of SNPs on quantitative traits using data from case-control association studies: (1) controls only; (2) cases only; (3) combined sample of cases and controls; (4) meta-analysis of cases and controls; (5) joint analysis of cases and controls adjusted for the disease status. Methods (1) and (2) are restricted to controls and cases, respectively. Method (3) analyzes cases and controls together and ignores the disease status. In method (4), cases and controls are analyzed separately and the results are combined by a meta-analytic procedure. Method (5) analyzes cases and controls together and includes the disease status as a covariate in the model.

None of the aforementioned analysis methods is statistically correct. Because cases and controls are selected at different rates from their respective subpopulations, the case-control sample does not constitute a random sample of the general population. As a result, the population association between a SNP and a secondary trait can be distorted in the case-control sample. Thus, method (3) can be grossly misleading, especially when the secondary trait is strongly correlated with the disease and the sampling rates are very different between cases and controls. The other four methods are conditional on the disease status and are thus unaffected by the biased case-control sampling. However, the associations between a SNP and a secondary trait in the case and control groups can be quite different from the association in the general population if the secondary trait is correlated with the disease.

To illustrate the above points, we consider a dichotomous secondary trait taking the values 0 and 1 with equal probability and a SNP with minor allele frequency (MAF) of 0.2. Assume that the disease rate is 10%, the odds ratio of disease with the SNP is 1.5 under the dominant mode of inheritance, and the odds ratio of disease with the secondary trait is 2. If the SNP is unrelated to the secondary trait in the general population (i.e., the odds ratio is 1), then the odds ratios of the secondary trait with the SNP will be approximately 0.975 in the case and control groups, and the odds ratio in the combined sample of cases and controls with an equal number of cases and controls will be approximately 1.045; see Table I for details. In other words, there exist (spurious) associations between the SNP and the secondary trait in the case and control groups, as well as in the combined sample, despite the absence of association at the population level. This phenomenon implies that methods (1), (2) and (3) are all biased; methods (4) and (5) are also biased because they combine the biased results from the case and control groups. Because GWA studies typically have large sample sizes, even modest levels of bias can lead to grossly inflated false-positive rates, especially in meta-analysis.

TABLE I.

Probability distributions of disease status, genotype score and secondary trait in a case-control setting

General population
Genotype score	Secondary trait
	0	1
0	0.32	0.32
1	0.18	0.18
Odds ratio = 1

Cases
Genotype score	Secondary trait
	0	1
0	0.0192	0.0362
1	0.0157	0.0289
Odds ratio = 0.975

Controls
Genotype score	Secondary trait
	0	1
0	0.3008	0.2838
1	0.1643	0.1511
Odds ratio = 0.975

Case-control sample
Genotype score	Secondary trait
	0	1
0	0.2631	0.3387
1	0.1698	0.2285
Odds ratio = 1.045

The fact that method (3) is biased seems to contradict with the universally accepted practice of performing standard logistic regression on case-control data. Standard logistic regression analysis of case-control data indeed yields correct maximum likelihood estimates of odds ratios, although the estimate of the disease rate is generally biased [Prentice and Pyke, 1979]. This remarkable result, however, applies only to the primary disease outcome that defines the case-control status, and not to a secondary outcome that is correlated with the disease.

We have developed valid and efficient statistical methods to analyze secondary phenotype data in case-control association studies. Our methods are based on likelihood functions that properly reflect the case-control sampling. The corresponding maximum likelihood estimates are approximately unbiased and normally distributed. Furthermore, the estimates are statistically efficient in that they have the smallest variances among all valid estimates, and the corresponding association tests are the most powerful among all valid tests.

In the next section, we describe in more detail the ingredients of the new methods and the pitfalls of standard methods, particularly methods (1)-(5). In the subsequent Results section, we use Monte Carlo simulation to quantify the bias of standard methods in common situations and to evaluate the operating characteristics of the new methods. We relegate the technical details about the new and standard methods to Appendices A and B, respectively.

METHODS

NEW METHODS

Let D denote the case-control status (1 = disease; 0 = no disease) and Y denote the secondary phenotype. Also, let X denote the genotype score for a SNP of interest. Under the additive mode of inheritance, X is the number of minor alleles; under the dominant (recessive) model, X indicates, by the values 1 versus 0, whether or not the individual carries at least one minor allele (two minor alleles). We use a generalized linear model to formulate the effects of X on Y, and write the conditional density of Y given X as P(Y|X). If Y is a quantitative trait, we use the linear regression model, which specifies that the conditional distribution of Y given X is normal with mean β₀ + β₁X and variance σ². If Y is a dichotomous trait, we use the logistic regression model, under which

$$P\left(Y=1|X\right)=\frac{e^{{\beta }_0+{\beta }_{1}X}}{1+e^{{\beta }_0+{\beta }_{1}X}}.$$

We relate Y and X to D through the logistic regression model

$$P\left(D=1|X,Y\right)=\frac{e^{{\gamma }_0+{\gamma }_{1}X+{\gamma }_{2}Y}}{1+e^{{\gamma }_0+{\gamma }_{1}X+{\gamma }_{2}Y}}.$$

We are mainly interested in β₁.

For a case-control study with a total of n subjects, the data consist of (D_i, Y_i, X_i) (i = 1,…, n). Because the sampling is conditional on the case-control status, the likelihood function takes the retrospective form, ${\mathrm{\Pi }}_{i=1}^{n}P\left(Y_i,X_i|D_i\right),$ which is

$$\underset{i=1}{\overset{n}{\mathrm{\Pi }}}{\left\{\frac{P\left(D_i=1|X_i,Y_i\right)P\left(Y_i|X_i\right)P\left(X_i\right)}{P\left(D_i=1\right)}\right\}}^{D_i}{\left\{\frac{P\left(D_i=0|X_i,Y_i\right)P\left(Y_i|X_i\right)P\left(X_i\right)}{P\left(D_i=0\right)}\right\}}^{1-D_i},$$

where P(D_i = 1) = Σ_yΣ_x P(D_i = 1|x, y)P (y|x)P(x), P(D_i = 0) = 1 − P(D_i = 1), and P(D_i = 0|X_i, Y_i) = 1 − P(D_i = 1|X_i, Y_i). We maximize this function by the Newton-Raphson algorithm. Likelihood-based statistics (i.e., Wald, score and likelihood-ratio statistics) can be used to make inference about the parameter of main interest β₁.

The estimation of γ₀ may be unstable, especially for dichotomous Y. When the disease is rare such that P(D = 1|X, Y) ≈ e^{γ₀+γ₁X+γ₂Y}, the parameter γ₀ cancels in the numerator and denominator of the likelihood function. When the disease is not rare but the disease rate is known approximately, we can incorporate the information about the disease rate into the estimation. We can include environmental covariates in the models for Y and for D, but then the probability distribution of continuous environmental covariates will enter into the likelihood function as a high-dimensional nuisance parameter. We eliminate such nuisance parameters through the profile-likelihood approach. The interested readers are referred to Appendix A for the theoretical and computational details of the new methods.

STANDARD METHODS

As described in the Introduction section, standard statistical methods have been applied to the secondary phenotype data from case-control studies in five different ways, which we will refer to as methods (1)-(5). Methods (1)-(3) are based on the prospective likelihood function Π_i P(Y_i|X_i), where the product is taken over the controls, the cases or all study subjects. The maximization of this function yields the classical least-squares estimation for quantitative traits and the standard logistic regression for dichotomous traits. Method (4) combines the least-squares or odds ratio estimates of the case and control samples through the inverse-variance meta-analysis procedure. Method (5) is based on the prospective likelihood function ${\mathrm{\Pi }}_{i=1}^{n}P(Y_i|X_i,D_i),$ which is a parametric way of combining the results of the case and control samples.

We have conducted a thorough investigation into the properties of the five standard methods. We state here the main conclusions while relegating the details to Appendix B. If the secondary phenotype is not related to the case-control status, or more precisely, D is independent of Y given X (i.e., γ₂ = 0), then all five methods are valid. If the SNP is not associated with the case-control status, or more precisely, D is independent of X given Y (i.e., γ₁ = 0), then all five methods yield correct estimates of odds ratios for dichotomous traits, but the least-squares estimates for quantitative traits produced by the five methods are biased unless β₁ = 0 or γ₂ = 0. When the disease is rare in that the probability of disease is virtually 0, all standard methods except (3) are approximately valid.

The fact that standard methods are generally invalid unless γ₁ = 0 or γ₂ = 0 is disconcerting. Most secondary phenotypes are strongly correlated with the case-control status, so that γ₂ ≠ 0. Thus, any SNPs that are associated with the case-control status will tend to be detected as being associated with secondary phenotypes by standard methods even when the latter associations do not exist. When the associations truly exist, all five methods may produce estimates that are biased toward the null and thus reduce statistical power.

RESULTS

We conducted extensive simulation studies to assess the performance of the standard and new methods in the analysis of secondary quantitative traits. We considered a SNP with MAF of 0.3 and additive mode of inheritance. For the model of the secondary quantitative trait, we set β₀ = σ² = 1, and let β₁ = 0 and −0.12 under the null and alternative hypotheses, respectively; β₁ = −0.12 means that each copy of the minor allele decreases the trait value by 12% of its standard deviation. For the disease-risk model, we set γ₂ = log 2, varied the value of γ₁ from 0 to log 2, and chose the value of γ₀ to yield a disease rate of 1% or 5%. Note that γ₁ pertains to the change in the log odds ratio of disease for each copy of the minor allele of the SNP and γ₂ to the change in the log odds ratio of disease for one standard-derivation increase of the quantitative trait. The choice of γ₂ = log 2 represents a strong, but not uncommon, association between the secondary phenotype and the disease. For each combination of simulation parameters, we generated 1,000,000 data sets with 1,000 cases and 1,000 controls. We compared the new method to standard methods (1)-(3), i.e., the least-squares methods based on the data from the control group, the case group, and the combined sample of cases and controls. We focused on methods (1)-(3) because methods (4) and (5) are closely related (1) and (2).

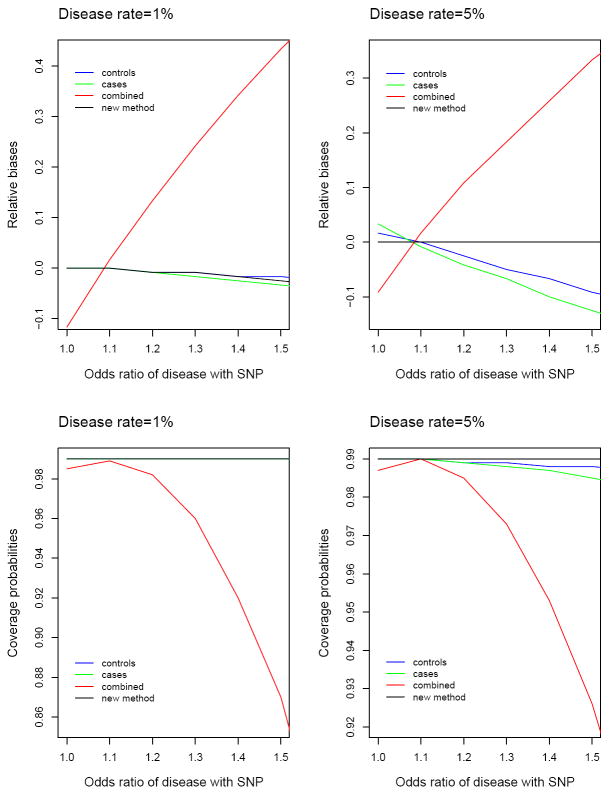
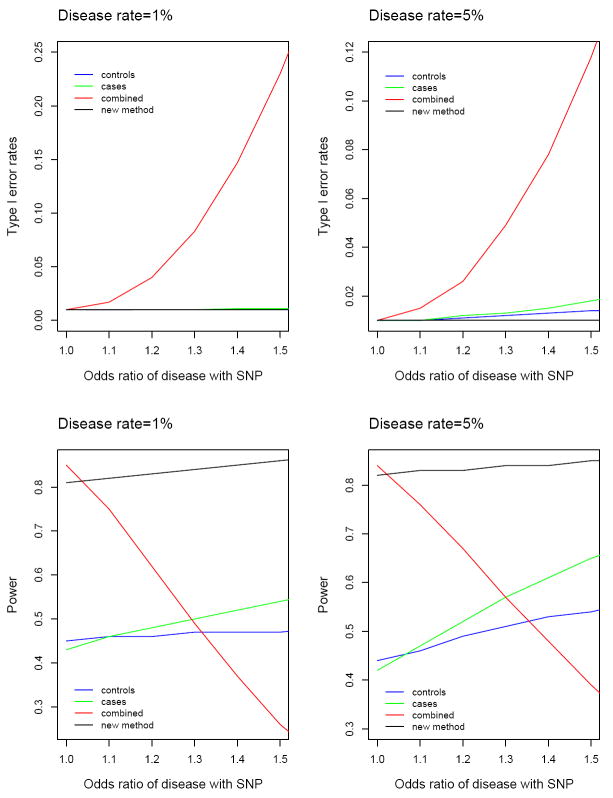
We summarize the key results in Figures 1 and 2. Figure 1 shows the biases of effect estimates and the coverage probabilities of 99% confidence intervals for β₁ as a function of the odds ratio of disease with the SNP (i.e., e^γ₁) under the alternative hypothesis (i.e., β₁ = −0.12). Figure 2 displays the type I error and power for testing the null hypothesis of β₁ = 0 at the nominal significance level of 1%. We restricted the horizontal axis to 1.5 because the odds ratios that have been observed in GWA studies thus far are mostly less than 1.5 although the odds ratios may be higher in candidate genes studies.

Figure 1.

Relative biases of effect estimates and coverage probabilities of 99% confidence intervals for four analysis methods: least-squares methods based on controls only, cases only and combined sample of cases and controls versus the new method. The relative bias is the bias divided by the effect size. The odds ratio of disease with the SNP (i.e., e^γ₁) was varied from 1 to 1.5 with 0.1 increment. Each result is based on 1,000,000 simulated data sets. For disease rate of 1%, least-squares methods based on controls only and cases only and the new method all yield coverage probabilities of virtually 99% at all values of the odds ratio of disease with the SNP, so the three curves are indistinguishable.

Figure 2.

Type I error rates and power of association tests at the 1% nominal significance level for four analysis methods: least-squares methods based on controls only, cases only and combined sample of cases and controls versus the new method. The odds ratio of disease with the SNP (i.e., e^γ₁) was varied from 1 to 1.5 with 0.1 increment. Each result is based on 1,000,000 simulated data sets. For disease rate of 1%, least-squares methods based on controls only and cases only and the new method all yield type I error rates of virtually 1% at all values of the odds ratio of disease with the SNP, so the three curves are indistinguishable.

The new method performs very well. The effect estimates are virtually unbiased, and the variance estimates accurately reflect the true variations (latter data not shown). A a result, the confidence intervals have proper coverage probabilities, and the association tests have correct type I error rates. The power of the new method is always above 80%.

The least-squares method based on the combined sample of cases and controls, i.e., method (3), can be very wrong, especially when the SNP is strongly related to the disease. The effect estimates are biased, the confidence intervals have poor coverage probabilities, and the type I error is inflated. The problems associated with this method are more severe for rarer diseases. The type I error rates are 8 times and 5 times the nominal significance level under the disease rates of 1% and 5%, respectively, when the odds ratio of disease with the SNP is 1.3. This strategy may be more powerful or less powerful than the new method, dependent on how the SNP affects the disease status and the secondary phenotype. Figure 2 shows that this strategy can be substantially less powerful than the new method.

When the disease is rare, say less than 1%, the least-squares methods based on controls only and cases only, i.e., methods (1) and (2), are appropriate in that the effect estimates are approximately unbiased, the confidence intervals have adequate coverage probabilities, and the association tests have reasonable type I error rates. These two methods, however, use half of the study subjects and are thus much less powerful than the new method. For relatively common diseases, methods (1) and (2) yield biased effect estimates, improper confidence intervals and inflated type I error, especially when the SNP is strongly related to the disease. When the disease rate is 5% and the odds ratio of disease with the SNP is 1.5, the type I error rates for methods (1) and (2) are about 1.3% and 1.8%, respectively.

All the aforementioned results pertain to MAF of 0.3, γ₂ of log 2, 1,000 cases and 1,000 controls, and nominal significance level of 1%. We also considered other combinations of simulation parameters. The new methods continued to perform well. The performance of standard methods became worse as MAF, γ₂ or sample size was increased and as the nominal significance level was lowered. In addition, the performance of methods (1) and (2) became worse as the disease rate was increased.

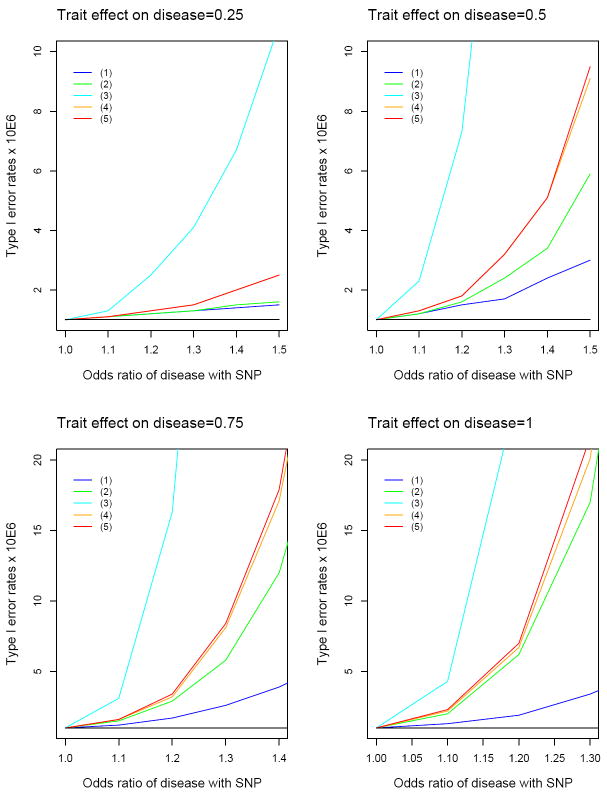
Figure 3 displays the type I error rates of the five standard methods for MAF of 0.2, disease rate of 7%, 2,000 cases and 2,000 controls, and nominal significance level of 10⁻⁶. The type I error rates for all five methods increase rapidly with increasing values of γ₁ and γ₂ and are seriously inflated even with moderate values of γ₁ and γ₂. Under γ₁ = log 1.3 and γ₂ = 0.5, the type I error rates of methods (1)–(5) are, respectively, 1.7, 2.4, 20, 3.2 and 3.2 times the nominal significance level; under γ₁ = log 1.2 and γ₂ = 1, the five type I error rates are 1.9, 6.2, 25, 6.7 and 7 times the nominal significance level. Controls-only analysis has the least inflation of type I error, followed by cases-only analysis. Meta-analysis of cases and controls has higher type I error than cases-only and controls-only analyses, mainly because it has twice the sample size. The joint analysis of cases and controls with the disease status as a covariate in the linear model has slightly higher inflation of type I error than the meta-analysis. The analysis of the combined sample without adjusting for the disease status, i.e., method (3), performs much worse than the other four methods.

Figure 3.

Type I error rates (×10⁶) at the nominal significance level of 10⁻⁶ for five linear regression methods: (1) controls only; (2) cases only; (3) combined sample of cases and controls; (4) meta-analysis of cases and controls; (5) joint analysis of cases and controls with adjustment for the disease status. The odds ratio of disease for the SNP (i.e., e^γ₁) was varied from 1 to 1.5 with 0.1 increment. Trait effect on disease (γ₂) pertains to the change in the log odds ratio of disease for one-standard derivation increase in the quantitative trait. Each result is based on 100,000,000 simulated data sets. For γ₂ of 0.25, the type I error rates are virtually identical between methods (3) and (5), so the two curves are indistinguishable. The nominal significance level of 10⁻⁶ is indicated by the black line in each panel.

DISCUSSION

The purpose of this article is two-fold: to evaluate the standard methods and to develop better methods for the analysis of secondary phenotype data in case-control association studies. We have demonstrated both analytically and numerically that all the standard methods can have severely inflated type I error and reduced power in practical situations. The new methods provide accurate control of the type I error and have the highest efficiency/power among all valid methods. We have developed efficient numerical algorithms to implement the new methods and posted the software online. With our software, analysis of a GWA study (with 500K-1,000K SNPs) can be completed in a few hours.

As mentioned in the Introduction section, the recent publications on human height, BMI and lipid levels relied on standard linear regression analysis of quantitative trait data from case-control studies of complex diseases. We are not challenging the conclusions of those publications because some of the initial results were validated in cross-sectional or cohort data, but the effect estimates and P-values reported in the papers might be questionable. Using valid and efficient statistical methods in the initial scans would reduce the number of false positives and increase the number of true positives among the initial results and thus enhance the success rates of validation efforts. It would be even more important to use proper statistical methods in any validation analysis.

When the disease is rare, all standard methods except (3) are approximately valid. Our simulation studies revealed that this assumption is problematic when the disease rate is appreciably higher than 1%. As shown in Figures 1 and 2, methods (1) and (2) have serious problems when the disease rate is 5%. We recommend to use the rare disease assumption only when the disease rate is less than 2%.

Many of the complex diseases currently under study are relatively common (5-10%), so the results of Figure 3 are particularly relevant. If the disease is type 2 diabetes, then γ₂ is close to 1 for BMI and triglyceride levels and close to 0 for height. Thus, standard linear regression analysis of BMI and triglyceride levels in case-control studies of type 2 diabetes would be more biased than that of height. The most recent publications on quantitative traits were based on meta-analyses of tens of thousands of subjects, so the inflation of type I error would be much more profound than what is seen in Figure 3.

Although only a small fraction of SNPs are truly associated with a complex disease, any SNPs that are associated with the disease in the observed data (mostly by chance) will tend to be spuriously associated with secondary traits in the case and control groups as well as in the combined sample; therefore, all five standard methods can cause large-scale increases of false positive results in GWA studies. Indeed, the quantile-quantile plots in several publications [Weedon et al., 2007; Weedon et al., 2008; Gudbjartsson et al., 2008] showed substantial deviations of observed statistics from the expected (after correcting for population stratification), even at the 0.01 level of significance.

APPENDIX A: THEORETICAL AND COMPUTATIONAL ASPECTS OF NEW STATISTICAL METHODS

We provide theoretical and computational details for the new statistical methods. In the main text of this article, X pertains to a single SNP. In this appendix, we expand X to contain all genetic and environmental factors of interest (including gene-environment interactions). We use P_θ(y|x) to denote the conditional density of Y given X = x, which is formulated through a parametric model with a set of parameters θ. We assume that

$$P\left(D=1|X,Y\right)=\frac{e^{{\gamma }_0+{\gamma }_1^{\mathrm{T}}X+{\gamma }_{2}Y}}{1+e^{{\gamma }_0+{\gamma }_1^{\mathrm{T}}X+{\gamma }_{2}Y}},$$

where γ₁ is now a vector.

The data consist of (D_i, Y_i, X_i) (i = 1,…, n). The likelihood function is

$${\begin{array}{c}\prod _{i=1}^n\left\{\frac{P_{\theta }\left(Y_i|X_i\right)P\left(X_i\right)e^{{\gamma }_0+{\gamma }_1^{\mathrm{T}}{X}_i+{\gamma }_2{Y}_i}/(1+e^{{\gamma }_0+{\gamma }_1^{\mathrm{T}}{X}_i+{\gamma }_2{Y}_i})}{P\left(D_i=1\right)}\right\}\\ \times \underset{i=1}{\overset{n}{\mathrm{\Pi }}}{\left\{\frac{P_{\theta }\left(Y_i|X_i\right)P\left(X_i\right)/\left(1+e^{{\gamma }_0+{\gamma }_1^{\mathrm{T}}{X}_i+{\gamma }_2{Y}_i}\right)}{P\left(D_i=0\right)}\right\}}^{1-D_i},\end{array}}^{D_i}$$

where P(x) is the density of X, and

$$P\left(D=0\right)={\mathit{\int }}_{y,x}{P}_{\theta }\left(y|x\right)P\left(x\right)/\left(1+e^{{\gamma }_0+{\gamma }_1^{\mathrm{T}}x+{\gamma }_{2}y}\right)\mathit{dydx}.$$

For discrete components, the integration is replaced by the summation.

Before deriving estimation methods, we need to determine which parameters are estimable or identifiable. We wish to show that two sets of parameters {γ₀, γ₁, γ₂, θ, P(x)} and {γ₀^*, γ₁^*, γ₂^*, θ*, P*(x)} are identical if they yield the same likelihood. It is natural to assume that P_θ(Y|X) = P_θ*(Y|X) if and only if θ = θ* and that the data matrix for (1, X, Y) is of full rank.

We first consider the case in which the disease is rare such that P(D = 1|X, Y) ≈ e^{γ₀+γ₁TX+γ₂Y} and P(D = 0|X, Y) ≈ 1. Then the likelihood function becomes

$$\prod _{i=1}^n{\left\{\frac{P_{\theta }\left(Y_i|X_i\right)P\left(X_i\right)e^{{\gamma }_1^{\mathrm{T}}{X}_i+{\gamma }_2{Y}_i}}{{\mathit{\int }}_{y,x}{P}_{\theta }\left(y|x\right)P\left(x\right)e^{{\gamma }_1^{\mathrm{T}}x+{\gamma }_{2}y}\mathit{dydx}}\right\}}^{D_i}\times \prod _{i=1}^n{\{P_{\theta }(Y_i|X_i)P(X_i)\}}^{1-D_i}.$$

We let D = 0 to obtain P_θ(Y|X)P(X) = P_θ*(Y|X)P*(X), which implies P(X) = P*(X) and θ = θ*. We let D = 1 to obtain γ₁^TX + γ₂Y = γ₁^*TX + γ₂^*Y + c, where c is a constant. Because the data matrix for (1, X, Y) is of full rank, this equation yields γ₁ = γ₁^* and γ₂ = γ₂^* (implying c = 0). Thus, all parameters are identifiable.

Next, we consider the case in which the disease rate is known. Since P(D = 1) is known,

$$P_{\theta }\left(Y|X\right)P\left(X\right)\frac{e^{D\left({\gamma }_0+{\gamma }_1^{\mathrm{T}}X+{\gamma }_{2}Y\right)}}{1+e^{{\gamma }_0+{\gamma }_1^{\mathrm{T}}X+{\gamma }_{2}Y}}=P_{{\theta }^{\ast }}\left(Y|X\right)P^{\ast }\left(X\right)\frac{e^{D\left({\gamma }_0^{\ast }+{\gamma }_1^{\ast \mathrm{T}}X+{\gamma }_2^{\ast }Y\right)}}{1+e^{{\gamma }_0^{\ast }+{\gamma }_1^{\ast \mathrm{T}}X+{\gamma }_2^{\ast }Y}}.$$

Summing over D = 0 and 1 yields P_θ(Y|X)P(X) = P_θ*(Y|X)P*(X), which implies θ = θ* and P(X) = P*(X). This further implies γ₀ + γ₁^TX + γ₂Y = γ₀^* + γ₁^*TX + γ₂^*Y. Hence, all parameters are identifiable.

The remaining case is when the disease is not rare and the disease rate is unknown. It can be shown that γ₁ = γ₁^*, γ₂= γ₂^*, and

$$P_{\theta }\left(y|x\right)P\left(x\right)=c_0{P}_{{\theta }^{\ast }}\left(y|x\right)P^{\ast }\left(x\right)\frac{1+e^{{\gamma }_0+{\gamma }_1^{\mathrm{T}}x+{\gamma }_{2}y}}{1+e^{{\gamma }_0^{\ast }+{\gamma }_1^{\mathrm{T}}x+{\gamma }_{2}y}},$$

where c₀ is a constant [Roeder et al., 1996]. In most cases, the above equation implies θ = θ*. (In particular, we can show that θ = θ* for continuous traits satisfying the linear regression model; this is also true for dichotomous traits satisfying the logistic regression model if γ₂ = 0 or if γ₂ ≠ 0 and there is a continuous component of X that is related to D.) Then

$$P\left(x\right)=c_0{P}^{\ast }\left(x\right)\frac{1+e^{{\gamma }_0+{\gamma }_1^{\mathrm{T}}x+{\gamma }_{2}y}}{1+e^{{\gamma }_0^{\ast }+{\gamma }_1^{\mathrm{T}}x+{\gamma }_{2}y}}.$$

If γ₂ ≠ 0, then the above equation clearly implies γ₀= γ₀^* and P(x) = P*(x), so all parameters are identifiable. If γ₂ = 0, we have

$$P\left(x\right)=c_0{P}^{\ast }\left(x\right)\frac{1+e^{{\gamma }_0+{\gamma }_1^{\mathrm{T}}x}}{1+e^{{\gamma }_0^{\ast }+{\gamma }_1^{\mathrm{T}}x}},$$

so γ₁, γ₂ and θ are identifiable while P(x)/(1 + e^{γ₀+γ₁Tx}) is identifiable up to some constant.

In all cases, we estimate the parameters by maximizing the likelihood functions. Because P(x) is potentially high-dimensional, we use the profile likelihood approach. We provide estimation procedures separately for the three cases discussed above.

We first consider the rare-disease case. Write p_i = P (X_i). By differentiating the log-likelihood function with respect to p_i, we obtain

$$\frac{1}{p_i}-n_1\frac{{\mathit{\int }}_y{P}_{\theta }\left(y|X_i\right)e^{{\gamma }_1^{\mathrm{T}}{X}_i+{\gamma }_{2}y}\mathit{dy}}{{\mathit{\int }}_{y,x}{P}_{\theta }\left(y|x\right)P\left(x\right)e^{{\gamma }_1^{\mathrm{T}}x+{\gamma }_{2}y}\mathit{dydx}}-\lambda =0,$$

where λ is the Lagrange multiplier for the constraint Σ_i p_i = 1, and n₁ is the number of cases. Multiplying the above equation by p_i and summing over i, we see λ = n − n₁. Thus,

$$p_i=\frac{1}{n-n_1+n_1\xi {\mathit{\int }}_y{P}_{\theta }\left(y|X_i\right)e^{{\gamma }_1^{\mathrm{T}}{X}_i+{\gamma }_{2}y}dy’}$$

where

$$\xi ={\left\{{\mathit{\int }}_{y,x}{P}_{\theta }\left(y|x\right)P\left(x\right)e^{{\gamma }_1^{\mathrm{T}}x+{\gamma }_{2}y}\mathit{dydx}\right\}}^{-1}.$$

By the arguments of Lin and Zeng [2006], maximizing the likelihood function is equivalent to maximizing

$$\begin{array}{c}\sum _{i=1}^n\left\{\log P_{\theta }\left(Y_i|X_i\right)+D_i({\gamma }_1^{\mathrm{T}}{X}_i+{\gamma }_2{Y}_i)\right\}+n_1\log \xi \\ -\sum _{i=1}^n\log \left\{1-\frac{n_1}{n}+\frac{n_1}{n}\xi {\mathit{\int }}_y{P}_{\theta }\left(y|X_i\right)e^{{\gamma }_1^{\mathrm{T}}{X}_i+{\gamma }_{2}y}\mathit{dy}\right\},\end{array}$$

which is called the profile log-likelihood function for γ₁, γ₂, θ and ξ.

When the disease rate is known, we maximize

$$\prod _{i=1}^n\left\{P_{\theta }\left(Y_i|X_i\right)p_i\frac{e^{D_i\left({\gamma }_0+{\gamma }_1^{\mathrm{T}}{X}_i+{\gamma }_2{Y}_i\right)}}{1+e^{{\gamma }_0+{\gamma }_1^{\mathrm{T}}{X}_i+{\gamma }_2{Y}_i}}\right\}$$

subject to the constraints that Σ_i p_i = 1 and

$$\sum _{i=1}^n{p}_i{\mathit{\int }}_y{P}_{\theta }\left(y|X_i\right)\frac{e^{{\gamma }_0+{\gamma }_1^{\mathrm{T}}{X}_i+{\gamma }_{2}y}}{1+e^{{\gamma }_0+{\gamma }_1^{\mathrm{T}}{X}_i+{\gamma }_{2}y}}\mathit{dy}={\xi }_0,$$

where ξ₀ is the known value of P(D = 1). By using the Lagrange multipliers, we see that the estimate for p_i satisfies

$$\frac{1}{p_i}-\lambda {\mathit{\int }}_y{P}_{\theta }\left(y|X_i\right)\frac{e^{{\gamma }_0+{\gamma }_1^{\mathrm{T}}{X}_i+{\gamma }_{2}y}}{1+e^{{\gamma }_0+{\gamma }_1^{\mathrm{T}}{X}_i+{\gamma }_{2}y}}\mathit{dy}-\stackrel{\sim }{\lambda }=0.$$

The two constraints imply λξ₀ + λ̃ = n; therefore,

$$p_i={\left\{\lambda {\mathit{\int }}_y{P}_{\theta }\left(y|X_i\right)\frac{e^{{\gamma }_0+{\gamma }_1^{\mathrm{T}}{X}_i+{\gamma }_{2}y}}{1+e^{{\gamma }_0+{\gamma }_1^{\mathrm{T}}{X}_i+{\gamma }_{2}y}}\mathit{dy}+\left(n-\lambda {\xi }_0\right)\right\}}^{-1},$$

where λ satisfies Σ_i p_i = 1. Thus, the profile log-likelihood function for θ, γ₀, γ₁ and γ₂ is

$$\begin{array}{c}\sum _{i=1}^n\left\{\log P_{\theta }\left(Y_i|X_i\right)+D_i({\gamma }_0+{\gamma }_1^{\mathrm{T}}{X}_i+{\gamma }_2{Y}_i)-\log (1+e^{{\gamma }_0+{\gamma }_1^{\mathrm{T}}{X}_i+{\gamma }_2{Y}_i})\right\}\\ -\sum _{i=1}^n\log \left\{\lambda {\mathit{\int }}_y{P}_{\theta }\left(y|X_i\right)\frac{e^{{\gamma }_0+{\gamma }_1^{\mathrm{T}}{X}_i+{\gamma }_{2}y}}{1+e^{{\gamma }_0+{\gamma }_1^{\mathrm{T}}{X}_i+{\gamma }_{2}y}}\mathit{dy}+(n-\lambda {\xi }_0)\right\},\end{array}$$

where λ is determined by the equation

$$\sum _{i=1}^n{\left\{\lambda {\mathit{\int }}_y{P}_{\theta }\left(y|X_i\right)\frac{e^{{\gamma }_0+{\gamma }_1^{\mathrm{T}}{X}_i+{\gamma }_{2}y}}{1+e^{{\gamma }_0+{\gamma }_1^{\mathrm{T}}{X}_i+{\gamma }_{2}y}}\mathit{dy}+(n-\lambda {\xi }_0)\right\}}^{-1}=1$$

under the constraint that each term in the summation is positive.

Finally, we deal with the case in which the disease is not rare and the disease rate is unknown. If γ₂ = 0, we can use standard statistical methods; see Appendix B. Suppose that γ₂ ≠ 0. By introducing the Lagrange multiplier λ, we differentiate the log-likelihood function to obtain

$$\frac{1}{p_i}-\frac{n_1}{P\left(D=1\right)}{\mathit{\int }}_y{P}_{\theta }\left(y|X_i\right)P\left(D=1|X_i,y\right)\mathit{dy}-\frac{n_0}{P\left(D=0\right)}{\mathit{\int }}_y{P}_{\theta }\left(y|X_i\right)P\left(D=0|X_i,y\right)\mathit{dy}-\lambda =0,$$

where n₁ and n₀ are the numbers of cases and controls. It is easy to see that λ = 0, so

$$p_i={\left\{\frac{n_1}{\xi }{\mathit{\int }}_y{P}_{\theta }\left(y|X_i\right)P\left(D=1|X_i,y\right)\mathit{dy}+\frac{n_0}{\left(1-\xi \right)}{\mathit{\int }}_y{P}_{\theta }\left(y|X_i\right)P\left(D=0|X_i,y\right)\mathit{dy}\right\}}^{-1},$$

where ξ = P(D = 1). Plugging this expression into the log-likelihood function yields the profile log-likelihood function for γ₀, γ₁, γ₂, θ and ξ

$$\begin{array}{c}\sum _{i=1}^n\left\{D_i({\gamma }_0+{\gamma }_1^{\mathrm{T}}{X}_i+{\gamma }_2{Y}_i)-\log (1+e^{{\gamma }_0+{\gamma }_1^{\mathrm{T}}{X}_i+{\gamma }_2{Y}_i})+\log P_{\theta }\left(Y_i|X_i\right)\right\}\\ -\sum _{i=1}^n\log \left\{\frac{n_1}{\xi }{\mathit{\int }}_y{P}_{\theta }\left(y|X_i\right)\frac{e^{{\gamma }_0+{\gamma }_1^{\mathrm{T}}{X}_i+{\gamma }_{2}y}}{1+e^{{\gamma }_0+{\gamma }_1^{\mathrm{T}}{X}_i+{\gamma }_{2}y}}\mathit{dy}+\frac{n_0}{\left(1-\xi \right)}{\mathit{\int }}_y{P}_{\theta }\left(y|X_i\right)\frac{1}{1+e^{{\gamma }_0+{\gamma }_1^{\mathrm{T}}{X}_i+{\gamma }_{2}y}}\mathit{dy}\right\}\\ -n_1\log \xi -n_0\log \left(1-\xi \right).\end{array}$$

In all three cases, we maximize the profile log-likelihood functions via the Newton-Raphson algorithm or optimization algorithms. By the arguments used in the proofs of Theorems 2 and 3 of Lin and Zeng [2006], we can show that the maximum likelihood estimators are consistent and asymptotically normal. In addition, the limiting covariance matrix attains the efficiency bound and can be consistently estimated by the inverse of the negative Hessian matrix of the profile log-likelihood function.

APPENDIX B: THEORETICAL PROPERTIES OF STANDARD STATISTICAL METHODS

We investigate the validity of standard statistical methods. Let P denote the true probability, and let P_obs denote the observed probability under the case-control design. Since

$$P_{\mathit{obs}}\left(Y|X\right)=\frac{P_{\mathit{obs}}\left(Y,X|D=1\right)P_{\mathit{obs}}\left(D=1\right)+P_{\mathit{obs}}\left(Y,X|D=0\right)P_{\mathit{obs}}\left(D=0\right)}{P_{\mathit{obs}}\left(X\right)}$$

and P_obs(Y, X |D) = P(Y, X |D), we have

$$P_{\mathit{obs}}\left(Y|X\right)=\left\{\frac{P_{\mathit{obs}}\left(D=1\right)}{P\left(D=1\right)}\frac{e^{{\gamma }_0+{\gamma }_1^{\mathrm{T}}X+{\gamma }_{2}Y}}{1+e^{{\gamma }_0+{\gamma }_1^{\mathrm{T}}X+{\gamma }_{2}Y}}+\frac{P_{\mathit{obs}}\left(D=0\right)}{P\left(D=0\right)}\frac{1}{1+e^{{\gamma }_0+{\gamma }_1^{\mathrm{T}}X+{\gamma }_{2}Y}}\right\}P\left(Y|X\right)\frac{P\left(X\right)}{P_{\mathit{obs}}\left(X\right)}.$$ (1)

Likewise,

$$P_{\mathit{obs}}\left(Y|X,D=0\right)=\frac{1}{P\left(D=0\right)}\frac{1}{1+e^{{\gamma }_0+{\gamma }_1^{\mathrm{T}}X+{\gamma }_{2}Y}}P\left(Y|X\right)\frac{P\left(X\right)}{P_{\mathit{obs}}\left(X|D=0\right)},$$ (2)

and

$$P_{\mathit{obs}}\left(Y|X,D=1\right)=\frac{1}{P\left(D=1\right)}\frac{e^{{\gamma }_0+{\gamma }_1^{\mathrm{T}}X+{\gamma }_{2}Y}}{1+e^{{\gamma }_0+{\gamma }_1^{\mathrm{T}}X+{\gamma }_{2}Y}}P\left(Y|X\right)\frac{P\left(X\right)}{P_{\mathit{obs}}\left(X|D=1\right)}.$$ (3)

If P_obs(Y |X) = P(Y |X), then the usual (prospective) likelihood based on the combined sample of cases and controls will yield correct estimates of θ as well as correct variance estimates. The sufficient and necessary condition for this equality is that Y is independent D conditional on X, i.e., γ₂ = 0. To show the sufficiency, we note that equation (1) under γ₂ = 0 entails

$$P_{\mathit{obs}}\left(X\right)=P\left(X|D=0\right)\{e^{{\gamma }_0+{\gamma }_1^{\mathrm{T}}X}{P}_{\mathit{obs}}\left(D=1\right)/P\left(D=1\right)+P_{\mathit{obs}}\left(D=0\right)/P\left(D=0\right)\}P\left(D=0\right).$$

Similarly, P(X) = P(X |D = 0)(e^{γ₀+γ₁TX} + 1)P(D = 0). Plugging these two expressions into equation (1), we see P_obs(Y |X) = P (Y |X). We show that γ₂ = 0 is the necessary condition by contradiction. Suppose that P_obs(Y|X) = P(Y|X) but γ₂ ≠ 0. Then equation (1) implies

$$\frac{P_{\mathit{obs}}\left(D=1\right)}{P\left(D=1\right)}=\frac{P_{\mathit{obs}}\left(D=0\right)}{P\left(D=0\right)}.$$

This is false since P_obs(D = 1) is arbitrary under the case-control design. Using equations (2) and (3), we can show that γ₂ = 0 is also the necessary and sufficient condition for the standard analysis based on controls only or cases only to be valid. In most case-control studies, secondary phenotypes are correlated with the disease status, so that γ₂ ≠ 0.

What happens if D is independent of X conditional on Y, i.e., γ₁ = 0? We first consider dichotomous traits. By switching the roles of X and Y in the above derivation, we see P_obs(X|Y) = P(X|Y) under γ₁ = 0; similar calculations show that P_obs(X |Y, D) is proportional to P(X|Y). Therefore, standard logistic regression analysis based on cases only, controls only, or the combined sample yields correct estimates of the odds ratios in the general population. For quantitative traits, the linear model specifies that Y = β₀ + β₁^TX + ∈, where ∈ is zero-mean normal with variance σ². Write Ỹ = Y − β₁^TX. Clearly, Ỹ is independent of X, so standard linear regression will estimate β₁ correctly if and only if P_obs(Ỹ |X) has mean zero. In light of equation (1), this means

$${\mathit{\int }}_y\frac{y}{1+e^{{\gamma }_0+{\left({\gamma }_1+{\gamma }_2{\beta }_1\right)}^{\mathrm{T}}X+{\gamma }_{2}y}}{P}_{\mathit{obs}}\left(y\right)\mathit{dy}=0$$

for all X, implying γ₁ = −γ₂β₁. Thus, standard regression analysis is biased under γ₁ = 0 unless β₁ = 0 or γ₂ = 0. This explains the patterns of bias seen in Figure 2.

We now investigate the bias of including the case-control status as a predictor in a regression model. It follows from equations (2) and (3) that for dichotomous traits,

$$\log \frac{P_{\mathit{obs}}\left(Y=1|X,D\right)}{P_{\mathrm{obs}}\left(Y=0|X,D\right)}={\beta }_0+{\beta }_1^{\mathrm{T}}X+{\gamma }_{2}D-\log \frac{1+e^{{\gamma }_0+{\gamma }_1^{\mathrm{T}}X+{\gamma }_2}}{1+e^{{\gamma }_0+{\gamma }_1^{\mathrm{T}}X}},$$

and for continuous traits,

$$E_{\mathit{obs}}\left[Y|X,D=0\right]={\mathit{\int }}_{y}yP\left(y|X\right){\left(1+e^{{\gamma }_0+{\gamma }_1^{\mathrm{T}}X+{\gamma }_{2}y}\right)}^{-1}dy/c_0\left(X\right),$$

$$E_{\mathit{obs}}\left[Y|X,D=1\right]=\frac{{\beta }_0+{\beta }_1^{\mathrm{T}}X-{\mathit{\int }}_{y}yP\left(y|X\right){\left(1+e^{{\gamma }_0+{\gamma }_1^{\mathrm{T}}X+{\gamma }_{2}y}\right)}^{-1}dy}{1-c_0\left(X\right)},$$

where c₀(X) = ∫_y P(y|X)(1 + e^{γ₀+γ₁TX+γ₂y})⁻¹dy. Thus, the logistic regression of Y on X and D is not a valid analysis of the effects of X on Y in the general population unless γ₁ = 0 or γ₂ = 0, whereas the linear regression of Y on X and D generally yields biased estimates of the effects of X on Y in the general population unless γ₁ = 0 and γ₂ = 0.

Finally, we consider rare disease. When the disease is rare, equation (1) becomes

$$P_{\mathit{obs}}\left(Y|X\right)\approx \left\{\frac{P_{\mathit{obs}}\left(D=1\right)}{\mathit{\int }{e}^{{\gamma }_1^{\mathrm{T}}x+{\gamma }_{2}y}P\left(y|x\right)P\left(x\right)\mathit{dydx}}{e}^{{\gamma }_1^{\mathrm{T}}X+{\gamma }_{2}Y}+\frac{P_{\mathit{obs}}\left(D=0\right)}{P\left(D=0\right)}\right\}P\left(Y|X\right)\frac{P\left(X\right)}{P_{\mathit{obs}}\left(X\right)}.$$

Clearly, P_obs(Y|X) is not equivalent to P(Y|X) unless γ₂ = 0. That is, standard analysis based on the combined sample is generally invalid. For rare disease, equation (2) becomes

$$P_{\mathit{obs}}\left(Y|X,D=0\right)\approx \frac{1}{P\left(D=0\right)}P\left(Y|X\right)\frac{P\left(X\right)}{P_{\mathit{obs}}\left(X|D=0\right)}\approx P\left(Y|X\right).$$

Thus, standard analysis based on controls only is approximately valid. On the other hand, equation (3) becomes

$$P_{\mathit{obs}}\left(Y|X,D=1\right)\approx \frac{1}{\mathit{\int }{e}^{{\gamma }_1^{\mathrm{T}}x+{\gamma }_{2}y}P\left(y|x\right)P\left(x\right)\mathit{dydx}}{e}^{{\gamma }_1^{\mathrm{T}}x+{\gamma }_{2}y}P\left(Y|X\right)\frac{P\left(X\right)}{P_{\mathit{obs}}\left(X|D=1\right)}.$$

Thus, P_obs(Y|X, D = 1) is not equivalent to P(Y |X) unless γ₂ = 0. Interestingly, when Y is dichotomous,

$$\frac{P_{\mathit{obs}}\left(Y=1|X,D=1\right)}{P_{\mathit{obs}}\left(Y=0|X,D=1\right)}\approx e^{{\gamma }_2}\frac{P\left(Y=1|X\right)}{P\left(Y=0|X\right)},$$

so standard logistic regression based on cases only yields approximately correct estimates of odds ratios. If Y is continuous satisfying the linear model, then P_obs (Y |X, D = 1) is approximately proportional to exp{−(Y − β₁^TX − β₀ − σ²γ₂)²/2σ²}; therefore, standard linear regression based on cases only is approximately correct for rare disease. Whether the trait is dichotomous or continuous, the regression means between cases and controls differ only by a constant, so (for rare disease) the regression of Y on X and D yields approximately correct estimation of the effects of X on Y in the general population.