Abstract
Fine particulate matter (PM2.5) is a mixture of pollutants that has been linked to serious health problems, including premature mortality. Since the chemical composition of PM2.5 varies across space and time, the association between PM2.5 and mortality could also change with space and season. In this work we develop and implement a statistical multi-stage Bayesian framework that provides a very broad, flexible approach to studying the spatiotemporal associations between mortality and population exposure to daily PM2.5 mass, while accounting for different sources of uncertainty. In stage 1, we map ambient PM2.5 air concentrations using all available monitoring data (IMPROVE and FRM) and an air quality model (CMAQ) at different spatial and temporal scales. In stage 2, we examine the spatial temporal relationships between the health end-points and the exposures to PM2.5 by introducing a spatial-temporal generalized Poisson regression model. We adjust for time-varying confounders, such as seasonal trends. A common seasonal trends model is to use a fixed number of basis functions to account for these confounders, but the results can be sensitive to the number of basis functions. In this study, the number of the basis functions is treated as an unknown parameter in our Bayesian model and we use a space-time stochastic search variable selection approach. We apply our methods to a data set in North Carolina for the year 2001.
Keywords: air pollution, Bayesian hierarchical models, conditional autoregressive models, computer models, spatial epidemiology
1 Introduction
Spatiotemporal analyses have generated core epidemiologic data and provided important scientific basis for the recently tightened PM2.5 (particulate matter with an aerodynamic diameter of < 2.5μm) air quality standard. Over the last decade, multi-city time-series studies have shown consistent associations of increased cardiopulmonary mortality and morbidity with short-term elevations of ambient PM2.5. Some of the recent epidemiologic studies suggest that exposures to PM may result in tens of thousands of excess deaths per year, and many more cases of illness among the U.S. population (e.g. Bates et al., 1990; Dockery et al., 1992; Ostro et al., 1991; Schwartz, 1994; Pope et al., 1995; American Thoracic Society and Bascom, 1996a,b). However, the work by Smith et al. (2000) on fine particles, PM2.5 (< 2.5μm in diameter), provided evidence of lack of significant association between fine PM and mortality. All this seems to suggest that more studies are needed, since there are remaining uncertainties and methodological challenges in understanding PM-related health effects, with respect to the uncertainty of exposure measurement errors using environmental monitoring data.
Most of the previous analyses of PM health effects have been conducted in urban areas; very little is known about the rural PM-related health effects. One reason for this is that, monitoring data are not only sparse across space but also time, since most stations only measure PM2.5 every third or sixth day. We overcome this limitation by supplementing monitoring data with atmospheric deterministic models (e.g. CMAQ). CMAQ predicts air pollution levels at any given location and time. However, these numerical models could have a significant bias that needs to be quantified. Also, numerical models provide areal pollution estimates, rather than spatial point estimates. Thus, we have a change of support problem (see e.g. Gotway and Young, 2002), since monitoring data and numerical models do not have the same spatial resolution. From our previous work on fine particles, we have developed a multi-stage spatiotemporal modeling approach which allows us to address these knowledge gaps, the change of support problem, and related uncertainties in assessing fine PM concentrations and health effects.
Recently, rigorous statistical time series modelling approaches have been used to better control for potential confounders in the epidemiological analysis of mortality associated with elevated ambient air pollutant levels. Furthermore, sophisticated analytical techniques have been introduced to adjust for seasonal trends in the data, culminating in the introduction of the generalized additive models (GAM). Although temporal trends can be explicitly included in the model, non parametric local smoothing methods (LOESS) based on GAM were widely used to take into account such trends in the analysis. Dominici et al. (2002b) suggested another approach using parametric natural cubic splines in the GAM model instead of the LOESS. One of the main limitations of this type of time series modelling approach is that it is necessary to choose the time span in the LOESS smoothing process, or the degrees of freedom of the cubic splines, and the results can be very sensitive to how that is done. In our framework, we use an alternative approach which does not involve the selection of the number of basis functions or the degrees of freedom. We estimate the shape of time-varying confounders by introducing a stochastic search variable selection (SSVS) approach (George and McCulloch, 1993) in a space-time context, while characterizing the spatial association of the time-varying confounders. SSVS was originally introduced for linear regression models and has been adopted for generalized linear models (George and McCulloch, 1997), log-linear models (Ntzoufras et al., 1997), and multivariate regression models (Brown et al., 1998). Smith and Kohn (1996) used Bayesian variable selection in a nonparametric regression model. The work presented here is the first attempt to extend Smith and Kohn’s idea to model spatiotemporal data, by randomly including/excluding basis functions from the model.
The PM2.5 chemistry changes with space and time so its association with mortality could change across space and time. Dominici et al. (2002a) showed that different cities have different relative risk of mortality due to PM2.5 exposure. Fuentes et al. (2006) smoothed the relative risk spatially. Lee and Shaddick (2007) smoothed the risk across time. This is the first study to combine these two approaches. In our framework we allow the relative risk of mortality due to exposure to PM2.5 vary across space and time, taking into account spatial dependencies of the mortality data and the pollution data. We show using different model performance criteria (such as DIC) that this is a better model.
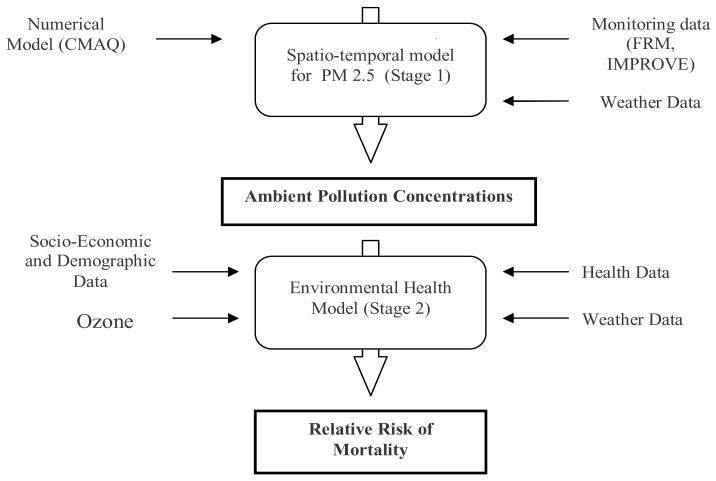
In this work we introduce an innovative hierarchical framework for spatial-temporal prediction and modelling of fine particulate matter (PM2.5) integrating atmospheric numerical models with monitoring data, and we investigate the adverse health outcomes associated with population exposure to fine particulate matter (see Figure 1). We characterize geographic differences in the PM2.5 health effects across the state of North Carolina for the year 2001. In the first stage we incorporate multi-source and multi-level information and knowledge (monitoring network [FRM, IMPROVE], meteorological data, air quality numerical model) about ambient environment into a flexible Bayesian space-time modeling framework for estimating ambient fine PM concentrations. These refined exposure indices of PM2.5 mass (from stage 1) are incorporated in a likelihood-based version of Poisson regression models (stage 2) to estimate the relative risks and to characterize the population susceptibility for PM2.5 associated increases in mortality. The hierarchical framework introduced here to combine different sources of spatial-temporal data, while characterizing uncertainty and bias associated to them, is adopted to obtain more reliable estimates of air pollution levels and to reduce the variability of the relative risk parameter, that explains the association between pollution and mortality. To the best of our knowledge, this is the first study to use numerical model output in studying the association between PM2.5 and mortality. However, this framework is flexible enough that can be adopted and implemented in many other situations where we have spatial (or spatial-temporal) information from different sources. For these data, adding CMAQ data reduces the posterior standard deviation of the relative risk for PM2.5 by as much as 50%.
Fig. 1.
Hierarchical Bayesian framework to study the spatial and temporal association between fine particulate matter and mortality.
This article is organized as follows. In Section 2, we describe the different sources of data used in this study. In Section 3, we present our hierarchical Bayesian framework to study the association between PM2.5 and mortality. In Section 4 we presents the results of this study. Finally, we provide a general discussion in Section 5.
2 Data Description
In this study we use the available PM2.5 data in North Carolina for the year 2001. The data were provided by the U.S. Environmental Protection Agency (EPA). The first source of PM2.5 data has been obtained from the Federal Reference Method (FRM) monitoring network, which includes rural and urban sites and collects PM2.5 samples either every day, every third day, or every sixth day. The second source of information for PM2.5 is from the Interagency Monitoring of Protected Visual Environments (IMPROVE) network. The IMPROVE network sites are located at national parks and wilderness areas, this network collect samples either every day, every third day, or every sixth day.
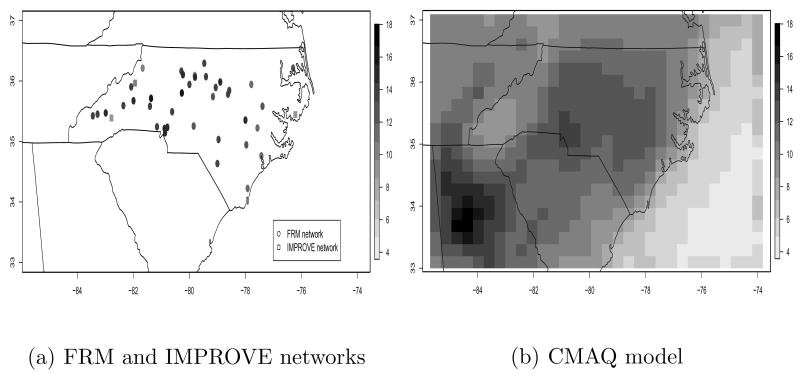
Figure 2 (a) presents the yearly average of total PM2.5 mass (μg/m3) at the 38 FRM monitoring sites and 3 IMPROVE monitoring sites in North Carolina for the year 2001.
Fig. 2.
Yearly average of total PM2.5 mass (μg/m3) from (a) FRM network and IMPROVE network and (b) CMAQ model for 2001.
Another important source of PM2.5 over large areas can obtained from three-dimensional (3-D) regional scale air quality models such as the U.S. EPA Community Multiscale Air Quality (CMAQ) modeling system (Binkowski and Roselle, 2003; Byun and Schere, 2006). CMAQ simulations over an airshed of interest provide gridded hourly concentrations and dry/wet deposition fluxes of major air pollutants such as PM2.5. In this study we use CMAQ output from the surface layer. Figure 2 (b) presents the yearly average of CMAQ’s total gridded PM2.5 mass (μg/m3) for the year 2001. The CMAQ resolution used in this study is 36km × 36km, each CMAQ value represents the averaged pollution levels within each grid cell.
Several co-pollutants (e.g. O3) are monitored (on the hourly basis) through the State and Local Air Monitoring Stations (SLAMS), National Air Monitoring Stations (NAMS), and Clean Air Status and Trends Network (CAST-NET). We have access to the SLAMS/NAMS measurements (http://www.epa.gov/oar/oaqps/qa/monprog.html), and CASTNET (http://www.epa.gov/castnet/) and we use them to study the influence of these co-pollutants as possible causative factors of adverse health effects. We determine the co-pollutants and fine particles effects jointly.
Daily meteorological data in North Carolina have been obtained from the U.S. National Climate Data Center. We use the following weather variables: minimum temperature (°C), maximum temperature (°C), dew point temperature (°C), wind speed (m/s), and pressure (hPa).
We obtained daily mortality data in North Carolina from the Odum Institute at the University of North Carolina (http://www.irss.unc.edu). These data include daily deaths from natural and cardiovascular causes by county in North Carolina for the year 2001.
3 Statistical Models
Our hierarchical framework has two main stages (see flowchart in Figure 1). In the first stage we model and estimate the PM2.5 concentrations, that are used in the health model proposed in stage 2. Fitting this complex hierarchical framework is done stage-by-stage, we take the interim posteriors from one stage as the priors for the next. Within each stage we use a fully Bayesian approach to get the interim posterior distributions. As the implementation is based on the sequential version of the Bayesian theorem, the corresponding model uncertainties are captured at the final stage of our hierarchical model. This is the approach known as cut (Best (2007)) in WinBUGS. Gelman (2004) has also described the benefits of this type of directional Bayesian approach. It not only offers computational benefits, but in settings like the one presented here, the lack of an iteration between stages 1 and 2 might be desired. For example, we would not want the health data (Stage 2) help us to explain the pollution variables (Stage 1).
3.1 Stage 1: Model for fine particulate matter
We introduce a spatial-temporal model for PM2.5 using both observed data and numerical model output; this is an extension of the approach presented by Fuentes and Raftery (2005) in a purely spatial setting. We do not consider FRM measurements to be the “true” values because they are measured with error. Thus, we denote the observed total PM2.5 mass at location s ∈ D1 on day t ∈ D2 from the FRM network by ẐF (s, t), where D1 = {s: s1, …, sNs} ⊂ ℝ2 and D2 = {t: 1, …, T} ⊂ ℝ, and it is modeled as
| (1) |
where Z(s, t) is the unobserved “true” underlying spatial-temporal process at location s and at time t. The measurement error is assumed to be independent of the true underlying process.
We use a similar representation for the observed PM2.5 measurements from the IMPROVE network, which is denoted by ẐI. We have
| (2) |
where is the measurement error and is assumed to be independent of the processes Z(s, t) and eF(s, t).
Since the CMAQ values are averages over grid squares, not point measurements, we model the PM2.5 CMAQ values, Z˜(Bb, t), where subregions B1, …, BB cover the spatial domain B, as follows:
| (3) |
where a(Bb) is the additive bias of the CMAQ output in subregion Bb and is assumed to be a polynomial function of the centroid of the subregion, sb, with a vector of coefficients, a0. The process accounts for the random deviation with respect to the underlying true process and is independent of eF (s, t), eI (s, t), and Z(s, t).
The true underlying process Z is modeled as a function of the weather covariates:
| (4) |
where M(s, t) is a vector of meteorological variables (minimum temperature, maximum temperature, dew point temperature, wind speed, and pressure) with a coefficient vector ζ. The weather information is obtained from weather stations, that are not necessarily at the same locations at which we have air pollutation data, thus, we have a spatial misalignment problem. To deal with this problem, we add in our hierarchical framework another level, stage 0, in which we introduce a statistical model for the weather variables and we predict these variables at the locations of interest for stages 1 and 2. The statistical model used for these spatial-temporal processes is the same as for the PM2.5 in stage 1, except for not using numerical models.
In order to predict Z(s0, t0), the true PM2.5 value at space s0 and time t0, given the data, Ẑ = (ẐF, ẐI, Z˜) and M, we need the posterior predictive distribution of Z(s0, t0),
| (5) |
where ΘZ is a collection of all parameters considered in the PM2.5 model. The posterior predictive distribution (5) given the data is approximated using Markov Chain Monte Carlo (MCMC) algorithms. We use a blocking Gibbs sampling algorithm to simulate values from the posterior distribution of the parameters ΘZ (using WinBUGS). Our Gibbs sampling algorithm has three steps. We alternate between the coefficients for the weather covariates and the covariance parameters of the spatial-temporal process ez (s, t) (Step 1), the parameters for the measurement error and bias components of the observed data (Step 2), and the values of Z at all monitoring sites (Step 3). The predictive distribution is obtained using the Rao-Blackwellized estimator (Gelfand and Smith, 1990)
| (6) |
where is the draw from the posterior distribution.
The quantities of interest are the true total PM2.5 averaged over a spatial domain Cj within a county j on day t denoted by Zj (t),
| (7) |
The estimate of Zj (t) is obtained by averaging estimates of true PM2.5 values at several locations randomly chosen within a county j on day t. These estimates are used in the second stage.
Spatial priors
We use uniform priors, Unif(0,5), for σF and σI. We set these priors based on the information provided by EPA (U.S. EPA, 1997) regarding the precision of the instrumentation used in these networks. Based on analysis of other similar datasets, we impose a uniform prior, Unif(0,5), for σN. Based on exploratory analysis, ez (·, t) = (ez (s1, t), …, ez (sNs, t) is normal with mean ψez (·, t − 1) and exponential covariance , where h1 = ||s − s′|| (in km). We use a N(0,0.1) prior (0.1 is the precision) for ψz and we use uniform priors, Unif(1,500) and Unif(0,100), for φz and σz, respectively.
3.2 Stage 2: Environmental Health Model
There are various statistical methods for modeling mortality data in the literature (e.g. Dominici et al., 2002a). The commonly-used model to study the association between air pollution and human health outcomes is a standard Poisson regression model with an independence assumption for the counts. However, an assumption of the Poisson model is that the mean and variance of the response variable are equal for each observation. This may be too restrictive. For example, the variance of the count data can be either smaller (under-dispersion) or larger (over-dispersion) than the mean. In this case, Poisson regression models might not be reasonable.
We use a generalized Poisson regression model (Famoye, 1993; Fuentes et al., 2006) to characterize the potential over-dispersion or under-dispersion of the mortality data. Let Yj (t) be the number of natural deaths of county j for day t, for j = 1, …, J and t = 1, …, T. We assume that Yj (t) follows a generalized Poisson distribution (GPoi) with dispersion parameter α, mean parameter μj (t), and V ar[Yj (t)] = μj (t)[1 + αμj (t)]2. Based on the generalized Poisson distribution for mortality, we develop a hierarchical regression model to investigate the association between different timescales of PM2.5 and mortality across space and season.
An important issue when studying the association between ambient PM2.5 concentrations and daily mortality counts is whether the increased mortality associated with higher PM2.5 levels is restricted to very frail people for whom life expectancy is short even in the absence of PM2.5 exposure. This possibility is called the “harvesting hypothesis” (also known as mortality displacement). We introduce a space-time model to estimate the association between PM2.5 and mortality that is resistant to short-term harvesting. The method is a spatial adaption of the approach by Dominici et al. (2003) in a purely temporal context, and it is based on the assumption that harvesting alone creates associations only at shorter time scales. We use a spectral approach for the log-linear regression to decompose the information about the pollution-mortality association into distinct time scales taking into account the spatial dependency structure of the mortality and pollution data, our relative risk estimates are harvesting-resistant because we exclude the short-term information that is affected by harvesting. Thus, we decompose the daily time series of PM2.5 estimates for county j, Zj (t), into L orthogonal different timescales components, Zj1(t), …, ZjL(t), using a discrete Fourier transform method (see Appendix).
The effect of each orthogonal decomposition of the PM2.5 time series is allowed to vary by county and by season. The index k refers to the seasons; we set k = 1 for the winter season (January–March), k = 2 for the spring season (April–June), k = 3 for the summer season (July–September), and k = 4 for the fall season (October–December). The parameter βjlk represents the effect of air pollution for county j on the timescale l and for season k; the log relative risk (RR) parameter is defined as βjlk * 103. We assume
| (8) |
The function fj (t) adjusts for the seasonality of mortality, which varies with county j. In addition to the orthogonal PM2.5 predictions, we also consider the co-pollutant Oj (t), the daily ozone for county j and day t, imputed using a similar spatial-temporal model as in Section 3.1. The Si’s are smooth functions of the weather covariates (temperature, dew point temperature, and wind speed) with the degrees of freedom (df) per year (dfi’s). These weather variables are important covariates to explain air pollution.
Confounders
We consider the following confounders: age, gender, race, and hispanic/non-hispanic. Each confounder is treated as a categorical variable in our health model. We study the potential impact of these confounders on the RR by allowing an interaction between our estimated PM2.5 component and the different confounders. In this study the groups for each confounder are:
Age: 0 – 14 years old (children), 15 – 64 (adults), ≥ 65 (senior adults).
Gender: male, female.
Race: white, black, American Indian, Other.
Hispanic: Non-hispanic, hispanic.
Spatial priors
Since the number of deaths for each county may depend on its population size, we assume that the intercept parameter γj is a spatial random effect representing the baseline log relative risk of mortality for each county j. We use a conditional autoregressive (CAR) prior (Besag et al., 1991) for γ = (γ1, …, γJ)T,
| (9) |
where is the overall variance parameter and ρ is the spatial association parameter. The matrix B = (Bjj′) includes the neighboring information, where Bjj′ = 1 if county j is adjacent to county j′, and Bjj′ = 0 otherwise. The matrix B+ is a J × J diagonal matrix with elements mj = ∑j′Bjj′, j = 1, …, J. Thus, mj is the number of “neighbors”(adjacent counties) of county j. The mean parameter μγ has a normal prior, N (0, 0.01) (0.01 is the precision). The parameter has an inverse gamma prior, IG(0.5,0.0005), as recommended by Kelsall and Wakefield (1999), the parameter ρ has a uniform prior with bounds which are determined in order to guarantee that the variance matrix of γ is symmetric positive definite (Banerjee et al., 2004).
To account for the spatial and temporal similarity of the effect of PM2.5 for each timescale l, the multivariate CAR prior for βl = (β1l, …, βnl)T, with βjl = (βjl1, …, βjl4)T would be proper. Jin et al. (2007) introduce a general approach for multivariate modelling, offering different alternatives to model the prior process for βl. In this study, we use a particular case of a multivariate CAR, called a multivariate intrinsic autoregressive (MIAR) prior (Gelfand and Vounatsou, 2002), that corresponds to a relatively smooth spatial process (a CAR model without including the ρ parameter),
| (10) |
where the positive definite 4 × 4 matrix Σβl accounts for the conditional variability as well as cross-covariance relationships between the different seasons given the neighboring sites for each time scale l. Even though the MIAR is improper, the posterior will be proper under some regulatory conditions (see e.g. Sun et al., 1999).
For the βl parameter we did not include the ρ parameter in the CAR model, corresponding to a smoother surface, because the effect of the P M2.5 should not vary dramatically from one county to the next, whereas the intercept γ accounts for many missing spatial confounders and thus may be more variable.
Seasonality of mortality
Selecting the number of basis functions to adjust for the seasonal trend of mortality is always problematic. Here, we propose an approach that avoids fixing the number of basis functions. We write the seasonal trend for county j, fj (t), using a Fourier basis (same for all counties), Cq (t), q = 1, …, Q,
| (11) |
where Q is the number of basis functions and the cjq’s are unknown regression parameters that control the shape of the seasonal trend at each county j. Instead of selecting the number of basis functions, we assume that Q is large enough to capture the true model and we use a Bayesian variable selection technique to stochastically include/exclude terms from the seasonal trend. We introduce a binary variable, wjq, and a continuous spatial variable, rjq, and express cjq as
where the vectors of coefficients rq = (r1q, …, rJq), for q = 1, …, Q, follow independent CAR priors. If wjq = 0, then cjq = 0, and the corresponding basis function is not included in the model. If wjq = 1, then cjq = rjq, and cjq is non-zero. We summarize the model complexity using the posterior of , which is the number of basis functions included in the model for county j.
4 Application
We apply our statistical framework to data in North Carolina for the year 2001 to study the spatial-temporal association between daily natural and cardiovascular deaths and PM2.5. We compare seasonal patterns in the effects of PM2.5 and its different timescales on mortality. We study the effects of ozone on mortality. Here, we decompose the daily time series of PM2.5 into five orthogonal components: < 3.5 days, 3.5 – 6 days, 7 – 13 days, 14 – 29 days, and ≥ 30 days (Dominici et al., 2003).
The prior distribution of the spatial models in stages 1 and 2 are described in Sections 3.1 and 3.2. In the mortality model, we use natural cubic splines for the smooth functions Si’s with B-spline basis functions (Eilers and Marx, 1996). To select the degrees of freedom (dfi’s), we considered up to 10 df per year for each smooth function. This value seemed to be large enough based on preliminary analysis. We found that 6 df per year for temperature and 3 df per year for dew point temperature and wind speed seemed appropriate using the deviance information criterion (DIC) of Spiegelhalter et al. (2002). Since we use 1-year data, we set the number of basis functions Q = 30. We obtained the results using WinBUGS (http://www.mrc-bsu.cam.ac.uk/bugs) and R (http://www.r-project.org/). For all MCMC sequences, we conducted a MCMC convergence diagnosis using the Gelman and Rubin (1992) convergence diagnostics, autocorrelation functions, and trace plots. For each stage, we ran two chains with 5000 iterations each, we discarded as burn-in the first 3000 iterations of each chain. The computing time could be reduced by running our model in Fortran or C++, in R using a Pentitum PC with 3.2 GHz and 1 GB RAM takes a couple of days to run.
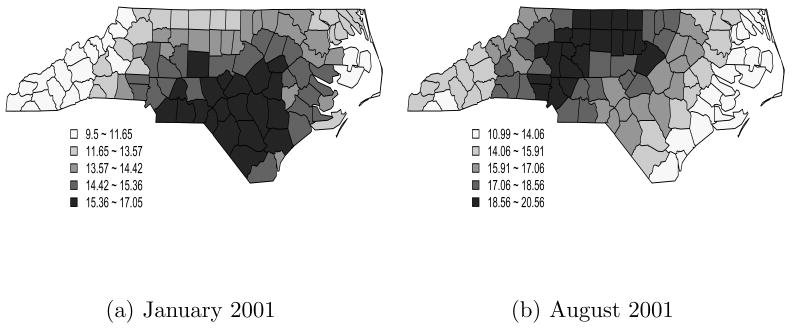
Figure 3 maps the posterior mean of the monthly average of the PM2.5 concentrations for January 2001 and August 2001. The estimated PM2.5 values in January and August were the highest in the central part of NC. Overall, the estimated PM2.5 concentrations in January were lower than in August. On average, the PM2.5 concentrations were 13.76μg/m3 for January and 16.26μg/m3 for August.
Fig. 3.
Maps of the monthly average of the estimated PM2.5 concentrations for (a) January 2001 and (b) August 2001.
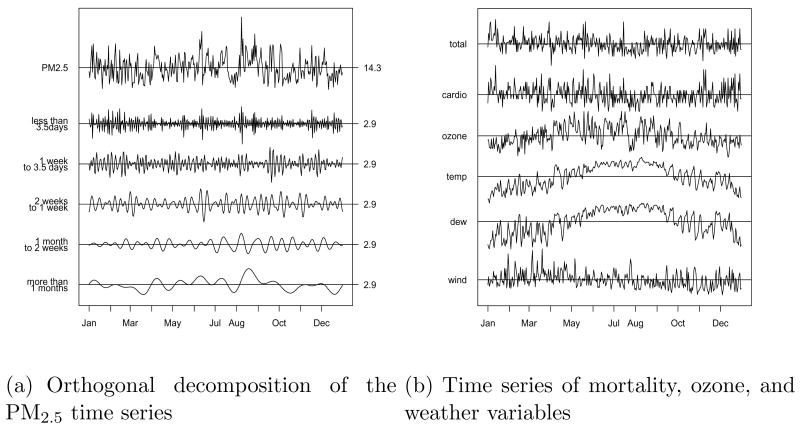
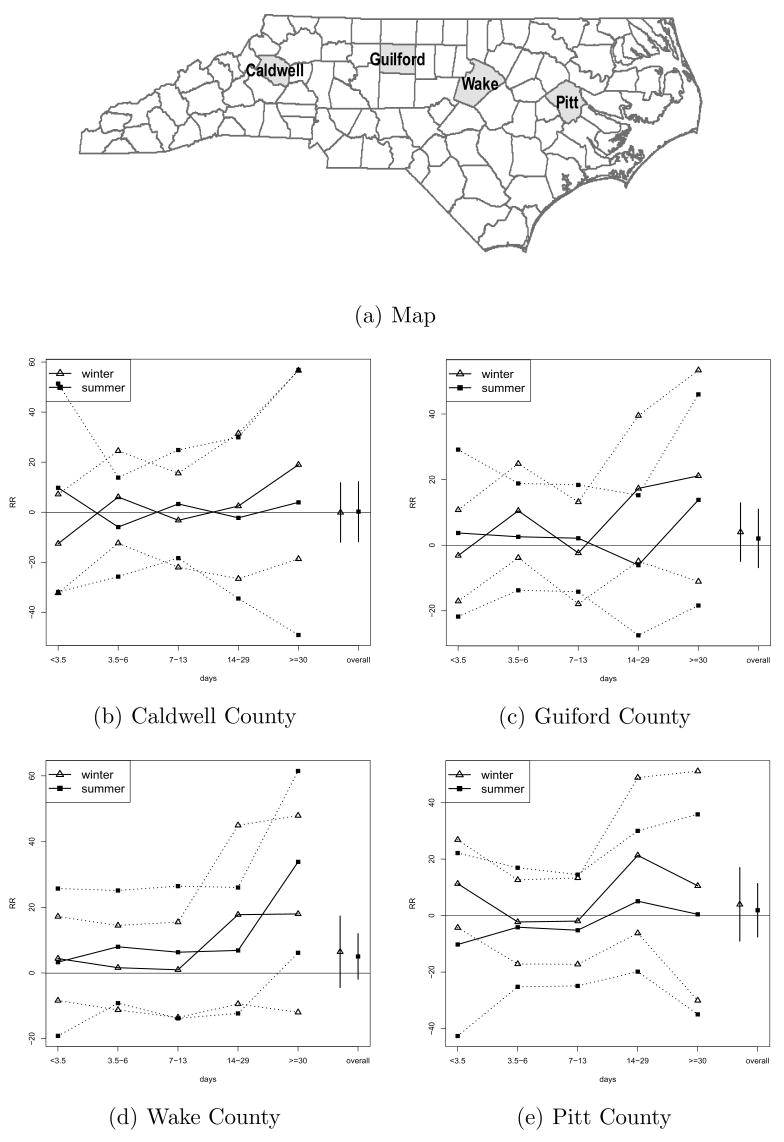
Figure 4 (a) presents the time series of the estimated PM2.5 and its different timescales for Wake County. As expected, the plots of the short-term timescales vary rapidly from day to day, while the time series plots for the long-term timescales are fairly smooth. The PM2.5 value for each day is the same as the value obtained by adding the values of the five timescales for that day. Figure 4 (b) shows the daily time series of mortality (total and cardiovascular disease), ozone, temperature, dew point temperature, and wind speed for Wake County. The estimated RRs at different timescales for 4 counties are presented in Figure 5. We found that the estimated RR values at longer timescale variations (> = 14 days) are larger than those at shorter timescale variations (< 14 days) in winter and summer, with few exceptions. The standard deviation (SD) of the RR is the highest for the longest timescale (> = 30 days), due to the potential correlation with the seasonal trend term. We also obtained estimated RR values of current day mortality using nondecomposed PM2.5 time series. The effects of PM2.5 on mortality in the winter and in the summer seem to be similar. The RR values of mortality by season for Wake County are summarized in Table 1. For all seasons, the RR at timescales greater than 1 month was larger than those at timescales less than 3.5 days. The effect of PM2.5 on current day mortality in the spring was the smallest among all seasons.
Fig. 4.
(a) Orthogonal decomposition of the PM2.5 time series and (b) time series of total natural deaths (total), cardiovascular deaths (cardio), ozone, temperature (temp), dew point (dew), and wind speed (wind) for Wake County in the year 2001. Horizontal lines show the mean value. For Wake County, the mean of the estimated PM2.5 is 14.3μg/m3 and the mean of each timescale is 2.9μg/m3.
Fig. 5.
Map shows the location of 4 counties in NC. Mean of the posterior distribution and 95% prediction intervals for the log relative rates of mortality at different timescales (percent increase in mortality per increase of 10μg/m3 of PM2.5 concentrations) in winter and summer. The values presented at “overall” are the estimates of log relative rates of mortality due to same-day PM2.5 exposure.
Table 1.
Posterior mean (SD) of log relative rates of mortality (percent increase in mortality per increase of 10μg/m3 of PM2.5 concentrations) for Wake County by season.
| Winter | Spring | Summer | Fall | |
|---|---|---|---|---|
| ≥ 30 | 18.0 (15.3) | 6.5 (21.1) | 33.8 (14.1) | 9.9 (13.7) |
| 14 – 29 | 17.8 (13.9) | 0.9 (12.2) | 6.9 (9.8) | −13.3 (7.7) |
| 7 – 13 | 1.0 (7.4) | −2.7 (8.0) | 6.3 (10.3) | 10.1 (7.6) |
| 3.5 – 6 | 1.6 (6.6) | 1.2 (8.5) | 8.0 (8.7) | −7.4 (7.6) |
| < 3.5 | 4.4 (6.5) | −3.2 (7.8) | 3.3 (11.4) | −3.1 (8.2) |
| overall | 6.5 (5.5) | 0.3 (6.1) | 5.1 (3.5) | 3.5 (5.4) |
We also studied the RR parameter of cardiovascular mortality by season. We found a similar pattern for all seasons, greater effects at timescales greater than 1 month than at timescales less than 3.5 days, with few exceptions. The spatial pattern of the RR for cardiovascular mortality due to PM2.5 was similar to that of the RR for natural mortality.
We studied the impact of ozone on the association between PM2.5 and mortality. Ozone did not seem to have a significant effect (results not shown here). For each season, the differences in the RR parameter when ozone is included in the model and when ozone is not included were small relative to the SD of the RR parameter. The 95% posterior interval was (−0.0009, 0.0061).
We examine the model complexity using the estimated Wj for each county j. This index is based on the adjustment for the seasonal trend of mortality. The posterior mean of the number of basis functions varied considerably by county. On average, the estimated number of basis functions included in the model across all counties was 10, and its SD was 2.3.
None of the confounders appeared to have a significant impact on the RR. The interaction term between the estimated PM2.5 for the 5 timescales and the confounders was not significant across space. We conducted another study to examine the significance of the interaction term between same day PM2.5 values and the confounders, and it was not significant either.
CMAQ
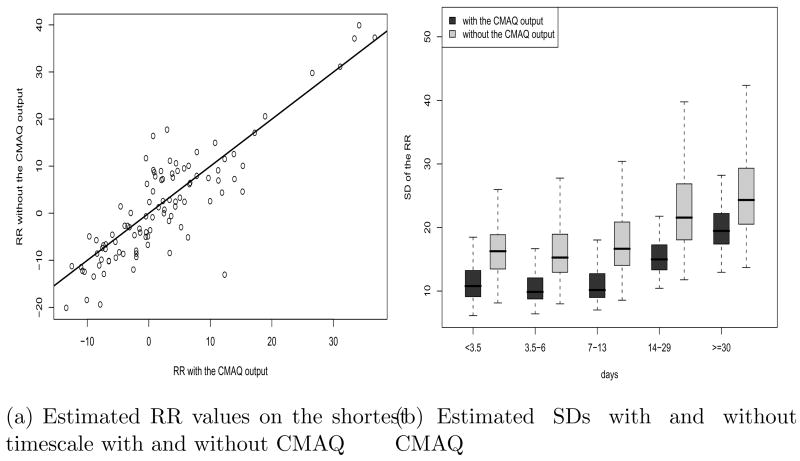
In order to examine the contribution of CMAQ to the relative risk, we repeated the analysis without the CMAQ output for PM2.5. The posterior means of the RR parameter when the CMAQ output was not used in our model were similar to those from the full model (Figure 6 (a)). However, Figure 6 (b) shows that including the CMAQ output substantially reduces the posterior SDs of the RR. Thus, it seems that including the numerical model output improves our estimate of the effect of PM2.5 on mortality.
Fig. 6.
(a) Estimated RR values on the shortest timescale in the winter with and without using CMAQ output in our model and (b) Standard deviations of the estimated RR in the winter when the CMAQ output was used in the model and when the CMAQ output were not used. The solid line in (a) shows y = x.
Model Diagnostics and Calibration
In our generalized Poisson model, the posterior mean of the dispersion parameter α was 0.049, and the 95% posterior interval was (0.040, 0.057). This provides some evidence that the data might overdispersed and that a generalized Poisson model is needed. We compare three different statistical models using the DIC and the root mean squared prediction error (RMSPE). The RMSPE is defined as , where Oi are the observed values at each monitoring station location, and Pi are the predicted values (using the mean of the predictive posterior distribution). We also present in parentheses the estimated effective number of parameters, pD. The DIC for our full model was 96327 (pD = 1038) and the DIC for the model with a constant RR across space was 96974 (pD = 1009). The RMSPE value was also smaller for the full model (2.749) compared to the model with a RR constant across space (2.781). This justifies the need of a model that allows for spatial temporal variation in the RR, even within the relatively small geographic domain of this study. In addition, we considered a generalized linear model (GLM) in order to assess the need for our more complex Bayesian space-time framework. We fit a traditional GLM with a Poisson model for the number of deaths and we allowed the regression coefficients to be independent over space and time, the RMSPE value of this model was 6.998. The fact that the RMSPE was almost 3 times the value obtained using our space-time model justifies the importance and relevance of taking into consideration the spatial temporal structure of the data and uncertainties associated to them.
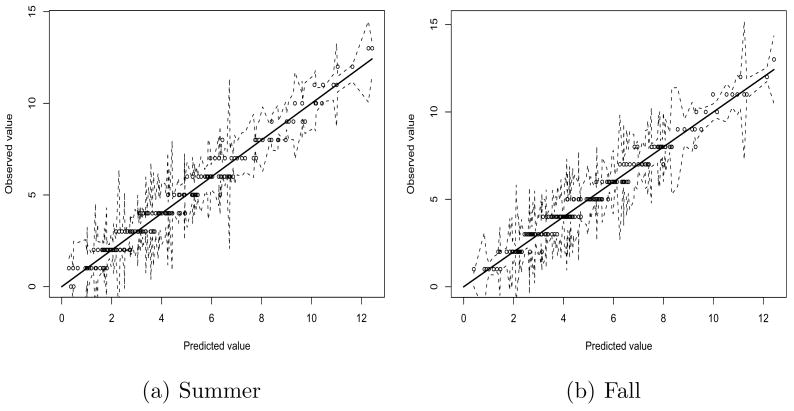
In addition, we did calibration analysis. In Figure 7, we present at a couple of randomly selected counties (Catawba and Durham) calibration plots for the mortality analysis during the summer and the fall seasons. The percentage of the observed values that are outside the interval is 10% for the summer and 6% for the fall. Similar results were obtained at other locations. We conclude our model is well calibrated.
Fig. 7.
Model diagnostics for mortality (a) during the summer and (b) during the fall: The dotted lines show the 95% prediction intervals.
We conducted sensitivity analysis to study the sensitivity of the estimated RR with respect to degrees of freedom used to explain the role of the weather variables. We fit several models using 3 and 9 dfs per year for temperature and using 6 and 9 dfs per year for the dew point temperature and wind speed. When we fit each model, we used the same functions for the other weather variables. The effects at the shorter timescales were similar in all cases, while the effects at the longer timescales were slightly different. Overall, there was not a significant impact on the RR by using different dfs per year.
5 Discussion
This article presents a Bayesian framework to investigate the spatial-temporal association between PM2.5 and daily mortality. We introduce a spatial-temporal model to obtain daily PM2.5 concentrations by combining observed PM2.5 data and numerical model output for PM2.5. We estimate the association between daily mortality and different timescales of PM2.5 to investigate the harvesting effect. Our approach to adjust for time-varying confounders does not require the selection of the number of basis functions. This hierarchical framework takes into account the spatial and temporal dependency in the pollution and mortality data, and different sources of uncertainty about them.
The PM2.5 and mortality association in NC is inconsistent with the harvesting-only hypothesis, and our harvesting resistant estimates of the relative risk are actually larger, not smaller, than the ordinary estimates. Our results are consistent with some other harvesting analysis (Zeger et al., 1999; Schwartz, 2000; Dominici et al., 2003). We found a similar association between different timescales and mortality for all seasons in NC. However, the association of PM2.5 and the current day mortality in the winter is higher than in the spring in NC.
In this study, we used sparse monitoring PM2.5 data (across space and time) as well as the CMAQ output for PM2.5. Our results show that adding the CMAQ output reduces the amount of uncertainty in our estimated relative risk parameter.
The framework introduced here is the first step to illustrate the benefits of combining different sources of information using a hierarchical framework that allows for a space-time varying risk assessment. This approach could easily be implemented for other geographic domains, including data for the conterminous U.S. and for longer time windows.
Appendix
The daily time series of PM2.5 for county j, Zj (t), t = 0, . . . ., T − 1, is decomposed into L orthogonal timescale components Zj1(t), Zj2(t), …, ZjL(t), where . For each county j, the discrete Fourier transform is defined as
| (12) |
where 1 ≤ m ≤ T − 1, i is the imaginary unit (i2 = −1), and T is the length of the time series Zj (t). The mth Fourier frequency is ωm = 2πm/T, where 0 ≤ ωm ≤ 2π, and it has m cycles in the length of the data. Note that for m ≥ T/2, , where is the complex conjugate of dj (ωm).
The inverse discrete Fourier transform is given by
| (13) |
Let [0 = ω0, ω1, …, ωl, …, ωL, π] be a partition of the interval [0, π], and we set Il = (ωl−1, ωl] ∪ [ωT −l, ωT −l+1). Then, the equation (13) is represented as
| (14) |
Thus, Zj (t) can be decomposed into Zjl’s using the following algorithm, for l = 1, …, L,
Compute the discrete Fourier transform of Zj (t) and obtain dj (ωm).
Let , if ωm ∈ Il, and , if ωm ∉ Il.
Obtain Zjl by the inverse of the discrete Fourier transform using , m = 1, …, T/2.
References
- Bascom R American Thoracic Society. Health effects of outdoor air pollution. Part 1. American Journal of Respiratory and Critical Care Medicine. 1996a;153:3–50. doi: 10.1164/ajrccm.153.1.8542133. [DOI] [PubMed] [Google Scholar]
- Bascom R American Thoracic Society. Health effects of outdoor air pollution. Part 2. American Journal of Respiratory and Critical Care Medicine. 1996b;153:477–498. doi: 10.1164/ajrccm.153.2.8564086. [DOI] [PubMed] [Google Scholar]
- Banerjee S, Carlin BP, Gelfand AE. Hierarchical modeling and analysis for spatial data. Chapman and Hall; New York: 2004. [Google Scholar]
- Bates DV, Baker-Anderson M, Sizto R. Asthma Attack Periodicity: A Study of Hospital Emergency Visits in Vancouver. Environmental Research. 1990;51:51–70. doi: 10.1016/s0013-9351(05)80182-3. [DOI] [PubMed] [Google Scholar]
- Besag J, York J, Mollie A. Bayesian image restoration, with two applications in spatial statistics (With discussion) Annals of the Institute of Statistical Mathematics. 1991;43:1–59. [Google Scholar]
- Best NG. Cutting feedback in Bayesian full probability models. Technical report at Imperial College; London. U.K: 2007. http://www.math.helsinki.fi/openbugs/IceBUGS/Presentations/BestIceBUGS.pdf. [Google Scholar]
- Binkowski FS, Roselle SJ. Models-3 community multiscale air quality (CMAQ) model aerosol component, 1. Model description. Journal of Geophysical Research. 2003;108:4183. doi: 10.1029/2001JD001409. [DOI] [Google Scholar]
- Brown PJ, Vannucci M, Fearn T. Multivariate Bayesian selection and prediction. Journal of the Royal Statistical Society B. 1998;60:627–641. [Google Scholar]
- Byun DW, Schere KL. Review of the governing equations, computational algorithms and other components of the Models-3 Community Multiscale Air Quality (CMAQ) Modeling System. Applied Mechanics Reviews. 2006;59:51–77. [Google Scholar]
- Dockery DW, Schwartz J, Spengler JD. Air pollution and daily mortality: associations with particulates and acid aerosols. Environmental Research. 1992;59:362–373. doi: 10.1016/s0013-9351(05)80042-8. [DOI] [PubMed] [Google Scholar]
- Dominici F, Daniels M, Zeger SL, Samet JM. Air Pollution and Mortality: Estimating Regional and National Dose-Response Relationships. Journal of the American Statistical Association. 2002a;97:100–111. [Google Scholar]
- Dominici F, McDermott A, Zeger SL, Samet JM. On the use of generalized additive models in time series of air pollution and health. American Journal of Epidemiology. 2002b;156:193–203. doi: 10.1093/aje/kwf062. [DOI] [PubMed] [Google Scholar]
- Dominici F, McDermott A, Zeger SL, Samet J. Airborne particulate matter and mortality: Timescale effects in four US cities. American Journal of Epidemiology. 2003;157:1055–1065. doi: 10.1093/aje/kwg087. [DOI] [PubMed] [Google Scholar]
- Eilers P, Marx B. Flexible smoothing with B-splines and penalties. Statistical Science. 1996;11:89–121. [Google Scholar]
- Famoye F. Restricted generalized Poisson regression model. Communication in Statistics-Theory and Methods. 1993;22:1335–1354. [Google Scholar]
- Fuentes M, Raftery AE. Model Evaluation and Spatial Interpolation by Bayesian Combination of Observations with Outputs from Numerical Models. Biometrics. 2005;61:36–45. doi: 10.1111/j.0006-341X.2005.030821.x. [DOI] [PubMed] [Google Scholar]
- Fuentes M, Song H, Ghosh SK, Holland DM, Davis JM. Spatial association between speciated fine particles and mortality. Biometrics. 2006;62:855–863. doi: 10.1111/j.1541-0420.2006.00526.x. [DOI] [PubMed] [Google Scholar]
- Gelfand AE, Vounatsou P. Proper multivariate conditional autoregressive models for spatial data analysis. Biostatistics. 2002;4:11–25. doi: 10.1093/biostatistics/4.1.11. [DOI] [PubMed] [Google Scholar]
- Gelfand AE, Smith AFM. Sampling-based approaches to calculating marginal densities. Journal of the American Statistical Association. 1990;85:398–409. [Google Scholar]
- Gelman A, Rubin DB. Inference from iterative simulation using multiple sequences. Statistical Science. 1992;7:457–72. [Google Scholar]
- Gelman A. Parameterization and Bayesian Modelling. Journal of the American Statistical Association. 2004;99:537–545. [Google Scholar]
- George EI, McCulloch RE. Variable selection via Gibbs sampling. Journal of The American Statistical Association. 1993;88:881–889. [Google Scholar]
- George EI, McCulloch RE. Approaches for Bayesian variable selection. Staistica Sinica. 1997;7:339–373. [Google Scholar]
- Gotway CA, Young LJ. Combining incompatible spatial data. Journal of the American Statistical Association. 2002;97:632–648. [Google Scholar]
- Jin X, Banerjee S, Carlin BP. Order-free coregionalized lattice models with application to multiple disease mapping. Journal of the royal Statistical Society series B. 2007;69:817–838. doi: 10.1111/j.1467-9868.2007.00612.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kelsall JE, Wakefield JC. Discussion of ”Bayesian models for spatially correlated disease and exposure data”. In: Bernardo JM, Berger JO, Dawid AP, Smith AFM, editors. Bayesian Statistics. Vol. 6. Oxford: Oxford University Press; 1999. p. 151. [Google Scholar]
- Lee D, Shaddick G. Time-Varying Coeffcient Models for the Analysis of Air Pollution and Health Outcome Data. Biometrics. 2007 doi: 10.1111/j.1541-0420.2007.00776.x. [DOI] [PubMed] [Google Scholar]
- Ntzoufras I, Forster JJ, Dellaportas P. Stochastic search variable selection for log-linear models. Technical Report. Faculty of Mathematics, Southampton University; Southampton, UK: 1997. [Google Scholar]
- Ostro BD, Lipsett MJ, Wiener MB, Selner JC. Asthmatic responses to airborne acid aerosols. American Journal of Public Health. 1991;81:694–702. doi: 10.2105/ajph.81.6.694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pope CA, Dockery D, Schwartz J. Review of epidemiological evidence of health effects of particulate air pollution. Inhalation Toxicology. 1995;47:1–18. [Google Scholar]
- Schwartz J. Air pollution and daily mortality: a review and meta analysis. Environmental research. 1994;64:36–52. doi: 10.1006/enrs.1994.1005. [DOI] [PubMed] [Google Scholar]
- Schwartz J. Harvesting and long-term between exposure effects in the relationship between air pollution and mortality. American Journal of Epidemiology. 2000;151:440–448. doi: 10.1093/oxfordjournals.aje.a010228. [DOI] [PubMed] [Google Scholar]
- Smith M, Kohn R. Nonparametric regression using Bayesian variable selection. Journal of Econometrics. 1996;75:317–343. [Google Scholar]
- Smith RL, Kim Y, Fuentes M, Spitzner D. Threshold dependence of mortality effects for fine and coarse particles in Phoenix, Arizona. Journal of the Air and Waste Management Association. 2000;50:1367–1379. doi: 10.1080/10473289.2000.10464172. [DOI] [PubMed] [Google Scholar]
- Spiegelhalter DJ, Best NG, Carlin BP, van der Linde A. Bayesian measures of model complexity and fit (with discussion) Journal of the Royal Statistical Society B. 2002;64:583–639. [Google Scholar]
- Sun D, Tsutakawa RK, Speckman P. Posterior distribution of hierarchical models using CAR (1) distributions. Biometrika. 1999;86:341–390. [Google Scholar]
- U.S. Environmental Protection Agency, 1997. National Ambient Air Quality Standards for Particulate Matter; Final Rule, Part II. Federal Register 40, CFR Part 50.
- Zeger SL, Dominici F, Samet J. Harvesting-resistant estimates of air pollution effects on mortality. Epidemiology. 1999;10:171–175. [PubMed] [Google Scholar]