Identification of differentially expressed spatial clusters using humoral response microarray data

Abstract

The antibody microarray is a powerful chip-based technology for profiling hundreds of proteins simultaneously and is used increasingly nowadays. To study humoral response in pancreatic cancers, Patwa et al. (2007) developed a two-dimensional liquid separation technique and built a two-dimensional antibody microarray. However, identifying differential expression regions on the antibody microarray requires the use of appropriate statistical methods to fairly assess the large amounts of data generated. In this paper, we propose a permutation-based test using spatial information of the two-dimensional antibody microarray. By borrowing strength from the neighboring differentially expressed spots, we are able to detect the differential expression region with very high power controlling type I error at 0.05 in our simulation studies. We also apply the proposed methodology to a real microarray dataset.

1 Introduction

Microarray technologies have been utilized extensively in scientific and medical experiments to assess the global expression patterns of multiple samples simultaneously. Most microarray platforms assay for expression of transcript mRNA, copy number or single nucleotide polymorphisms. However, in thinking of human diseases such as cancer, the major molecules that are of interest are proteins. In this paper, we deal with a particular type of microarray known as an antibody microarray.

Antibody microarrays are currently the method mostly adopted in studying cancer immune responses on a protein level. A microarray consisting of antibodies is probed with serum from normal or diseased patients to determine which set of samples differentially elicits an immune response. Typically, such a method is used assuming that the proteins (antibodies) are known. Here, we use a new technology, developed by (Patwa et al., 2007) in which proteins from a pancreatic cancer cell line as well as pancreatic cancer tissue were separated by a two-dimensional liquid separation technique after which they were arrayed on nitrocellulose slides. The slides were then probed with serum from normal individuals as well as patients diagnosed with pancreatic cancer. Only after a fraction of the spots are selected are the proteins then identified using a mass spectrometric-based technology.

The data can be summarized in the form of “Digital Western blots,” as given in Figure 1. Each point corresponds to a two-statistic comparison between cases and controls for a protein at a given pH level and isoelectric point. A common problem is to determine which spots are differentially expressed between the cases and controls. The statistical analysis method of choice in such studies typically involves the use of a two sample t-test to assess differences between normal and diseased states. While many statistical methods exist for assessing differential expression in gene expression data (e.g. Ge et al. (2003)), there is an element of spatial correlation that we would like to exploit in differential expression analyses with antibody arrays. This is evident from Figure 1. Thus, we wish to use spatial information in our differential expression analyses, which renders this microarray analysis problem different from most studied in the literature. In this article, we develop tests of differential expression in which the goal is to find differentially expressed regions on the antibody microarray. We adapt an approach developed by Tango (2007) for identifying differentially expressed spatial clusters. A complication to direct application of this methodology involves choice of the appropriate null distribution for assessing significance. We develop a new permutation-based procedure for assessing the null distribution of the test statistics in this problem. The structure of this paper is as follows. In Section 2, we describe the calculation of the test statistics in this problem; further details of this can be found in Tango (2007). The development of the permutation distribution occurs in Section 3. We report on the results of some simulation studies and data analyses in Section 4. Finally, we conclude with some discussion in Section 5.

Fig. 1.

Wilcoxon rank sum statistics are calculated for each grid to assess differences between cancer and normal sera. Each pH/fraction combination was tested and the p-values are plotted in the above figure. The red/orange section at low fractions of pH 5.1 through 5.7 indicates a possible region in which cancer is expressing above normal.

2 Proposed Methodology

We assume that there are two different experimental conditions that we wish to compare. Let there be n₁ samples from the first condition and n₂ samples from the second. We denote the spatial location as a two-dimensional parameter (g, h), g = 1, … , m; h = 1, …, l. There is a total of m × l combinations of grid points.

We are interested in detecting if there are any significant differentially expressed clusters. The null hypothesis can be expressed as the union of the following three hypotheses: H₀₁: There are no differential expressions for any points on the grid; H₀₂: All m × l grid points are differentially expressed; H₀₃: Some grids are differentially expressed, but there is no cluster of significant differential expressions. For simplicity, we combine these three null hypotheses into one null hypothesis, H₀: There are no differentially expressed points or there is no cluster of differential expressions.

At each grid point, we have measurements on (n₁ + n₂) samples. We calculate a summary statistic of differential expression between the two groups. It could be the t-statistic or a Wilcoxon rank-sum statistic. Here and in the sequel, we use the latter, but the proposed framework could easily handle the former as well. We then modify the approach of Tango (Tango, 2007) and calculate the two-dimensional statistic vector for a cluster S

$$T_s\left(\theta \right)=[{\mathbf{A}}_s^T\left(\theta \right){\mathbf{A}}_s\left(\theta \right){]}^{-1}{\mathbf{A}}_s^T\left(\theta \right)\delta$$ (1)

where δ is an m × l by 2 matrix of scoring function which will be defined in Section 3, and A(θ) is an m × l by m × l matrix that denotes the closeness between any two locations, with θ parametrizing the distance model used. Here A_s(θ) denotes the sth column of matrix A(θ). We consider several choices for A:

1. The modified k nearest neighbors model: A = [a_ij], where

   $$a_{ij}\left(k\right)=\{\begin{array}{cc}1,\hfill & \mathit{if}\mid g_i-g_j\mid \le k\mathit{or}\mid h_i-h_j\mid \le k\hfill \\ 0,\hfill & \mathit{else}\hfill \end{array}\phantom{\}}$$

   In this model θ = k.
2. The extended modified (k, r)nearest neighbors model:

   $$a_{ij}(k,r)=\{\begin{array}{cc}1\hfill & \mathit{if}\mid g_i-g_j\mid \le k\mathit{or}\mid h_i-h_j\mid \le r\hfill \\ 0,\hfill & \mathit{else}\hfill \end{array}\phantom{\}}$$

3. Fixed area of (k, r)nearest neighbors model: This is the same as (2), with the constraint that k + r = c, where c is a pre-defined constant.

3 Assessing significance

Recall that our goal is to test for the presence of differentially expressed clusters between two conditions. To do this, we use an idea applied in a completely different setting by Efron and Tibshirani (2007). For each cluster S with t grids, we calculate the following two-dimensional scoring function:

$$s_i\left(z_i\right)=\{s_i^{+}\left(z_i\right),s_i^{-}\left(z_i\right)\},(i=1,\cdots ,t)$$

where z_i is the summary statistic obtained from t-test or Wilcoxon rank-sum test; s⁺(z) = max(z, 0) and s^-(z) = - min(z, 0). Define the “maxmean” test statistic:

$$S_{\max }=\max \{{\stackrel{‒}{s}}^{+},{\stackrel{‒}{s}}^{-}\},$$

where ${\stackrel{‒}{s}}^{+}=t^{-1}{\sum }_{i=1}^t{s}_i^{+}\left(z_i\right)$ and ${\stackrel{‒}{s}}^{-}=t^{-1}{\sum }_{i=1}^t{s}^{-}\left(z_i\right)$. Therefore, the maxmean statistic for a cluster S in formula (1) is

$$T_{\max }\left(\theta \right)=\max T_s\left(\theta \right)$$

Large values of the maxmean statistic indicate evidence against the null hypothesis.

While our object of inference are the clusters, note that the independent units are the samples. Under the null hypothesis, if we permute the grid locations, then we will be underestimating the true variability, since the grid locations are not statistically independent. If we permute the sample labels, then we are not directly estimating the null distribution of the clusters.

To adjust the null distribution of the cluster statistics, we do a restandardization as in Efron and Tibshirani (2007). The restandardization is applied separately to ${\stackrel{‒}{s}}^{+}$ and ${\stackrel{‒}{s}}^{-}$. Then, the two statistics are combined to give ${\tilde{S}}_{\max }^{\ast }=\max \{{\tilde{s}}^{+},{\tilde{s}}^{-}\}$. Note that the means and standard deviations for maxmean statistic can be computed from the grid-wise means and standard deviations.

A permutation test is conducted for comparison of observed test statistic with test statistics under null hypotheses. The labels of the (n₁+n₂) protein samples are permuted and the test statistics ${\tilde{S}}_{\max }^{\ast }$ are obtained by the same method described above. P-values are calculated for each cluster S after 1000 permutations. Q-values (Storey (2002)) are obtained to adjust for multiple testing of the m × l clusters.

In practice, there may be some situations in which the size parameter k is difficult to determine beforehand. In that case, we may repeat the test using different k's (i.e. k can take values ranging from 1 to a user-defined upper bound k_U), and consequently, lead to multiple testing problems again. In Tango (2007), he introduced an efficient robust test called the Max test to control for this problem. The Max test is defined as the maximum of the test statistic considered, which is equivalent to the minimum of p-values. As the value of k varies from 1 to k_U, the test statistic Pmin is defined as:

$$\begin{array}{cc}\hfill Pmin& =\min Pr\{{\tilde{S}}_{\max }^{\ast }\left(k\right)\ge S_{\mathit{max}}^{\ast }\left(k\right)\mid H_0,k\}\hfill \\ \hfill & =Pr\{{\tilde{S}}_{\max }^{\ast }\left(k\right)\ge S_{\mathit{max}}^{\ast }\left(k\right)\mid H_0,k=k^{\ast }\}\hfill \end{array}$$ (2)

where ${\tilde{S}}_{\max }^{\ast }\left(k\right)$ is the test statistic under null hypothesis; $S_{\max }^{\ast }\left(k\right)$ is the observed test statistic at k and k^* is where we obtain the minimum p-values of $S_{\max }^{\ast }\left(k\right)$. The minimum is chosen in the parameter space {k : 1 ≤ k ≤ k_U}. k_U should be chosen such that the cluster sizes that will be considered are reasonable in specific problem settings. For example, in proteomic studies, proteins will only be expressed differentially for cancer and normal cells under certain pH and isoelectric conditions. Thus, the cluster size will usually not be too large. In this case, we choose the upper bound to be an appropriate value which ensures that a testing cluster size is at most of 50% of total grids.

If the null hypothesis is rejected, local cluster is identified as the one having a significant p-value after FDR adjustment as well as Max test. The best cluster size for that cluster is determined by certain k value where the minimum p-value is attained.

4 Numerical Examples

4.1 Real Data Example

We analyzed 30 protein samples after a two-dimensional liquid separation. In that dataset, there were 15 pancreatic cancer samples and 15 normal samples. Those protein samples were separated by chromatofocusing (CF) from pH 9.2 to 4.3 and each CF fraction was further separated by non-porous reversed-phase HPLC. The pH levels are denoted as 1, 2, 3, . 19, and the fractions separated by NPS-RP-HPLC are labeled as 1, 2, 3..70. The data are cleaned by an analysis of variance method, described in Patwa et al. (2007). Test statistic z is computed by using Wilcoxon Rank-Sum test for each combination of fractions and pH conditions. The location matrix and maxmean statistics are calculated as described in Section 2 and 3 by using the modified k nearest neighbor's model for k from 1 to 12. B-H FDR method and Max test are applied to control multiplicity testing problems. The results show that none of the p-values are smaller than 0.05, which indicates that there are no differential expressed clusters identified. If we fix one condition and try to identify potential clusters when the other condition varies and apply the extended modified (k, r) nearest neighbor's model with r equal to 0, all the tests still yield non-significant results. In fact, the smallest p value of the Wilcoxon Rank-Sum tests between cancer and normal sera under 1012 combinations of two conditions (There are missing data for the rest of 318 combinations of two conditions) is 0.00315, which will be considered to be non-significant if we control the multiplicity testing problem by either conservative method: Bonferroni correction or liberal method: B-H FDR method. This may explain the reason that we cannot find any significant clusters by using neither the modified k nearest neighbor's model nor the extended modified (k, r) nearest neighbor's model.

4.2 Simulation Studies

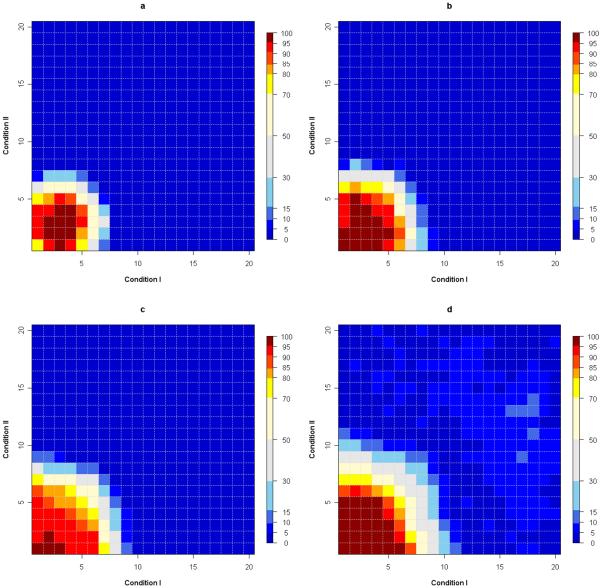
To validate this method, data simulation analyses are performed and powers of this test are calculated based on 100 data simulations. Assume all the data are generated under two conditions with 20 levels of each. For alternative hypothesis, a pre-designed square cluster of size 36 grids (i.e. pH 1 to 6 and fractions 1 to 6) is sampled with 15 cancer protein intensities from N(1, 1) and 15 controls from N(0, 1). Among the rest of the 364 grids, 100 grids picked randomly are included as noises with cancer sampled from N(1, 1) and normal sampled from N(0, 1); the other 264 grids have 30 cancer and normal protein intensities all sampled from standard normal distribution. The same methods are performed for k from 1 to 8. Since the true signal matrix is 6 by 6, We choose the upper bound of k to be a little bit larger than 6. Controlling type I error rate at 0.05, powers of this test are calculated for each of k's separately as well as for all Ks combined using formula (2). When k is equal to 3, 4, or 5, our method performs the best with very high powers detecting nearly all the differentially expressed clusters (Figure 2a-2c). For most of the simulated true clusters, the probabilities of identifying them range from 0.80 to 1.00. When all eight k values are considered together by using formula (2), the probability of detecting differential expressed cluster of any size is even larger compared with the power for any specific k value (Figure 2d).

Fig. 2.

(a). Heatmap of the powers of alternative hypothesis testing for k = 3controlling type I error at 0.05. All the powers (the probability of identifying a cluster with ith grid as the center and size determined by specific k = 3; i=1, 2, ⋯, 400) are shown in percentage in the plot. For example, for k = 3, if the first grid is in dark red, that means the cluster with first grid as the center and including grids within 3 units (row and column indexes) away from the center is identified as differentially expressed region more than 95% of the times.(b). Heatmap of the powers of alternative hypothesis testing for k = 4 controlling type I error at 0.05. (c). Heatmap of the powers of alternative hypothesis testing for k = 5 controlling type I error at 0.05. (d). Heatmap of the powers of alternative hypothesis testing for all k(1 - 8) considered together by using formula (2), controlling type I error at 0.05. When all eight k values are considered together, the probability of detecting differential expressed cluster of any size is even larger compared with the power for any specific k value.

However, our method does not show a satisfactory performance in terms of detecting clusters close to and on the boundary of the true signal matrix (Figure 2a-2d). This may be explained by small sample sizes of our simulation studies as well as a small signal-to-noise ratio (e.g. Of 400 grids total, 9% are signals and 25% are noises). Thus, we carry out further simulation analyses by increasing either the sample size or the signal-to-noise ratio. Figure 3a-3b show the results from the two simulation studies. By increasing the sample size 10 times larger, or incorporating only 50 noises sampled from N(1,1), the performance of our method is improved comparing with the simulation results in Figure 2a and it identifies true clusters more than 95% of time with fewer poor detections near the boundary. In Figure 3c, we introduce 50 noises sampled from N(-1, 1) and 50 noises sampled from N(1, 1) and the simulation results indicate even better performance of our method as the case when we increase the signal-to-noise ratio by 50% in Figure 3b.

Fig. 3.

(a). Heatmap of the powers of alternative hypothesis testing for k = 3with sample size 10 folds larger, controlling type I error at 0.05. (b). Heatmap of the powers of alternative hypothesis testing for k = 3with signal-to-noise ratio increased by 50%, controlling type I error at 0.05. (c). Heatmap of the powers of alternative hypothesis testing for k = 3 with 50 noises sampled from N(-1, 1)controlling type I error at 0.05.

For null hypotheses, data are simulated under three specific null hypotheses as previously described. Under H₀₁, 30 samples from all the 400 grids are sampled from standard normal distribution. Under H₀₂, 30 samples from all the 400 grids are sampled with 15 cancers from N(1, 1) and 15 controls from N(0, 1). Under H₀₃, of 36 randomly selected grids among all 400 grids, 15 cancers are sampled from N(1, 1) and 15 controls from N(0, 1). For k from 1 to 8, the same methods are applied. After repeating 100 times for each of three null hypotheses, the powers of all the tests are calculated for each k separately as well as for all eight Ks combined and turn out to be less than 0.05 (There are only two exceptions with power equal to 0.06 for testing H₀₂ when all eight Ks are considered together; Figure 4a-4c).

Fig. 4.

(a). Heatmap of the powers of null hypothesis I testing for all k(1 - 8) considered together by using formula (2), controlling type I error at 0.05. (b). Heatmap of the powers of null hypothesis II testing for all k(1 - 8) considered together by using formula (2), controlling type I error at 0.05. (c). Heatmap of the powers of null hypothesis III testing for all k(1 - 8) considered together by using formula (2), controlling type I error at 0.05.

The results of our simulation studies may be summarized as follows: (i) our method have very high powers to detect differentially expressed regions controlling type I error rate at 0.05. (ii) As the sample size or signal-to-noise ratio increases (the noises are sampled from the same distribution as signals), our method shows much better performance in detecting both the clusters in the center of the signal matrix and the clusters near the boundary of signal matrix. (iii) Incoporating noises sampled from distributions in the opposite direction of signals' improves the performance of our method comparing with increasing signal-to-noise ratio. (iv) If the effect size of expression level of cancer versus normal proteins is small, we may need large sample size to detect differentially expressed clusters.

5 Discussion

We have developed tests of identifying differentially expressed regions on the two-dimensional antibody microarray. By borrowing strength from neighboring differential grids, our method shows very high powers in terms of detecting differentially expressed regions from our simulation studies. We apply our method to the real data, but do not find any significant clusters with k ranging from 1 to 12.

The simulation studies mainly focus on computing test statistics with spatial matrix A(θ) defined by the k nearest neighbors model (model (1)), which only tests for clusters of square shapes. But our methods can be easily extended to testing of clusters of rectangle shapes or fixed sizes with model (2) and (3). The simulation results indicate good performance of these modifications (results not shown). The k nearest neighbors model that we mainly used in this article gives equal weight to all the nearest neighbors of each gird. We may also use a gradual decline, which is described in Tango (2000), to define the spatial matrix so that we can distinguish the adjacent grids from boundary grids and focus mainly on the center of the clusters.

In this paper, we use maxmean statistic as the cluster statistic to identify differential expressed spatial cluster. In the context of brain imaging, Bullmore et al. (1999) introduced two cluster statistics: cluster area and cluster mass. The cluster area statistic calculates the two-dimensional (2-D) area of a suprathreshold cluster and the cluster mass statistic sums up all the suprathreshold statistics of a 2-D cluster. The three statistics capture different characteristics of clusters. The maxmean statistic is more sensitive to clusters with high density of signals (i.e., large maxmean statistic). By contrast, the cluster area statistic is sensitive when the cluster size is significantly large and the cluster mass statistic combines the information of the density of signals and the area of clusters. Therefore, a cluster will be identified as significant by cluster area statistics if the cluster size is large enough even though the statistic density for that cluster is moderately low. On the other hand, the cluster mass statistic has great sensitivity for a combination of marginally significant cluster density and cluster extent, but may not be able to detect signals when only one of them is highly significant. With the maxmean statistic, we mainly focus on the densities of signals of clusters and allow the comparability of clusters with different sizes.

Another important feature of the cluster area and cluster mass methods is that Bullmore et al. (1999) obtain cluster statistics by arbitrarily thresholding maps of original statistics and considering the properties of the spatial clusters of suprathresholded parts. By doing this, they reduced the number of testing clusters and ease the computational burden. Our method can also be extended by adopting their thresholding ideas and calculate the suprathresholded maxmean statistics to test the clusters which are identified by thresholding rather than determined by k nearest neighbors model. However, this brings up the issue that the determination of threshold is sometimes very subjective and diffcult to be verified. Sensitivity analysis may be required to provide a valid inference. Moreover, the identified clusters by thresholding may be of special shapes besides regular square or rectangular shapes. This can be regarded as one advantage of thresholding such that it allows the detection of clusters with flexible shapes, but may also not be reasonable and interpretable in some biological scenarios such as protein microarrys.

Our methods are permutation-based tests and the advantages of permutation testing have been well recognized: it generally conditions on far fewer assumptions and can be readily devised for any statistic of interest. However, the computational cost will increase as the dimension of spatial matrix gets larger. It will not be efficient to deal with a fine grid large two-dimensional matrix or even three-dimensional space with moderate size. In that case, we may treat the measurements of each protein under all combinations of two conditions as the two-dimensional functional data and think of transforming this two-dimensional functional data into some functional space (e.g. wavelet space) with the goal of reducing dimensions (e.g, see Mager et al. (2007), Aston et al. (2006) for applications of wavelet space to imaging data). This area merits further investigation.