Thermodynamic basis of the enhanced specificity of structured DNA probes

Abstract

Molecular beacons are DNA probes that form a stem-and-loop structure and possess an internally quenched fluorophore. When they bind to complementary nucleic acids, they undergo a conformational transition that switches on their fluorescence. These probes recognize their targets with higher specificity than probes that cannot form a hairpin stem, and they easily discriminate targets that differ from one another by only a single nucleotide. Our results show that molecular beacons can exist in three different states: bound to a target, free in the form of a hairpin structure, and free in the form of a random coil. Thermodynamic analysis of the transitions between these states reveals that enhanced specificity is a general feature of conformationally constrained probes.

We have developed DNA probes, called “molecular beacons,” that become fluorescent when they bind to complementary nucleic acids (1). These probes are single-stranded DNA molecules that form a stem-and-loop structure (see Fig. 1). A fluorophore is linked to one end of the molecule and a quencher is linked to the other end. Consequently, fluorescence is quenched when the probe is in the stem-and-loop conformation. However, when the probe sequence in the loop anneals to a complementary nucleic acid target sequence, the longer and stronger probe–target duplex overcomes the shorter hairpin stem, leading to a conformational reorganization. The rigidity of the probe–target helix forces the hairpin stem to unwind, resulting in the separation of the fluorophore and quencher, and fluorescence is switched on. Typically, the fluorescence of the probe increases 100-fold when it binds to its target.

Figure 1.

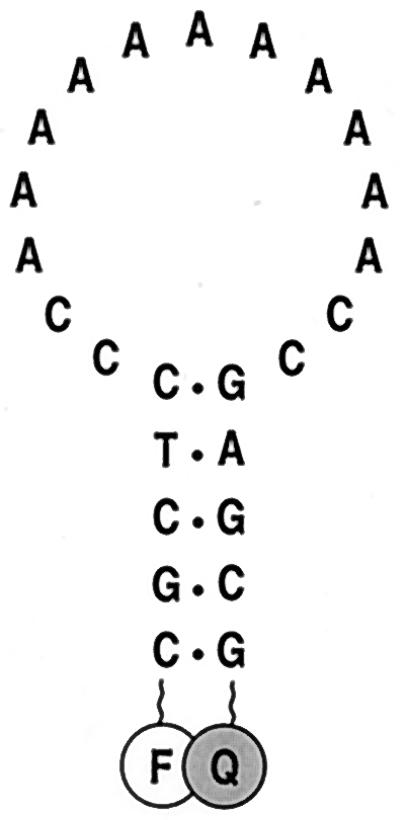
Schematic representation of the molecular beacon used in these experiments. The molecule has an oligoadenosine probe sequence embedded within complementary arm sequences. The arms form a hairpin stem and the probe sequence is located in the hairpin loop. A fluorophore (F) is covalently linked to the end of one arm and a quencher (Q) is covalently linked to the end of the other arm.

Oligonucleotide probes are commonly used to identify complementary strands in the presence of unrelated nucleic acids. However, their specificity is limited when they are used to discriminate targets that differ from one another by only a single nucleotide. As the length of the probe is increased, the free energy penalty resulting from a mismatched base pair in the probe–target duplex represents a smaller and smaller fraction of the total free energy of binding (2). Consequently, for oligonucleotides that are sufficiently long to distinguish a particular sequence in the presence of unrelated DNA the size of a genome, a mismatched base pair will have only a marginal effect on the stability of the duplex. This limitation often necessitates the use of proteins or chemical agents to assist in the identification of mismatched base pairs (3–5).

In this report, we show that molecular beacons readily distinguish targets that differ by only a single nucleotide, and that they are significantly more specific than conventional oligonucleotide probes of equivalent length. We demonstrate that their enhanced specificity is due to their ability to form a stem-and-loop structure. Utilizing a thermodynamic approach, we constructed a phase diagram that illustrates how molecular beacons behave at different temperatures in the presence of perfectly complementary targets and in the presence of targets that contain a mismatched nucleotide. This analysis reveals that enhanced specificity is a general feature of structurally constrained probes.

MATERIALS AND METHODS

Construction of Molecular Beacons.

Molecular beacons were synthesized from modified synthetic oligonucleotides that contained a primary amino group covalently attached to their 3′ end and a sulfhydryl group protected by a trityl moiety covalently attached to their 5′ end. The quencher, 4-([4′-(dimethylamino)phenyl]azo)benzoic acid (dabcyl), was coupled to the 3′ end of the oligonucleotides by reacting a succinimidyl ester of dabcyl (Molecular Probes) to the primary amino group. The reaction products were passed through a NAP-5 Sephadex column (Pharmacia Biotech) to remove unreacted dabcyl and to exchange buffers. The derivatized oligonucleotides were then purified by high-pressure liquid chromatography through a reverse-phase column. The protective trityl moiety was then removed from the sulfhydryl group and an iodoacetamide derivative of fluorescein (Molecular Probes) was conjugated to the reduced thiol. Molecular beacons possessing both a fluorophore and a quencher were isolated by gel-exclusion chromatography and high-pressure liquid chromatography. A detailed protocol for synthesizing molecular beacons is available on the internet at http://www.molecular-beacons.org.

Thermal Denaturation Profiles.

The fluorescence of solutions of a molecular beacon (fluorescein-5′-CGCTCCCA₁₁CCGAGCG-3′-dabcyl), in the presence or absence of synthetic target oligonucleotides, was measured as a function of temperature. All measurements were made in 100-μl solutions containing 50 nM molecular beacon, 100 mM KCl, 1 mM MgCl₂, 10 mM Tris⋅HCl (pH 8.0), and no target, 300 nM perfectly complementary target (5′-GGT₁₁GG-3′), or 300 nM mismatched target (5′-GGT₅GT₅GG-3′). The fluorescence of these reaction mixtures was measured by excitation with a 488-nm laser light source in a spectrofluorometric thermal cycler (Applied Biosystems Prism 7700). The temperature was increased in steps of 1°C, from 15°C to 80°C, with each step lasting 5 min. To confirm that nonequilibrium hysteresis did not occur, the temperature was then decreased in 1°C steps from 80°C to 15°C, with each step lasting 5 min. Fluorescence was measured during the last 30 sec of each step.

The intrinsic fluorescence of fluorescein varies with temperature. We therefore measured the fluorescence of a dabcyl-less analogue of the molecular beacon as a function of temperature, and these data were used to correct the thermal denaturation profiles so that the adjusted fluorescence intensities were independent of the intrinsic variation of fluorescein fluorescence. Furthermore, to compare different thermal denaturation profiles, the fluorescence intensities of each profile were divided by the fluorescence intensity measured at 80°C. Consequently, all profiles were normalized to a value of 1.00 at 80°C.

Equilibrium Analysis.

Molecular beacons in solution with their targets can exist in three states: bound to target (phase 1), free of target in the form of a hairpin (phase 2), and free of target in the form of a random coil (phase 3). At equilibrium:

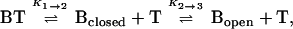where BT is the probe–target duplex, B_closed is the molecular beacon in the form of a hairpin, B_open is the molecular beacon in the form of a random coil, and T is the free target. The fluorescence of the solution at a given temperature, F, is the sum of the fluorescence of the molecular beacons in each of the three states:

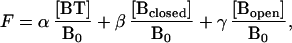1

where α, β, and γ are the characteristic fluorescence intensities of the molecular beacons in each state, and

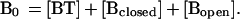The equilibrium constant for the dissociation of the hairpin stem is described by the equation

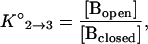and the equilibrium constant for the dissociation of the probe–target duplex is described by the equation

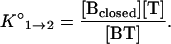2

When the total concentration of targets, T₀, is much greater than the total concentration of molecular beacons, B₀, as is the case in our experiments, T₀ can be substituted for [T] in Eq. 2, and the fraction of molecular beacons in each state as a function of temperature can be expressed in terms of the two equilibrium constants as follows:

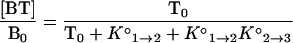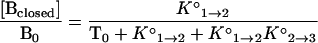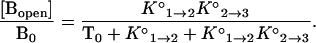Substituting these three expressions into Eq. 1, the fluorescence of a solution of molecular beacons in equilibrium with its target is fully described by the equation

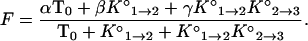3

Thermodynamic Measurements of the Hairpin to Random-Coil Transition.

The thermodynamic parameters that describe the transition from a stem-and-loop structure (phase 2) to a random coil (phase 3), enthalpy (ΔH°_2→3) and entropy (ΔS°_2→3), were determined by analyzing the fluorescence data obtained from the thermal denaturation profile of a 50 nM solution of molecular beacons incubated in the absence of targets. The equilibrium constant for this transition can be expressed in terms of the fluorescence measured in the experiments by taking T₀ = 0 in Eq. 3 and rearranging:

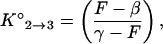where F is the fluorescence intensity at a given temperature, β is the characteristic fluorescence intensity of the molecular beacons in the form of a hairpin (obtained from the fluorescence measured at 15°C), and γ is the characteristic fluorescence intensity of the molecular beacons in the form of a random coil (obtained from the fluorescence measured at 80°C). Since ΔG° = −Rθ ln K(θ) = ΔH° − θ ΔS°, where ΔG° is the free energy, R is the gas constant, and θ is the temperature in kelvin, the fluorescence–temperature data could be fitted to a straight line having the equation

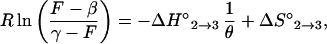where −ΔH°_2→3 is the slope and ΔS°_2→3 is the intercept. This method assumes an all-or-none transition between the stem-and-loop structure and the random coil, and it assumes that enthalpy and entropy do not vary with temperature (6).

Thermodynamic Measurements of the Dissociation of Probe–Target Duplexes.

The thermodynamic parameters that describe the dissociation of a probe–target duplex (phase 1) into a free target and a molecular beacon in the form of a hairpin (phase 2), ΔH°_1→2 and ΔS°_1→2, were determined by analyzing the fluorescence data obtained from the thermal denaturation profiles of 50 nM solutions of molecular beacons incubated in the presence of six different concentrations of added target oligonucleotide (between 300 nM and 300 μM). The analysis was based on the determination of the melting temperature of the probe–target duplexes, θ_m, at each target concentration. θ_m was determined by fitting all of the data in each thermal denaturation profile to Eq. 3, which fully describes fluorescence at every temperature in terms of the two equilibrium constants. At the melting temperature of the duplex, [B_closed] = [BT], and from Eq. 2, K°_1→2equals [T], whose value at θ_m is T₀ − 0.5B₀. Since ΔG° = −R θ ln K(θ) = ΔH° − θ ΔS°, the melting temperature data could be fitted to a straight line having the equation

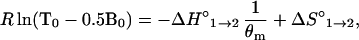where −ΔH°_1→2 is the slope and ΔS°_1→2 is the intercept.

The following rearrangement of Eq. 3 illustrates why θ_m could be obtained from the fluorescence–temperature data:

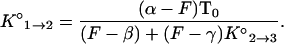The value of β and the values of ΔH°_2→3 and ΔS°_2→3, which are needed to calculate K°_2→3 at each temperature, were obtained from the measurements made with molecular beacons incubated in the absence of targets. For each target concentration, the value of α was obtained from the fluorescence measured at 15°C and the value of γ was obtained from the fluorescence measured at 80°C. Therefore, the fluorescence–temperature data could be used to calculate the value of K°_1→2 at every temperature, and θ_m is the temperature at which K°_1→2 equals T₀ − 0.5B₀.

RESULTS

Characteristics of Molecular Beacons.

The principal feature that distinguishes molecular beacons from conventional nucleic acid probes is the presence of a hairpin stem. The complementary arms are so close to one another in the stem-and-loop configuration that direct coupling takes place between the fluorophore and the quencher (7). Consequently, nonhybridized molecular beacons are quenched, while hybridized molecular beacons fluoresce, eliminating the need to isolate probe–target hybrids from nonhybridized probes to determine the number of probes that are bound to targets. The most intriguing feature of molecular beacons is that they are considerably more specific than the corresponding “linear” probes. Targets that differ from one another by as little as a single nucleotide substitution can readily be distinguished (7, 8). To understand the basis of this enhanced specificity, we carried out a series of thermodynamic measurements that compared the behavior of molecular beacons in the presence of perfectly complementary target oligonucleotides to their behavior in the presence of targets whose sequence created a single mismatched base pair in the probe–target duplex. The experiments were designed to take advantage of the change in fluorescence intensity that occurs upon thermal dissociation of the probe–target duplexes (9–11).

Design of the Probes.

A molecular beacon was synthesized that possessed a 15-nucleotide loop and 5-nucleotide arms. The nucleotide sequence of the loop consisted of an 11-adenosine homo-oligomer flanked by two cytidines at each end (Fig. 1). This homogeneous probe sequence was chosen to reduce the probability of secondary structures forming within the loop and to avoid any context dependence in studies on the effect of mismatch position on the stability of probe–target duplexes. The cytidines at the ends of the loop sequence served to minimize the sliding of the hybridized target oligonucleotide along the probe sequence. The molecular beacons were labeled with fluorescein and dabcyl. When an excess of targets was added to a solution of the molecular beacons, fluorescence increased 50-fold.

Thermal Denaturation Profiles of Molecular Beacons in Equilibrium with Their Targets.

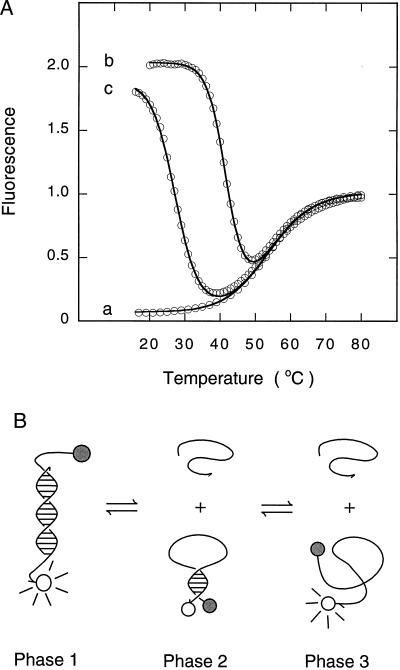
We first monitored the fluorescence of a solution of molecular beacons incubated in the absence of targets at different temperatures. The results (Fig. 2A, trace a) demonstrate that at lower temperatures the molecular beacons are in a closed state, the fluorophore and the quencher are held in close proximity to each other by the hairpin stem, and the molecular beacons do not fluoresce. However, at high temperatures the helical order of the stem gives way to a random-coil configuration, separating the fluorophore from the quencher, restoring fluorescence. This transition occurred at 54°C.

Figure 2.

Phase transitions in solutions containing molecular beacons. (A) Thermal denaturation profiles of solutions containing molecular beacons: trace a, in the absence of targets; trace b, in the presence of a 6-fold excess of perfectly complementary targets; and trace c, in the presence of a 6-fold excess of mismatched targets. The data were fitted to Eq. 3 and plotted as continuous lines. (B) Schematic representation of the phases. As the temperature is raised, the fluorescent probe–target duplex (phase 1) dissociates into a nonfluorescent molecular beacon in a closed conformation and a randomly coiled target oligonucleotide (phase 2). As the temperature is raised even higher, the hairpin stem of the molecular beacon unravels into a fluorescent randomly coiled oligonucleotide (phase 3).

This experiment was repeated in the presence of a 6-fold excess of single-stranded DNA targets that were perfectly complementary to the loop sequence in the molecular beacon. The results (Fig. 2A, trace b) show that the molecular beacons fluoresce brightly at low temperatures, but as the temperature is slowly raised fluorescence diminishes significantly, followed by an increase in fluorescence at the highest temperatures. Fig. 2B summarizes the phase transitions that occur. At low temperatures, probe–target duplexes form spontaneously. Since the hairpin stem is less stable than the probe–target helix, the stem unwinds to allow the probe to bind to its target (Fig. 2B, phase 1). Thus, molecular beacons in duplexes are open and fluorescent, whereas nonhybridized molecular beacons are closed and nonfluorescent. As the temperature is raised, the probe–target duplexes become destabilized, the molecular beacons are released, returning to their closed conformation, and fluorescence decreases (Fig. 2B, phase 2). For the molecular beacons used in our experiments, the transition from phase 1_P (duplexes with perfectly complementary targets) to phase 2 occurred at 42°C. As the temperature is raised further, the closed molecular beacons melt into fluorescent random coils (Fig. 2B, phase 3). This transition occurred at the same temperature (54°C) as the transition seen when the molecular beacons were incubated in the absence of targets. The temperature–fluorescence profile of the probe–target mixture was fitted to Eq. 3, which was derived from this two-phase-transition model. The resulting curve, plotted in Fig. 2A, closely correlates with the experimental data, validating the model.

This experiment was also repeated in the presence of a 6-fold excess of single-stranded DNA targets that were complementary to the probe sequence except for one nucleotide (mismatched targets). Similar changes in fluorescence were observed as the temperature was raised (Fig. 2A, trace c). However, the transition from phase 1_M (duplexes with mismatched targets) to phase 2 occurred at a significantly lower temperature, 28°C, than the transition from phase 1_P to phase 2, which occurred at 42°C. This result reflects the lower stability of probe–target duplexes that contain a mismatched base pair. The difference between the melting temperature of perfectly complementary probe–target duplexes and the melting temperature of mismatched probe–target duplexes was 14°C. Within this temperature range, perfectly complementary targets form duplexes that lead to fluorescence, while mismatched targets do not form duplexes and no fluorescence occurs. The range of temperatures within which perfectly complementary targets form hybrids but mismatched targets do not form hybrids is significantly wider than the corresponding range observed for conventional probes (12–14).

Determination of Thermodynamic Parameters.

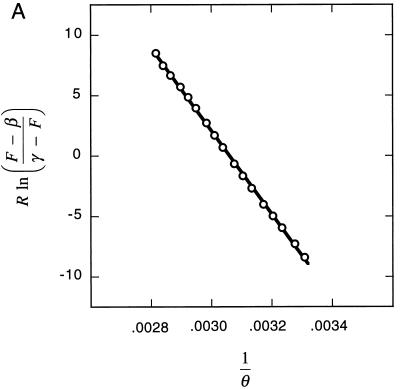
To understand why molecular beacons are able to distinguish closely related target sequences with higher specificity than linear probes can, we measured the thermodynamic parameters that describe the phase transitions that occur when the temperature of a mixture of molecular beacons and oligonucleotide targets is slowly increased. The increase in fluorescence that accompanies dissociation of the hairpin stems (phase 2 to phase 3) in a 50 nM solution of molecular beacons was used to determine the enthalpy and entropy describing this transition (Fig. 3A). We found that ΔH°_2→3 = 34 ± 1 kcal/mol and ΔS°_2→3 = 104 ± 3 cal/mol⋅K (1 cal = 4.18 J).

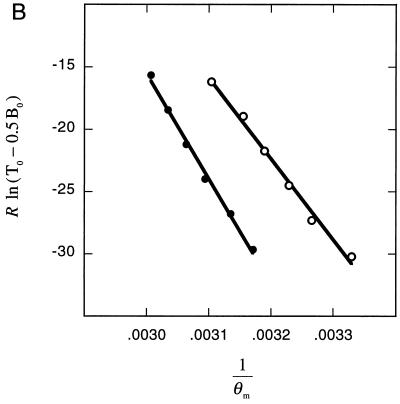
Figure 3.

Determination of thermodynamic parameters. (A) The increase in fluorescence that accompanies the melting of the molecular beacon’s hairpin stem was used to determine the thermodynamic parameters that describe this transition. The slope of the fitted line is equal to the negative value of the enthalpy (−ΔH°_2→3) and the intercept is equal to the entropy (ΔS°_2→3). (B) The increase in the melting temperature of the probe–target duplex that results from increasing the concentration of target oligonucleotides was used to determine the thermodynamic parameters that describe the dissociation of probe–target duplexes. Separate determinations were carried out with perfectly complementary duplexes (●) and with mismatched duplexes (○). The slope of each fitted line is equal to the negative value of the enthalpy (−ΔH°_1→2) and the intercept is equal to the entropy (ΔS°_1→2). In this graph, the independent variable, R ln(T₀ − 0.5B₀), is plotted on the ordinate and the dependent variable, 1/θ_m, is plotted on the abscissa, to illustrate the similarities in the manner in which the enthalpies and entropies were determined for the dissociation of probe–target duplexes and for the dissociation of hairpin stems.

To determine the enthalpy and entropy describing the dissociation of probe–target duplexes (phase 1 to phase 2), we measured the melting temperature of the duplex as a function of the concentration of target oligonucleotides. We obtained temperature–fluorescence profiles from a series of solutions containing 50 nM molecular beacons and different excess concentrations of target oligonucleotides (between 300 nM and 300 μM). The higher the concentration of the target oligonucleotides, the greater the melting temperature of the probe–target duplexes. Since at higher target concentrations it is difficult to distinguish the decrease in fluorescence due to the dissociation of the probe–target duplexes from the increase in fluorescence due to the unwinding of the molecular beacon stems, we utilized Eq. 3, which describes the entire temperature–fluorescence profile, to accurately determine the melting temperature of the duplexes. The resulting melting temperatures were then used to calculate the thermodynamic parameters that describe the transition from phase 1 to phase 2 (Fig. 3B). For the dissociation of probe–target duplexes formed from perfectly complementary target oligonucleotides, we found that ΔH°_1P→2 = 84 ± 3 kcal/mol and ΔS°_1P→2 = 237 ± 9 cal/mol⋅K; and for the dissociation of probe–target duplexes formed from mismatched target oligonucleotides, we found that ΔH°_1M→2 = 65 ± 3 kcal/mol and ΔS°_1M→2 = 185 ± 10 cal/mol⋅K.

Phase Diagram for Solutions Containing Molecular Beacons and Targets.

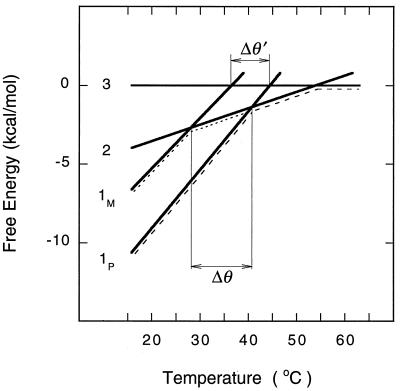
We constructed a diagram showing free energy for the three phases of molecular beacons in equilibrium with their targets (Fig. 4). The free energy of each phase was plotted as a function of temperature (ΔG = ΔH − θ ΔS). Phase 3 was chosen as the reference state (ΔG₃ = 0), because the molecular beacons and the target oligonucleotides are present as disorganized random coils. Since ΔG₂ = ΔG₃ − ΔG_2→3, the free energy of phase 2 is calculated to be ΔG₂ = −ΔH°_2→3 + θ ΔS°_2→3; and since ΔG₁ = ΔG₃ − ΔG_2→3 − ΔG_1→2, the free energy of phase 1 is calculated to be ΔG₁ = −(ΔH°_2→3 + ΔH°_1→2) + θ(ΔS°_2→3 + ΔS°_1→2 − R lnT₀). The predominant phase at each temperature is the phase with the lowest free energy. From the diagram it can be seen that in a system of molecular beacons and perfectly complementary targets at temperatures below 42°C, phase 1_P predominates; at temperatures between 42°C and 54°C, phase 2 predominates; and at temperatures above 54°C, phase 3 predominates (this progression is indicated in the figure by a line containing long dashes). By contrast, in a solution containing mismatched targets, the transition from phase 1_M to phase 2 (indicated by a line containing short dashes) occurs at a significantly lower temperature (θ_M = 28°C) than the corresponding transition from phase 1_P to phase 2 (θ_P = 42°C). Consequently, in the range between these temperatures (Δθ = θ_P − θ_M = 14°C), perfectly complementary targets can be distinguished from mismatched targets.

Figure 4.

Free energy of the three phases of a solution of molecular beacons in equilibrium with target oligonucleotides. Although this phase diagram was calculated for a solution containing a particular molecular beacon at 50 nM and its target at 300 nM, the relative positions of the phase lines are generally the same for all molecular beacons under all conditions. The equation of each line is ΔG = ΔH − θ ΔS, where ΔG₃ = 0; ΔG₂ = 0.104 θ − 34 kcal/mol; ΔG_1P = 0.371 θ − 118; and ΔG_1M = 0.320 θ − 99. The difference between the melting temperatures of perfectly matched duplexes (phase 1_P) and mismatched duplexes (phase 1_M) is greater if the probe can form a structure after dissociation (Δθ = 14°C) than it is if the probe cannot form a structure (Δθ′ = 8°C).

The phase diagram illustrates why molecular beacons are able to distinguish closely related target sequences with higher specificity than the corresponding linear probes can. If we had used a probe with the same loop sequence, but with arm sequences that cannot form a hairpin structure (unstructured probe), then phase 2 could not occur, and the only phase change would have been a direct transition from phase 1 to phase 3. From the phase diagram it can be seen that if unstructured probes had been used to form perfectly complementary probe–target duplexes, the transition from phase 1_P to phase 3 would have occurred at 45°C (at the intersection of the line describing the free energy of phase 1_P with the line describing the free energy of phase 3); and if unstructured probes had been used to form mismatched probe–target duplexes, the transition from phase 1_M to phase 3 would have occurred at 37°C. The difference between these two transitions is relatively small (Δθ′ = 8°C). A comparison of Δθ with Δθ′ shows that probes possessing a stem-and-loop structure distinguish mismatches over a wider range of temperatures than do unstructured probes.

Although the phase diagram was constructed from thermodynamic parameters determined for a particular molecular beacon, the relative placement of the lines that describe the free energy of each phase is common to all molecular beacons, and more generally, to all probes that can form a structured intermediate when they dissociate from their target. Since enthalpy is dependent on the number of base pairs formed, the enthalpies of each phase will always occur in the following order: 0 = ΔH°₃ > ΔH°₂ > ΔH°_1M > ΔH°_1P. Similarly, entropy is dependent on the number of configurations that can be assumed by the probe in each phase: 0 = ΔS°₃ > ΔS°₂ > ΔS°_1M > ΔS°_1P. In particular, the number of configurations that can be assumed by an unstructured probe (ΔS₃) is substantially higher than the number of configurations that can be assumed by a structured probe (ΔS₂). Consequently, the phase diagram will look similar for all structured probes. It is thus generally true that if a probe can form a structure after dissociating from its target, phase 2 will occur, and the line describing phase 2 will intersect the lines describing phase 1_M and 1_P over a wider range of temperatures than the corresponding intersections with the line describing phase 3. Since molecular beacons are constrained polymers, upon dissociation (or formation) of probe–target duplexes they undergo a greater reorganization than do unstructured probes, leading to a higher sensitivity to the presence of a mismatch. Similarly, all conformationally constrained probes should display higher specificity in molecular recognition than unconstrained probes.

Effect of Mismatch Position and Mismatch Identity.

We assumed an all-or-none mechanism for the formation of probe–target hybrids. However, when a molecular beacon hybridizes to its target its stem must unwind, so it is not clear whether its hybridization is a one-step or a multistep process. The all-or-none mechanism predicts that the position of a mismatch should have little effect on the stability of the probe–target duplex, as long as the mismatch is flanked on either side by at least one base pair (6). To check whether the all-or-none mechanism of hybridization applies to molecular beacons, we prepared a series of target oligonucleotides whose sequences (5′-GGT_5+nGT_5−nGG-3′, where −4 ≤ n ≤ 4) created a G-A mismatch (instead of a complementary T⋅A base pair) at different positions within the duplex formed by the molecular beacon shown in Fig. 1. Sequence-dependent effects on hybrid stability were minimized because, irrespective of location, the mismatches were always embedded within neighboring T⋅A base pairs. For each target, we obtained a thermal denaturation profile at six different target concentrations (between 300 nM and 300 μM) and used the results to determine the enthalpy and entropy for the dissociation of its probe–target duplex. We then calculated the melting temperature of the duplex in the presence of 300 nM target. The results show that the position of the mismatched base pair has a negligible effect on melting temperature (Table 1), implying that molecular beacons form hybrids through an all-or-none mechanism. To determine whether the identity of the mismatched base pair influences the stability of the hybrid, we also prepared targets containing different nucleotides at the position corresponding to the central nucleotide of the probe sequence (5′-GGT₅NT₅GG-3′, where N = A, C, or G), and we studied the dissociation of their probe–target hybrids in the same manner. The results show that the identity of the mismatched base pair does not have an appreciable effect on the melting temperature of the hybrid (Table 1). Since the melting temperatures of the mismatched duplexes are similar, and since they are all significantly lower than the melting temperature of the perfectly complementary duplex, molecular beacons can easily detect the presence of a mismatch, yet they are insensitive to variations in identity and position. These features greatly simplify the detection of point mutations.

Table 1.

Enthalpies, entropies, and melting temperatures for the dissociation of a perfectly complementary probe–target duplex (first entry), probe–target duplexes containing different mismatched base pairs at the same position (next three entries), and probe–target duplexes containing the same mismatched base pair at different positions (last nine entries)

Mismatch	Position (n)	ΔH°, kcal/mol	ΔS°, cal/mol⋅K	θm, °C
T⋅A	0	84	237	42
A-A	0	69	201	27
C-A	0	61	175	23
G-A	0	65	185	28
G-A	−4	75	218	30
G-A	−3	68	194	29
G-A	−2	78	228	30
G-A	−1	72	208	29
G-A	0	65	185	28
G-A	+1	74	213	29
G-A	+2	74	213	29
G-A	+3	74	212	29
G-A	+4	77	221	31

Standard enthalpies and standard entropies are shown for solutions containing 50 nM molecular beacons and 1 M target oligonucleotides in the presence of 100 mM KCl and 1 mM MgCl₂. Melting temperatures are shown for solutions containing 50 nM molecular beacons and 300 nM target oligonucleotides. The errors associated with ΔH° and ΔS° averaged ±6%. 

DISCUSSION

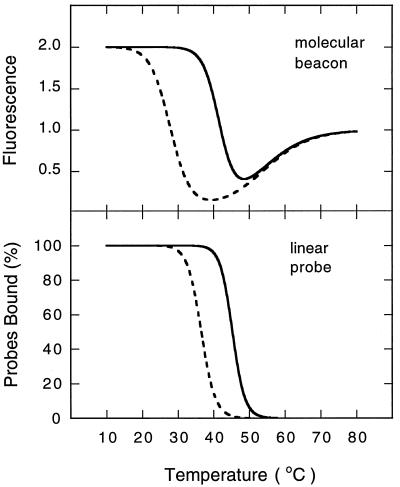
The phase diagram for mixtures of molecular beacons and targets (Fig. 4) predicts the melting temperatures of the probe–target duplexes that would be formed by the corresponding linear probes. Utilizing the measured thermodynamic parameters, we reconstructed the complete thermal denaturation profiles of duplexes formed from linear probes and compared them with the reconstructed profiles of duplexes formed from molecular beacons (Fig. 5). The figure shows that the range of temperatures within which discrimination between the two targets is possible is wider for molecular beacons than it is for the corresponding linear probes.

Figure 5.

Comparison of the window of mismatch discrimination observed for molecular beacons with the window of discrimination predicted for the corresponding linear probes. These curves were calculated for mixtures of 50 nM probes and 300 nM targets, utilizing the thermodynamic parameters measured for molecular beacons. Continuous lines identify perfectly complementary probe–target duplexes and broken lines identify mismatched probe–target duplexes.

The phase diagram (Fig. 4) shows that structural constraints on probe conformation lead to enhanced specificity. This result implies that the specificity of molecular beacons and other oligonucleotide probes can be modulated by altering the degree of constraint placed on their conformation. We found that increasing the length (or strength) of the stem of molecular beacons increases the difference between the melting temperatures of perfectly complementary duplexes and mismatched duplexes. Thus, the presence of the stem offers a means of maximizing the specificity of the probe, without needing to alter experimental conditions. There is, however, a limitation on the length to which the stem can be extended. When the stems become too long, hybridization kinetics are slow and the probes tend to remain closed while bound to their targets, particularly at lower temperatures. This problem can be overcome by extending the probe sequence in such a manner that one arm of the stem also binds to the target.

Other methods of constraining the flexibility of oligonucleotide probes should be fruitful. Some of these have been described—for example, circularization of a probe (15) or the introduction of secondary structures into a probe (16) enhances the specificity of formation of triple helices. Moreover, structural constraints that enhance the specificity of molecular recognition may occur in nature. For example, the high specificity of recognition between codons in a messenger RNA and the anticodon loop of transfer RNAs may be enabled by structural constraints inherent in the anticodon stem (17, 18). Furthermore, enhanced specificity due to structural constraint is probably not limited to nucleic acids, and should be present in other macromolecular interactions.

The high specificity of structured probes suggests their use in a variety of practical applications. Molecular beacons can be used for simple and accurate genetic analyses in which single-nucleotide polymorphisms need to be detected. Molecular beacons will also be useful as recognition elements in molecular computation (19). Hairpin-shaped oligonucleotide primers will be useful for enhancing the specificity of nucleic acid amplification reactions. And finally, antisense oligonucleotides used for the inhibition of gene expression (20) can be embedded within a hairpin structure, increasing their ability to selectively inhibit the pathogenic effects of point mutations.

ABBREVIATION

dabcyl

4-([4′-(dimethylamino)phenyl]azo)benzoic acid