Cascading extinctions and community collapse in model food webs

Abstract

Species loss in ecosystems can lead to secondary extinctions as a result of consumer–resource relationships and other species interactions. We compare levels of secondary extinctions in communities generated by four structural food-web models and a fifth null model in response to sequential primary species removals. We focus on various aspects of food-web structural integrity including robustness, community collapse and threshold periods, and how these features relate to assumptions underlying different models, different species loss sequences and simple measures of diversity and complexity. Hierarchical feeding, a fundamental characteristic of food-web structure, appears to impose a cost in terms of robustness and other aspects of structural integrity. However, exponential-type link distributions, also characteristic of more realistic models, generally confer greater structural robustness than the less skewed link distributions of less realistic models. In most cases for the more realistic models, increased robustness and decreased levels of web collapse are associated with increased diversity, measured as species richness S, and increased complexity, measured as connectance C. These and other results, including a surprising sensitivity of more realistic model food webs to loss of species with few links to other species, are compared with prior work based on empirical food-web data.

1. Introduction

The threat of extensive current and future biodiversity loss due to major anthropogenic perturbations such as climate change, habitat destruction and species introductions is widely appreciated (Ceballos & Ehrlich 2002; Thomas et al. 2004a,b; Clavero & García-Berthou 2005; Pimm et al. 2006; Pounds et al. 2006), including implications for ecosystem properties, services and functioning (Naeem et al. 1994; Chapin et al. 2000; Solan et al. 2004; Zavaleta & Hulvey 2004; Bunker et al. 2005; Dobson et al. 2006; Worm et al. 2006). However, the impact of primary species loss on the potential for other species to go secondarily extinct, through coextinctions of tightly dependent species (Koh et al. 2004; Biesmeijer et al. 2006; Rezende et al. 2007; Lafferty & Kuris 2009) and extinctions that cascade through ecological communities via complex networks of species interactions, is a critical component of understanding the true magnitude of the extinction crisis that we face. Research focused on cascading secondary extinctions has been referred to collectively as ‘community viability analysis’ or CVA (Ebenman et al. 2004; Ebenman & Jonnson 2005). CVA ranges from empirically grounded evaluations of the effects of losing particular species in actual communities to theoretical treatments of simulated species loss in model systems, with many gradations in between (for review, see Ebenman & Jonnson 2005). Such research has even been extended to ancient paleocommunities (Roopnarine 2006; Roopnarine et al. 2007).

The present study falls on the theoretical end of that spectrum, and focuses on simulated species loss in structural food-web models, i.e. models that generate networks of unweighted feeding interactions by distributing L links among S species according to a few simple rules (e.g. Cohen & Newman 1985; Williams & Martinez 2000, 2008). This approach fills a gap between research that simulates extinctions in empirically-based datasets that document the complex link topologies of actual ecological communities (Solé & Montoya 2001; Dunne et al. 2002a, 2004a; Allesina & Bodini 2004; Memmott et al. 2004; Srinivasan et al. 2007; Petchey et al. 2008), and research that simulates extinctions in dynamical models of species interactions, which typically use Lotka-Volterra type dynamics and focus on low-diversity communities (S<15) with simplified network structures (Pimm 1979, 1980; Borrvall et al. 2000; Lundberg et al. 2000; Jordan et al. 2002; Ebenman et al. 2004; Eklöf & Ebenman 2006; Jonsson et al. 2006; Petchey et al. 2008).

Because researchers cannot do the obvious canonical experiments by going into natural ecosystems, inducing the extinctions of single or multiple populations in controlled, replicated, multi-factor ways at useful spatial scales, and then tracking the whole community over an appropriate time period for secondary extinctions, they have to use various other approaches to evaluate secondary extinction risk. No particular method will give a singularly correct or general answer, and different methods often provide apparently conflicting results for the same or closely related questions. However, much can be learned by employing a wide range of methods and comparing their results with an understanding of each method's assumptions, limitations and utilities (Dunne et al. 2004b). Thus, we suggest that a certain proliferation of methods for evaluating cascading extinctions in ecological communities is a good thing at this time, although it will be important to weed out more irrelevant results and approaches and weave together a coherent understanding from what is left standing (Ebenman & Jonnson 2005).

One central issue is whether diversity and complexity influence the susceptibility of communities to secondary extinctions. This question is an outgrowth of inquiries on the relationship of community stability to diversity and complexity that date back decades (e.g. MacArthur 1955; May 1973), which have spawned a wide range of current research (McCann 2000; Ives & Carpenter 2007) of which studies focused on species interaction networks are one off shoot. Here, as in a number of related studies, we focus on the simplest formulations of diversity, defined as species richness (S), and complexity, defined as connectance (C), the proportion of possible links among S species that are actually realized (L/S²). A variety of other, more complex ways of characterizing aspects of community organization are possible, such as ‘trophic diversity’ (Petchey et al. 2008). Susceptibility to secondary extinctions is also quantified in a simple way—‘structural robustness’ (R) is the proportion of primary extinctions that lead to a particular proportion of total extinctions, equal to primary plus secondary extinctions (Dunne et al. 2002a, 2004a; Srinivasan et al. 2007). A species goes secondarily extinct if it loses all its resource species. This is an obviously limited view of extinction risk, since the loss of top predators cannot lead to secondary extinctions, and basal species (plants) cannot go secondarily extinct. Studies focused on species dynamics suggest that structural robustness defines a minimum level of secondary extinctions that might be experienced by a community (e.g. Eklöf & Ebenman 2006). By ignoring dynamics and interaction strengths, structural approaches trade one kind of ecological ‘realism’ for another—the study of systems with more realistic levels of species richness and more realistic topologies than dynamical models can presently accommodate.

Analysis of structural robustness has thus far been limited to simulations of species loss in empirical food webs compiled from ‘real-world’ data for trophic interactions among co-occurring species in particular habitats (Dunne et al. 2002a, 2004a; Srinivasan et al. 2007). However, the apparent topological complexities of empirical food webs appear relatively well described by various recent network structure models based on simple resource assignment rules with stochastic elements (Williams & Martinez 2000, 2008; Stouffer et al. 2005; Allesina et al. 2008). Such models provide a framework for assessing aspects of structural robustness of idealized food webs in a more systematic way than can be achieved with existing data, which is variable, limited and can be biased in idiosyncratic ways (Dunne et al. 2004a). The fact that proposed models vary in some of their resource distribution assumptions can be used to potentially untangle some general structural features of communities that tend to promote or reduce robustness and other aspects of food-web structural integrity. With these various issues in mind, we address several interrelated questions in this study. First, are there differences among models in their robustness, as well as in their responses to different extinction sequences? Second, is there any indication that particular model assumptions are related to differences in robustness among models? Third, how does robustness relate to how well various models appear to fit present empirical data? Fourth, how does robustness in the more realistic models compare with robustness of empirical food webs (Dunne et al. 2002a)? Fifth, what is the relationship of structural robustness to diversity (S) and complexity (C) in model food webs? Because we are working with sets of model food webs, we also quantify the propensity of webs to collapse completely as species are lost, and the relationship of such community collapse to the various factors of interest—type of model, type of extinction sequence, diversity and complexity. Additional aspects of structural integrity discussed include the shape of secondary extinction curves and the presence and magnitude of initial threshold periods of primary species losses that lead to no or few secondary extinctions.

2. Material and methods

We studied sequential species loss in networks generated by four different food-web models—the cascade model (Cohen & Newman 1985), the generalized cascade model (Stouffer et al. 2005), the niche model (Williams & Martinez 2000) and the nested hierarchy model (Cattin et al. 2004). All four models have as input parameters the number of species S and the directed connectance (Martinez 1991) C=L/S², where L is the number of links in the network. Each model orders all S species according to a uniformly random ‘niche value’ (n_i) assigned to each species, which randomly places the species somewhere along a ‘niche dimension’ from 0 to 1 (0≤n_i≤1). The models differ in how they distribute links among species and in particular, how they assign prey, or ‘resources’, among species.

In the cascade model, each species i has probability p=2CS/(S−1) of consuming only resource species j with niche values less than its own (i.e. n_j<n_i) (Cohen & Newman 1985; Williams & Martinez 2000). The generalized cascade model (Stouffer et al. 2005) is similar to the cascade model except that it allows for cannibalism (i.e. n_j≤n_i), and species consume potential resource species with a probability equal to a random number with mean 2C drawn from a beta distribution. In the niche model (Williams & Martinez 2000), a consumer eats all species whose niche values fall within a range (r_i) whose centre (c_i) is a uniformly random number between r_i/2 and min(n_i, 1−r_i/2). This constraint on c_i ensures that r_i is placed entirely on the niche dimension, that the centre of r_i is less than n_i, and that the diet of the consumer is strongly biased towards resource species with lower niche values than the consumer. The niche range r_i=xn_i and 0≤x≤1 is a random variable with a beta-distributed probable density function p(x)=β(1−x)^(β−1) with β=(1/2C)−1. This ensures that the average of all species' r_i equals C. The nested hierarchy model (Cattin et al. 2004) assigns each consumer i's number of resource species j using the same rules as the niche model, but assigns the locations of the links to resources in a multi-step process. First, j are randomly chosen from among species with n_j<n_i until i obtains all of its specified number of j or it obtains a j that already has at least one consumer. When the latter occurs, i joins the group of j's consumers, defined as the group of all consumers sharing at least one j, with at least one consumer of that group feeding on j. Subsequent j of i are chosen randomly from the set of j of this group until all of i's links have been assigned or all j of the group have been chosen. If i still requires more j, they are randomly chosen from the remaining j with no consumers and n_j<n_i. If all links are still not assigned, more j are chosen randomly from species with n_j≥n_i.

In plainer language, what do these models share and how do they differ? The generalized cascade, niche and nested hierarchy models all distribute links to resources according to a beta distribution, in contrast to the resource distribution of the earlier cascade model. The beta distribution was introduced in the niche model (Williams & Martinez 2000), retained by the nested-hierarchy model (Cattin et al. 2004) and justified in the generalized cascade model as a fundamental driver of the success of the previous two models (Stouffer et al. 2005) because it generates approximately exponential link distributions (i.e. the distribution of total links—links to resources plus links from consumers), similar to what is observed in empirical food webs (Camacho et al. 2002; Dunne et al. 2002b; Stouffer et al. 2005). These types of distributions are less skewed than the power-law distributions often observed in other real-world networks (Albert & Barabási 2002). The resource distribution rule of the cascade model produces a less skewed link distribution than the other three models, since every node (species) has the same expected connectivity, and few or no species end up with low or high numbers of links. All four of the food-web models result in hierarchical feeding, where there is a strong tendency to eat resource species with lower niche values than the consumer (i.e. n_j<n_i). However, they differ in the strictness of the hierarchy—the cascade model imposes a strict hierarchy, the other three models allow for cannibalism (i.e. n_j=n_i) and the niche and nested-hierarchy models also allow for looping (i.e. n_j>n_i), although it rarely occurs in the nested-hierarchy model. The niche model differs from the other three models because it imposes intervality in how links to resource species are assigned—taxa, arranged along a single-dimension interval, have contiguous feeding ranges r_i represented as segments of the interval. In this paper, we sometimes refer collectively to the niche model, nested hierarchy model and generalized cascade model as ‘beta/hierarchical’ models since they share the beta distribution and hierarchical feeding.

We also studied sequential species loss in a fifth ‘null’ model, the random beta model (Dunne et al. 2008). The random beta model assigns the number of resources for each species according to a beta-distributed probability density function, as used in the generalized cascade, niche and nested hierarchy models, and assigns links to resources randomly across all species. It therefore does not have any hierarchical feeding constraint and also lacks the intervality constraint of the niche model. The five models differ in how well corroborated they are by empirical data. The random beta model provides a poor fit to data (Dunne et al. 2008). The cascade model, while providing a much better fit to data than a model that distributes links among species randomly, fits data much worse than the niche model (Williams & Martinez 2000). The niche, nested hierarchy and generalized cascade models generate the same degree distributions that are equally similar to empirically observed distributions (Stouffer et al. 2005), but given a broader suite of network structure properties, the niche model appears to slightly outperform the other two models (Stouffer et al. 2007; Williams & Martinez 2008). Another analysis approach that focuses on the topology of food webs as a whole reinforces prior results by showing that the niche model has a higher likelihood than the cascade and nested hierarchy models of reproducing empirical food-web data (Allesina et al. 2008). The basic similarities and differences in underlying assumptions of the five models are summarized in table 1.

Table 1.

Characteristics of five models of food-web structure. (n_j refers to the niche value of a resource species j; n_i refers to the niche value of a consumer species i; n_j=n_i indicates that cannibalism is possible; n_j≥n_i indicates that cannibalism and looping are possible).

			hierarchical feeding
	beta distribution	intervality	hierarchy	exceptions
random beta	yes	no	no	—
cascade	no	no	yes	no
generalized cascade	yes	no	yes	nj=ni
niche	yes	yes	yes	nj≥ni
nested hierarchy	yes	no	yes	nj≥ni

We simulated primary species loss and resulting secondary extinctions in model food webs by sequentially removing species using one of three criteria: removal of (i) the most-connected species, (ii) the least-connected species and (iii) randomly chosen species. The most-connected and least-connected criteria are based on the ‘degree’ of species that refers to the total number of links to resources plus links from consumers for each species. If following a primary removal, any remaining species lost all of their resources species, or any cannibalistic species lost all of their resource species except the cannibalistic link, they dropped from the web and were recorded as a secondary extinction. We then removed the next appropriate species, determining the most- and least-connected species based on the web remaining after all prior primary removals and secondary extinctions occurred. This process continued until all species disappeared from the web. Removal of the most-connected and random species follows research on network tolerance to ‘attacks’ and ‘errors’ (Albert et al. 2000; Jeong et al. 2001) and as investigated for empirical food webs (Solé & Montoya 2001; Dunne et al. 2002a, 2004a; Srinivasan et al. 2007), in which least-connected species removals have also been studied (Dunne et al. 2002a, 2004a; Srinivasan et al. 2007). While such extinction sequences are not necessarily realistic representations of either anthropogenic or natural species loss (Srinivasan et al. 2007), degree-based and random extinction sequences are useful as a systematic way to assess any differences in the models to divergent patterns of species loss.

Sequential species removals were conducted in each type of model food web at four levels of S (25, 50, 100 and 200) and C (0.05, 0.10, 0.15 and 0.30), resulting in 16 combinations of S and C for each of five types of model webs, except for the combination of S=25 and C=0.05 for the niche, nested hierarchy and generalized cascade models. That combination of S and C imposes such a low L/S (1.25) that fully connected webs of those types are rarely generated. We chose these S and C levels to span the ranges of observed values for trophic-species versions of cumulative community webs, typically used for comparative food-web structure research (Dunne 2006). For each model at each level of S and C, we generated two sets of 500 webs and one set of 50 webs. We conducted most-connected species removals in one set of 500 webs, least-connected species removals in the other set of 500 webs and ten random sequences of random species removals in each of the 50 webs. For each type of species removal, the average number of secondary extinctions was calculated for each step of species loss. If a web in the ensemble collapsed and disappeared at some point during the removal sequence, its loss was recorded and its total number of secondary extinctions was retained in computations of the mean number of secondary extinctions on subsequent deletion steps.

Robustness (R) of food webs to species loss was quantified as the proportion of species subjected to primary removals that resulted in a total loss (i.e. primary removals plus secondary extinctions) of some specified proportion of the species. We focus here on R₅₀, primary extinctions that result in at least 50 per cent of total species loss (Dunne et al. 2002a, 2004a; Srinivasan et al. 2007). Thus, a maximally robust community undergoes no secondary extinctions (R₅₀=0.50), and a minimally robust community has extensive secondary extinctions (i.e. at least S/2−1) after the loss of just one species (R₅₀=1/S). In addition, during the removal sequence, sometimes one or more of the webs in an ensemble would collapse, due to every species going extinct. As a measure of a model's likelihood of whole-community collapse, which we refer to as ‘web collapse’ (WC), we recorded the cumulative fraction of 500 initial webs in a particular ensemble that collapsed out of existence at the point at which some proportion of the species in the webs went extinct (i.e. primary removals plus secondary extinctions). We focus on WC₈₀, the cumulative proportion of webs that collapsed at the point at which at least 80 per cent of taxa went extinct. The rationale for WC₈₀ rather than some other level is discussed in the results.

3. Results

(a) Secondary extinction curves

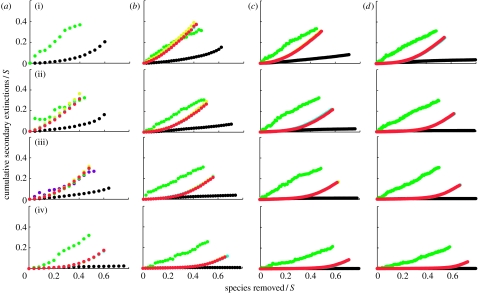
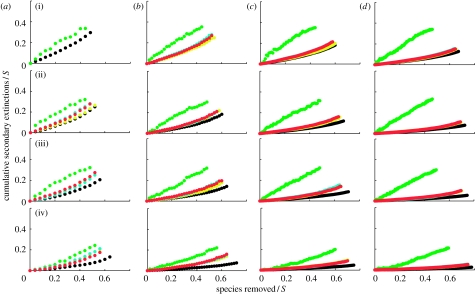
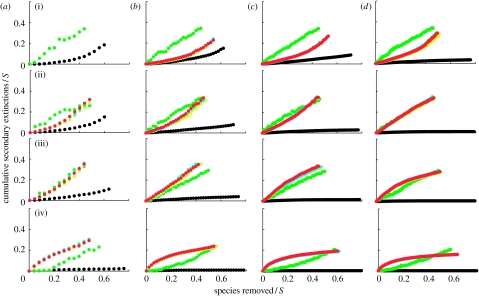
Figures 1–3 show cumulative secondary extinctions as a function of primary species loss under the three species removal sequences for the five models at the 16 combinations of S and C. We refer to S=25 as ‘low’ S, S=50 or 100 as ‘intermediate’ S and S=200 as ‘high’ S, with the same distinctions for C=0.05, 0.10 or 0.15 and 0.30. Secondary extinction curves end where total species loss equals approximately 80 per cent of the original S, at which point complete collapse is imminent. Lower curves reflect lower accumulations of secondary extinctions. The shape of the curves reflects an increasing (convex), constant (linear) or decreasing (concave) rate of secondary extinctions. We summarize the results by model.

Figure 1.

Secondary extinctions resulting from the primary loss of most-connected species. S refers to species richness and C refers to connectance. The generalized cascade data (yellow circles) and nested hierarchy data (blue circles) are generally obscured by overlapping niche model data (red circles). The cascade data are shown by the upper green circles and the random beta data are shown by the lower black circles that sometimes overlap the lower border of the graph when there are no secondary extinctions. Each data point represents a mean across 500 model webs. Panels are shown in order of increasing connectance ((i) C=0.05, (ii) C=0.10, (iii) C=0.15 and (iv) C=0.30) and increasing species richness ((a) S=25, (b) S=50, (c) S=100 and (d) S=200). Secondary extinction curves end at the point at which approximately 80% of all taxa have gone extinct.

Figure 2.

Secondary extinctions resulting from the primary loss of random species. S refers to species richness and C refers to connectance. The generalized cascade data (yellow circles) and nested hierarchy data (blue circles) are generally obscured by overlapping niche model data (red circles). The cascade data are shown by the upper green circles and the random beta data are shown by the lower black circles that sometimes overlap the lower border of the graph when there are no secondary extinctions. Each data point represents the mean of 10 random deletion sequences in 50 model webs. Panels are shown in order of increasing connectance ((i) C=0.05, (ii) C=0.10, (iii) C=0.15 and (iv) C=0.30) and increasing species richness ((a) S=25, (b) S=50, (c) S=100 and (d) S=200). Secondary extinction curves end at the point at which approximately 80% of all taxa have gone extinct.

Figure 3.

Secondary extinctions resulting from the primary loss of least-connected species. S refers to species richness and C refers to connectance. The generalized cascade data (yellow circles) and nested hierarchy data (blue circles) are generally obscured by overlapping niche model data (red circles). The cascade data are shown by the upper green circles and the random beta data are shown by the lower black circles that sometimes overlap the lower border of the graph when there are no secondary extinctions. Each data point represents a mean across 500 model webs. Panels are shown in order of increasing connectance ((i) C=0.05, (ii) C=0.10, (iii) C=0.15 and (iv) C=0.30) and increasing species richness ((a) S=25, (b) S=50, (c) S=100 and (d) S=200). Secondary extinction curves end at the point at which approximately 80% of all taxa have gone extinct.

In general, random beta webs display the lowest secondary extinctions among the five models. Across all the three species removal sequences, secondary extinctions in random beta webs decrease with increasing S and C, and except for cases where secondary extinctions are very low and increase linearly if at all, they accumulate at a slowly increasing rate. Random beta webs display nearly identical responses to the loss of most- and least-connected species (figures 1 and 3), accumulating few secondary extinctions. The greatest accumulation of secondary extinctions is approximately 20 per cent of species, given primary removals of approximately 60 per cent of species in webs with low S and C. Few if any secondary extinctions occur for webs with high S, or high C, or intermediate levels of S and C. Random beta webs are more sensitive to removal of random species (figure 2) than to degree-based removals (figures 1 and 3) at all levels of S and C, with a very small number of secondary extinctions even at high S and C. The highest accumulation of secondary extinctions is approximately 30 per cent of species, given primary removals of approximately 50 per cent of species in webs with low S and C (figure 2).

Cascade webs generally have the highest secondary extinction curves and thus display the greatest accumulations of secondary extinctions, given primary species loss among the five models (figures 1–3). The response of cascade webs to all three species removal sequences is extremely similar, and secondary extinctions tend to accumulate approximately linearly. The highest accumulations of secondary extinctions approach 40 per cent of species for primary loss of 40 per cent of species. The only obvious sensitivity to S or C in cascade webs is a decrease in secondary extinctions at C=0.30.

Niche, generalized cascade and nested hierarchy webs display nearly indistinguishable responses to primary species loss (figures 1–3). Response of these beta/hierarchical model webs to loss of most-connected and random species is generally intermediate to the responses of random beta and cascade webs (figures 1 and 2). The exception are webs with S=50 and C=0.05 subjected to loss of most-connected species, which show similar levels of secondary extinctions to cascade webs (figure 1). The beta/hierarchical model webs are generally more sensitive to loss of most-connected species than to random species except for webs with high C. Accumulation of secondary extinctions decreases with increasing S and C for both most-connected and random species removals (figures 1 and 2). Secondary extinctions tend to accumulate near linearly with random species removals (figure 2). By contrast, they accumulate at an increasing rate with the removal of most-connected species, with an initial ‘threshold period’ of no or negligible secondary extinctions (except for webs with low S and intermediate C or vice versa) that extends out further with increasing S and/or C (figure 1). For webs with high S and C, the threshold period extends through primary loss of approximately 50 per cent of species. For webs with combinations of S and C that include intermediate values of either, this threshold period extends through primary loss of approximately 10–40 per cent of species.

The response of the beta/hierarchical model webs to loss of least-connected species is more complicated (figure 3). At low C, their response is intermediate to the random beta and cascade responses. At intermediate C, their response is similar to the cascade response. At high C, their response is higher than the cascade response, with the difference decreasing to 0 at primary species removal levels of approximately 50 per cent for webs with S≥50. The beta/hierarchical webs tend to be more sensitive to loss of least-connected species than to loss of most-connected or random species, except for webs with low C and intermediate S or vice versa. Low C webs display increasing rates of secondary extinctions, intermediate C webs display linear or near-linear rates and high C webs display decreasing rates (figure 3). Webs with intermediate C also display the greatest accumulation of secondary extinctions, reaching close to 40 per cent of species undergoing secondary extinctions for primary removal of approximately 40 per cent of species.

How do the beta/hierarchical model secondary extinction curves compare with results for similar simulations done with empirically documented food web datasets? We focus on extinctions in six community food webs known to be relatively well fit by the niche model and its variants (St Marks Estuary, St Martin Island, Little Rock Lake, Bridge Brook Lake, Coachella Valley and Skipwith Pond; Williams & Martinez 2000, 2008), and match up empirical web curves (fig. 1 in Dunne et al. 2002a) with model web curves for similar S and C combinations (i.e. S=50 and C=0.10 for St Marks and St Martin, S=100 and C=0.10 for Little Rock, S=25 and C=0.15 for Bridge Brook and S=25 and C=0.30 for Coachella and Skipwith). We excluded a few webs known to be well fit by the niche model (Chesapeake Bay, Benguela, Caribbean Reef, N.E. U.S. Shelf) that have been analysed for secondary extinctions (Dunne et al. 2002a, 2004a) because their S and C combinations were too far from the ones used here. The three empirical webs with C≈0.1 (St Marks, St Martin, Little Rock) accumulate many more secondary extinctions due to loss of most-connected species than seen in the comparable beta/hierarchical model webs—they each have secondary losses of approximately 40 per cent of species for primary losses of approximately 40 per cent of species, compared with a 20/60 per cent split in the model webs. Secondary extinction curves for the three higher C empirical webs (Bridge Brook, Coachella and Skipwith) are similar to model web curves. There are similar threshold effects for secondary extinctions due to loss of most-connected species in both empirical and model webs. For random species losses, the empirical and model webs display similar secondary extinction curves in all six cases. For loss of least-connected species, the six empirical webs generally show much lower accumulation of secondary extinctions than the comparable beta/hierarchical model webs.

(b) Robustness and web collapse

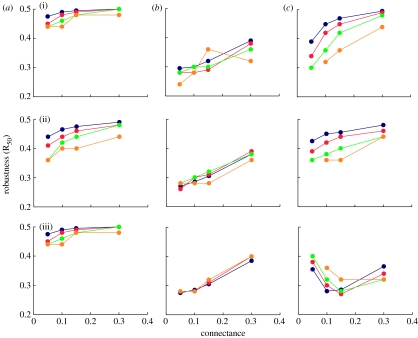
The robustness results shown in figure 4 provide a convenient way to summarize and easily compare the relative sensitivity of model webs to primary extinctions in relationship to S and C. Higher lines reflect higher robustness of webs to primary species loss, flatter lines reflect lower sensitivity of robustness to changes in C and high overlap of the four differently coloured lines within any given panel reflects lower sensitivity of robustness to changes in S. Owing to the close overlap of secondary extinction curves for the niche, nested hierarchy and generalized cascade models, we show only robustness results for the niche model.

Figure 4.

Robustness of model food webs to primary species loss. R₅₀ refers to the proportion of species that have to undergo primary removal to achieve a total loss of at least 50% of taxa (primary removals plus secondary extinctions). Panels in columns (a), (b) and (c) show results for the random beta, cascade and niche models respectively. Results are not shown for the generalized cascade or nested hierarchy models because they are nearly indistinguishable from niche model results (figures 1–3). Different coloured lines (blue, S=200; red, S=100; green, S=50; orange, S=25) show robustness trends for different levels of species richness (S) as a function of increasing connectance. Panels in rows (i), (ii) and (iii) show results for loss of most-connected, random and least-connected species respectively. Data points represent means across 500 model webs (for most- and least-connected removal sequences) or means for 10 random removal sequences in 50 model webs.

The two most unrealistic models, the random beta and cascade models, display the most and least robustness, respectively. The random beta model is highly robust to degree-based species removal sequences. Both models display increasing robustness with increasing connectance, although this effect is stronger in the cascade webs, with an increase of approximately 0.10 in R₅₀ as C increases from 0.05 to 0.30. The robustness of these two models also sometimes increases with S, but not consistently or in every case. The strongest and the most consistent increases with S are displayed by the random beta model in response to random species losses, where there is an increase in R₅₀ of approximately 0.10 as S increases from 25 to 200. Thus, given an approximate order of magnitude change in S or C, there can be a similar increase of R₅₀ by approximately 0.10 (i.e. 10% additional species have to be primarily removed to achieve total loss of 50% of species), although this change is much more consistent for changes in C. The niche model displays increases of robustness with both C and S in response to loss of most-connected or random species. R₅₀ increases by approximately 0.10–0.20 with C and by approximately 0.10–0.15 with S, given the loss of most-connected species, and shows smaller increases given random species losses. With loss of least-connected species, niche model webs show the opposite trends—there are initial decreases in robustness with increasing S and C. However, robustness then increases as S goes from 100 to 200 and C goes from 0.15 to 0.30.

Figure 5 similarly shows a summary of WC and its relationship to S and C. Unlike the secondary extinction results, we do not show the web extinction curves as they are easy to summarize. The cascade results are approximately linear and very similar with regard to different species removal sequences. For the other four models, there are basically no WCs until total species losses are greater than 50 per cent, with few but increasing collapses at levels of total species losses from approximately 50–90 per cent and increasingly comprehensive collapses beyond that. Using 80 per cent total species loss as the point at which we quantify web collapse (WC₈₀) seemed to catch an early point of rapidly increasing rates of collapse for the non-cascade models, and did not obscure the general difference between the cascade model and the other models. We show separate results for all the three beta/hierarchical models.

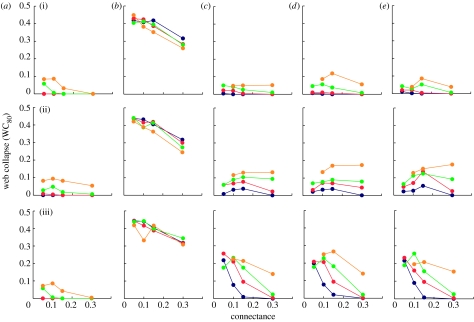
Figure 5.

Collapse of model food webs in response to species loss. WC₈₀ refers to the proportion of 500 webs that have completely collapsed at the point at which 80% of total taxa in the webs have gone extinct. Panels in columns (a), (b), (c), (d) and (e) show results for the random beta, cascade, niche, generalized cascade and nested hierarchy models respectively. Panels in rows (i), (ii) and (iii) show results for loss of most-connected, random and least-connected species respectively. Different coloured lines (blue circles, S=200; red circles, S=100; green circles, S=50; orange circles, S=25) show web collapse trends for different levels of species richness (S) as a function of increasing connectance. Data points represent means across 500 model webs (for most- and least-connected removal sequences) or means for 10 random removal sequences in 50 model webs.

Similar to results for robustness, the random beta and cascade models show the lowest and the highest levels of WC, respectively. Random beta webs display WC₈₀ values between 0 and 0.10, with a slight trend towards fewer collapsed webs as C and S increase. They display marginally more collapses with loss of random species. Cascade model webs display WC₈₀ values between approximately 0.25 and 0.45, with a strong trend of fewer collapses with increasing C. Responses to S are weak and variable. The niche, generalized cascade and nested hierarchy models display WC₈₀ values that range from 0 to approximately 0.30, with the fewest webs collapsing in response to removal of most-connected species, slightly more webs collapsing in response to removal of random species and the most webs collapsing in response to removal of least-connected species, except at high levels of C where levels of collapse are similar to those for webs with random species removed. WC is not consistently sensitive to changes in C for most-connected and random species losses, but decreases strongly with C for loss of least-connected species. In most cases, increases in S are associated with decreases in WC, particularly with regard to loss of random and least-connected species, where the percentage of collapsed webs decreases from as much as approximately 20–30 per cent to as little as 0 per cent as S increases from 25 to 200. WC results are more variable among the three beta/hierarchical models than are the secondary extinction and robustness results, but are still quite similar.

4. Discussion

A central outcome of comparing the impact of primary species losses on the topology of various model food webs is that hierarchical feeding, a fundamental characteristic of food-web structure, appears to impose a cost in terms of robustness and other aspects of structural integrity. This is suggested by the fact that, out of the five models considered, the random beta model is the most robust to primary species loss, and also displays the lowest rates of complete WC. This null model is based on the beta distribution that is central to the three most empirically well-corroborated food-web models (niche, nested hierarchy and generalized cascade), but lacks the hierarchical feeding constraint present in all four food-web models. While there is no strict correspondence between hierarchy in network structure models and actual hierarchy of a particular ecological trait, it has been suggested that it may be closely related to body size (e.g. Woodward et al. 2005). Simulations of nonlinear trophic dynamics for networks of 20 to 40 species with cascade, niche and nested hierarchy structure, combined with empirical data on predator–prey body mass ratios, suggest that hierarchical arrangements of naturally occurring body masses of consumers and resources, at least within the non-parasite portion of species assemblages, confer stability on and increase persistence of complex food webs (Brose et al. 2006; see also Otto et al. 2007). This suggests that the structural robustness costs of hierarchical feeding arrangements revealed by the current analysis are outweighed by dynamical stability benefits of such organization.

Comparing the four food-web models that incorporate hierarchical feeding suggests that the more skewed and realistic exponential-type link distributions of the niche, nested hierarchy and generalized cascade models confer greater structural robustness in most cases than the more narrowly constrained link distribution of the cascade model. Compared with the other three models, the cascade model is always more sensitive to loss of random species, is usually more sensitive to loss of most-connected species, except for webs with lower levels of S and C and is more sensitive to loss of least-connected species in webs with low connectance. In general, cascade webs respond similarly, and with great sensitivity, to any type of primary species loss, displaying the same low robustness and high levels of WC. The unchanging nature of the cascade model's response to the three types of primary species loss is because every species in a cascade web has a set probability of interacting with resource species. As a result, whether species are picked randomly or based on their total number of links, they effectively are removed at random from the hierarchy. Thus, no matter what species removal sequence is used, the chances of inducing secondary extinctions and WC are the same. The structural integrity differences between cascade and the other three food-web models attributable to degree distribution may be reinforced by aspects of dynamical stability. A nonlinear dynamical study of model food webs with S=30 and C=0.15 found that webs with niche structure had higher species persistence than webs with cascade structure, with approximately 30–50 per cent more species persisting in niche-structured webs (Martinez et al. 2006).

There is little difference in the responses of the three hierarchical, beta-distributed food-web models to species loss, which suggests that their distinguishing features—a small probability of looping in the nested hierarchy and niche models and interval feeding in the niche model—have little effect on the structural robustness, the likelihood of WC and other aspects of structural integrity in the face of species loss. This is perhaps not surprising, given the relative subtlety of the structural differences induced by such additional constraints (Williams & Martinez 2008). We did not consider some other possible additional models, in particular two recent variants of the niche model referred to as the ‘relaxed niche model’ (Williams & Martinez 2008) and the ‘minimum potential niche model’ (Allesina et al. 2008), both of which relax the interval feeding constraint of the niche model so there can be gaps in consumers' diets. Such models are general in that they generate networks in which all links are compatible with empirical data that are not the case with the niche, nested hierarchy and generalized cascade models (Allesina et al. 2008). Depending on the evaluation method, these recent niche model variants have been shown either to slightly outperform, based on total log likelihood for the overall fit (Allesina et al. 2008), or slightly underperform, based on normalized model errors for a suite of network properties (Williams & Martinez 2008), compared with the niche model for presently available empirical community food-web data. Given the lack of differences in the responses of the niche, nested hierarchy and generalized cascade models to primary species loss, it seems unlikely that allowing for a slightly ‘gappy’ niche model is likely to affect such responses significantly, but this is something that can be investigated in more detail in the future.

We now focus on the effects of connectance and species richness on robustness, secondary extinction rates, secondary extinction thresholds and WC in niche (and by extension, the nested hierarchy and generalized cascade) model webs subjected to different types of species loss. Consistent with prior results for species loss simulations in empirical food webs (Dunne et al. 2002a, 2004a), structural robustness increases with connectance for niche model webs, given primary loss of most-connected or random species, with the model webs showing lower robustness to loss of most-connected species at lower levels of connectance. Empirical webs with C≈0.1 are less robust to loss of most-connected species than expected for niche-type webs of that C. Empirical and model webs with higher C have similar robustness to loss of most-connected species and empirical and model webs at any C have similar robustness to loss of random species. Threshold periods, during which zero or very few secondary extinctions occur until some level of primary species loss is reached, appear in both empirical and niche-type model webs in response to loss of most-connected species. As with robustness, such threshold periods extend with increasing connectance. However, connectance does not appear to influence the magnitude of niche model WC in response to loss of most-connected or random species. The percentage of collapsed webs, given total loss of 80 per cent of species, ranges from 0 to approximately 10 per cent with the most-connected species removals or from 0 to approximately 20 per cent with random species removals. The basic shape of secondary extinction curves also does not change with connectance. Loss of random species results in near constant rates of secondary extinctions, and loss of most-connected species results in increasing rates of secondary extinctions.

A very different picture emerges for the relationship of connectance to the impacts from loss of least-connected species on robustness, secondary extinction rates, thresholds and WC in niche webs. No relationship was found between robustness and connectance in empirical webs, where few secondary extinctions occur, resulting in higher robustness than with removal of random species (Dunne et al. 2002a). By contrast, in niche model webs, robustness to loss of least-connected species is always much lower than robustness to random species loss. Robustness decreases substantially with increasing C through intermediate levels of connectance, and then increases as C increases from intermediate to high levels. Also, the shape of the secondary extinction curves for model webs, which lack threshold periods, changes systematically with connectance, with increasing rates of secondary extinctions in low C webs transforming into decreasing rates of secondary extinctions in high C webs, resulting in a non-monotonic relationship between robustness and connectance. WC levels for niche webs in response to loss of least-connected species decrease from approximately 20 per cent to nearly 0 with increasing connectance, except in the smallest webs, which show modest decreases. While the surprise in the earlier empirical web study was that occasionally a web would experience a sudden surge of secondary extinctions following losses of least-connected species, which otherwise led to few such extinctions (Dunne et al. 2002a), the surprise here is how sensitive niche and related model webs are to the loss of least-connected species, as well as associated sharp decreases in robustness as connectance increases from 0.05 to 0.15. While the ‘surprises’ from the earlier and current study are different, the message is the same—species with few links cannot be dismissed a priori as unimportant, and in fact their loss may have significant and/or unexpected negative impacts on the structural integrity of food webs. This effect may be related to finer grained structure within such webs, for example if species with few links have dependent species that themselves have many dependent species. The dissasortativity of empirical (Newman 2002) and niche model food webs (Stouffer et al. 2005), where species with few links tend to links to species with many links, may be a factor driving this effect.

Contrary to prior results for empirical webs which showed no relationship of robustness with species richness (Dunne et al. 2002a), structural robustness of niche, nested hierarchy and generalized cascade webs increases with increasing S for primary removals of most-connected and random species, with a stronger response of robustness to S for loss of most-connected species. The magnitude of changes in robustness as a function of S or C is similar, with responses to C slightly greater, given a near order of magnitude change in either factor. Also similar to connectance, species richness displays a non-monotonic relationship with model web robustness to loss of least-connected species, although it is weaker than that seen for C. Thus, more speciose webs have reduced robustness at low and intermediate C, with the reverse true at high C. The length of secondary extinction threshold periods in response to loss of most-connected species increases with increasing S, as with C. There is a tendency for the rate of secondary extinctions in response to loss of least-connected species to shift from increasing to decreasing rates with increasing S, but it is again weaker than the connectance effect. Unlike with connectance, the levels of WC for all three types of species loss in model webs tend to decrease with increasing species richness, with the greatest S effects seen for loss of least-connected species, the one WC case where there is also a positive connectance effect.

How specific to niche and the other two beta/hierarchical webs are the relationships of connectance and species richness to various aspects of food-web structural integrity? The cascade and random beta webs display increased robustness and decreased WC with increased C, although the trends are weak in the random beta webs, where even at low C robustness is already close to the maximum robustness of 0.50 and WC is less than 10 per cent. Thus, increased network structural integrity with increasing connectance appears to be a general feature of networks, at least those that incorporate either a beta distribution or hierarchical link organization, with the latter leading to stronger connectance–integrity relationships. Deviations from this trend in niche and related webs, in particular the non-monotonic relationship between C and robustness to loss of least-connected species and the lack of a relationship between C and WC in response to loss of most-connected and random species, must result from the dual constraints of beta-distributed links to resources plus hierarchical feeding. In terms of species richness, random beta webs do display consistent increases in robustness and decreases in WC with increasing S, but any such trends for cascade webs tend to be more muddled, marginal or non-existent. This suggests that many of the observed trends such as increasing robustness and decreasing WC with increasing S in niche and related webs are more attributable to the beta distribution constraint. As with connectance, the non-monotonic relationship of niche model robustness to S in response to loss of least-connected species appears to reflect interplay between the beta distribution and hierarchical feeding constraints.

Various factors may have led to the differences in response to S between niche and related model webs and empirical webs that appear to have niche-like topology. One possibility is that the difference is an artefact of the empirical webs studied. The earlier study (Dunne et al. 2002a) looked at a mix of cumulative, community-type webs well fit by the niche model and other types of webs such as Grassland and Scotch Broom, two very low connectance ‘source’ webs with degree distributions that are markedly more skewed than what is observed in other webs (Dunne et al. 2002b). Out of 16 webs in that study, only seven are known unequivocally to be well fit by the niche model (Williams & Martinez 2000, 2008; Dunne et al. 2008), and are an inadequate sample for evaluating the relationship of robustness to S—6 have S of 25–48 and one has S of 91. Another way to think about this is that the effect of C is so strong that it emerges even in sub optimal mixed ensembles of webs, regardless of the relative shape of their degree distributions, which seems to be more important for the observed effect of S. Another possibility is that actual differences in the structure of niche model and empirical webs, particularly the level of herbivory which is severely underestimated by the niche model (Williams & Martinez 2008), lead to different secondary extinction responses. Clearly, we would like to know whether the actual relationship of food-web structural integrity to S in empirical webs is similar to the strong positive relationship observed in niche and related model webs, as is the case for connectance, but this will require a wider range of comparable datasets, and a careful assessment of the role of herbivory, if any, in driving observed differences in response to S. Until that research occurs, the model-based analysis clearly presents a strong hypothesis that most aspects of structural integrity in the face of species loss of webs with niche structure generally increases with S.

The type of model-based study presented here, including comparisons with studies based on empirical data, is important because it would be extremely useful from a conservation perspective to know whether we can use simplified views of ecosystems to understand the vulnerability of ecosystems to extinctions, which types of extinctions are likely to be the most damaging, and what if any simple characteristics of ecosystems augment their ability to withstand extinctions. In this case, we are exploring two core simplifications—focusing just on the topology of feeding interactions, and using simple models that reproduce many but not all aspects of empirical food-web structure. If such simplifications can provide a way to faithfully capture some basic aspects of the response of actual communities to perturbations such as species loss, risk assessment becomes a much easier, quicker and cheaper process, at least for cases that can be shown to be reasonably represented by the simplified approaches. Studies such as this one, and further studies that relate the results from studies of simple structural models to more complex dynamical models (e.g. Martinez et al. 2006; Williams 2008), will help to determine whether and when such approximations can be reliably used for evaluating the potential disruption of the integrity of ecological communities, given loss of species for whatever reason.

Along these lines, there is a great deal of interesting and useful research to be done in the future. As mentioned, we need to understand why niche model web and empirical web species removal results are so different with regard to the effect of species richness and the loss of least-connected species. What are the features of the structure of empirical webs that are not being captured by the niche model or what are the artefacts driven by bias in the presently available data that drive differences in responses to species loss? More needs to be done to systematically model species extinctions in dynamical models that encompass nonlinear functional responses, more realistic numbers of species and more realistic network structures. Computational approaches built on a framework for consumer–resource dynamics developed by Yodzis & Innes (1992) appear to be one promising methodology for bridging the gap between structural extinction studies and the simplified Lotka-Volterra dynamical studies discussed in the introduction (e.g. Brose et al. 2006; Martinez et al. 2006; Williams et al. 2007; Williams 2008). Future integrated structural–dynamical studies should also look at more than just the ability of species to persist and coexist, and move towards looking more explicitly at the effect of extinctions on ecosystem function. Virgo and colleagues (2006) looked at the development of ecosystem function during food-web assembly; it would be interesting to look at the breakdown of ecosystem function during sequential extinctions. This would also be an opportunity to see how changes in system function are related to changes in system composition (i.e. number and role of species) and whether system composition is a useful surrogate for ecosystem function.