The assembly and disassembly of ecological networks

Abstract

Global change has created a severe biodiversity crisis. Species are driven extinct at an increasing rate, and this has the potential to cause further coextinction cascades. The rate and shape of these coextinction cascades depend very much on the structure of the networks of interactions across species. Understanding network structure and how it relates to network disassembly, therefore, is a priority for system-level conservation biology. This process of network collapse may indeed be related to the process of network build-up, although very little is known about both processes and even less about their relationship. Here we review recent work that provides some preliminary answers to these questions. First, we focus on network assembly by emphasizing temporal processes at the species level, as well as the structural building blocks of complex ecological networks. Second, we focus on network disassembly as a consequence of species extinctions or habitat loss. We conclude by emphasizing some general rules of thumb that can help in building a comprehensive framework to understand the responses of ecological networks to global change.

1. Introduction

Global change is one of the leading problems faced by humankind. Decades of severe overfishing, habitat transformation, biotic invasions, contamination and changes on atmospheric gases are producing a severe biodiversity crisis (Sala et al. 2000). While the nature of these changes and the tragic consequences for the persistence of life on Earth and the services provided are beyond any doubt, we still know little of the community-wide implications of human-induced perturbations. Partly, this is owing to the fact that the bulk of studies on global change have focused on population abundance, distribution shifts and organism physiology (Sala et al. 2000), while very little is known on the changes of such global change drivers on the network of interactions among species (Tylianakis et al. 2008). This lack of information also reflects the still unknown relationship between network structure and dynamics. There is a need of a system-level conservation ecology which requires a cross-fertilization across multiple lines of investigation including both network structure and dynamics.

A fundamental initial goal is to better understand ecological network structure and how these networks are assembled from their basic building blocks. However, to truly examine the ecological consequences of change, we must examine how these networks disassemble as a result of human actions, or environmental perturbations, direct or indirect. There appear, then, to be two apparently independent questions in food web research, which ideally have the same long-term intent. Here we review recent work aimed at one or the other goal, while emphasizing the connections between these two seemingly disparate research agendas.

2. Assembly of ecological networks

(a) Dynamics of network build-up

Empirical research on ecological networks has been eminently static, describing networks either as a snapshot in time or an amalgamation across time (Polis 1991). This is because, in general, there is very little empirical data regarding the temporal aspects of whole food webs. Similar criticism can be made of the spatial dimension of these networks. Thus, the traditional approach in ecology has been to indirectly infer a process or mechanism from a fixed pattern. For example, ecologists in the last few years have described the skewed distribution of the number of interactions per species (Solé & Montoya 2001; Dunne et al. 2002a; Jordano et al. 2003). This pattern describes a heterogeneous community where the bulk of species have only a few interactions, but a few species are much more connected than expected by chance. While there are simple models of network formation that can account for these patterns, it is risky to infer process from pattern. Recently, however, there have appeared a few papers that describe the temporal dynamics of ecological networks and lead us in this direction.

Olesen et al. (2008) were able to analyse the day-to-day dynamics of a pollination network, taking advantage of the severe seasonality of the Zackenberg Research Station in Greenland. The soil is covered by snow for approximately 10 consecutive months, which leaves a wonderful opportunity to witness the entire network assembly process from the beginning of each season. Jens Olesen and a group of students recorded the species and interactions every day, allowing the characterization of the attachment process of this network.

Physicists proposed a simple model that is able to generate these skewed connectivity distributions, the so-called preferential attachment (Simon 1955; Barabasi & Albert 1999). Roughly speaking, this model proceeds as follows. Let us imagine an initial set of nodes and interactions. When a new node is introduced to the network, it interacts with an existing node selected at random, proportional to the existing node's number of interactions. If this process is repeated, small initial differences in the number of interactions of each node are amplified; this is a kind of ‘rich gets richer’ process (Barabasi & Albert 1999). In some sociological and physical examples, this process could be tested, but this had not previously been the case in ecology.

Olesen et al. (2008) showed that the attachment is intermediate between preferential and random. Importantly, this process is compatible with the skewed truncated power-law connectivity distributions previously reported (Jordano et al. 2003). From an ecological point of view, the results by Olesen et al. (2008) are telling us that the ecological network is assembled so that new species tend to interact predominantly with already well-connected species because these species are either more abundant or have a higher phenophase. In this community, plant abundance explains only 12 per cent of plant linkage level, while phenophase length explains between 50 and 70 per cent of the variance.

The previous field experiment provides insight into the assembly of a real pollination network at a species level. One could argue that many mechanistic models developed to explain ecological network structure, such as the cascade model of Cohen (1989) or the niche model of Williams & Martinez (2000), similarly provide insight into food web assembly at a species level. This argument relies on the idea that these models use heuristic rules for how predators in an ecological community select their prey. An intriguing, but heretofore untested, question is whether one can empirically measure if those heuristic mechanisms that can explain the entire food web structure are the same mechanisms undergone during the assembly of the ecosystem, or the same mechanisms, for example, that would be used by invasive species in the community.

Another indirect way to explore instances of network assembly is through careful field exclusion experiments. One of these experiments was developed in the Tuesday Lake by Cohen et al. (2003). In 1985, three species of planktivorous fishes were removed and one species of piscivorous fish was introduced. Comparisons of the data from 1984 and 1986 show that the manipulation produced at most minor differences in the structure of the food web, despite the fact that species composition changed, as did relative abundance among species categories. This pattern is quite similar to the pattern found in pollination networks. Both Olesen et al. (2008) and Petanidou et al. (2008) analysed the temporal dynamics of two pollination networks across several years. Interestingly enough, these independent studies arrive at the same conclusion: there is high turnover in both species and interactions between years, yet the overall network architecture remains quite constant. This robustness of network architecture in front of sampling effort both in time and in space was also concluded in a more local study by Nielsen & Bascompte (2007).

A complementary approach in between the scale of individual species and complete networks examines the basic building blocks of complex networks. While this recent set of studies does not provide information on dynamics, they provide a step in the right direction by examining the relative frequency of each one of these structural and dynamic components.

(b) Network motifs: the basic building blocks of complex networks

An influential paper by Milo et al. (2002) first introduced the idea of the network motifs that are subgraphs of interconnections that appear significantly more often than expected by chance in complex networks. These motifs can then be viewed as the fundamental building blocks of the representative complex networks (figure 1). When examining the complete set of unique connected subgraphs for a specified number of nodes, it was additionally observed that some classes of complex networks exhibit conserved patterns of subgraphs that appear significantly more—motifs—and that appear significantly less than expected by chance (Milo et al. 2004).

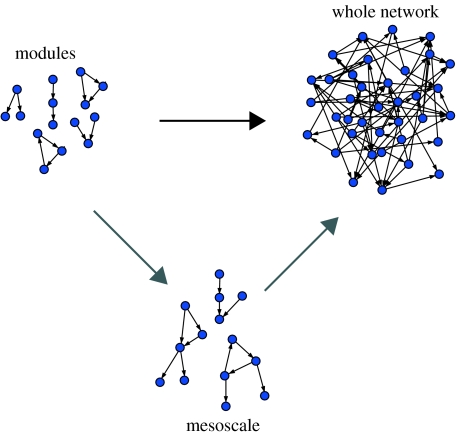
Figure 1.

The different approaches to food web research. Traditionally, ecologists have either studied the dynamics of simple trophic modules (left) or the statistical properties of entire food webs (right). In the last few years, ecologists have tried to bridge between these two research agendas by exploring how well represented are these trophic modules in entire food webs (black arrow). Some of these modules are over-represented; they are called networks motifs and can be regarded as the basic building blocks of complex food webs. The next step in understanding network assembly is to focus on the mesoscale by exploring how trophic modules relate to each other and what components of food web stability can be explained by the stability of the basic blocks versus the stability of their combination (grey arrows).

In ecology, there is a long tradition of studying simple trophic modules such as tri-trophic food chains, omnivory or intraguild predation (Pimm & Lawton 1977; Holt 1997; McCann et al. 1998). Ecologists have largely focused on these simple trophic modules because of known, or at times presumed, ecological relevance and either analytical tractability or experimental practicability.

Unfortunately, there exists a large gap between the dynamic study of trophic modules and the static empirical descriptions of entire food webs (Bascompte & Melián 2005). One must ask to what extent are these dynamic studies relevant for our understanding of entire food webs? A first step in answering this question could be to state that this depends on how relevant—or frequent—each of these trophic modules are in entire food webs (Bascompte & Melián 2005; Stouffer et al. 2007). It is interesting to note that while research on complex networks has first quantified motifs and then explored the dynamical implications (Prill et al. 2005), the reverse has occurred in ecology.

It is not a stretch to argue that the relationship between trophic modules and network motifs is also relevant for our understanding of the assembly of ecological networks. In §2a, we addressed this assembly from the point of view of the dynamics, while here we examine assembly from another point of view, namely considering what are the blocks from which one may assemble an ecological network. This line of research shows that some trophic modules are over-represented in food webs—they are truly fundamental motifs—while others are found less often than that in appropriate randomizations (Bascompte & Melián 2005; Stouffer et al. 2007). For example, apparent competition and intraguild predation were found to be over-represented in several large food webs, while the frequency of omnivory greatly varied across food webs (Arim & Marquet 2004; Bascompte & Melián 2005; Stouffer et al. 2007).

Intriguingly, it was demonstrated that, similar to other types of complex networks (Milo et al. 2004), there is a conserved pattern of over-representation and under-representation of trophic modules that is shared by food webs from a variety of habitat types: estuarine; freshwater; marine; and terrestrial (Camacho et al. 2007; Stouffer et al. 2007). This pattern was also demonstrated to be independent of other factors that distinguished the various food webs, such as the number or composition of species present. Nonetheless, while we observe that these food webs share a similar make-up, we do not yet understand the historical assembly process, the seemingly complex manner in which these various pieces come together, beyond the level discussed earlier with regard to the mechanistic food web models.

Largely trophic modules in food webs have been examined as structural components only, i.e. one ignored or did not consider the strength of the interactions. It is now known that the strength of the interactions between predators and their preys may strongly determine the stability of ecological communities. Thus, a subsequent investigation of the studies on network motifs considered motifs defined by the intensity of the interactions among species (Bascompte et al. 2005). In order to assess the likelihood of a trophic cascade (i.e. indirect changes in biomass across more than one trophic link) following the overfishing of sharks, Bascompte et al. (2005) examined how over-represented strongly interacting tri-trophic food chains were. These chains are those with two consecutive strong interaction strengths in the food chain. When chains exhibit such co-occurrence of strong interactions, trophic cascades are more probable.

It was shown that a large Caribbean marine food web showed a significantly lower number of these combinations than that would be expected at random, given the observed interactions and interaction strengths. Furthermore, in the few cases in which two strong interaction strengths occur, these were statistically associated with strong omnivory (Bascompte et al. 2005). These structural patterns are of relevance for our understanding of the consequences of overfishing of top predators. The under-representation of highly interacting tri-trophic food chains and the over-representation of strong omnivory in the few cases in which two strong interaction strengths co-occur simultaneously reduce the likelihood of trophic cascades as observed in a biologically parametrized bioenergetic model (Bascompte et al. 2005).

As detailed, the study of network motifs can thus be seen as relevant when understanding not only the basic building blocks that form complex food webs, but the stability of these food webs. However, the implications should be viewed with caution. Thus far, we can speak only about the stability of these basic blocks in isolation, despite the temptation to scale up these results and infer the stability of the entire food web. There is still a large gap in our understanding of this problem. We must examine in greater detail to what extent the stability of the entire food web can be explained by the stability of its simple components (Garcia-Domingo & Saldaña 2007; Allesina & Pascual 2008). In addition, we remain to build a concrete understanding at the mesoscale level regarding how these network motifs interrelate with each other (figure 1), and whether the manner in which they combine influences the stability of the whole assembly.

(c) Network modularity: community structure of mutualistic networks

A related search for the basic organization of complex networks has also been performed in mutualistic networks such as those relating flowering plants with their insect pollinators (Olesen et al. 2007). The approach is different, however, than the one described for trophic food webs while the ultimate goal and consequences are quite similar. In this case, Olesen et al. (2007) characterized the degree of modularity of these networks. A modular network is that organized in different modules so that species within a module tend to interact among themselves more frequently that they do with species from other modules (Guimerà & Amaral 2005). Olesen et al. (2007) found significant evidence for modularity in the bulk of the large pollination networks they studied. The observed modules constitute small groups of plants and animals. For example, some of these compartments are formed by a few Diptera species and mainly white flowers, while others are composed by one plant species and several butterfly species (Olesen et al. 2007). Interestingly enough, these modules can be considered the fundamental functional units of these pollination networks, candidates for coevolutionary units.

The mapping of modules can explain how previous research on basic groups of coevolving species relates to the other research agenda based on entire networks. One particularly interesting result relating to network assembly is the particular pattern by which these modules are interlinked between themselves. This interlinking will also tell us how different patterns are compatible in the same network. In particular, one observes that these functional units interact through the generalist species—which are found in the core of the nested matrix—that glue the modules into a single coherent, cohesive network (Olesen et al. 2007).

Interestingly enough, this cohesive wiring pattern is very similar to that found in food webs when they are analysed using their distribution in k-subwebs. A k-subweb is defined as a subset of species that are connected to at least k species of the same subweb. Melián & Bascompte (2004) found the existence of a single, most dense subweb having most interactions despite being formed by a small number of species. The cohesive nature of these food webs is defined by the fact that all other subwebs in the network are connected to this most dense subweb. The removal of this most dense subweb was translated into the fragmentation of the food web in as many as 57 parts (Melián & Bascompte 2004). Thus, ecological networks seem to have a well-defined pattern of interactions where modules or subwebs are attached to a core of the network that acts as the glue providing cohesion.

In summary, from the above subsections, we have seen the sort of ideas that could be considered basic ingredients of network assembly and that a ‘network engineer’ could follow. First, on a temporal scale, it seems that the assembly of mutualistic networks takes place by a preferential attachment of new species to already well-connected species, probably mediated by ecological variables such as phenophase length (Olesen et al. 2008). Second, from a structural point of view, there are well-defined patterns of interconnectivity, which form the basic building blocks of food webs (Bascompte & Melián 2005; Stouffer et al. 2007). These blocks are connected in a particular way, so that they are attached to a central group of generalist species that not only interact among themselves within this core, but also with other species through the network (Melián & Bascompte 2004; Olesen et al. 2007).

Each of these topics relates to the assembly of an ecological network and the formation of these networks. The alternative concept, of network disassembly, relates directly to the consequences of global change in biodiversity. At what rate will these networks collapse as the intensity of a perturbation is increased? We will turn to recent research into network disassembly in §3.

3. Disassembly of ecological networks

(a) Network disassembly and coextinction cascades

Studies on the disassembly of ecological networks are mainly based on simulations in which a progressive number of species are driven extinct, or a progressive fraction of the habitat is destroyed. These approaches follow the influential paper by Albert et al. (2000). In that paper, the authors tried to understand how the architecture of the Internet makes it more robust to server failure and attack. An increasing number of nodes were removed, and the authors targeted that point at which the network becomes fragmented in a series of disjoint networks. This clearly demonstrated that there is a well-defined relationship between network structure and robustness, and was followed by ecologists using food web data (Solé & Montoya 2001; Dunne et al. 2002b). The motivation, once more, was to better understand the relationship between network structure and dynamics. Network robustness was quite different if one deleted the most specialist species or targeted the most generalist ones, again echoing the paper by Albert et al. (2000). One main result was that ecological networks were quite robust to the extinction of the most specialist species, but quite fragile if the most generalized species were the ones going extinct (Solé & Montoya 2001; Dunne et al. 2002b). In addition, whereas secondary extinctions increase gradually as a result of randomly removing species, the removal of the most connected species produces a sharp increase in secondary extinctions after an initial period of minimal secondary extinctions (Dunne et al. 2002b). In both cases, however, there is an increased sensitivity with greater removal level (Dunne et al. 2002b). Thus, the consequences of perturbations are higher as the intensity of the perturbation is gradually increased. This result, therefore, calls for caution since we cannot directly extrapolate the consequences of global change at the first stages with those at the latter stages.

The above robustness of food webs to random species extinctions has largely been explained by their heterogeneous structure (Albert et al. 2000; Solé & Montoya 2001). However, motivated by the finding that the majority of food webs do not exhibit skewed distributions of connections (Camacho et al. 2002; Dunne et al. 2002a; Stouffer et al. 2005). Dunne et al. (2002b) showed that as a rule of thumb, the higher the connectance of the food web, the higher its robustness (Dunne et al. 2002a).

One might question whether these patterns of robustness or fragility are a consequence of the simple extinction sequences used. To address this concern, Srinivasan et al. (2007) used a biologically realistic and informed extinction scenario in 34 freshwater, pelagic food webs. Here, species widely distributed across all lakes are assumed to be more environmentally tolerant—and so less likely to be driven extinct—than species that inhabit only one or a few such lakes. This extinction order not only indicated marked robustness of food webs but also significant fragility to the reverse sequence.

Beyond food webs, Memmott et al. (2004) extended these extinction simulations to two pollination networks. These authors showed that the architecture of these networks makes them increasingly robust to species extinction. Again, the networks were more robust to the random extinction of species than to the extinction of the most generalist ones; however, in this case, the decay was linear and no thresholds of sudden collapse were found.

This lack of network collapse with the extinction of the most connected species was suggested to imply that other factors beyond a heterogeneous degree distribution were at work. Among these, the nested structure of these networks was related to this tolerance to species extinction (Memmott et al. 2004). However, as noted by the authors, this difference between food webs and mutualistic networks may be a consequence of the different methodologies. In the study of Memmott et al. (2004), the ranking of extinctions is within the species of the same trophic level while in food webs species removed may belong to different trophic levels (Solé & Montoya 2001; Dunne et al. 2002a). When species are removed according to generalization level and across both plants and animals, a similar network collapse happens as that observed for food webs (Memmott et al. 2004). The take-home message was again that ecological networks are robust to the random extinction of species, but may be quite fragile if generalist species prove to be the most susceptible. In mutualistic networks, the heterogeneous degree distribution and the nested structure confer this robustness.

The structure of mutualistic networks also confers robustness to habitat loss. Using a simple model of metacommunity dynamics that preserved the exact pattern of interactions of two real mutualistic networks, Fortuna & Bascompte (2006) showed that the metacommunity was more persistent to habitat loss than equivalent models where the structure of the network was randomized. Similarly, there was a sudden decay in biodiversity for a given destruction level. Empirically, Ashworth et al. (2004) also adduced to the structure of mutualistic networks to explain plant responses to habitat fragmentation. Specifically, the asymmetric specialization observed in these networks (specialists interact with generalists) makes that, contrary to expectation, both specialists and generalist plant species decay at the same values of habitat loss. Even when specialists interact with only one or a few pollinator species, these are generalists and widely distributed, which assures the persistence of plant specialists almost as long as some patches are occupied by generalists (Ashworth et al. 2004).

There are other consequences of species extinctions beyond the size of the coextinction cascade. Some species have key roles in the network of interactions and their disappearance may induce structural changes in the remaining network. This is related to the roles of species in the network. In §2c, we have already described the modules or basic building blocks of mutualistic networks. Modularity analysis also describes the role of each species in the network (Guimerà & Amaral 2005). This provides a classification of the role of species in relation to this modular organization: some species are irrelevant both within their module and across modules; others are within-module hubs but do not interact at all with species in other modules; others have a small number of interactions and yet contribute to the connection of several such modules; and finally a few species are both within-module hubs and connectors (Guimerà & Amaral 2005). Olesen et al. (2007) analysed the modularity of pollination networks and found that a small fraction of the species in these networks are network hubs (i.e. they are very important within their modules and also connecting different modules). Among the insects, only 1 per cent of the species have this particular role. These species are exclusively Hymenoptera and Diptera. Thus, the extinction of these species, besides the potential coextinction of other species depending on them, may change the structural properties of the network in the sense of making it less cohesive. The modules would become more isolated, and this may affect the robustness of the network to further perturbation (Olesen et al. 2007).

(b) Network disassembly and the loss of evolutionary history

A further implication beyond the size of secondary coextinction cascades has to do with the rate at which past evolutionary history, or functional groups are lost. In order to assess this effect, one must integrate network structure and biological attributes by examining the precise identity of the species going extinct. Rezende et al. (2007) first demonstrated that there is a significant phylogenetic signal on species' roles in the network of interactions. Specifically, one-third of the communities have a strong phylogenetic signal (i.e. a tendency of phylogenetically similar species to have similar roles in the network of interactions) relative to the number of interactions per species, while half of the communities have a strong signal relative to the identity of the species one interacts with (Rezende et al. 2007).

The results of Rezende et al. (2007) imply that, in order to consider the mechanisms leading to the formation of network patterns, one must take into account the past evolutionary history of the species forming such networks. Thus, the dynamical process of network assembly described earlier appears to need a phylogenetic basis. This perhaps also relates to the predominance of some of the network building blocks we have discussed and whether or not they also have an evolutionary basis.

Another main implication of the phylogenetic signal on network patterns has to do with the nature of the coextinction cascades described in §3a. In the absence of a phylogenetic signal on network patterns, these coextinction cascades would prune homogeneously through the phylogenies as there clearly would not be any phylogenetic correlation between the species going coextinct. However, due to the observed phylogenetic signal, coextinction cascades tend to involve phylogenetically related species: since phylogenetically related species tend to interact with the same other species, they will suffer similarly from the extinction of their common resources. This translates into a biased pruning of the evolutionary tree and a more pronounced loss of evolutionary history than previous research anticipated. Although the structure of ecological networks makes them more robust to species extinctions, the phylogenetic signal on network patterns is translated into a risk of substantial loss of evolutionary history.

In short, the rate and mode of network disassembly has started to be anticipated through simple simulation models. These very preliminary results tell us that the architecture of ecological networks is important in understanding disassembly. In addition, the interaction between network and phylogenetic structure is important when exploring the consequences of this network collapse. Similarly, it would be important to superimpose functional groups or life-history attributes on top of these networks to get insight into how ecosystem function is mapped into network structure (Dobson et al. 2006).

4. Assembly and disassembly: are there general rules?

In this paper, we have reviewed some preliminary results on both the assembly of ecological networks and its collapse after perturbations. The reader should recognize, however, that this knowledge is still very fragmented and many questions remain to be solved. For example, how relevant is the information of the first part to understand the second? To some extent, this question is akin to asking whether these processes are reversible. This possibility appears to be unlikely, if untested. Nevertheless, despite these limitations, we are in a position to outline a few important facts that underlie our understanding of the response of biodiversity to global change summarized in the following points.

1. In the only instance in which there is detailed temporal information of the network build-up, a mutualistic network exhibits a temporal assembly in which newly appearing species tend to interact with already well-connected species.

2. There are trophic and mutualistic modules that act as the basic building blocks of complex ecological networks. Assembly seems to proceed by a combination of such building blocks increasing the cohesion of the network; these modules are attached to a core of species by interactions that act as the glue of the network.

3. The structure of ecological networks imparts robustness to the random extinction of species but is similarly responsible for their fragility to the extinction of generalist species.

4. The disassembly of ecological networks leads to thresholds where upon the network collapses. The consequences of species extinction become amplified and self-reinforcing as more and more species have been extirpated.

5. Despite network robustness to species extinctions, the phylogenetic signal on network patters confers a faster loss of evolutionary history and a biased pruning of the tree of life.