Abstract
Here, we synthesize a number of recent empirical and theoretical papers to argue that food-web dynamics are characterized by high amounts of spatial and temporal variability and that organisms respond predictably, via behaviour, to these changing conditions. Such behavioural responses on the landscape drive a highly adaptive food-web structure in space and time. Empirical evidence suggests that underlying attributes of food webs are potentially scale-invariant such that food webs are characterized by hump-shaped trophic structures with fast and slow pathways that repeat at different resolutions within the food web. We place these empirical patterns within the context of recent food-web theory to show that adaptable food-web structure confers stability to an assemblage of interacting organisms in a variable world. Finally, we show that recent food-web analyses agree with two of the major predictions of this theory. We argue that the next major frontier in food-web theory and applied food-web ecology must consider the influence of variability on food-web structure.
Keywords: variability, adaptive food webs, mobile consumers, trophic structure, fast and slow pathways, stability
1. Introduction
Ecologists and naturalists have long been aware of the indescribably complex set of animal and plant interactions that make up nature's ecosystems (Darwin 1859; Polis 1991). At the same time, ecologists have recognized the remarkable consistency of the species and the structures that compose these tangled networks (Elton 1958; Dunne 2006; Dunne et al. 2008). Despite the intuitively pleasing notion that the world's ecosystems harbour a great steadiness, most biologists would be quick to argue that ecological systems are notoriously variable (Elton 1958; Levin 1998). In this sense, stability may be more about the non-equilibrium persistence (i.e. species remain above zero densities) of an assemblage than long-standing equilibrium notions of stability (e.g. eigenvalue stability). As such, one can envision the natural world as a constantly changing mosaic (i.e. population densities, interaction strength) with a stable assemblage of interacting organisms over ecologically relevant time scales. It is this aspect of variability and stability (i.e. persistence) that this paper addresses.
Early food-web empiricism tended to make the implicit assumption that food webs can be envisioned as static entities (Cohen 1978). This approach was consistent with early theory that relied heavily on equilibrium assumptions (May 1973). These early simplifying assumptions are reasonable starting points; however, a number of empirical ecologists have since made cogent arguments for the potential importance of space and time in governing food-web dynamics (Winemiller 1990; Polis & Winemiller 1996). Furthermore, a growing body of complex systems theory has argued that some of the most fundamental aspects behind the persistence and functioning of complex systems, in general, may be their ability to adapt in the face of perturbations (Levin 1998). While a very interesting general theory, it has proven somewhat elusive to concretely map this abstract set of ideas to specific food-web structures. This paper is a preliminary attempt at piecing together existing evidence to argue that variability (in space, time and food-web structure) and the ability to rapidly respond to such variation (i.e. organismal behaviour) are critical to the maintenance of one of nature's most amazingly diverse and complex entities—the food web.
Recently, empirical and theoretical ecologists have begun the intrepid task of incorporating spatial and temporal aspects into food-web ecology (Winemiller 1990; Woodward & Hildrew 2002; Holt & Barfield 2003; McCann et al. 2005; Thompson & Townsend 2005). Although the early empirical results have been enticing (Eveleigh et al. 2007; Tylianakis et al. 2007), ecologists are in no position to empirically tackle this baroque problem rapidly using the modest number of food-web studies that exist. Food-web data rarely have been gathered with the required spatial and temporal gradients in mind (Martinez 1991). Additionally, documenting food webs in space and time is a monumental task. While traditional methods of gathering food-web data still need to be brought to bear on this issue, a number of researchers are currently using body size and behavioural attributes of organisms to begin to predict food-web architecture across space and time (Emmerson & Raffaelli 2004; Petchey et al. 2008; Rooney et al. 2008). Such an approach promises the potential to make progress with a large body of existing empirical data. This organismal-level approach to food webs has the added benefit of allowing ecologists to synthesize an enormous amount of existing empirical data on lower level biological entities (e.g. individual species attributes and behaviour), with the sparse amount of existing data capable of looking at large-scale empirical patterns (e.g. food-web structure). In a sense, one is asking whether empirically derived attributes of organisms predict food-web structures that are actually found in existing food-web data. Where this has been done, there have been some interesting consistencies across scales (Petchey et al. 2008; Rooney et al. 2008), suggesting that some unification of different sub-disciplines may be possible within the food-web framework.
In the following, we put together a body of recent research which argues that individual attributes such as size and behaviour can be used to predict the architecture of a broad range of food webs. Preliminary empirical data show that food-web attributes are consistent with predictions based on patterns in organismal attributes. We then explore some novel stochastic theory and review theory within the context of a variable world and a behaviourally adaptive food-web structure. We show that this collective food-web theory hinges on two critical assumptions: (i) the ‘bird feeder’ effect, whereby consumers move to sudden outbreaks in a resource density (i.e. consumers behave adaptively), and (ii) resources in space are not synchronized (i.e. consumers have something to adapt to). Together, these assumptions and the empirically motivated food-web structure suggest that nature's diverse food webs are composed in such a way as to promote the persistence of these complex assemblages. We end by interpreting two recent empirical studies in terms of these two major underlying theoretical assumptions. A recent example of boreal insect food webs that was measured over space and time shows the existence of the bird feeder effect at the whole food-web level, while a classic empirical example of seasonal plankton dynamics shows how food-web structure can readily generate asynchronous resources even when abiotic forces synchronize resources (Sommer et al. 1986). We end by interpreting this general theory within the context of human modifications influencing food-web structure.
2. Individual traits and food-web structure
There is a long-standing research axis in ecology that has sought out the ecological implications of body size (e.g. Peters 1983; Brown et al. 2004). This largely empirical literature provides a powerful base for understanding organismal traits and thus puts us in a position to make predictions about a food-web structure that must adhere to these empirical relationships (Rooney et al. 2008). Ecologists have also produced an impressive body of research on individual foraging behaviours (MacArthur & Pianka 1966; Charnov 1976) that can be placed within the food-web framework. Taken together, body size and foraging behaviour allow us to predict the three following attributes of food webs (Rooney et al. 2008; discussed in further detail below):
food webs ought to have mobile generalist consumers coupling spatially isolated resources repeated over a range of spatial scales (figure 1a; hereafter referred to as a hump-shaped trophic structure since the empirical manifestation of this idea produces a hump-shaped figure; figure 1b; §2a),
mobile consumers, the apex of the hump-shaped trophic structure, couple sub-webs and adaptively respond to resource variation in space (§2b), and
sub-webs tend to have asymmetric flux rates that readily generate spatial resource asynchrony (§2c).
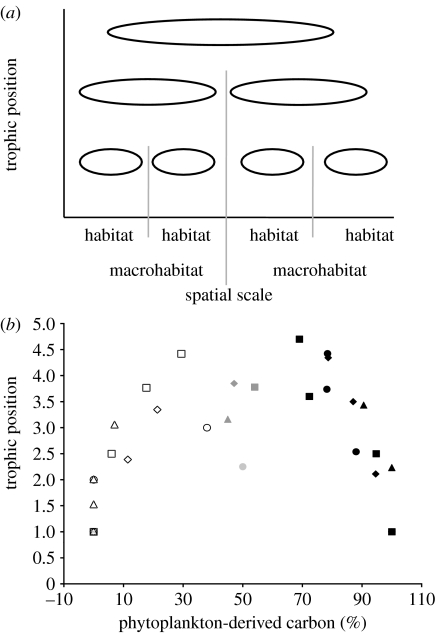
Figure 1.
(a) The simple architecture of food webs predicted by empirical body-size relationships and foraging theory. Sub-food webs (effectively habitats) are hierarchically coupled by consumers such that, at the highest trophic level, consumers couple regional habitats or macrohabitats. (b) Four well-resolved aquatic webs, which display the predicted hump-shaped architecture over the macrohabitat scale (i.e. relative amount of carbon from pelagic versus benthic). Each symbol represents mean trophic position and carbon content from each trophic guild: white circles, Chile detrital channel; white squares, Cantabrian detrital channel; white triangles, Chesapeake phytoplankton channel; white diamonds, Bering detrital channel; black circles, Chile phytoplankton channel; black squares, Cantabrian phytoplankton channel; black triangles, Chesapeake detrital channel; black diamonds, Bering phytoplankton channel; grey circles, Chile couplers; grey squares, Cantabrian couplers; grey triangles, Chesapeake couplers; grey diamonds, Bering couplers.
In the following, we further outline the logic behind each of these predictions and the empirical data that speak to these food-web predictions.
(a) Hump-shaped trophic structure
It is commonly asserted that size correlates positively with trophic position. The data generally agree with this intuition but occasionally the trend between size and trophic position is weak (Jennings et al. 2001). Not surprisingly, this aspect of individual biology (i.e. body size and trophic position) frequently plays into food-web models that have successfully reproduced patterns in natural food webs (e.g. Cohen & Newman 1985; Williams & Martinez 2000).
It is also simultaneously the case that larger organisms tend to be more mobile (Peters 1983). Empirical research has found that transport is more cost efficient, on average, in larger organisms (Peters 1983). Thus, larger, higher trophic-level organisms are also more mobile on average, and so operate over a larger spatial scale. These relationships between body size, trophic position and spatial scale immediately set up a hierarchy of interactions in ecological space (figure 1a). As a result of these empirical relationships, we predict that small organisms are more isolated in space since they are less mobile than larger, higher trophic-level organisms (McCann et al. 2005). This reasoning immediately suggests that, as one moves up the trophic structure, we expect each new trophic level, on average, to progressively couple spatially restricted organisms at the trophic level below them (figure 1a). Thus, in lower trophic levels, consumers effectively couple sub-webs at a microhabitat scale, while higher trophic-level consumers effectively couple sub-webs at a macrohabitat scale. This very simple logic sets up a hierarchical hump-shaped trophic plot whereby each consumer connects resources in space (the humped-shape is the consumer coupling relatively isolated resources). If this is true, then we predict that behind nature's reticulate food webs lies a relatively simple repeated architecture—the hump-shaped trophic structure (figure 1a,b).
To empirically assess this food-web structure, Rooney et al. (2006) used eight of the most well-compiled webs that include estimates of flux rates between species. In all cases, they followed the fate of carbon from distinct spatial habitats through the food web. As an example, for aquatic food webs, they asked whether carbon for any given species came from benthic macrohabitats (i.e. the benthic sub-web) or pelagic macrohabitats (i.e. the pelagic sub-web). Similarly, they identified common microhabitats in soil webs (i.e. the dry soil fungal sub-web and the moist soil bacterial sub-web) and followed the fate of carbon in these webs. Rooney et al. (2006) then plotted each species according to where they derived their carbon (i.e. percentage carbon derived from habitat A) against their trophic position. Figure 1b displays the average relationships across trophic levels for the four aquatic webs they investigated. If the gross architecture of these reticulate webs acts as predicted, then one expects a hump-shaped plot of species carbon acquisition for any given food web. Figure 1b shows that this hump-shaped pattern occurs consistently in all four aquatic webs. The four terrestrial soil webs also consistently show the identical hump-shaped pattern (Rooney et al. 2006). Organisms that derive relatively equal amounts of carbon from distinct habitats in figure 1b (e.g. the shaded grey symbols) are the mobile food-web couplers of these otherwise relatively distinct habitats.
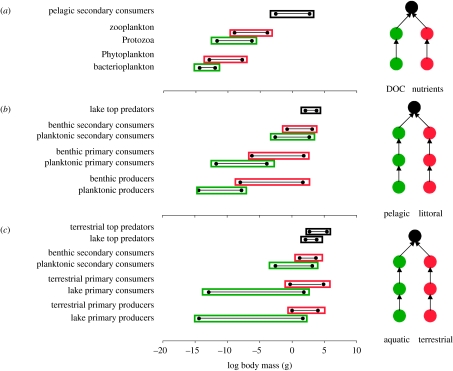
It would be interesting to further explore the role of relatively distinct habitats in carbon flux. As discussed above, given an increasing spatial scale of consumers as we move up the food chain, then one predicts that the hump-shaped curve ought to be invariant across spatial scales. To highlight this prediction, let us consider an aquatic example (figure 2). Over a range of spatial scales from within the water column (i.e. the pelagic sub-web; figure 2a), to within the lake ecosystem (i.e. the pelagic–littoral sub-web; figure 2b), to between ecosystems (i.e. the terrestrial–aquatic food web; figure 2c), this pattern of relatively separate pathways coupled by higher order consumers repeats itself. Starting from the pelagic sub-web (figure 2a), we find that the dissolved organic carbon (DOC) pathway and the phytoplankton pathway are coupled by zooplankton (Sherr & Sherr 1988). As we move beyond this trophic level, we return to the whole lake web, which is coupled by mobile fishes that move between littoral and pelagic habitats (Vander Zanden & Vadeboncoeur 2002). Finally, at the landscape scale, we find couplers, such as birds and mammals, that integrate across terrestrial and aquatic prey (e.g. Hebert et al. 2008). Thus, at each spatial scale, we have pathways connected by higher order consumers (i.e. the hump-shaped trophic structure repeats itself). Note, in addition to this, that, in all cases, one pathway tends to consistently have a smaller range in body sizes than the other pathway (e.g. DOC versus phytoplankton, pelagic versus littoral, aquatic versus terrestrial; figure 2). We will return to this intriguing body-size pattern shortly in order to predict another food-web consequence of these different individual traits within the different pathways or sub-webs.
Figure 2.
The hump-shaped structure of food webs occurs at a variety of scales from (a) within the pelagic, (b) within a lake and (c) between lakes and terrestrial ecosystems. Green and red delineate energy channels and the size range of the resident species. Note that in all cases, there appears to be consistent size differences between pathways such that one pathway is consistently smaller at all trophic levels until the top of the hump-shaped trophic structure whereby both pathways are coupled by predators. Adapted from Rooney et al. (2008). DOC, dissolved organic carbon.
(b) Mobile adaptive consumer responses
The foregoing discussion clearly identifies that mobile organisms couple networks in space and may do so at a variety of spatial scales. The consumer's ability to move between distinct resources that have different habitat demands puts them in a position to make foraging decisions within their sub-web. Thus, the food-web arrangement, in a sense, is a recursive optimal foraging and habitat choice problem. As such, if spatially distinct habitats vary in resource quantity, then we expect the consumers to adopt behaviour that tracks this resource variability (i.e. consumers move from lower density prey habitat to higher density habitat). The food web in the low resource density habitat therefore is expected to have a lower trophic position than the food web in the high resource density habitat—the food web, in a sense, expands and contracts vertically on the landscape as an accordion. This notion of the food web as an accordion has been called the bird feeder effect by Eveleigh et al. (2007) for the simple reason that organisms flock to areas of high resource densities as birds flock to a bird feeder. Here, we have concentrated on a food web's ability to adapt rapidly (i.e. behaviourally) and so play a potent role in governing population dynamics of the underlying assemblage of species. Clearly, it is of interest, but beyond the scope of this paper, to also consider the role of adaptive processes across evolutionarily time scales (i.e. from relatively rapid morphotype responses to slower speciation responses) in maintaining complex ecosystems (Levin 1998; Johnson & Agrawal 2003).
(c) Asymmetric flux rates
We alluded above to the fact that the food web in figure 2 has the interesting property that each sub-web tends to be composed of different-sized organisms with common couplers. This again puts us in a position to consider the implications of different-sized organisms by turning to the extensive empirical literature on body size and organismal traits. Specifically, the allometry literature has pointed out that small organisms tend to have high turnover rates while large organisms have lower turnover rates (Peters 1983). In a sense, the range in body sizes forms a slow–fast metabolic continuum whereby small organisms have a heightened cost of living (BMR/weight is relatively high) and so require high consumption and growth rates to match this high energetic cost. The result of such simple mathematical relationships is necessarily a higher, on average, turnover rate in smaller organisms (Brown et al. 2004). These simple empirical and theoretically reasonable relationships immediately imply that pathways with very different-sized organisms also ought to have very different rates of turnover. We expect, therefore, that pathways with small organisms have higher turnover rates (fast pathways) and larger organisms have lower turnover rates (slow pathways).
Recent research has found this to be precisely the case for four aquatic and four soil food webs (Rooney et al. 2006). The above body-size relationships across scales (figure 2), coupled with empirical body-size relationships, would further suggest that we have such fast–slow pathways across the range of food-web scaling (i.e. from within sub-food webs at a microhabitat scale to food webs that span entire ecosystems). This prediction has yet to be fully explored, but early empirical analysis, and the consistent difference in body size between sub-webs, suggests that it may occur frequently in ecological networks.
We now consider the stability implications of the above three aspects of food-web structure.
3. Theoretical implications
Much recent theory has found that weak interactions, properly placed, can act to mute out the destabilizing potential of strong interactions (McCann et al. 1998; McCann 2000; Neutel et al. 2002). The food-web structure we have outlined above is an interesting combination of fast pathways (or strong interactions) and slow pathways (or weak interactions). Furthermore, the adaptable aspect of the food web has been long seen as a stabilizing force in population ecology (Murdoch 1969; Oaten & Murdoch 1975), but has only recently been placed as a potent stabilizing force within a whole food-web context (Kondoh 2003; McCann et al. 2005). The adaptable consumer effectively preys upon the resources when resources are plentiful and releases resources from predation when resources are scarce. This predatory coupling and decoupling at appropriate times can greatly stabilize dynamics (McCauley et al. 1999). Clearly though, if there is a considerable lag in the consumer's response to changes in resource density, then the stabilizing influences are compromised.
The theory required to explicate the implications of the above food-web structure relies critically on the underlying food-web module of an adaptive mobile consumer that feeds on multiple competing resources in space. The underlying module, as suggested above, repeats itself at a variety of spatial scales. With this in mind, we explore some stochastic models and highlight theoretical results from deterministic models that come out of this very simple module.
(a) Stochastically driven resources
Here, for heuristic reasons, we explore a very simple stochastic model to show that variability in space can strongly stabilize consumer dynamics (i.e. bound their dynamics away from low densities). The stochastic model assumes that the consumer has no effect on the resource densities, rather resource densities are purely modulated by abiotic conditions. Later, we will consider the case of dynamical resources and therefore this case serves as a conceptual endpoint whereby resource dynamics are driven entirely by abiotic factors. Under this simplification, the model can be constructed as
| (3.1) |
where Fa is the density-dependent preference function (Chesson 1983),
| (3.2) |
and C is the consumer density; m is the density-dependent mortality rate; e is the conversion efficiency; ω is the preference for species 1; and ai is the attack rate of the consumer on resource species, Ri. Furthermore, for simplification, we have assumed that the underlying resources are identical in terms of consumer growth rates (i.e. a1=a2=a and e are equivalent for both R's). The consumer is self-damped (i.e. −mC2) to stop the biologically unrealistic case of uncapped population growth or decay. We now consider two informative endpoint cases of this stochastic model.
(i) Case 1: synchronized forcing of resources
Without loss of generality, let us assume that the initial condition is R1=R2. Furthermore, let us assume that the resources cycle with a given period described by the sine function . Since R1 is also equivalent to R2 in terms of C's growth rate, we can rearrange equation (3.1) to the following:
| (3.3) |
where RT(t) is the sum of R1(t) and R2(t) at time, t.
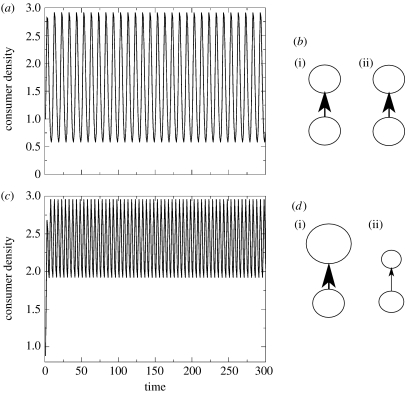
From this simple model, we immediately recognize that the consumer is driven to oscillations as it passively follows the temporal fluctuations in resources (figure 3a). If we ask how this simple food web adapts in each patch to these fluctuations on the two-patch landscape, we recognize that the food web is the same in both patches (figure 3b). This occurs despite the fact that the consumer has the ability to adapt. The reasoning for this result is trivial, but informative, the synchronization of resources in space eliminates variability in space. Without variability in space, there is nothing for the consumer to adapt to. Hence, the food web is static in space under synchronous resource dynamics. Large unstable resource fluctuations, therefore, transmit through the consumer as large unstable consumer fluctuations (figure 3a). Some degree of asynchrony is therefore critical for stabilizing interactions in space.
Figure 3.
(a) Completely synchronous resources have wildly fluctuating consumer densities. (b) The completely synchronous C–R interactions with flux rates (arrows) in space at a given time when R's are relatively high ((i) patch 1 and (ii) patch 2). Interactions are symmetric in space such that there are equal numbers of consumers and resources as well as identical consumption rates in both patches. (c) Completely asynchronous resource dynamics result in much more bounded consumer fluctuations. (d) Consumer resource interaction in each patch at a given time (relatively high resource densities in (i) patch 1). Interactions are asymmetric in space such that (i) patch 1 is a two-trophic-level system and (ii) patch 2 more closely resembles a one-trophic-level system. Parameters: a=1.0; e=1.0; m=0.50; and ω=0.5.
(ii) Case 2: asynchronized forcing and the bird feeder effect
Figure 3c displays the dynamics of the same consumer foraging on resources that are completely asynchronized in space. Under the above assumptions, the consumer still fluctuates, but it is easy to see that fluctuations in consumers are strongly muted relative to the individual resource fluctuations. A more bounded solution means a more persistent assemblage since the dynamics are not as sensitive to abiotic variation that can drive dangerously low population densities to extinction. Note here, though, that the dynamics never get completely stabilized. In fact, what tends to happen is that the minima of the plot in figure 3c are lifted and the maxima are reduced when compared with figure 3a. This makes sense in the light of the preference-based foraging decision modelled above. Organisms are tending to reside most of the time in higher density patches and so elevate there minima relative to the synchronized case. Furthermore, owing to imperfect foraging decisions, some organisms remain in the low density patch and so reduce the maxima relative to the synchronized case (figure 3a).
Changing the precise foraging decision does not qualitatively modify this result unless an organism forages severely sub-optimally. For example, even a random foraging decision would allow the consumer to average over the two patches and so be effectively quite stabilizing. On the other hand, if all consumers dispersed from high resource density patches to low resource density patches, then this would drive the consumer population to consistently low densities. Clearly, such sub-optimal foraging would lower the chances that such a consumer persists.
If we return to figure 3c to ask how the food web adapts on each patch in the two-patch landscape model above, we find that, for asynchronous resources, the food web consistently changes in both patches. If R1 is high, and R2 is low, then patch 1 has a strong C–R interaction and patch 2 has a relatively few consumers feeding on R2 (figure 3d). Patch 2 is effectively acting as a single trophic level (figure 3d). The asynchronization of resources in space and time allows the adaptability of this greatly simplified network to promote more stable consumer dynamics. The food web on each patch expands as an accordion back and forth according to local resource densities. When resource densities are high, a bird feeder effect occurs attracting consumers, and when resource densities are low, consumers leave the patch for the alternative higher density patch. There is a cost to such movement, omitted from the model, but given even modest spatial variability and finite costs, the stabilizing result robustly remains.
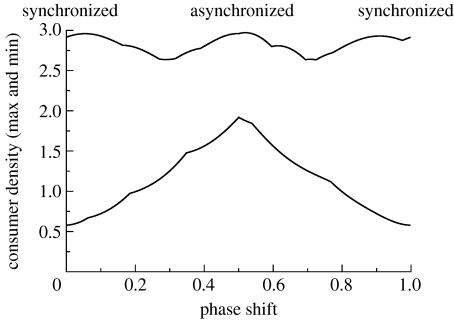
To more generally explore the role of asynchrony further, we plotted local maxima and local minima of consumer density as a function of the phase shift between resource dynamics (i.e. from a zero period shift to a full period shift). Clearly, the result discussed above is general (figure 4). As the resource dynamics get less synchronized, the consumer dynamics approach a more bounded solution (note that completely asynchronized case in figure 4 occurs at a phase shift equivalent to a half period). Any amount of spatial resource variability, therefore, promotes the stability of such an adaptive mobile consumer (figure 4).
Figure 4.
Consumer density, maxima and minima, after a transient of 200 time units as a function of the phase shift (period) between the two resources. Resources are completely synchronized at 0 and 1 full period, and completely asynchronized at a 0.5 period phase shift. The greatest stability occurs with the greatest asynchrony. Parameters: a=1.0; e=1.0; m=0.50; and ω=0.5.
It is worth pointing out that if the consumer does not have to make a preference in space (i.e. can forage simultaneously on all resources), then this asynchrony is also stabilizing. Since two completely asynchronized resources sum to a constant density (i.e. RT, defined above, is a constant), it is easy to reduce equation (3.1) to the following:
| (3.4) |
It is straightforward to see that this results in a stable consumer population with an equilibrium population and a negative eigenvalue (λ=−eaRT). This latter case is akin to the averaging effect and therefore can be seen as an extension of much single trophic-level theory (Doak et al. 1998; Tilman et al. 1998). While averaging means the result does not rely on space or switching, recent theory has shown that consumers that can average over resources in space tend to synchronize the resource dynamics in the patches (McCann et al. 2005). Once synchronized, the stabilizing influence of the consumer is lost (McCann et al. 2005). Hence, the switching aspect of this result is critical to the stability.
(b) Biotically driven resource dynamics
We now turn to the alternative endpoint case where resource dynamics are biotically driven. The model system under these assumptions can be written as
| (3.5) |
where all consumer parameters and functions are already defined above; ri is the rate of increase of species i; K is the carrying capacity of both resource species; and αij is the competition coefficient of species j on i. This model is effectively an example of the diamond-shaped food-web module (Holt 1996; McCann et al. 1998). McCann et al. (1998) analysed a very similar model and found that a strong food chain pathway (e.g. R1 strongly outcompetes R2 and R1 is fed on strongly by C) can be muted by a weak pathway (e.g. R2 weakly competes with R1 and R2 is fed on weakly by C). In such a case, the overall dynamics are greatly stabilized by the weak pathway (McCann 2000; Rooney et al. 2006).
The reasons for this are twofold. First, a weak competitor that can persist effectively shunts energy away from the otherwise strong pathway (McCann et al. 1998). This, in essence, reverses the paradox of enrichment and so tends to stabilize the potentially strong C−R1 interaction (McCann et al. 1998). Second, and more interesting for the discussion here, the differential competing pathways coupled by a predator readily generate asynchronous responses in the two resources. As we have seen above, this asynchrony has the ability to effectively take the wobble out of a consumer's dynamics capable of averaging across the two patches (McCann 2000). As an example of this, figure 5a shows the dynamic response of a fast–slow parametrization of model system (3.5) after a synchronized perturbation (see figure 5 for parameters). The perturbation here is a modest but sustained increase in both resources carrying capacity, K.
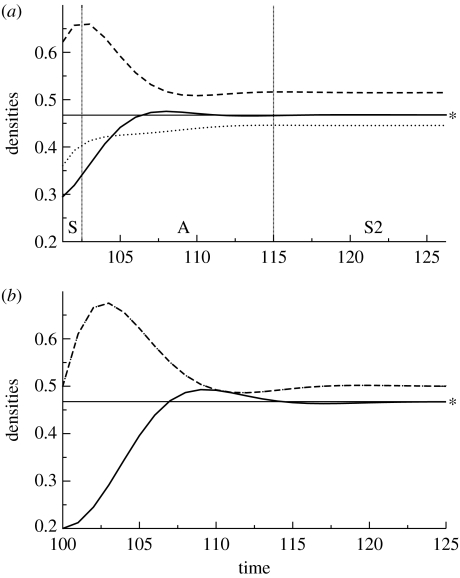
Figure 5.
The densities of a consumer (solid lines) and two resources (R1 (dashed lines) and R2 (dotted lines)) plotted after a perturbation at time 100. The horizontal line indicates the new equilibrium consumer density (asterisk). (a) Asymmetric energy flux through two resources results in weak–strong interaction pathways (parameters: r=1.0; K=1.0; a1=2.50; a2=1.50; α12=0.10; α21=1.1; e=1.0; m=0.50; and ω=0.5). Post-perturbation dynamics starts with resources characterized by synchronous dynamics (region S) followed by asynchronous dynamics (region A) and then back to synchronous but stable dynamics (S2). (b) Symmetric flux through two resources results in the two resources being synchronized throughout the post-perturbation period (r=1.0; K=1.0; a1=2.0; a2=2.0; α12=0.60; α21=0.6; e=1.0; m=0.50; and ω=0.5). Note that the greatest stability (quickest return time) occurs with (a) the asynchrony case as indicated by the consumer density approaching equilibrium faster. Note also that in (b) the completely synchronous case, the consumer, C, overshoots the new equilibrium (asterisk) to a greater extent than in (a) the asynchronous case.
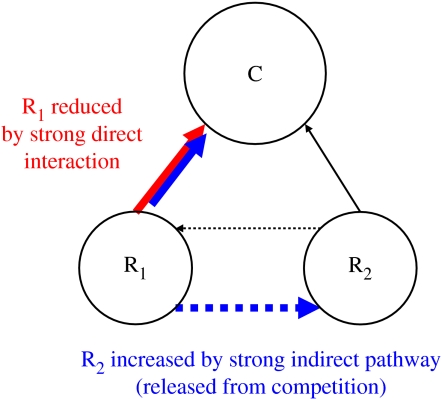
The resources initially both increase in synchrony after the perturbation, delineated by the first region S denoted in figure 5a. This synchrony soon changes to asynchronous resources dynamics (region A in figure 5a). This occurs because any increase in total R is soon met with an increase in C. As C preferentially consumes the best competitor, R1, it obviously reduces R1 (figure 6). As R1 declines, R2 is freed from the competitive grips of R1, and so increases (region A in figure 5a). R2 increases since the direct loss due to increased consumption by C (which is weak) has less negative effect than the indirect gains from the relaxation of the strong competitive pathway (C–R1–R2; figure 6). This is a classic example of indirect interactions outweighing a direct interaction (figure 6). Clearly, if C is reduced instead of increased, a similar set of reasoning drives asynchronous resources dynamics.
Figure 6.
Weak and strong pathways within the simple diamond food-web module. Increased consumers have a strong influence on edible resources (red pathway). This, in turn, drives a strong indirect pathway that releases less edible resources from competition (blue pathway). This differential response requires the appropriate trade-offs such that the more edible resource is also the better competitor.
The key to this asynchronous response and the rapid return to equilibrium in figure 5a is the differential pathways. To highlight this, we choose parameters for system (3.5) that created two symmetric pathways with moderate interaction strengths. This symmetric set of interactions was chosen in such a way that C still received approximately the same amount of potential production from both resources in order to isolate the change in pathway strength alone. Figure 5b shows that, in this case, the two resources stay synchronized for all times after the perturbation. Consistent with recent theory (McCann 2000; Rooney et al. 2006), the fast–slow (also referred to as strong–weak) pathway scenario returns to the equilibrium (line marked by an asterisk in figure 5a,b) more rapidly than the symmetric model scenario (see text in figure 5 for details). Furthermore, the symmetric pathway overshoots the new equilibrium line to a greater extent than the fast–slow pathway (i.e. the C trajectory in figure 5a barely rises above the equilibrium line while the trajectory in figure 5b rises considerably more above the equilibrium line). The fast–slow pathway, therefore, takes the wobble out of the consumer, which averages over the asynchronized resource variance increasing return time and reducing overshoot dynamics.
Above, we have argued that this fast–slow pathway may occur at a variety of spatial scales within the food web (figure 2). If this is the case, the ability for such webs to ‘generate resource asynchrony’ and buffer consumers is large and redundant within the food web. Importantly, much life-history theory also argues that the existence of such fast–slow pathways ought to be ubiquitous (e.g. defensive structures make an organism less competitive but also less edible; Chase 1999). We do not review this extensive literature, but its general result is very consistent with the ubiquitous existence of slow–fast pathways in food webs.
(c) Summary
We have outlined two major theoretical implications of the empirically determined food-web architecture. First, the bird feeder effect allows food webs to adapt to variability in the landscape in such a way as to promote stability and persistence as long as resource patches on the landscape are sufficiently out of phase (i.e. not synchronized). Second, given that abiotic mechanisms may occasionally synchronize resources in space, the existence of fast–slow pathways coupled by mobile adaptive predators readily generates spatial asynchrony in the resources. Taken altogether, we have identified some simple empirically motivated food-web structures that react to variability in a way that promotes balance in a variable world. Thus, we argue here that food webs are constructed such that they operate on the variability, and even produce spatial variability, that in turn buffers adaptive consumers. We now turn to some empirical examples to ask if food webs do, indeed, display (i) the bird feeder effect and (ii) the ability to internally generate asynchrony through fast–slow pathways.
4. Some emerging empirical evidence
(a) Eveleigh's balsam fir food web and the bird feeder effect
In a recent empirical paper, Eveleigh et al. (2007) were able to explicitly test the bird feeder effect within the context of a complex boreal insect food web. In an enormous field effort, Eveleigh et al. (2007) collected and analysed 20 plot-years of interaction data (over 100 000 rearings). This extensive catalogue enabled them to build a series of food-web snapshots over a wide range in budworm densities. This enormous research effort therefore had the data to catalogue how the food web adapts as a function of resource variability. Additionally, the data were gathered from both heterogeneous forest stands (mixed hardwood and softwood) and homogenized forest stands (almost all balsam firs).
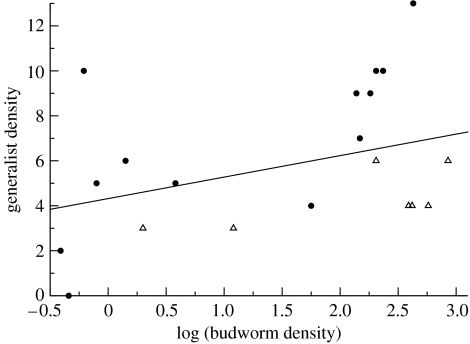
Recalling the theory laid out above, we expect the bird feeder effect within a variable spatial landscape of resources to make the food webs expand and contract according to local resource densities. Furthermore, we expect the effect to be most dramatically driven by higher order consumers in the web. Consistent with this bird feeder effect, Eveleigh et al. (2007) found that the balsam fir food web expanded vertically locally when budworm densities were high and contracted when budworm densities were low. Specifically, higher order generalist predators and parasitoids were responding in space to the outbreaks (figure 7). Curiously, the homogenized plot consistently showed weaker bird feeder effects (the open triangles below the solid circles in figure 7). Thus, these data suggest that human homogenization on the landscape may weaken this stabilizing mechanism. In this case, Eveleigh et al. (2007) found that parasitism rates were higher in the heterogeneous plots, suggesting budworm were being reduced by the onslaught of parasitic diversity.
Figure 7.
The balsam fir food webs response to changing budworm densities. The number of secondary and tertiary generalist parasitoids increase with increasing budworm density. Thus, as with a bird feeder effect, a cascade of higher order parasitoids appear at high budworm densities. Note that the open triangles (homogenized balsam fir plot) tend to lie below the filled circles (heterogeneous stands).
To further experimentally test this result, Eveleigh et al. (2007) then created a localized budworm outbreak. The web before the outbreak was depauperate and truncated, shortly after the localized outbreak the web became more reticulated with higher maximum trophic position. In all cases, it appeared as though secondary and tertiary generalist parasitoids were responsible for the expanding and contracting of the food web. While some of this numerical response of these generalist consumers may have been dynamical in nature, the response of the consumers was so rapid that movement on the landscape must have played a significant role. This is an especially intriguing test of some of the ideas of the theory as this web is not structured by size in the general way suggested above. That is to say that the higher trophic-level parasitoids tend to be smaller than their lower level hosts. Nonetheless, there are still mechanisms that promote their movement on the larger landscape (e.g. chemical cues), and so the theory of higher order food-web adaptability to changing lower level budworm variability remains the case in this empirical example.
(b) Pelagic sub-webs generate asynchronous resource dynamics
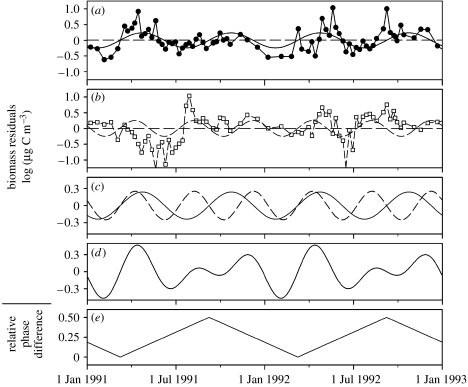
Limnologists have long noted both the synchronization of plankton in early spring followed by the decoupling of edible and relatively inedible plankton in the summer (PEG model of succession; Sommer et al. 1986). In the spring, nutrients sweep in off the landscape and make plentiful conditions for phytoplankton to flourish, the small edible plankton rising the most but other larger less edible plankton also rise (Vasseur et al. 2005). As a result, abiotic conditions readily promote a period of algal synchrony. Consistent with the simple diamond model presented above though, the herbivorous cladoceran density soon responds to these bountiful resource conditions and rises in density. This rise in herbivore density intensifies herbivory, especially on the small more edible phytoplankton (Vasseur et al. 2005). Taken altogether, we have the perfect conditions for asynchrony generation in that we have high consumptive pressure on two competing resources, and the existence of fast–slow pathways (i.e. fast-growing edible algal functional group that is preferentially consumed and a slow growing less edible algal functional group that is weakly consumed). Vasseur et al. (2005) examined 20 years of data in Lake Constance and noted this well-known seasonal succession with spring algal synchronization, followed by algal asynchronization (figure 8).
Figure 8.
Asynchrony generation. Using statistical techniques to decompose time series into underlying periodicities, Vasseur et al. (2005) continuously estimated phase shift in edible and less edible phytoplankton (0 is in phase or synchronous and 0.5 is out of phase or asynchronous). The plankton tend to respond by asynchronizing during the summer after a strong synchronizing event in spring. (a) Edible plankton dynamics; (b) less edible plankton; (c) dominant periodicities of edible and less edible trajectories plotted together; (d) summed dynamics; and (e) estimated phase difference. Adapted from Vasseur et al. (2005).
To more thoroughly examine the mechanisms behind the coherent and compensatory dynamics, Vasseur et al. (2005) examined the 20 years of Lake Constance plankton data by employing a number of sophisticated time-series techniques that allowed them to continuously estimate the degree of synchrony between edible versus less edible plankton in the planktonic sub-web. Vasseur et al. (2005) then plotted both nutrient conditions (soluble reactive phosphorus) and cladoceran density versus degree of synchrony. The results showed a strong relationship such that low phosphorus and high cladoceran density correlated with asynchrony, while high nutrient conditions and low cladoceran density correlated with synchronous dynamics. These are precisely the results one predicts from the fast–slow food-web diamond module (figure 5). In a sense, the spring nutrient pulse ultimately heightens both herbivory and competition later in the season, and this simultaneously strong herbivory and competition generates resource asynchrony (figure 5a).
This example is consistent with ‘asynchrony generation’ within a sub-web, an empirical idea with a long history in limnological work (Sommer et al. 1986). It remains, though, to show that asynchrony generation can occur on larger spatial scales as well. A recent empirical analysis has found a range of bird-switching responses operating on asynchronous invertebrate and fruit dynamics (Carnicer et al. 2008). The strong switching responses documented by these authors leave open the possibility that this is a larger scale example of resource asynchrony generation as the temporal period this unfolds over and appears more rapid than seasonal dynamics alone.
The above theory, which relies so heavily on variability in space, also suggests that it will be fruitful to re-examine existing temporal and spatial data on a variety of resources to more fully understand both synchronous resource dynamics (Hornfeldt 1978) and asynchronous resource dynamics (Carnicer et al. 2008; Owen-Smith & Mills 2008). We have concentrated on the role of weak–strong pathways but other environmental mechanisms (such as differential response to abiotic conditions) may frequently be responsible for generating resource asynchrony. This aspect of asynchrony is firmly part of the theory presented here; we have focused on asynchrony generation as it is an intriguing way systems can respond in the face of synchronizing environmental conditions. Further empirical and experimental work determining patterns in synchrony/asynchrony within trophic levels, and what drives these patterns, will significantly aid the ideas presented here.
5. Discussion
Here, we have synthesized a number of recent theoretical and empirical contributions to suggest that food webs have an adaptable underlying framework that plays a major role in maintaining the persistence of complex interacting assemblages in a naturally variable world. By using organismal traits that scale to body size, we have shown that food webs are constructed of a hump-shaped architecture such that spatially localized lower trophic levels are increasingly coupled by more mobile higher trophic-level organisms. This pattern implies that as we move up food webs, we are in fact increasingly coupling organisms in space (McCann et al. 2005). Importantly, this hump-shaped architecture appears to be invariant, repeating itself at different resolutions within food webs (within habitats, between habitats and between ecosystems). Furthermore, metabolic theory predicts asymmetric energy flux between coupled energy channels at each level of resolution, as the body sizes of organisms occupying coupled energy channels consistently differ (figure 3).
This invariant hump-shaped trophic structure with adaptable apex consumers appears to have important consequences for food-web dynamics. We first looked at the role of stochastic resources on the simple food-web module (i.e. C–R1–R2) that underlies the invariant hump-shaped trophic observation. In a purely stochastic resource model, we found that asynchronous resources in space and time are muted by an adaptable consumer reacting to this variability. More synchronized resources weaken and eventually remove this stabilizing effect because they reduce the ability for an organism to adapt and average over the environment. We then revisited deterministic food-web theory to show that slow (weak) pathways play not only a critical role in deflecting energy away from potentially fast (strong) unstable interactions (McCann et al. 1998) but also the combination of fast–slow pathways readily generate resource asynchrony (McCann 2000). This result is consistent with other fast–slow models containing higher numbers of species that found similar stabilizing results (Post et al. 2000; Rooney et al. 2006). This general theory resonates with MacArthur's suggestion that generalists play a critical buffering role in food webs (MacArthur 1955). Both the theory discussed here and within MacArthur (1955) do not account for the generalism that occurs due to resource switching by life stage. Here, the rapid behavioural mechanism that drives stability no longer necessarily holds. Further work is needed to understand how this different aspect of generalism plays out in whole food webs.
Our empirical work on aquatic food webs and terrestrial soil food webs revealed some strong consistencies across both environments in the food-web architecture. More empirical analysis, though, across a broader range of terrestrial ecosystems is required. Some important recent work has revealed that there are both fundamental similarities and differences between aquatic and terrestrial ecosystems (Cebrian 2004; Cebrian & Latrigure 2004; Shurin et al. 2006). These differences are not inconsistent with our observations here but importantly point out that the magnitude of different pathways can vary considerably between aquatic and terrestrial webs (e.g. detrital). Nonetheless, differences noted in Shurin et al. (2006; body size and growth rates) agree with our arguments above that terrestrial dynamics are probably a slow channel relative to aquatic flux rates.
While we primarily have focused on how this theory works, there are obvious exceptions and omissions that require reconciliation. The above theory does not make any attempt to embed the role of positive interactions in food webs. This is critical, and fortunately recent research has made significant progress in this area (e.g. Bascompte & Jordano 2007). Integration across antagonistic and mutualistic work remains a challenge. Additionally, not all food webs are organized so strictly by size as suggested above (e.g. Lafferty et al. 2006). Insect food webs seem to be an obvious exception to this rule with many higher trophic-level organisms, such as parasitoids, much smaller than their prey. There is clearly a demand for future theory to also more rigorously embed parasites in food webs (Lafferty et al. 2006). Consistent with the general theory discussed here though, Eveleigh et al.'s (2007) empirical example found that adaptability within a parasitoid food web occurred in the higher trophic levels. Another obvious exception comes in the form of large mobile herbivores on the terrestrial landscape. Ungulates, for example, often migrate enormous distances, potentially turning the hump-shaped trophic structure upside down. In a sense, the same pieces of the puzzle that confer stability remain. Here, the large herbivores move across the landscape decoupling themselves from their own resources before depleting them and simultaneously removing themselves from their localized predators before they overconsume the herbivores. Recent work has found that lions appear to employ switching behaviour based on the fluctuations in major herbivore prey, and so here top predators are also adaptively responding on the landscape (Owen-Smith & Mills 2008). Similarly, deBruyn et al. (2004) found that major predators in the St Lawrence River responded on rapid behavioural time scales to a sewage-enriched food web.
Food-web ecology has frequently adopted a static view of empirical food webs. In this paper, we have argued that the food-web change noted by some empiricists (Winemiller 1990) may in fact be extremely important for understanding what sustains ecological networks. Unfortunately, gathering the long-term food-web data to test this prediction is an onerous and slow task. However, ecologists may be able to switch this temporal axis to a spatial axis to explore the influence of variability on food-web dynamics and afford us glimpses into the workings of these amazingly complex entities. To accomplish this, ecologists can examine food-web variability by empirically examining how specific ecosystems, with relatively consistent species assemblages, change across gradients in environmental conditions. These gradients can be natural (e.g. lake size, latitude) or human-driven (e.g. human density). Understanding variability across such gradients may also enable us to begin to predict the consequences of human modification on the structure and functioning of ecological systems (McCann 2007).
It is worth considering the role of human modifications on the landscape within the context of the framework laid out here. The above theory argues that the variation in lower trophic-level species allows for an ecosystem to maintain a range of responses to a variable world while mobile organisms act to integrate across this landscape of species variability, and do so in such a way as to prevent any lower level organisms from monopolizing space and energy. The large organisms thus promote the balance and maintenance of a diverse and variable assemblage of organisms. Given this, it is of concern that much human activity frequently homogenizes resources in space (e.g. agriculture, silviculture) and also removes higher order consumers by harvesting and habitat fragmentation (Pauly et al. 1998; Tylianakis et al. 2007). The synchronization of resources and the removal of the flexible apex consumers therefore remove some of the potent stabilizing forces outlined here. Human modification may be attacking the very aspect of food-web structure that makes it so robust.
It may be that such human actions will be countered by the differential response of fast and slow pathways generating asynchronous variability in prey in space. Here too, though, the human influence frequently is strongly skewing the nature of such fast–slow pathways. As an example, nutrient loading often drives complete dominance by the planktonic web in the form of an algal bloom that shades out littoral production. The system is no longer a balance of littoral and pelagic production but becomes largely a fast pelagic channel process. In this case, the planktonic channel ultimately responds and tends to be relatively low in diversity and dominated by large, inedible blue-green algae. The usually fast pelagic channel is thus changed into a larger, slower, weakly consumed pathway dominated by lower trophic levels. The once persistent diverse pelagic habitat is then transformed into a monoculture of inedible algae, where the fate of primary production is detritus, resulting in increased bacterial decomposition rates. Thus, many aquatic ecosystems with high nutrient loading are now creating dead zones wherein massive bacterial respiration rates remove oxygen from large areas once hospitable to a diverse assemblage of organisms (Moffat 1998). Other examples exist; agricultural systems effectively skew energy towards fast bacterial pathways and away from slower fungal pathways (Hendrix et al. 1986), while Layman et al. (2007) have documented niche width collapse in a top predator coinciding with the homogenization of energy flows following fragmentation. Human modifications may not be just homogenizing variability in space but also appear to be homogenizing production in many ecosystems and, in doing so, slowly decaying the upper trophic structure of ecosystems and their services (Dobson et al. 2006).
It is possible that the much impacted ecosystems may ultimately be stabilized by similar mechanisms to those argued above. As an example, the enhancement of the fast pelagic pathway by nutrient run-off may in turn be stabilized by the development of primary production based on largely inedible, or weakly consumed, phytoplankton (i.e. the pelagic channel becomes composed of weak interactions in such a case). However, under such potentially stable conditions, many species will be held at greatly reduced densities. At this point, the question may turn away from stability and more to ecosystem function. In this particular case, the aquatic ecosystem probably experiences greatly reduced function along some fundamental axes (e.g. large anoxic areas, greatly reduced fish production, reduced zooplankton productivity). The stability we have discussed in this paper does not speak to which system is the most stable, but rather how food-web structure helps maintain nature's diverse assemblages. It is possible, although not examined here, that the repeatable hump-shaped structures discussed create a functional system redundancy that enhances the stability of a complex network over a simple network. If so, biological outcomes such as runaway blue-green algae and bacteria may be the final expression of a defeated ecosystem. Curiously, the fate of most aquatic microcosms, perhaps the ultimate homogenized ecosystem, is a similar detrital and bacterial takeover.
Acknowledgments
We would like to thank Stefano Allesina and Mercedes Pascual for organizing an excellent symposium that allowed us to think about many of the issues addressed here. This research was sponsored by an NSERC discovery grant to K.S.M.
Footnotes
One contribution of 15 to a Theme Issue ‘Food-web assembly and collapse: mathematical models and implications for conservation’.
References
- Bascompte J., Jordano P. Plant–animal mutualistic networks: the architecture of biodiversity. Annu. Rev. Ecol. Evol. Syst. 2007;38:567–593. doi:10.1146/annurev.ecolsys.38.091206.095818 [Google Scholar]
- Brown J., Gillooly J.F., Allen P., Savage V.M., West G.B. Towards a metabolic theory of ecology. Ecology. 2004;85:1771–1789. doi:10.1890/03-9000 [Google Scholar]
- Carnicer J., Abrams P.A., Jordano P. Switching behavior, coexistence and diversification: comparing empirical community-wide evidence with theoretical predictions. Ecol. Letts. 2008;11:802–808. doi: 10.1111/j.1461-0248.2008.01195.x. doi:10.1111/j.1461-0248.2008.01195.x [DOI] [PubMed] [Google Scholar]
- Cebrian J. Role of first-order consumers in ecosystem carbon flow. Ecol. Lett. 2004;7:232–240. doi:10.1111/j.1461-0248.2004.00574.x [Google Scholar]
- Cebrian J., Latrigure J. Patterns of herbivory and decomposition in aquatic and terrestrial ecosystems. Ecol. Monogr. 2004;74:237–259. doi:10.1890/03-4019 [Google Scholar]
- Charnov E. Optimal foraging, the marginal value theorem. Theor. Popul. Biol. 1976;9:129–136. doi: 10.1016/0040-5809(76)90040-x. doi:10.1016/0040-5809(76)90040-X [DOI] [PubMed] [Google Scholar]
- Chase J.M. To grow or reproduce? The role of life history plasticity in food web dynamics. Am. Nat. 1999;154:571–586. doi: 10.1086/303261. doi:10.1086/303261 [DOI] [PubMed] [Google Scholar]
- Chesson J. The estimation and analysis of preference and its relationship to foraging models. Ecology. 1983;64:1297–1304. doi:10.2307/1937838 [Google Scholar]
- Cohen J.E. Princeton University Press; Princeton, NJ: 1978. Food webs and niche space, monographs in population biology. [PubMed] [Google Scholar]
- Cohen J.E., Newman C.M. A stochastic theory of community food webs. I. Models and aggregated data. Proc. R. Soc. B. 1985;224:421–448. doi:10.1098/rspb.1985.0042 [Google Scholar]
- Darwin C.S. J. Murray; London, UK: 1859. The origin of the species. [Google Scholar]
- deBruyn A.M.H., McCann K.S., Rasmussen J.B. Migration supports uneven consumer control in a sewage enriched river food web. J. Anim. Ecol. 2004;73:737–746. doi:10.1111/j.0021-8790.2004.00845.x [Google Scholar]
- Doak D.F.D., Bigger D., Harding E.K., Marvier M.A., O'Malley R.E., Thompson D. The statistical inevitability of stability–diversity relationships in community ecology. Am. Nat. 1998;151:264–276. doi: 10.1086/286117. doi:10.1086/286117 [DOI] [PubMed] [Google Scholar]
- Dobson A.P., et al. Habitat loss, trophic collapse, and the decline of ecosystem services. Ecology. 2006;87:1915–1924. doi: 10.1890/0012-9658(2006)87[1915:hltcat]2.0.co;2. doi:10.1890/0012-9658(2006)87[1915:HLTCAT]2.0.CO;2 [DOI] [PubMed] [Google Scholar]
- Dunne J.A. The network structure of food webs. In: Pascual M., Dunne J.A., editors. Ecological networks: linking structure to dynamics in food webs. Oxford University Press; Oxford, UK: 2006. pp. 27–86. [Google Scholar]
- Dunne J.A., Williams R.J., Martinez N.D., Wood R.A., Erwin D.E. Compilation of network analyses of Cambrian food webs. PLoS Biol. 2008;6:e102. doi: 10.1371/journal.pbio.0060102. doi:10.1371/journal.pbio.0060102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elton C. Methuen; London, UK: 1958. The ecology of invasions by plants and animals. [Google Scholar]
- Emmerson M.C., Raffaelli D.G. Body size, patterns of interaction strength and the stability of a real food web. J. Anim. Ecol. 2004;73:399–409. doi:10.1111/j.0021-8790.2004.00818.x [Google Scholar]
- Eveleigh E.S., et al. Fluctuations in density of an outbreak species drive diversity cascades in food webs. Proc. Natl Acad. Sci. USA. 2007;104:16 976–16 981. doi: 10.1073/pnas.0704301104. doi:10.1073/pnas.0704301104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hebert C.E., Weseloh D.V.C., Idrissi A., Arts A.T., O'Gorman R.O., Gorman O.T., Locke B., Madenjian C.P., Roseman E.F. Restoring piscivorous fish populations in the Laurentian Great Lakes causes seabird dietary change. Ecology. 2008;89:891–897. doi: 10.1890/07-1603.1. doi:10.1890/07-1603.1 [DOI] [PubMed] [Google Scholar]
- Hendrix P.F., Parmelee R.W., Crossley D.A., Coleman D.C., Odum E.P., Groffman P.M. Detritus food webs in conventional and no-tillage agroecosystems. Bioscience. 1986;36:374–380. doi:10.2307/1310259 [Google Scholar]
- Holt R.D. In: Multitrophic interactions. Begon M., Gange A., Brown V., editors. Chapman and Hall; London, UK: 1996. [Google Scholar]
- Holt R.D., Barfield M. Impacts of temporal variation on apparent competition and coexistence in open systems. Context-dependence in plant–herbivore interactions. Oikos. 2003;101:49–58. doi:10.1034/j.1600-0706.2003.12570.x [Google Scholar]
- Hornfeldt B. Synchronous population fluctuations in voles, small game, owls, and tularemia in northern Sweden. Oecologia. 1978;32:141–152. doi: 10.1007/BF00366068. doi:10.1007/BF00366068 [DOI] [PubMed] [Google Scholar]
- Jennings S., Pinnegar J.K., Nicholas V.C., Boon T.W. Weak cross-species relationships between body size and trophic level belie powerful size-based trophic structuring in fish communities. J. Anim. Ecol. 2001;70:934–944. doi:10.1046/j.0021-8790.2001.00552.x [Google Scholar]
- Johnson M.T.J., Agrawal A. The ecological play of predator–prey dynamics in an evolutionary theatre. Trends Ecol. Evol. 2003;18:549–551. doi:10.1016/j.tree.2003.09.001 [Google Scholar]
- Kondoh M. Foraging adaptation and the relationship between food-web complexity and stability. Science. 2003;299:1388–1391. doi: 10.1126/science.1079154. doi:10.1126/science.1079154 [DOI] [PubMed] [Google Scholar]
- Lafferty K.D., Dobson A.P., Kuris A.M. Parasites dominate food web links. Proc. Natl Acad. Sci. USA. 2006;103:11 211–11 216. doi: 10.1073/pnas.0604755103. doi:10.1073/pnas.0604755103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Layman C.A., Quattrochi J.P., Peyer C.M., Allgeier J.E. Niche width collapse in a resilient top predator following ecosystem fragmentation. Ecol. Lett. 2007;10:937–944. doi: 10.1111/j.1461-0248.2007.01087.x. doi:10.1111/j.1461-0248.2007.01087.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levin S.A. Ecosystems and the biosphere as complex adaptive systems. Ecosystems. 1998;1:431–436. doi:10.1007/s100219900037 [Google Scholar]
- MacArthur R.H. Fluctuations of animal populations and a measure of community stability. Ecology. 1955;36:533–536. doi:10.2307/1929601 [Google Scholar]
- MacArthur R.H., Pianka E.R. On the optimal use of a patchy environment. Am. Nat. 1966;100:603–610. doi:10.1086/282454 [Google Scholar]
- Martinez N. Artifacts artifacts or attributes? Effects of resolution on the little rock lake food web. Ecol. Monogr. 1991;61:367–392. doi:10.2307/2937047 [Google Scholar]
- May R. Princeton University Press; Princeton, NJ: 1973. Stability and complexity in model systems. [Google Scholar]
- McCann K.S. The diversity–stability debate. Nature. 2000;405:228–233. doi: 10.1038/35012234. doi:10.1038/35012234 [DOI] [PubMed] [Google Scholar]
- McCann K.S. Protecting biostructure. Nature. 2007;446:29. doi: 10.1038/446029a. doi:10.1038/446029a [DOI] [PubMed] [Google Scholar]
- McCann K.S., Hastings A., Huxel G.R. Weak trophic interactions and the balance of nature. Nature. 1998;395:794–798. doi:10.1038/27427 [Google Scholar]
- McCann K.S., Rasmussen J.R., Umbanhowar J. The dynamics of spatially coupled food webs. Ecol. Lett. 2005;8:513–523. doi: 10.1111/j.1461-0248.2005.00742.x. doi:10.1111/j.1461-0248.2005.00742.x [DOI] [PubMed] [Google Scholar]
- McCauley E., Nisbet R.M., Murdoch W.W., de Roos A.M., Gurney W.S.C. Large-amplitude cycles of Daphnia and its algal prey in enriched environments. Nature. 1999;42:653–656. doi:10.1038/45223 [Google Scholar]
- Moffat A.S. Global nitrogen overload problem grows critical. Science. 1998;279:988–989. doi:10.1126/science.279.5353.988 [Google Scholar]
- Murdoch W.W. Switching in general predators: experiments of predator specificity and stability of prey. Ecol. Monogr. 1969;39:335–354. doi:10.2307/1942352 [Google Scholar]
- Neutel A., Heesterbeek J.A.P., de ruiter P. Stability in real food webs: weak links in long loops. Science. 2002;296:1120–1123. doi: 10.1126/science.1068326. doi:10.1126/science.1068326 [DOI] [PubMed] [Google Scholar]
- Oaten A., Murdoch W.W. Switching, functional response, and stability in predator–prey systems. Am. Nat. 1975;109:299–318. doi:10.1086/282999 [Google Scholar]
- Owen-Smith N., Mills M.G.L. Shifting prey selection generates contrasting herbivore dynamics within a large-mammal predator–prey web. Ecology. 2008;89:1120–1133. doi: 10.1890/07-0970.1. doi:10.1890/07-0970.1 [DOI] [PubMed] [Google Scholar]
- Pauly D., Christensen V., Dalsgaard J., Froese R., Torres F. Fishing down marine food webs. Science. 1998;279:860–863. doi: 10.1126/science.279.5352.860. doi:10.1126/science.279.5352.860 [DOI] [PubMed] [Google Scholar]
- Petchey O., Beckerman A.P., Riede J.O., Warren P.H. Size, foraging and food web structure. Proc. Natl Acad. Sci. USA. 2008;105:4191–4196. doi: 10.1073/pnas.0710672105. doi:10.1073/pnas.0710672105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peters R. Cambridge University Press; Cambridge, UK: 1983. The ecological implications of body size. [Google Scholar]
- Polis G.A. Complex trophic interactions in deserts: an empirical critique of food-web theory. Am. Nat. 1991;138:123. doi:10.1086/285208 [Google Scholar]
- Polis G.A., Winemiller K.O. Chapman and Hall; New York, NY: 1996. Food webs: integration of patterns and dynamics. [Google Scholar]
- Post D., Conners M.E., Goldberg D.S. Prey preference by a top predator and the stability of linked food chains. Ecology. 2000;81:8–14. doi:10.2307/177129 [Google Scholar]
- Rooney N., McCann K.S., Gellner G., Moore J.C. Structural asymmetry and the stability of diverse food webs. Nature. 2006;442:265–269. doi: 10.1038/nature04887. doi:10.1038/nature04887 [DOI] [PubMed] [Google Scholar]
- Rooney N., McCann K.S., Moore J.C. A landscape theory for food web architecture. Ecol. Lett. 2008;11:867–881. doi: 10.1111/j.1461-0248.2008.01193.x. doi:10.1111/j.1461-0248.2008.01193.x [DOI] [PubMed] [Google Scholar]
- Sherr E.B., Sherr B.F. Roles of microbes in pelagic food webs: a revised concept. Limnol. Oceanogr. 1988;33:1225–1227. [Google Scholar]
- Shurin J.B., Druner D.S., Hillebrand H. All wet or dried up? Real differences between aquatic and terrestrial food webs. Proc. R. Soc. B. 2006;273:1–9. doi: 10.1098/rspb.2005.3377. doi:10.1098/rspb.2005.3377 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sommer U., Gliwicz Z.M., Lampert W., Duncan A. PEG-model of seasonal succession of planktonic events in fresh waters. Arch. Hydrobiol. 1986;106:433–471. [Google Scholar]
- Thompson R.M., Townsend C.R. Food web topology varies with spatial scale in a patchy environment. Ecology. 2005;86:1916–1925. doi:10.1890/04-1352 [Google Scholar]
- Tilman D., Lehman C.L., Bristow C.E. Diversity–stability relationships: statistical inevitability or ecological consequence? Am. Nat. 1998;151:277–282. doi: 10.1086/286118. doi:10.1086/286118 [DOI] [PubMed] [Google Scholar]
- Tylianakis J.M., Tscharntke T., Lewis O.T. Habitat modification alters the structure of tropical host–parasitoid food webs. Nature. 2007;455:202–205. doi: 10.1038/nature05429. doi:10.1038/nature05429 [DOI] [PubMed] [Google Scholar]
- Vander Zanden M.J., Vadeboncoeur Y. Fishes as integrators of benthic and pelagic food webs in lakes. Ecology. 2002;83:2152–2161. doi:10.1890/0012-9658(2002)083[2152:FAIOBA]2.0.CO;2 [Google Scholar]
- Vasseur D., Gaedke U., McCann K. A seasonal alteration in compensatory and coherent dynamics occurs in phytoplankton. Oikos. 2005;110:507–514. doi:10.1111/j.0030-1299.2005.14006.x [Google Scholar]
- Williams R.J., Martinez N. Simple rules yield complex food webs. Nature. 2000;404:180–183. doi: 10.1038/35004572. doi:10.1038/35006555 [DOI] [PubMed] [Google Scholar]
- Winemiller K. Spatial and temporal variation in tropical fish trophic networks. Ecol. Monogr. 1990;60:331–367. doi:10.2307/1943061 [Google Scholar]
- Woodward G., Hildrew A.G. Food web structure in riverine landscapes. Freshw. Biol. 2002;47:777–798. doi:10.1046/j.1365-2427.2002.00908.x [Google Scholar]