Micromagnetic study of domain wall dynamics in bit-patterned nanodots

Abstract

Domain wall dynamics in magnetic nanodots is critical to the understanding of the magnetization reversal mechanisms in bit-patterned arrays, the issues of writeablility, data rate maximization, and bit stability. In this work, micromagnetic simulations were carried out to investigate the dynamics of domain walls in disk-shaped nanostructures with large built-in perpendicular anisotropy. Due to the strong demagnetizing effect, the domain wall motion falls into the supercritical regime. A 90° phase shift of the wall velocity is developed due to the finite thicknesses. The mean value of the wall velocity increases as the domain wall propagates away from the center. This induced asymmetry causes the frequency of the wall oscillations to be halved. At large diameters, the wall acceleration deceases and the periodicity is lost. The in-plane magnetization configuration shows that multiple spin wave modes are present. The absence of the coherency in the magnetization orientations causes phase canceling. The out-of-phase motion of neighboring segments reduces the wall acceleration.

INTRODUCTION

The physics of magnetic patterned arrays has attracted significant attention to support the research in bit-patterned medium recording, magnetic random access memories, and magnetic logic applications.^{1, 2, 3, 4, 5, 6, 7, 8, 9, 10} It has been shown that the magnetization switching within the patterned dots can often be characterized by the nucleation of domains at the defects or sites due to edge roughness or grain misalignment, followed by the rapid motion of the domain walls.^{11, 12} Therefore, an understanding of domain wall dynamics is crucial to the description of magnetization switching in nanostructures and is closely related to the issues of writeablility, data rate maximization, and data stability.^{13, 14, 15, 16, 17}

The analytical approach of domain wall dynamics applied to a one-dimensional (1D) bulk system with a Bloch type domain wall has been well established.¹⁸ There exists a critical field H_c=2παM₀, below which the domain wall approaches the static solution asymptotically and above which the domain wall oscillates while propagating. However, extending the analytical approach to the study of domain wall dynamics in the nanodots is difficult. First, the round shape of the nanostructure will cause the domain wall to corrugate.¹⁹ Further, the domain wall in the nanodot is at least two dimensional. Therefore, a wall profile in a simple form of mathematical expression can be hardly obtained. Second, when the diameter of the nanodot becomes large, multiple spin wave modes can be excited along the domain wall, which complicates the phase relations among the spins as the domain wall propagates. In this work, the micromagnetic method was adopted to study the details of domain wall dynamics in nanodots with large perpendicular anisotropy.

MICROMAGNETIC MODEL DETAILS

The nanostructure under investigation is illustrated in Fig. 1. The three-dimensional micromagnetic code of OOMMF (Ref. ²⁰) was used to carry out the simulations. A right circular cylinder is used as a model for a single bit of a patterned medium with a constant thickness of 10 nm and variable diameter d. This medium parameters were chosen consistent with those measured off the (Co∕Pd)₁₀ multilayers reported elsewhere:²¹K_u=5.4×10⁶ erg∕cm³, M_s=420 emu∕cm³, A=3.0×10⁻⁶ erg∕cm, and maximized intergranular exchange coupling (the material is considered to be magnetically continuous). The anisotropy axis was defined to be parallel to the rotation axis of the cylinder. The micromagnetic model element size was chosen to be 2×2×2 nm³ (further subdivisions did not result in quantitative data improvements). No thermal effects are considered. The initial configuration of the magnetization consisted of two equally sized antiparallel domains along the anisotropy axis separated by a linear domain wall. It was from this state we allowed the magnetization to evolve.

Figure 1.

Schematics of a patterned nanodot with a linear domain wall in the middle. The z axis is parallel to the uniaxial anisotropy axis.

RESULTS AND DISCUSSION

Figure 2 shows the evolution of the magnetization orthogonal to the anisotropy axis. The initial 180° domain wall immediately excites background spin waves, superimposed on the domain wall propagation. These background spin waves are initially excited near the domain wall before propagating perpendicular to it in either in-plane direction. When they hit the bit edge boundary, at certain distance, the long wave fronts break into chains of vortices. As energy dissipates away, the transverse wavelength increases and the vortices within the chains merge and annihilate. This dissipation and annihilation process is extremely rapid compared to the propagation of the domain wall.

Figure 2.

In-plane magnetization orientations at (a) 0.0016 ns, (b) 0.013 ns, (c) 0.0357 ns, and (d) 0.0433 ns of simulation time.

The critical field was computed to be 266 Oe based on the parameters used in the simulation. The demagnetization field for nanodot with d=100 nm is 2.68 kOe (3.62 kOe) when it is in multidomain (single domain) state. In Fig. 3a, the evolution of energies and the mean domain wall velocity for the nanodot of d=150 nm are plotted. The domain wall velocity oscillates approximately in phase with the demagnetization energy, and they are 180° out of phase with the anisotropy and exchange energy. In Fig. 3b, the changing of perpendicular component of magnetization evaluated at multiple locations of the same nanodot is illustrated. Curve (a) clearly shows the oscillation of the domain wall, which is consistent with the description of supercritical characteristics. In Fig. 4, the in-plane magnetization orientation within the domain wall are plotted at one period of oscillation of demagnetization energy and wall velocity, clearly showing that the internal configuration of the wall changes during propagation. When demagnetization energy is half way between the maximum and minimum, the spins are aligned along the domain wall (Bloch wall configuration) [Figs. 4(2) and 4(4)]. At demagnetization energy maximum, the spins are perpendicular to the domain wall curvature and pointing to the domain with smaller area [Fig. 4(3)]. At demagnetization energy minimum, the spins are also perpendicular to the domain wall curvature but pointing to the domain with larger area [Figs. 4(1) and 4(5)] (Neel wall configuration). If a localized coordinate system is placed at the middle of the domain wall with x axis pointing to the smaller domain, it is found that the maximum wall velocity occurred when the azimuthal angle φ(t) is close to 0 instead of π∕2, as in the case of 1D bulk system. This phase shift is caused by the finite thickness of the nanodot, in which Neel type of domain wall is more energetically favorable.²² Also, as the domain wall propagates away from the center, the domains are no longer symmetric. From Figs. 4(1)–4(5), it can be observed that it takes a full rotation to fulfill a period of oscillation as opposed to a half rotation in the 1D bulk case. As a result, the frequency of the wall velocity oscillation is halved. In addition, the propagation of the domain wall increases the demagnetization field within the nanodot, rendering both the oscillation period and the mean value of the domain wall velocity increase as domain wall propagates [Fig. 3a], which differs from the bulk case.¹⁸

Figure 3.

Evolution of (a) energies and domain wall velocity and (b) M_z evaluated at multiple locations as functions of simulation time.

Figure 4.

(a) wall velocity and energies within one period of oscillation. [(1)–(5)] Spin configurations within the domain wall evaluated at the instances indicated in (a). d=150 nm. (The displaying lattice is much greater than the computation lattice for clearer presentation.)

In Fig. 5, the mean domain wall velocity for nanodots with d=100, 150, 300, and 500 nm are plotted. As d increases, the acceleration of the domain wall decreases and the periodicity is obscured. If the in-plane magnetization configuration at a wall velocity maximum within one period oscillation is plotted for d=150 nm and d=300 nm, as in Figs. 6a, 6b, the magnetization precesses coherently in the smaller dot while the phase information among the spins of the larger dot is complex. In Fig. 6c, the in-plane magnetization both parallel and perpendicular to the S coordinate along the domain wall is plotted together with its Fourier transformation. For d=150 nm nanodot, the magnetization components are almost uniform. For d=300 nm nanodot, two faster precession modes are observed at each end of the domain wall, while a much slower precession is seen in the middle. Although fast Fourier transform (FFT) cannot fully represent spin wave modes within the domain wall due to the limited length and the possible nonlinearities, it does show that for d=300 nm, complex frequency components exist. If the spins within the domain walls are considered as 1D system in the S coordinate, for nanodots with greater diameter d, the multiple modes of spin waves within the domain wall mix the phase relationships. The overall velocity loses periodicity due to phase canceling among the spins. The out-of-phase motion of the neighboring segments of the domain wall produces drag that inhibits the wall’s acceleration.

Figure 5.

Domain wall velocity as functions of simulated time for d=100, 150, 300, and 500 nm. The inset shows that, for d=300 nm, after certain time instances, the exchange, anisotropy, and demagnetization energy regain the periodicities.

Figure 6.

In-plane magnetization configurations along the domain wall for (a) d=150 nm and (b) d=300 nm nanodots. (c) The parallel and perpendicular in-plane magnetization along the domain wall and their FFTs for d=150 nm and d=300 nm.

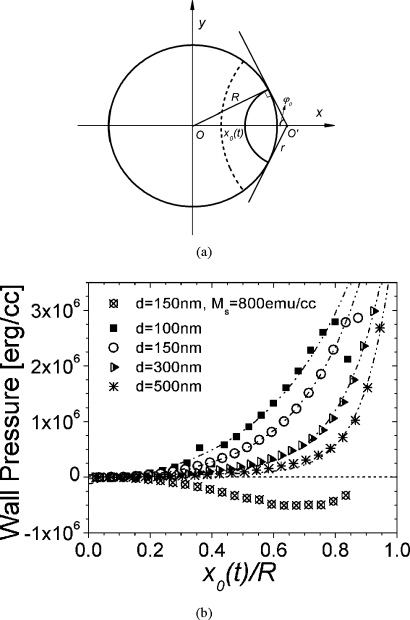
The driving force and the acceleration of the domain wall were further studied by computing the energy differences as the domain wall propagates. The domain wall was modeled as circular and propagates strictly along the x axis. Each end of the domain wall intercepts the boundary of the nanodot and is perpendicular to the edge. This is due to that, from a very local point of view, the spins on either side of the domain wall near the edge should experience symmetry. Under this assumption, as domain wall propagates, the center O^′ and the radius r of the domain wall change [Fig. 7a]. If x₀ is the position of domain wall on the x axis and R is the radius of the nanodot, then $r=\left(R^2-x_0^2\right)∕2x_0$ and ${\phi }_0=\arctan \left[2R{x}_0∕\left(R^2-x_0^2\right)\right]$. The total energy density can be expressed as E=E_a+E_ex+E_d=K sin²(θ)+A(∇θ)²+E_d.

Figure 7.

(a) Schematics of the circular domain wall. (b) Wall pressure as a function of reduced wall position for d=100, 150, 300, and 500 nm (M_s=420 emu∕cc) and d=150 nm (M_s=800 emu∕cc).

Here we strip out the oscillations in the wall velocity and only consider when the spins are aligned along the domain wall (Bloch type wall), which corresponds to the midpoint (average value) of the wall velocity. By assuming the 1D analytical profile θ=2 arctan{exp[a(r−r^′)∕Δ]}, where Δ is the domain wall width, r^′ is the radius in the cylindrical coordinate originated at O^′, and a is a proportional constant.

The anisotropy energy is then equal to

$$W_a=\int E_{a}dv=h{\int }_{-{\phi }_0}^{{\phi }_0}d\phi {\int }_{r-\Delta ∕2}^{r+\Delta ∕2}K{\text{sin}}^2\theta r^{\prime }d{r}^{\prime },$$ (1)

where h is the thickness of the nanodot. Thus, we get

$$W_a=8Kh{\phi }_0{\int }_{r-\Delta ∕2}^{r+\Delta ∕2}\frac{e^{2a\left(r-r^{\prime }\right)∕\Delta }}{{\left[1+e^{2a\left(r-r^{\prime }\right)∕\Delta }\right]}^2}{r}^{\prime }d{r}^{\prime }.$$ (2)

Let y=exp[(2a(r−r^′))∕Δ], then dr^′=−(Δ∕2ay)dy and r^′=r−(Δ∕2a)ln y.

Substituting the above equation into Eq. 2, we obtain

$$W_a=8Kh{\phi }_0\left[{\int }_{e^{-a}}^{e^a}\frac{\Delta }{2a}\frac{r}{{\left(1+y\right)}^2}dy-{\int }_{e^{-a}}^{e^a}\frac{{\Delta }^2}{4a^2}\frac{1}{{\left(1+y\right)}^2}\text{ln}ydy\right].$$ (3)

Carrying out the integral, we can express the anisotropy as

$$W_a=\frac{4Khr\Delta {\phi }_0}{a}\left(\frac{e^a-e^{-a}}{e^a+e^{-a}+2}\right)-\frac{2Kh{\Delta }^2{\phi }_0}{a^2}\left[a+\text{ln}\left(\frac{1+e^{-a}}{1+e^a}\right)\right].$$ (4)

For exchange energy,

$$E_{\text{ex}}=A{\left(\nabla \theta \right)}^2=A{\left(\frac{\partial \theta }{\partial r^{\prime }}\right)}^2+A\frac{{\text{sin}}^2\theta }{r^{\prime 2}}.$$ (5)

Then,

$$W_{\text{ex}}=\int E_{\text{ex}}dv=h{\int }_{-{\phi }_0}^{{\phi }_0}d\phi {\int }_{r-\Delta ∕2}^{r+\Delta ∕2}\left[A{\left(\frac{\partial \theta }{\partial r^{\prime }}\right)}^2+A\frac{{\text{sin}}^2\theta }{r^{\prime 2}}\right]r^{\prime }d{r}^{\prime }.$$ (6)

Similarly, we get

$$W_{\text{ex}}=\frac{4Ahra{\phi }_0}{\Delta }\left(\frac{e^a-e^{-a}}{e^a+e^{-a}+2}\right)-2Ah{\phi }_0\left[a+\text{ln}\left(\frac{1+e^{-a}}{1+e^a}\right)\right]+\frac{4Ah\Delta }{a}{\int }_{e^{-a}}^{e^a}\frac{1}{\left(1+y^2\right)\left(r-\frac{\Delta }{2a}\text{ln}y\right)}dy.$$ (7)

The magnetostatic energy was determined by the method described in Refs. ^{20, 23} The integral in Eq. 7 was also evaluated numerically. Wall pressure is expressed as P=(1∕lh)(∂W∕∂r^′), where l(t) is the domain wall length. When x(t) approaches R, r becomes increasingly small. The denominator in Eq. 7 can be singular. Also, at small r, W_ex increases significantly due to the rapid increase in domain wall curvature. At these situations, the circular domain wall assumption may no longer hold since the domain wall would deform to release the large exchange energy. By removing these points from the evaluations, the domain wall pressure as a function of reduced domain wall position x(t)∕R is plotted in Fig. 7b. For nanodots with saturation magnetization M_s=420 emu∕cc, the wall pressure increases as the domain wall travels toward the edge; this holds for the nanostructures under study. As d increases, the pressure decreases, consistent with the decrease in wall acceleration rate shown in Fig. 5. If a nanodot has M_s=800 emu∕cc, the wall pressure is strictly negative. Since P should be odd in x(t), the original domain wall position is a stable state at the bottom of a potential well. The wall pressure is the restoring force that brings the domain wall back to the central position if it is perturbed away from this state. Micromagnetic simulation of the domain wall dynamics of a nanodot with d=150 nm and M_s=800 emu∕cc shows that the domain wall is of Neel type all the time and the precession of the spins around the anisotropy axis is suppressed by the large additional magnetostatic energy of deviations from the Neel wall configuration. The domain wall moves with low velocity, stopped at particular location on positive x axis, and travels back to the origin.

SUMMARY

The domain wall dynamics in magnetic nanostructures were studied by micromagnetic simulations. It was found that the domain wall velocity oscillates in phase with the demagnetization energy and they are about 180° out of phase with the anisotropy and exchange energy. As the diameter of the nanodot increases, the wall acceleration decreases and the periodicity is lost. Multimode excitations of spin waves along the domain wall may cause phase canceling and out-of-phase movement of the neighboring segments drags the wall propagation. The decrease in energy gain as the diameter increases may also account for the decrease in wall accelerations.