Abstract
With an increasing interest in RNA therapeutics and for targeting RNA to treat disease, there is a need for the tools used in protein-based drug design, particularly DOCKing algorithms, to be extended or adapted for nucleic acids. Here, we have compiled a test set of RNA–ligand complexes to validate the ability of the DOCK suite of programs to successfully recreate experimentally determined binding poses. With the optimized parameters and a minimal scoring function, 70% of the test set with less than seven rotatable ligand bonds and 26% of the test set with less than 13 rotatable bonds can be successfully recreated within 2 Å heavy-atom RMSD. When DOCKed conformations are rescored with the implicit solvent models AMBER generalized Born with solvent-accessible surface area (GB/SA) and Poisson–Boltzmann with solvent-accessible surface area (PB/SA) in combination with explicit water molecules and sodium counterions, the success rate increases to 80% with PB/SA for less than seven rotatable bonds and 58% with AMBER GB/SA and 47% with PB/SA for less than 13 rotatable bonds. These results indicate that DOCK can indeed be useful for structure-based drug design aimed at RNA. Our studies also suggest that RNA-directed ligands often differ from typical protein–ligand complexes in their electrostatic properties, but these differences can be accommodated through the choice of potential function. In addition, in the course of the study, we explore a variety of newly added DOCK functions, demonstrating the ease with which new functions can be added to address new scientific questions.
Keywords: scoring functions, structure-based drug design, RNA DOCKing, binding mode prediction, validation
INTRODUCTION
In the past few years, knowledge of the role of RNA in cellular processes has greatly expanded. No longer is RNA known simply for transporting genetic information from the nucleus to the cytoplasm for translation. Rather, it has been shown to be an integral part of many biological processes. For example, in ribosomes, RNA has been shown to be responsible for a wide range of functions including catalyzing the formation of nascent peptide bonds (Polacek and Mankin 2005; Frank and Spahn 2006). Other RNA molecules, like TAR from HIV and bacterial riboswitches, recruit and bind proteins to regulate reproduction of the HIV genome and the production of various processes, respectively (Frankel and Young 1998; Bannwarth and Gatignol 2005; Tucker and Breaker 2005). These and other RNA–protein interactions are critical for cellular function and thus present potential drug targets.
Several drug design efforts for targeting RNA have already been attempted with various levels of success (see, for example, Johansson et al. 2005; Mayer and James 2005; Renner et al. 2005; Yu et al. 2005; Mayer et al. 2006; Nakatani et al. 2006). With the increasing evidence of the importance of RNA in regulation of the cell, these efforts will increase as well. As a result, there is a need for the same tools that are used in drug design for protein targets, in particular DOCKing algorithms, to be adapted and extended for nucleic acids. Some other DOCKing algorithms have already been adapted for fast screening of small molecules against RNA targets (Filikov et al. 2000; Detering and Varani 2004; Morley and Afshar 2004; Pfeffer and Gohlke 2007; Guilbert and James 2008). Previous studies suggest that poor modeling of the highly localized charges in the polyanionic RNA targets through both the scoring function and the estimation of charge may limit the success of DOCKing algorithms (Lind et al. 2002; Detering and Varani 2004). The newest release of the DOCK suite of programs, version 6, is ideally suited to address the issues for targeting RNA using physics-based scoring functions.
The release of DOCK, version 6, is an important extension of previous versions of the code. Version 5 was a reimplementation of version 4 algorithms in a modular, extendable format (Moustakas et al. 2006). This newest release is a direct application of that extensibility with the addition of a number of new features, including DOCK 3.5 scoring, Hawkins–Cramer–Truhlar (HCT) generalized Born with solvent-accessible surface area (GB/SA) solvation scoring with optional salt screening, Poisson–Boltzmann with solvent-accessible surface area (PB/SA) solvation scoring, and AMBER molecular mechanics with GB/SA solvation scoring and optional receptor flexibility. All of these new features have been added to the basic core of the original DOCKing code. In this paper, we will focus on the newly implemented AMBER GB/SA and PB/SA scoring functions in addition to the previously available Grid Score; DOCK 3.5 scoring and HCT GB/SA scoring will be described elsewhere.
AMBER Score implements molecular mechanics GB/SA simulations with the traditional all-atom AMBER force fields and the generalized AMBER force field (Wang et al. 2004; Case et al. 2005). This method calculates the energy terms for the entire AMBER force field, including bond, angle, and dihedral terms, as well as Coulomb's Law and the Lennard-Jones potential for the ligand, receptor, and complex. The solvation energy can be calculated using one of several generalized Born (GB) solvation models. The surface area term is derived using a fast linear combination of pairwise overlap (LCPO) algorithm (Weiser et al. 1999). Because the internal energy is calculated, a full thermodynamic cycle is employed (i.e., Score = Ecomplex – [Ereceptor + Eligand]). Minimization via the conjugate gradient method is also available in lieu of the simplex minimizer used with other scoring functions. In addition, Langevin molecular dynamics (MD) simulations at constant temperature can be performed. As a result of both the new minimizer and the molecular dynamics capabilities, the AMBER Score function now allows for both ligand and receptor flexibility during scoring.
PB/SA is an implicit solvent model that uses the Poisson–Boltzmann equation to account for the hydrophilic effect on electrostatic screening and the exposed surface area of the complex as an approximation of the hydrophobic effect. In DOCK 6, the van der Waals (VDW) component of the scoring function is computed between the ligand and receptor using a grid-based form of the Lennard-Jones potential as implemented in the Grid Score from previous versions (Moustakas et al. 2006). For the electrostatic and surface area portion of the energy function, the Zap Tool Kit from OpenEye has been employed. ZAP uses Gaussian-based maps, which preserves the speed of grid-based solutions to PB but avoids the pitfalls of discrete dielectrics (Grant et al. 2001).
There have been several studies published that explore DOCKing libraries of small molecules to RNA targets (Filikov et al. 2000; Lind et al. 2002; Detering and Varani 2004; Morley and Afshar 2004; Pfeffer and Gohlke 2007; Guilbert and James 2008). As in this prior work, we have developed a structure-based test set of both X-ray crystallographic and NMR structures of ligand–RNA complexes, which was used to optimize the sampling methods and compare various scoring functions. A combination of optimized ligand sampling and more advanced scoring functions has vastly improved DOCK's ability to predict binding poses for RNA.
RESULTS
Designing the structure-based test set
The initial structure-based test set of 70 complexes was compiled from coordinates deposited in the Protein Data Bank (see Table 1; Materials and Methods). We included aminoglycosides in our test set because they are an important class of RNA binders. However, as a result of these large, floppy molecules, the number of rotatable bonds in our test set covered a very wide range. We examined the ability of DOCK to reproduce the experimental binding pose within 2 Å heavy-atom RMSD with flexible ligand DOCKing as well as the cumulative average time of the calculations (Fig. 1). The success rate dropped off dramatically from 100% after three rotatable bonds and then leveled off just under 20% after 12 bonds. However, when looking at the average length of the calculation, the less floppy molecules' time increased relatively linearly with the number of rotatable bonds, whereas the additional sampling required for ligands with more than 12 rotatable bonds results in an increase that was greater than linear. Because the length of time was so much greater for the larger molecules, we chose to focus on the subset of the test set with less than 13 rotatable bonds (L13, total of 38 complexes), which is a reasonable limit for current sampling strategies.
TABLE 1.
List of PDB codes for all RNA–ligand complexes in test set
FIGURE 1.
Effect of number of rotatable bonds on DOCKing success rate (●) (defined as the percent of test set with best scoring pose reproducing the experimental structures with 2 Å heavy-atom RMSD) and average length of DOCKing calculation (○) using sampling parameters optimized for proteins in DOCK 5.
Modification and optimization of ligand sampling algorithms
DOCK 6 uses a sampling algorithm called anchor-and-grow to flexibly build ligands into the active site of the biomolecular target (Fig. 2). In anchor-and-grow, the largest rigid portion of the ligand (anchor) is identified and oriented in the active site. The flexible portions of the ligand are then systematically grown from the anchor, clustering at each layer of growth to maximize geometric diversity, until a full molecule is formed. Previous studies indicated that this clustering-based algorithm could be improved by modifying the number and quality of anchors and layers to be brought to the next stage of growth (Moustakas et al. 2006). To address this problem, we modified the sampling algorithm by softening the VDW interaction energy during the sampling procedure and by ranking only, skipping clustering, when layers are selected for the next stage of growth (see Materials and Methods for more details). We hypothesize these modifications, which we term the ranking-based sampling algorithm, guide the sampling algorithm to identify the correct pose, while avoiding other traps on the surface of the receptor. We then reoptimized the sampling parameters for the ranking-based algorithm to obtain maximal success rates, where success is defined as the highest ranking pose being within 2.0 Å RMSD of the experimentally determined structure. Both the clustering-based and ranking-based sampling algorithms are included in the DOCK 6 code base.
FIGURE 2.
Diagram identifying rigid anchor (Layer 1) and flexible layers for growth.
To reduce the length of the calculation, we then applied a bump filter, which quickly filters anchor orientations and layer growths with exceptionally high clashes with the receptor. Improvements to where and when the clash checking occurs resulted in a useful restriction of the search (see Modification of bump filter in Materials and Methods). By modification and optimization of the sampling algorithm in conjunction with the bump filter, for the L13 test set we improved success rates and length of calculation from 18% (7/38) in 32 min to 26% (10/38) in 16 min.
In drug design efforts targeting proteins, the number of rotatable bonds in the ligand is typically limited to 6–10 to reduce the loss of entropy upon binding and to increase the possibility that the molecule will be bioavailable (Lipinski 2000; Wunberg et al. 2006). In addition, a preliminary analysis of ligands that were unable to be reDOCKed indicated that there was a sharp decrease in success rate for ligands with less than seven rotatable bonds (Fig. 3A). Therefore, we subdivided the L13 subset into a set including only those compounds with less than seven rotatable bonds (L7, total of 10 complexes). With the modification and optimization of the sampling algorithm in conjunction with the bump filter for the L7 test set, we were able to increase the success rate from 60% (6/10) to 70% (7/10). There was no significant change for the average length of the calculation (5 min) between either of the sampling methods.
FIGURE 3.
Analysis of reDOCKing and rescoring successes and failures. Successes (striped) and failures (open) are compared for DOCKing using the ranking-based sampling method with Grid Score and receptor in vacuum as (A) a function of the number of rotatable ligand bonds or (B) formal charge of the ligand. (C) Cumulative success rates for Gasteiger (▲), AM1BCC (▼), and RESP (■) charge models are compared as a function of the number of rotatable bonds for the AMBER score using the clustering-based sampling method with explicit water molecules and counterions. (D) Success rates for Gasteiger (horizontal stripes), AM1BCC (diagonal stripes), and RESP (solid) charge models are compared as a function of the ligand formal charge for the AMBER rescoring methodology. Success is defined by the top-scoring pose being within 2 Å heavy-atom RMSD from the experimental structure.
Examination of ensemble of generated orientations
To explore the variety of conformations generated by each sampling method, we also looked at the entire list of conformations that were generated by both the clustering- and ranking-based sampling algorithms. The more advanced scoring functions now available in DOCK take a nontrivial amount of processor time to score even a single pose. We were also, therefore, interested in determining if the sampling algorithm generated conformations close to the experimental orientation, regardless of how the conformation scored, and, thus, how many ranked conformations would need to be rescored to access the experimental conformation. Finally, we compared the effect of reDOCKing of Gasteiger–Hückel, AM1-BCC, and RESP methods for computing ligand charges as well as use of explicit water molecules and counterions.
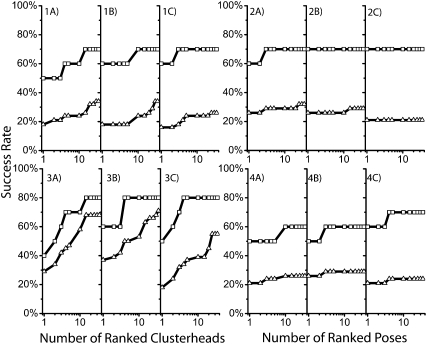
First, we examined results obtained without explicit waters or ions. For the clustering-based method, we first looked at the highest-ranking poses. For the various charge models, the highest success rate was 60% (6/10) for the L7 test set (AM1-BCC and RESP) and 18% (7/38) (Gasteiger–Hückel and AM1-BCC) for the L13 test set (Fig. 4, 1A–1C). If we look at all of the conformations generated, the success rate improves, reaching a maximum of 70% (7/10) (all three charge models) for the L7 set and 34% (13/38) (Gasteiger–Hückel and AM1-BCC) for the L13 set. For the ranking-based sampling method, the success rate for the best-scoring pose is 70% (7/10) for the L7 test set (AM1-BCC and RESP) and 26% (12/38) for the L13 test set (Gasteiger–Hückel) (Fig. 4, 2A–2C). While these rates (70%/26% versus 60%/18%) are better than the clustering-based sampling method, the range of conformations generated was less diverse. Here, the success rates reach a maximum at 70% (7/10) for the L7 test set (all charge models) and 32% (12/38) (Gasteiger–Hückel) for the L13 test set. We expected this result, as the ranking-based method is designed to enrich for orientations with similar scores that are typically close in Cartesian space, whereas the clustering-based algorithm is designed to enrich for diversity.
FIGURE 4.
Exploration of entire list of generated conformations. Success is defined as any pose in the cumulative list being within 2 Å heavy-atom RMSD from the experimental structure. (1A–4A) Gasteiger–Hückel, (1B–4B) AM1-BCC, and (1C–4C) RESP ligand charge models are compared for each analysis. (1) Cumulative success rates of clusterheads (lowest-scoring member of each cluster) for clustering-based sampling methods with receptor in vacuum. (2) Cumulative success rates for ranked list of conformations for ranking-based sampling method with receptor in vacuum. (3) Cumulative success rates of clusterheads for clustering-based sampling methods with the receptor plus explicit water molecules and counterions. (4) Cumulative success rates for ranked list of conformations for ranking-based sampling method with the receptor plus explicit water molecules and counterions. Test set is divided into less than seven (□) and less than 13 (△) rotatable bonds.
Further analysis of ligands that were unable to be DOCKed correlated with ligands in the test set with a positive formal charge (Fig. 3B). We hypothesized that the naked charges on the backbone of the RNA targets were creating artificial energy wells that were being scored as false positives, even with the more advanced solvation models. To address the issue, we added sodium counterions to neutralize the backbone charge and two shells of explicit water molecules to shield the charges. We then repeated the comparison of the two sampling methods (Fig. 4, 3A–3C, 4A–4C). Because the active sites were more occluded with the addition of the explicit water molecules and counterions, the bump filter removed too many conformations during DOCK runs and was not used.
With the clustering-based algorithm, the success rate for the highest-ranking pose stayed at 60% (6/10) for the L7 test set (AM1-BCC) and improved to 37% (14/38) for the L13 test set (AM1-BCC). In addition, for all conformations generated, there is an improvement in the success rate with fewer conformations for all three ligand charge models for the clustering-based algorithm, reaching a maximum of 80% (8/10) (all charge models) for the L7 set and 71% (27/38) (AM1-BCC) for the L13 test set. There was some, less dramatic improvement in sampling for the ranking-based algorithm as well. Finally, we compared whether the increase in success rate for the clustering-based algorithm for the L13 test was a subset of the successes from the vacuum calculations (Table 2). As expected, all but one of the vacuum calculation successes were maintained in the water plus counterion calculation successes.
TABLE 2.
Analysis of changes in success due to scoring function
The results from the clustering-based algorithm suggest that the sampling algorithm is sufficient to identify the experimental orientations for the L7 test set, but the scoring function has problems properly ranking these orientations. For the L13 test set, there is a need to improve the sampling algorithm as well as the scoring function to ensure the experimental orientation is sampled as well as scored properly. The ranking-based algorithm performs better than the clustering-based algorithm for top-ranked poses, but still needs improvement in both sampling and scoring.
Comparison to protein test set
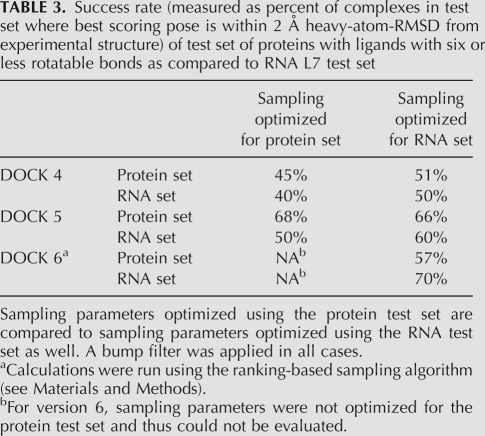
Previous studies of the DOCK algorithms have explored the ability to predict ligand orientation with proteins (Moustakas et al. 2006). Because the previous protein test set was restricted to ligands with seven or less rotatable bonds and performed without explicit waters or counterions, we compared the success rates of the L7 RNA test set with the receptor in vacuum to the success rates of a subset of the protein test set with less than six rotatable bonds (101 complexes). Also, because the sampling parameters are slightly different for proteins and for RNA, we compared how the success rate for each test set performed using each set of sampling parameters (Table 3). In DOCK versions 4 and 5 (clustering-based algorithm), the protein test set success rates were better than RNA success rates. This result was expected as the number of complexes in the protein test set is much higher and more diverse, thus giving less emphasis to any one particular failure or fold class. For version 6 (ranking-based sampling algorithm), the RNA test set success rate was better than the protein test set. This result may not be surprising as the ranking-based sampling method was optimized specifically for RNA targets.
TABLE 3.
Success rate (measured as percent of complexes in test set where best scoring pose is within 2 Å heavy-atom-RMSD from experimental structure) of test set of proteins with ligands with six or less rotatable bonds as compared to RNA L7 test set
We also compared the diversity of generated conformations for both proteins and RNA targets for the clustering-based algorithm (Fig. 5). As expected from the success rate based on the top-scoring conformation, the RNA conformational ensemble does not generate as diverse a set as for proteins when the standard receptor preparation is used for sampling. However, when the counterion-solvent preparation is used, the success rate for the ensemble of conformations approaches that of the protein set. Because the same sampling method was used in each case, these results indicate that the counterions and explicit solvent are critical for properly modeling the energy landscape for RNA targets.
FIGURE 5.
Comparison of the success rates for reDOCKing of generated conformational ensembles for protein (closed symbols) and RNA test sets (open symbols). Success is defined as any pose in the cumulative list being within 2 Å heavy-atom RMSD from the experimental structure. All ligands have six or less rotatable bonds and AM1-BCC partial charges. Both sets were DOCKed using the clustering-based sampling algorithm. The protein test set (●) was DOCKed with receptors in a vacuum. The RNA test set was DOCKed both with receptors in a vacuum (□) and with two shells of explicit water molecules plus sodium counterions (◇).
Rescoring ensembles of generated orientations
As a first comparison, we rescored just the best-scoring pose using AMBER GB/SA and PB/SA with minimization for both the clustering- and ranking-based sampling algorithms. There was no change in the success rate for the test set, indicating that simply minimizing and rescoring with a more advanced scoring function does not rescue bad poses. However, in all members of the test set for all charge models, the interaction energy between the ligand and receptor changes became less negative in the vast majority of cases. This result was expected as, by design, both the AMBER GB/SA and PB/SA scoring functions are more sophisticated in shielding electrostatics than Grid Score.
Next, we explored rescoring all poses generated with the AMBER GB/SA Score. For the ranking-based clustering algorithm, there was minimal change in the success rate, regardless of the number of poses rescored (data not shown). This result was not surprising, as the conformational ensemble for the rankings was less geometrically diverse than for the clustering-based algorithm. For the clustering-based algorithm using receptors in a vacuum, the success rate did not improve for any of the charge models regardless of how many poses were rescored. In fact, the more poses that were rescored, the worse the success rate became, emphasizing once again that explicit waters and counterions were critical for properly modeling the energy landscape of RNA targets, even in the presence of more sophisticated implicit water models.
For receptors with explicit waters and counterions, we first compared minimizing the ligand alone using the conjugate gradient method while the receptor was kept frozen. The average length of the rescoring calculation increased slightly from 17 to 21 min per complex for the L13 test set. The success rate improved quickly as more conformations were rescored, achieving a converged success rate of 50% (5/10) (Gasteiger and RESP) for the L7 test set and 42% (16/38) (Gasteiger) for the L13 test set.
Because there was some improvement in the success rate with minimization only, we also examined using molecular dynamics in combination with minimization of the ligand, keeping the receptor rigid. Here, the length of the calculation increased significantly from 75 to 112 min per calculation for the L13 test set. However, as with the minimization-only protocol, success rates converged at 50% (5/10) (RESP) for the L7 test set. More impressively, success rates converged at 58% (22/38) (Gasteiger) for the L13 test set.
We next examined the effect of allowing portions of the receptor to move during rescoring. We compared allowing receptor residues from 1 to 7 Å of the spheres to move to the ligand alone (Fig. 6). As the number of flexible residues increased, the trend indicated an initial improvement in success rates for a distance threshold ≤2 Å with greater thresholds yielding progressively worse rates. Using the 2 Å distance as representative, the success rates once again converged at 50% (5/10) (Gasteiger) for the L7 test set and 50% (19/38) (Gasteiger) for the L13 test set when the minimization protocol was applied. For the minimization/MD/minimization (MDM) protocol (see AMBER GB/SA scoring function in Materials and Methods), the success rates once again converged at 50% for both the L7 (RESP) and L13 (Gasteiger) test sets (Table 4). Here, the addition of solvent and counterions increased the length of the calculation from 27 to 46 min for the minimization protocol and from 106 to 191 min for the MD protocol for the L13 test set. Greater radii yielded progressively worse success rates and longer calculation times. We hypothesize that the decrease in success rate as increasing amounts of the receptor are allowed to move indicates that the experimental structure is not fully equilibrated prior to DOCKing studies.
FIGURE 6.
Effect of allowing increasing portions of receptor to move using the MDM protocol during rescoring with AMBER GB/SA Score. Ligand alone (0 Å) is compared to the ligand plus all residues within 1–7 Å of the spheres. Ligand charge models Gasteiger–Hückel (—), AM1-BCC (–), and RESP (···) were compared.
TABLE 4.
Success rate (measured as percent of complexes in test set where best scoring pose is within 2 Å heavy-atom RMSD from experimental structure)
Using the 2 Å cutoff as a model, we also calculated the heavy-atom RMSD of receptor residues within 13 Å of the ligand to verify whether the lower success rates were due to the receptor moving even if the ligand was DOCKed properly. In all cases, the receptor moved <1 Å heavy-atom RMSD from the experimental structure. In addition, in all cases, the receptor residues moved about the same amount for all poses in the ensemble and regardless of the ligand charge models. However, as the radius around the receptor was increased, the RMSD increased as well, but only in structures solved by NMR. We hypothesize the success rates when the receptor is allowed to move in increasing amounts would improve if the experimental structure were fully equilibrated before DOCKing.
Finally, we explored rescoring all poses generated with PB/SA Score. As for the AMBER Score, there was only minimal improvement in the success rate for the ranking-based clustering algorithm, regardless of the number of poses rescored as well as a decrease in the success rate for the clustering-based algorithm for receptors in vacuum (data not shown). However, for receptors with explicit water and counterions, success rates improved for all test sets with all charge models, converging at 80% (8/10) (AM1-BCC and RESP) for the L7 test set and at 47% (18/37) (Gasteiger and AM1-BCC) for the L13 test sets (Table 4). There was only a small effect on the length of the rescoring calculation, increasing from 1.8 to 2.2 min for the L13 test set.
In an attempt to explain the differences in the scoring functions, we investigated the contributions of the various components of the scoring functions. For the AMBER score, the bond, angle, and torsion terms cancel to several places past the decimal point in vacuum and to somewhat less with explicit waters and counterions. This result is expected as there is very little change in any of these values for the receptor and ligand upon complex formation. The VDW energy for all three scoring functions was also very similar. This result, too, is not surprising as the Lennard-Jones function for PB/SA and Grid is a grid-based simplification of that used for AMBER. There was some difference in the electrostatics between the methods, with both AMBER GB/SA and PB/SA values tending to be more negative than the Grid Score's distance-dependent dielectric, as expected from the more advanced solvation models. The largest contribution to the difference in the AMBER GB/SA and PB/SA scores, however, was the solvent-accessible surface area term; for the former, these are in the range of −1 kcal/mol to −5 kcal/mol with a mean of −2.7; for the latter, these are in the range of 0 kcal/mol to −30 kcal/mol with a mean of −20. These results suggest that the solvent-accessible surface area for AMBER GB/SA could be improved to better discriminate ligands and active sites of different shapes and sizes.
We also compared the subsets of complexes that were successes for both the AMBER GB/SA and PB/SA scoring function (Table 2). A total of 15 out of the 22 AMBER GB/SA and 18 PB/SA complexes were the same for both sets. Those complexes that the AMBER GB/SA scoring function, but not PB/SA, were correctly able to identify had seven or more rotatable bonds. This result supports the hypothesis from the scoring breakdown that the solvent-accessible surface area portion of the PB/SA scoring function needs to be improved, particularly for large, floppy molecules.
Comparison to other DOCKing methods
As mentioned above, developers of AutoDock and DrugScoreRNA have also evaluated their DOCKing algorithms against rigid receptors using similar test sets. Based on these data, the success rate for the L13 test set with the receptor in a vacuum, 26%, is below that of AutoDock's and DrugScoreRNA's success rates of 44% on 16 RNA–ligand complexes and 42% on 32 RNA–ligand complexes, respectively (Table 5). However, for DOCK using AMBER rescoring with ligand minimization and rigid receptors with explicit waters and counterions, the success rate of 58% is comparable to the other algorithms for a larger, more diverse test set. Unfortunately, neither code base has posted the RMSD-based results for their test sets, so a direct comparison cannot be made.
TABLE 5.
Comparison to other DOCKing methods
Analysis of remaining failures
Even with improvement in the success rate by rescoring with a more advanced scoring function, there were several ligands that could not be reDOCKed. In general, the rescored cumulative success rates for the L13 test set as a function of rotatable bonds is much flatter than the success rate based on simple DOCKing (Fig. 3C). Looking more specifically, there appears to be two types of behavior. For ligands with six or less rotatable bonds, both the Gasteiger and AM1-BCC charge models behave similarly, moving between 40% and 60% success rates, as compared to RESP charges that decrease from 50% to 35% by six rotatable bonds. After six rotatable bonds, the Gasteiger charge model success rates remain between 55% and 60%. However, the AM1-BCC charges continue to decrease, mimicking the behavior of RESP charges and decreasing from 43% to 32%. However, as it is not entirely clear why the charge models would behave differently based on the number of rotatable bonds, other factors were required to explain these failures.
When broken down by ligand formal charge, it becomes apparent that the Gasteiger charge model had a better success rate for positively charged ligands, which is the predominant species in this test set, than in either AM1-BCC or RESP models (Fig. 3D). It was not entirely apparent why this would be the case, as previous studies have shown that RESP in combination with PB/SA is a better predictor of experimental hydration-free energies, a standard model for determining the accuracy of the charge model, than Gasteiger (Rizzo et al. 2006). We hypothesize that, because Gasteiger partial charges tend to be smaller, the electrostatics were effectively down-weighted, possibly mimicking screening. Previous studies found improvement in fitting known ligands to RNA targets when electrostatic contributions were substantially reduced (Lind et al. 2002)
Finally, we compared success rates as a function of the experimental method used to generate each structure. In all three charge models, success rates for X-ray structures were substantially better than for NMR structures (76%, 19/25 complexes, success rate for X-ray versus 23%, 3/13 complexes for NMR). We hypothesize that this result is due to the fact that the NMR structures are of lower resolution than X-ray structures and possibly because the receptor–ligand complex came from a structural ensemble rather than the crystal structure single solution; there is no guarantee that our representative single structure choice from the NMR ensemble is the best structure for DOCKing purposes. This problem could potentially be addressed by DOCKing to the minimized lowest-energy NMR structure, or cross-DOCKing within an ensemble of structures and developing a method for combining the scores (Knegtel et al. 1997).
DISCUSSION
In the course of this study, we optimized the DOCK clustering-based sampling algorithm for RNA ligands. We also developed a ranking-based sampling algorithm that addressed some previously identified issues in the clustering-based algorithm. Based on our results, the ranking-based method should be applied in cases where time is critical, as the calculation is faster and has a higher success rate when looking at just the top-scoring pose. However, the clustering-based algorithm generates a more diverse set of conformations, which is more appropriate when rescoring with more advanced scoring functions. When we compare the success rate for ligands with less than seven rotatable bonds using the most simplified scoring function, Grid Score, to a similar study with protein complexes, we see that the success rate for the RNA set, 70%, is comparable to that of proteins, 68%.
Knowing that RNA–small molecule interactions are dominated by electrostatics, we explored more advanced methods for modeling charges as well as the contribution of solvent. We determined that the addition of explicit water molecules and sodium counterions increased the number of poses in each individual conformational ensemble placed close to the active site even with the most basic scoring function, Grid Score. We also found that neither a more advanced implicit solvent model, AMBER GB/SA nor PB/SA, was sufficient to counteract the naked phosphate charges on the backbone. Rather, explicit waters plus counterions in combination with more advanced implicit solvent models are critical for properly modeling the RNA energy landscape. With both models in combination, success rates increase to 80% with PB/SA for ligands with less than seven rotatable bonds and 58% with AMBER GB/SA and 47% with PB/SA for ligands with less than 13 rotatable bonds. We also determined that AM1-BCC charges were optimal for ligands with charges close to neutral, confirming results from a recent study on absolute free energies of hydration, and that Gasteiger charges perform better with highly positively charged ligands (Rizzo et al. 2006).
An additional underlying purpose of this paper is to show the ease of extensibility of DOCK. In the course of this study, we were able to add a range of new functionalities to the code, which was critical to the improved success rate for the RNA test set. Specific to this study, we found that DOCK can be successfully employed for binding mode prediction for RNA–ligand complexes and should be useful in the drug design setting. More generally, we believe that DOCK is a dynamic tool for a wide variety of structure-based drug design projects both because of the range of currently available functionality as well as the ease with which new functions can be added to address project-specific problems.
In this study, we have focused on rapid DOCKing to a rigid RNA target. However, we have recently described a promising new program, MORDOR, which enables flexibility in the ligand and limited flexibility in the RNA receptor for an induced fit (Guilbert and James 2008). MORDOR performed well on a test set and in discovering ligands for a novel target (Gómez Pinto et al. 2008; Guilbert and James 2008). MORDOR performed better than DOCK 6 on ligands in the test set with a large number of rotatable bonds. As suggested by our studies, such large ligands may need some degree of RNA flexibility in order to be accommodated in the complex. While a rigorous comparison has not been carried out, local experience suggests that DOCK 6 screens ∼3–10 times faster than MORDOR. Therefore, DOCK 6 is most useful for screening a large database of ligands, while MORDOR is most useful for screening a more focused database.
In looking forward toward using DOCK in combination with other DOCKing programs in a setting in which RNA is the target, we would recommend that the libraries being explored be subjected to the same constraints as typical protein screens (e.g., Lipinski Rule of 5), restricting ligands to fall within the definition of our more successful less than seven test set as well as restricting the partial charge of the ligands. For bigger, more complicated molecules, we would recommend using DOCKing algorithms only in the context of a larger modeling effort with support from more extensive sampling methodologies, like full molecular dynamics simulations, or methods that do not depend on energetic evaluation, such as QSAR.
MATERIALS AND METHODS
Preparation of structure-based test set
To generate the test set, we collected all NMR and X-ray crystal structures with both an RNA molecule and a ligand from the Protein Data Bank (PDB) (Berman et al. 2000). X-ray structures with resolution <3.0 Å were removed, as were all complexes where the “ligands” were either ions or artifacts of the structural determination method (e.g., ethanol). To bias toward biologically relevant structures, all receptors with <15 residues were also removed. Next, complexes with chemistries not available in our parameter set, including cobalt and receptors with modified or incompletely built nucleic acid bases, were removed. Four complexes had more than two ligands bound to a single receptor, which led us to remove them from the test set due to nonspecific binding. Of the remaining complexes, 15 had two ligands bound in two separate active sites. Each active site was treated as unique and prepared separately.
Receptor preparation
To identify a single structure from the NMR ensembles, we selected the structure in the ensemble that was closest to the average by RMSD. Receptor structures were processed with the Dock Prep module in Chimera (Pettersen et al. 2004). The graphical interface allows control over which tasks are performed, in this case: solvent deletion, deletion of alternate positions (retaining only the highest-occupancy positions), hydrogen addition, partial charge assignment, and output in Mol2 format. Hydrogen atoms were positioned to avoid clashes and to form hydrogen bonds where possible; this was done in the presence of bound ligand (Moustakas et al. 2006). Standard residues (receptor nucleotides) were assigned AMBER parm99 partial charges (Cornell et al. 1995). AM1-BCC charges were computed for the receptor cofactors with ANTECHAMBER, which is included in Chimera (Jakalian et al. 2000; Wang et al. 2006). Dock Prep recognizes which residues are standard and nonstandard, and presents options accordingly. The formal charge of each nonstandard residue can be specified prior to the charge calculation.
Active site identification
Active sites were identified and prepared following the procedure described previously, resulting in an average of 130 ± 29 spheres per active site (Moustakas et al. 2006). Spheres selected at different distances from 1 to 10 Å from the ligand were explored. We found that there was no change in the success rate using anything between 1 and 10 Å and only minimal changes in the energy (−98.9 ± 2.5 kcal/mol) and length of calculation (1207 ± 3 sec). We therefore selected the 10 Å radius from the ligand for historical purposes to compare with the results from the protein test set. Next, to account for the receptor contribution to the score during DOCKing, grids that store the VDW and electrostatic values for the receptor were calculated, also using procedures previously described. The final grids, with 0.15 Å spacing, averaged ∼40 × 103 Å3 in volume.
Counterions and explicit waters
Counterions and explicit waters were added to each receptor–ligand complex using LEaP, an AMBER accessory (Pearlman et al. 1995). Sodium ions were added along the backbone to neutralize the phosphate charges as well as any other negatively charged species. In some cases, chloride ions were added to attain overall neutrality when charged ligands or cofactors were present. LEaP uses a Coulombic potential grid to calculate the location for each ion. An octagon of TIP3P water was then built around each receptor such that the shortest distance between the walls of the octahedron and the closest receptor atom was 5 Å (Jorgensen et al. 1983). Solvent molecules were placed according to an equilibrated room temperature molecular dynamics simulation of a bubble of TIP3P water. Chimera was used to remove any waters >5 Å from any receptor atom, resulting in approximately two shells of water molecules plus counterions in the final structures. The ligands were removed and the receptors and active sites were once again prepared following the procedure described above.
Ligand preparation
The ligands were protonated and assigned AM1-BCC charges with Chimera's Dock Prep module, as described above for the receptors. For the comparison and evaluation of the scoring functions, Gasteiger–Hückel and RESP partial charges were calculated using the ANTECHAMBER accessory in AMBER for ligands with less than 13 rotatable bonds (Gasteiger and Marsili 1980; Bayly et al. 1993; Jakalian et al. 2000; Wang et al. 2004, 2006). Finally, each ligand was minimized while keeping the receptor rigid to detect complexes that were not stable with our scoring function. The ligands that moved >2 Å heavy-atom RMSD from the starting structure, a total of six structures, were removed from the set. The final set had a total of 70 structures (53 structures without the multiple binding sites) (Table 1).
Modifications in sampling and Grid Score
The ligand flexibility sampling algorithm is an incremental construction method called anchor-and-grow. In this method, the ligand is first divided into the largest rigid portion and layers of flexible regions (see Fig. 2, for example). The largest rigid portion of the ligand, or anchor, is identified and then oriented in the active site and minimized. All orientations with scores >1000 kcal/mol were removed and the remaining ranked by score, then clustered by RMSD using a greedy algorithm (cluster-based pruning). One layer of flexible bonds is then grown from each cluster, minimized, ranked, and clustered again. The growth phase is repeated until the molecule is fully built. In a previous study, we had shown that the pruning portion of the algorithm was limiting sampling during growth and preventing energy convergence. In addition, we found that flexible sampling failures often occurred as a result of minor clashes between the ligand and the protein receptor, which we hypothesized were due to clashes resulting from overly coarse sampling (Moustakas et al. 2006).
To address the limitations of cluster-based pruning, we compared several different clustering algorithms. In the end, it was determined that the clustering itself was limiting the sampling, because all anchors that were close to the correct position fell into the same cluster. Thus, in the worst case, only one of these anchors would be propagated to the next stage even though several were generated by the sampling algorithm. Instead of clustering, we found that using a simple scoring cutoff of 25 kcal/mol and a hard upper limit of 100 ranked orientations increased the number of orientations near the active site in the final list. To overcome the clashes due to coarse sampling, we scaled down the radius of each atom used for the repulsive term in the Lennard-Jones potential. This modification shifts the energy function toward lower energy but maintains the overall functional shape.
Modification of bump filter
In previous versions of DOCK, the bump filter could be applied to remove orientations that significantly overlap with receptor atoms before minimization. Because minimization is the most time-consuming portion of the calculation, filtering helps to increase the speed of the calculation by directing sampling toward more productive routes. In DOCK 6, we have implemented the same filtering by bump during growth, in this case between torsional sampling and minimization. Because the number of atoms in the anchor is much larger than in each flexible layer, we added user parameters to separately control the maximum number of bumps allowed for both the anchor and growth stages.
Optimization of parameters for DOCKing
Parameters for both the clustering- and ranking-based sampling methods as well as for the bump filter were optimized according to the protocol used for the protein test set (Moustakas et al. 2006). The final version of the code, including all functions described in this paper, was posted to the DOCK website as version 6.3 (http://dock.compbio.ucsf.edu) and will be referred to as DOCK 6 for convenience. All experiments performed with the previous versions of DOCK used version 4.0.1 and version 5.4.0 and will be referred to as DOCK 4 and DOCK 5, respectively. All sampling calculations were run on AMD Opteron 248 dual processors. All rescoring calculations were performed on the Ohio Supercomputer Center's IBM Cluster 1350, which includes AMD Opteron multicore technologies and the new IBM cell processors. The code was compiled using open-source GNU compilers (http://www.gnu.org).
AMBER GB/SA scoring function
The AMBER scoring function employs the Nucleic Acid Builder (NAB) library (Macke and Case 1998). As stated in the introduction, the AMBER GB/SA score is calculated via a thermodynamic cycle. The Cornell and colleagues force field was used (Cornell et al. 1995). The solvation component of the score can be calculated using: (1) Hawkins, Cramer, and Truhlar model with parameters described by Tsui and Case, (2) Onufriev, Bashford, and Case model, and (3) Onufriev, Bashford, and Case model with modified parameters (Hawkins et al. 1995, 1996; Onufriev et al. 2000; Tsui and Case 2000; Feig et al. 2004; Onufriev et al. 2004). For these studies, model 3 was used. The library also enables conjugate gradient minimization and molecular dynamics simulations. In the current implementation, this increased sampling functionality is only available for the AMBER Score function. The NAB library is constructed using the lex and yacc language specification, which has special support for macromolecules and has a C-like syntax. It is included in the distribution of DOCK, but can also be downloaded from the Case laboratory website (http://www.ambermd.org/).
Many sampling protocols are possible with the AMBER GB/SA score. Initial development began with a minimization only approach. Later work by Graves and colleagues developed a minimization/MD/minimization formulation (MDM protocol) (Graves et al. 2008). For the simulations with minimization only, ligands were minimized to a convergence criterion of 0.01 followed by a final energy evaluation (Min protocol). The convergence criterion was computed as the root-mean-square of the components of the energy gradient and was selected based on the convergence of the test set success rate. For simulations including molecular dynamics, we performed 100 steps of minimization with a conjugate gradient method followed by 3000 steps of molecular dynamics simulation (Langevin molecular dynamics at a constant temperature of 300 K), another 100 steps of minimization, and a final energy evaluation (Graves et al. 2008).
The flexible parts of the receptor–ligand complex are denoted by the parameter movable_region. Four movable regions are available: (1) nothing—all ligand and receptor atoms were frozen; (2) ligand—all ligand atoms were movable and all receptor atoms were frozen; (3) distance—all ligand atoms and all receptor atoms in residues that were within a user-defined distance of the ligand were movable and all other receptor atoms were frozen; (4) everything—all ligand and receptor atoms were movable. Note that for the distance movable region the movable receptor residues were predefined and thus independent of any particular ligand molecule or conformation.
PB/SA scoring function
The Poisson–Boltzmann with solvent-accessible surface area (PB/SA) scoring function is an implementation of the ZAP library from OpenEye (Grant et al. 2001). The VDW interactions are modeled by interpolating values from a precomputed grid, as in Grid Score. The solvent potential comes from the solution for the Poisson–Boltzmann equation in combination with atomic point charges summed over each atom in the system. Finally, the hydrophobic component is calculated using the solvent-accessible surface area multiplied by an interfacial surface-free energy obtained from partition coefficients of nonpolar solutes transferred from a low-dielectric solvent to water. The ZAP library is object-oriented and written in ANSI C and is free to most academics and government institutions. It is available in the form of a linkable library and prepackaged binaries for Linux, Windows, and Cygwin platforms and can be accessed from the OpenEye website (http://eyesopen.com). The implementation of the library in DOCK as well as the defaults are based on the “Solvation Energies: PBSA” example from the ZAP library documentation.
ACKNOWLEDGMENTS
We thank Brian Shoichet for helpful conversations. I.D.K., D.A.C., and P.T.L. are supported by NIH grant GM 56531 (Paul Ortiz de Montellano, PI). D.A.C. is also supported by NIH grant RR12255. P.T.L. would like to thank the American Foundation for Pharmaceutical Education, the Burroughs-Wellcome Foundation, and NIH grants AI46967, which also supported T.L.J., for additional support. E.F.P. and E.C.M. are supported by NIH grant P41 RR-01081. R.C.R. acknowledges NYSTAR (#C040031), the OVPR at Stony Brook University, and the Computational Science Center at BNL for support. This work was supported in part by an allocation of computing time from the Ohio Supercomputer Center.
Footnotes
Article published online ahead of print. Article and publication date are at http://www.rnajournal.org/cgi/doi/10.1261/rna.1563609.
REFERENCES
- Bannwarth S., Gatignol A. HIV-1 TAR RNA: The target of molecular interactions between the virus and its host. Curr. HIV Res. 2005;3:61–71. doi: 10.2174/1570162052772924. [DOI] [PubMed] [Google Scholar]
- Bayly C.I., Cieplak P., Cornell W.D., Kollman P.A. A well-behaved electrostatic potential based method using charge restraints for deriving atomic charges: The RESP model. J. Phys. Chem. 1993;97:10269–10280. [Google Scholar]
- Berman H.M., Westbrook J., Feng Z., Gilliland G., Bhat T.N., Weissig H., Shindyalov I.N., Bourne P.E. The Protein Data Bank. Nucleic Acids Res. 2000;28:235–242. doi: 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Case D.A., Cheatham T.E., III, Darden T., Gohlke H., Luo R., Merz K.M., Onufriev A., Simmerling C., Wang B., Woods R. The Amber biomolecular simulation programs. J. Comput. Chem. 2005;26:1668–1688. doi: 10.1002/jcc.20290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cornell W.D., Cieplak P., Bayly C.I., Gould I.R., Merz K.M., Ferguson D.M., Spellmeyer D.C., Fox T., Caldwell J.W., Kollman P.A. A second generation force field for the simulation of proteins, nucleic acids, and organic molecules. J. Am. Chem. Soc. 1995;117:5179–5197. [Google Scholar]
- Detering C., Varani G. Validation of automated docking programs for docking and database screening against RNA drug targets. J. Med. Chem. 2004;47:4188–4201. doi: 10.1021/jm030650o. [DOI] [PubMed] [Google Scholar]
- Feig M., Im W., Brooks C.L., III Implicit solvation based on generalized Born theory in different dielectric environments. J. Chem. Phys. 2004;120:903–911. doi: 10.1063/1.1631258. [DOI] [PubMed] [Google Scholar]
- Filikov A.V., Mohan V., Vickers T.A., Griffey R.H., Cook P.D., Abagyan R.A., James T.L. Identification of ligands for RNA targets via structure-based virtual screening: HIV-1 TAR. J. Comput. Aided Mol. Des. 2000;14:593–610. doi: 10.1023/a:1008121029716. [DOI] [PubMed] [Google Scholar]
- Frank J., Spahn C.M.T. The ribosome and the mechanism of protein synthesis. Rep. Prog. Phys. 2006;69:1383–1417. [Google Scholar]
- Frankel A.D., Young J.A. HIV-1: Fifteen proteins and an RNA. Annu. Rev. Biochem. 1998;67:1–25. doi: 10.1146/annurev.biochem.67.1.1. [DOI] [PubMed] [Google Scholar]
- Gasteiger J., Marsili M. Iterative partial equalization of orbital electronegativity—A rapid access to atomic charges. Tetrahedron. 1980;36:3219–3288. [Google Scholar]
- Gómez Pinto I., Guilbert C., Ulyanov N.B., Stearns J., James T.L. Discovery of ligands for a novel target, the human telomerase RNA, based on flexible-target virtual screening and NMR. J. Med. Chem. 2008;51:7205–7215. doi: 10.1021/jm800825n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grant J.A., Pickup B.T., Nicholls A. A smooth permittivity function for Poisson–Boltzmann solvation methods. J. Comput. Chem. 2001;22:608–640. [Google Scholar]
- Graves A.P., Shivakumar D.M., Boyce S.E., Jacobson M.P., Case D.A., Shoichet B. Rescoring docking hit lists for model cavity sites: Predictions and experimental testing. J. Mol. Biol. 2008;337:914–934. doi: 10.1016/j.jmb.2008.01.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guilbert C., James T.L. Docking to RNA via root-mean-square-deviation-driven energy minimization with flexible ligands and flexible targets. J. Chem. Inf. Model. 2008;48:1257–1268. doi: 10.1021/ci8000327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hawkins G.D., Cramer C.J., Truhlar D.G. Pairwise solute descreening of solute charges from a dielectric medium. Chem. Phys. Lett. 1995;246:122–129. [Google Scholar]
- Hawkins G.D., Cramer C.J., Truhlar D.G. Parametrized models of aqueous free energies of solvation based on pairwise descreening of solute atomic charges from a dielectric medium. J. Phys. Chem. 1996;100:19824–19839. [Google Scholar]
- Jakalian A., Bush B.L., Jack D.B., Bayly C.I. Fast, efficient generation of high-quality atomic charges. AM1-BCC model: I. Method. J. Comput. Chem. 2000;21:132–146. doi: 10.1002/jcc.10128. [DOI] [PubMed] [Google Scholar]
- Johansson D., Jessen C.H., Pohlsgaard J., Jensen K.B., Vester B., Pedersen E.B., Nielsen P. Design, synthesis and ribosome binding of chloramphenicol nucleotide and intercalator conjugates. Bioorg. Med. Chem. Lett. 2005;15:2079–2083. doi: 10.1016/j.bmcl.2005.02.044. [DOI] [PubMed] [Google Scholar]
- Jorgensen W.L., Chandrasekhar J., Madura J.D., Impey R.W., Klein M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983;79:926–935. [Google Scholar]
- Knegtel R.M.A., Kuntz I.D., Oshiro C.M. Molecular docking to ensembles of protein structures. J. Mol. Biol. 1997;266:424–440. doi: 10.1006/jmbi.1996.0776. [DOI] [PubMed] [Google Scholar]
- Lind K.E., Du Z., Fujinaga K., Peterlin B.M., James T.L. Structure-based computational database screening, in vitro assay, and NMR assessment of compounds that target TAR RNA. Chem. Biol. 2002;9:185–193. doi: 10.1016/s1074-5521(02)00106-0. [DOI] [PubMed] [Google Scholar]
- Lipinski C.A. Drug-like properties and the causes of poor solubility and poor permeability. J. Pharmacol. Toxicol. Methods. 2000;44:235–249. doi: 10.1016/s1056-8719(00)00107-6. [DOI] [PubMed] [Google Scholar]
- Macke T.J., Case D.A. Modeling unusual nucleic acid structures. In: Leontis N.B., SantaLucia J. Jr, editors. Molecular modeling of nucleic acids. American Chemical Society; Washington, DC: 1998. pp. 379–393. [Google Scholar]
- Mayer M., James T.L. Discovery of ligands by a combination of computational and NMR-based screening: RNA as an example target. Methods Enzymol. 2005;394:571–587. doi: 10.1016/S0076-6879(05)94024-X. [DOI] [PubMed] [Google Scholar]
- Mayer M., Lang P.T., Gerber S., Madrid P.B., Pinto I.G., Guy R.K., James T.L. Synthesis and testing of a focused phenothiazine library for binding to HIV-1 TAR RNA. Chem. Biol. 2006;13:993–1000. doi: 10.1016/j.chembiol.2006.07.009. [DOI] [PubMed] [Google Scholar]
- Morley S.D., Afshar M. Validation of an empirical RNA-ligand scoring function for fast flexible docking using RiboDock (R) J. Comput. Aided Mol. Des. 2004;18:189–208. doi: 10.1023/b:jcam.0000035199.48747.1e. [DOI] [PubMed] [Google Scholar]
- Moustakas D.T., Lang P.T., Pegg S., Pettersen E., Kuntz I.D., Brooijmans N., Rizzo R.C. Development and validation of a modular, extensible docking program: DOCK 5. J. Comput. Aided Mol. Des. 2006;20:601–619. doi: 10.1007/s10822-006-9060-4. [DOI] [PubMed] [Google Scholar]
- Nakatani K., Horie S., Goto Y., Kobori A., Hagihara S. Evaluation of mismatch-binding ligands as inhibitors for Rev-RRE interaction. Bioorg. Med. Chem. 2006;14:5384–5388. doi: 10.1016/j.bmc.2006.03.038. [DOI] [PubMed] [Google Scholar]
- Onufriev A., Bashford D., Case D.A. Modification of the generalized Born model suitable for macromolecules. J. Phys. Chem. B. 2000;104:3712–3720. [Google Scholar]
- Onufriev A., Bashford D., Case D.A. Exploring protein native states and large-scale conformational changes with a modified generalized Born model. Proteins. 2004;55:383–394. doi: 10.1002/prot.20033. [DOI] [PubMed] [Google Scholar]
- Pearlman D.A., Case D.A., Caldwell J.W., Ross W.S., Cheatham T.E., III, DeBolt S., Ferguson D., Seibel G., Kollman P. AMBER, a package of computer programs for applying molecular mechanics, normal mode analysis, molecular dynamics, and free energy calculations to simulate the structural and energetic properties of molecules. Comput. Phys. Commun. 1995;91:1–41. [Google Scholar]
- Pettersen E.F., Goddard T.D., Huang C.C., Couch G.S., Greenblatt D.M., Meng E.C., Ferrin T.E. UCSF Chimera—A visualization system for exploratory research and analysis. J. Comput. Chem. 2004;25:1605–1612. doi: 10.1002/jcc.20084. [DOI] [PubMed] [Google Scholar]
- Pfeffer P., Gohlke H. DrugScore(RNA)—Knowledge-based scoring function to predict RNA-ligand interactions. J. Chem. Inf. Model. 2007;47:1868–1876. doi: 10.1021/ci700134p. [DOI] [PubMed] [Google Scholar]
- Polacek N., Mankin A.S. The ribosomal peptidyl transferase center: Structure, function, evolution, inhibition. Crit. Rev. Biochem. Mol. Biol. 2005;40:285–311. doi: 10.1080/10409230500326334. [DOI] [PubMed] [Google Scholar]
- Renner S., Ludwig V., Boden O., Scheffer U., Gobel M., Schneider G. New inhibitors of the Tat-TAR RNA interaction found with a “fuzzy” pharmacophore model. ChemBioChem. 2005;6:1119–1125. doi: 10.1002/cbic.200400376. [DOI] [PubMed] [Google Scholar]
- Rizzo R.C., Aynechi T., Case D.A., Kuntz I.D. Estimation of absolute free energies of hydration using continuum methods: Accuracy of partial, charge models and optimization of nonpolar contributions. J. Chem. Theory Comput. 2006;2:128–139. doi: 10.1021/ct050097l. [DOI] [PubMed] [Google Scholar]
- Tsui V., Case D.A. Molecular dynamics simulations of nucleic acids with a generalized Born solvation model. J. Am. Chem. Soc. 2000;122:2489–2498. [Google Scholar]
- Tucker B.J., Breaker R.R. Riboswitches as versatile gene control elements. Curr. Opin. Struct. Biol. 2005;15:342–348. doi: 10.1016/j.sbi.2005.05.003. [DOI] [PubMed] [Google Scholar]
- Wang J., Wolf R.M., Caldwell J.W., Kollman P.A., Case D.A. Development and testing of a general amber force field. J. Comput. Chem. 2004;25:1157–1174. doi: 10.1002/jcc.20035. [DOI] [PubMed] [Google Scholar]
- Wang J., Wang W., Kollman P.A., Case D.A. Automatic atom type and bond type perception in molecular mechanical calculations. J. Mol. Graph. Model. 2006;25:247–260. doi: 10.1016/j.jmgm.2005.12.005. [DOI] [PubMed] [Google Scholar]
- Weiser J., Shenkin P.S., Still W.C. Approximate atomic surfaces from linear combinations of pairwise overlaps (LCPO) J. Comput. Chem. 1999;20:217–230. [Google Scholar]
- Wunberg T., Hendrix M., Hillisch A., Lobell M., Meier H., Schmeck C., Wild H., Hinzen B. Improving the hit-to-lead process: Data-driven assessment of drug-like and lead-like screening hits. Drug Discov. Today. 2006;11:175–180. doi: 10.1016/S1359-6446(05)03700-1. [DOI] [PubMed] [Google Scholar]
- Yu X.L., Lin W., Pang R.F., Yang M. Design, synthesis and bioactivities of TAR RNA targeting β-carboline derivatives based on Tat-TAR interaction. Eur. J. Med. Chem. 2005;40:831–839. doi: 10.1016/j.ejmech.2005.01.012. [DOI] [PubMed] [Google Scholar]