Real-Time Quantitative RT-PCR: Design, Calculations, and Statistics

Two recent letters to the editor of The Plant Cell (Gutierrez et al., 2008; Udvardi et al., 2008) highlighted the importance of following correct experimental protocol in quantitative RT-PCR (qRT-PCR). In these letters, the authors outlined measures to allow precise estimation of gene expression by ensuring the quality of material, refining laboratory practice, and using a normalization of relative quantities of transcripts of genes of interest (GOI; also called target genes) where multiple reference genes have been analyzed appropriately. In this letter, we build on the issues raised by considering the statistical design of qRT-PCR experiments, the calculation of normalized gene expression, and the statistical analysis of the subsequent data. This letter comprises advice for taking account of, in particular, the first and the last of these three vital issues. We concentrate on the situation of comparing transcript levels in different sample types (treatments) using relative quantification, but many of the concerns, particularly those with respect to design, are equally applicable to absolute quantification.

STATISTICAL DESIGN

As mentioned by Udvardi et al. (2008), an experiment ideally should encompass at least three independent biological replicates of each treatment. For each biological replicate, it is common to run at least two technical replicates of each PCR reaction. Each sample provides material for both GOI and reference gene reactions, so these are paired for each biological replicate. Ideally, a full experiment (i.e., all primer pairs for the GOI and reference genes on all samples) would be analyzed on a single (typically 96-well) plate. However, an experiment with many treatments and/or GOIs and reference genes requires a design strategy for multiple plates. Such a design was investigated by Hellemans et al. (2007) where they compared gene maximization to sample maximization; but to enable effective statistical comparison of treatments, a strategy that may be termed “treatment maximization” is required. As a plate can be viewed as a statistical block, the best option would be to separate complete biological replicates (i.e., one biological sample of each treatment) on each plate, so that the design is then a randomized block (see, for example, Mead, 1988). Larger experiments may necessitate an unbalanced design (i.e., without a complete replicate of all the treatments on a given plate), which must be constructed so that treatment comparisons of greatest interest are seen most frequently together on the same plate. It is then beneficial to use inter-run calibrators (IRCs) on each plate to improve the assessment of plate-to-plate variation (described in Hellemans et al., 2007). When many GOIs and reference genes are analyzed using the same samples, it will be more economical to analyze different genes on different plates (sample maximization). Although this is common practice and even supported by qPCR software packages, from a statistical point of view, it is not correct to separate the paired reactions of the samples. Whichever of the above setups is chosen, it is, in principle, advisable to use a full randomization of the reactions within each plate to counteract the effects of systematic variations occurring within a plate as introduced during the PCR setup or PCR run. However, because within-plate variation introduced during the PCR run should be minimal in the current generation of real-time PCR cyclers, it may now be less of a problem to use a more practical, nonrandom plate setup.

CALCULATIONS

The reaction (amplification) curve formed during the PCR run is exponential in its early phase, the progress of this curve being determined by the amplification efficiency, E. The basic formula applying to qRT-PCR aims to convert the number of cycles at a threshold level of fluorescence (more generally termed the quantification cycle or Cq; Hellemans et al., 2007) into a relative quantity of input template present at the start of the PCR. If we take the relative amount of fragments at the Cq as 1, then the relative quantity of template in the original sample (RQ) can be calculated as follows:

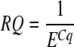In the optimal situation, E equals 2, and, in many studies, E is taken arbitrarily as 2. However, in reality, E may vary considerably between primer pairs and between plates. Hence, it is more accurate to estimate E for each primer pair through analysis of a dilution curve or, more commonly, by analyzing the amplification curves of all reactions (e.g., Ramakers et al., 2003; Ruijter et al., 2009). Usually the error in E estimation from a single reaction will be greater than the real difference in E values between samples for a given primer pair on the same plate. Accordingly, it has been shown that the most precise results are obtained by assuming the same E for all reactions with the same primer pair on the same plate (Cook et al., 2004), calculated as the mean of E values. Nevertheless, variation in E values should be inspected to check for obvious and systematic outliers. Currently, it is advisable to discard such outliers, although progress is being made to improve E estimation for individual reactions (e.g., Alvarez et al., 2007; Durtschi et al., 2007; Spiess et al., 2008). The variation in Cq for technical replicates also should be assessed, and the mean Cq of technical replicates then can be used in subsequent calculations. After calculating the RQ of a GOI, this needs to be normalized for the total amount of cDNA that was used in the reaction, as discussed by Gutierrez et al. (2008). This provides the normalized RQ (NRQ) of the GOI for each biological replicate.

STATISTICS

Before meaningful statistical analysis can be performed, the NRQ data need transformation. Specifically, on the RQ and NRQ scale, qPCR data are nonlinear and typically suffer from heterogeneity of variance across biological replicates within treatments and across treatments. This usually can be accounted for by applying a log transformation (Gomez and Gomez, 1984) to the NRQ data, the result of which may be termed Cq′ (as it brings the data back to the Cq scale):

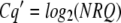Following a single-plate experiment or a balanced-design experiment across a number of plates, analysis of variance (ANOVA) can be used to compare treatments using the Cq′ values calculated above. This reduces to a t test if there are only two treatments run on a single plate. One benefit of applying ANOVA is that if the treatment structure consists of two or more treatment factors (for example, three genotypes as one factor by two environmental conditions as the other factor), the method can assess the variation due to each of these (as main effects) and then the interaction between them. Also, ANOVA automatically accounts for block effects such as interplate variation. Performed on the Cq′ values of the biological replicates, the mean for each treatment is output and used to make a statistical comparison of the treatments based on the standard error of the difference (SED) between means using the estimate of random variation at the level of biological replication. Hence, from the SED, the least significant difference (LSD) can be calculated at a particular level of significance (e.g., 5%) and used to compare treatments of a priori biological importance from the full set of possible comparisons.

Data (Cq′ values) from an unbalanced design where not all treatments may occur together on plates precludes the use of ANOVA and requires modeling to estimate the means one would have expected if the design had been balanced. Such modeling employs the method of residual maximum likelihood (Patterson and Thompson, 1971) to provide the means and appropriate SEDs for comparison of any pair of treatments. The relative size of these SEDs reflects degree of imbalance, so treatments never seen on the same plate will be compared with the greatest SED/LSD. Repeating an identical sample on all plates (i.e., using IRCs) will help in the assessment of plate-to-plate variation and hence in controlling the size of SEDs in the analysis of unbalanced designs. In some cases, variances may still be heterogeneous after log transformation (e.g., in experiments that include samples with a very low transcript level [high Cq], which inherently have a higher error). The influence of such samples could be inspected by inclusion/omission from the statistical analysis. Alternatively, nonparametric tests, such as Friedman's ANOVA (which accounts for block effects), Kruskal-Wallis ANOVA (which does not account for block effects), or the Mann-Whitney test in the situation of only two treatments (in one block) can be applied (note that all these tests require a balanced design).

It is possible to process and analyze qRT-PCR data using standard database/spreadsheet and statistics software such as R (freely available), SAS, and GenStat. Alternatively, dedicated qRT-PCR analysis software packages are available (both commercially and as freeware), although careful checking is required to determine whether they are tailored for the experimental setup (e.g., whether they can handle multiple levels of replication [i.e., biological and technical] and whether they can perform an appropriate statistical analysis of the data). An up-to-date overview of qPCR software can be found at http://www.gene-quantification.info or in Pfaffl et al. (2009).

PRESENTATION

Although NRQ data should not be used for inferential statistics (the analyses/comparisons are done on a different scale; see above), the mean NRQ and corresponding standard error for each treatment, as calculated from the replicate NRQ observations, are commonly used (graphically) to represent qRT-PCR results. When using a randomized block design, the NRQs may first be corrected to account for block effects (e.g., plate-to-plate variation). To do this, it is important to note that the block effects are not additive on the NRQ scale (hence, the transformation to Cq′ that was required). For a balanced randomized block design, the block effects can be taken out manually by subtracting the mean Cq′ of a given block from each individual Cq′ in that same block. In the case of an unbalanced design, it is not possible to take out the block effects manually using block means, but the Cq′ values can be corrected at least partially by subtracting from each individual Cq′ in a block the Cq′ of an IRC in the block. NRQ data for presentation then may be calculated by back-transforming the corrected Cq′ values to the NRQ scale. Usually the mean (corrected) NRQs and corresponding standard errors are presented all rescaled by the same quantity for convenient display (e.g., such that the rescaled mean NRQ of one of the treatments equals 1). In cases where all treatments are only compared with a common control (or calibrator) sample, it may be appropriate to calculate and present only the ratios between the mean NRQs of the treatments and the control. If this is done, the standard error of the ratios, using the standard errors of the mean NRQs, should be correctly calculated as given below:

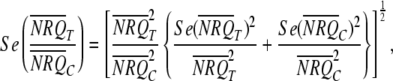where , , , 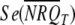and 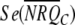are the means and standard errors for treatment T and control treatment C.

CONCLUSION

To make a valid comparison of treatments in qRT-PCR experiments, it is essential to begin with a statistical design that incorporates the concepts of randomization, blocking, and adequate (biological) replication. Subsequently, data analysis will benefit from appropriate data transformation and proper accounting of sources of variation due to the experimental design prior to making a statistical assessment of differences between treatments. Finally, it should be kept in mind that the strategy of relative quantification, as dealt with here, is only suitable for comparing results from a given primer pair between treatments and not for comparing results obtained with different primer pairs to each other.