Pseudosymmetry, high copy number and twinning complicate the structure determination of Desulfovibrio desulfuricans (ATCC 29577) flavodoxin

Complications to molecular replacement resulting from a poor starting search model, pseudosymmetry, twinning and a high copy number in the asymmetric unit made the determination of the structure of D. desulfuricans (ATCC 29577) flavodoxin in two crystal forms challenging.

Abstract

The crystal structure of oxidized flavodoxin from Desulfo­vibrio desulfuricans (ATCC 29577) was determined by molecular replacement in two crystal forms, P3₁21 and P4₃, at 2.5 and 2.0 Å resolution, respectively. Structure determination in space group P3₁21 was challenging owing to the presence of pseudo-translational symmetry and a high copy number in the asymmetric unit (8). Initial phasing attempts in space group P3₁21 by molecular replacement using a poor search model (46% identity) and multi-wavelength anomalous dispersion were unsuccessful. It was necessary to solve the structure in a second crystal form, space group P4₃, which was characterized by almost perfect twinning, in order to obtain a suitable search model for molecular replacement. This search model with complementary approaches to molecular replacement utilizing the pseudo-translational symmetry operators determined by analysis of the native Patterson map facilitated the selection and manual placement of molecules to generate an initial solution in the P3₁21 crystal form. During the early stages of refinement, application of the appropriate twin law, (−h, −k, l), was required to converge to reasonable R-factor values despite the fact that in the final analysis the data were untwinned and the twin law could subsequently be removed. The approaches used in structure determination and refinement may be applicable to other crystal structures characterized by these complicating factors. The refined model shows flexibility of the flavin mononucleotide coordinating loops indicated by the isolation of two loop conformations and provides a starting point for the elucidation of the mechanism used for protein-partner recognition.

1. Introduction  

Flavodoxins are small single-domain flavoproteins that bind a single flavin mononucleotide (FMN) and participate in electron-transfer pathways at low redox potentials (Mayhew & Ludwig, 1975 ▶). Flavodoxins have been isolated from a wide distribution of bacteria and a few species of algae and are classified into two groups based on size: long-chain flavodoxins (23 kDa) and short-chain flavodoxins (15 kDa). The sequences of flavodoxins from various organisms, even within the same group, share little sequence homology. The difference between the long-chain and short-chain flavodoxins can mainly be attributed to the presence of a 20–25-residue loop that interrupts the fifth β-strand. Although flavodoxins are not found in eukaryotes, the descendants of the flavodoxin protein are conserved in multi-domain proteins such as human cytochrome P450 reductase (Zhao et al., 1999 ▶).

Although the sequence homology between flavodoxins is low, the overall fold consisting of a central β-sheet flanked by α-helices on both sides is highly conserved. The FMN molecule is bound at the periphery between two flexible loops through stacking interactions with Trp60 and Tyr98 and a number of hydrogen bonds (Lostao et al., 2000 ▶; Maldonado et al., 1998 ▶). Both long-chain and short-chain flavodoxins are represented in the collection of X-ray crystal structures that have been solved to date; examples of long-chain flavodoxin structures are those from Azotobacter vinelandii (Alagaratnam et al., 2005 ▶) and Anabaena (Rao et al., 1992 ▶) and examples of short-chain flavodoxin structures are those from Desulfovibrio vulgaris (Watt et al., 1991 ▶) and Clostridum beijerinckii (Ludwig et al., 1969 ▶).

In solving the structure of D. desulfuricans (ATCC 29577) flavodoxin, several complications were encountered: twinning, pseudosymmetry and the presence of a large number of molecules in the asymmetric unit. Twinning is a condition that results from crystal growth in which crystal domains are oriented by a symmetry operation in which the molecular spacings match at the face where the domains meet (Yeates, 1997 ▶). In the case of merohedral twinning, the twin domains are superimposable in three-dimensional space and each intensity is the sum of two crystallographically distinct reflections weighted by the twin fraction α (Yeates, 1997 ▶). Merohedral twinning cannot be readily detected by inspection of the diffraction pattern, but can be evaluated by inspection of the intensities. Several programs can be used to detect twinning, including the Merohedral Crystal Twinning Server (Yeates, 1997 ▶), TRUNCATE in the CCP4 suite (Collaborative Computational Project, 1994 ▶) and phenix.xtriage (Adams et al., 2002 ▶). If twinning is undetected, it can complicate structure solution in a number of ways, including incorrect space-group assignment and the convergence of refinement at unexpectedly high R-factor values.

An additional complication that was present in the D. desulfuricans (ATCC 29577) flavodoxin crystals was translational pseudosymmetry, a form of noncrystallographic symmetry. When noncrystallographic symmetry operators are very close to true crystallographic symmetry operators, the situation is referred to as pseudosymmetry (Zwart et al., 2008 ▶). In other words, translational pseudosymmetry occurs when two molecules are related by translational symmetry but have orientations that differ by a root-mean-square displacement (r.m.s.d.) that is below a certain threshold (3 Å; Zwart et al., 2008 ▶). If the translational pseudosymmetry operator is very close to the lattice-centering operators, for example 1/2, 1/3 or 1/4 of a unit-cell dimension, the effect is pseudocentering (Zwart et al., 2008 ▶). Pseudocentering causes an increase in very high and low intensities at low resolution (Chook et al., 1998 ▶; Vajdos et al., 1997 ▶).

Either twinning or pseudosymmetry can complicate structure solution on its own and combination of the two further compounds these problems, in part because both have an impact on the intensities of the data (Chook et al., 1998 ▶; Yeates, 1997 ▶). The presence of translational pseudosymmetry can mask the effects of twinning on the intensity statistics, making it more difficult to detect (Zwart et al., 2008 ▶). Twinning usually decreases the number of very weak intensities; this effect is offset by translational pseudosymmetry, which gives rise to systematically weak and strong intensities (Lebedev et al., 2006 ▶). Pseudosymmetry can also mimic twinning at low resolution in that crystallographically distinct reflections show similarities in intensities in both cases.

Here, we report the process used to determine the crystal structure of flavodoxin from D. desulfuricans (ATCC 29577) in two crystal forms. Pseudo-translational symmetry accompanied by the presence of eight copies in the asymmetric unit complicated solution of the structure in the crystal form initially obtained, P3₁21; initial attempts at phasing by both molecular replacement and multiwavelength anomalous dispersion failed. Since a better search model could provide a solution to the difficulties in phasing by molecular replacement, a second crystal form was obtained in space group P4₃. This second form was characterized by near-perfect twinning, but refinement was straightforward using twin-specific applications. The refined P4₃ structure was then successfully used together with an approach complementary to molecular replacement to generate an initial model for the P3₁21 data. Interestingly, the application of an appropriate twin law was essential to refinement of the P3₁21 structure, although the final solution confirmed that no significant twinning was present. The effects of both twinning and pseudosymmetry were investigated to determine how they complicate structure solution and to develop insights into dealing with these factors for future structural studies. For clarity, the results and discussion section is divided by crystal form and does not follow the chronological order of determination as outlined in this paragraph.

2. Methods  

2.1. Expression and purification  

The gene encoding D. desulfuricans (ATCC 29577) flavodoxin had previously been cloned into a pET-24c(+) vector conferring kanamycin resistance. The plasmid pET-24c(+)-Ddflavo was expressed in Escherichia coli grown in Luria–Bertani (LB) medium containing 30 µg ml⁻¹ kanamycin at 310 K. At an optical density of 0.8 at 590 nm, the cells were induced with isopropyl β-d-1-thiogalactopyranside (IPTG) at a final concentration of 1 mM. The cells were harvested 4 h after induction by centrifugation and the pellets were stored at 193 K.

The frozen cell pellet was thawed on ice and resuspended in buffer A (20 mM sodium citrate pH 5.2). Cell lysis was performed by pulsed sonication. Insoluble material was pelleted by centrifugation at 16 000 rev min⁻¹ for 25 min. The supernatant was filtered and applied onto two stacked 5 ml HiTrap Q HP cartridges (Amersham Pharmacia) equilibrated in buffer A. The protein was eluted using a gradient of 0–40% buffer B (20 mM sodium citrate pH 5.2, 2 M sodium chloride) over eight column volumes. Fractions containing flavodoxin were pooled and exogenous flavin mononcleotide (FMN) and potassium ferricyanide were added to the sample. The sample was concentrated using a 10 000 molecular-weight cutoff Vivaspin 20 ml centrifugal concentrator and applied onto a Superose 12 10/300 GL column (Amersham Biosciences) equilibrated with GF buffer (20 mM potassium phosphate pH 7.0). Fractions containing flavodoxin were pooled and concentrated to 47 mg ml⁻¹ for crystallization. The purified protein was separated into 50 µl aliquots, flash-frozen in liquid nitrogen and stored at 193 K.

Selenomethionine-substituted D. desulfuricans flavodoxin was expressed and purified as described above with the following modifications. Cells transformed with pET-24c(+)-Ddflavo were grown in M9 minimal medium containing 20 µg ml⁻¹ kanamycin at 310 K. When an optical density of 0.75 at 590 nm was reached, the following were added: 50 mg l⁻¹ isoleucine, leucine and valine, 100 mg l⁻¹ lysine, phenylalanine and threonine and 50 mg l⁻¹ selenomethionine. After 15 min incubation in the dark, IPTG was added to a final concentration of 1 mM (Doublié, 1997 ▶). To maintain reduced conditions, β-mercaptoethanol at a final concentration of 5 mM was added to the resuspended cells before lysis and to all purification buffers (Sharff et al., 2000 ▶; Smith & Thompson, 1998 ▶).

2.2. Crystallization  

Both the native and selenomethionine-substituted flavodoxins crystallized in space group P3₁21 using 0.2 M potassium thiocyanate pH 6.5 and 2.2–2.4 M ammonium sulfate. Crystals in space group P4₃ were obtained for the native flavodoxin using 0.1 M sodium citrate pH 8.8 and 2.4 M ammonium sulfate. All crystals used for data collection were grown using the hanging-drop vapor-diffusion method with a 2 µl drop and a 1:1 ratio of protein to well solution. Crystals were obtained within one week of incubation at 293 K.

2.3. Data collection and processing  

Native and selenomethionine-substituted crystals in the P3₁21 crystal form were cryoprotected by serial transfers to 20%(v/v) glycerol containing 0.2 M potassium thiocyanate and 2.2 M ammonium sulfate as stabilizers and finally to 30%(v/v) glycerol containing the same stabilizers; they were then flash-frozen in liquid nitrogen. Crystals in space group P4₃ were cryoprotected by the same method but with 0.1 M sodium citrate and 2.2 M ammonium sulfate as stabilizers.

The crystals of native and selenomethionine-substituted flavodoxin diffracted to 1.8 Å resolution. Data for the native crystals were collected on our home source using a Rigaku R-­AXIS IV⁺⁺ detector and a Rigaku Denki RU-H3R rotating copper-anode generator with a wavelength of 1.54 Å and Osmic Mirrors and at the Cornell High Energy Synchrotron Source (CHESS) on the A1 and F2 beamlines using a Dual ADSC Quantum 4 CCD at a wavelength of 0.9791 Å. Data for the selenomethionine-substituted crystals were collected on Advanced Light Source (ALS) beamline 4.2.2 using a NOIR-1 MBC detector. A three-wavelength multiwavelength anomalous dispersion (MAD) experiment was performed. Data for the P4₃ crystal form were collected on our home source as described above with Rigaku VariMax HF optics. All data were collected at 100 K using a nitrogen cryostream.

The P3₁21 native data sets were processed using DENZO and SCALEPACK (Otwinowski & Minor, 1997 ▶). The seleno­methionine-derivative data sets were processed using MOSFLM and SCALA from the CCP4 suite (Leslie, 1992 ▶; Collaborative Computational Project, Number 4, 1994 ▶). The unit-cell parameters for all P3₁21 data sets were a = b = 94, c = 237 Å, α = β = 90, γ = 120°. Ultimately, the structure was solved by molecular replacement using the peak-wavelength data set from the selenomethionine-substituted flavodoxin crystals. The P4₃ data set was processed using CrystalClear and d*TREK (Pflugrath, 1999 ▶) in point groups P4 and P4₁2₁2 with unit-cell parameters a = b = 71, c = 113 Å, α = β = γ = 90°. Analysis using phenix.xtriage determined the data in P4₃2₁2 to be over-merged and P4₃ was chosen as the correct space group. The data-collection statistics for the original crystal form (P3₁21, peak wavelength) and second crystal form (P4₃) data sets used for structure determination are shown in Table 1 ▶.

Table 1. Data-collection and processing statistics for the two flavodoxin crystal forms.

Values in parentheses are for the highest resolution shell.

Space group	P3121	P43
Unit-cell parameters
a ()	94.71	71.06
b ()	94.71	71.06
c ()	237.96	112.99
()	90	90
()	90	90
()	120	90
No. of molecules in the ASU	8	4
Beam source	ALS 4.2.2†	Home
Resolution range	202.5	202.0
No. of total reflections	454921	117212
No. of unique reflections	43662	19078
Completeness (%)	99.8 (100.0)	99.1 (98.6)
Redundancy	10.4 (8.0)	6.14 (5.89)
R merge ‡ (%)	10.9 (24.3)	9.0 (22.7)
I/(I)	19.3 (9.8)	11.8 (3.3)

^†Advanced Light Source beamline 4.2.2 at Lawrence Berkeley National Laboratory.

^‡ R _merge = .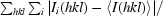

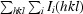2.4. Phasing and refinement  

Initial molecular-replacement trials were attempted using CNS (Brünger et al., 1998 ▶; Brunger, 2007 ▶) and Phaser (McCoy et al., 2007 ▶; Collaborative Computational Project, Number 4, 1994 ▶) with the original crystal form (P3₁21) data and the structure of D. vulgaris flavodoxin (PDB code 1azl; Watenpaugh et al., 1972 ▶; Watt et al., 1991 ▶), which is 46% identical, as a search model, without success. The programs SOLVE (Terwilliger & Berendzen, 1999 ▶), SHARP and AutoSHARP (Vonrhein et al., 2007 ▶; de La Fortelle & Bricogne, 1997 ▶) and phenix.hyss (Adams et al., 2002 ▶) were used for initial phasing efforts by multiwavelength anomalous dispersion (MAD). The second crystal form (P4₃) was solved by molecular replacement using Phaser and was then used as a search model to solve the structure in the original crystal form (P3₁21) by molecular replacement using Phaser with manual selection of correct solutions and manual placement.

Refinement of both structures was performed using CNS and PHENIX. The early stages of refinement were carried out in CNS and included rigid-body and positional refinement. A 2F _o − F _c composite OMIT map was calculated and used for model rebuilding in O (Jones et al., 1991 ▶). Several rounds of refinement and rebuilding followed including positional and individual B-factor refinement and simulated annealing until the R factors converged in the low thirties. phenix.refine was then used for several rounds of refinement with the imposition of noncrystallographic sym­metry (NCS) restraints and application of the appropriate twin law (−h, −k, l for the P3₁21 data and h, −k, −l for the P4₃ data). In the final rounds of refinement the NCS restraints were released as well as the specified twin law for the P3₁21 crystal. Refinement statistics for the final models in both space groups are shown in Table 2 ▶.

Table 2. Statistics for atomic refinement of oxidized flavodoxin.

Space group	P3121	P43
Resolution ()	202.5	202.0
R (%)	21.98	21.12
R free (%)	27.87	24.91
Twin fraction	0.047	0.475
No. of atoms
Protein	8992	4496
Solvent	307	343
Average B factor (2)
Protein	65.65	30.58
Solvent	68.65	34.34
R.m.s. deviations
Bonds ()	0.006	0.005
Angles ()	1.010	0.944
Ramachandran analysis
Favored	88.6	91.5
Additionally allowed	11.4	8.6
Disallowed	0	0

3. Results and discussion  

3.1. P4₃ crystal form  

3.1.1. Initial characterization of P4₃ data  

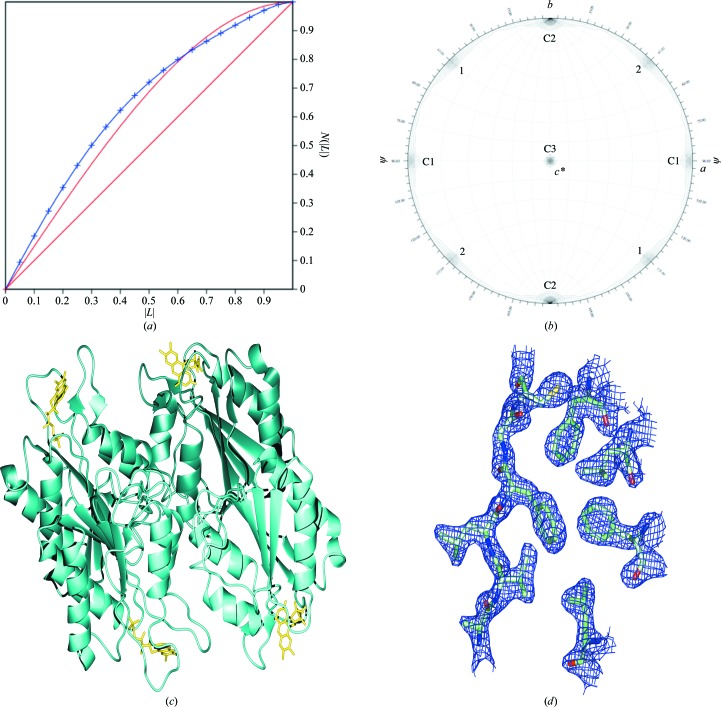
The data were processed in space group P4₃ and analyzed using twinning tests, calculations of a self-rotation function and native Patterson map and phenix.xtriage. The contents of the asymmetric unit were estimated by analysis of the Matthews co­efficient. The most likely composition was judged to be four molecules with 46% solvent content, which correlated with a V _M of 2.27 ų Da⁻¹. Twinning was detected by the L-test using the Merohedral Crystal Twinning Server: Padilla–Yeates Algorithm (Padilla & Yeates, 2003 ▶; Fig. 1 ▶ a) and phenix.xtriage; in both cases near-perfect twinning was indicated with an estimated twin fraction of 0.45 with the twin fractions related by the twin law h, −k, −l.

Figure 1.

P4₃ data analysis and final model. (a) Twinning analysis using the L-test performed with the Merohedral Crystal Twinning Server: Padilla–Yeates Algorithm (Padilla & Yeates, 2003 ▶) shows almost perfect twinning. The curve for the observed data (blue) more closely resembles the curve for theoretically perfectly twinned data (red curve) than that for theoretically untwinned data (red line). The twin fraction related by the twin law h, −k, −l was estimated at 0.45. (b) The self-rotation function plot at κ = 180 shows two noncrystallographic rotational symmetry axes labelled 1 and 2. Peaks corresponding to crystallographic twofold axes for this space group are labelled C. Despite the presence of higher rotational symmetry, assignment of a higher symmetry space group to the data resulted in over-merging. (c) The final model contained four copies in the asymmetric unit, each in unique orientations related by two twofold rotational axes. (d) Representative density from a 2F _o − F _c σ_A-weighted map calculated in Phenix is shown for the final model.

Owing to the high degree of twinning, as demonstrated by the overall intensity statistics (Fig. 1 ▶ a), the data set could be reduced nearly as well in P4₃22 as in P4₃. The merging R value was only slightly higher, 0.098 versus 0.090, and the higher apparent symmetry was also evident in a self-rotation function (Fig. 1 ▶ b). When near-422 rotational symmetry arises from twinning, the presumptive true space group is a tetragonal one with rotational symmetry 4, since these space groups allow true merohedral twinning. Furthermore, the observed systematic absences (00l = 4n) require the presence of a true 4₁ or 4₃ crystallographic symmetry axis. The data were therefore reduced in this symmetry and used in molecular-replacement calculations, testing both P4₁ and P4₃.

3.1.2. Molecular replacement and refinement  

The structure was solved by molecular replacement using the autosearch mode in Phaser with the modified D. vulgaris flavodoxin (PDB code 1azl) as a search model. The flavin mononucleotide was deleted from the search model and the side chains were pruned to the last common atom using CHAINSAW in CCP4 (Collaborative Computational Project, Number 4, 1994 ▶). All solutions found had rotation-function Z scores above 5 and translation-function Z scores above 8; no packing violations were observed for any of the solutions in the sets. All log-likelihood gains increased with the subsequent location of additional copies and were >1600; the top solution LLG was 1821. The top solution as scored by Phaser was used for refinement. Upon calculation of a 2F _o − F _c composite OMIT map, density was observed for each FMN and the side chains of residues absent from the search model, confirming the correct positions of each copy. Refinement was carried out in CNS and then in phenix.refine with the twin law imposed.

3.1.3. Description of the final model  

The final model contained four copies in the asymmetric unit, each in a different orientation, related by two twofold rotational axes (Fig. 1 ▶ c). All were nearly identical, with r.m.s. deviations of <0.2 Å. The final twin fraction refined to 0.488. Density was not observed for the N-terminal methionine, so its coordinates were not included in the final structure. The final R and R _free values were 21.12% and 24.91%, respectively, and structure verification with PROCHECK showed that the model falls well within allowed values (Table 2 ▶); representative density from a 2F _o − F _c σ_A-weighted map for the final model is shown in Fig. 1 ▶(d) (PDB code 3f6r).

3.2. P3₁21 crystal form  

3.2.1. Initial characterization of space group P3₁21 data  

Matthews coefficient analysis suggested that six to eight copies could comprise the asymmetric unit, with V _M values of 3.30 and 2.47 ų Da⁻¹, respectively, and corresponding solvent contents of 62.73 and 50.31%. Since it is impossible to distinguish the exact composition on the basis of Matthews coefficient analysis alone, subsequent data handling was carried out using a wide range of cell-content definitions.

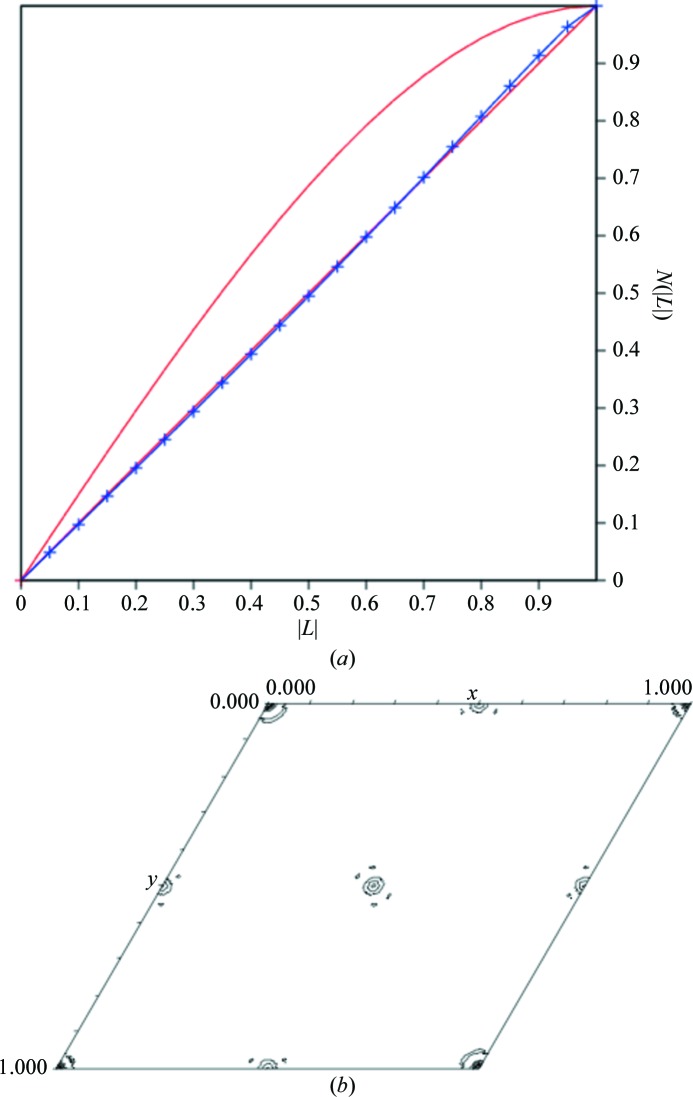
One twin law is applicable for space group P3₁21, the merohedral twin law (−h, −k, l), so we first tested the data for twinning using four different programs: The Merohedral Crystal Twinning Server: Padilla–Yeates Algorithm (Padilla & Yeates, 2003 ▶), TRUNCATE, DETWIN (Collaborative Com­putational Project, Number 4, 1994 ▶) and phenix.xtriage (Adams et al., 2002 ▶). The results from these programs indicated that the data were untwinned (Fig. 2 ▶ a) except for those from phenix.xtriage, which showed a possible twin fraction of approximately 0.25. TRUNCATE, DETWIN and phenix.xtriage use the H-test to examine the cumulative distribution of intensities for twin law-related reflections. The Merohedral Crystal Twinning Server: Padilla–Yeates Algorithm uses the L statistic, which is a modification of the H-test in which the intensies from two reflections related by very close Miller indices rather than a twin law are compared. It has been observed that the H-test is more accurate at estimating the twin fraction, while the L-test has been designed to be more robust in detecting twinning when anisotropy or pseudo-centering exist (Padilla & Yeates, 2003 ▶).

Figure 2.

Tests for twinning and pseudo-translational symmetry in space group P3₁21. (a) The L-test for twinning for the P3₁21 data was performed using the Merohedral Crystal Twinning Server: Padilla–Yeates Algorithm (Padilla & Yeates, 2003 ▶). Theoretical plots are shown in red and the plot for the observed data is shown in blue. No significant twinning was detected as the plot for the observed data overlays with the plot for theoretical untwinned data. (b) The pseudo-translational symmetry operators were determined by analysis of the native Patterson map generated with xfft from the XtalView suite (McRee, 1999 ▶) showing the unique region using a resolution range of 20–4 Å and contoured at 5σ. Off-origin peaks with decreased heights (35%) compared with the origin peak are present at (0.5, 0, 0), (0, 0.5, 0) and (0.5, 0.5, 0), indicating pseudo-translational symmetry.

phenix.xtriage also detected the presence of an off-origin peak representing pseudo-translational symmetry at x, y + ½, z that was 35% of the origin peak. To confirm the presence of pseudo-translational symmetry, a native Patterson map was calculated using the program xfft from the XtalView suite (McRee, 1999 ▶) using the resolution range 20–4 Å (Fig. 2 ▶ b). Off-origin peaks were observed at three positions, (0.5, 0, 0), (0, 0.5, 0) and (0.5, 0.5, 0), with heights of 6888 compared with 27 375 for the origin. These peaks corresponded to the off-origin peak detected by phenix.xtriage. Since the off-origin peak heights are less than the origin peak height, the non­crystallographic symmetry is a pseudo-translation rather than a true translation. No additional rotational symmetry was detected by the calculation of a self-rotation function.

Additionally, analysis of the ratio of the average magnitude of structure factors, 〈F _even〉/〈F _odd〉, in parity groups by resolution range indicated the presence of pseudo-translational symmetry (Table 3 ▶). In this case, 〈F _even〉/〈F _odd〉 over the entire resolution range was 1.8, 1.7 and 2.0 for the h, k and h + k parity groups, respectively. The 〈F _even〉/〈F _odd〉 are higher in the low-resolution bins for these parity groups than in higher resolution bins. For data without the presence of pseudo-translation 〈F _even〉/〈F _odd〉 should be close to 1.0 for all parity groups regardless of resolution; when translational pseudosymmetry is present, 〈F _even〉/〈F _odd〉 is >1 in certain parity groups with a stronger effect at low resolution that breaks down at high resolution (Chook et al., 1998 ▶). Thus, the existence of systematically weak odd reflections further confirms the presence of pseudo-centering symmetry in the direction of x + ½ and y + ½.

Table 3. Statistics of F _even/F _odd in parity groups by resolution.

F _even or F _odd is the averaged magnitude of observed structure factors for reflections with even or odd indices. Only reflections with k 6 were used in the statistics.

Parity group	Resolution ()	F even	No. of even reflections	F odd	No. of odd reflections	F even/F odd
h + k + l	20.06.0	305.21	1576	296.84	1580	1.03
	6.04.0	377.87	2994	394.39	2988	0.96
	4.03.5	416.14	1740	406.16	1738	1.02
	3.53.0	344.47	2746	350.73	2744	0.98
	3.02.5	251.67	4642	255.21	4655	0.99
h + k	20.06.0	431.60	1571	171.58	1585	2.52
	6.04.0	541.79	2984	231.18	2998	2.34
	4.03.5	564.93	1730	258.96	1748	2.18
	3.53.0	461.81	2747	233.22	2743	1.98
	3.02.5	331.25	4646	175.71	4651	1.88
h + l	20.06.0	305.44	1579	296.59	1577	1.03
	6.04.0	377.84	2990	394.40	2992	0.96
	4.03.5	416.18	1737	406.14	1741	1.02
	3.53.0	344.31	2746	350.89	2744	0.98
	3.02.5	251.63	4648	255.25	4649	0.99
k + l	20.06.0	306.50	1574	295.56	1582	1.04
	6.04.0	378.85	2992	393.40	2990	0.96
	4.03.5	415.73	1741	406.56	1737	1.02
	3.53.0	345.32	2741	349.86	2749	0.99
	3.02.5	251.26	4655	255.62	4642	0.98
h	20.06.0	438.60	1566	165.51	1590	2.65
	6.04.0	535.78	2988	236.76	2994	2.26
	4.03.5	557.72	1731	265.93	1747	2.10
	3.53.0	461.29	2745	233.90	2747	1.97
	3.02.5	327.11	4642	179.97	4655	1.82
k	20.06.0	406.77	1791	162.26	1365	2.51
	6.04.0	485.69	3404	254.65	2578	1.91
	4.03.5	498.11	1987	295.27	1491	1.69
	3.53.0	411.47	3138	262.38	2352	1.57
	3.02.5	294.41	5293	199.29	4004	1.48
l	20.06.0	305.83	1575	296.22	1581	1.03
	6.04.0	379.09	2994	393.16	2988	0.96
	4.03.5	415.15	1740	407.14	1738	1.02
	3.53.0	344.30	2747	350.90	2743	0.98
	3.02.5	351.43	4653	255.45	4644	0.98

3.2.2. Initial attempts at phasing by molecular replacement and multiwavelength anomalous dispersion  

Attempts to locate molecular-replacement solutions using the native P3₁21 data sets were carried out in CNS and Phaser, but the large number of molecules, the presence of pseudo-translational symmetry and a poor search model (46% identity) complicated initial attempts at structure solution. With eight copies in the asymmetric unit, the individual contribution of each copy is low, in turn leading to lower scores for the possible solutions for a single copy. The degree of homology between the search model and target proteins was also low; D. desulfuricans (ATCC 29577) flavodoxin is only 46% identical to the D. vulgaris protein. To generate improved search models, differing side chains were pruned to the last common atom or to the γ atom using the program CHAINSAW (Collaborative Computational Project, Number 4, 1994 ▶). After a number of trials with the various models and altering the search parameters, it was presumed that the combination of the low-homology model together with the large number of copies in the asymmetric unit complicated structure solution to the point that phasing by molecular replacement would not be successful. We therefore decided to pursue phasing by multiwavelength anomalous dispersion (MAD).

D. desulfuricans (ATCC 29577) flavodoxin contains four methionines: one N-terminal, one in a predicted loop and two in core regions of the protein. Several programs were used in attempts to locate the Se sites using the MAD data, including SOLVE (Terwilliger & Berendzen, 1999 ▶), phenix.hyss (Adams et al., 2002 ▶) and SHARP/autoSHARP (de La Fortelle & Bricogne, 1997 ▶; Vonrhein et al., 2007 ▶), but all were unsuccessful. The figures of merit were typically ≤0.4 and the maps produced were not interpretable although they contained some regions of contiguous density. Similarly, in the structure determination of superoxide dismutase from Pyrobaculum aerophilum initial molecular-replacement and MAD phasing attempts failed and were attributed to the high copy number (24) in the asymmetric unit, twinning and pseudosymmetry (Lee et al., 2003 ▶).

Combined with the large number of copies in the asymmetric unit, pseudo-translational symmetry can help to explain why initial attempts at phasing by both molecular replacement and multiwavelength anomalous dispersion failed. Although molecular replacement using Phaser is robust at handling large copy numbers in the asymmetric unit, these data were complicated by the presence of pseudo-translational sym­metry (McCoy, 2007 ▶). In the case of MAD phasing, the pseudo-translational symmetry may have reduced the signal-to-noise ratio, leading to the failed attempts to correctly locate the positions of the Se atoms.

3.2.3. Successful molecular replacement in space group P3₁21  

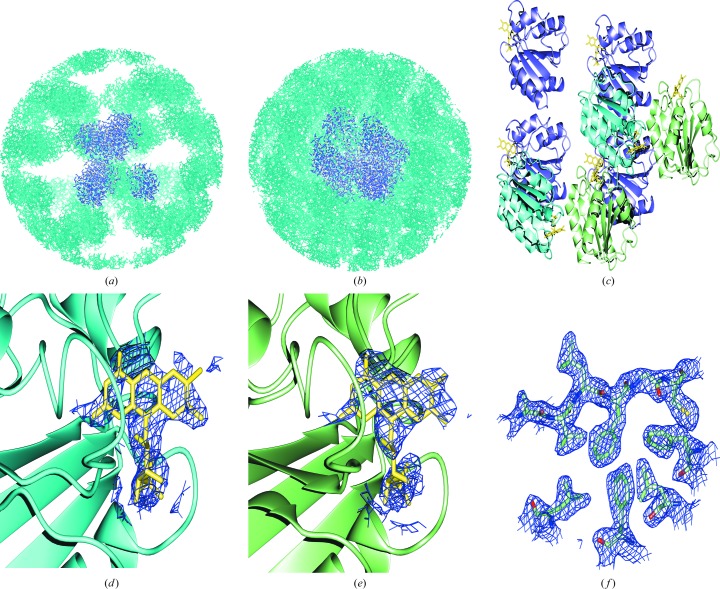
Determination of the structure of D. desulfuricans flavodoxin in the other crystal form, P4₃, provided a much improved search model compared with the D. vulgaris flavodoxin model. Even with an improved search model, finding a molecular-replacement solution was not trivial. Alternative approaches to molecular replacement were used incorporating the positions derived from the pseudo-translational symmetry apparent from the native Patterson map. Molecular-replacement searches were carried out in Phaser (McCoy, 2007 ▶; Collaborative Computational Project, Number 4, 1994 ▶) using the peak-wavelength data set from the MAD experiment. The top solution set as ranked by Phaser was inspected for agreement with the pseudo-translational symmetry operators; six of eight solutions within the top set were offset by the pseudo-translational symmetry operators (x, y, z), (x + ½, y, z), (x, y + ½, z), (x + ½, y + ½, z) and were chosen for incorporation in the starting model. A 2F _o − F _c composite OMIT map in CNS was then calculated and the packing was analyzed by generating a 100 Å sphere of crystallographic symmetry mates in Coot (Emsley & Cowtan, 2004 ▶; Figs. 3 ▶ a and 3 ▶ b). Unoccupied density was observed that coincided with large spaces in the symmetry sphere, suggesting the presence of additional copies in the asymmetric unit. Clear density for the eight FMN molecules that had been excluded from the search model was identifiable and two molecules were placed manually using this density as a guide (Figs. 3 ▶ d and 3 ▶ e). The correct model was composed of eight copies (four copies in one orientation, two copies in a second orientation and two copies in a third orientation); pseudo-translational symmetry operators related molecules in the same orientation (Fig. 3 ▶ c). The addition of the two final copies gave a Matthews coefficient of 2.47 ų Da⁻¹ and 50.3% solvent content.

Figure 3.

Spheres of crystallographic symmetry-related molecules used to analyze packing in the P3₁21 crystal. A 100 Å sphere of crystallographic symmetry mates was generated in Coot from (a) the six copies chosen from the molecular-replacement solution set obtained from Phaser and (b) after manually placing the final two copies in the asymmetric unit. The copies in the model are shown in purple and symmetry mates are shown in cyan. (c) The final model contains eight copies in three unique orientations. Molecules related by pseudo-translational symmetry are shown in the same color. (d, e) Representative density is shown from a 2F _o − F _c composite OMIT map calculated from the six-copy solution set chosen from Phaser drawn for a 2.0 Å region around the FMN molecule which was excluded from the search model and map calculation for (d) a copy located by Phaser and (e) a copy placed manually. (f) Representative density from a 2F _o − F _c σ_A-weighted map calculated in Phenix is shown for the final model.

During refinement, the R factors converged at high values of 35–40%. The application of NCS restraints significantly improved the R factors. The best results were obtained by specifying each set of pseudo-translational symmetry-related molecules as separate NCS groups and the NCS restraints were released before the final rounds of refinement. In order to further refine the structure, it was also necessary to apply the twin law, (−h, −k, l), in phenix.refine. Since the twinning fraction of the final structure refined to less than 0.05, twinning was not responsible for the complications and application of the twin law was then removed for final rounds of refinement. Although the data were not twinned, application of the twin law was essential to overcoming convergence at high R factors. In a similar case of molecular replacement with multiple molecules and pseudo-translation, application of the twin law was necessary for refinement, although twinning was not detected by twinning tests (Lee et al., 2003 ▶). Possible explanations for why the twin law improves refinement are that the pseudo-translational symmetry prevents the detection of twinning by conventional means or was in effect an approximate crystallographic operator and this phenomenon is itself a structural basis for the presence of twinning (Zwart et al., 2008 ▶).

In this case, refinement was carried out in CNS until the R factors converged and was then continued with phenix.refine. The choice of refinement program, application of the twin law and application of NCS restraints were necessary for refining the model to reasonable R-factor values.

3.2.4. Description of the final model  

The final model con­tained eight copies in three orientations (four in one orientation and two sets of two in additional orientations), each related to another by the pseudo-translational symmetry operator x, y + ½, z (Fig. 3 ▶ c). The Trp60-containing loop (residues 60–65) had two conformations; in four copies the loop was straight as observed for all copies in the P4₃ structure and in four copies there was a strong bend of 90°. Copies related by pseudo-translational symmetry also have the same Trp60-containing loop conformation and show the lowest r.m.s. deviations (<0.35 Å). No density was present for the N-­terminal methionine, so its coordinates were excluded from the final structure. The final R and R _free values were 21.98% and 27.87%, respectively. In order to test for systematic bias in the calculation of R _free resulting from the skewed intensities of h and k (Table 3 ▶), the existing R _free test set was split into separate parity groups and new R _free values were calculated against the final model following a round of refinement. If h _odd or k _odd (systematically low) are excluded the R _free decreases by 1.0%, while if h _even or k _even (systematically high) are excluded the R _free rises by 1.0%, suggesting a small but detectable bias. The statistics from PROCHECK show that the structure falls within reasonable ranges for each criterion (Table 2 ▶) and representative density from a 2F _o − F _c σ_A-weighted map is shown for the final model in Fig. 3 ▶(f) (PDB code 3f6s).

Based on the final model, a native Patterson map was calculated from F _calc; as in the observed native Patterson map, off-origin peaks with reduced height compared with the origin (60%) are present at (0.5, 0, 0), (0, 0.5, 0) and (0.5, 0.5, 0) as expected when pseudo-translational symmetry is present, consistent with half the contents of the unit cell being related by pseudo-translational symmetry. Both the expected relative heights of Patterson peaks and the F ratios between parity groups are dependent on the fraction of the cell affected by pseudo-translations.

3.3. Description of oxidized flavodoxin structure  

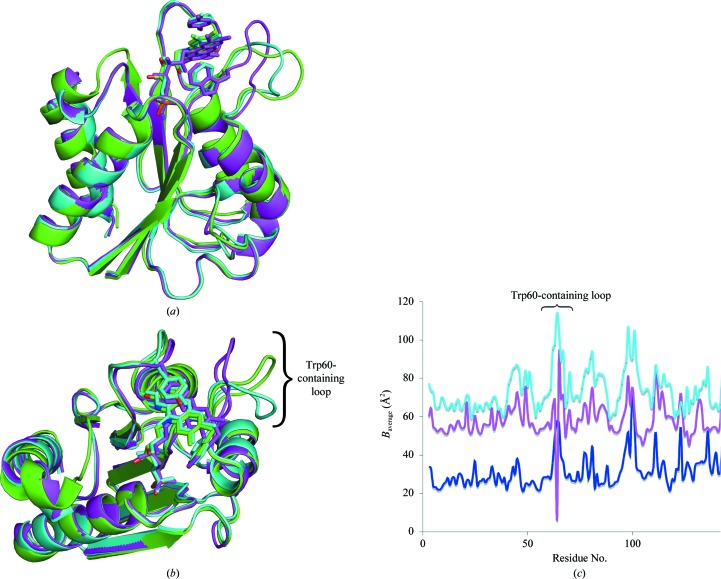
The refined structures of D. desulfuricans (ATCC 29577) flavodoxin in both crystal forms, P4₃ and P3₁21, show the conserved topology of this class of proteins: a five-stranded parallel β-sheet flanked by two α-helices on each side (Fig. 4 ▶). The flavin mononucleotide (FMN) is bound at the periphery between two coordinating loops, with the ribityl group pointing into the molecule. Stacking interactions are formed between the FMN isoalloxazine ring and two residues, Trp60 and Tyr98, contained in the loops that coordinate the FMN. The tyrosine phenyl ring lies almost parallel to the isoalloxazine ring and the Trp60 indole ring is positioned at an angle of approximately 45° relative to that of the isoalloxazine.

Figure 4.

Superposition of ribbon diagrams of the D. desulfuricans (ATCC 29577) flavodoxin structures with two loop conformations with the D. vulgaris flavodoxin. The D. desulfuricans (ATCC 29577) flavodoxin structure with the straight (purple) and bent (cyan) Trp60-containing loop conformations shows (a) high similarity (r.m.s.d. 1.3 Å) to the D. vulgaris flavodoxin structure (PDB code 1azl; green). The major difference lies in the Trp60-containing loop. In (b) the structures are rotated to highlight the flexibility of the Trp60-containing loop. In all three structures the position of Trp60 (sticks) that coordinates the flavin mononucleotide is maintained. The atomic displacement parameters (ADPs) for the Trp60-containing loop are significantly higher than the overall ADP as shown in (c), a plot of the ADP by residue number for the P4₃ (blue), the P3₁21 straight-loop (magenta) and P3₁21 bent-loop (cyan) crystal structures, supporting the conclusion of loop flexibility.

Flavodoxins have been shown to play a role in a number of cellular processes (Gangeswaran & Eady, 1996 ▶; Gulati et al., 1997 ▶; Hoover et al., 1997 ▶; Lawson et al., 2004 ▶; Stok & De Voss, 2000 ▶; Hughes et al., 1995 ▶). The structural details of the interactions between flavodoxin and its specific protein partners are just beginning to be elucidated. Since flavodoxin interacts with a variety of proteins, the residues that are involved in recognition are of great interest. Two conformations of the Trp60-containing loop were identified in the crystal structure of flavodoxin in the P3₁21 crystal form, one with the loop straight as determined in space group P4₃ and one with the loop bent at an approximately 90° angle (Figs. 4 ▶ a and 4 ▶ b). This loop also has significantly higher atomic displacement parameters (ADPs) than the overall structure in both crystal forms, supporting loop flexibility. The overall ADP in the P4₃ crystal structure was 34 Ų compared with 50 Ų for the Trp60-containing loop (residues 61–65) and the overall ADP in the P3₁21 crystal structure was 65 Ų compared with 94 Ų for the Trp60-containing loop (Fig. 4 ▶ c). Although the overall ADP for the P3₁21 structure is very high, the differences in the overall ADP and the ADP for the Trp60-containing loop in the P4₃ structure are still significant, indicating flexibility of the loop in general. Such flexibility was predicted by molecular-dynamics simulations (Muralidhara et al., 2005 ▶) and has also been reported in previously solved flavodoxin structures from Anabaena, C. beijerinckii and D. vulgaris (Martinez-Julvez et al., 2007 ▶; Steensma & van Mierlo, 1998 ▶; Langdon et al., 2001 ▶; Ludwig et al., 1997 ▶). The flexibility of the Trp60-containing loop observed in two conformations in the structure described here may be a starting point for elucidating the residues that are involved in protein-partner recognition. Similarly, it has been proposed that E. coli flavodoxin uses the same loop for partner recognition (Hall et al., 2001 ▶), as was elucidated from its interactions with flavodoxin reductase and cobalamin-dependent methionine synthase (Wan & Jarrett, 2002 ▶; Hall et al., 2001 ▶). It is likely that the flexible loop near the flavin mononucleotide may play a role in this process.

The overall structure is very similar to the structure of D. vulgaris flavodoxin; the average r.m.s. deviation between C^α atoms is 1.3 Å. A ribbon diagram of the D. desulfuricans (ATCC 29577) flavodoxin structures with both the bent and straight conformations of the Trp60-containing loop superimposed with the D. vulgaris flavodoxin structure (PDB code 1azl; Watt et al., 1991 ▶; O’Farrell et al., 1998 ▶) is shown in Figs. 4 ▶(a) and 4 ▶(b). The major differences between the two are in the loop regions that are close to the flavin mononucleotide, but the positions of the Trp60 and Tyr98 relative to the isoalloxazine ring are conserved.

3.4. Interactions with the flavin mononucleotide  

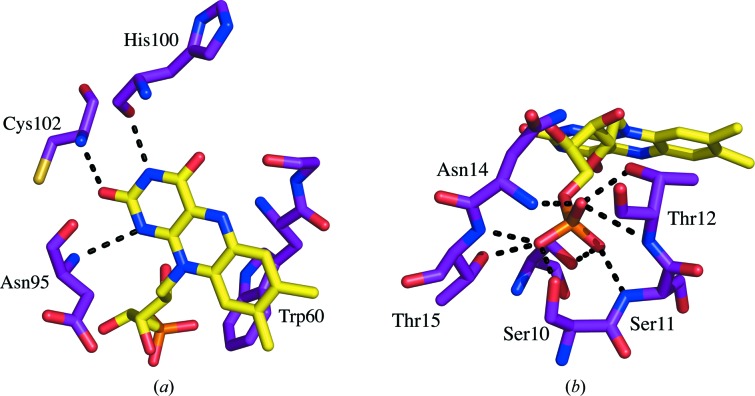
In addition to the stacking interaction with Trp60 and Tyr98, a number of contacts are made between the protein and the FMN molecule, leading to very tight binding (Muralidhara & Wittung-Stafshede, 2005 ▶; Muralidhara et al., 2005 ▶). The hydrogen bonds and estimated distances between atoms calculated using the WHAT IF online server for interatomic contacts are listed in Table 4 ▶ (Rodriguez et al., 1998 ▶). Hydrogen bonds are formed between the backbone atoms of Asp95, His100 and Cys102 and the atoms of the FMN iso­alloxine ring (Fig. 5 ▶ a). Asp95 forms two hydrogen bonds: one with the FMN N1 atom and one with the FMN O2 atom. The Asp95–FMN O2 bond is not observed in all copies and the distance to the FMN N1 atom is quite long (3.2 Å). This non-optimal distance is also found in the D. desulfuricans (ATCC 27774) flavodoxin structure (Romero et al., 1996 ▶). Hydrogen bonds are also formed between the ribityl and phosphate groups of the flavin mononucleotide. No electrostatic contacts are made as might be expected with the phosphate group; the residues surrounding the phosphate group are negatively charged. Instead, a number of hydrogen bonds are made to free NH groups and hydroxy amino-acid side chains forming ion–dipole interactions (Fig. 5 ▶ b; Vyas et al., 2003 ▶; Pflugrath & Quiocho, 1985 ▶).

Table 4. Hydrogen-bond distances () between flavodoxin with both the straight and bent Trp60-containing loop conformations and the flavin mononucleotide.

Bond distances were calculated using the WHAT IF online server (Rodriguez et al., 1998 ▶). The values shown are for a single copy for each loop conformation in the asymmetric unit.

FMN atom	Flavodoxin atom	Straight loop	Bent loop
N1	Asp95 N	3.19	2.92
N3	His100 O	2.93	2.71
O2	Cys102 N	3.01	3.03
O2	Ala59 O	2.63	2.47
O4	Ser93 O	2.63	2.66
O4	Asn14 N2	3.26	3.68
OP1	Thr12 N	2.99	2.77
OP1	Thr12 O	2.55	2.61
OP1	Asn14 N	2.85	2.94
OP2	Ser11 N	2.77	2.81
OP2	Ser58 O	2.91	2.74
OP3	Ser10 O	2.80	2.69
OP3	Thr15 N	3.02	2.74
OP3	Thr15 O1	2.78	2.87

Figure 5.

Hydrogen bonds formed between the flavodoxin and flavin mononucleotide. Hydrogen bonds are illustrated as dashed lines between the flavodoxin atoms and (a) the isoalloxazine ring and (b) the phosphate group of the flavin mononucleotide. The hydrogen-bond network is conserved in both the straight and bent Trp60-containing loop conformations observed. The flavodoxin residues are labeled.

Apoflavodoxin has a high affinity for the flavin mononucleotide cofactor (Mayhew & Tollin, 1992 ▶). Cofactor binding generally stabilizes the protein. However, in the case of D. desulfuricans (ATCC 29577) little or no stabilization was observed upon flavin mononucleotide binding (Apiyo et al., 2000 ▶). The opposite is the case for D. vulgaris, A. vinelandii and Anabaena flavodoxins; in these species the flavodoxin–flavin mononucleotide complex was found to be far more stable than the apoprotein (Bollen et al., 2005 ▶; Campos & Sancho, 2006 ▶). The lower stabilization in the D. desulfuricans flavodoxin may be the consequence of a lower affinity of the flavin mononucleotide for this flavodoxin and corresponds to the fewer interactions observed in the structure presented here compared with flavodoxins from other species.

3.5. Revisiting initial phasing attempts  

The primary complicating factors in solving the structure of D. desulfuricans (ATCC 29577) flavodoxin in the P3₁21 crystal form were (i) the presence of pseudo-centering translational noncrystallographic symmetry and (ii) a high copy number in the asymmetric unit (eight). The previous phasing attempts by molecular replacement and multiwavelength anomalous dispersion were revisited to determine how these two com­plications adversely affected the structure solution and to develop insights into dealing with these factors for future structural studies.

A number of trials were carried out in order to determine what is required of the model and Phaser search variables in order to correctly locate and recognize a partial molecular-replacement solution for at least four copies unrelated by the pseudo-translational symmetry operator that can be used for the complete structure solution. In retrospect, some solutions were located with the pruned model, allowing ten clashes with the rotation-search cutoff reduced to 65% of the top peak. One copy from all three orientations of pseudo-translated copies was represented and could have been used to place additional copies. However, this analysis was only successful in retrospect and required knowledge of the ‘right’ answer as these ‘correct’ solutions were well down the peak list.

As a test of the phasing power of the MAD data, additional searches were performed using the list of known selenium sites from the solved structure as input to SHARP and SOLVE. The fact that the known sites were removed from the site list implies that anomalous data had either been adversely affected by the presence of pseudo-translations or were poorly measured, because the known sites should directly correspond with the detected peaks.

As a further test, the refined model was used to generate a three-wavelength MAD data set using the GENERATE command in SOLVE (Terwilliger & Berendzen, 1999 ▶). 23 of the 24 selenium sites were successfully located with a figure of merit of 0.72. The highest figure of merit obtained from the phasing attempts using the measured data was only 0.41 and appeared to result from a lower than expected anomalous signal at low resolution. The values of both the correlation coefficients and the completeness were relatively similar to those for the observed data. However, the signal-to-noise ratios for anomalous and dispersive differences were much higher for the calculated data compared with the observed data. The successful location of the selenium sites using the calculated data implies that the previous failures are the consequence of errors in the experimentally measured intensities and not the method itself. As discussed previously, translational pseudosymmetry directly affects the diffraction measurements by increasing the number of very weak and very strong intensities observed, essentially increasing the noise present in the data and thus obscuring the very small differences necessary for the successful determination of the anomalously scattering atom positions.

4. Conclusions  

Twinning and pseudo-translational symmetry are two factors that can limit structure solution in crystallography; however, when detected, approaches can be taken to favor a successful outcome. A variety of programs and methods are available for the detection of both twinning and pseudosymmetry, including but not limited to, phenix.xtriage (Adams et al., 2002 ▶), The Merohedral Crystal Twinning Servers (Padilla & Yeates, 2003 ▶; Yeates, 1997 ▶), the self-rotation function (Rossmann & Blow, 1962 ▶) and native Patterson maps (Patterson, 1934 ▶). Since different algorithms are used by different programs and have different strengths, more than one test should be performed in each case. In cases where the detection of twinning is prevented by the presence of pseudo-translational symmetry application of the appropriate twin law in refinement should be investigated.

Complementary approaches to molecular replacement can be used to identify an initial solution. If the pseudo-translational symmetry operator is known, it should be used to identify correct molecular-replacement solutions in a solution set or to place additional copies after initial solutions have been defined. The R factors for an initial solution may be higher than expected for a correct solution (Vajdos et al., 1997 ▶), so initial solutions should not be discarded based on this value alone.

In addition, the signal-to-noise ratio for the data may be reduced by pseudo-translational symmetry. The success of a molecular-replacement search is therefore highly dependent on the quality of the search model, since low-homology models also reduce the signal present in a manner that is generally proportional to the agreement between the search model and the target. Improvements can be made to a search model by modifying the side chains and averaging multiple structures to use as the search ensemble (Schwarzenbacher et al., 2004 ▶). Searches can be additionally complicated by a large number of copies in the asymmetric unit, particularly when they are related by pseudo-translational symmetry (McCoy, 2007 ▶).

Overcoming the challenge of pseudosymmetry in solving the X-ray crystal structure of D. desulfuricans (ATCC 29577) flavodoxin was greatly aided by a careful analysis of pseudosymmetry as well as improvements to the initial search model and the application of an appropriate twin law. It is important to begin to develop insights about the complications in crystallography in­voked by challenging factors such as pseudo-translational symmetry. As more structures are solved that exhibit pseudo-translational symmetry, the methods and programs employed will inevitably improve.

Supplementary Material

PDB reference: flavodoxin, 3f6r, r3f6rsf

PDB reference: 3f6s, r3f6ssf