Abstract
The principle that the standard deviation of estimates scales with the mean estimate, commonly known as the scalar property, is one of the most broadly accepted fundamentals of interval timing. This property is measured using the coefficient of variation (CV) calculated as the ratio between the standard deviation and the mean. In 1997, John Gibbon suggested that different time measurement mechanisms may have different levels of absolute precision, and would therefore be associated with different CVs. Here, we test this proposal by examining the CVs produced by human subjects timing a broad range of intervals (68 ms to 16.7 min). Our data reveal no evidence for multiple mechanisms, but instead show a continuous logarithmic decrease in CV as timed intervals increase. This finding joins other recent reports in demonstrating a systematic violation of the scalar property in timing data. Interestingly, the estimated CV of circadian judgements fits onto the regression of decreasing CV, suggesting a link between short interval and circadian timing mechanisms.
Keywords: time perception, scalar timing, precision, consistency
1. Introduction
Time measurement is used for different purposes at different ranges of duration. For instance, estimation of milliseconds is used in co-ordination with multi-limb movements and muscle contractions, while estimation of tens of seconds to minutes may be used to predict when a foraging area will run out of prey items (Brunner et al. 1997) or how long it will take for a flower to refill with nectar (Pyke et al. 1977). Owing to these disparate functions, it would make sense if different time measurement mechanisms were used for intervals in different temporal ranges (Ivry & Schlerf 2008). This arrangement would also be practical in terms of engineering constraints: since most clock models deal with large interval ranges by adding extra units, e.g. additional pacemakers, accumulators (Gibbon et al. 1984) or decay units (Staddon & Higa 1999).
The hypothesis of multiple clock mechanisms is strongly supported by data showing dissociation in the effect of pharmacological agents upon discrimination thresholds. For instance, drugs, which are known to disrupt working memory, such as benzodiazepine and remoxipride, impair discrimination in the range of seconds without affecting the millisecond range (Rammsayer 1994, 1997, 1999). Conversely, alcohol degrades performance on the same task at the millisecond but not second range (Rammsayer & Vogel 1992). Furthermore, the dopamine antagonist haloperidol impairs timing in both ranges, but ceases to affect the seconds range if body temperature is raised above normal (Rammsayer 1997). Lesion work adds to this literature by showing that damage to the cerebellar hemispheres impairs the performance of rats on a discrimination task of 0.2–0.8, but not of 2–8 s (Breukelaar & Dalrymple-Alford 1999; but see Malapani et al. 1998). Our own investigations with functional magnetic resonance imaging have shown that different regions are associated with measurement of sub- and supra-second intervals (Lewis & Miall 2003a,b). If the gist of the multiple-clock argument is correct and different timing mechanisms are used for measuring intervals of different durations, it is imperative that we determine where the switches from one mechanism to another occur. Knowledge about the location of these ‘break points’ will allow further study of each clock in isolation, and help to minimize the confusion that may otherwise be caused by differences between mechanisms that have not been identified as separate.
One way to search for break points between mechanisms relies upon analysing the distribution of errors associated with timing of intervals at different lengths. Weber's Law is widely believed to apply to time measurement data. Dubbed the ‘scalar property’ within the field of interval timing (Gibbon 1977), this concept predicts that the relative precision of temporal measurement, measured using the coefficient of variation (CV) that is calculated as the standard deviation in estimates divided by the mean estimate, should remain constant across a range of intervals. Although it predicts a constant CV for intervals timed by any single mechanism, the scalar property does not imply that different mechanisms should be associated with identical values for this ratio. In fact, it would be unreasonable to make this assumption as different mechanisms may involve quite different processes and might therefore be associated with different types and magnitudes of error. Instead, it seems more logical to assume that distinct mechanisms do not produce precisely the same value for CV. If this is the case, then the boundaries between the temporal ranges of mechanisms could be marked by sudden changes in relative precision (CV).
Using the scalar property, we can therefore predict that CV remains constant across the durations measured by any single mechanism, but jumps to a new value wherever a switch in mechanisms occurs. If it is possible to find the break points between the operating ranges of different clocks by examining relative precision, then they should be apparent as jumps in CV. This general idea was suggested by Gibbon et al. (1997a) in a review investigating the possibility that distinct mechanisms may be used to measure different temporal durations. Later, work testing the possibility of distinct mechanisms for different tasks (Lejeune & Wearden 2006) or task properties (Merchant et al. 2008) draws on the same principle. It should be noted that CV data can only be interpreted meaningfully under this method if shifts are detected. A flat CV with no shifts or jumps across a temporal scale could arise from multiple mechanisms producing temporal estimates with similar or overlapping CVs and cannot, therefore, be taken as evidence for the use of a single timing mechanism for the whole scale.
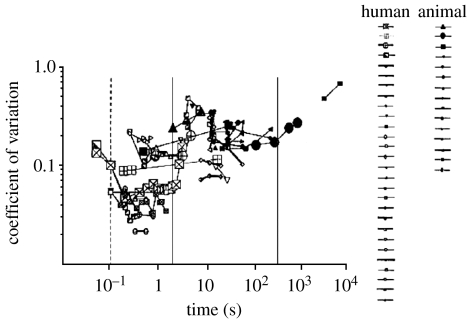
Because no single experiment has characterized the behaviour of CV across a wide range of temporal magnitudes, Gibbon et al. pooled data from a plethora of different sources. Unfortunately, few of these individual reports encompass more than a couple of orders of temporal magnitude, making it necessary to extrapolate from one to the next in order to get an idea about how CV changes over a larger range. This extrapolation led to the confusing picture shown in figure 1. However, two suggestions do emerge from these data. The first is of a gradual increase in CV with longer intervals; the second is of a break point at approximately 100 ms and perhaps another at 1.5 s (figure 1, Gibbon et al. 1997a). These suggested locations for a switch of mechanism are tantalizing, but the noisy nature of the data from which they are drawn means they constitute a tentative hypothesis at best.
Figure 1.
Modified from Gibbon et al. (1997a), this shows CV from a variety of different studies plotted against the target intervals. Gibbon suggests that the pattern may imply two changes or ‘jumps’ in CV, at approximately 0.1 and 1.5 s.
In order to better characterize the behaviour of the CV across a broad range of intervals, it would be necessary to perform a study that used a single task across several orders of magnitude. In the current paper, we have attempted to do precisely this. We describe a series of human studies, each encompassing a broad range of temporal durations (the largest of these spans 68 ms to 16.7 min) and investigate the relative precision of temporal judgements across these durations. Our analysis includes a careful search for break points between mechanisms, as indexed by CV.
2. Material and methods
(a) Experiment 1
This experiment aimed to provide information about the relative precision with which subjects can estimate a number of intervals ranging from 68 ms to 16.7 min. The paradigm employed a temporal reproduction task in which subjects were first presented with an interval, then asked to reproduce it by pressing and holding a button (figure 2).
Figure 2.
Paradigm for the reproduction task used in experiment 1. (a) During the initial presentation phase, changes in screen colour were dictated by the program, which showed a red screen for the interval that was to be timed. Subjects initiated this presentation with a keypress, and were required to release the key when it was terminated by a white screen. (b) The reproduction phase followed and was initiated when subjects depressed the response button again. They held it down for the duration that they thought had passed during presentation. In this figure, the subject overestimates the interval by a small percentage. The number reading distraction task was performed throughout the time that the screen was red or blue.
(i) Subjects
Five healthy female subjects between 20 and 30 years of age participated in this study. They were paid for their time.
(ii) Task
We used 26 intervals, equally spaced on a logarithmic axis. The shortest was 68 ms (4× the screen refresh interval of 16.6 ms), the longest 16.7 min, and the other 24 fell in between (figure 3). This resulted in a geometric series with the modulus 101/6≈1.4678. Each trial consisted of three phases: presentation, reproduction and report (figure 2). Presentation was initiated by a key press and hold, which changed the screen colour from blue to red for the fixed duration of the given interval. When this elapsed, the screen turned white to indicate termination, then returned to blue when the key was released. A second key press and hold initiated the reproduction phase, which continued for as long as the key was held down. When the key was released, the duration of key holding was recorded as the ‘press estimate’, and the subject was prompted to report a ‘typed estimate’ of how long they thought the interval had lasted. For the latter, they typed in an estimate of the interval in milliseconds using the computer keyboard. The computer then returned to the blue pre-presentation state, waiting for initiation of the next trial. Because report data are subject to interval-dependent rounding errors (Huttenlocher et al. 1990), typed estimates were not analysed.
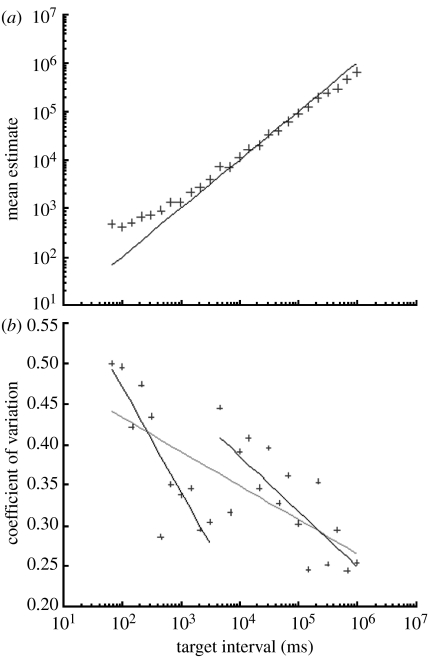
Figure 3.
(a) Demonstrates the relative accuracy with which subjects produced the intervals by plotting the mean of produced durations (calculated by averaging estimates within each subject and then across subjects), against the target (solid line) intervals. (b) Shows the CV for each subject plotted against the target intervals. The grey line represents a simple logarithmic regression. The two black lines represent a two part logarithmic regression. The parameters for all three regression lines, as well as the break point between the two black regression lines, were chosen using an iterative least-squares fitting method.
(iii) Data collection
The 26 intervals in this experiment were tested in two separate blocks of 13, each repeated 10 times. Ranking the intervals from the shortest to the longest, the 13 even ranked intervals fell into one block and the 13 odd ranked intervals fell into the other. These were then presented in pseudorandom order in each test session. It took subjects approximately 1 hour to complete a block, which is to reproduce each of 13 intervals once. Subjects completed both even and odd blocks each day, starting the first at 14.00 and the second at 19.00 or within 30 min of these times, on 10 separate days within a 15 day period. The design was counter-balanced such that each block was completed five times in the afternoon and five times in the evening. Subjects worked alone in a quiet darkened room.
(iv) Distraction task
Throughout the presentation and reproduction phases, subjects performed a distraction task that was intended to prevent them from subdividing the interval by counting. For the purpose of this task, random numbers ranging from 1 to 6 digits in length appeared on the screen. Subjects were asked to read the numbers out loud in long format, i.e. 628 was ‘six-hundred and twenty-eight’ not ‘six-two-eight’, this ensured that the reading did not contain rhythmicity that could be used as a timing cue. Subjects began reading numbers before initiating either presentation or reproduction of an interval. They were instructed to initiate those phases only when comfortable with the number reading task. This ensured that, even for intervals too short for complete reading of one number, subjects were already in the middle of the reading task. Each number appeared for a random length of time chosen from a beta distribution with a minimum of 12 s, a maximum of 9.29 s and mean of 3.3 s. The beta distribution had a long thin tail such that the longer intervals occurred only occasionally. The disappearance of each number was followed by a random interval chosen from the same distribution before the next number appeared. A dictaphone was used to record the oral responses and tapes were scanned to ensure that the task had been performed faithfully.
(v) Apparatus
A computer program written in C and running under DOS on a PC was used to present stimuli and collect responses for this task. This set-up had a temporal precision of approximately 1 ms.
3. Results: experiment 1
As shown in figure 3a, subjects tended to overestimate the short intervals and underestimate the long ones. This is a classic characteristic of timing data know as the ‘central tendency’ (Hollingworth 1913; Treisman 1963); however, the errors were very large for the shortest intervals, with a mean overestimate of approximately 500 per cent on 68 ms, but much smaller on the long intervals, with a mean underestimate of approximately 35 per cent on 16.7 min.
Figure 3b shows a plot of the CV for each subject against the target intervals. Two logarithmic regression lines were fit to these data using an iterative least-squares method performed by a Matlab script that tried every possible combination of parameters and chose the one associated with the smallest residuals. The grey line shows a simple logarithmic regression with a slope of −0.042 (p<0.001, R2=0.132, s.e.=0.01). The solid line shows a bisegmental regression containing two different logarithmic segments, each with its own parameters (slope for the first is −0.129, for the second is −0.068). The break point between these segments falls between the data points at 3.2 and 4.6 s, together with parameters for all line segments as chosen using an iterative least-squares method that tested all possible break points.
An F-test was used to compare the residuals resulting from the simple regression to those resulting from the bisegmental regression, taking the three additional degrees of freedom associated with the latter into account (Clarke & Cooke 1998). This gave an F-statistic of 0.461 (p>0.05), showing that the bisegmental version does not provide a significantly better fit than the simple regression.
4. Discussion: experiment 1
(a) Hypothesized breaks in coefficient of variation
Gibbon et al.'s (1997a) review suggested that the CV may increase abruptly at approximately 100 ms and again at approximately 1.5 s. The two-part regression analysis in figure 3 shows that the best possible break point for our data falls between 3.2 and 4.6 s, quite a distance from the predicted 1.5 s. Furthermore, according to the F-test, the fit provided by this double regression is not significantly better than that provided by the single regression, suggesting that the apparent jump in CV at approximately 4 s is not significant. It is not possible to draw a conclusion about the hypothesized 100 ms jump based upon these data because only one data point (68 ms) falls at a shorter interval.
(b) Violation of the scalar property
The CV does not appear to remain constant even across small ranges of duration, which might be expected to rely upon a single mechanism. Instead, the simple regression shows a logarithmic decrease. This non-scalar timing is unexpected and interesting. Because the slope of this decrease is shallow, it may have been overlooked by past investigators who examined smaller ranges of intervals. Because the scalar property is widely accepted, it seems prudent to treat this initial finding with caution and even some suspicion. Furthermore, the CVs observed here are quite large, with a mean of 0.35, while those reported in fig. 1 from Gibbon et al. (1997a) have a mean closer to 0.1 over a similar range of intervals. This may not be surprising as the task we used was quite difficult: subjects experienced each interval just once before having to produce it, and they were never able to refer to semantic memory representations of the required time because they were never informed as to the durations of target intervals in terms of a standard measure such as minutes or seconds. In addition, they were actively engaged in a secondary task during both the presentation and reproduction phases. The overall difficulty of the task probably leads to the observed low level of accuracy and high level of variance. It is therefore possible that the somewhat uneven pattern of CV decrease can be explained by noise relating to the paradigm rather than to the underlying clock properties, which the experiment aimed to examine.
On these grounds, it seemed important to perform additional experiments to examine the same issue of declining CV. We chose a lower variance paradigm with the aim that a higher proportion of the total variance would be linked to underlying clock properties, that the overall CV would be lower and that this would lead to a tidier pattern of CV values with which to examine the questions of break point and apparent decrease. An obvious way to check for interference due to the distraction task might have been to run the same timing paradigm and simply instruct subjects not to count instead of having them do the distracter task. It would, however, have been impossible to ensure compliance using this method, and we therefore decided upon a more robust approach (see below).
5. Methods: experiments 2–4
(a) Experiment 2
This experiment aimed to examine the behaviour of CV across a similar range of intervals as experiment 1. The paradigm employed a production task wherein subjects were first trained extensively with feedback, then asked to produce the intervals without feedback. This training/production design was intended to provide data with a higher degree of relative precision, and thus lower CV values and less extraneous noise.
(i) Subjects
Twelve naive subjects (six male and six female) participated. They were aged 16–26, had regular sleep/wake patterns, had no history of neurological disease and were not taking any neuroactive medications at the time of the experiment. Subjects were instructed to abstain from food, drink (other than water) and smoking for 1 hour prior to the experiment. They were paid for their help.
(ii) Apparatus
The same equipment used for experiment 1 was also used here. Two new C programs were written: one for training and one for testing.
(iii) Intervals
Ten time intervals, equally spaced on a logarithmic scale between 215 ms and 3.59 min (215 400 ms), were examined. These intervals were divided into ‘even’ and ‘odd’ rank groups as in experiment 1. Subjects were also divided into two groups, the SHORT group, trained on even numbered intervals, and the LONG group, trained on odd numbered intervals. Four subjects (two male and two female) performed both short and long in separate testing sessions, while the remaining eight performed either short or long.
(iv) Train
Subjects were trained with feedback at the start of the first session. They were trained on all intervals, one by one, in random order. The training programme first indicated the length of the interval with a text message, i.e. ‘the first interval is 10 s’, then the subject initiated presentation of the interval, wherein a button press caused the screen to change colour for the relevant duration. Subjects were next prompted to reproduce the duration by pressing and holding a button. After each such estimate, subjects were informed via a text message of the actual duration produced, the percentage of the desired interval produced (produced/target) and whether or not they were within 85 per cent accuracy. Subjects continued to produce estimates of the same interval until a minimum of 10 estimates had been made, and they produced three out of the last four within 85 per cent of the target interval. At this point they were informed that training was complete for this interval and started on the next.
(v) Test
Subjects produced each interval six times in a row without feedback by pressing and holding the button. The order in which intervals were requested was randomized, but once one estimate of any given interval was made, the subject had to complete all six estimates before moving to the next interval. Three separate test sessions were performed in this way (6×3=18 estimates total for each interval) on a single day of testing.
(vi) Distraction task
The same distraction task used in experiment 1 was used throughout training and testing in experiment 2.
(b) Experiment 3
The paradigm of this experiment was identical to experiment 2, but different intervals were chosen. The data were collected as part of another experiment testing the effects of nicotine on time estimation. Because nicotine had no significant impact on mean estimates, these data are compatible with data from experiment 1.
(i) Subjects
Six healthy subjects aged 16–22 (three males and three females) participated. All were self-reported heavy smokers, consuming more than 10 cigarettes per day, but had no history of neurological trauma and were taking no medications at the time of the experiment. They were paid for their help.
(ii) Task
Only four intervals were tested: 463, 2153, 10 000, and 46 345 ms (0.77 min). These intervals are equally spaced on a logarithmic axis, similar to the intervals used in experiments 1 and 2 (figure 4).
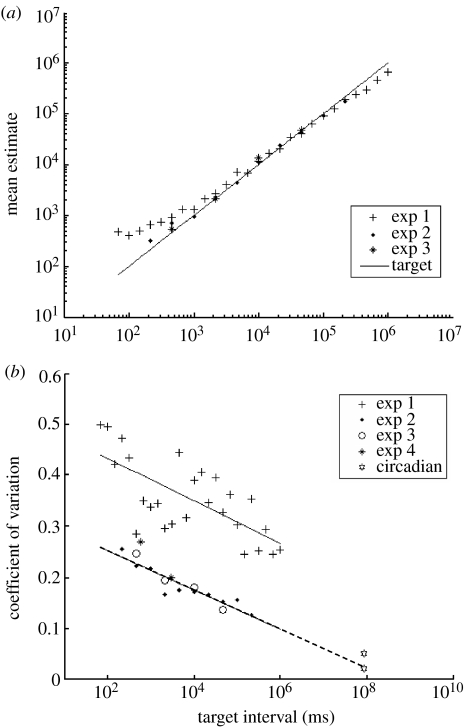
Figure 4.
(a) The mean estimate of within and across the subjects in experiment 1 (pluses), experiment 2 (diamonds) and experiment 3 (asterisks) is plotted against the target interval (solid line). (b) Mean coefficients of variation (averaged within and then across subjects) for experiments 1–4 are plotted against target intervals. The grey line is a simple logarithmic regression of experiment 1 (pluses). The CV of circadian timing has been added (stars). These data were taken from (Wever 1979; Gibbon et al. 1997b). It is interesting to note that the circadian CV commonly observed in free-running circadian timing fit onto the dashed extrapolation of the regression line from experiments 2 to 4.
(c) Experiment 4
This experiment used a comparison paradigm to find the disparity threshold (e.g. the difference between a standard and probe interval), which allowed a subject to accurately determine which of these was longer 85 per cent of the time. Two different standard durations were examined: 3 and 0.6 s. These data have been partially reported in a previous write-up (Lewis & Miall 2003b).
(i) Subjects
Eight healthy subjects aged 20–35 participated. Three were female and five were male. All were paid for their time.
(ii) Task
In each trial, subjects were first presented with a standard cue—a white line that appeared on the screen for the relevant standard duration, then with a probe—a similar line that appeared for the same duration as the standard plus or minus some amount. During the probe presentation, the physical length of the line was increased or reduced by a random fraction of the target mean length (less than or equal to 20% of the mean, with uniform distribution), with each new length presented for a random interval chosen from a beta distribution (mean=322 ms, s.d.=207 ms), constrained to the overall duration required. Subjects ignored fluctuations in line length and responded ‘>’ or ‘<’, using the keyboard, to indicate whether the probe was longer or shorter than the standard. A Kaernbach staircase procedure (Kaernbach 1991) was used to modulate the difficulty of this task and to find a value for the precise disparity between standard and probe at which subjects were accurate 85 per cent of the time. This procedure worked by adjusting the disparity used in each new trial on the basis of performance on the prior trial. Correct responses led to an increase in difficulty, accomplished by making the next probe more similar to the standard by one step (7 ms). Incorrect responses led to a decrease in difficulty by five steps. Each subject performed the staircase at least four times with standards (training), and at least once without (test) for each target duration. If the threshold did not increase by more than 50 per cent when standards were omitted, training ceased and the final disparity threshold was accepted. Otherwise, subjects repeated the staircase with standards, and again without, until the test performance remained stable within 50 per cent of the threshold.
(iii) Analysis
The percentage of each standard interval, which was required as disparity between standard and probe in order to judge correctly 85 per cent of the time, was taken as a measure of precision equivalent to CV. This is known as the difference limen and is often used as a measure of precision (Nichelli et al. 1996).
6. Results: experiments 2–4
The plot of accuracy (figure 4a) shows that experiments 2 and 3 produced data with a higher mean accuracy than experiment 1. The central tendency was observed in these data, but the mean errors were comparatively small, with the largest mean overestimate on short intervals at 44 per cent and the largest mean underestimate of a long interval at 19 per cent.
The plot of CVs shows a lower mean in experiments 2 and 3 than in experiment 1. A single simple regression line was fit to data from experiments 2 and 3 because they used the same task (figure 4b). This line's logarithmic slope of −0.0386 (p<0.001, R2=0.86, s.e.=0.001) is very similar to the −0.0419 slope of the simple regression fit to data from experiment 1. Since the standard error of the slope calculated in experiment 1 is 0.01, the standard errors overlap and these two slopes are therefore statistically indistinguishable.
If the shortest intervals (less than 4.6 s) that might potentially be effected by delays associated with the motor portion of the task are removed from the analysis, and a logarithmic regression is performed on data from the 4.6 s duration and longer, a slope of −0.027 (p<0.001, R2=0.74, s.e. is 0.007) is found. The two data points from experiment 4 do not fit perfectly onto the simple regression line but they are quite near to it, and show a marked decrease from 600 to 3000 ms.
7. Discussion: experiments 2–4
The increase in accuracy and decrease in CV of data in experiments 2 and 3 (figure 4) when compared with experiment 1 show that subjects in the second two studies were less variable and made estimates closer to the target intervals. Because subjects were trained with feedback until they reached an 85 per cent accuracy criterion in the training/testing design, this paradigm forced them to form a solid representation of the intervals before test data were collected. It is therefore unsurprising that the estimates produced during the test phase of experiments 2 and 3 were less variable than the data collected in experiment 1 where intervals were presented just once before each reproduction. The ensuing reduction in non-timing-related confounds means that a much higher proportion of the surviving variance in these experiments is relevant to mechanisms of interest. The data from experiments 2 and 3 are therefore more reliable and informative when used to search for the presence of sudden changes in CV than data from experiment 1.
(a) Absence of break points
Whereas the plot of CV from experiment 1 (figure 3b) weakly suggests a break point between 3.2 and 4.6 s, experiments 2 and 3 show a smoothly decreasing CV (figure 4b). Since the latter dataset is less noisy, we can reasonably accept the smoothly decreasing model over the break point possibility. The fact that the slope calculated in the simple regression for experiment 1 and that calculated for experiments 2 and 3 are statistically indistinguishable supports this conclusion by showing that the gradually decreasing slope is replicable. The observation that the double regression fit to experiment 1 does not provide a significant improvement when compared to the simple regression further supports this conclusion.
(b) Increasing precision/decreasing CV
The trend to decreased CV with increased duration is not only replicated in experiments 2 and 3, it is also much clearer in these data than in experiment 1. The similarity of slopes observed in experiments 2 and 3 makes this replication particularly convincing. The two data points produced by experiment 4 also indicate greater precision when timing longer intervals. Although no regression was fit to these points, it is clear from figure 4 that the slope of such a line would be steeper than those of the other regressions. This steeper slope could be due to either the difference in paradigm and measure of precision or the fact that only two data points were collected. Taken together, experiments 2–4 strongly support increased precision of timing on longer intervals, and this is replicably indexed by the decrease in the CV along a logarithmic slope close to −0.04 as timed intervals become longer.
8. General discussion
As introduced above, constancy of the Weber fraction across different durations (at least for those intervals measured by the same mechanism) is commonly considered to be a fundamental property of interval timing (Gibbon 1977; Buhusi & Meck 2005). Despite this dogma, CV has frequently been observed to vary with interval duration. Most of the studies in figure 1, for instance, show some variation. A decrease in CV for increased durations, as revealed here, has been previously reported at least twice, but was dismissed as a possible artefact of paradigm in one case (Wearden et al. 1998) and as a characteristic of timing very short durations (under 300 ms) in another (Mauk & Buonomano 2004). Interestingly, several recent studies have observed an increase in CV for longer durations (Zeiler & Hoyert 1989; Lejeune & Wearden 1991; Zeiler & Powell 1994), and one observed a U-shaped function (Bizo et al. 2006), with CV decreasing from 1 to 4 s and then increasing again from 8 to 64 s. The authors of this latter study argue that data from a number of other reports also support a U-shaped function, citing Gibbon et al.'s (1997a) review as an example of this (figure 1). Under this line of argument, the short interval data (up to 104 ms) from our own experiment 1 could be loosely interpreted as showing a U shape; however, this is not supported by the regression analysis that shows negative slopes for both halves of the bisegmental regression. Moreover, the bisegmental model was not significantly better than a single linear regression.
Because the studies showing increasing (Zeiler & Hoyert 1989; Lejeune & Wearden 1991; Zeiler & Powell 1994) U-shaped (Bizo et al. 2006) or flat (Mauk & Buonomano 2004) CVs examine just a small segment of the temporal scale, we feel that it would be incorrect to base broad generalizations on any of them. Our own study covers a much wider range of intervals, allowing us to conclude that, at least within the range of 68 ms to 16.7 min, CV decreases as intervals get longer. Because our test intervals were evenly spaced across a log scale, it will be necessary to sample at a higher resolution to determine whether the apparent local increase at approximately 3–5 s is real.
(a) Possibility 1: a single mechanism
The concurrence of timing data with Weber's law is so widely accepted that almost every existing model of time measurement predicts it. The possibility raised here that a single mechanism used across a range of durations, which violates this law, causes problems for most of these models, but these problems are not grave. Subtle adaptations of the noise parameters within most models will accommodate the observed pattern. For instance, the scalar expectancy theory (SET) model (Gibbon 1977) produces scalar timing by combining a memory encoding error (k*), Poisson variance of the pacemaker and ratio comparisons between current and remembered numbers of pacemaker counts. Tweaking the relative contributions of these parameters in a time-independent manner can easily produce a gradually decreasing CV (Gibbon 1991). Similarly, multiple time scales (MTS) (Staddon & Higa 1999) relies upon the slope of the decaying memory function to produce scalar timing. A slight increase in this slope would predict the observed behaviour of CV (Staddon & Higa 1999).
Although SET predicts the scalar property, a simplified version of the same oscillator/accumulator system in which Poisson variance of the oscillator is the only source of error would show an exponential decrease in CV with an increasing number of pacemaker counts (Gibbon 1992). Data following this pattern would strongly support the concept of a pacemaker system with a Poisson pacemaker, unfortunately the observed logarithmic slope of approximately −0.04 is far too shallow to fit this model and does not, therefore, support the Poisson hypothesis.
(b) Possibility 2: multiple mechanisms
It is important to note that the absence of break points from our findings does not argue against the multiple-clock hypothesis. Although the gradual decreasing curve that we describe could be produced by a single clock with gradually increasing precision, it could equally represent an envelope function containing a number of overlapping mechanisms with similar CVs. In this latter case, each multiple mechanisms could either display a decrease or display scalar timing, but be overlapped such that their summation gives the appearance of a continuous decrease at the resolution of our data.
(c) Confounds due to response times and distraction task
One potential confound to experiments 1–3 relates to response times. Movement associated with pressing and releasing the response button can reasonably be expected to involve a variance of up to approximately 200 ms, which is constant across intervals. Such added variance would greatly increase the CV at the briefest intervals, but have no significant effect at durations longer than 2 or 3 s. This type of confound could explain the disproportionate variance associated with the shortest intervals in experiment 1. Importantly, however, this confound could not be responsible for the negative slope seen across the remainder of our data since truncating figure 4b to include only intervals of 4.6 s and above does not remove the negative slope. We can therefore be certain that the gradual reduction in CV across our entire range of intervals is not an artefact of motor confound.
The number reading distraction task is a second potential confound to experiments 1–3 since it could induce differential amounts of variance between very short intervals, where subjects have time to read only one or two numbers, and medium length or long intervals where there is time to read 10 or more such that reading becomes semi-automatic. It is unlikely, however, that the task has differential effects on variance between medium, long and very long intervals where subjects are reading more than 20 numbers in each case. Because the CV continues to decrease across these longer durations, for instance, between 68 s and 7.7 min (where a mean of 40 and 156 numbers are read, respectively), it seems fair to assume that the influence of this variation in distracted attention upon its negative slope is minimal.
Importantly, the comparison task (experiment 4) involved neither motor response nor number reading and could not, therefore, have been effected by these confounds. The measured response in this task reflects the result of discrimination and comes after both stimulus intervals had been presented, thus the perceptual decision cannot be affected by motor delays. Since no distraction task was used, the results are not affected by that type of confound either. The main weakness of these data is their scarcity—since they were collected for only two points of the entire curve. It would be nice to have more points, but the fact that the two intervals that were investigated fit quite well onto the regression of data from experiments 3 and 4 increases confidence in their validity as well as supporting the overall result.
(d) Implications of circadian CV
Two estimates of the CV for circadian timing have been added to the plot of experiments 1–4 in figure 4. These represent the upper and lower limit of the CV observed for circadian timing by humans (Wever 1979; Gibbon et al. 1997b). As shown in the figure, these points straddle the extrapolated regression line fit to data from experiments 2 and 3. This shared regression of precision measures implies a similarity between short interval and circadian timing mechanisms, which are in keeping with work suggesting that there may be interplay between these systems. These include a clinical study describing a human with an suprachiasmatic nucleus (SCN) lesion who showed abnormal variability in tapping continuation of 550 ms intervals and impaired duration discrimination of 400 ms, while tone intensity discrimination was unaffected (Cohen et al. 1997). Furthermore, the drug phospho fluoridate perturbs both circadian rhythm and duration comparisons (Raslear et al. 1988). Also, 1 hour estimates in human subjects correlate with changes in the length of the circadian period during temporal isolation (Aschoff & Kremer 1998). Finally, but of more tentative relevance to mammals, work on fruitflies (Kyriacou & Hall 1980; Kyriacou et al. 1990) shows that timing of short intervals is disrupted in circadian mutants. These flies produce a ‘love song’ that is used in courtship. The song is rhythmic and contains 60 s cycles, which is disrupted such that changes in circadian period correlate with changes in song cycle duration.
One possibility that is consistent with the data cited above is that the circadian pacemaker is simply one in an array of mechanisms, which complement each other in terms of precision and which interact in subtle yet complicated ways. Unfortunately, this suggestion is not in perfect accord with studies demonstrating that brief interval and circadian timing are independent (Lewis et al. 2003; Crystal & Baramidze 2007). Another possible interpretation of the observation that circadian and short interval CV's fall on the same regression is that whatever physiological or engineering principle allows the gradual increase in precision at the millisecond to minutes range also applies to the circadian system.
(e) Summary
We examined human timing across a broad range of intervals (68 ms to 16.7 min) in hopes of detecting jumps in the precision of measurement, which would support the hypothesis that distinct clock mechanisms are used for different subsets of this range. Our data provide no evidence for such a jump. Instead, our four experiments all demonstrate a gradual increase in precision of timing as the intervals measured increase. These findings are significant in that they add to a growing literature demonstrating systematic violations of the scalar property, a fundamental precept of timing. Our data also provide tentative evidence for a link between short interval and circadian timing since the relative precision of the latter fits perfectly onto our regression of increasing precision for the timing for longer intervals.
Acknowledgments
These experiments were approved by the appropriate Oxford Regional Ethics Board.
Footnotes
One contribution of 14 to a Theme Issue ‘The experience of time: neural mechanisms and the interplay of emotion, cognition and embodiment’.
References
- Aschoff A., Kremer P. Determining the best cerebrospinal fluid shunt valve design: the pediatric valve design trial. Neurosurgery. 1998;42:949–951. doi: 10.1097/00006123-199804000-00160. doi:10.1097/00006123-199804000-00160 [DOI] [PubMed] [Google Scholar]
- Bizo L.A., Chu J.Y., Sanabria F., Killeen P.R. The failure of Weber's law in time perception and production. Behav. Process. 2006;71:201–210. doi: 10.1016/j.beproc.2005.11.006. doi:10.1016/j.beproc.2005.11.006 [DOI] [PubMed] [Google Scholar]
- Breukelaar J.W., Dalrymple-Alford J.C. Effects of lesions to the cerebellar vermis and hemispheres on timing and counting in rats. Behav. Neurosci. 1999;113:78–90. doi: 10.1037//0735-7044.113.1.78. doi:10.1037/0735-7044.113.1.78 [DOI] [PubMed] [Google Scholar]
- Brunner D., Fairhurst S., Stolovitzky G., Gibbon J. Mnemonics for variability: remembering food delay. J. Exp. Psychol. Anim. Behav. Process. 1997;23:68–83. doi: 10.1037//0097-7403.23.1.68. doi:10.1037/0097-7403.23.1.68 [DOI] [PubMed] [Google Scholar]
- Buhusi C.V., Meck W.H. What makes us tick? Functional and neural mechanisms of interval timing. Nat. Rev. Neurosci. 2005;6:755–765. doi: 10.1038/nrn1764. doi:10.1038/nrn1764 [DOI] [PubMed] [Google Scholar]
- Clarke G.M., Cooke D. Arnold; New York, NY: 1998. A basic course in statistics. [Google Scholar]
- Cohen R.A., Barnes H.J., Jenkins M., Albers H.E. Disruption of short-duration timing associated with damage to the suprachiasmatic region of the hypothalamus. Neurology. 1997;48:1533–1539. doi: 10.1212/wnl.48.6.1533. [DOI] [PubMed] [Google Scholar]
- Crystal J.D., Baramidze G.T. Endogenous oscillations in short-interval timing. Behav. Process. 2007;74:152–158. doi: 10.1016/j.beproc.2006.10.008. doi:10.1016/j.beproc.2006.10.008 [DOI] [PubMed] [Google Scholar]
- Gibbon J. Scalar expectancy theory and Weber's law in animal timing. Psychol. Rev. 1977;84:279–325. doi:10.1037/0033-295X.84.3.279 [Google Scholar]
- Gibbon J. Origins of scalar timing. Learn. Motiv. 1991;22:3–38. doi:10.1016/0023-9690(91)90015-Z [Google Scholar]
- Gibbon J. Ubiquity of scalar timing with a Poisson clock. J. Math. Psychol. 1992;36:283–293. doi:10.1016/0022-2496(92)90041-5 [Google Scholar]
- Gibbon J., Church R.M., Meck W.H. Scalar timing in memory. Ann. NY Acad. Sci. 1984;423:52–77. doi: 10.1111/j.1749-6632.1984.tb23417.x. doi:10.1111/j.1749-6632.1984.tb23417.x [DOI] [PubMed] [Google Scholar]
- Gibbon J., Malapani C., Dale C.L., Gallistel C. Toward a neurobiology of temporal cognition: advances and challenges. Curr. Opin. Neurobiol. 1997a;7:170–184. doi: 10.1016/s0959-4388(97)80005-0. doi:10.1016/S0959-4388(97)80005-0 [DOI] [PubMed] [Google Scholar]
- Gibbon J., Fairhurst S., Boldberg B. Cooperation, conflict, and compromise between circadian and interval clocks in pigeons. In: Stelmach G.E., Vroon P.A., editors. Time and behaviour. Elsevier; New York, NY: 1997b. pp. 329–385. [Google Scholar]
- Hollingworth H.L. The central tendency of judgement. Arch. Psychol. 1913;4:44–52. doi:10.2307/2012819 [Google Scholar]
- Huttenlocher J., Hedges L.V., Bradburn N.M. Reports of elapsed time: bounding and rounding processes in estimation. J. Exp. Psychol. Learn. Mem. Cogn. 1990;16:196–213. doi: 10.1037//0278-7393.16.2.196. doi:10.1037/0278-7393.16.2.196 [DOI] [PubMed] [Google Scholar]
- Ivry R.B., Schlerf J.E. Dedicated and intrinsic models of time perception. Trends Cogn. Sci. 2008;12:273–278. doi: 10.1016/j.tics.2008.04.002. doi:10.1016/j.tics.2008.04.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaernbach C. Simple adaptive testing with the weighted up-down method. Percept. Psychophys. 1991;49:227–229. doi: 10.3758/bf03214307. [DOI] [PubMed] [Google Scholar]
- Kyriacou C.P., Hall J.C. Circadian rhythm mutations in Drosophila melanogaster affect short-term fluctuations in the male's courtship song. Proc. Natl Acad. Sci. USA. 1980;77:6729–6733. doi: 10.1073/pnas.77.11.6729. doi:10.1073/pnas.77.11.6729 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kyriacou C.P., van den Berg M.J., Hall J.C. Drosophila courtship song cycles in normal and period mutant males revisited. Behav. Genet. 1990;20:617–644. doi: 10.1007/BF01065875. doi:10.1007/BF01065875 [DOI] [PubMed] [Google Scholar]
- Lejeune H., Wearden J.H. The comparative psychology of fixed-interval responding: some quantitative analyses. Learn. Motiv. 1991;22:84–111. doi:10.1016/0023-9690(91)90018-4 [Google Scholar]
- Lejeune H., Wearden J.H. Scalar properties in animal timing: conformity and violations. Q. J. Exp. Psychol. (Colchester) 2006;59:1875–1908. doi: 10.1080/17470210600784649. doi:10.1080/17470210600784649 [DOI] [PubMed] [Google Scholar]
- Lewis P.A., Miall R.C. Distinct systems for automatic and cognitively controlled time measurement: evidence from neuroimaging. Curr. Opin. Neurobiol. 2003a;13:250–255. doi: 10.1016/s0959-4388(03)00036-9. doi:10.1016/S0959-4388(03)00036-9 [DOI] [PubMed] [Google Scholar]
- Lewis P.A., Miall R.C. Brain activation patterns during measurement of sub- and supra-second intervals. Neuropsychologia. 2003b;41:1583–1592. doi: 10.1016/s0028-3932(03)00118-0. doi:10.1016/S0028-3932(03)00118-0 [DOI] [PubMed] [Google Scholar]
- Lewis P.A., Miall R.C., Daan S., Kacelnik A. Interval timing in mice does not rely upon the circadian pacemaker. Neurosci. Lett. 2003;348:131–134. doi: 10.1016/s0304-3940(03)00521-4. doi:10.1016/S0304-3940(03)00521-4 [DOI] [PubMed] [Google Scholar]
- Malapani C., Rakitin B., Levy R., Meck W.H., Deweer B., Dubois B., Gibbon J. Coupled temporal memories in Parkinson's disease: a dopamine-related dysfunction. J. Cogn. Neurosci. 1998;10:316–331. doi: 10.1162/089892998562762. doi:10.1162/089892998562762 [DOI] [PubMed] [Google Scholar]
- Mauk M.D., Buonomano D.V. The neural basis of temporal processing. Annu. Rev. Neurosci. 2004;27:307–340. doi: 10.1146/annurev.neuro.27.070203.144247. doi:10.1146/annurev.neuro.27.070203.144247 [DOI] [PubMed] [Google Scholar]
- Merchant H., Zarco W., Prado L. Do we have a common mechanism for measuring time in the hundreds of millisecond range? Evidence from multiple-interval timing tasks. J. Neurophysiol. 2008;99:939–949. doi: 10.1152/jn.01225.2007. doi:10.1152/jn.01225.2007 [DOI] [PubMed] [Google Scholar]
- Nichelli P., Alway D., Grafman J. Perceptual timing in cerebellar degeneration. Neuropsychologia. 1996;34:863–871. doi: 10.1016/0028-3932(96)00001-2. doi:10.1016/0028-3932(96)00001-2 [DOI] [PubMed] [Google Scholar]
- Pyke G.H., Pulliam H.R., Charnov E.L. Optimal foraging: a selective review of the theory and tests. Q. Rev. Biol. 1977;52:137–152. doi:10.1086/409852 [Google Scholar]
- Rammsayer T.H. Effects of practice and signal energy on duration discrimination of brief auditory intervals. Percept. Psychophys. 1994;55:454–464. doi: 10.3758/bf03205302. [DOI] [PubMed] [Google Scholar]
- Rammsayer T.H. Effects of body core temperature and brain dopamine activity on timing processes in humans. Biol. Psychol. 1997;46:169–192. doi: 10.1016/s0301-0511(97)05251-4. doi:10.1016/S0301-0511(97)05251-4 [DOI] [PubMed] [Google Scholar]
- Rammsayer T.H. Neuropharmacological evidence for different timing mechanisms in humans. Q. J. Exp. Psychol. B. 1999;52:273–286. doi: 10.1080/713932708. doi:10.1080/027249899391070 [DOI] [PubMed] [Google Scholar]
- Rammsayer T.H., Vogel W.H. Pharmacologic properties of the internal clock underlying time perception in humans. Neuropsychobiology. 1992;26:71–80. doi: 10.1159/000118899. doi:10.1159/000118899 [DOI] [PubMed] [Google Scholar]
- Raslear T.G., Shurtleff D., Simmons L. The effects of diisopropyl phosphorofluoridate (DFP) on time perception in rats. Physiol. Behav. 1988;43:805–813. doi: 10.1016/0031-9384(88)90380-0. doi:10.1016/0031-9384(88)90380-0 [DOI] [PubMed] [Google Scholar]
- Staddon J.E., Higa J.J. Time and memory: towards a pacemaker-free theory of interval timing. J. Exp. Anal. Behav. 1999;71:215–251. doi: 10.1901/jeab.1999.71-215. doi:10.1901/jeab.1999.71-215 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Treisman M. Temporal discrimination and the indifference interval. Psychol. Monogr. 1963;77:1–31. doi: 10.1037/h0093864. [DOI] [PubMed] [Google Scholar]
- Wearden J.H., Edwards H., Fakhri M., Percival A. Why ‘sounds are judged longer than lights’: application of a model of the internal clock in humans. Q. J. Exp. Psychol. B. 1998;51:97–120. doi: 10.1080/713932672. [DOI] [PubMed] [Google Scholar]
- Wever R. Springer; New York, NY: 1979. The circadian system of man: results of experiments under temporal isolation. [Google Scholar]
- Zeiler M.D., Hoyert M.S. Temporal reproduction. J. Exp. Anal. Behav. 1989;52:81–95. doi: 10.1901/jeab.1989.52-81. doi:10.1901/jeab.1989.52-81 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeiler M.D., Powell D.G. Temporal control in fixed-interval schedules. J. Exp. Anal. Behav. 1994;61:1–9. doi: 10.1901/jeab.1994.61-1. doi:10.1901/jeab.1994.61-1 [DOI] [PMC free article] [PubMed] [Google Scholar]