Abstract
DiProDB (http://diprodb.fli-leibniz.de) is a database of conformational and thermodynamic dinucleotide properties. It includes datasets both for DNA and RNA, as well as for single and double strands. The data have been shown to be important for understanding different aspects of nucleic acid structure and function, and they can also be used for encoding nucleic acid sequences. The database is intended to facilitate further applications of dinucleotide properties. A number of property datasets is highly correlated. Therefore, the database comes with a correlation analysis facility. Authors having determined new sets of dinucleotide property values are invited to submit these data to DiProDB.
INTRODUCTION
Nucleic acid properties are governed by the corresponding nucleotide sequence. More specifically, many properties such as nucleic acid stability, for example, seem to depend primarily on the identity of nearest-neighbour nucleotides (1). The corresponding nearest-neighbour model is also the basis for RNA secondary structure prediction by free-energy minimization (2). It is known that not only thermodynamic but also conformational nucleotide properties may play a role. It has been shown, for example, that promoter locations can be predicted adopting dinucleotide stiffness parameters derived from molecular dynamic simulations (3). Also, curved DNA is known to play a role in prokaryotic gene expression (4). In addition, physical DNA profiles have been used for an improved promoter prediction (5,6). There are numerous other examples. It is, however, beyond the scope of this brief database description to provide a comprehensive overview. Currently, we are developing a Genome Browser that encodes complete eukaryotic or prokaryotic genomes by thermodynamic and conformational dinucleotide properties. In this context, we have collected more than 100 sets of dinucleotide properties from the literature. Currently, there are two related data collections, the PROPERTY DB (srs6.bionet.nsc.ru/srs6bin/cgi-bin/wgetz?-page+LibInfo+-id+1pFZP1TuQpU+-lib+PROPERTY) with about 30 property sets (7) and plot.it (hydra.icgeb.trieste.it/dna/plot_it.html) with about 50 sets (Vlahovicek,K. and Pongor,S., unpublished data). Both of these databases do not include many of the existing datasets and, in addition, it is difficult to trace back the original data sources. Also, both of them are not included in the NAR Database Collection. Therefore, we have set up the database DiProDB, which is aimed to be a one-stop resource for these properties. With DiProDB we want to provide reliable, easily accessible and comprehensive information on dinucleotide properties that may stimulate the application of these data to a diversity of biological problems.
DATABASE CONTENT
DiProDB currently includes 115 dinucleotide datasets. They were collected from the literature and are classified according to nucleic acid type (DNA and RNA), strand information (double or single), how the data were obtained (experimental, theoretical/calculated) and also according to the general type of the dinucleotide property: thermodynamical (e.g. free energy), conformational (e.g. twist) or letter-based (e.g. GC content). We include the letter-based data to demonstrate relations to thermodynamical and conformational properties. Moreover, most of the current motif discovery approaches are letter-based. An example from our work refers to the identification of significant purine–pyrimidine patterns in restriction enzyme binding sites (8). The number of datasets for each category is shown in Table 1. For each dataset, the 16 dinucleotide values, the unit of measurement, the reference, the classification features as well as comments are provided. If a dataset refers to RNA, it is mentioned in the corresponding property name, if the name does not mention a nucleic acid, it always refers to DNA.
Table 1.
Number of dinucleotide property datasets for each category
| Nucleic acid type |
Strand information |
Mode of property determination |
Property type |
||||||
|---|---|---|---|---|---|---|---|---|---|
| DNA | DNA/RNA | RNA | Double | Single | Experimental | Theoretical/calculated | Thermo-dynamical | Conformational | Letter-based |
| 93 | 7 | 15 | 103 | 12 | 33 | 82 | 34 | 74 | 7 |
USER INTERFACE
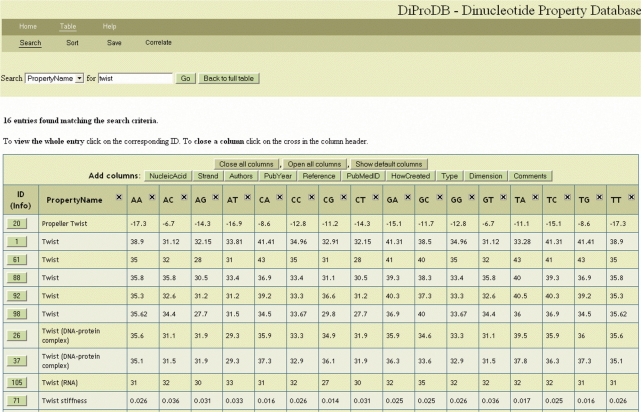
DiProDB displays all data in a single table, see Figure 1. The number and type of columns shown can be customized by the user. When clicking on the ID button in the first column a new page pops up containing all relevant information about the corresponding property. The database entries can be sorted according to three different criteria. There is also a search option for all or for specific columns. The complete table or parts of it can be saved as text file or in a format directly importable into the Genome Browser mentioned in the Introduction section. The DiProDB website contains a Submit button, where users can submit new property datasets.
Figure 1.
Screenshot of the DiProDB table displaying search results for the term ‘twist’ (conformational dinucleotide property) in the property name.
DATA ANALYSES
The DiProDB website contains a Correlate option, where users can calculate Pearson's or Spearman's rank correlation coefficients for all or selected properties. This allows easy identification of dependencies between different dinucleotide properties. As an example in Figure 2, Spearman's correlation data are shown for five different datasets quantifying the twist in B-DNA. All datasets are clearly correlated to each other. However, the extent of correlation is rather different. Correlation coefficients >0.58 are considered as statistically significant (P < 0.01, t-test).
Figure 2.
Pearson's correlation coefficients for five sets of twist angles. ID (Ref.): 1 (9), 61 (10), 88 (11), 92 (12) and 98 (13). Correlation coefficients >0.8 are coloured in green.
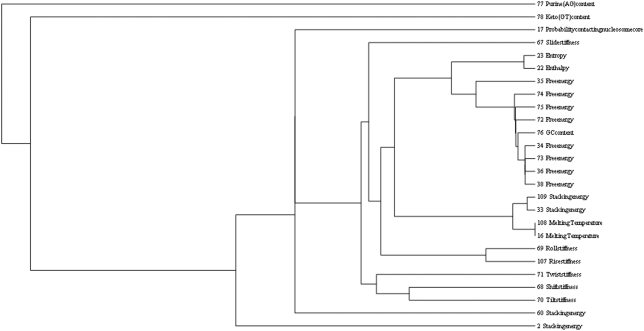
Based on these correlations, we have done different hierarchical clustering analyses to get a deeper insight into the overall correlation of the datasets. Figure 3 shows a single linkage hierarchical clustering of all 23 B-DNA double-strand thermodynamical properties together with the three-dinucleotide letter-based quantities GC content, purine (GA) content and keto (GT) content. This clustering is based on the distance measure 1−|rPearson|, because it is just the absolute value of the correlation, which indicates whether two properties contain similar information. Other correlation measures like Spearman or Kendall-Tau give very similar results. It can be seen that all free-energy data contain more or less the same information and that this is basically equivalent to the GC content. This is very likely due to the simple fact that GC pairs have three H-bonds instead of two in AT base pairs. The complete single-linkage hierarchical clustering of all 115 properties is given in the Supplementary Material (Table 2), where also a corresponding Ward clustering (14) is shown. The latter one shows a separation between a free energy/entropy/enthalpy/stacking energy/melting temperature cluster and another cluster containing all the conformational datasets. The complete single linkage clustering reveals that the most uncorrelated dinucleotide properties are direction, inclination, twist–rise (conformational), stacking energy, tilt, shift, propeller twist and rise.
Figure 3.
Hierarchical clustering of all 23 B-DNA double-strand physicochemical properties and the three-dinucleotide letter-based quantities GC content, purine (GA) content and keto (GT) content. The property sets are designated by their IDs and names.
Table 2.
Content of supplementary material
| Figure S1 | Single linkage hierarchical clustering of 115 dinucleotide properties. |
| Figure S2 | Ward hierarchical clustering of 115 dinucleotide properties. |
| Figure S3 | 115 dinucleotide properties in the first two principal components. |
| Figure S4 | 115 dinucleotide properties in the first and third principal component. |
| Figure S5 | The 16 dinucleotides in the first two principal components. |
| Table S1 | Percentage of importance of the 15 PCs carrying >10−14% of information. |
| Table S2 | Percentage of importance of the first 10 dinucleotide properties in the first 15 PCs in decreasing order. |
| Table S3 | Involvement of the 10 most important dinucleotide properties in the PCs 1–15. |
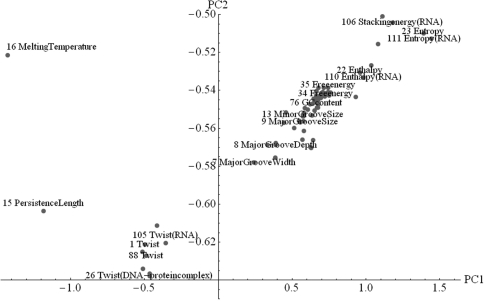
In order to gain more insights into the data, we performed two principal component analyses (PCA) (15). The complete data of 115 properties for 16 dinucleotides corresponds to 115 points in 16-dimensional space (or 16 points in 115-dimensional space). PCA helps to reveal the internal structure of such high-dimensional data by providing lower dimensional pictures of the ‘cloud’ in coordinates corresponding to maximum variance of the data (http://en.wikipedia.org/wiki/Principal_components_analysis). The cloud of all 115 properties in the first two principal components (PCs, the new coordinates) is shown in Figure 4. Only the most uncorrelated property ‘direction’ lies outside the shown region: (PC1,PC2)Direction = (0.1,1.6) (the complete figure containing direction and a PC1–PC3 projection are given in the Supplementary Material; note also that only the first three PCs carry relevant information: PC1 78.5%, PC2 16.9%, PC3 3.3%). The other two outliers are melting temperature and persistence length. This indicates that especially these three properties carry information quite different from the others. Note that the latter two properties are not amongst the outliers according to the above mentioned single linkage clustering, because each one has (at least) one better correlation to other datasets (melting temperature to stacking energy, and persistence length to tilt–shift). Figure 4 also indicates three clusters containing all other properties, one stacking energy/entropy cluster, a twist cluster and the central main cluster.
Figure 4.
All dinucleotide properties plotted in the first two PCs. A few of them are designated by property name and ID.
Finally, we also performed a PCA calculating the 115 principal components for the 16 dinucleotides. The first 15 PCs carry information (23%, 21%, 14%, 12%, 6%, etc.), roughly indicating that about this number of low correlated properties is needed to represent all information of the complete set of 115 properties. The Supplementary Material also contains a corresponding PC1–PC2 plot, together with all detailed information about the performed PCAs.
OUTLOOK
So far the DiProDB database contains 115 sets of dinucleotide properties. In the future, this number is to be increased. We also invite other authors to submit their measured or calculated dinucleotide properties to DiProDB.
SUPPLEMENTARY DATA
Supplementary data are available at NAR Online.
FUNDING
Funding for open access charge: Biotechnology and Biological Sciences Research Council (BBSRC)IFR Core Strategic Grant.
Conflict of interest statement. None declared.
ACKNOWLEDGEMENTS
We are grateful to Friedrich Haubensak for setting up the database and to Rolf Hühne for helpful comments on the database layout.
REFERENCES
- 1.SantaLucia J., Jr A unified view of polymer, dumbbell, and oligonucleotide DNA nearest-neighbour thermodynamics. Proc. Natl Acad. Sci. USA. 1998;95:1460–1465. doi: 10.1073/pnas.95.4.1460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Mathews DH, Turner DH. Prediction of RNA secondary structure by free energy minimization. Curr. Opin. Struct. Biol. 2006;16:270–278. doi: 10.1016/j.sbi.2006.05.010. [DOI] [PubMed] [Google Scholar]
- 3.Goñi JR, Pérez A, Torrents D, Orozco M. Determining promoter location based on DNA structure first-principles calculations. Genome Biol. 2007;8:R263. doi: 10.1186/gb-2007-8-12-r263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Pérez-Martín J, Rojo F, de Lorenzo V. Promoters responsive to DNA bending: a common theme in prokaryotic gene expression. Microbiol. Rev. 1994;58:268–290. doi: 10.1128/mr.58.2.268-290.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Abeel T, Saeys Y, Rouzé P, Van de Peer Y. ProSOM: core promoter prediction based on unsupervised clustering of DNA physical profiles. Bioinformatics. 2008;24:i24–i31. doi: 10.1093/bioinformatics/btn172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Florquin K, Saeys Y, Degroeve S, Rouzé P, Van de Peer Y. Large-scale structural analysis of the core promoter in mammalian and plant genomes. Nucleic Acids Res. 2005;33:4255–4264. doi: 10.1093/nar/gki737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Ponomarenko JV, Ponomarenko MP, Frolov AS, Vorobyev DG, Overton GC, Kolchanov NA. Conformational and physicochemical DNA features specific for transcription factor binding sites. Bioinformatics. 1999;15:654–668. doi: 10.1093/bioinformatics/15.7.654. [DOI] [PubMed] [Google Scholar]
- 8.Nikolajewa S, Beyer A, Friedel M, Hollunder J, Wilhelm T. Common patterns in type II restriction enzyme binding sites. Nucleic Acids Res. 2005;33:2726–2733. doi: 10.1093/nar/gki575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Karas H, Knüppel R, Schulz W, Sklenar H, Wingender E. Combining structural analysis of DNA with search routines for the detection of transcription regulatory elements. Comput. Appl. Biosci. 1996;12:441–446. doi: 10.1093/bioinformatics/12.5.441. [DOI] [PubMed] [Google Scholar]
- 10.Pérez A, Noy A, Lankas F, Luque FJ, Orozco M. The relative flexibility of B-DNA and A-RNA duplexes: database analysis. Nucleic Acids Res. 2004;32:6144–6151. doi: 10.1093/nar/gkh954. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Gorin AA, Zhurkin VB, Olson WK. B-DNA twisting correlates with base-pair morphology. J. Mol. Biol. 1995;247:34–48. doi: 10.1006/jmbi.1994.0120. [DOI] [PubMed] [Google Scholar]
- 12.Suzuki M, Yagi N, Finch JT. Role of base-backbone and base-base interactions in alternating DNA conformations. FEBS Lett. 1996;379:148–152. doi: 10.1016/0014-5793(95)01506-x. [DOI] [PubMed] [Google Scholar]
- 13.Shpigelman ES, Trifonov EN, Bolshoy A. CURVATURE: software for the analysis of curved DNA. Comput. Appl. Biosci. 1993;9:435–440. doi: 10.1093/bioinformatics/9.4.435. [DOI] [PubMed] [Google Scholar]
- 14.Ward JH. Hierarchical grouping to optimize an objective function. J. Am. Stat. Assoc. 1963;58:236–244. [Google Scholar]
- 15.Pearson K. On lines and planes of closest fit to systems of points in space. Philos. Magazine. 1901;2:559–572. [Google Scholar]