Hormone Therapy Improves Femur Geometry Among Ethnically Diverse Postmenopausal Participants in the Women's Health Initiative Hormone Intervention Trials

Abstract

Loss of bone strength underlies osteoporotic fragility fractures. We hypothesized that hormone interventions significantly improve the structural geometry of proximal femur cross-sections. Study participants were from the Women's Health Initiative hormone intervention trials: either the conjugated equine estrogen (CEE) only (N _placebo = 447, N _CEE = 422) trial or the estrogen (E) plus progestin (P) (N _placebo = 441, N _E+P = 503) trial, who were 50–79 yr old at baseline and were followed up to 6 yr. BMD scans by DXA were conducted at baseline, year 1, year 3, and year 6. Femur geometry was derived from hip DXA scans using the hip structural analysis (HSA) method. Mixed effects models with the intent-to-treat analysis approach were used. There were no significant differences in treatment effects between the E-alone and the E + P trial, so the analyses were conducted with participants combined from both trials. Treatment benefits (p < 0.05) on femur geometry were observed as early as 1 yr after the intervention. From baseline to year 6, section modulus (a measure of maximum bending stress) was preserved, and buckling ratio (an index of cortical instability under compression) was reduced by hormone interventions (p < 0.05); the differences in the percent changes from baseline to year 6 between women on hormone intervention versus women on placebo were 2.3–3.6% for section modulus and –5.3% to – 4.3% for buckling ratio. Hormone interventions led to favorable changes in femur geometry, which may help explain the reduced fracture risk observed in hormone interventions.

INTRODUCTION

Adramatic decline in endogenous female hormone levels after menopause has been linked to a greater loss of BMD and a heightened risk of fractures with aging. Whereas estrogen therapy in postmenopausal women has been shown to reduce rates of all fractures by >20% and hip fractures by >30%,(1,2) the potential for elevated risk of breast cancer and stroke contradicts its use in osteoporosis prevention. Nevertheless, further evaluations of existing study data on estrogen effects on bone may clarify mechanisms of interventions using similar biological pathways. One important question is why the 2–4% treatment effect on BMD measured by DXA seems to be inconsistent with the larger effect on fracture incidence. This disconnect seems to be shared by other antiresorptive therapies; indeed, the meta-analysis of Delmas and Seeman(3) showed no relationship between treatment effects on fracture rates and change in BMD.

At the simplest level, an effective treatment could reduce fractures by making falls less likely or by making bones stronger so that fractures are less likely when falls do occur. Hormone therapy does seem to have effects that might reduce the likelihood of falls. For example, estrogen treatment improves preservation of body lean mass after menopause,(4) increases muscle strength,(5) and improves postural balance.(6,7) However, the magnitudes of these effects are also quite small. On the other hand, there is a wealth of animal and human data showing that bone strength declines with estrogen depletion and is improved by restoration.(8) Although a useful clinical surrogate, BMD is not itself a property that governs mechanical strength, although it certainly correlates in a general way with the strength of osteoporotic bones. It may be that underlying dimensional changes alter bone strength in ways that are not always apparent in BMD.

Bone strength (see glossary for more details) is the force required to cause mechanical failure. It cannot actually be measured on bones within individuals but can be predicted from engineering models. Basically, an engineering model is a simulation using dimensions of an object (geometry) and information about its material to predict behavior under load. At present, noninvasive methods cannot evaluate tissue material properties, so models must assume constant values from ex vivo experiments. It is also difficult to image the complex internal geometry of bones for simulations, especially the fine structural details that can only be imaged with sufficient resolution at peripheral sites. Even when imaged with adequate resolution, engineering simulations with an accurate level of structural detail are prohibitively complex even for current computational resources.(9) Practical engineering methods applied to bones in vivo generally assume simplified geometric models that can be reasonably well specified from current CT methods. Those higher radiation dose methods are not often used in large clinical trials, and most studies have even more restricted information on skeletal effects. For example, the bulk of the in vivo evidence on estrogen effects comes from completed studies that mainly evaluated treatments with DXA BMD. Whereas not sufficient for 3D engineering models, it is possible to extract limited geometric information to provide insights into strength effects by reanalyzing archived DXA scans with special software.

The hip structure analysis (HSA) software used in this study has been used to evaluate treatment effects on the proximal femur in clinical trials and observational studies.(10–12) Although the specific effects of hormone therapy on femur geometry are not completely clear, positive effects have been reported from an observational study(13) and a small clinical trial of older women.(10) One advantage of the method is that it presents both the conventional BMD and the geometry of three selected cross-sections through the proximal femur. Thus, the changes in outer dimensions or in the amount of bone that can independently alter BMD in a cross-section can be teased apart, and the distribution effects that influence bending properties can also be evaluated. These data from a larger Women's Health Initiative (WHI) placebo-controlled trial with a longer follow-up and including younger postmenopausal women should permit a clearer picture of hormone therapy on femur BMD and on the underlying geometric strength at a site where the most costly osteoporotic fractures occur.

MATERIALS AND METHODS

The WHI study

The WHI is the largest women's health study in the United States. Details regarding the inclusion and exclusion criteria, recruitment procedures, participants characteristics, hormone intervention regimens, randomization, blinding, and follow-up can be found in the previously published papers.(1,2,14)

Briefly, U.S. women who were 50–79 yr old, postmenopausal, and not likely to change residence or die within 3 yr at the time of enrollment were recruited from 40 clinical centers nationwide between 1993 and 1998. The WHI is made up of an observational study, two hormone trials (estrogen alone or estrogen plus progestin), a calcium and vitamin D supplement trial, and a dietary modification trial. The study protocol and consent forms were approved by the institutional review boards for all participating institutions.

WHI hormone trials

The two WHI hormone trials evaluated estrogen plus progestin (E + P) or estrogen alone (E alone) interventions. To be eligible for the hormone trials, the women had to be free of cancer within the preceding 10 yr except for non-melanoma skin cancers. In addition, if women were using hormones at initial screening, a 3-mo washout period was required before randomization.

In the E + P trial, 16,608 postmenopausal women with an intact uterus were randomized by clinical center into either an intervention group (conjugated equine estrogen 0.625 mg/d and medroxyprogesterone acetate 2.5 mg/d) or a placebo group. These women were followed for an average of 5.2 yr through May 31, 2002. The E + P intervention was terminated ∼3 yr before the planned date because of an adverse effect on breast cancer and a global index showing that the risks exceeded benefits.(2)

In the E-alone trial, 10,739 postmenopausal women with prior hysterectomy were randomly assigned by clinical center to receive either 0.625 mg/d conjugated equine estrogen (CEE) or placebo. Results from interim data analysis by the WHI Data and Safety Monitoring Board suggested that CEE increases stroke and decreases the risk of hip fractures but does not provide overall benefit for chronic disease prevention in postmenopausal women who had hysterectomy. Hence, the E-alone trial was terminated by February 2004 after an average follow-up time of 6.8 yr, 1 yr before the scheduled closeout date (March 2005).(1)

Participants in this study

This study included a subgroup of participants (n = 1813) in the WHI hormone trials who were recruited from three WHI BMD clinical centers (Pittsburgh, PA, USA; Birmingham, AL, USA; and Tucson/Phoenix, AZ, USA) and who received total body, spine, and hip bone scans by DXA (QDR 2000, 2000+, or 4500W; Hologic, Waltham, MA, USA). The BMD centers were chosen to enrich the data with information on minority women.

DXA scans and HSA

DXA scans were conducted at baseline and at years 1, 3, and 6 during the intervention. Standard protocols for positioning and analysis were used by technicians who were trained and certified by the DXA manufacturer and by the WHI DXA coordination center at the University of California at San Francisco. The ongoing quality assurance program monitored spine and hip phantom scans and reviewed a random sample of all subject scans and flagged those with specific problems. Hardware and software changes were tracked with in vitro and in vivo cross-calibrations and by scans of calibration phantoms across instruments and clinical sites.

HSA was conducted on archived scans at the Johns Hopkins University under the supervision of TJB. A separate cross-calibration was conducted on all WHI BMD sites using a special phantom provided by TJB.

In a DXA image, pixels are expressed in grams per square centimeter and represent mineral in grams summed along the X-ray path to the pixel location. Conventional BMD simply averages pixels over a defined region after excluding values below a certain threshold. The strength of an object is typically evaluated using measurements of the load supporting surface of cross-sections through sites where fractures are likely. The HSA software uses a principle first described by Martin and Burr(15) that a line of pixel values in a bone mass image is a projection of the mineral in the cross-section. Assuming that the mineral is distributed as it is in adult cortical bone, the profile integral is a measure of the total bone surface, thus its resistance to axially directed loads. The distribution of the bone surface along the profile can then be used to derive the cross-sectional moment of inertia (CSMI) for resisting bending in the frontal plane of the hip. The CSMI can be used to evaluate bending stress at any point within the cross-section but one is usually interested in the maximum bending stress which is always on the surface at the point farthest from the center of mass (d_max). Maximum bending stress is inversely related to the section modulus (SM), computed as CSMI/d_max. The HSA program computes geometry from five parallel lines one pixel (∼1 mm) apart traversing the bone axis at each of three femur cross-sections that are then averaged. Analysis sites include the narrow neck (NN) across the femur neck at its narrowest point; the shaft, across the shaft at a distance of 1.5 times minimum neck width distal to the intersection of the neck and shaft axes; and the intertrochanter (IT) along the bisector of the angle produced by neck and shaft axes. The HSA program also computes conventional BMD, bone outer diameter (OD), and the location of the center of mass of each cross-section, as well as femur neck length and neck shaft angle. The preceding parameters are directly measured from the mass profiles, but an estimate of buckling ratio (BR) is also generated as an index of susceptibility to local cortical buckling under compressive loads. First, an estimate of mean cortical thickness (CT) is computed using circular (NN or shaft) or elliptical annulus models of the cross-section with a fixed proportion of the measured CSA in the cortical shell (i.e., 60%, 70%, and 100% for NN, IT, and shaft, respectively). The scan-plane outer diameter of the shaft is used as the minor axis outer diameter of the IT ellipse model for BR. Whereas admittedly crude, the estimated BR has been shown to provide a mechanical explanation for the predictive value of low BMD in elderly bones.(16,17) The centroid position generated in computing the CSMI has been shown to be of some value because it is shifted medially with advancing age caused by greater bone loss in the lateral cortex, and this effect is greater among hip fracture cases.(17,18) For the purposes of display, the parameter is expressed as the ratio of distance from the centroid to the medial cortex over outer diameter (result is dimensionless).

Data collection for other covariates

Questionnaires were used at baseline and follow-up to collect information on age, years since menopause, race/ethnicity, smoking, recreational physical activities, energy intake, and alcohol use. Age at menopause was defined as the minimum age at which the participant last reported any menstrual bleeding, had a bilateral oophorectomy, or began using postmenopausal hormone therapy. Caloric intake was assessed using a validated food frequency questionnaire based on instruments previously used in large-scale dietary intervention trials.(19,20) Recreational physical activity was assessed by questions on the frequency and duration of several types of recreational activity, and metabolic equivalent task (MET) scores (defined as the ratio of work metabolic rate to a standard resting metabolic rate, with 1 MET roughly equivalent to the resting metabolism while sitting quietly) were computed as the product of days per week, minutes per day, and MET value for each activity.(21) Physical function was measured using the 10-item Medical Outcomes Study Scale(22) for which a higher score indicates better physical function. Weight was measured to the nearest 0.1 kg on a balance beam scale with the participant dressed in indoor clothing without shoes. Height was measured to the nearest 0.1 cm using a wall-mounted stadiometer. Body mass index (BMI) was calculated as weight (kg)/height (m)².

Statistical analysis

Descriptive analyses and group comparisons (t-test for continuous variables or χ² test for categorical variables) were conducted by intervention for selected characteristics of the study participants at baseline. The intent-to-treat principle was used in the analyses to test intervention effects on BMD and geometry measurements by each hormone trial and for a combined cohort of both trials.

Mixed effects models (random effects models) were used to test the average differences in hip BMD and geometry and in differences in the slope of change with time between the intervention and the placebo groups. A preliminary analysis showed no significant differences in the intervention effects between the E and E + P trials; hence, data were combined in the final analysis. In evaluation of potential confounding factors and interaction terms, models examined baseline age, height, weight, BMD, ethnicity, previous hormone use, years since menopause, smoking, alcohol use, fracture history, osteoporosis history, hip replacement history, total calcium consumption, total vitamin D consumption, physical function, diabetes, and total body percent lean soft tissue mass from DXA. Marginal analyses were used to evaluate each covariate separately, and variables with p < 0.1 were examined in the models with other covariates.

Sensitivity analyses were conducted by including only women who had taken 80% of their assigned pills during the trials. Analyses were also conducted after excluding all ethnicities other than non-Hispanic white women to confirm the findings from the complete cohort.

Scans conducted 6 mo after stopping the trial were excluded from all the analyses and, because few women had year 9 follow-up information, we used only the first 6 yr of follow-up data. All statistical analyses were conducted using STATA (version 9.2).

RESULTS

Characteristics of the study participants at baseline

Participants' baseline characteristics are presented by intervention assignment in Table 1. A total of 441 and 503 women were from the placebo and the intervention arms of the E + P, respectively. In the E-alone trial, 447 women from the placebo and 422 from the intervention arm were included. In the E + P trial, the percentage of black women was higher in the placebo arm than in the intervention arm (11.3% versus 7.6%). In contrast, the percent of Hispanic women was lower in the placebo arm than in the intervention arm (4.5% versus 7.2%; p = 0.039). No significant differences in other measures were observed between the intervention and the placebo arm in either the E + P or E-alone trials.

Table 1.

Baseline Characteristics of the Study Participants [Mean ± SD or N(%)]

	E + P			E alone
	Placebo (N = 441)	Treatment (N = 503)	P	Placebo (N = 447)	Treatment (N = 422)	P
Age at screening (yr)	63.7 ± 7.0	63.4 ± 7.3	0.589	63.5 ± 7.6	63.4 ± 7.7	0.878
Years since menopause	14.2 ± 8.1	14.3 ± 9.4	0.877	19.4 ± 10.1	19.4 ± 10.0	0.943
Height (kg)	161.5 ± 5.9	161.4 ± 5.9	0.724	161.5 ± 6.1	160.9 ± 6.3	0.122
Weight (cm)	73.9 ± 16.2	73.1 ± 14.4	0.406	77.8 ± 15.6	77.8 ± 15.6	0.970
Body mass index (kg/m2)	28.3 ± 5.8	28.1 ± 5.2	0.491	29.8 ± 5.6	30.0 ± 5.6	0.478
Dietary energy (kcal)	1696.0 ± 713.4	1717.0 ± 700.9	0.655	1673.0 ± 767.6	1679.6 ± 740.9	0.900
Total expenditure from physical activity(METS)	12.2 ± 14.7	10.9 ±13.2	0.223	9.4 ±11.5	10.0 ± 13.0	0.501
Total calcium intake (mg)	1036.5 ± 33.1	1029.7 ± 30.4	0.880	922.7 ± 28.1	956.6 ± 32.1	0.427
Total vitamin D intake (μg)	8.9 ± 0.4	8.7 ± 0.3	0.71	7.8 ± 0.3	8.0 ± 0.3	0.723
Total body lean mass (kg)	38.2 ± 5.5	37.7 ± 5.1	0.150	38.8 ± 5.6	38.5 ± 5.5	0.442
Total body percent fat (%)	43.5 ± 7.3	43.8 ± 7.2	0.515	45.7 ± 6.5	46.1 ± 6.7	0.396
Hologic total body BMD (g/cm2)	0.99 ± 0.10	0.99 ± 0.10	0.769	1.01 ± 0.11	1.00 ± 0.11	0.549
Hologic spine BMD (g/cm2)	0.95 ± 0.16	0.94 ± 0.15	0.261	0.98 ± 0.17	0.97 ± 0.16	0.622
Hologic hip BMD (g/cm2)	0.84 ± 0.14	0.83 ± 0.12	0.374	0.86 ± 0.15	0.86 ± 0.13	0.852
Ethnicity
White	363 (82.3%)	418 (83.1%)	0.039	317 (70.9%)	317 (75.1%)	0.123
Black	50 (11.3%)	38 (7.6%)		93 (20.8%)	67 (15.9%)
Hispanic	20 (4.5%)	36 (7.2%)		32 (7.2%)	31 (7.4%)
Native American	6 (1.4%)	3 (0.6%)		4 (0.9%)	3 (0.7%)
Asian/Pacific Islander	0 (0.00%)	4 (0.8%)		1 (0.2%)	0 (0.0%)
Other	2 (0.5%)	4 (0.8%)		0 (0.0%)	4 (1.0%)
Smoking
Never	225 (52.7%)	239 (56.9%)	0.797	238 (54.0%)	239 (56.9%)	0.686
Past	160 (37.5%)	177 (35.5%)		151 (34.2%)	135 (32.1%)
Current	42 (9.8%)	53 (10.6%)		52 (11.8%)	46 (11.0%)
Physical function
<90	263 (61.7%)	302 (60.9%)	0.792	310 (70.5%)	302 (73.8%)	0.272
≥90	163 (38.3%)	194(39.1%)		130 (29.6%)	107 (26.2%)
Hormone use
Never	347 (78.7%)	397 (79.1%)	0.851	281 (62.9%)	251 (59.5%)	0.130
Past	76 (17.2%)	88 (17.5%)		133 (29.8%)	149 (35.3%)
Current	18 (4.1%)	17 (3.4%)		33 (7.4%)	22 (5.2%)
Duration of prior hormone use
None	347 (78.7%)	397 (78.9%)	0.922	281 (62.9%)	251 (59.5%)	0.867
<5 yr	70 (15.9%)	81 (16.1%)		99 (22.2%)	105 (24.9%)
5 to <10 yr	13 (3.0%)	14 (2.8%)		32 (7.2%)	33 (7.8%)
10 to <15 yr	8 (1.8%)	6 (1.2%)		14 (3.1%)	14 (3.3%)
15+ yr	3 (0.7%)	5 (1.0%)		21 (4.7%)	19 (4.5%)

Baseline BMD and femur geometry measures were similar between the intervention and the corresponding placebo group in both trials, but there were significant differences in BMD and femur geometry between the two trials.

Changes in BMD and geometry caused by interventions

The average follow-up time was 4.4 ± 2.2 yr for the participants included in this analysis; the E + P trial stopped earlier than the E-alone trial, resulting in an average follow-up time of 4.2 ± 2.2 versus 4.5 ± 2.2 yr for the E-alone trial. E-alone and E + P trials were combined in all the analysis because no significant difference in treatment effects between the two trials was found (data not shown). BMD and femur geometric measures from baseline to year 6 are shown in Table 2. Group t-tests were used to examine the differences in HSA measures between the hormone intervention and the placebo group at each visit. The results showed that BMD was increased and that the underlying geometry of femur cross-sections was altered in the direction of greater strength with the hormone intervention. Starting at year 1 of the intervention, BMD, cortical thickness, cross-sectional area (CSA), and section modulus at all three femoral sites became higher in the intervention arm in comparison with the placebo arm, although not all the differences reached the statistical significance at α = 0.05. Outer diameters were slightly narrower in the intervention group, but the differences between the intervention and the placebo group were very small, and none of them were statistically significant. BRs at all regions became significantly smaller in the intervention arm in comparison with the placebo arm, with the exception at year 3 at the intertrochanter and shaft region. Centers of mass (centroids) of each cross-section were displaced significantly toward the center of the bone (value closer to 0.5) with treatment, indicating that the distribution of bone tissue in cross-sections was altered to be more symmetrical.

Table 2.

Proximal Femur BMD and Geometry Measurements From Baseline to Year 6 by Hormone Intervention

	Baseline		Year 1		Year 3		Year 6
	Placebo (N = 888)	Hormone (N = 925)	Placebo (N = 806)	Hormone (N = 820)	Placebo (N = 702)	Hormone (N = 733)	Placebo (N = 603)	Hormone (N = 523)
Femoral narrow neck
BMD (g/cm2)	0.71 ± 0.13	0.71 ± 0.12	0.71 ± 0.13	0.73 ± 0.13*	0.72 ± 0.14	0.75 ± 0.13*	0.71 ± 0.13	0.74 ± 0.13*
Cross-sectional area (cm2)	2.04 ± 0.37	2.03 ± 0.35	2.04 ± 0.37	2.08 ± 0.36†	2.07 ± 0.40	2.14 ± 0.38*	2.05 ± 0.41	2.12 ± 0.38*
Outer diameter (cm)	3.01 ± 0.21	3.01 ± 0.21	3.03 ± 0.23	3.02 ± 0.21	3.04 ± 0.25	3.02 ± 0.21	3.05 ± 0.24	3.04 ± 0.23
Section modulus (g/cm3)	0.91 ± 0.20	0.91 ± 0.19	0.92 ± 0.21	0.94 ± 0.19	0.95 ± 0.25	0.97 ± 0.20	0.94 ± 0.22	0.97 ± 0.21
Cortical thickness (cm)	0.14 ± 0.03	0.14 ± 0.02	0.14 ± 0.03	0.14 ± 0.03*	0.14 ± 0.03	0.14 ± 0.03*	0.13 ± 0.03	0.14 ± 0.03*
Buckling ratio	12.55 ± 2.91	12.51 ± 2.69	12.68 ± 2.92	12.24 ± 2.66*	12.58 ± 3.01	11.88 ±2.59*	12.84 ± 3.03	12.18 ± 2.71*
Centroid position	0.459 ± 0.016	0.458 ± 0.016	0.458 ± 0.015	0.458 ± 0.016	0.457 ± 0.017	0.459 ± 0.016†	0.456 ± 0.019	0.458 ± 0.018
Intertrochanter
BMD (g/cm2)	0.72 ± 0.14	0.71 ± 0.13	0.72 ± 0.14	0.73 ± 0.13	0.72 ± 0.15	0.75 ± 0.13*	0.71 ± 0.14	0.74 ± 0.13*
Cross-sectional area (cm2)	3.50 ± 0.69	3.48 ± 0.64	3.51 ± 0.69	3.57 ± 0.65	3.55 ± 0.73	3.66 ± 0.66*	3.52 ± 0.72	3.62 ± 0.65*
Outer diameter (cm)	5.12 ± 0.33	5.13 ± 0.34	5.13 ±0.41	5.14 ± 0.35	5.15 ± 0.36	5.13 ± 0.32	5.19 ± 0.41	5.16 ± 0.34
Section modulus (g/cm3)	2.91 ± 0.63	2.89 ± 0.61	2.93 ± 0.68	2.98 ± 0.63	2.97 ± 0.67	3.06 ± 0.63†	2.98 ± 0.71	3.03 ± 0.62†
Cortical thickness (cm)	0.29 ± 0.06	0.29 ± 0.06	0.29 ± 0.06	0.30 ± 0.10	0.29 ± 0.06	0.31 ± 0.11*	0.29 ± 0.06	0.30 ± 0.06*
Buckling ratio	10.43 ± 2.4	10.52 ± 2.29	10.37 ± 2.35	10.18 ± 2.21	10.4 ± 2.47	9.86 ± 2.09*	10.66 ± 2.44	10.11 ± 2.18*
Centroid position	0.435 ± 0.017	0.434 ± 0.017	0.435 ± 0.017	0.436 ± 0.017	0.433 ± 0.018	0.435 ± 0.017†	0.433 ± 0.019	0.434 ± 0.017
Shaft
BMD (g/cm2)	1.14 ± 0.19	1.13 ± 0.18	1.15 ± 0.19	1.16 ± 0.18	1.17 ± 0.20	1.19 ± 0.18†	1.14 ± 0.20	1.18 ± 0.18†
Cross-sectional area (cm2)	3.10 ± 0.53	3.09 ± 0.50	3.13 ± 0.53	3.15 ± 0.52	3.18 ± 0.56	3.23 ± 0.51	3.12 ± 0.56	3.22 ± 0.50
Outer diameter (cm)	2.87 ± 0.18	2.87 ± 0.19	2.87 ± 0.18	2.86 ± 0.21	2.87 ± 0.18	2.86 ± 0.20	2.88 ± 0.18	2.86 ± 0.19
Section modulus (g/cm3)	1.63 ± 0.31	1.62 ± 0.29	1.65 ± 0.31	1.66 ± 0.30	1.69 ± 0.32	1.71 ± 0.30	1.67 ± 0.32	1.70 ± 0.30
Cortical thickness (cm)	0.40 ± 0.08	0.40 ± 0.08	0.41 ± 0.08	0.41 ± 0.08	0.42 ± 0.09	0.43 ± 0.08†	0.40 ± 0.08	0.42 ± 0.08†
Buckling ratio	3.78 ± 0.93	3.78 ± 0.92	3.73 ± 0.88	3.68 ± 0.87	3.67 ± 0.91	3.53 ± 0.80*	3.80 ± 0.94	3.57 ± 0.81*
Centroid position	0.496 ± 0.010	0.497 ± 0.010†	0.496 ± 0.010	0.498 ± 0.010†	0.497 ± 0.010	0.499 ± 0.010*	0.497 ± 0.010	0.499 ± 0.01†

* p < 0.01 and ^† p < 0.05: significant levels for the difference between the hormone intervention and the placebo group.

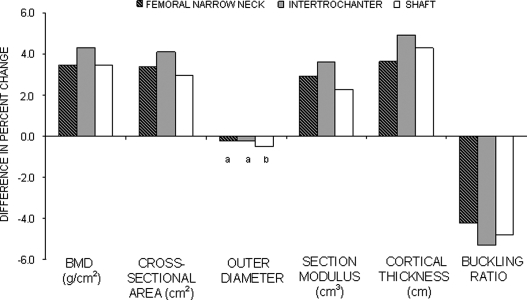
Figure 1 compares the differences in the percent changes from baseline to year 6 between women on hormone intervention versus women on placebo. These data suggested significant positive intervention effects (p < 0.05) from baseline to year 6 on all measures with the exception of the outer diameter at the femoral narrow neck and intertrochanter regions. With the exception of shaft outer diameter, overall effects of hormone interventions seemed to be greater in magnitude at the intertrochanter region in comparison with the other two femoral regions.

FIG. 1.

Difference in percent change in hip BMD and geometry between the intervention and placebo groups from baseline to year 6. All p < 0.01 except ^a p > 0.05 and ^b p < 0.05 for the difference in percent changes between the hormone intervention and the placebo group.

Longitudinal data analysis on intervention effects

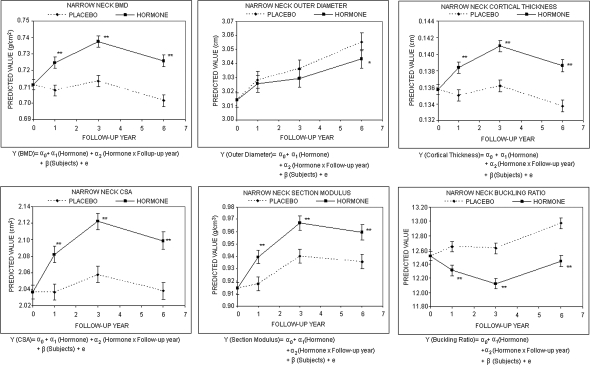
Mixed effects models were used to examine intervention effects on the geometric parameters and BMD in the three femoral regions. For the longitudinal data analysis, each measure from the HSA program was the dependent variable in the corresponding random effects model. The independent variables were hormone treatment, visit (0, 1, 3, 6), and the interaction term between hormone treatment and visit. Figure 2 shows the intervention effect on BMD and geometry at the femur narrow neck. The predicted values from the mixed effects model indicated that women who received hormone interventions had higher BMD, CSA, cortical thickness, and section modulus and lower BR compared with their placebo counterparts. The effects on femur BMD and geometry at the intertrochanter and shaft regions were similar to the narrow neck region (data not shown). Results from these longitudinal models confirmed significant hormone effects on most of the HSA parameters except for outer diameter.

FIG. 2.

Predicted proximal femur geometry by intervention based on the random effects model (mean and SE). “Predicted value” is the predicted mean of HSA measurement based on the random effects model. α, fixed effects parameters; β, random effects parameters; e, residual error. *p < 0.05, **p < 0.01.

No significant confounding factors were identified for the relationship between hormone intervention and femur BMD or geometry. Adding age, ethnicity, height, weight, total body percent lean mass, and smoking did not alter the findings of these mixed effects models, although model fitness was modestly improved (data not shown). Intervention effects were not significantly different by ethnic group as indicated by nonsignificant interaction terms between ethnicity and treatment (data not shown).

Sensitivity analysis

Sensitivity analyses were conducted by restricting the analysis to women who had taken at least 80% of the assigned study pills. Results from the sensitivity analyses showed the same direction but stronger treatment effects (data not shown), supporting the findings of the intent-to-treat analyses.

DISCUSSION

As in other studies,(23–25) we showed modest improvements in femur BMD caused by treatment with conjugated equine estrogen either alone (E-alone) or in combination with progestin (E + P) when contrasted with placebo. None of the effects on BMD or on the underlying geometry differed significantly between E-alone and E + P, suggesting that the treatment effects were exclusively caused by estrogen. The geometric changes underlying the increase in femur BMD were significant but were also both subtle and complex.

Our data suggested that diameters of femur cross-sections in treatment groups expanded more slowly with time (Figs. 1 and 2), but differences only reached significance at the shaft. Femur cross-sections in treatment groups did show significant increases in the amount of bone surface as well as an alteration of the distribution of the material within cross-sections evident as a shift in the centroid. Our interpretations of these effects and their mechanical significance are as follows.

Indirect effects on bone strength

It is well established that bone tissue responds to mechanical load and that the load is primarily mediated by muscle forces. Because estrogen has positive effects on muscle strength,(26) it might stimulate a positive skeletal adaptation response independent of its direct effects on bone tissue. If geometry effects were eliminated by adjusting for body lean mass, this would suggest that the skeletal effects were entirely indirect. Correction for percent lean mass did not eliminate the geometry effect. Hence, we conclude that treatment effects of hormone therapy are mainly caused by a direct influence on bone rather than to an adaptation to a treatment induced increase in muscle load.

Estrogen and load sensitivity

Mechanostat theory holds that bone geometry adapts to ensure that maximum tissue strains (deformations) from prevalent loads remain within certain limits.(27) Strains are proportional to stresses, which under a given loading condition are determined by geometry. A number of investigators,(28) Frost among them,(29) have speculated that estrogen influences mechanostat thresholds, perhaps by altering the sensitivity of bone cells to mechanical stimuli. A bone cell culture assay by Bakker et al.(30) showed that, in the presence of estradiol, cultures produced higher signal levels under equivalent mechanical stimulus. Higher signal levels for a given stimulus should effectively reduce the level of strain necessary for an osteogenic effect; thus, the response should alter geometry so that maximum stresses are reduced for a given load (assuming no effect on the elastic modulus that could not be measured). Our observation that section moduli are higher in women on hormone therapy suggests that their bending stresses are lower when subjected to an equivalent muscle load. This is consistent with the conjecture that estrogen increases the load sensitivity of bone tissue and is worthy of further study.

Effects on centroid position

Several studies have shown that bone loss in the aging proximal femur is not uniform and tends to be greater on the superior-lateral than on the inferior medial regions of cross-sections. Indeed, the cross-sectional analysis of cadaver femur necks by Mayhew et al.(18) could not show any age trends in cortical thinning on the inferior-medial surfaces of the femoral neck in either men or women. One effect of preferential bone loss from lateral regions is that the center of mass of the cross-section shifts toward the medial cortex. A medial shift in the centroid position was evident in the NHANES survey of the U.S. population in both men and women.(18) The effect was greater in femoral necks of women with fractures of the hip(31) and in femoral neck biopsies of fracture cases(18) than unfractured controls. A treatment-induced lateral shift in the centroid position reduces maximum distance to the outer cortical surface (d_max), causing positive effects on SM and on BR.

Effects on susceptibility to local buckling

The generalized expansion of femur diameter accompanying the aging process seems to preserve bending strength (SM) in the presence of net bone loss, but it is achieved with progressively less bone mass (thinner cortices) as diameter increases. If carried too far, strength begins to be compromised by susceptibility to local buckling under compressive loads. In smooth thin-walled hollow tubes, this occurs when the ratio of outer diameter to wall thickness (BR) exceeds a factor of 10.(32) BR can only be crudely estimated from DXA data by combining measured dimensions with a model and, because proximal femurs are not strictly hollow, it is uncertain what values estimated by this method are actually unstable. If local buckling does contribute to strength loss, a treatment-induced reduction in susceptibility should supplement positive treatment effects on CSA and section modulus. A definitive conclusion on the strength contribution of local buckling would require more sophisticated 3D engineering methods(33) than are possible to construct from 2D DXA data. Nevertheless, DXA estimates of BRs seem to explain why low BMD is predictive of hip fracture and why men fracture at higher BMD levels than women.(16,34) The observation that hormone therapy significantly reduces BR suggests that treatment improves cortical stability in the proximal femur, supplementing its positive effects on CSA and SM. It may be important to note that, although BRs are reduced with treatment at early time points, they return to baseline after 6 yr, whereas values in untreated individuals continue to rise. This may suggest that hormone therapy produces an age displacement in the onset of fragility, but consistent with the epidemiological evidence, does not prevent it entirely.

Comparison with results from other studies

The results from this study support previous findings on positive effects of hormone interventions on femur geometry from an observational study(13) and from a 3-yr intervention study.(10) Despite the differences in age groups and duration of interventions, our results are similar to the 3-yr study Greenspan et al. in older women, suggesting significant treatment effects by hormones on bone CSA, SM, CT, and BR in the femoral narrow neck, intertrochanter, and shaft regions, although there were some differences in results. For example, whereas BRs after treatment were significantly smaller in all regions than placebo in this study, the smaller study on an older cohort by Greenspan et al. did not observe a positive effect at the NN and IT regions where buckling would be likely. We also note that consistent with the report of Greenspan et al.,(10) geometric effects of hormone therapy were greatest at the IT region in comparison with the NN and shaft. Interestingly, this was also evident in the alendronate cohort of Greenspan et al. and with both alendronate and denosumab treatments in a report on postmenopausal women by Beck et al.(35) The greater effect may have something to do with the interaction between treatment and load response at that highly stressed site and may be worthy of further study.

This is the first study of this kind that included multi-racial/ethnic groups. This paper is also unique in its study population, interventions, measurements, and longitudinal analysis approach for evaluating effects on femur geometry in a large cohort of postmenopausal women.

Study limitations

Our primary interest was in delineating treatment effects on femur geometry, but there are limitations to the DXA-based methodology for that purpose. Because the geometry is derived from a 2D image, the method can only evaluate resistance to bending in the plane of the DXA image, and one cannot be certain that treatment effects are equivalent with respect to bending in other directions. Difficulties in achieving consistent positioning of the femur in that plane make the method relatively imprecise.(36) Although we suspect that hormone therapy has a small suppressive effect on periosteal apposition, the imprecision of this method is likely behind our inability to definitively conclude that this is so. One possible confounder is that the HSA algorithms assume that bone tissue mineralization is that of normal adult bone tissue, and this may have an effect on the results. The magnitude of the effect of hormone therapy on mean tissue mineralization based on biopsy data seems to be small,(37) but if femurs of untreated postmenopausal women are undermineralized, the HSA method may overestimate the geometric change caused by treatment. Note that the mineralization effect would not influence treatment changes in outer diameter or location of the centroid, which do not require the assumption.

We should also point out that experience with HSA in large observational studies indicate that predictive models using femur geometry only equal the performance of BMD on the same population.(16,17) The problem with BMD is it is nonspecific, because a given value may be produced by several different underlying factors. Furthermore BMD has been far less useful in treatment monitoring than in fracture prediction.(3,38) The HSA method extends the value of the DXA data by providing mechanical insights into the underlying effects that alter the BMD as well as into the changes in bone tissue distribution that are not evident in BMD.

The study showed that both E-alone and E + P significantly improved femur strength as estimated from hip structure analysis in age and ethnically diverse postmenopausal women during an intervention lasting >5 yr. Intervention effects were very similar between the two hormone trials, although the study participants differed in some baseline characteristics and in baseline BMD and femur geometry. With multiple time points of measurements during the intervention, this study showed that the magnitude of the hormone intervention effects on hip geometry may vary with time as suggested by a significant interaction term of intervention assignment and years of intervention. Nevertheless, the differences in rates of changes were small between time points and should be interpreted with caution. We were able to examine a large number of covariates including age, race/ethnicity, BMI, baseline hormone use, and body composition as confounding factors and effect modifiers. The results from this study indicate that the intervention effects of hormones on femur geometry were not significantly confounded or modified by these covariates in this WHI cohort.

Conclusions

A geometric assessment of the effects of hormone intervention on the proximal femur indicated significant increases in the amount of bone tissue in measured cross-sections that should improve resistance to axially directed loads. There were also significant treatment effects on the scan plane distribution of that tissue. Medial shifts in the center of mass associated with preferential bone loss on lateral surfaces were reversed with treatment. This had positive effects on resistance to bending loads and on estimates of susceptibility to local bucking. We were only able to detect suppressed periosteal apposition by hormone therapy at the proximal femur shaft but not at the narrow neck and intertrochanter regions, where the effect might further reduce buckling susceptibility. Overall, there were positive effects of hormone therapy on the structure of the femur underlying the changes in BMD.

APPENDIX 1: GLOSSARY OF TERMS

Centroid: location of the center of mass of the hard tissue in the cross-section and where bending stresses are zero (also called neutral axis); measured by HSA from the mineral mass profile. Used in computing the CSMI and SM, but also useful in evaluating the symmetry of a cross-section, because fragile NN and IT cross-sections are more asymmetric because of greater differences in cortical thickness on opposite margins.

Cross-sectional area (CSA): total bone surface in a cross-section, exclusive of soft tissue spaces and pores. Forces directed along a long bone (axial forces) are distributed over the CSA; hence, axial compressive stress varies inversely with CSA.

Cross-sectional moment of inertia (CSMI): The cross-sectional surface weighted by the square of distance from the center of mass of the cross-section. Bending stress within a cross-section depends inversely on the CSMI divided by the distance from the center of mass.

Geometric strength: that component of strength that governs stresses and not the ability of the material to withstand them (which currently cannot be measured by noninvasive methods). A method that evaluates only geometry (HSA and CT-based methods) can only assess geometric strength.

Geometry or structural geometry: the dimensions of the supporting material within an object, expressed in engineering terms especially within cross-sections.

Local buckling: A failure mode where thin, relatively flat regions of a structure under compressive loads may bend (fold or crumple) locally leading to complete failure.

Section modulus (SM): maximum bending stress in a cross-section is located at maximum distance from the center of mass (d_max) and is thus inversely related to the SM, where SM = CSMI/d_max.

Strength: the loading force applied under a specific condition that causes internal stresses to exceed the material limits. Two material endpoints are commonly used: ultimate strength is the force that causes complete material failure, whereas yield strength is the force that causes permanent material damage to initiate. The latter is usually used in predictive models because of the large variability in behavior of complex objects like bones between yield and complete failure.

Stress: force concentrations (per unit area) within an object from applied loads. Types of stress (i.e., tension, compression, torsion and shear) depend on how loads are applied, but magnitudes depend entirely on geometry of the object.

APPENDIX 2: SHORT LIST OF WHI INVESTIGATORS

Program Office: (National Heart, Lung, and Blood Institute, Bethesda, MD) Elizabeth Nabel, Jacques Rossouw, Shari Ludlam, Linda Pottern, Joan McGowan, Leslie Ford, and Nancy Geller.

Clinical Coordinating Center (Fred Hutchinson Cancer Research Center, Seattle, WA): Ross Prentice, Garnet Anderson, Andrea LaCroix, Charles L. Kooperberg, Ruth E. Patterson, Anne McTiernan; (Wake Forest University School of Medicine, Winston-Salem, NC) Sally Shumaker; (Medical Research Labs, Highland Heights, KY) Evan Stein; (University of California at San Francisco, San Francisco, CA) Steven Cummings. Clinical Centers: (Albert Einstein College of Medicine, Bronx, NY) Sylvia Wassertheil-Smoller; (Baylor College of Medicine, Houston, TX) Jennifer Hays; (Brigham and Women's Hospital, Harvard Medical School, Boston, MA) JoAnn Manson; (Brown University, Providence, RI) Annlouise R. Assaf; (Emory University, Atlanta, GA) Lawrence Phillips; (Fred Hutchinson Cancer Research Center, Seattle, WA) Shirley Beresford; (George Washington University Medical Center, Washington, DC) Judith Hsia; (Los Angeles Biomedical Research Institute at Harbor-UCLA Medical Center, Torrance, CA) Rowan Chlebowski; (Kaiser Permanente Center for Health Research, Portland, OR) Evelyn Whitlock; (Kaiser Permanente Division of Research, Oakland, CA) Bette Caan; (Medical College of Wisconsin, Milwaukee, WI) Jane Morley Kotchen; (MedStar Research Institute/Howard University, Washington, DC) Barbara V. Howard; (Northwestern University, Chicago/Evanston, IL) Linda Van Horn; (Rush Medical Center, Chicago, IL) Henry Black; (Stanford Prevention Research Center, Stanford, CA) Marcia L. Stefanick; (State University of New York at Stony Brook, Stony Brook, NY) Dorothy Lane; (The Ohio State University, Columbus, OH) Rebecca Jackson; (University of Alabama at Birmingham, Birmingham, AL) Cora E. Lewis; (University of Arizona, Tucson/Phoenix, AZ) Tamsen Bassford; (University at Buffalo, Buffalo, NY) Jean Wactawski-Wende; (University of California at Davis, Sacramento, CA) John Robbins; (University of California at Irvine, CA) F. Allan Hubbell; (University of California at Los Angeles, Los Angeles, CA) Howard Judd; (University of California at San Diego, LaJolla/Chula Vista, CA) Robert D. Langer; (University of Cincinnati, Cincinnati, OH) Margery Gass; (University of Florida, Gainesville/Jacksonville, FL) Marian Limacher; (University of Hawaii, Honolulu, HI) David Curb; (University of Iowa, Iowa City/Davenport, IA) Robert Wallace; (University of Massachusetts/Fallon Clinic, Worcester, MA) Judith Ockene; (University of Medicine and Dentistry of New Jersey, Newark, NJ) Norman Lasser; (University of Miami, Miami, FL) Mary Jo O'Sullivan; (University of Minnesota, Minneapolis, MN) Karen Margolis; (University of Nevada, Reno, NV) Robert Brunner; (University of North Carolina, Chapel Hill, NC) Gerardo Heiss; (University of Pittsburgh, Pittsburgh, PA) Lewis Kuller; (University of Tennessee, Memphis, TN) Karen C. Johnson; (University of Texas Health Science Center, San Antonio, TX) Robert Brzyski; (University of Wisconsin, Madison, WI) Gloria E. Sarto; (Wake Forest University School of Medicine, Winston-Salem, NC) Denise Bonds; (Wayne State University School of Medicine/Hutzel Hospital, Detroit, MI) Susan Hendrix.